A Dynamic Framework for Modelling Set-Shifting Performances
Abstract
1. Introduction
2. Materials and Methods
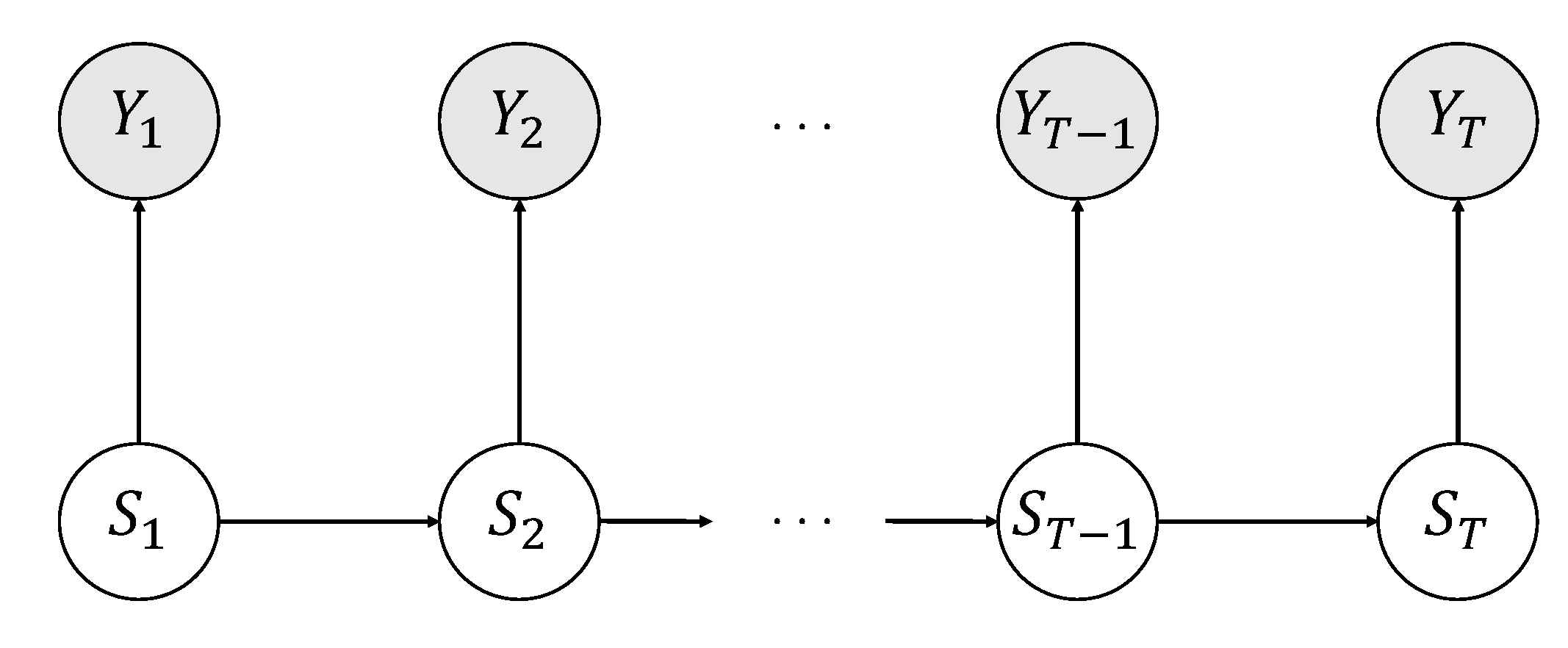
2.1. The Formal Framework
2.2. Model Application
2.3. Participants
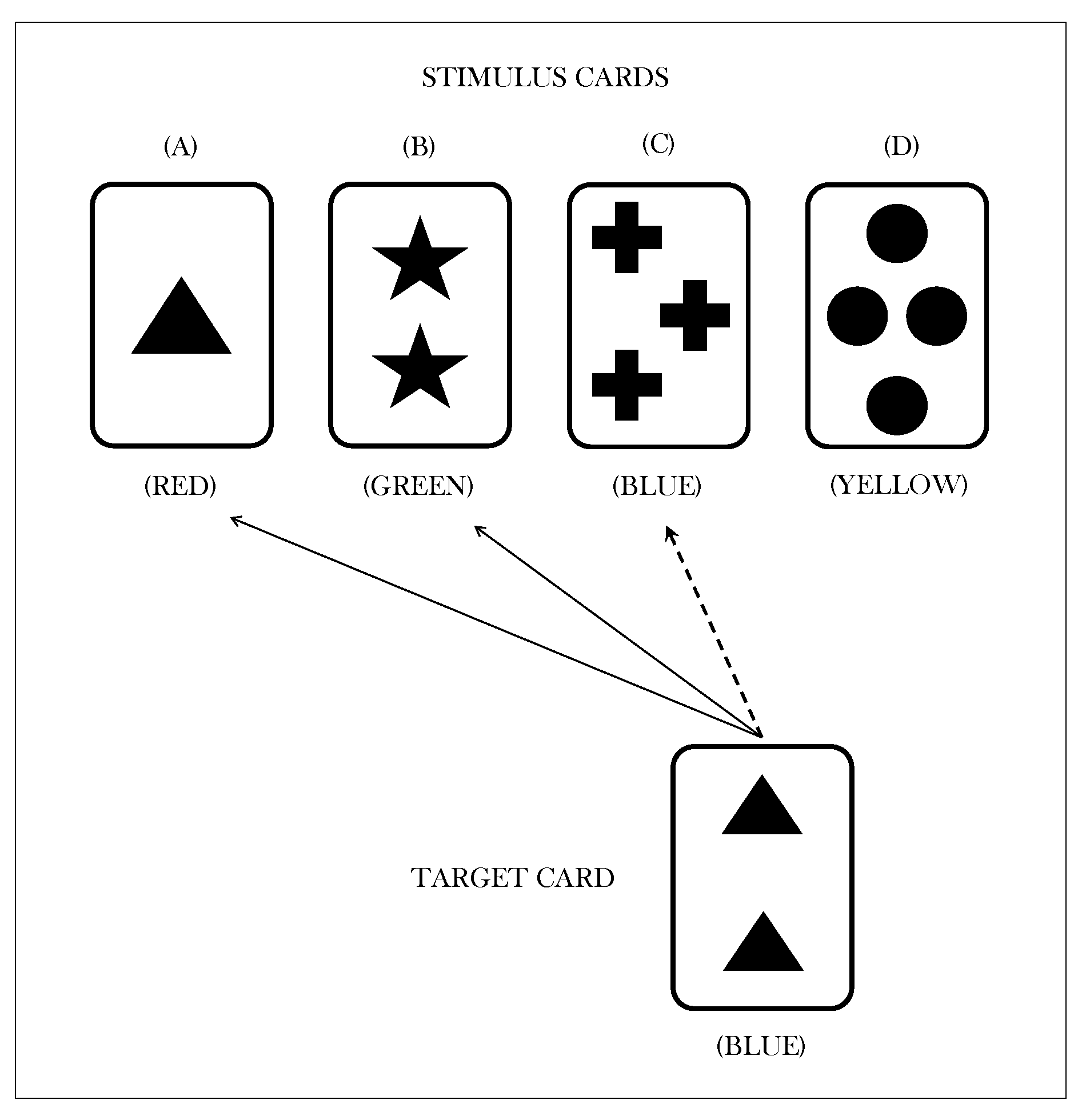
2.4. Task Procedure
2.5. Data Modelling
- (i)
- the conditional response probabilitieswhere and . This parameters set characterizes the measurement model which concerns the conditional distribution of the possible responses given the latent process. It is assumed that the measurement model is conditionally independent of the covariate. Here we are not interested in explaining heterogeneity in the response model between the two groups, since in our view only dynamics in the latent process are responsible for differences in performance trend between groups;
- (ii)
- the initial probabilitieswhere . This parameter characterizes a distribution for the initial state across the (latent) states. In particular, and refer to the initial probabilities vectors of the states for the control group and for the substance dependent group, respectively;
- (iii)
- the transition probabilitieswhere and . This parameter characterizes the conditional probabilities of transitions between latent states across the task phases. In particular, and refer to the transition probabilities for the control group and the substance dependent group, respectively. Here we assume that a specific covariate entails the characterization of a sub-population with its own initial and transition probabilities of the latent process. In this way, accounting for differences in performance trend relies on explaining heterogeneity in the latent states process between the two groups;
3. Results
3.1. Conditional Response Probabilities
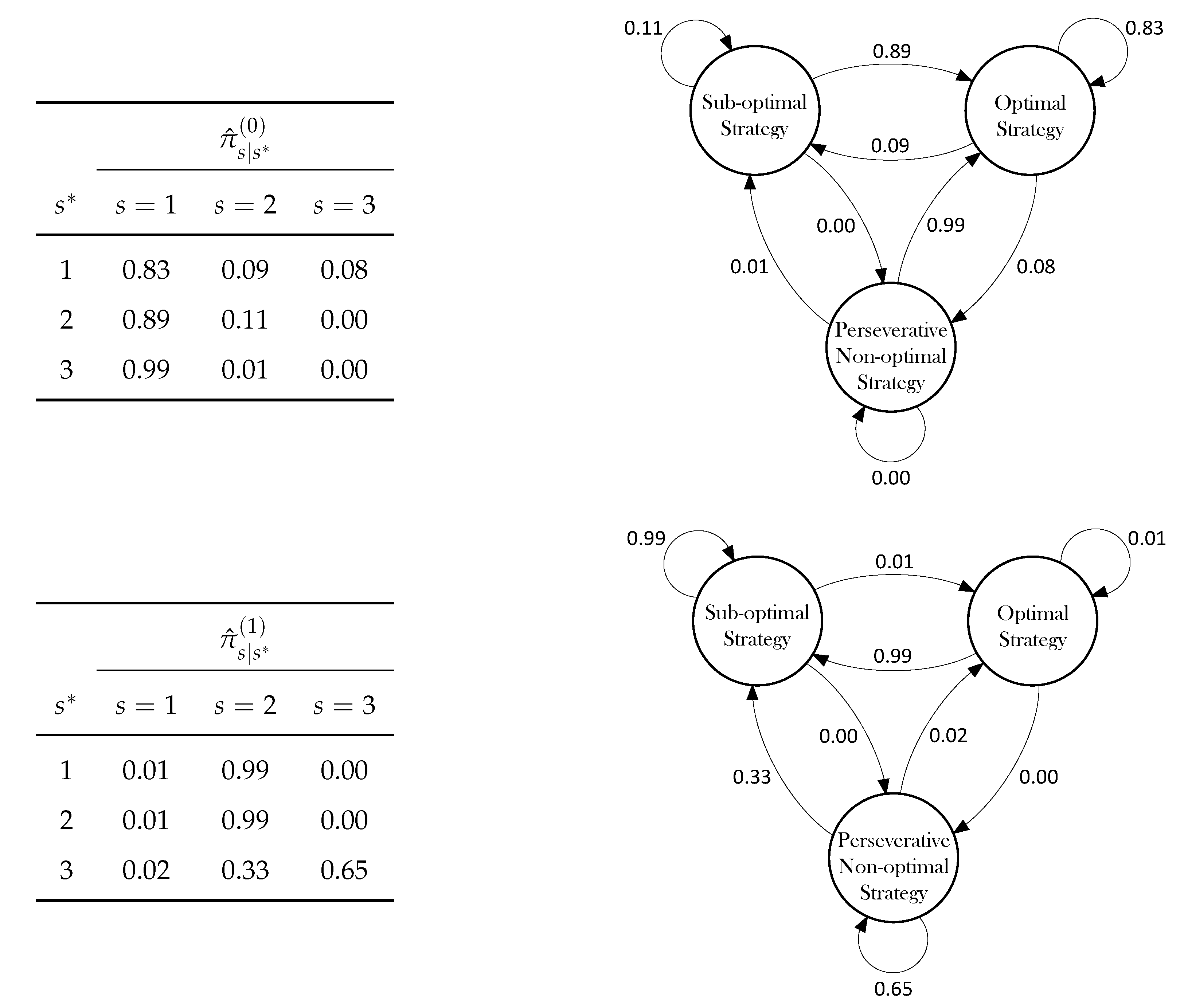
3.2. Initial Probabilities
3.3. Transitions Probabilities
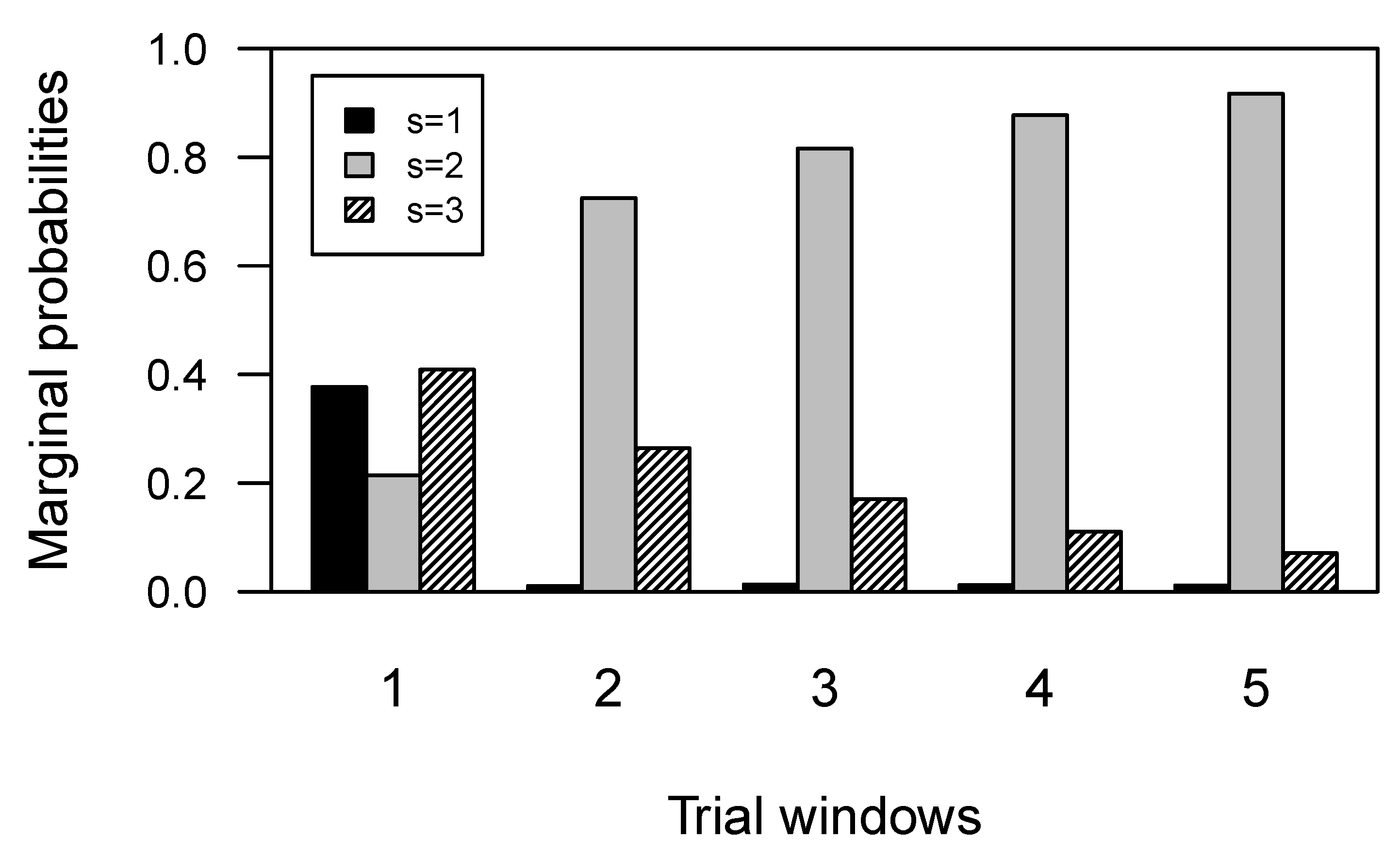
3.4. Marginal Latent States Distributions
4. Discussion of Results
5. General Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LMM | Latent Markov Model |
| WCST | Wisconsin Card Sorting Test |
Appendix A
References
- Dehaene, S.; Changeux, J.P. The Wisconsin card sorting test: Theoretical analysis and modeling in a neuronal network. Cereb. Cortex 1992, 1, 62–79. [Google Scholar] [CrossRef] [PubMed]
- Busemeyer, J.R.; Stout, J.C. A contribution of cognitive decision models to clinical assessment: Decomposing performance on the Bechara gambling task. Psychol. Assess. 2002, 14, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Yechiam, E.; Goodnight, J.; Bates, J.E.; Busemeyer, J.R.; Dodge, K.A.; Pettit, G.S.; Newman, J.P. A formal cognitive model of the go/no-go discrimination task: Evaluation and implications. Psychol. Assess. 2006, 18, 239–249. [Google Scholar] [CrossRef] [PubMed]
- Hull, R.; Martin, R.C.; Beier, M.E.; Lane, D.; Hamilton, A.C. Executive function in older adults: A structural equation modeling approach. Neuropsychology 2008, 22, 508–522. [Google Scholar] [CrossRef] [PubMed]
- Bartolucci, F.; Solis-Trapala, I.L. Multidimensional Latent Markov Models in a developmental study of inhibitory control and attentional flexibility in early childhood. Psychometrika 2010, 75, 725–743. [Google Scholar] [CrossRef]
- Bishara, A.J.; Kruschke, J.K.; Stout, J.C.; Bechara, A.; McCabe, D.P.; Busemeyer, J.R. Sequential learning models for the wisconsin card sort task: Assessing processes in substance dependent individuals. J. Math. Psychol. 2010, 54, 5–13. [Google Scholar] [CrossRef]
- Zelazo, P.D.; Muller, U.; Frye, D.; Marcovitch, S. The development of executive function: Cognitive complexity and control-revised. Monogr. Soc. Res. Child Dev. 2003, 68, 93–119. [Google Scholar] [CrossRef]
- Busemeyer, J.R.; Stout, J.C.; Finn, P. Using computational models to help explain decision making processes of substance abusers. In Cognitive and Affective Neuroscience of Psychopathology; Barch, D., Ed.; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Bechara, A.; Damasio, H. Decision-making and addiction (part I): Impaired activation of somatic states in substance dependent individuals when pondering decisions with negative future consequences. Neuropsychologia 2002, 40, 1675–1689. [Google Scholar] [CrossRef]
- Zakzanis, K.K. The subcortical dementia of Huntington’s desease. J. Clin. Exp. Neuropsychol. 1998, 40, 565–578. [Google Scholar] [CrossRef]
- Braff, D.L.; Heaton, R.K.; Kuck, J.; Cullum, M. The generalized pattern of neuropsychological deficits in outpatients with chronic schizophrenia with heterogeneous Wisconsin Card Sorting Test results. Arch. Gen. Psychiatry 1991, 48, 891–898. [Google Scholar] [CrossRef]
- Heaton, R.K.; Chelune, G.J.; Talley, J.L.; Kay, G.G.; Curtiss, G. Wisconsin Card Sorting Test Manual: Revised and Expanded; Psychological Assessment Resources Inc.: Odessa, FL, USA, 1993. [Google Scholar]
- Buchsbaum, B.R.; Greer, S.; Chang, W.L.; Berman, K.F. Meta-analysis of neuroimaging studies of the Wisconsin card-sorting task and component processes. Hum. Brain Mapp. 2005, 25, 35–45. [Google Scholar] [CrossRef]
- Berg, E.A. A simple objective technique for measuring flexibility in thinking. J. Gen. Psychol. 1948, 39, 15–22. [Google Scholar] [CrossRef]
- Demakis, G.J. A meta-analytic review of the sensitivity of the Wisconsin Card Sorting Test to frontal and lateralized frontal brain damage. Neuropsychology 2003, 17, 255–264. [Google Scholar] [CrossRef]
- Tarter, R.E. An analysis of cognitive deficits in chronic alcoholics. J. Nerv. Ment. Dis. 1973, 157, 138–147. [Google Scholar] [CrossRef]
- Dai, J.; Pleskac, T.J.; Pachur, T. Dynamic cognitive models of intertemporal choice. Cogn. Psychol. 2018, 104, 29–56. [Google Scholar] [CrossRef]
- Gershman, S.J. A Unifying Probabilistic View of Associative Learning. PLoS Comput. Biol. 2015, 11, e1004567. [Google Scholar] [CrossRef]
- Wallsten, T.S.; Pleskac, T.J.; Lejuez, C.W. Modeling Behavior in a Clinically Diagnostic Sequential Risk-Taking Task. Psychol. Rev. 2005, 112, 862–880. [Google Scholar] [CrossRef]
- Kruschke, J. Models of Categorization. In The Cambridge Handbook of Computational Psychology; Sun, R., Ed.; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Wiggins, L.M. Panel Analysis: Latent Probability Models for Attitude and Behavior Processes; Elsevier: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Bartolucci, F.; Farcomeni, A.; Pennoni, F. Latent Markov Models for Longitudinal Data; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Smallwood, J.; Schooler, J.W. The science of mind wandering: Empirically navigating the stream of consciousness. Annu. Rev. Psychol. 2014, 66, 487–518. [Google Scholar] [CrossRef]
- Hawkins, G.E.; Mittner, M.; Forstmann, B.U.; Heathcote, A. On the efficiency of neurally-informed cognitive models to identify latent cognitive states. J. Math. Psychol. 2017, 76, 142–155. [Google Scholar] [CrossRef]
- Taghia, J.; Cai, W.; Ryali, S.; Kochalka, J.; Nicholas, J.; Chen, T.; Menon, V. Uncovering hidden brain state dynamics that regulate performance and decision-making during cognition. Nat. Commun. 2018, 9, 2505. [Google Scholar] [CrossRef]
- Maarten, S.; Lagnado, D.A.; Wilkinson, L.; Jahanshahi, M.; Shanks, D.R. Models of probabilistic category learning in Parkinson’s disease: Strategy use and the effects of L-dopa. J. Math. Psychol. 2010, 54, 123–136. [Google Scholar]
- Pennoni, F. Issues on the Estimation of Latent Variable and Latent Class Models: With Applications in the Social Sciences; Scholars’ Press: Saarbucken, Germany, 2014. [Google Scholar]
- Visser, I. Seven things to remember about hidden Markov models: A tutorial on Markovian models for time series. J. Math. Psychol. 2011, 55, 403–415. [Google Scholar] [CrossRef]
- First, M.B.; Spitzer, R.L.; Gibbon, M.; Williams, J.B.W. Structured Clinical Interview for DSM-IV Axis I Disorders, Research Version, Non-Patient Edition (SCID-I:NP); Biometrics Research: New York, NY, USA, 1997. [Google Scholar]
- Nagahama, Y.; Okina, T.; Suzuki, N.; Nabatame, H.; Matsuda, M. The cerebral correlates of different types of perseveration in the Wisconsin Card Sorting Test. J. Neurol. Neurosurg. Psychiatry 2005, 76, 169–175. [Google Scholar] [CrossRef]
- Miller, H.L.; Ragozzino, M.E.; Cook, E.H.; Sweeney, J.A.; Mosconi, M.W. Cognitive set shifting deficits and their relationship to repetitive behaviors in autism spectrum disorder. J. Autism Dev. Disord. 2015, 45, 805–815. [Google Scholar] [CrossRef]
- Flashman, L.A.; Horner, M.D.; Freides, D. Note on scoring perseveration on the Wisconsin card sorting test. Clin. Neuropsychol. 1991, 5, 190–194. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, AC-19, 716–723. [Google Scholar] [CrossRef]
- de Haan-Rietdijk, S.; Kuppens, P.; Bergeman, C.S.; Sheeber, L.B.; Allen, N.B.; Hamaker, E.L. On the use of mixed Markov models for intensive longitudinal data. Multivar. Behav. Res. 2017, 52, 747–767. [Google Scholar] [CrossRef]
- Bartolucci, F.; Pandolfi, S.; Pennoni, F. LMest: An R Package for Latent Markov Models for Longitudinal Categorical Data. J. Stat. Softw. 2017, 81, 1–38. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Figueroa, I.J.; Youmans, R.J. Failure to Maintain Set A Measure of Distractibility or Cognitive Flexibility? Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2013, 57, 828–832. [Google Scholar] [CrossRef]
- Dobrow, R.P. Introduction to Stochastic Processes with R; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]

| Model | BIC | AIC |
|---|---|---|
| 1-state | 8792 | 8781 |
| two-state | 8561 | 8490 |
| three-state | 8608 | 8493 |
| Model | BIC | AIC |
|---|---|---|
| Basic | 8858 | 8691 |
| Covariate | 8608 | 8493 |
| C | 0.93 | 0.80 | 0.44 |
| E | 0.02 | 0.10 | 0.38 |
| PE | 0.05 | 0.10 | 0.18 |
| 0.57 | 0.14 | 0.29 | |
| 0.38 | 0.21 | 0.41 |
| C | E | PE | |
|---|---|---|---|
| Control | 66.34 (0.64) | 5.25 (0.29) | 4.65 (0.42) |
| SDI | 72.34 (2.17) | 10.57 (0.96) | 14.28 (1.52) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Alessandro, M.; Lombardi, L. A Dynamic Framework for Modelling Set-Shifting Performances. Behav. Sci. 2019, 9, 79. https://doi.org/10.3390/bs9070079
D’Alessandro M, Lombardi L. A Dynamic Framework for Modelling Set-Shifting Performances. Behavioral Sciences. 2019; 9(7):79. https://doi.org/10.3390/bs9070079
Chicago/Turabian StyleD’Alessandro, Marco, and Luigi Lombardi. 2019. "A Dynamic Framework for Modelling Set-Shifting Performances" Behavioral Sciences 9, no. 7: 79. https://doi.org/10.3390/bs9070079
APA StyleD’Alessandro, M., & Lombardi, L. (2019). A Dynamic Framework for Modelling Set-Shifting Performances. Behavioral Sciences, 9(7), 79. https://doi.org/10.3390/bs9070079





