Brain Myelin Covariance Networks: Gradients, Cognition, and Higher-Order Landscape
Abstract
1. Introduction
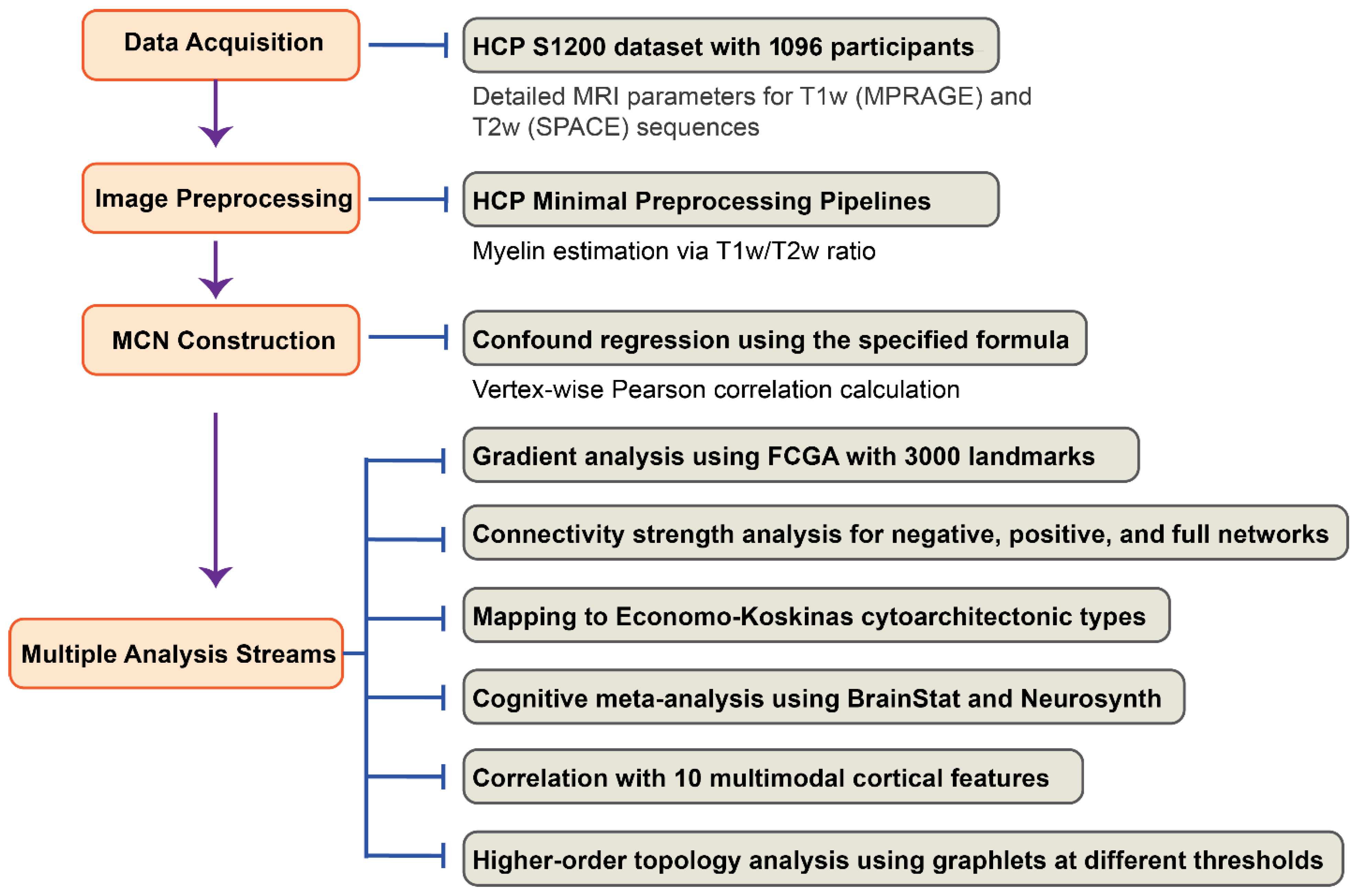
2. Materials and Methods
2.1. Study Design
2.2. Participants
2.3. MRI Acquisition
2.4. Image Preprocessing
2.5. Myelin Covariance Network Construction
2.6. Gradients of Vertex-Wise Myelin Covariance Network
2.7. Connectivity Strength of Vertex-Wise Myelin Covariance Network
2.8. Mapping Gradients and Connectivity Strength to Economo–Koskinas Cytoarchitecture
2.9. Cognitive Meta-Analysis
2.10. Correlation of Gradients and MCN Connectivity with Multimodal Cortical Features
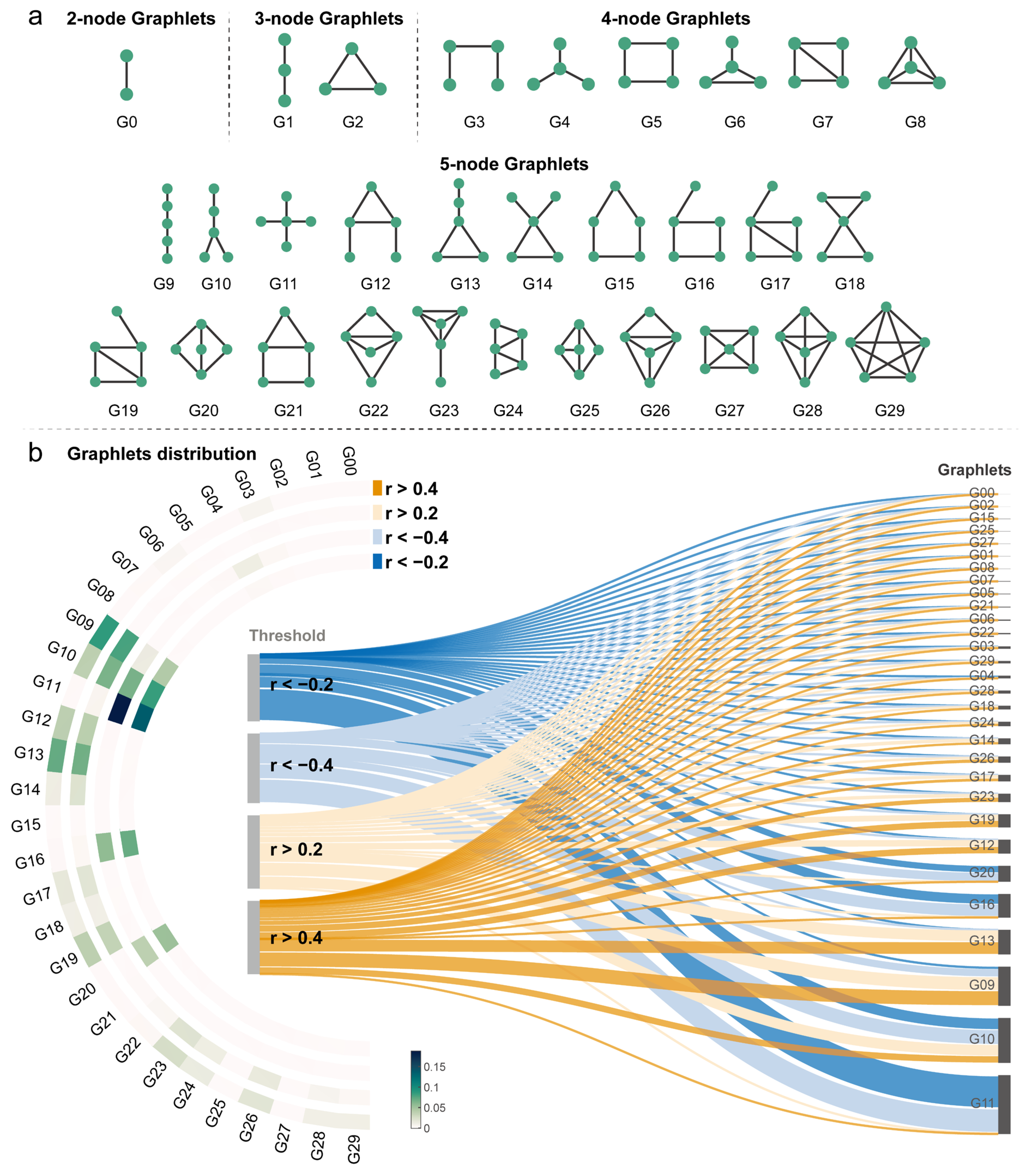
2.11. Higher-Order Landscape in Vertex-Wise MCN
3. Results
3.1. Gradients and MCN Connectivity Strength Maps
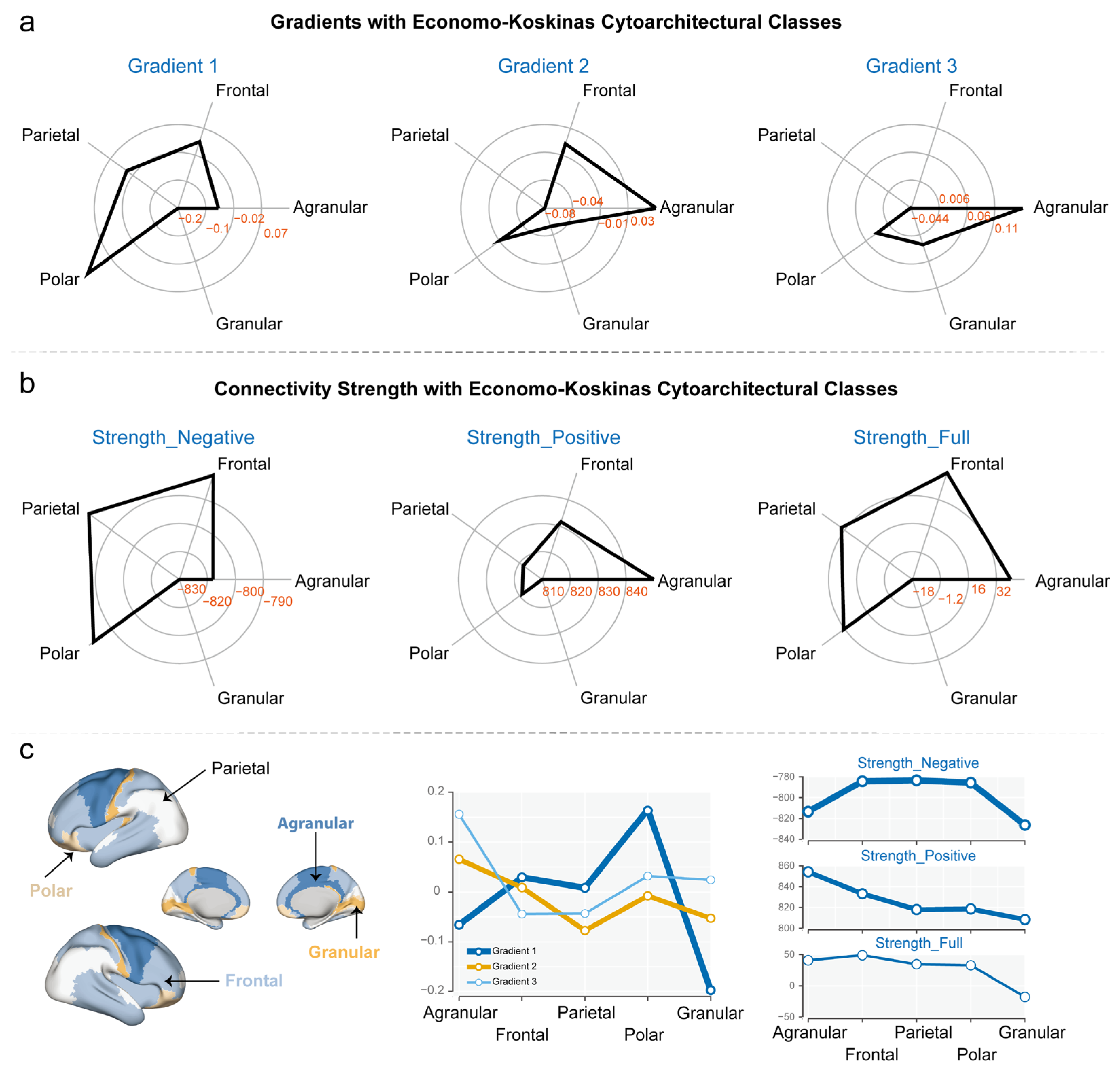
3.2. Gradients and Connectivity Strength with Economo–Koskinas Cytoarchitectural Classes
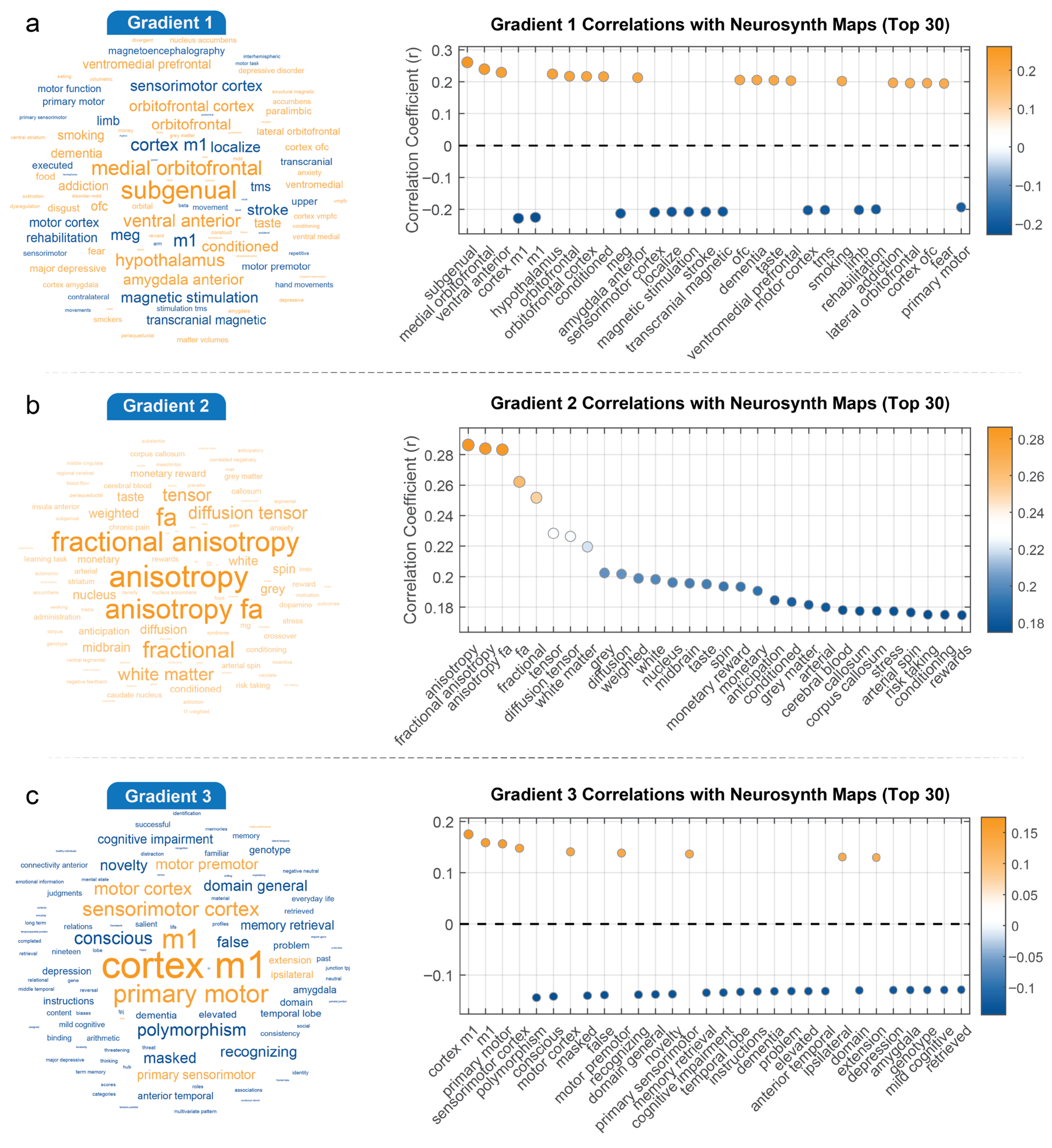
3.3. Interpreting Gradients and Connectivity Strength in the Context of Cognitive Maps
3.4. Gradients and MCN Connectivity with Multimodal Cortical Features
3.5. Higher-Order Topological Landscape of MCN
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alexander-Bloch, A., Giedd, J. N., & Bullmore, E. (2013). Imaging structural co-variance between human brain regions. Nature Reviews Neuroscience, 14(5), 322–336. [Google Scholar] [CrossRef] [PubMed]
- Badre, D., & D’Esposito, M. (2007). Functional magnetic resonance imaging evidence for a hierarchical organization of the prefrontal cortex. Journal of Cognitive Neuroscience, 19(12), 2082–2099. [Google Scholar] [CrossRef] [PubMed]
- Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A., Young, J.-G., & Petri, G. (2020). Networks beyond pairwise interactions: Structure and dynamics. Physics Reports, 874, 1–92. [Google Scholar] [CrossRef]
- Bright, A., Akay, L. A., Blanchard, J., & Tsai, L. H. (2025). Emerging connections between myelin and Alzheimer’s disease. Nature Cell Biology, 27(7), 1049–1051. [Google Scholar] [CrossRef]
- Buckner, R. L., & Krienen, F. M. (2013). The evolution of distributed association networks in the human brain. Trends in Cognitive Sciences, 17(12), 648–665. [Google Scholar] [CrossRef]
- Burt, J. B., Demirtas, M., Eckner, W. J., Navejar, N. M., Ji, J. L., Martin, W. J., Bernacchia, A., Anticevic, A., & Murray, J. D. (2018). Hierarchy of transcriptomic specialization across human cortex captured by structural neuroimaging topography. Nature Neuroscience, 21(9), 1251–1259. [Google Scholar] [CrossRef]
- Cai, Y., Pinheiro-de-Sousa, I., Slobodyanyuk, M., Chen, F., Huynh, T., Kanyo, J., Tang, P., Fuentes, L. A., Braker, A., Welch, R., Huttner, A., Tong, L., Yuan, P., Lam, T. T., Petsalaki, E., Reimand, J., Nairn, A. C., & Grutzendler, J. (2025). Myelin-axon interface vulnerability in Alzheimer’s disease revealed by subcellular proteomics and imaging of human and mouse brain. Nature Neuroscience, 28(7), 1418–1435. [Google Scholar] [CrossRef]
- Coronel-Oliveros, C., Migeot, J., Lehue, F., Amoruso, L., Kowalczyk-Grebska, N., Jakubowska, N., Mandke, K. N., Seabra, J. P., Orio, P., Campbell, D., Gonzalez-Gomez, R., Prado, P., Cuadros, J., Tagliazucchi, E., Cruzat, J., Legaz, A., Medel, V., Hernandez, H., Fittipaldi, S., … Ibanez, A. (2025). Creative experiences and brain clocks. Nature Communications, 16(1), 8336. [Google Scholar] [CrossRef]
- Du, G., Lewis, M. M., Sica, C., Kong, L., & Huang, X. (2019). Magnetic resonance T1w/T2w ratio: A parsimonious marker for Parkinson disease. Annals of Neurology, 85(1), 96–104. [Google Scholar] [CrossRef]
- Fornito, A., Arnatkeviciute, A., & Fulcher, B. D. (2019). Bridging the Gap between connectome and transcriptome. Trends in Cognitive Sciences, 23(1), 34–50. [Google Scholar] [CrossRef]
- Fotiadis, P., Cieslak, M., He, X., Caciagli, L., Ouellet, M., Satterthwaite, T. D., Shinohara, R. T., & Bassett, D. S. (2023). Myelination and excitation-inhibition balance synergistically shape structure-function coupling across the human cortex. Nature Communications, 14(1), 6115. [Google Scholar] [CrossRef]
- Frisoni, G. B., Hansson, O., Nichols, E., Garibotto, V., Schindler, S. E., van der Flier, W. M., Jessen, F., Villain, N., Arenaza-Urquijo, E. M., Crivelli, L., Fortea, J., Grinberg, L. T., Ismail, Z., Minoshima, S., Ossenkoppele, R., Zetterberg, H., Petersen, R. C., & Dubois, B. (2025). New landscape of the diagnosis of Alzheimer’s disease. The Lancet, 406(10510), 1389–1407. [Google Scholar] [CrossRef]
- Furtjes, A. E., Cole, J. H., Couvy-Duchesne, B., & Ritchie, S. J. (2023). A quantified comparison of cortical atlases on the basis of trait morphometricity. Cortex, 158, 110–126. [Google Scholar] [CrossRef] [PubMed]
- Ganjgahi, H., Haring, D. A., Aarden, P., Graham, G., Sun, Y., Gardiner, S., Su, W., Berge, C., Bischof, A., Fisher, E., Gaetano, L., Thoma, S. P., Kieseier, B. C., Nichols, T. E., Thompson, A. J., Montalban, X., Lublin, F. D., Kappos, L., Arnold, D. L., … Holmes, C. C. (2025). AI-driven reclassification of multiple sclerosis progression. Nature Medicine, 31(10), 3414–3424. [Google Scholar] [CrossRef] [PubMed]
- Glasser, M. F., Smith, S. M., Marcus, D. S., Andersson, J. L., Auerbach, E. J., Behrens, T. E., Coalson, T. S., Harms, M. P., Jenkinson, M., Moeller, S., Robinson, E. C., Sotiropoulos, S. N., Xu, J., Yacoub, E., Ugurbil, K., & Van Essen, D. C. (2016). The Human Connectome Project’s neuroimaging approach. Nature Neuroscience, 19(9), 1175–1187. [Google Scholar] [CrossRef]
- Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S., Fischl, B., Andersson, J. L., Xu, J., Jbabdi, S., Webster, M., Polimeni, J. R., Van Essen, D. C., & Jenkinson, M. (2013). The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80, 105–124. [Google Scholar] [CrossRef]
- Glasser, M. F., & Van Essen, D. C. (2011). Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2-weighted MRI. Journal of Neuroscience, 31(32), 11597–11616. [Google Scholar] [CrossRef]
- Grydeland, H., Walhovd, K. B., Tamnes, C. K., Westlye, L. T., & Fjell, A. M. (2013). Intracortical myelin links with performance variability across the human lifespan: Results from T1- and T2-weighted MRI myelin mapping and diffusion tensor imaging. Journal of Neuroscience, 33(47), 18618–18630. [Google Scholar] [CrossRef]
- Hahn, S., Owens, M. M., Yuan, D., Juliano, A. C., Potter, A., Garavan, H., & Allgaier, N. (2022). Performance scaling for structural MRI surface parcellations: A machine learning analysis in the ABCD Study. Cerebral Cortex, 33(1), 176–194. [Google Scholar] [CrossRef]
- He, Y., Chen, Z. J., & Evans, A. C. (2007). Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cerebral Cortex, 17(10), 2407–2419. [Google Scholar] [CrossRef]
- Hill, J., Inder, T., Neil, J., Dierker, D., Harwell, J., & Van Essen, D. (2010). Similar patterns of cortical expansion during human development and evolution. Proceedings of the National Academy of Sciences of the United States of America, 107(29), 13135–13140. [Google Scholar] [CrossRef] [PubMed]
- Hočevar, T., & Demčar, J. (2016). Computation of graphlet orbits for nodes and edges in sparse graphs. Journal of Statistical Software, 71(10), 1–24. [Google Scholar] [CrossRef]
- Hunt, B. A., Tewarie, P. K., Mougin, O. E., Geades, N., Jones, D. K., Singh, K. D., Morris, P. G., Gowland, P. A., & Brookes, M. J. (2016). Relationships between cortical myeloarchitecture and electrophysiological networks. Proceedings of the National Academy of Sciences of the United States of America, 113(47), 13510–13515. [Google Scholar] [CrossRef]
- Huntenburg, J. M., Bazin, P. L., & Margulies, D. S. (2018). Large-scale gradients in human cortical organization. Trends in Cognitive Sciences, 22(1), 21–31. [Google Scholar] [CrossRef]
- Khundrakpam, B. S., Lewis, J. D., Zhao, L., Chouinard-Decorte, F., & Evans, A. C. (2016). Brain connectivity in normally developing children and adolescents. NeuroImage, 134, 192–203. [Google Scholar] [CrossRef]
- Kulkarni, S., & Bassett, D. S. (2025). Toward principles of brain network organization and function. Annual Review of Biophysics, 54(1), 353–378. [Google Scholar] [CrossRef]
- Lariviere, S., Bayrak, S., Vos de Wael, R., Benkarim, O., Herholz, P., Rodriguez-Cruces, R., Paquola, C., Hong, S. J., Misic, B., Evans, A. C., Valk, S. L., & Bernhardt, B. C. (2023). BrainStat: A toolbox for brain-wide statistics and multimodal feature associations. NeuroImage, 266, 119807. [Google Scholar] [CrossRef]
- Lariviere, S., Paquola, C., Park, B. Y., Royer, J., Wang, Y., Benkarim, O., Vos de Wael, R., Valk, S. L., Thomopoulos, S. I., Kirschner, M., Lewis, L. B., Evans, A. C., Sisodiya, S. M., McDonald, C. R., Thompson, P. M., & Bernhardt, B. C. (2021). The ENIGMA Toolbox: Multiscale neural contextualization of multisite neuroimaging datasets. Nature Methods, 18(7), 698–700. [Google Scholar] [CrossRef]
- Li, Y., Wang, N., Wang, H., Lv, Y., Zou, Q., & Wang, J. (2021). Surface-based single-subject morphological brain networks: Effects of morphological index, brain parcellation and similarity measure, sample size-varying stability and test-retest reliability. NeuroImage, 235, 118018. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y., Wang, H., Duan, Y., Huang, J., Ren, Z., Ye, J., Dong, H., Shi, F., Li, K., & Wang, J. (2017). Functional brain network alterations in clinically isolated syndrome and multiple sclerosis: A graph-based connectome study. Radiology, 282(2), 534–541. [Google Scholar] [CrossRef] [PubMed]
- Luo, A. C., Sydnor, V. J., Pines, A., Larsen, B., Alexander-Bloch, A. F., Cieslak, M., Covitz, S., Chen, A. A., Esper, N. B., Feczko, E., Franco, A. R., Gur, R. E., Gur, R. C., Houghton, A., Hu, F., Keller, A. S., Kiar, G., Mehta, K., Salum, G. A., … Satterthwaite, T. D. (2024). Functional connectivity development along the sensorimotor-association axis enhances the cortical hierarchy. Nature Communications, 15(1), 3511. [Google Scholar] [CrossRef]
- Ma, Z., & Zhang, N. (2017). Cross-population myelination covariance of human cerebral cortex. Human Brain Mapping, 38(9), 4730–4743. [Google Scholar] [CrossRef] [PubMed]
- Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg, J. M., Langs, G., Bezgin, G., Eickhoff, S. B., Castellanos, F. X., Petrides, M., Jefferies, E., & Smallwood, J. (2016). Situating the default-mode network along a principal gradient of macroscale cortical organization. Proceedings of the National Academy of Sciences of the United States of America, 113(44), 12574–12579. [Google Scholar] [CrossRef]
- Matute, C., & Verkhratsky, A. (2025). Brain myelin as a deficient energy source in aging and disease. Trends in Endocrinology and Metabolism, 36(9), 781–784. [Google Scholar] [CrossRef] [PubMed]
- Melie-Garcia, L., Slater, D., Ruef, A., Sanabria-Diaz, G., Preisig, M., Kherif, F., Draganski, B., & Lutti, A. (2018). Networks of myelin covariance. Human Brain Mapping, 39(4), 1532–1554. [Google Scholar] [CrossRef] [PubMed]
- Mesulam, M. M. (1998). From sensation to cognition. Brain, 121(Pt 6), 1013–1052. [Google Scholar] [CrossRef]
- Nenning, K. H., Xu, T., Tambini, A., Franco, A. R., Margulies, D. S., Colcombe, S. J., & Milham, M. P. (2024). Fast connectivity gradient approximation: Maintaining spatially fine-grained connectivity gradients while reducing computational costs. Communications Biology, 7(1), 697. [Google Scholar] [CrossRef]
- Paquola, C., Seidlitz, J., Benkarim, O., Royer, J., Klimes, P., Bethlehem, R. A. I., Lariviere, S., Vos de Wael, R., Rodriguez-Cruces, R., Hall, J. A., Frauscher, B., Smallwood, J., & Bernhardt, B. C. (2020). A multi-scale cortical wiring space links cellular architecture and functional dynamics in the human brain. PLoS Biology, 18(11), e3000979. [Google Scholar] [CrossRef]
- Patel, Y., Shin, J., Gowland, P. A., Pausova, Z., Paus, T., & IMAGEN Consortium. (2019). Maturation of the human cerebral cortex during adolescence: Myelin or dendritic arbor? Cerebral Cortex, 29(8), 3351–3362. [Google Scholar] [CrossRef]
- Pei, H., Jiang, S., Hou, C., Li, H., Yang, Z., Rodriguez-Labrada, R., Duan, M., Yao, D., & Luo, C. (2025). Accelerated ageing unfolds along the sensorimotor-association cortical axis in schizophrenia: Multi-site study. The British Journal of Psychiatry, 1–9. [Google Scholar] [CrossRef]
- Presigny, C., & De Vico Fallani, F. (2022). Colloquium: Multiscale modeling of brain network organization. Reviews of Modern Physics, 94(3), 031002. [Google Scholar] [CrossRef]
- Przulj, N. (2007). Biological network comparison using graphlet degree distribution. Bioinformatics, 23(2), e177–e183. [Google Scholar] [CrossRef]
- Rahmanzadeh, R., Lu, P. J., Barakovic, M., Weigel, M., Maggi, P., Nguyen, T. D., Schiavi, S., Daducci, A., La Rosa, F., Schaedelin, S., Absinta, M., Reich, D. S., Sati, P., Wang, Y., Bach Cuadra, M., Radue, E. W., Kuhle, J., Kappos, L., & Granziera, C. (2021). Myelin and axon pathology in multiple sclerosis assessed by myelin water and multi-shell diffusion imaging. Brain, 144(6), 1684–1696. [Google Scholar] [CrossRef] [PubMed]
- Reardon, P. K., Seidlitz, J., Vandekar, S., Liu, S., Patel, R., Park, M. T. M., Alexander-Bloch, A., Clasen, L. S., Blumenthal, J. D., Lalonde, F. M., Giedd, J. N., Gur, R. C., Gur, R. E., Lerch, J. P., Chakravarty, M. M., Satterthwaite, T. D., Shinohara, R. T., & Raznahan, A. (2018). Normative brain size variation and brain shape diversity in humans. Science, 360(6394), 1222–1227. [Google Scholar] [CrossRef] [PubMed]
- Revell, A. Y., Silva, A. B., Arnold, T. C., Stein, J. M., Das, S. R., Shinohara, R. T., Bassett, D. S., Litt, B., & Davis, K. A. (2022). A framework For brain atlases: Lessons from seizure dynamics. NeuroImage, 254, 118986. [Google Scholar] [CrossRef] [PubMed]
- Romero-Garcia, R., Whitaker, K. J., Vasa, F., Seidlitz, J., Shinn, M., Fonagy, P., Dolan, R. J., Jones, P. B., Goodyer, I. M., Consortium, N., Bullmore, E. T., & Vertes, P. E. (2018). Structural covariance networks are coupled to expression of genes enriched in supragranular layers of the human cortex. NeuroImage, 171, 256–267. [Google Scholar] [CrossRef]
- Saberi, M., Khosrowabadi, R., Khatibi, A., Misic, B., & Jafari, G. (2021). Topological impact of negative links on the stability of resting-state brain network. Scientific Reports, 11(1), 2176. [Google Scholar] [CrossRef]
- Sandrone, S., Aiello, M., Cavaliere, C., Thiebaut de Schotten, M., Reimann, K., Troakes, C., Bodi, I., Lacerda, L., Monti, S., Murphy, D., Geyer, S., Catani, M., & Dell’Acqua, F. (2023). Mapping myelin in white matter with T1-weighted/T2-weighted maps: Discrepancy with histology and other myelin MRI measures. Brain Structure & Function, 228(2), 525–535. [Google Scholar] [CrossRef]
- Satterthwaite, T. D., Shinohara, R. T., Wolf, D. H., Hopson, R. D., Elliott, M. A., Vandekar, S. N., Ruparel, K., Calkins, M. E., Roalf, D. R., Gennatas, E. D., Jackson, C., Erus, G., Prabhakaran, K., Davatzikos, C., Detre, J. A., Hakonarson, H., Gur, R. C., & Gur, R. E. (2014). Impact of puberty on the evolution of cerebral perfusion during adolescence. Proceedings of the National Academy of Sciences of the United States of America, 111(23), 8643–8648. [Google Scholar] [CrossRef]
- Schaffner, E., Bosch-Queralt, M., Edgar, J. M., Lehning, M., Strauss, J., Fleischer, N., Kungl, T., Wieghofer, P., Berghoff, S. A., Reinert, T., Krueger, M., Morawski, M., Mobius, W., Barrantes-Freer, A., Stieler, J., Sun, T., Saher, G., Schwab, M. H., Wrede, C., … Stassart, R. M. (2023). Myelin insulation as a risk factor for axonal degeneration in autoimmune demyelinating disease. Nature Neuroscience, 26(7), 1218–1228. [Google Scholar] [CrossRef]
- Scholtens, L. H., de Reus, M. A., de Lange, S. C., Schmidt, R., & van den Heuvel, M. P. (2018). An MRI Von Economo—Koskinas atlas. NeuroImage, 170, 249–256. [Google Scholar] [CrossRef]
- Sebenius, I., Seidlitz, J., Warrier, V., Bethlehem, R. A. I., Alexander-Bloch, A., Mallard, T. T., Garcia, R. R., Bullmore, E. T., & Morgan, S. E. (2023). Robust estimation of cortical similarity networks from brain MRI. Nature Neuroscience, 26(8), 1461–1471. [Google Scholar] [CrossRef]
- Shen, X., Finn, E. S., Scheinost, D., Rosenberg, M. D., Chun, M. M., Papademetris, X., & Constable, R. T. (2017). Using connectome-based predictive modeling to predict individual behavior from brain connectivity. Nature Protocols, 12(3), 506–518. [Google Scholar] [CrossRef]
- Shin, H. G., Oh, S. H., Fukunaga, M., Nam, Y., Lee, D., Jung, W., Jo, M., Ji, S., Choi, J. Y., & Lee, J. (2019). Advances in gradient echo myelin water imaging at 3T and 7T. NeuroImage, 188, 835–844. [Google Scholar] [CrossRef]
- Sydnor, V. J., Larsen, B., Bassett, D. S., Alexander-Bloch, A., Fair, D. A., Liston, C., Mackey, A. P., Milham, M. P., Pines, A., Roalf, D. R., Seidlitz, J., Xu, T., Raznahan, A., & Satterthwaite, T. D. (2021). Neurodevelopment of the association cortices: Patterns, mechanisms, and implications for psychopathology. Neuron, 109(18), 2820–2846. [Google Scholar] [CrossRef] [PubMed]
- Vaishnavi, S. N., Vlassenko, A. G., Rundle, M. M., Snyder, A. Z., Mintun, M. A., & Raichle, M. E. (2010). Regional aerobic glycolysis in the human brain. Proceedings of the National Academy of Sciences of the United States of America, 107(41), 17757–17762. [Google Scholar] [CrossRef] [PubMed]
- van der Weijden, C. W. J., Garcia, D. V., Borra, R. J. H., Thurner, P., Meilof, J. F., van Laar, P. J., Dierckx, R., Gutmann, I. W., & de Vries, E. F. J. (2021). Myelin quantification with MRI: A systematic review of accuracy and reproducibility. NeuroImage, 226, 117561. [Google Scholar] [CrossRef] [PubMed]
- Vandewouw, M. M., Hunt, B. A. E., Ziolkowski, J., & Taylor, M. J. (2021). The developing relations between networks of cortical myelin and neurophysiological connectivity. NeuroImage, 237, 118142. [Google Scholar] [CrossRef]
- Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E., Yacoub, E., & Ugurbil, K. (2013). The WU-Minn Human Connectome Project: An overview. NeuroImage, 80, 62–79. [Google Scholar] [CrossRef]
- Vasa, F., Seidlitz, J., Romero-Garcia, R., Whitaker, K. J., Rosenthal, G., Vertes, P. E., Shinn, M., Alexander-Bloch, A., Fonagy, P., Dolan, R. J., Jones, P. B., Goodyer, I. M., Consortium, N., Sporns, O., & Bullmore, E. T. (2018). Adolescent tuning of association cortex in human structural brain networks. Cerebral Cortex, 28(1), 281–294. [Google Scholar] [CrossRef]
- Vojdani, A., Almulla, A. F., Vojdani, E., Li, J., Zhang, Y., & Maes, M. (2025). Autoimmune responses to myelin-associated proteins as diagnostic and prognostic biomarkers of relapsing-remitting multiple sclerosis: Associations with human herpesvirus-6 and Epstein-Barr virus reactivation. Journal of Advanced Research. [Google Scholar] [CrossRef]
- Wagstyl, K., Ronan, L., Goodyer, I. M., & Fletcher, P. C. (2015). Cortical thickness gradients in structural hierarchies. NeuroImage, 111, 241–250. [Google Scholar] [CrossRef]
- Wang, J., Zuo, X., Dai, Z., Xia, M., Zhao, Z., Zhao, X., Jia, J., Han, Y., & He, Y. (2013). Disrupted functional brain connectome in individuals at risk for Alzheimer’s disease. Biological Psychiatry, 73(5), 472–481. [Google Scholar] [CrossRef] [PubMed]
- Wang, P., Zhao, J., Zhang, X., Li, Z., Cheng, J., Lui, J. C. S., Towsley, D., Tao, J., & Guan, X. (2018). MOSS-5: A fast method of approximating counts of 5-node graphlets in large graphs. IEEE Transactions on Knowledge and Data Engineering, 30(1), 73–86. [Google Scholar] [CrossRef]
- Weiskopf, N., Edwards, L. J., Helms, G., Mohammadi, S., & Kirilina, E. (2021). Quantitative magnetic resonance imaging of brain anatomy and in vivo histology. Nature Reviews Physics, 3(8), 570–588. [Google Scholar] [CrossRef]
- Wu, H., Fan, S., Yan, C., & Wang, H. (2024). Cortical microstructural brain network mediates the association between personality trait of agreeableness and life satisfaction. Cerebral Cortex, 34(1), bhad410. [Google Scholar] [CrossRef]
- Wu, H., Wang, H., & Lü, L. (2018). Individual T1-weighted/T2-weighted ratio brain networks: Small-worldness, hubs and modular organization. International Journal of Modern Physics C, 29(05), 18400077. [Google Scholar] [CrossRef]
- Yarkoni, T., Poldrack, R. A., Nichols, T. E., Van Essen, D. C., & Wager, T. D. (2011). Large-scale automated synthesis of human functional neuroimaging data. Nature Methods, 8(8), 665–670. [Google Scholar] [CrossRef]
- Zhan, L., Jenkins, L. M., Wolfson, O. E., GadElkarim, J. J., Nocito, K., Thompson, P. M., Ajilore, O. A., Chung, M. K., & Leow, A. D. (2017). The significance of negative correlations in brain connectivity. Journal of Comparative Neurology, 525(15), 3251–3265. [Google Scholar] [CrossRef]
- Zitnik, M., Li, M. M., Wells, A., Glass, K., Morselli Gysi, D., Krishnan, A., Murali, T. M., Radivojac, P., Roy, S., Baudot, A., Bozdag, S., Chen, D. Z., Cowen, L., Devkota, K., Gitter, A., Gosline, S. J. C., Gu, P., Guzzi, P. H., Huang, H., … Milenkovic, T. (2024). Current and future directions in network biology. Bioinformatics Advances, 4(1), vbae099. [Google Scholar] [CrossRef]


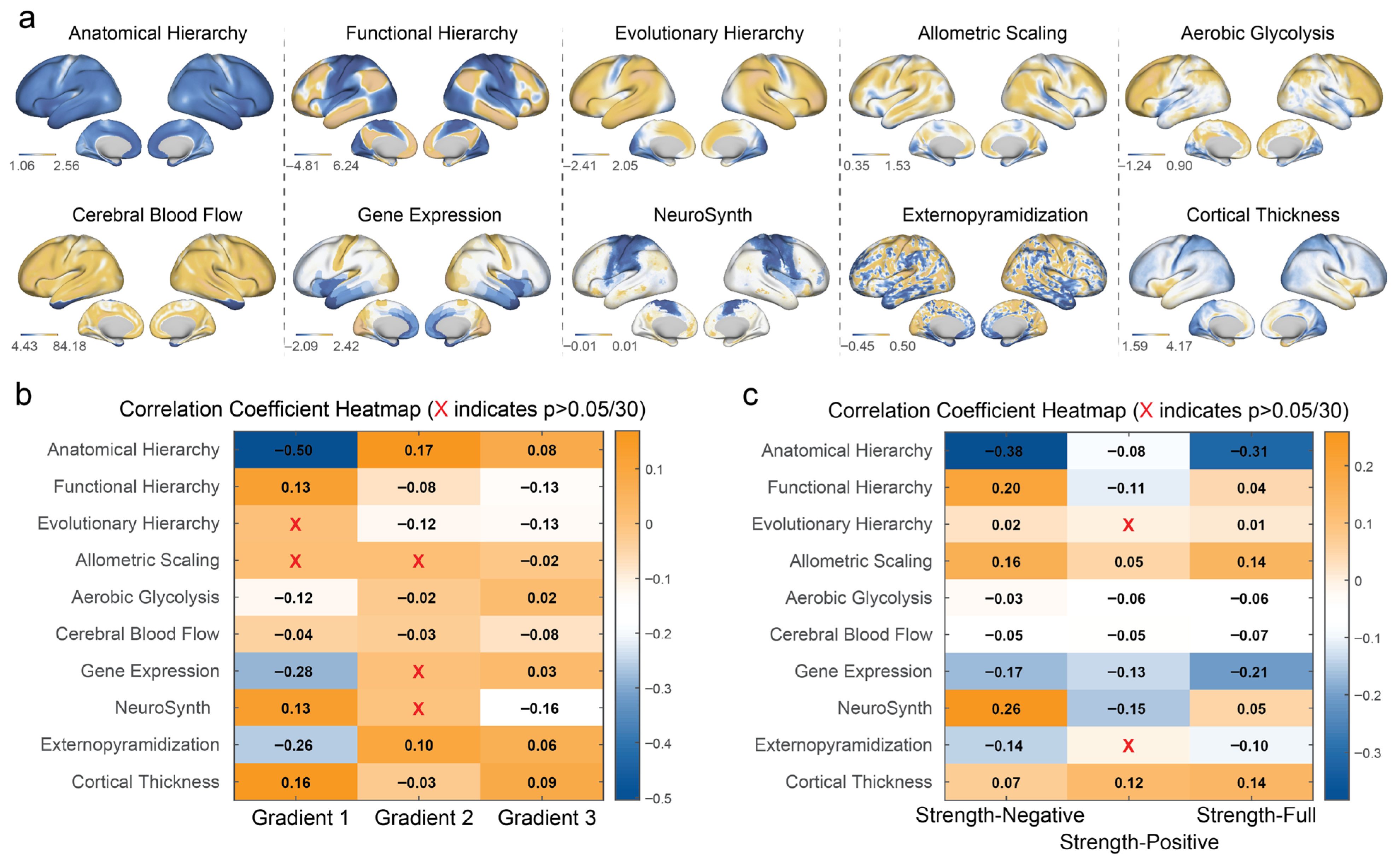
| Feature Name | Description | Corresponding GitHub Filename |
|---|---|---|
| Anatomical Hierarchy | A measure of hierarchical organization (often proxied by T1w/T2w myelination maps). | T1T2ratio.dscalar.nii |
| Functional Hierarchy | The principal gradient (G1) of functional connectivity variation across the cortex. | G1.fMRI.dscalar.nii |
| Evolutionary Hierarchy | A map reflecting the evolutionary expansion of the cerebral cortex. | Evolution.Expansion.dscalar.nii |
| Allometric Scaling | A measure related to how brain properties scale with brain size. | AllometricScaling.PNC20mm.dscalar.nii |
| Aerobic Glycolysis | A metabolic map indicating the rate of aerobic glycolysis, measured via PET. | PET.AG.dscalar.nii |
| Cerebral Blood Flow | A map of resting-state cerebral blood flow (CBF). | CBF.dscalar.nii |
| Gene Expression | The first principal component (PC1) of cortical gene expression from the Allen Human Brain Atlas (AHBA). | PC1.AHBA.dscalar.nii |
| NeuroSynth | The first principal component (PC1) of NeuroSynth meta-analytic decodings. | PC1.Neurosynth.dscalar.nii |
| Externopyramidization | A microstructural measure related to cytoarchitecture, often studied using high-resolution histology like the BigBrain dataset. | BigBrain.Histology.dscalar.nii |
| Cortical Thickness | A structural measure of the thickness of the cerebral cortex. | Cortical.Thickness.dscalar.nii |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Church, A.; Jiang, X.; Labus, J.S.; Yan, C.; Mayer, E.A.; Wang, H. Brain Myelin Covariance Networks: Gradients, Cognition, and Higher-Order Landscape. Behav. Sci. 2025, 15, 1466. https://doi.org/10.3390/bs15111466
Wu H, Church A, Jiang X, Labus JS, Yan C, Mayer EA, Wang H. Brain Myelin Covariance Networks: Gradients, Cognition, and Higher-Order Landscape. Behavioral Sciences. 2025; 15(11):1466. https://doi.org/10.3390/bs15111466
Chicago/Turabian StyleWu, Huijun, Arpana Church, Xueyan Jiang, Jennifer S. Labus, Chuyao Yan, Emeran A. Mayer, and Hao Wang. 2025. "Brain Myelin Covariance Networks: Gradients, Cognition, and Higher-Order Landscape" Behavioral Sciences 15, no. 11: 1466. https://doi.org/10.3390/bs15111466
APA StyleWu, H., Church, A., Jiang, X., Labus, J. S., Yan, C., Mayer, E. A., & Wang, H. (2025). Brain Myelin Covariance Networks: Gradients, Cognition, and Higher-Order Landscape. Behavioral Sciences, 15(11), 1466. https://doi.org/10.3390/bs15111466






