Firstly, a continuous-time utility model is constructed to describe the decision-making process between parents’ self-consumption and investment in children’s education. By maximizing the utility function, it is shown that the optimal consumption growth rate and the optimal investment growth rate of parents have the characteristics of independence for a given level of total consumption or total investment. It is also shown that the two decisions of focusing on the sum of the utilities of children’s human capital outputs in each period and focusing on the final level of children’s human capital generally cannot coexist. The conclusions are then based on the use of a three-period utility model to calculate inter-period optimal decisions. Finally, the model incorporates children’s future transfers and draws conclusions about revealed preferences for decision-making under different situations.
3.1. Continuous-Time Utility Modeling
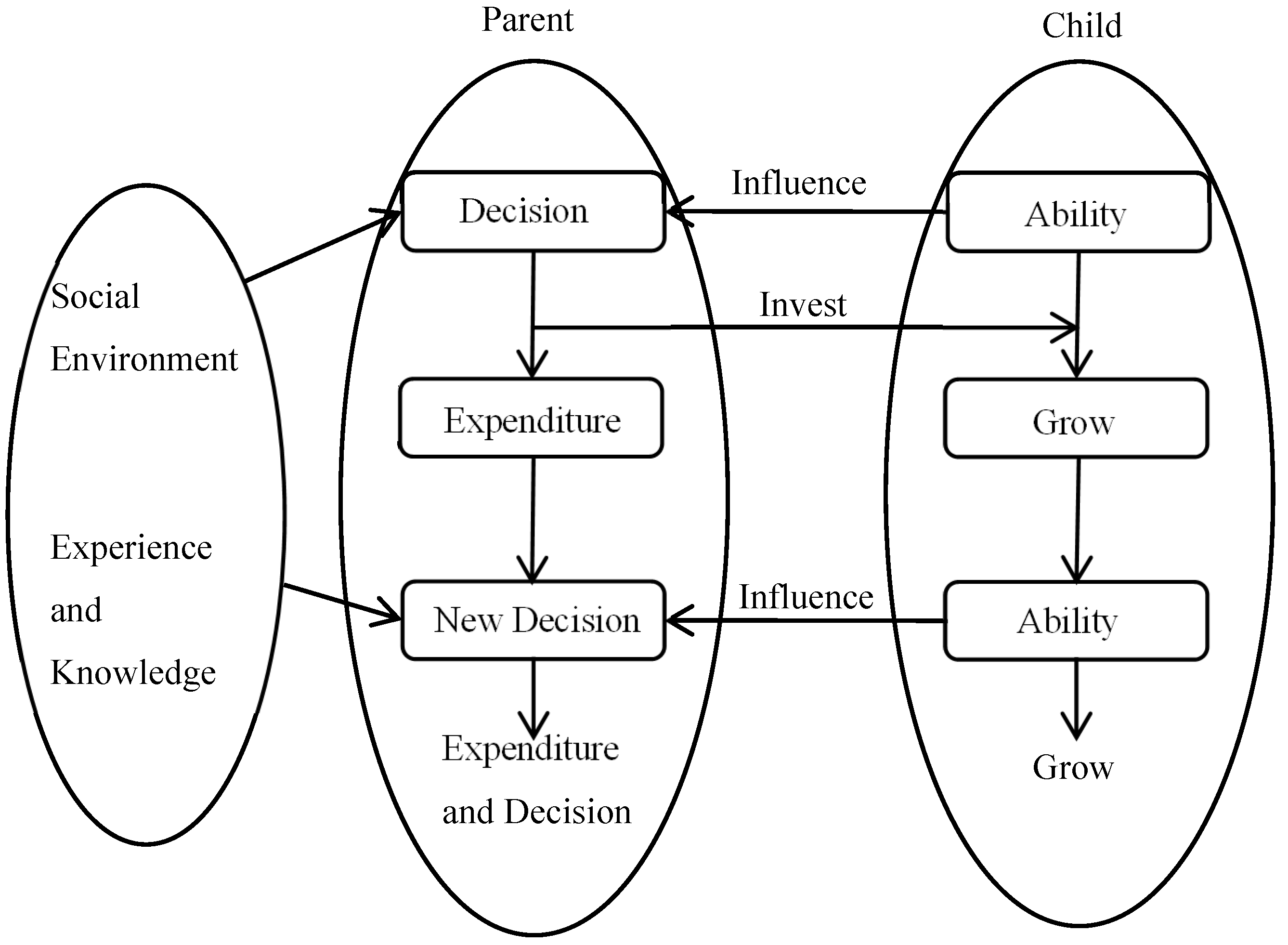
Assuming that a typical family consists of parents with stable jobs and one child, at the moment
t, the level of consumption of the parents is
, the level of expenditure on investment in the education of the child is
, and the level of wages used for consumption and investment in education
. In the classical theory of human capital, when the study period is [0,
T], the equation of human capital accumulation by children has the following form
is the incremental human capital at time t. means a human capital production function. δ is the level of human capital depreciation, and is the level of parental investment in education. Function F may have a more complex structure. It can deal with endogenous factors such as family time investment and school investment. These favorable factors for enhancing children’s growth can be simplified into exogenous technological progress and the increase of children’s environmental endowment.
When there is no borrowing, per-period parents have a strict budget constraint is:
In a complete financial market, parents are able to borrow money and make decisions freely. In reality, with the help of others, parents are usually able to make such behavioral choices. Here, we assume that the average family budget cannot exceed lifetime income. The total lifetime income that can be used for investing in education and self-consumption is
W. This thus yields budget constraints.
r is the discount parameter. Parents maximize their utility function by choosing future consumption paths
and investment paths
.
The total utility of parents consists of the consumption utility function and the utility function of the new growth component of children’s human capital . It satisfies , , , and . denotes the subjective discount rate of utility. R denotes the value of a unit of human capital. is an altruistic parameter that reflects the degree of utility preference between self-consumption and investment in education. It may also reflect the relative value of the utility of consumption and investment. also includes parents’ well-being.
The linear assumption of the value of human capital follows the classic theory of Ben Porath [
41]. And our discussion focuses on the paths of consumption paths
and investment paths
. In each period, human capital additions give parents the satisfaction and utility of investment. If parents derive greater well-being from their children’s education over a period of time, they decide to invest more in education. This change is given by Equation (4)
, which means
increases or
has a higher marginal value for the level of children’s human capital. Therefore, the marginal utility of consumption and education investment is equal when maximizing Equation (4). It means parents choose a decline in consumption and an increase in education investment. Obviously, parental entertainment consumption is also part of total consumption. If they have higher entertainment utility, then
in Equation (4) decreases, which implies parents choose higher self-consumption with less investment in children’s education.
In anticipation of the future, the forgotten regression is usually ignored by the parents, and the human capital invested in the next period when the children are educated is the net of the forgotten regressions. Then, the regression is seen as a depreciation of human capital. Equations (1)–(4) constitute the main model.
The objective of Equation (4) reflects the fact that the utility of parents consists of two components: the utility of consumption and the utility of the new growth of children’s human capital in each period. Here, the growth of children can be interpreted as the return on investment in the current period. The η in Equation (4) can also be interpreted as the degree of parental motivation to invest in education, and the larger η is, the higher the utility that parents get from investing in their children’s education. The behavior that optimizes Equation (4) to maximize the total utility of the expenditure is called “Decision one”.
The total utility Equation (4) takes on a different form when the parents’ concern is the ultimate level of their children’s human capital. It means parents have no clear preference for the time of the formation of competence in their children’s lives. The only aim is to see the best level of their children’s human capital
at moment
T. The choice of the path is called “Decision two”. The utility function takes the form
In addition, Equation (4) has a deformation as
Equation (4) is used to describe the utility generated by the overall progress of children relative to the previous period. The interest is in the addition of children’s human capital, not the value-creating function of capital. Typically, depreciation is not observed, and parental decision-making usually considers the effects achieved by education inputs rather than a comprehensive evaluation. Thus, both functions have important uses. In particular, human capital can be expressed as an integral form of multi-period accumulation.
Equations (4) and (4a) can capture the dual choice of consumption and investment in parental decision-making. The difference is that Equation (4) captures the instant gratification utility to parents from the increase in their children’s human capital. The decision-making behavior typically describes parents’ planned choice of investment in their children’s future education at various stages, and the value of the returns to achieving their investment goals at each period. Equation (4a) describes the process of education and development of their children, where parents do not care about the timing of their children’s acquisition of competences. These parents are more concerned about the expected level of their children’s human capital and will choose the best investment path for their children’s growth under a defined investment spending plan.
In contrast, the investment in education in Equation (4) is an investment process with continuous returns, whereas Equation (4a) resembles a phased forward investment with special returns in the future. From a parental perspective, investment and consumption are not completely free substitutes, and the decision-making process often pre-determines the total amount of investment or the total amount of consumption. The point of the decision is to achieve a higher level of self-consumption and a better upbringing for the children.
3.2. Principles of Decision-Making in Consumption and Investment
Under complete financial markets, using Equation (3) as a constraint, the Hamiltonian function of Equation (4) is
The maximization conditions are
The transverse condition is
. Then, we calculate
Notice that , thus, Equation (8) is a necessary condition for the maximization of Equation (4). includes consumption only, so only relate to time t. We can draw an important conclusion.
Conclusion 1. Under the basic assumptions, when maximizing the objective Equations (4) and (4a), the growth rate of the parents’ optimal consumption path is relevant to time t only. isn’t dependent on the level of human capital of the offspring and the parent’s investment path Once the optimal initial consumption level is chosen, the optimal consumption path is also determined.
Then, Corollary 1 can be described as follows:
Corollary 1 (Principle of independent decision-making). The optimal paths of consumption and investment in education can be decided independently at decision time t, when either the total consumption or the total investment is selected.
The total level of consumption is the factor that affects the family education investment decision. Corollary 1 expresses the fact that the optimal investment in children’s education can be transformed into a local optimization problem after parents have chosen an initial level of consumption. The opportunity cost of consumption and investment is the marginal cost of the entire decision-making period. Because the level of consumption is set, the level of investment ability
K is only related to the level of initial investment and lifetime income. We make
Assuming that the consumption path is given, then maximizing Equation (4a) at this point is also equivalent to maximizing the final level of children’s human capital. For the two alternative decisions of maximizing the sum of individual utilities in each period or maximizing the expected utility of the children’s human capital, the limit method is used to obtain Conclusion 2.
Conclusion 2 (Principle of incompatibility of decision-making). Under the basic assumptions, the optimal investment paths obtained under the maximizing objective Equations (4) and (4a) will not be identical, given the level of total parental consumption.
Proof of Conclusion 2. A simple proof process is stated as follows: If the utility functions of the two decisions are the same, from the first-order condition
We substitute two equations into Equation (5).
The above equation holds for any time t. Then, or . The former implies that, for a given growth path, the utility function is only a specific function of time. However, the parameter of the utility function in the generalization discussion is free, and the utility function cannot be just a function of time t. Moreover, the latter implies zero inputs due to the cumulative nature of human capital. The contradiction is obvious. □
Conclusion 2 illustrates that, in most cases, the future growth path of investing in education will vary depending on the decisions. Usually the two decisions cannot coexist, so the choice of decision can even show a display of preference in different discussions. In particular, it is shown that the elimination of the altruism parameter in the first-order conditional Equations (10) and (11) also suggests that altruistic choice means a trade-off between consumption and investment in education and that the structure of investment over time is irrelevant. Parents’ preference for their children’s education only determines the distribution of total consumption and total investment in education.
So far, we have constructed a continuous-time utility model under two decisions and obtained two important conclusions by mathematical means. And when the total investment or consumption is selected, it is clear from Corollary 1 that the utility level is at least locally optimal under different decisions.
3.3. Three-Period Logarithmic Utility Models and Decision-Making Mechanisms
In the decision-making process, intertemporal choice is an important element. Based on the assumption that the continuous-time model is difficult to solve, a three-period logarithmic utility model is developed to analyze the problem in order to reflect the inter-period comparison.
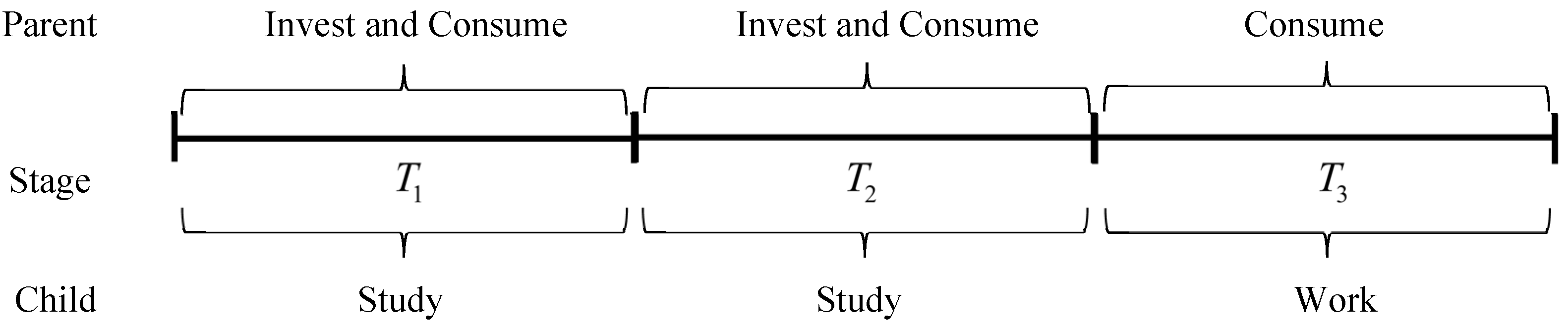
Assuming a classic intergenerational structure where a family chooses to invest in the education of a child, it will go through three stages of consumption and investment, as shown in
Figure 3. Stage 1 and stage 2 parents will consume and invest in their child’s education, and the child will learn to increase his or her level of human capital but will not generate income, usually by attending school. In the third stage, children rely on their level of human capital to generate income, and parents only need to satisfy self-consumption. Usually, the initial level of human capital of the child is not zero.
Based on the structure of Equation (4), a logarithmic utility function is used. The objective function for maximizing utility is
Here,
, parents have three period consumption variables
,
,
and two period investment variables
,
.
R is the value of a unit of human capital.
is the altruism parameter.
ρ is the discounted level of utility. And
r is the discounted level of capital.
W is the level of total income available to the parent for investment and consumption in the three periods, and the budget constraint is
In the first two stages of human capital formation, simply, the growth of children is an output of the investment in education, and the effects of the individual state in both stages are treated exogenously. We set that
and
. So, the net increase in the level of human capital in the two periods is
and
. Where
and
are composite parameters of capacity,
δ is the depreciation rate, and
means the initial human capital level of the offspring. At the decision point, where parents are not fully certain of their children’s future potential, the process of human capital growth is perceived as an act of pre-investment, and the outcome of children’s growth generates satisfaction and utility for parents. In particular, the production function
F may have a richer form, and the calculation will be more complicated [
42].
Constructing a Lagrange function
is a Lagrange factor. Because
Combining Conclusion 1 with Equation (16), in the parent maximization decision, the consumption growth rate is equal to
. Once the parents have determined the appropriate initial level of consumption, the future plan of consumption is also determined, independent of the investment path. Continuing with the calculation of the maximization condition
Evidently,
and
. Equation (17) is the maximization condition of L. The investment decisions at this point can explain a phenomenon. In the early years of a child’s life, if parents believe that their child’s human capital growth results from the accumulation of knowledge and skills that investment can provide, then the optimal investment decision depends on the degree of parental preference for the child
, elasticity of capital output
α, and discount rates
ρ and
r. Because human capital factors such as the ability and potential of the offspring are not fully expressed at the initial stage, parents’ future investment decisions depend only on the characteristics of the current market environment and the initial level of consumption, and they aim to maximize the utility value of their investments. When the total amount of investment is given, parents choose their investment weights based on the expected capital output capacity
α at different stages of the process, rather than the unknown level of their children’s capacity
A.
At this point, the level of consumption, the level of investment, and the level of human capital in the objective function are uniquely determined. reflects the negative correlation between parents’ consumption levels and care for their children. reflects the decelerating decline in personal consumption when parents are more inclined to care for their children. and shows investment levels will show decelerated growth.
Parental concern increases the expectations of their children, but is still influenced by self-consumption, with a marginal diminution in the growth of investment. In particular, entertainment consumption can increase parental satisfaction. In different periods, parents’ preference for entertainment may lead to the decline of . At this time, consumption rises and investment falls. Families make decisions that take into account market characteristics, the expected learning ability of their children, and parental preferences for their children, which include growth rates and initial level choices.
From Corollary 1, the optimal behavior of investment is considered locally under a stable consumption path. Based on Equation (4a), the objective function becomes:
Maximizing the objective function
When , it means: .
A comparison of the two decisions reveals that the allocation ratio of investment is different. Because of the independent decision-making characteristics of consumption behavior and investment growth rate, global maximization of utility only requires choosing the appropriate initial level of consumption or investment. The optimization Equations (15) and (19) must satisfy that the marginal utility levels of consumption and investment are equal. Thus, the calculation can be obtained when choosing the global maximizing consumption and investment paths under the same conditions:
Equation (21) shows that the marginal utility of consumption in Decision 1 is greater than that of Decision 2, which then suggests that Decision 1 invests more in education and consumes less. One explanation is that Decision 1′s investment in education is inefficient for children. Parents lose the expectation of their children’s growth in order to satisfy the self-consumption utility. This illustrates that period-planned education decisions are not always optimal, and that sometimes temporary mediocrity is for the sake of better growth in the future. Here, there is uncertainty about the final level under both decisions due to the initial level of human capital.
From Equation (17), the proportion of investment allocated to the two periods of Decision 1 is independent of the child’s individual trait ability A and depends only on the ability α to use investment. Investment in this decision is treated as future multi-period consumption, and the output of human capital is the return on the productive utility of the investment in each period. In Decision 2, since the technical parameters and are uncertain, the structure of the function is influenced by the objective environment, current knowledge, perception of self, etc. Comparing the two decisions shows that when the level of investment under Equations (17) and (20) is different, parents in Decision 2 lose the intermediate period utility of their investment but allow their children to grow to maximize future expectations.
Take constraint Equation (20) into Equation (19) and derive . It has two typical situations. When children are at high levels of human capital, there is a sufficiently large to make . In the feasible domain of , the optimal solution is . It means children’s human capital is high, and parents will choose to make their own consumption without excessive investment in education. When is small, there is an optimal solution for the level of consumption. Parents will choose a suitable level of consumption and investment in education at the same time.
In short, in different growth stages, the marginal income of education decreases, and the optimal decision of parents will dynamically tend to choose self-consumption.
3.4. Future Transfer Payments
In the previous discussion, the budget constraint for parents was the level of total income available to the individual W. Variable W does not take into account the impact of child-related income. As kinship and care generate intergenerational income transfers, transfers from children are included in the model to analyze the impact on parental decisions.
In the future, children will spend part of their income on their parents’ retirement at
. Generally, the higher the level of children’s human capital is, the more they can earn. And more transfer payments will be made. Assuming that transfers from children are
,
denotes the transfer payment of unit human capital. The parent’s budget constraint Equation (14) becomes
Obviously, the level of transfers should also be within the children’s earning capacity. is usually low in real terms because of the children’s own consumption, investment, and other needs. Assuming that both parents have positive expectations of transfer payments, transfers from children are positive incentives. It directly increases parents’ lifetime budget constraints. It increases both the level of consumption and investment in education in each period. From Equation (18), for each unit of transfer payments, total parental consumption increases and total parental investment increases .
An increase in the level of expected transfers is accompanied by parents’ preference for investing in their children’s education, and as care for their children increases, parents allocate a portion of their future income to less consumption and more investment. Thus, in anticipation of future transfers for their children, parents will maximize upfront investment and consumption. This decision-making behavior of using present consumption in exchange for future returns increases both their self-consumption and their children’s human capital.
Equation (23) is an implicit function of and . At this point, we discuss a steady-state scenario with a given φ. Parents choose to rationally allocate the portion of future benefits given the future transfer ratios. means higher levels of initial human capital are associated with higher levels of future human capital, as well as higher returns to parents. Sometimes the initial level of human capital cannot be evaluated, and judgments based on the inheritance of traits, children’s performance, and life experience produce high evaluations that stimulate parents’ propensity to invest more.
When the objective decision is Equation (4), maximizing the utility of the parent will fail to maximize the level of human capital , as described earlier. At this point, the proportion of investments used for both periods can be adjusted to meet Equation (20). The child will have a higher level of human capital with higher transfers in the future. Thus, the budget of the father’s generation will increase further, but there will be no decline in the level of self-consumption. Parents can increase investment until the equilibrium in Equation (22) is satisfied and additional self-consumption is available. It also means that using Decision 2, parents can obtain a greater level of self-consumption, or their children can reach a higher level of human capital. Especially, parents’ consumption profiles or children’s human capital are expected to become better.
Conclusion 3 (Revealed preference). Assuming that the child is expected to give fixed transfers proportional to his own human capital, when parents have already decided on the level of total consumption or total investment, parents reveal their preferences for Decision 2.
Conclusion 3 is presented in two scenarios. In the first scenario, when the optimal investment ratio of Decision 1 satisfies Equation (20), given the parents’ consumption level, the optimal decision maximizes the parents’ total consumption utility while the children are able to obtain a high level of human capital in the future, which is a win-win outcome. In the second scenario, when the conditions are not met, parents use Decision 2 to make adjustments. The consumption level and the children’s human capital are expected to be better when the situation does not get worse. In both cases, parents can obtain child transfers to improve budget constraints.
Corollary 2. After parents have decided on the consumption path, the optimal decision to maximize the expected level of children’s human capital is to make the two-period level of investment in children satisfy Equation (20) and make Equation (22) hold.
Corollary 3. After parents have decided on the total amount of future investment, the optimal decision must be such that the two-period investment satisfies Equation (20) and parents can obtain the maximum utility level of total consumption.
Two corollaries suggest that the advent of transfers makes it possible for parents to be willing upfront, not only to increase their investment in their children, but also to increase their own consumption. Conclusion 3 reflects the important value of focusing on the education of children. When there are intergenerational exchanges proportional to children’s incomes, it is preferable for parents to invest wisely in their children in order to maximize rather than satisfy self-consumption utility. Conclusion 3 can be generalized to some extent. When parents wish to obtain greater self-consumption utility from a fixed investment in education, the local decision path of investment must be maximizing the human capital of children. The future transfers are favorable to parents. Otherwise, parents can benefit from adjusting their decision by adjusting the level of investment so that their children will give more transfers in the future.
When the level of transfers b is constant or independent of the level of children’s human capital, there are no deterministic revealed preferences for the two decisions based on maximizing Equations (4) and (4a). The actual situation is that parents expect to receive a fixed return from their children in the future without extravagant expectations. Transfers are only a fixed increase in the budget constraint. We illustrate the future return value of parents’ decisions to invest in education. The expectations of children can stimulate their current consumption choices. Selfish family decisions can turn out to be inefficient.