Pattern Recognition of Gene Expression with Singular Spectrum Analysis
Abstract
:1. Introduction
2. Singular Spectrum Analysis (SSA)
2.1. LS and MV Estimators
2.2. LS Estimate of
2.3. MV Estimate of
2.4. Weight Matrix W
3. Empirical Results
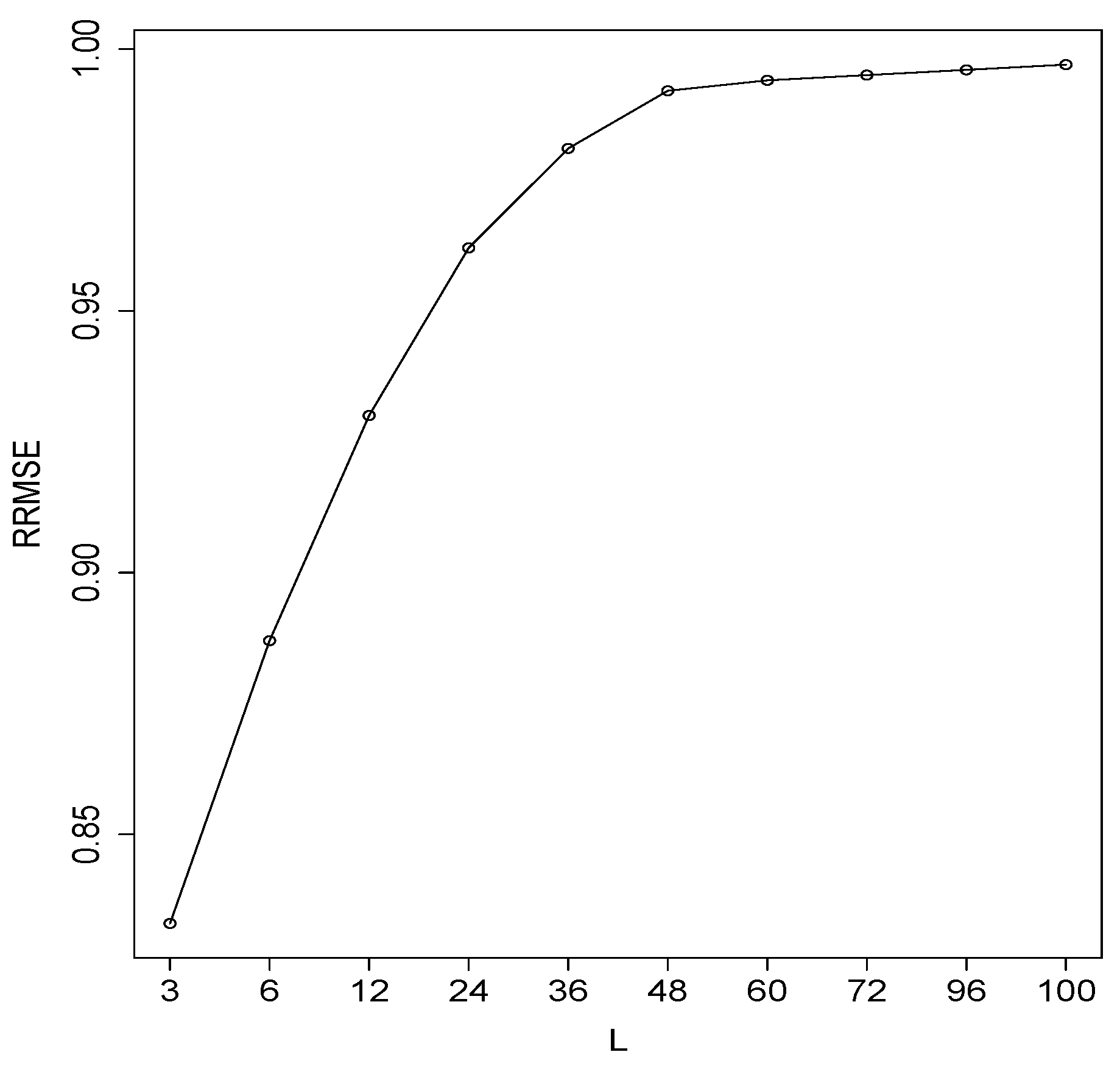
3.1. Simulated Series
| Parameter | Original Value | Average | S.D | Ratio | ||
|---|---|---|---|---|---|---|
| before | after | before | after | |||
| A | 200 | 204.2 | 202.6 | 4.19 | 2.64 | |
| λ | 20 | 19.57 | 19.76 | 0.41 | 0.26 | |

| Simulation Run | RMSE | RRMSE () | |
|---|---|---|---|
| SSA | SDD | ||
| 1 | 2.72 | 4.87 | 0.55 |
| 2 | 2.71 | 4.83 | 0.56 |
| 3 | 2.69 | 3.98 | 0.54 |
| 4 | 2.72 | 4.68 | 0.58 |
| 5 | 2.73 | 4.96 | 0.54 |
3.2. The Bicode Data
3.2.1. Data Description
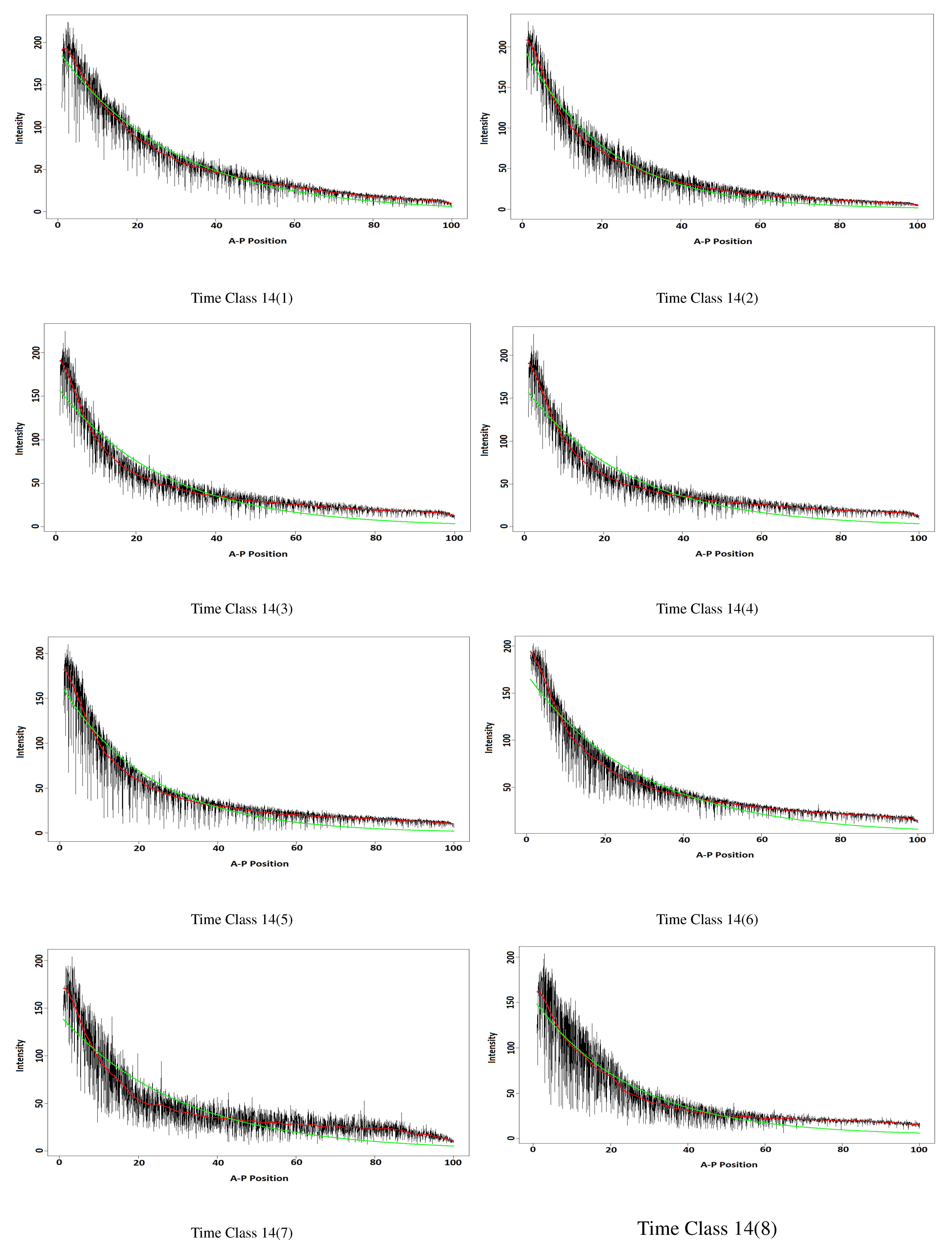
3.2.2. The Results
| Time Class | w-Correlation | Time Class | w-Correlation |
|---|---|---|---|
| 10 | 0.008 | 14(3) | 0.001 |
| 11 | 0.005 | 14(4) | 0.002 |
| 12 | 0.007 | 14(5) | 0.001 |
| 13 | 0.003 | 14(6) | 0.001 |
| 14(1) | 0.001 | 14(7) | 0.001 |
| 14(2) | 0.001 | 14(8) | 0.001 |

4. Conclusions
Conflicts of Interest
References
- How Instructors Request a Complimentary Sample. Available online: http://highered.mcgraw-hill.com (accessed on 30 June 2014).
- Surkova, S.; Kosman, D.; Kozlov, K.; Manu; Myasnikova, E.; Samsonova, A.A.; Spirov, A.; Vanario-Alonso, C.E.; Samsonova, M.; Reinitz, J. Characterization of the Drosophila segment determination morphome. Dev. Biol. 2007, 313, 844–862. [Google Scholar] [CrossRef] [PubMed]
- Wolpert, L. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol. 1969, 27, 1–47. [Google Scholar] [CrossRef]
- Nusslein-Volhard, C.; Wieschaus, E. Mutations affecting segment number and polarity in Drosophila. Nature 1980, 287, 795–801. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Niranjan, M. Gaussian process modelling for bicoid mRNA regulation in spatio-temporal Bicoid profile. Bioinformatics 2011, 28, 366–372. [Google Scholar] [CrossRef] [PubMed]
- Holloway, D.M.; Harrison, L.G.; Kosman, D.; Vanario-Alonso, C.E.; Spirov, A.V. Analysis of pattern precision shows that Drosophila segmentation develops substantial independence from gradients of maternal gene products. Dev. Dyn. 2006, 235, 2949–2960. [Google Scholar] [CrossRef] [PubMed]
- Nusslein-Volhard, C.N. The bicoid morphogen papers (I): Account from CNV. Cell 2004, 116, 1–5. [Google Scholar] [CrossRef]
- Grimm, O.; Coppey, M.; Wieschaus, E. Modelling the bicoid gradient. Development 2010, 137, 2253–2264. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; He, F.; Ma, J. Morphogen gradient formation and action. Fly 2011, 5, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Houchmandzadeh, B.; Wieschaus, E.; Leibler, S. Establishment of developmental precision and proportions in the early Drosophila embryo. Nature 2002, 415, 798–802. [Google Scholar] [CrossRef] [PubMed]
- Gregor, T.; Tank, D.W.; Wieschaus, E.F.; Bialek, W. Stability and Nuclear Dynamics of the Bicoid Morphogen Gradient. Cell 2007, 153, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Hilfinger, H.; Paulsson, J. Separating intrinsic from extrinsic fluctuations in dynamic biological systems. Proc. Natl. Acad. Sci. USA 2011, 108, 12167–12172. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H.; Zokaei, M.; von Rosenc, D.; Amiri, S.; Ghodsi, M. Does noise reduction matter for curve fitting in growth curve models? Comput. Methods Programs Biomed. 2009, 96, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H.; Dionisio, A.; Ghodsi, M. The effect of noise reduction in measuring the linear and nonlinear dependency of financial markets. Nonlin. Anal.: Real World Appl. 2010, 11, 492–502. [Google Scholar] [CrossRef]
- Du, L.P.; Wu, S.H.; Liew, A.W.C.; Smith, D.K.; Yan, H. Spectral Analysis of Microarray Gene Expression Time Series Data of Plasmodium Falciparum. Int. J. Bioinf. Res. Appl. 2008, 4, 337–349. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H. Singular spectrum analysis: Methodology and comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar]
- Hassani, H.; Thomakos, D. A review on singular spectrum analysis for economic and financial time series. Stat. Interface 2010, 3, 377–397. [Google Scholar] [CrossRef]
- Hassani, H.; Soofi, S.; Zhigljavsky, A. Predicting Inflation Dynamics with Singular Spectrum Analysis. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2012, 176, 743–760. [Google Scholar] [CrossRef]
- Golyandina, N.E.; Holloway, D.M.; Lopesc, F.J.P.; Spirov, A.V.; Spirova, E.N.; Usevich, K.D. Measuring gene expression noise in early Drosophila embryos: nucleus-to-nucleus variability. Int. Conf. Comput. Sci. 2012, 9, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Spirov, A.V.; Golyandina, N.E.; Holloway, D.M.; Alexandrov, T.; Spirova, E.N.; Lopes, F.J.P. Measuring Gene Expression Noise in Early Drosophila Embryos: The Highly Dynamic Compartmentalized Micro-environment of the Blastoderm Is One of the Main Sources of Noise. Evol. Comput. Mach. Learn. Data Mining Bioinf. 2012, 7246, 177–188. [Google Scholar]
- Holloway, D.M.; Lopes, F.J.P.; da Fontoura Costa, L.; Travencolo, B.A.N.; Golyandina, N.; Usevich, K.; Spirov, A.V. Gene Expression Noise in Spatial Patterning: Hunchback Promoter Structure Affects Noise Amplitude and Distribution in Drosophila Segmentation. PLoS Comput. Biol. 2011, 7, e1001069. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H. Singular spectrum analysis based on the minimum variance estimator. Nonlin. Anal.: Real World Appl. 2010, 11, 2065–2077. [Google Scholar] [CrossRef]
- Alexandrov, T.; Golyandina, N.; Sprov, A. Singular spectrum analysis of gene expression profiles of early drosophila embryo: Exponential-in-distance patterns. Res. Lett. Signal Process 2010, 2008, 5. [Google Scholar]
- Ghodsi, M.; Hassani, H.; Sanei, S.; Hicks, Y. The use of noise information for detection of temporomandibular disorder. Biomed. Signal Process. Control 2010, 4, 79–85. [Google Scholar] [CrossRef]
- Ghodsi, M.; Hassani, H.; Sanei, S. Extracting fetal heart signal from noisy maternal ECG by multivariate singular spectrum analysis. Stat. Interface 2010, 3, 399–411. [Google Scholar] [CrossRef]
- Vivian, T.; Tang, Y.; Yan, H. Noise Reduction in Microarray Gene Expression Data Based on Spectral Analysis. Int. J. Mach. Learning Cybern. 2012, 3, 51–57. [Google Scholar] [CrossRef]
- Mamou, J.; Feleppa, E.J. Singular Spectrum Analysis Applied to Ultrasonic Detection and Imaging of Brachytherapy Seeds. J. Acoust. Soc. Am. 2007, 121, 1790–1801. [Google Scholar] [CrossRef] [PubMed]
- De Moor, B. The singular value decomposition and long and short spaces on noisy matrices. IEEE Trans. Signal Process. 1993, 41, 2826–2838. [Google Scholar] [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A. Analysis of Time Series Structure: SSA and related techniques; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Hassani, H.; Heravi, H.; Zhigljavsky, A. Forecasting European Industrial Production with Singular Spectrum Analysis. Int. J. Forec. 2009, 25, 103–118. [Google Scholar] [CrossRef]
- Van Huffel, S. Enhanced resolution based on minimum variance estimation and exponential data modeling. Signal Process 1993, 33, 333–355. [Google Scholar] [CrossRef]
- A Database of Segmentation gene Expression in Drosophila. Available online: http://urchin.spbcas.ru/flyex/ (accessed on 30 June 2014).
- Pisarev, A.; Poustelnikova, E.; Samsonova, M.; Reinitz, J. FlyEx, the quantitative atlas on segmentation gene expression at cellular resolution. Nucl. Acids Res. 2008. [Google Scholar] [CrossRef] [PubMed]
- Poustelnikova, E.; Pisarev, A.; Blagov, M.; Samsonova, M.; Reinitz, J. A database for management of gene expression data in situ. Bioinformatics 2008, 20, 2212–2221. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hassani, H.; Ghodsi, Z. Pattern Recognition of Gene Expression with Singular Spectrum Analysis. Med. Sci. 2014, 2, 127-139. https://doi.org/10.3390/medsci2030127
Hassani H, Ghodsi Z. Pattern Recognition of Gene Expression with Singular Spectrum Analysis. Medical Sciences. 2014; 2(3):127-139. https://doi.org/10.3390/medsci2030127
Chicago/Turabian StyleHassani, Hossein, and Zara Ghodsi. 2014. "Pattern Recognition of Gene Expression with Singular Spectrum Analysis" Medical Sciences 2, no. 3: 127-139. https://doi.org/10.3390/medsci2030127
APA StyleHassani, H., & Ghodsi, Z. (2014). Pattern Recognition of Gene Expression with Singular Spectrum Analysis. Medical Sciences, 2(3), 127-139. https://doi.org/10.3390/medsci2030127




