Small Scale Rainfall Partitioning in a European Beech Forest Ecosystem Reveals Heterogeneity of Leaf Area Index and Its Connectivity to Hydro-and Atmosphere
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Design for Throughfall and Litter Sampling
2.3. Litter Biomass and Leaf Area
2.3.1. Measurement of Litter Fall
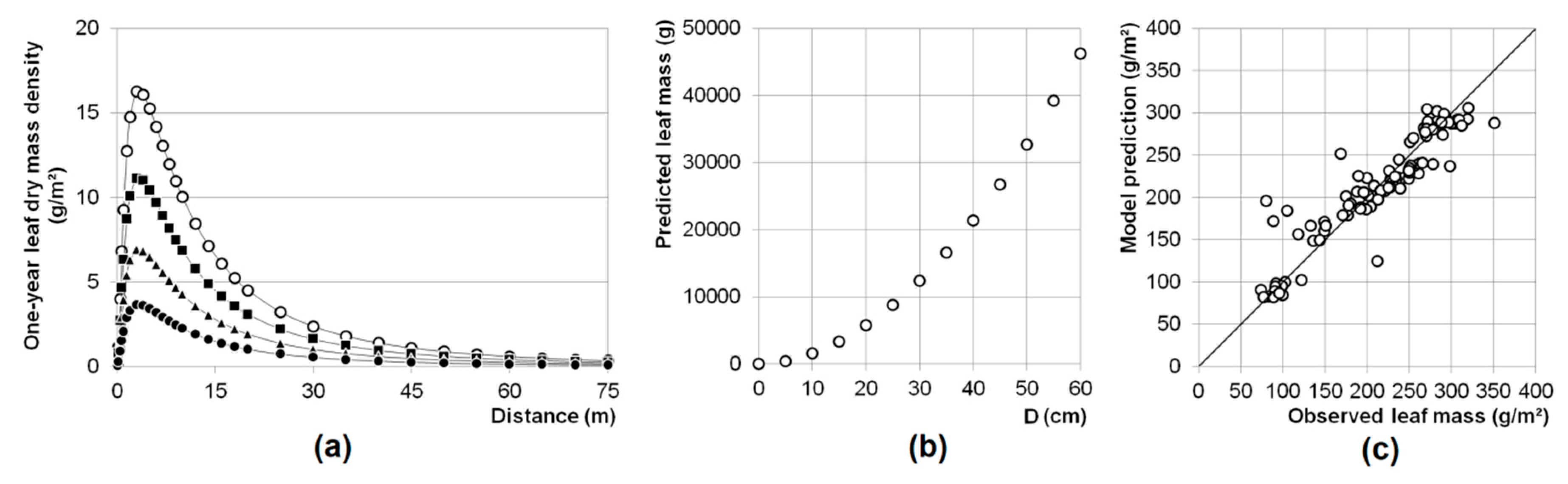
2.3.2. Calculating Leaf Dispersal and One-Year Single Tree Leaf Production
2.4. Gross Precipitation and Throughfall
2.4.1. Measurement of Gross Precipitation and Throughfall
2.4.2. Throughfall Data Inspection and Selection
2.5. Storage Capacity of Tree Biomass Compartments
2.5.1. Estimation of Canopy Storage Capacity, Leaf Storage Capacity, and Twig Storage Capacity
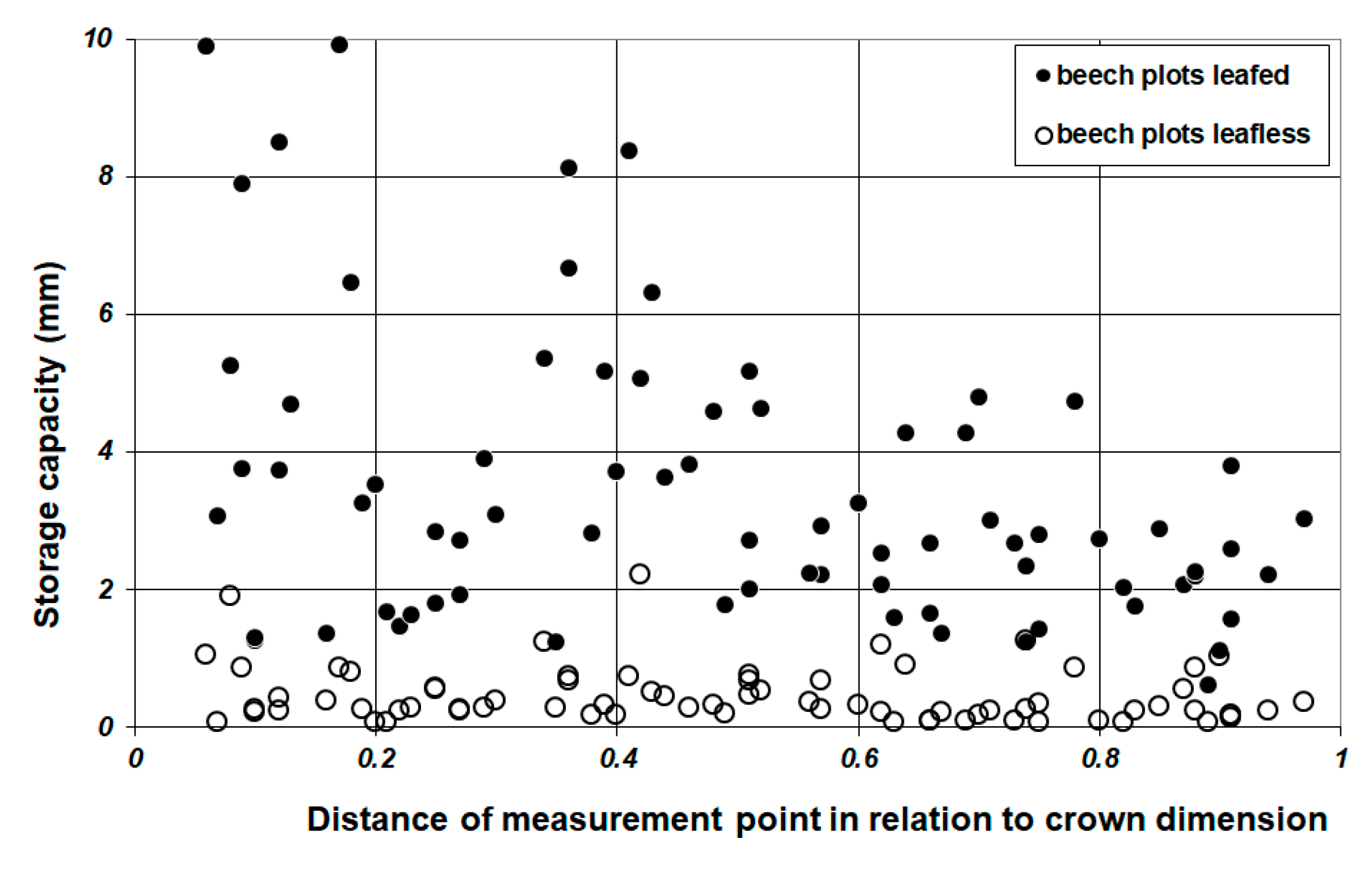
2.5.2. Spatial Analysis of Leaf Storage Capacity
3. Results
3.1. Leaf Mass
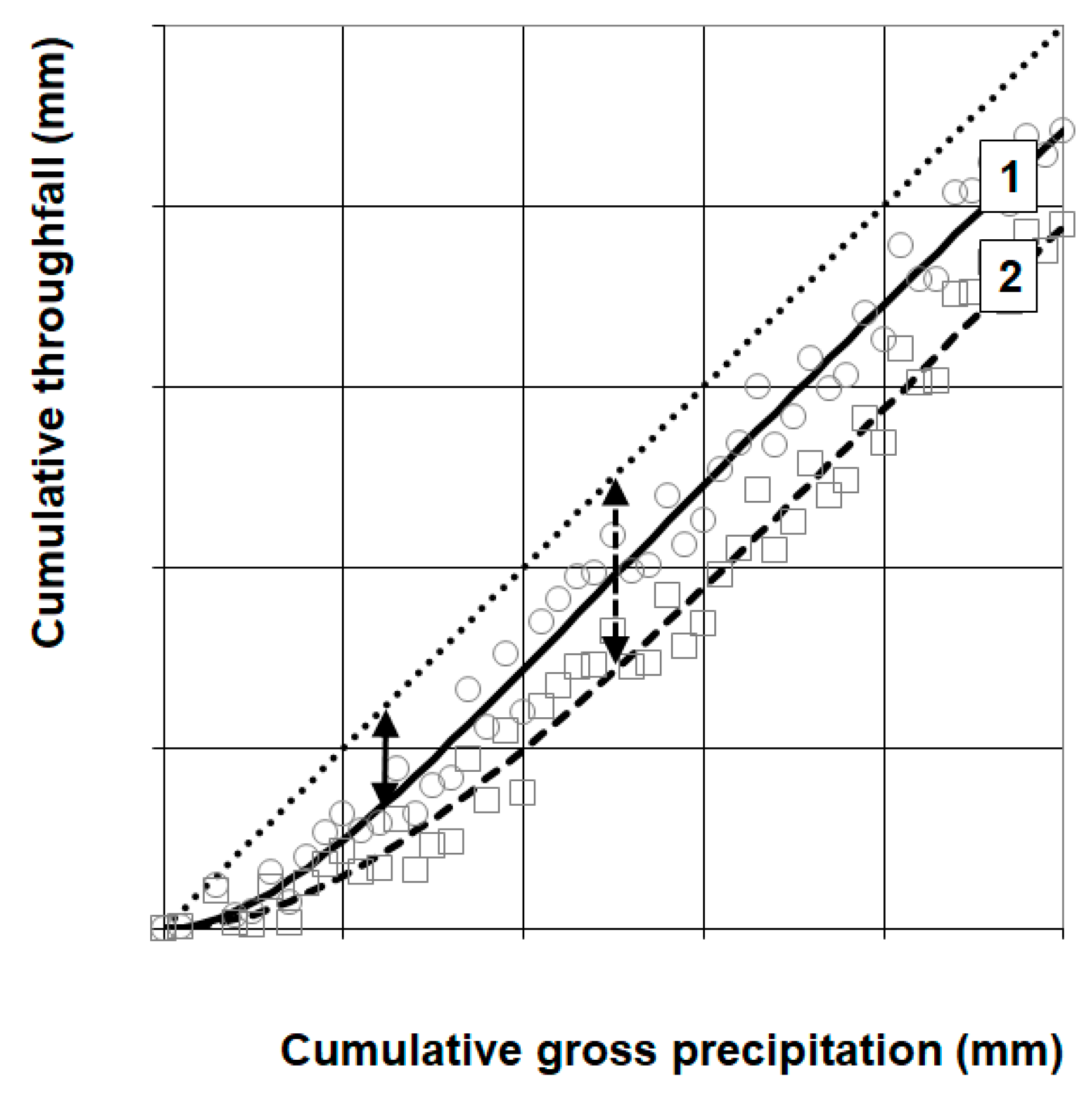
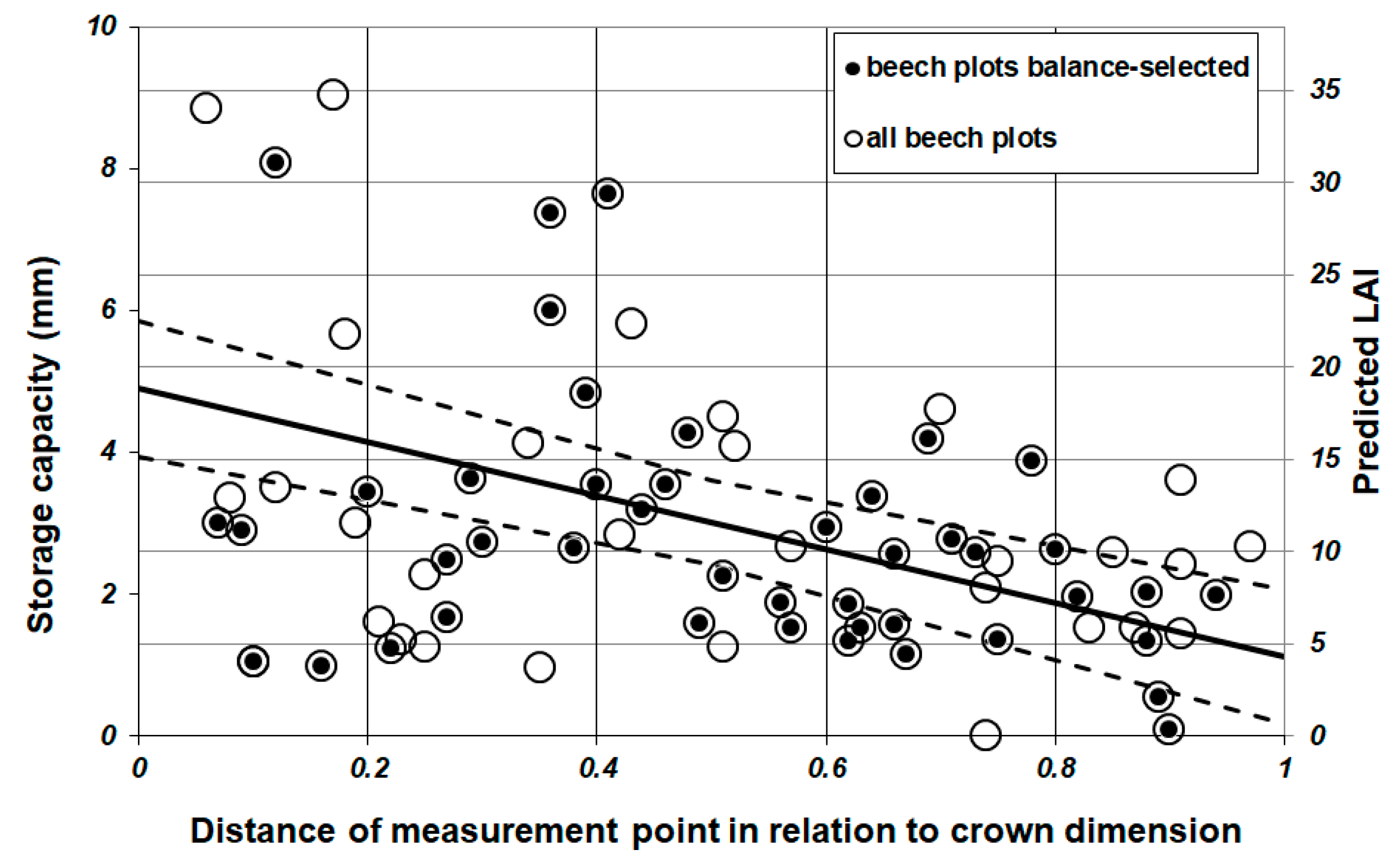
3.2. Throughfall and Storage Capacity
3.3. Leaf Area Index (LAI)
4. Discussion
4.1. Leaf Area Index (LAI) Estimation
4.2. Leaf Mass Prediction, Leaf Ratio Determination, and Leaf Dispersion
4.3. SCtwig and WAI Prediction
4.4. Throughfall Measurement and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Navar, J.; Bryan, R. Interception loss and rainfall redistribution by three semi-arid growing shrubs in Northeastern Mexico. J. Hydrol. 1990, 1150, 51–63. [Google Scholar] [CrossRef]
- Klaasen, W.; Bosveld, F.; de Water, E. Water storage and evaporation as constituents of rainfall interception. J. Hydrol. 1998, 212–213, 36–50. [Google Scholar] [CrossRef]
- André, F.; Jonard, M.; Jonard, F.; Ponette, Q. Spatial and temporal patterns of throughfall volume in a deciduous mixed-species stand. J. Hydrol. 2011, 400, 244–254. [Google Scholar] [CrossRef]
- Canham, C.D.; Finzi, A.C.; Pacala, S.W.; Burbank, D.H. Causes and consequences of resource heterogeneity in forests: Interspecific variation in light transmission by canopy trees. Can. J. For. Res. 1994, 24, 337–349. [Google Scholar] [CrossRef]
- Metzger, J.C.; Wutzler, T.; Dalla Valle, N.; Filipzik, J.; Grauer, C.; Lehmann, R.; Roggenbuck, M.; Schelhorn, D.; Weckmüller, J.; Küsel, K.; et al. Vegetation impacts soil water content patterns by shaping canopy water fluxes and soil properties. Hydrol. Processes 2017, 31, 3783–3795. [Google Scholar] [CrossRef]
- Crockford, R.H.; Richardson, D.P. Partitioning of rainfall into throughfall, stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Processes 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Barkman, J.J. Canopies and microclimate of tree species mixtures. In Special Publication Number 11 of the British Ecological Society; Cannell, M.G.R., Molcolm, D.C., Robertson, P.A., Eds.; Blackwell Scientific Publications: Oxford, UK, 1992; Volume 11, pp. 181–188. [Google Scholar]
- Bréda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2012, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Mottus, M.; Sulev, M.; Lang, M. Estimation of crown volume for a geometric radiation model from detailed measurements of tree structure. Ecol. Model. 2006, 198, 506–514. [Google Scholar] [CrossRef]
- Watson, D. Comparative physiological studies on the growth of field crops. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Brunner, A.; Rajkai, K.; Gacsi, Z.; Hagyo, A. Regenerator—A Forest Regeneration Model; NAT-MAN Working Report 46; University of Copenhagen: Copenhagen, Denmark, 2004. [Google Scholar]
- Pukkala, T.; Kolström, T. A Stochastic Spatial Regeneration Model for Pinus sylvestris. Scand. J. For. Res. 1992, 7, 377–385. [Google Scholar] [CrossRef]
- Wagner, S.; Fisher, H.; Huth, F. Canopy effects on vegetation caused by harvesting and regeneration treatments. Eur. J. For. Res. 2011, 130, 17–40. [Google Scholar] [CrossRef]
- Woodgate, W.; Disney, M.; Armston, J.D.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. An improved theoretical model of canopy gap probability for Leaf Area Index estimation in woody ecosystems. For. Ecol. Manag. 2015, 358, 303–320. [Google Scholar] [CrossRef]
- Wälder, K.; Frischbier, N.; Bredemeier, M.; Näther, W.; Wagner, S. Analysis of OF-layer humus mass variation in a mixed stand of European beech and Norway spruce: An application of structural equation modelling. Ecol. Model. 2008, 213, 319–330. [Google Scholar] [CrossRef]
- Labaz, B.; Galka, B.; Bogacz, A.; Waroszewski, J.; Kabala, C. Factors influencing humus forms and forest litter properties in the mid-mountains under temperate climate of southwestern Poland. Geoderma 2014, 230–231, 265–273. [Google Scholar] [CrossRef]
- Schua, K.; Wende, S.; Wagner, S.; Feger, K.H. Soil Chemical and Microbial Properties in a Mixed Stand of Spruce and Birch in the Ore Mountains (Germany)—A Case Study. Forests 2015, 6, 1949–1965. [Google Scholar] [CrossRef]
- Bartelink, H.H. Simulation for Growth and Competition in Mixed Stands of Douglas-Fir and Beech. Ph.D. Thesis, Landbouwuniversiteit Wageningen, Wageningen, The Netherlands, 1998. [Google Scholar]
- Grote, R.; Reiter, I.M. Competition-dependent modeling of foliage biomass in forest stands. Trees 2004, 18, 596–607. [Google Scholar] [CrossRef]
- Sinoquet, H.; Rivet, P. Measurement and visualization of the architecture of an adult tree based on a three-dimensional digitising device. Trees 1997, 11, 265–270. [Google Scholar] [CrossRef]
- Cohen, S.; Fuchs, M. The distribution of leaf area, radiation, photosynthesis and transpiration in a shamouti orange hedgerow orchard. Agric. For. Meteorol. 1987, 40, 123–144. [Google Scholar] [CrossRef]
- Cohen, S.; Mosoni, P.; Meron, M. Canopy clumpiness and radiation penetration in a young hedgerow apple orchard. Agric. For. Meteorol. 1995, 76, 185–200. [Google Scholar] [CrossRef]
- Mariscal, M.J.; Orgaz, F.; Villalobos, F.J. Modelling and measurement of radiation interception by olive canopies. Agric. For. Meteorol. 2000, 100, 183–197. [Google Scholar] [CrossRef]
- Bequet, R.; Campioli, M.; Kint, V.; Muys, B.; Bogaert, J.; Ceulemans, R. Spatial Variability of Leaf Area Index in Homogeneous Forests Relates to Local Variation in Tree Characteristics. For. Sci. 2012, 58, 633–640. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Xiang, W.; Pan, Q.; Zeng, Y.; Ouyang, S.; Lei, P.; Deng, X.; Fang, X.; Peng, C. Spatial and seasonal variations of leaf area index (LAI) in subtropical secondary forests related to floristic composition and stand characters. Biogeosciences 2016, 13, 3819–3831. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Liu, W.; Li, W.; Jiang, X.; Wu, J. Effects of rainfall on the spatial distribution of the throughfall kinetic energy on a small scale in a rubber plantation. Hydrol. Sci. J. 2018, 63, 1078–1090. [Google Scholar] [CrossRef]
- Chen, J.M.; Rich, P.M.; Gower, S.T.; Norman, J.M.; Plummer, S. Leaf area index of boreal forests: Theory, techniques, and measurements. J. Geophys. Res. 1997, 102, 29429–29443. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Xihan, M.; Donghui, X.; Zhang, W. Review of indirect methods for leaf area index measurement. J. Remote Sens. 2016, 20, 958–978. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Claders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef] [Green Version]
- Leblanc, S.G.; Fournier, R.A. Hemispherical photography simulations with an architectural model to assess retrieval of leaf area index. Agric. For. Meteorol. 2014, 194, 64–76. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Li, M.H. Quantifying Rainfall Interception Loss of a Subtropical Broadleaved Forest in Central Taiwan. Water 2016, 8, 14. [Google Scholar] [CrossRef]
- Fathizadeh, O.; Hosseini, S.M.; Zimmermann, A.; Keim, R.F.; Boloorani, A.D. Estimating linkages between forest structural variables and rainfall interception parameters in semi-arid deciduous oak forest stands. Sci. Total Environ. 2017, 601–602, 1824–1837. [Google Scholar] [CrossRef]
- Weber, Y.; Jolivet, V.; Gilet, G.; Nanko, K.; Ghazanfarpour, D. A phenomenological model for throughfall rendering in real-time. Eurograph. Sympos. Render. 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Hutchinson, I.; Roberts, M.C. Vertical variation in stemflow generation. J. Appl. Ecol. 1981, 18, 521–527. [Google Scholar] [CrossRef]
- Dijk, A.I.J.M.; Bruijnzeel, L.A. Modelling rainfall interception by vegetation of variable density using an adapted analytical model. Part 1. Model description. J. Hydrol. 2001, 247, 230–238. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Processes 2000, 14, 763–784. [Google Scholar] [CrossRef]
- Ford, E.D.; Deans, J.D. The effects of canopy structure on stemflow, throughfall and interception loss in a young sitka spruce plantation. J. App. Ecol. 1978, 15, 905–917. Available online: http://www.jstor.org/stable/2402786 (accessed on 10 July 2019). [CrossRef]
- Gash, J. An analytical model of rainfall interception over large areas. J. Clim. 1979, 6, 1002–1008. [Google Scholar]
- Frischbier, N.; Wagner, S. Detection, quantification and modelling of small-scale lateral translocation of throughfall in tree crowns of European beech (Fagus sylvatica L.) and Norway spruce (Picea abies (L.) Karst.). J. Hydrol. 2015, 522, 228–238. [Google Scholar] [CrossRef]
- Levia, D.F.; Germer, S. A review of stemflow generation dynamics and stemflow-environment interactions in forests and shrublands. Rev. Geophys. 2015, 53, 673–714. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Verstraete, M.; Pinty, B.; Gobron, N. Allometric Relationships of Selected European Tree Species. Parametrizations of Tree Architecture for the Purpose of 3-D Canopy Reflectance Models Used in the Interpretation of Remote Sensing Data; European Commission Joint Research Centre: Ispra, Italy, 2003. [Google Scholar]
- Konôpka, B.; Pajtík, J.; Marušák, R.; Bošel’a, M.; Lukac, M. Specific leaf area and leaf area index in developing stands of Fagus sylvatica L. and Picea abies Karst. For. Ecol. Manag. 2016, 364, 52–59. [Google Scholar] [CrossRef]
- Leuschner, C.; Voß, S.; Foetzki, A.; Clases, Y. Variation in leaf area index and stand leaf mass of European beech across gradients of soil acidity and precipitation. Plant Ecol. 2006, 186, 247–258. [Google Scholar] [CrossRef]
- Staelens, J.; Nachtergale, L.; Luyssart, S. Predicting the spatial distribution of leaf litterfall in a mixed deciduous forest. For. Sci. 2004, 50, 836–846. [Google Scholar] [CrossRef]
- Bigelow, S.W.; Canham, C.D. Litterfall as a niche construction process in a northern hardwood forest. Ecosphere 2015, 6, 1–14. [Google Scholar] [CrossRef]
- Canham, C.D.; Uriate, M. Analysis of neighbourhood dynamics of forest ecosystems using likelihood methods and modeling. Ecol. Appl. 2006, 16, 62–73. [Google Scholar] [CrossRef] [PubMed]
- Näther, W.; Wälder, K. Applying fuzzy measures for considering interaction effects in root dispersal models. Fuzzy Sets Syst. 2007, 158, 572–582. [Google Scholar] [CrossRef]
- Ribbens, E.; Silander, J.A.; Pacala, S.W. Seedling recruitment in forests: Calibrating models to predict patterns of tree seedling dispersion. Ecology 1994, 75, 1794–1806. [Google Scholar] [CrossRef]
- Bredemeier, M.; Cheussom, L.; Beese, F.O. Water balance of a mixed forest in central Germany-small-scale variability in dependence on pattern of local canopy cover. In Forstliche Schriftenreihe der Universität für Bodenkultur Wien, Österreichische Gesellschaft für Waldökoforschung und experimentelle Baumforschung; Band 18; University of Natural Resources and Life Sciences: Wien, Austria, 2004; pp. 143–156. [Google Scholar]
- Gomez, J.A.; Vanderlinden, K.; Giraldez, J.V.; Fereres, E. Rainfall concentration under olive trees. Agric. Water Manag. 2002, 55, 53–70. [Google Scholar] [CrossRef]
- Durocher, M.G. Monitoring spatial variability of forest interception. Hydrol. Processes 1990, 4, 215–229. [Google Scholar] [CrossRef]
- Frischbier, N. Study on the Single-Tree Related Small-Scale Variability and Quantity-Dependent Dynamics of Net Forest Precipitation Using the Example of Two Mixed Beech-Spruce Stands; TUDpress: Dresden, Germany, 2012. [Google Scholar]
- Zwanzig, M.; Schlicht, R.; Frischbier, N.; Berger, U. Data exploration and transformation: An outline on tasks and tools. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Forest-Water Interactions. Ecological Studies Series, No. [TBD]; Springer: Heidelberg, Germany, 2019; in press. [Google Scholar]
- Wagner, S.; Wälder, K.; Ribbens, E.; Zeibig, A. Directionality in fruit dispersal models for anemochorous forest trees. Ecol. Model. 2004, 179, 487–498. [Google Scholar] [CrossRef]
- Rhoads, A.G.; Hamburg, S.P.; Fahey, T.J.; Siccama, T.G.; Kobe, R. Comparing direct and indirect methods of assessing canopy structure in a northern hardwood forest. Can. J. For. Res. 2004, 34, 584–591. [Google Scholar] [CrossRef]
- van Putten, B.; Visser, M.D.; Muller-Landau, H.C.; Jansen, P.A. Distorted-distance models for directional dispersal: A general framework with application to a wind-dispersed tree. Methods Ecol. Evol. 2012, 3, 642–652. [Google Scholar] [CrossRef]
- Näther, W.; Wälder, K. Experimental Design and Statistical Inference for Cluster Point Processes—With Applications to the Fruit Dispersion of Anemochorous Forest Trees. Biom. J. 2003, 45, 1006–1022. [Google Scholar] [CrossRef]
- Wälder, K.; Näther, W.; Wagner, S. Improving inverse model fitting in trees-anisotropy, multiplicative effects, and Bayes estimation. Ecol. Model. 2009, 220, 1044–1053. [Google Scholar] [CrossRef]
- Batschelet, E. Circular Statistics in Biology; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Aradóttir, A.L.; Robertson, A.; Moore, E. Circular statistical analysis of birch colonization and the directional growth response of birch and black cottonwood in south Iceland. Agric. For. Meteorol. 1997, 84, 179–186. [Google Scholar] [CrossRef]
- Herrmann, I.; Herrmann, T.; Wagner, S. Improvements in anisotropic models of single tree effects in Cartesian coordinates. Ecol. Model. 2011, 222, 1333–1336. [Google Scholar] [CrossRef]
- MacKinnon, J. Bootstrap Hypothesis Testing; Queen’s Economics Department Working Paper No. 1127; Department of Economics, Queen’s University: Kingston, ON, Canada, 2007. [Google Scholar]
- Fox, J. Bootstrapping Regression Models: Appendix to “An R and S-PLUS Companion to Applied Regression”; Sage: Newcastle, UK, 2002. [Google Scholar]
- Faraway, J. Extending the Linear Model with R; Chapman and Hall: London, UK, 2006. [Google Scholar]
- Hall, P.; Wilson, S.R. Two Guidelines for Bootstrap Hypothesis Testing. Biometrics 1991, 47, 757–762. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www.r-project.org/ (accessed on 7 March 2019).
- Shuguang, L. A new model for the prediction of rainfall interception in forest canopies. Ecol. Model. 1997, 99, 151–159. [Google Scholar] [CrossRef]
- Herbst, M.; Rosier, P.; McNeil, D.; Harding, R.; Gowing, D. Seasonal variability of interception evaporation from the canopy of a mixed deciduous forest. Agric. For. Meteorol. 2008, 148, 1655–1667. [Google Scholar] [CrossRef]
- Chang, M. Forest Hydrology. An Introduction to Water and Forests; CRC Press: Washington, DC, USA, 2003. [Google Scholar]
- Staelens, J.; De Schrijver, A.; Verheyen, K.; Verhoest, N. Rainfall partitioning into throughfall, stemflow, and interception within a single beech (Fagus sylvatica L.) canopy: Influences of foliation, rain event characteristics, and meteorology. Hydrol. Processes 2008, 22, 33–45. [Google Scholar] [CrossRef]
- Rutter, A.; Kershaw, K.; Robins, P.; Morton, A. A predictive model of rainfall interception in forests. I. Derivation of the model from observations in a plantation of Corsican pine. Agric. For. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Gerrits, A.M.J.; Pfister, L.; Savenije, H.H.G. Spatial and temporal variability of canopy and forest floor interception in a beech forest. Hydrol. Process. 2010, 24, 3011–3025. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer: Dordrecht, The Netherlands, 2010; ISBN 9781441903181. [Google Scholar]
- Ross, J. The Radiation Regime and the Architecture of Plants Stands; Junk Publishers: The Hague, The Netherlands, 1981. [Google Scholar]
- Wagner, S. Relative radiance measurements and zenith angle dependent segmentation in hemispherical photography. Agric. For. Meteorol. 2001, 107, 103–115. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Bicheron, P.; Chen, J.M.; Leroy, M.; Cihlar, J. Investigation of Directional Reflectance in Boreal Forests with an Improved Four-Scale Model and Airborne POLDER Data. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1396–1414. [Google Scholar] [CrossRef]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating Leaf Area Index (LAI) at multiple spatial scales through lidar remote sensing: A case study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and bias in active and passive ground-based measurements of effective plant, wood and leaf area index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Müller-Dombois, D.; Ellenberg, H. Aims and Methods of Vegetation Ecology; Blackburn Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Godin, C. Representing and encoding plant architecture: A review. Ann. For. Sci. 2000, 57, 413–438. [Google Scholar] [CrossRef]
- Whitehead, D.; Grace, J.C.; Godfrey, M. Architectural distribution of foliage in individual Pinus radiata D. on crowns and the effect of clumping on radiation interception. Tree Physiol. 1990, 7, 135–155. [Google Scholar] [CrossRef] [PubMed]
- Deleuze, C.; Hervé, J.C.; Colin, F.; Ribeyrolles, L. Modelling crown shape of Picea abies: Spacing effects. Can. J. For. Res. 1996, 26, 1957–1966. [Google Scholar] [CrossRef]
- Anzola-Jürgenson, G.A. Linking Structural and Process-Oriented Models of Plant Growth. Ph.D. Thesis, Georg-August-Universität Göttingen, Göttingen, Germany, 2002. [Google Scholar]
- Grote, R. Foliage and branch biomass estimation of coniferous and deciduous tree species. Silva Fenn. 2002, 36, 779–788. [Google Scholar] [CrossRef]
- Kinerson, R.; Fritschen, L. Modeling a coniferous forest canopy. Agric. Meteorol. 1971, 8, 439–445. [Google Scholar] [CrossRef]
- Koppel, A.; Oja, T. Regime of diffuse solar radiation in an individual Norway spruce (Picea abies (L.) KARST.) crown. Photosynthetica 1984, 18, 529–535. [Google Scholar]
- Kull, O.; Broadmeadow, M.; Kruijt, B.; Meir, P. Light distribution and foliage structure in an oak canopy. Trees 1999, 14, 55–64. [Google Scholar] [CrossRef]
- Smolander, S.; Stenberg, P. A method to account for shoot scale clumping in coniferous canopy reflectance models. Remote Sens. Environ. 2003, 88, 363–373. [Google Scholar] [CrossRef] [Green Version]
- Stadt, K.J.; Lieffers, V.J.; Hall, R.J.; Messier, C. Spatially explicit modeling of PAR transmission and growth of Picea glauca and Abies balsamea in the boreal forests of Alberta and Quebec. Can. J. For. Res. 2005, 35, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chin, A.R.O.; Sillett, S.C. Within-crown plasticity in leaf traits among the tallest conifers. Am. J. Bot. 2019, 106, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Woodgate, W.; Armston, J.D.; Disney, M.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M. Quantifying the impact of woody material on leaf area index estimation from hemispherical photography using 3D canopysimulations. Agric. For. Meteorol. 2016, 226, 1–12. [Google Scholar] [CrossRef]
- Jochheim, H.; Einert, P.; Ende, H.P.; Kallweit, R.; Lüttschwager, D.; Schindler, U. Wasser- und Stoffhaushalt eines Buchen-Altbestandes im Nordostdeutschen Tiefland-Ergebnisse einer 4jährigen Messperiode. Arch. für Forstwes. und Landschaftsökologie 2007, 41, 1–14. [Google Scholar]
- Palán, L.; Křeček, J.; Sato, Y. Leaf area index in a forested mountain catchment. Hung. Geogr. Bull. 2018, 67, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Ahrends, B.; Schmidt-Walter, P.; Fleck, S.; Köhler, M.; Weis, W. Wasserhaushaltssimulation und Klimadaten; Berichte Freiburger Forstliche Forschung 101; Fakultät für Umwelt und Natürliche Ressourcen der Albert-Ludwigs-Universität Freiburg; Forstliche Versuchs- und Forschungsanstalt Baden-Württemberg: Freiburg, Germany, 2018; pp. 74–94. [Google Scholar]
- Dyderski, M.; Jagodziński, A. Functional traits of acquisitive invasive woody species differ from conservative invasive and native species. NeoBiota 2019, 41, 91–113. [Google Scholar] [CrossRef]
- Forrester, D.; Tachauer, I.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T.; et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Annighöfer, P.; Ameztegui, A.; Ammer, C.; Balandier, P.; Bartsch, N.; Bolte, A.; Coll, L.; Collet, C.; Ewald, J.; Frischbier, N.; et al. Species-specific and generic biomass equations for seedlings and saplings of European tree species. Eur. J. For. Res. 2016, 135, 313–329. [Google Scholar] [CrossRef]
- Stadt, K.J.; Lieffers, V.J. MIXLIGHT: A flexible PAR transmission model for mixed-species forest stands. Agric. For. Meteorol. 2000, 102, 235–252. [Google Scholar] [CrossRef]
- Staelens, J.; De Schrijver, A.; Verheyen, K.; Verhoest, N. Spatial variability and temporal stability of throughfall water under a dominant beech (Fagus sylvatica L.) tree in relationship to canopy cover. J. Hydrol. 2006, 330, 651–662. [Google Scholar] [CrossRef]
- Kato, H.; Onda, Y.; Nanko, K.; Gomi, T.; Yamanaka, T.; Kawaguchi, S. Effect of canopy interception on spatial variability and isotopic composition of throughfall in Japanese cypress plantations. J. Hydrol. 2013, 504, 1–11. [Google Scholar] [CrossRef]
- Hansen, K. In-Canopy throughfall measurements in Norway Spruce: Water flow and consequences for ion fluxes. Water Air Soil Pollut. 1995, 85, 2259–2264. [Google Scholar] [CrossRef]
- Gash, J.; Lloyd, C.; Lachaud, G. Estimating sparse forest rainfall interception with an analytical model. J. Hydrol. 1995, 170, 79–86. [Google Scholar] [CrossRef]
- Saito, T.; Matsuda, H.; Komatsu, M.; Xiang, Y.; Takahashi, A.; Shinohara, Y.; Otsuki, K. Forest canopy interception loss exceeds wet canopy evaporation in Japanese cypress (Hinoki) and Japanese cedar (Sugi) plantations. J. Hydrol. 2013, 507, 287–299. [Google Scholar] [CrossRef]
- Loustau, D.; Berbigier, P.; Granier, A. Interception lost, throughfall and stemflow in a maritime pine stand. II. An application of Gash’s analytical modell of interception. J. Hydrol. 1992, 138, 469–485. [Google Scholar] [CrossRef]
- Tischer, A.; Zwanzig, M.; Frischbier, N. Spatiotemporal statistics: Analysis of spatially and temporally-correlated throughfall data—Exploring and considering dependency and heterogeneity. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Forest-Water Interactions; Ecological Studies Series, No. [TBD]; Springer: Heidelberg, Germany, 2019; in press. [Google Scholar]
- Li, X.; Xiao, Q.; Niu, J.; Dymond, S.; van Doorn, N.S.; Yu, X.; Xie, B.; Lv, X.; Zhang, K.; Li, J. Process-based rainfall interception by small trees in Northern China: The effect of rainfall traits and crown structure characteristics. Agric. For. Meteorol. 2016, 218–219, 65–73. [Google Scholar] [CrossRef]
- Grote, R.; Korhonen, J.; Mammarella, I. Challenges for evaluating process-based models of gas exchange at forest sites with fetches of various species. For. Syst. 2011, 20, 389–406. [Google Scholar] [CrossRef]
- Deckmyn, G.; Verbeeck, H.; Op de Beeck, M.; Vansteenkiste, D.; Steppe, K.; Ceulemans, R. ANAFORE: A stand-scale process-based forest model that includes wood tissue development and labile carbon storage in trees. Ecol. Model. 2008, 215, 345–368. [Google Scholar] [CrossRef]
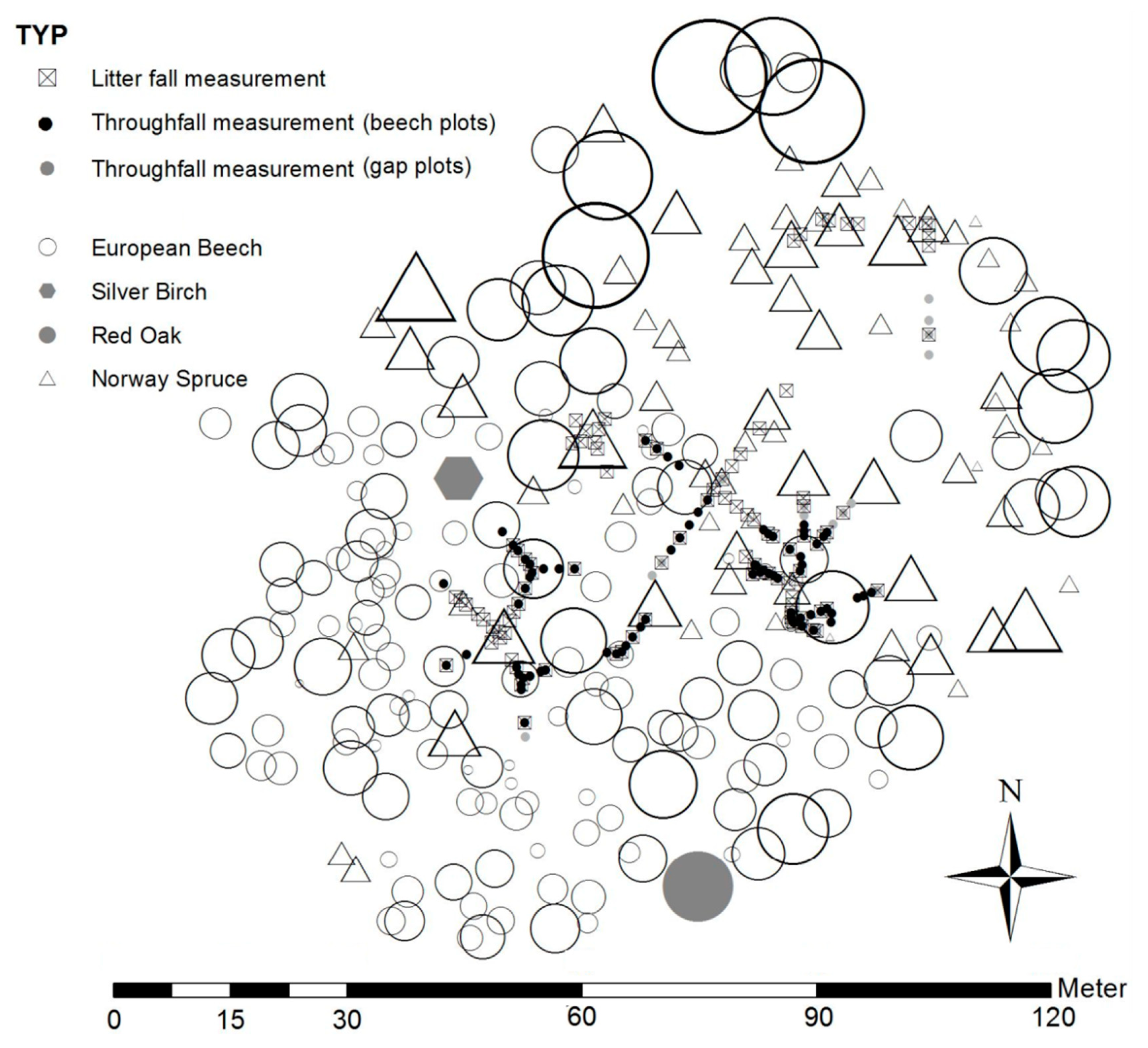

| Tree Species | Tree Number (ha−1) | Mean Tree Height (m) | D (cm) | Basal Area (m2·ha−1) | Growth Rate100 (m³·ha−1·a−1) 1 | Crown Length (% of Tree Height) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD 2 | Max. | Min. | Mean | SD | |||||
| Beech | 139 | 34.5 | 44.2 | 10.8 | 75.4 | 21.2 | 22.8 | 8.0 | 66.6 | ± 9.9 |
| Stand total | 227 | 35.8 | ||||||||
| Canopy Stratum | Sample Size (n) According to Relative Distance Class | Total n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–0.1 | 0.1–0.2 | 0.2–0.3 | 0.3–0.4 | 0.4–0.5 | 0.5–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–1.0 | ||
| Beech | 5 | 10 | 9 | 6 | 8 | 8 | 8 | 9 | 8 | 5 | 76 |
| Gap | 15 | ||||||||||
| Variable | Unit | n | Mean | SD |
|---|---|---|---|---|
| Observed one-year leaf dry mass per area | (g·m−2) | 99 | 216.7 | 70.5 |
| Leaf mass | (g·leaf−1) | 15 × 250 | 0.0799 | 0.0040 |
| Leaf area | (cm2·leaf−1) | 15 × 100 | 20.467 | 2.564 |
| Specific leaf area | (m2·kg−1) | 25.616 |
| Model | Clumping κ | Fecundity α | Fecundity z | Expected Value μ | Variance δ | Coherency β | Bootstrap 1 |
|---|---|---|---|---|---|---|---|
| iso-tropic | 10.67 | −1.41 | 1.9 | 3.72 | 1.23 | P = 0.354 | |
| aniso-tropic | 10.67 | −0.98 | 1.9 | 4.42 | 1.43 | 0.52 | |
| Model | Driftγ | Rotationψ | AIC | Loglike | r | p-Value | Bootstrap 1 |
| iso-tropic | 1036.3 | −515.2 | 0.935 | <2.2 × 10−16 | P = 0.354 | ||
| aniso-tropic | 0.62 | 2.67 | 1039.5 | −513.7 | 0.938 | <2.2 × 10−16 |
| D | Crown Radius | Crown Area | Leaf Area | SCtwig1 | SCleaf |
|---|---|---|---|---|---|
| (cm) | (m) | (m2) | (m2) | (l·tree−1) | (l·tree−1) |
| 15 | 1.62 | 8.2 | 85.1 | 3.6 | 19.6 |
| 20 | 2.16 | 14.7 | 146.9 | 6.3 | 34.8 |
| 25 | 2.70 | 22.9 | 224.5 | 9.9 | 54.4 |
| 30 | 3.24 | 33.0 | 317.5 | 14.2 | 78.3 |
| 35 | 3.78 | 44.9 | 425.5 | 19.3 | 106.6 |
| 40 | 4.32 | 58.6 | 548.4 | 25.3 | 139.2 |
| 45 | 4.86 | 74.2 | 685.9 | 32.0 | 176.1 |
| 50 | 5.40 | 91.6 | 838.0 | 39.5 | 217.4 |
| 55 | 5.94 | 110.8 | 1 004.3 | 47.8 | 263.1 |
| 60 | 6.48 | 131.9 | 1 184.9 | 56.9 | 313.1 |
| Type of Specific Wetting Capacity | Unit | Mean | SD |
|---|---|---|---|
| for leaf mass | (l·kg−1) | 6.656 | 0.044 |
| for leaf area | (l·m−2) | 0.260 | 0.002 |
| for leaf number | (l 1000 leaves−1) | 0.532 | 0.004 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frischbier, N.; Tiebel, K.; Tischer, A.; Wagner, S. Small Scale Rainfall Partitioning in a European Beech Forest Ecosystem Reveals Heterogeneity of Leaf Area Index and Its Connectivity to Hydro-and Atmosphere. Geosciences 2019, 9, 393. https://doi.org/10.3390/geosciences9090393
Frischbier N, Tiebel K, Tischer A, Wagner S. Small Scale Rainfall Partitioning in a European Beech Forest Ecosystem Reveals Heterogeneity of Leaf Area Index and Its Connectivity to Hydro-and Atmosphere. Geosciences. 2019; 9(9):393. https://doi.org/10.3390/geosciences9090393
Chicago/Turabian StyleFrischbier, Nico, Katharina Tiebel, Alexander Tischer, and Sven Wagner. 2019. "Small Scale Rainfall Partitioning in a European Beech Forest Ecosystem Reveals Heterogeneity of Leaf Area Index and Its Connectivity to Hydro-and Atmosphere" Geosciences 9, no. 9: 393. https://doi.org/10.3390/geosciences9090393
APA StyleFrischbier, N., Tiebel, K., Tischer, A., & Wagner, S. (2019). Small Scale Rainfall Partitioning in a European Beech Forest Ecosystem Reveals Heterogeneity of Leaf Area Index and Its Connectivity to Hydro-and Atmosphere. Geosciences, 9(9), 393. https://doi.org/10.3390/geosciences9090393





