Periodicity in Volcanic Gas Plumes: A Review and Analysis
Abstract
1. Introduction
2. Methods for Detecting Periodicity
2.1. Spectral Analysis
2.2. Autocorrelation
2.3. Fast Fourier Transform
2.4. Continuous Wavelet Transform
2.5. Worked Example
3. Previous Studies on Periodicity within Volcanic Plumes
3.1. Studies of Periodicity at Lava Lakes
3.2. Studies of Periodicity at Basaltic Volcanoes
3.3. Studies of Periodicity at Predominantly Non-Basaltic Volcanoes
4. Comparison of Volcanoes and Potential Drivers of Periodicity
4.1. Non-Volcanic Periodicity (C1)
4.2. Periodicities Generated within the Shallow Plumbing System (C2 and C3)
4.3. Periodicity in Magma Storage Region (C4)
4.4. Synthesis
4.5. Future Challenges in Periodicity Analysis
- What are the dominant controls on long-term stability of short-duration periodicity (< an hour)?
- Is there a relationship between total emission fluxes and either the magnitude or timescale of periodicity? If so, how can this help inform our understanding of subsurface processes?
- How do the properties of periodic behaviour change in the time before/after eruptive events, and can these be used to aid in hazard assessment and eruption forecasting?
- Do tidal forces have an effect on volcanoes and, if so, what is the magnitude of oscillation compared to volcanogenic mechanisms? What other external forcings should be considered?
- At multi-vent volcanoes, do the periodic characteristics of outgassing vary between craters? If so, what can this tell us about shallow subsurface plumbing systems?
- Do phase offsets exist between emissions of different gas species, i.e., highlighting a specific source depth for periodicity?
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shaw, H.R.; Wright, T.L.; Peck, D.L.; Okamura, R. The viscosity of basaltic magma; an analysis of field measurements in Makaopuhi lava lake, Hawaii. Am. J. Sci. 1968, 266, 225–264. [Google Scholar] [CrossRef]
- Parfitt, E.A. A discussion of the mechanisms of explosive basaltic eruptions. J. Volcanol. Geotherm. Res. 2004, 134, 77–107. [Google Scholar] [CrossRef]
- Sparks, R.S.J. The dynamics of bubble formation and growth in magmas: A review and analysis. J. Volcanol. Geotherm. Res. 1978, 3, 1–37. [Google Scholar] [CrossRef]
- Namiki, A.; Manga, M. Transition between fragmentation and permeable outgassing of low viscosity magmas. J. Volcanol. Geotherm. Res. 2008, 169, 48–60. [Google Scholar] [CrossRef]
- Cashman, K.V.; Scheu, B. Magmatic Fragmentation. Encycl. Volcanoes 2015, 459–471. [Google Scholar]
- McGonigle, A.J.S.; Pering, T.D.; Wilkes, T.C.; Tamburello, G.; D’Aleo, R.; Bitetto, M.; Aiuppa, A.; Willmott, J.R. Ultraviolet Imaging of Volcanic Plumes: A New Paradigm in Volcanology. Geosciences 2017, 7, 68. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Tsanev, V.I.; Braban, C.F.; Cox, R.A.; Adams, J.W.; Aiuppa, A.; Bobrowski, N.; Delmelle, P.; Barclay, J.; McGonigle, A.J.S.S. BrO formation in volcanic plumes. Geochim. Cosmochim. Acta 2006, 70, 2935–2941. [Google Scholar] [CrossRef]
- Schönhardt, A.; Richter, A.; Theys, N.; Burrows, J.P. Space-based observation of volcanic iodine monoxide. Atmos. Chem. Phys 2017, 17, 4857–4870. [Google Scholar] [CrossRef]
- Gutmann, A.; Bobrowski, N.; Roberts, T.J.; Rüdiger, J.; Hoffmann, T. Advances in Bromine Speciation in Volcanic Plumes. Front. Earth Sci. 2018, 6, 213. [Google Scholar] [CrossRef]
- Mori, T.; Burton, M. The SO2 camera: A simple, fast and cheap method for ground-based imaging of SO2 in volcanic plumes. Geophys. Res. Lett. 2006, 33, L24804. [Google Scholar] [CrossRef]
- Bluth, G.J.S.; Shannon, J.M.; Watson, I.M.; Prata, A.J.; Realmuto, V.J. Development of an ultra-violet digital camera for volcanic SO2 imaging. J. Volcanol. Geotherm. Res. 2007, 161, 47–56. [Google Scholar] [CrossRef]
- McGonigle, A.J.S.; Oppenheimer, C.; Galle, B.; Mather, T.A.; Pyle, D.M. Walking traverse and scanning DOAS measurements of volcanic gas emission rates. Geophys. Res. Lett. 2002, 29, 1–4. [Google Scholar] [CrossRef]
- Galle, B.; Oppenheimer, C.; Geyer, A.; McGonigle, A.J.; Edmonds, M.; Horrocks, L. A miniaturised ultraviolet spectrometer for remote sensing of SO2 fluxes: A new tool for volcano surveillance. J. Volcanol. Geotherm. Res. 2003, 119, 241–254. [Google Scholar] [CrossRef]
- Kantzas, E.P.; McGonigle, A.J.S. Ground Based Ultraviolet Remote Sensing of Volcanic Gas Plumes. Sensors 2008, 8, 1559–1574. [Google Scholar] [CrossRef]
- Tamburello, G.; Aiuppa, A.; McGonigle, A.J.S.; Allard, P.; Cannata, A.; Giudice, G.; Kantzas, E.P.; Pering, T.D. Periodic volcanic degassing behavior: The Mount Etna example. Geophys. Res. Lett. 2013, 40, 4818–4822. [Google Scholar] [CrossRef]
- Pering, T.D.; Tamburello, G.; McGonigle, A.J.S.; Aiuppa, A.; Cannata, A.; Giudice, G.; Patanè, D. High time resolution fluctuations in volcanic carbon dioxide degassing from Mount Etna. J. Volcanol. Geotherm. Res. 2014, 270, 115–121. [Google Scholar] [CrossRef]
- Pering, T.D.; Ilanko, T.; Wilkes, T.C.; England, R.A.; Silcock, S.R.; Stanger, L.R.; Willmott, J.R.; Bryant, R.G.; McGonigle, A.J.S. A Rapidly Convecting Lava Lake at Masaya Volcano, Nicaragua. Front. Earth Sci. 2019, 6, 241. [Google Scholar] [CrossRef]
- Campion, R.; Delgado-Granados, H.; Legrand, D.; Taquet, N.; Boulesteix, T.; Pedraza-Espitía, S.; Lecocq, T. Breathing and Coughing: The Extraordinarily High Degassing of Popocatépetl Volcano Investigated With an SO2 Camera. Front. Earth Sci. 2018, 6, 163. [Google Scholar] [CrossRef]
- Liu, E.J.; Wood, K.; Mason, E.; Edmonds, M.; Aiuppa, A.; Giudice, G.; Bitetto, M.; Francofonte, V.; Burrow, S.; Richardson, T.; et al. Dynamics of Outgassing and Plume Transport Revealed by Proximal Unmanned Aerial System (UAS) Measurements at Volcán Villarrica, Chile. Geochem. Geophys. Geosystems 2019, 20, 730–750. [Google Scholar] [CrossRef]
- Connor, C.B.; Stoiber, R.E.; Malinconico, L.L. Variation in sulfur dioxide emissions related to earth tides, Halemaumau Crater, Kilauea Volcano, Hawaii. J. Geophys. Res. Solid Earth 1988, 93, 14867–14871. [Google Scholar] [CrossRef]
- Nicholson, E.J.; Mather, T.A.; Pyle, D.M.; Odbert, H.M.; Christopher, T. Cyclical patterns in volcanic degassing revealed by SO2 flux timeseries analysis: An application to Soufrière Hills Volcano, Montserrat. Earth Planet. Sci. Lett. 2013, 375, 209–221. [Google Scholar] [CrossRef]
- Rymer, H.; Locke, C.A.; Brenes, J.; Williams-Jones, G. Magma plumbing processes for persistent activity at Poás volcano, Costa Rica. Geophys. Res. Lett. 2005, 32, L08307. [Google Scholar] [CrossRef]
- Christopher, T.; Edmonds, M.; Taisne, B.; Odbert, H.; Costa, A.; Hards, V.; Wadge, G. Periodic sulphur dioxide degassing from the Soufrière Hills Volcano related to deep magma supply. Geol. Soc. Lond. Spec. Publ. 2015, 410, 123–141. [Google Scholar] [CrossRef]
- Ilanko, T.; Oppenheimer, C.; Burgisser, A.; Kyle, P. Cyclic degassing of Erebus volcano, Antarctica. Bull. Volcanol. 2015, 77, 56. [Google Scholar] [CrossRef]
- Allard, P.; Burton, M.; Sawyer, G.; Bani, P. Degassing dynamics of basaltic lava lake at a top-ranking volatile emitter: Ambrym volcano, Vanuatu arc. Earth Planet. Sci. Lett. 2016, 448, 69–80. [Google Scholar] [CrossRef]
- Moussallam, Y.; Tamburello, G.; Peters, N.; Apaza, F.; Schipper, C.I.; Curtis, A.; Aiuppa, A.; Masias, P.; Boichu, M.; Bauduin, S.; et al. Volcanic gas emissions and degassing dynamics at Ubinas and Sabancaya volcanoes; implications for the volatile budget of the central volcanic zone. J. Volcanol. Geotherm. Res. 2017, 343, 181–191. [Google Scholar] [CrossRef]
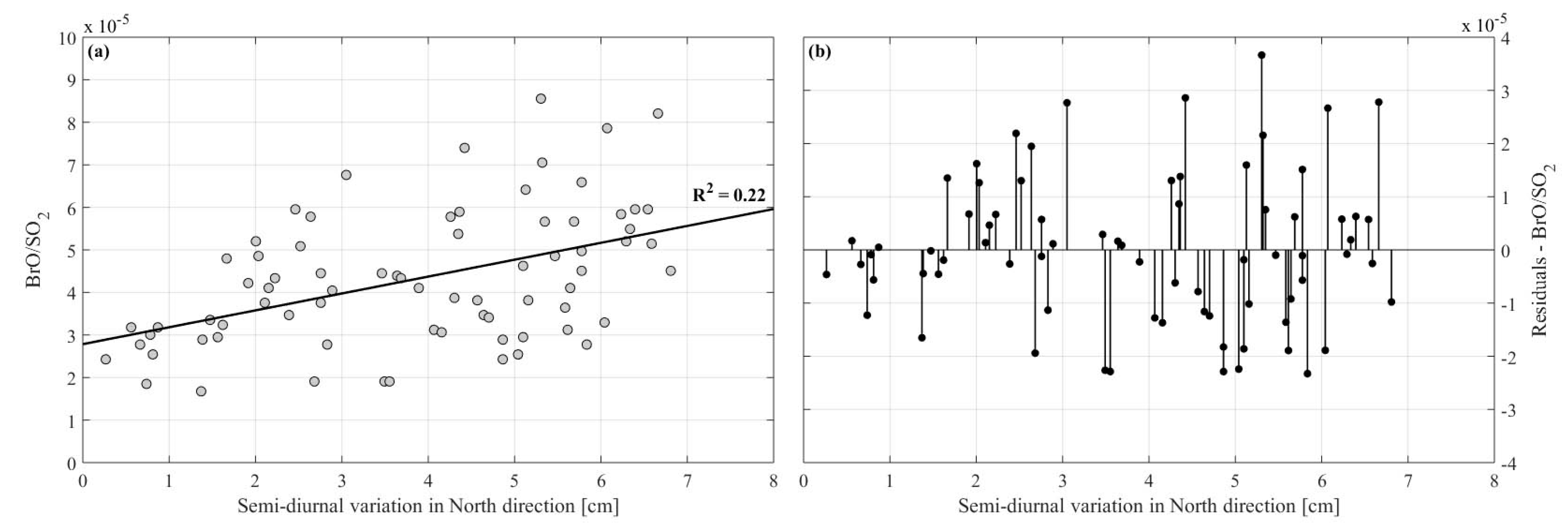
- Dinger, F.; Bobrowski, N.; Warnach, S.; Bredemeyer, S.; Hidalgo, S.; Arellano, S.; Galle, B.; Platt, U.; Wagner, T. Periodicity in the BrO/SO2 molar ratios in the volcanic gas plume of Cotopaxi and its correlation with the Earth tides during the eruption in 2015. Solid Earth 2018, 9, 247–266. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Francis, P.; Burton, M.; Maciejewski, A.J.H.; Boardman, L. Remote measurement of volcanic gases by Fourier transform infrared spectroscopy. Appl. Phys. B Lasers Opt. 1998, 67, 505–515. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Bani, P.; Calkins, J.A.; Burton, M.R.; Sawyer, G.M. Rapid FTIR sensing of volcanic gases released by Strombolian explosions at Yasur volcano, Vanuatu. Appl. Phys. B 2006, 85, 453–460. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Kyle, P.R. Probing the magma plumbing of Erebus volcano, Antarctica, by open-path FTIR spectroscopy of gas emissions. J. Volcanol. Geotherm. Res. 2008, 177, 743–754. [Google Scholar] [CrossRef]
- Burton, M.; Allard, P.; Mure, F.; La Spina, A. Magmatic Gas Composition Reveals the Source Depth of Slug-Driven Strombolian Explosive Activity. Science 2007, 317, 227–230. [Google Scholar] [CrossRef]
- La Spina, A.; Burton, M.; Allard, P.; Alparone, S.; Muré, F. Open-path FTIR spectroscopy of magma degassing processes during eight lava fountains on Mount Etna. Earth Planet. Sci. Lett. 2015, 413, 123–134. [Google Scholar] [CrossRef]
- Aiuppa, A.; Moretti, R.; Federico, C.; Giudice, G.; Gurrieri, S.; Liuzzo, M.; Papale, P.; Shinohara, H.; Valenza, M. Forecasting Etna eruptions by real-time observation of volcanic gas composition. Geology 2007, 35, 1115. [Google Scholar] [CrossRef]
- Aiuppa, A.; Federico, C.; Giudice, G.; Giuffrida, G.; Guida, R.; Gurrieri, S.; Liuzzo, M.; Moretti, R.; Papale, P. The 2007 eruption of Stromboli volcano: Insights from real-time measurement of the volcanic gas plume CO2/SO2 ratio. J. Volcanol. Geotherm. Res. 2009, 182, 221–230. [Google Scholar] [CrossRef]
- Aiuppa, A.; de Moor, J.M.; Arellano, S.; Coppola, D.; Francofonte, V.; Galle, B.; Giudice, G.; Liuzzo, M.; Mendoza, E.; Saballos, A.; et al. Tracking Formation of a Lava Lake From Ground and Space: Masaya Volcano (Nicaragua), 2014–2017. Geochem. Geophys. Geosystems 2018, 19, 496–515. [Google Scholar] [CrossRef]
- Edmonds, M. New geochemical insights into volcanic degassing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 4559–4579. [Google Scholar] [CrossRef]
- Burgisser, A.; Scaillet, B. Redox evolution of a degassing magma rising to the surface. Nature 2007, 445, 194–197. [Google Scholar] [CrossRef]
- Cochran, W.T.; Cooley, J.W.; Favin, D.L.; Helms, H.D.; Kaenel, R.A.; Lang, W.W.; Maling, G.C.; Nelson, D.E.; Rader, C.M.; Welch, P.D. What is the fast Fourier transform? Proc. IEEE 1967, 55, 1664–1674. [Google Scholar] [CrossRef]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Cooley, J.W.; Lewis, P.A.W.; Welch, P.D. The Fast Fourier Transform and Its Applications. IEEE Trans. Educ. 1969, 12, 27–34. [Google Scholar] [CrossRef]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Thomson, D.J. Spectrum estimation and harmonic analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W.; Buck, J.R. Discrete-Time Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1999; ISBN 0137549202. [Google Scholar]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory—Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Colestock, M.A. Wavelets-a new tool for signal processing analysts. In Proceedings of the [1993 Proceedings] AIAA/IEEE Digital Avionics Systems Conference, Fort Worth, TX, USA, 25–28 October 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 54–59. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Pering, T.D.; Tamburello, G.; McGonigle, A.J.S.; Hanna, E.; Aiuppa, A. Correlation of oscillatory behaviour in Matlab using wavelets. Comput. Geosci. 2014, 70, 206–212. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: New York, NY, USA, 2000; ISBN 9780521685085. [Google Scholar]
- Odbert, H.M.; Stewart, R.C.; Wadge, G. Chapter 2 Cyclic phenomena at the Soufrière Hills Volcano, Montserrat. Geol. Soc. Lond. Mem. 2014, 39, 41–60. [Google Scholar] [CrossRef]
- Nyquist, H. Certain Topics in Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Moussallam, Y.; Bani, P.; Curtis, A.; Barnie, T.; Moussallam, M.; Peters, N.; Schipper, C.I.; Aiuppa, A.; Giudice, G.; Amigo, Á.; et al. Sustaining persistent lava lakes: Observations from high-resolution gas measurements at Villarrica volcano, Chile. Earth Planet. Sci. Lett. 2016, 454, 237–247. [Google Scholar] [CrossRef]
- Pearson, K. On Further Methods of Determining Correlation (eBook, 1907) [WorldCat.org]; Cambridge University Press: London, UK, 1907. [Google Scholar]
- Odbert, H.M.; Wadge, G. Time series analysis of lava flux. J. Volcanol. Geotherm. Res. 2009, 188, 305–314. [Google Scholar] [CrossRef]
- Girona, T.; Costa, F.; Taisne, B.; Aggangan, B.; Ildefonso, S. Fractal degassing from Erebus and Mayon volcanoes revealed by a new method to monitor H2O emission cycles. J. Geophys. Res. Solid Earth 2015, 120, 2988–3002. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 1992; ISBN 0521431085. [Google Scholar]
- Schuster, A. The Periodogram and Its Optical Analogy. Proc. R. Soc. A Math. Phys. Eng. Sci. 1906, 77, 136–140. [Google Scholar]
- Alter, D. A Simple Form of Periodogram. Ann. Math. Stat. 1937, 8, 121–126. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Spectral analysis for Physical Applications: Multitaper and Conventional Univariate Techniques; Cambridge University Press: New York, NY, USA, 1993; ISBN 9780521435413. [Google Scholar]
- Bartlett, M.S. Smoothing Periodograms from Time-Series with Continuous Spectra. Nature 1948, 161, 686–687. [Google Scholar] [CrossRef]
- Park, J.; Lindberg, C.R.; Vernon, F.L., III. Multitaper Spectral Analysis of High-Frequency Seismogams. J. Geophys. Res. 1987, 92, 12675–12684. [Google Scholar] [CrossRef]
- Bredemeyer, S.; Hansteen, T.H. Synchronous degassing patterns of the neighbouring volcanoes Llaima and Villarrica in south-central Chile: the influence of tidal forces. Int. J. Earth Sci. 2014, 103, 1999–2012. [Google Scholar] [CrossRef]
- Flower, V.J.B.; Carn, S.A. Characterising volcanic cycles at Soufriere Hills Volcano, Montserrat: Time series analysis of multi-parameter satellite data. J. Volcanol. Geotherm. Res. 2015, 304, 82–93. [Google Scholar] [CrossRef][Green Version]
- Sweeney, D.; Kyle, P.R.; Oppenheimer, C. Sulfur dioxide emissions and degassing behavior of Erebus volcano, Antarctica. J. Volcanol. Geotherm. Res. 2008, 177, 725–733. [Google Scholar] [CrossRef]
- Philander, S.G. El Niño, La Niña, and the Southern Oscillation; Academic Press: Cambridge, MA, USA, 1990; ISBN 9780080570983. [Google Scholar]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Lockwood, M. Solar Influence on Global and Regional Climates. Surv. Geophys. 2012, 33, 503–534. [Google Scholar] [CrossRef]
- Sheppard, L.W.; Bell, J.R.; Harrington, R.; Reuman, D.C. Changes in large-scale climate alter spatial synchrony of aphid pests. Nat. Clim. Chang. 2016, 6, 610–613. [Google Scholar] [CrossRef]
- Cannata, A.; Montalto, P.; Patanè, D. Joint analysis of infrasound and seismic signals by cross wavelet transform: detection of Mt. Etna explosive activity. Nat. Hazards Earth Syst. Sci. 2013, 13, 1669–1677. [Google Scholar] [CrossRef][Green Version]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Rohatgi, A. Web Plot Digitizer. Available online: https://automeris.io/WebPlotDigitizer/citation.html. (accessed on 1 March 2019).
- GVP. Global Volcanism Program. Available online: https://volcano.si.edu/ (accessed on Jul 17 2019).
- Boichu, M.; Oppenheimer, C.; Tsanev, V.; Kyle, P.R. High temporal resolution SO2 flux measurements at Erebus volcano, Antarctica. J. Volcanol. Geotherm. Res. 2010, 190, 325–336. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Lomakina, A.S.; Kyle, P.R.; Kingsbury, N.G.; Boichu, M. Pulsatory magma supply to a phonolite lava lake. Earth Planet. Sci. Lett. 2009, 284, 392–398. [Google Scholar] [CrossRef]
- Bouche, E.; Vergniolle, S.; Staudacher, T.; Nercessian, A.; Delmont, J.; Frogneux, M. The role of large bubbles detected from acoustic measurements on the dynamics of Erta ’ Ale lava lake ( Ethiopia). Earth Planet. Sci. Lett. 2010, 295, 37–48. [Google Scholar] [CrossRef]
- Pering, T.D.; McGonigle, A.J.S.; Tamburello, G.; Aiuppa, A.; Bitetto, M.; Rubino, C.; Wilkes, T.C. A Novel and Inexpensive Method for Measuring Volcanic Plume Water Fluxes at High Temporal Resolution. Remote Sens. 2017, 9, 146. [Google Scholar] [CrossRef]
- Nadeau, P.A.; Palma, J.L.; Waite, G.P. Linking volcanic tremor, degassing, and eruption dynamics via SO2 imaging. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Aiuppa, A.; Giudice, G.; Liuzzo, M.; Tamburello, G.; Allard, P.; Calabrese, S.; Chaplygin, I.; McGonigle, A.J.S.; Taran, Y. First volatile inventory for Gorely volcano, Kamchatka. Geophys. Res. Lett. 2012, 39, 1–5. [Google Scholar] [CrossRef]
- Johnson, J.B.; Harris, A.J.L.; Hoblitt, R.P. Thermal observations of gas pistoning at Kilauea Volcano. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Orr, T.R.; Rea, J.C. Time-lapse camera observations of gas piston activity at Pu‘u ‘Ō‘ō, Kīlauea volcano, Hawai‘i. Bull. Volcanol. 2012, 74, 2353–2362. [Google Scholar] [CrossRef]
- Nadeau, P.A.; Werner, C.A.; Waite, G.P.; Carn, S.A.; Brewer, I.D.; Elias, T.; Sutton, A.J.; Kern, C. Using SO2 camera imagery and seismicity to examine degassing and gas accumulation at Kīlauea Volcano, May 2010. J. Volcanol. Geotherm. Res. 2015, 300, 70–80. [Google Scholar] [CrossRef]
- Patrick, M.R.; Orr, T.; Sutton, A.J.; Lev, E.; Thelen, W.; Fee, D. Shallowly driven fluctuations in lava lake outgassing (gas pistoning), Kīlauea Volcano. Earth Planet. Sci. Lett. 2016, 433, 326–338. [Google Scholar] [CrossRef]
- Battaglia, A.; Bitetto, M.; Aiuppa, A.; Rizzo, A.L.; Chigna, G.; Watson, I.M.; D’Aleo, R.; Juárez Cacao, F.J.; de Moor, M.J. The Magmatic Gas Signature of Pacaya Volcano, With Implications for the Volcanic CO2 Flux From Guatemala. Geochem. Geophys. Geosystems 2018, 19, 667–692. [Google Scholar] [CrossRef]
- Ripepe, M.; Harris, A.J.L.; Carniel, R. Thermal, seismic and infrasonic evidences of variable degassing rates at Stromboli volcano. J. Volcanol. Geotherm. Res. 2002, 118, 285–297. [Google Scholar] [CrossRef]
- Spampinato, L.; Oppenheimer, C.; Cannata, A.; Montalto, P.; Salerno, G.G.; Calvari, S. On the time-scale of thermal cycles associated with open-vent degassing. Bull. Volcanol. 2012, 74, 1281–1292. [Google Scholar] [CrossRef]
- Campion, R.; Martinez-Cruz, M.; Lecocq, T.; Caudron, C.; Pacheco, J.; Pinardi, G.; Hermans, C.; Carn, S.; Bernard, A. Space and ground-based measurements of sulphur dioxide emissions from Turrialba Volcano (Costa Rica). Bull. Volcanol. 2012, 74, 1757–1770. [Google Scholar] [CrossRef]
- Conde, V.; Bredemeyer, S.; Duarte, E.; Pacheco, J.F.; Miranda, S.; Galle, B.; Hansteen, T.H. SO2 degassing from Turrialba Volcano linked to seismic signatures during the period 2008–2012. Int. J. Earth Sci. 2014, 103, 1983–1998. [Google Scholar] [CrossRef]
- Bani, P.; Lardy, M. Sulphur dioxide emission rates from Yasur volcano, Vanuatu archipelago. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Kremers, S.; Wassermann, J.; Meier, K.; Pelties, C.; van Driel, M.; Vasseur, J.; Hort, M. Inverting the source mechanism of Strombolian explosions at Mt. Yasur, Vanuatu, using a multi-parameter dataset. J. Volcanol. Geotherm. Res. 2013, 262, 104–122. [Google Scholar] [CrossRef]
- Lev, E.; Ruprecht, P.; Oppenheimer, C.; Peters, N.; Patrick, M.; Hernández, P.A.; Spampinato, L.; Marlow, J. A global synthesis of lava lake dynamics. J. Volcanol. Geotherm. Res. 2019, 381, 16–31. [Google Scholar] [CrossRef]
- Gray, D.M.; Burton-Johnson, A.; Fretwell, P.T. Evidence for a lava lake on Mt. Michael volcano, Saunders Island (South Sandwich Islands) from Landsat, Sentinel-2 and ASTER satellite imagery. J. Volcanol. Geotherm. Res. 2019, 379, 60–71. [Google Scholar] [CrossRef]
- Peters, N.; Oppenheimer, C.; Kyle, P.; Kingsbury, N. Decadal persistence of cycles in lava lake motion at Erebus volcano, Antarctica. Earth Planet. Sci. Lett. 2014, 395, 1–12. [Google Scholar] [CrossRef]
- Le Losq, C.; Neuville, D.R.; Moretti, R.; Kyle, P.R.; Oppenheimer, C. Rheology of phonolitic magmas-the case of the Erebus lava lake. Earth Planet. Sci. Lett. 2015, 411, 53–61. [Google Scholar] [CrossRef]
- Moussallam, Y.; Oppenheimer, C.; Scaillet, B.; Gaillard, F.; Kyle, P.; Peters, N.; Hartley, M.; Berlo, K.; Donovan, A. Tracking the changing oxidation state of Erebus magmas, from mantle to surface, driven by magma ascent and degassing. Earth Planet. Sci. Lett. 2014, 393, 200–209. [Google Scholar] [CrossRef]
- Jones, L.K.; Kyle, P.R.; Oppenheimer, C.; Frechette, J.D.; Okal, M.H. Terrestrial laser scanning observations of geomorphic changes and varying lava lake levels at Erebus volcano, Antarctica. J. Volcanol. Geotherm. Res. 2015, 295, 43–54. [Google Scholar] [CrossRef]
- Sigurdsson, H.; Houghton, B.F. Encyclopedia of Volcanoes; Elsevier: Oxford, UK, 2015; ISBN 9780123859389. [Google Scholar]
- Galle, B.; Johansson, M.; Rivera, C.; Zhang, Y.; Kihlman, M.; Kern, C.; Lehmann, T.; Platt, U.; Arellano, S.; Hidalgo, S. Network for Observation of Volcanic and Atmospheric Change (NOVAC)—A global network for volcanic gas monitoring: Network layout and instrument description. J. Geophys. Res. 2010, 115, D05304. [Google Scholar] [CrossRef]
- Agnew, D.C. Treatise on Geophysics and Geodesy; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Wilkes, T.C.; Pering, T.D.; McGonigle, A.J.S.; Willmott, J.R.; Bryant, R.; Smalley, A.L.; Mims, F.M.; Parisi, A.V.; England, R.A. The PiSpec: A Low-Cost, 3D-Printed Spectrometer for Measuring Volcanic SO2 Emission Rates. Front. Earth Sci. 2019, 7, 65. [Google Scholar] [CrossRef]
- Gerlach, T.M. Exsolution of H2O, CO2, and S during eruptive episodes at Kilauea Volcano, Hawaii. J. Geophys. Res. Solid Earth 1986, 91, 12177–12185. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Fischer, T.P.; Scaillet, B. Volcanic Degassing: Process and Impact. In Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2014; pp. 111–179. [Google Scholar]
- Manga, M. Waves of bubbles in basaltic magmas and lavas. J. Geophys. Res. 1996, 101, 17457. [Google Scholar] [CrossRef]
- Gaudin, D.; Taddeucci, J.; Scarlato, P.; Harris, A.; Bombrun, M.; Del Bello, E.; Ricci, T. Characteristics of puffing activity revealed by ground-based, thermal infrared imaging: the example of Stromboli Volcano (Italy). Bull. Volcanol. 2017, 79, 24. [Google Scholar] [CrossRef]
- Gaudin, D.; Taddeucci, J.; Scarlato, P.; del Bello, E.; Ricci, T.; Orr, T.; Houghton, B.; Harris, A.; Rao, S.; Bucci, A. Integrating puffing and explosions in a general scheme for Strombolian-style activity. J. Geophys. Res. Solid Earth 2017, 122, 1860–1875. [Google Scholar] [CrossRef]
- Pering, T.D.; McGonigle, A.J.S. Combining Spherical-Cap and Taylor Bubble Fluid Dynamics with Plume Measurements to Characterize Basaltic Degassing. Geosciences 2018, 8, 42. [Google Scholar] [CrossRef]
- Pering, T.D.; McGonigle, A.J.S.; James, M.R.; Capponi, A.; Lane, S.J.; Tamburello, G.; Aiuppa, A. The dynamics of slug trains in volcanic conduits: Evidence for expansion driven slug coalescence. J. Volcanol. Geotherm. Res. 2017, 348, 26–35. [Google Scholar] [CrossRef]
- Christopher, T.; Edmonds, M.; Humphreys, M.C.S.; Herd, R.A. Volcanic gas emissions from Soufrière Hills Volcano, Montserrat 1995–2009, with implications for mafic magma supply and degassing. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Costa, A.; Melnik, O.; Sparks, R.S.J. Controls of conduit geometry and wallrock elasticity on lava dome eruptions. Earth Planet. Sci. Lett. 2007, 260, 137–151. [Google Scholar] [CrossRef]
- Christopher, T.E.; Blundy, J.; Cashman, K.; Cole, P.; Edmonds, M.; Smith, P.J.; Sparks, R.S.J.; Stinton, A. Crustal-scale degassing due to magma system destabilization and magma-gas decoupling at Soufrière Hills Volcano, Montserrat. Geochem. Geophys. Geosystems 2015, 16, 2797–2811. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Pardyjak, E.R. Field Studies Delve Into the Intricacies of Mountain Weather. Eos, Trans. Am. Geophys. Union 2013, 94, 313–315. [Google Scholar] [CrossRef]
- Dinger, F.; Bredemeyer, S.; Arellano, S.; Bobrowski, N.; Platt, U.; Wagner, T. On the link between Earth tides and volcanic degassing. Solid Earth 2019, 10, 725–740. [Google Scholar] [CrossRef]
- Manga, M.; Castro, J.; Cashman, K.V.; Loewenberg, M. Rheology of bubble-bearing magmas. J. Volcanol. Geotherm. Res. 1998, 87, 15–28. [Google Scholar] [CrossRef]
- Seyfried, R.; Freundt, A. Experiments on conduit flow and eruption behavior of basaltic volcanic eruptions. J. Geophys. Res. 2000, 105, 23727. [Google Scholar] [CrossRef]
- Gonnermann, H.M.; Manga, M. The Fluid Mechanics Inside a Volcano. Annu. Rev. Fluid Mech. 2007, 39, 321–356. [Google Scholar] [CrossRef]
- Valade, S.; Ripepe, M.; Giuffrida, G.; Karume, K.; Tedesco, D. Dynamics of Mount Nyiragongo lava lake inferred from thermal imaging and infrasound array. Earth Planet. Sci. Lett. 2018, 500, 192–204. [Google Scholar] [CrossRef]
- Divoux, T.; Vidal, V.; Ripepe, M.; Géminard, J.-C. Influence of non-Newtonian rheology on magma degassing. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef][Green Version]
- Belien, I.B.; Cashman, K.V.; Rempel, A.W. Gas accumulation in particle-rich suspensions and implications for bubble populations in crystal-rich magma. Earth Planet. Sci. Lett. 2010, 297, 133–140. [Google Scholar] [CrossRef]
- Rust, A.C.; Cashman, K.V. Permeability controls on expansion and size distributions of pyroclasts. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- Bachmann, O.; Bergantz, G.W. Gas percolation in upper-crustal silicic crystal mushes as a mechanism for upward heat advection and rejuvenation of near-solidus magma bodies. J. Volcanol. Geotherm. Res. 2006, 149, 85–102. [Google Scholar] [CrossRef]
- Berberich, G.M.; Berberich, M.B.; Ellison, A.M.; Wöhler, C. First Identification of Periodic Degassing Rhythms in Three Mineral Springs of the East Eifel Volcanic Field (EEVF, Germany). Geosciences 2019, 9, 189. [Google Scholar] [CrossRef]
- Giammanco, S.; Bonfanti, P. Cluster analysis of soil CO2 data from Mt. Etna (Italy) reveals volcanic influences on temporal and spatial patterns of degassing. Bull. Volcanol. 2009, 71, 201–218. [Google Scholar] [CrossRef]
- Granieri, D.; Chiodini, G.; Marzocchi, W.; Avino, R. Continuous monitoring of CO2 soil diffuse degassing at Phlegraean Fields (Italy): influence of environmental and volcanic parameters. Earth Planet. Sci. Lett. 2003, 212, 167–179. [Google Scholar] [CrossRef]
- Viveiros, F.; Vandemeulebrouck, J.; Rinaldi, A.P.; Ferreira, T.; Silva, C.; Cruz, J.V. Periodic behavior of soil CO2 emissions in diffuse degassing areas of the Azores archipelago: Application to seismovolcanic monitoring. J. Geophys. Res. Solid Earth 2014, 119, 7578–7597. [Google Scholar] [CrossRef]
- Oliveira, S.; Viveiros, F.; Silva, C.; Pacheco, J.E. Automatic Filtering of Soil CO2 Flux Data; Different Statistical Approaches Applied to Long Time Series. Front. Earth Sci. 2018, 6, 208. [Google Scholar] [CrossRef]
- Delle Donne, D.; Ripepe, M.; Lacanna, G.; Tamburello, G.; Bitetto, M.; Aiuppa, A. Gas mass derived by infrasound and UV cameras: Implications for mass flow rate. J. Volcanol. Geotherm. Res. 2016, 325, 169–178. [Google Scholar] [CrossRef]
- D’Aleo, R.; Bitetto, M.; Delle Donne, D.; Tamburello, G.; Battaglia, A.; Coltelli, M.; Patanè, D.; Prestifilippo, M.; Sciotto, M.; Aiuppa, A. Spatially resolved SO2 flux emissions from Mt Etna. Geophys. Res. Lett. 2016, 43, 7511–7519. [Google Scholar] [CrossRef]
- Kantzas, E.P.; McGonigle, A.J.S.; Tamburello, G.; Aiuppa, A.; Bryant, R.G. Protocols for UV camera volcanic SO2 measurements. J. Volcanol. Geotherm. Res. 2010, 194, 55–60. [Google Scholar] [CrossRef]
- Aiuppa, A.; Fischer, T.P.; Plank, T.; Bani, P. CO2 flux emissions from the Earth’s most actively degassing volcanoes, 2005–2015. Sci. Rep. 2019, 9, 5442. [Google Scholar] [CrossRef]
- Queißer, M.; Burton, M.; Theys, N.; Pardini, F.; Salerno, G.; Caltabiano, T.; Varnam, M.; Esse, B.; Kazahaya, R. TROPOMI enables high resolution SO2 flux observations from Mt. Etna, Italy, and beyond. Sci. Rep. 2019, 9, 957. [Google Scholar] [CrossRef]


| Technique | Ideal Use |
|---|---|
| Autocorrelation | Stationary periodicity, one clear and dominant period |
| Welch’s (FFT) | Non-stationary periodicity, but approx. stationary within window, requires prior knowledge of target periodicity timescale |
| Thomson’s Multitaper (FFT) | Stationarity required within an individual analysis window; but, can visualise non-stationary periodicity when employed in the form of the short-term Fourier transform (STFT) moving window method. Requires no prior knowledge of target periodicity timescale |
| Lomb-Scargle (FFT) | Non-stationary periodicity, for datasets with missing data points |
| Continuous Wavelet Transform | Non-stationary, good for visualizing temporal stability and strength of multiple concurrent periodicities. Requires no prior knowledge on the signal generating process. |
| Volcano | Magma Type | Period (units) | Notes | Key References |
|---|---|---|---|---|
| Ambrym | Basalt | 100–200, 480 s | Ratio data | [25] |
| Cotopaxi | Andesite/Basaltic-Andesite | 13.7 d | Ratio data | [27] |
| Erebus | Phonolite | 100–600 s 600 s 10–360 min | Fluxes and Ratio data | [24,56,67,76,77] |
| Erta Ale | Basalt | 1 h | Bubble volume | [78] |
| Etna | Basalt | 40–340 500–1200 s | SO2 flux and ratio data | [15,16,79] |
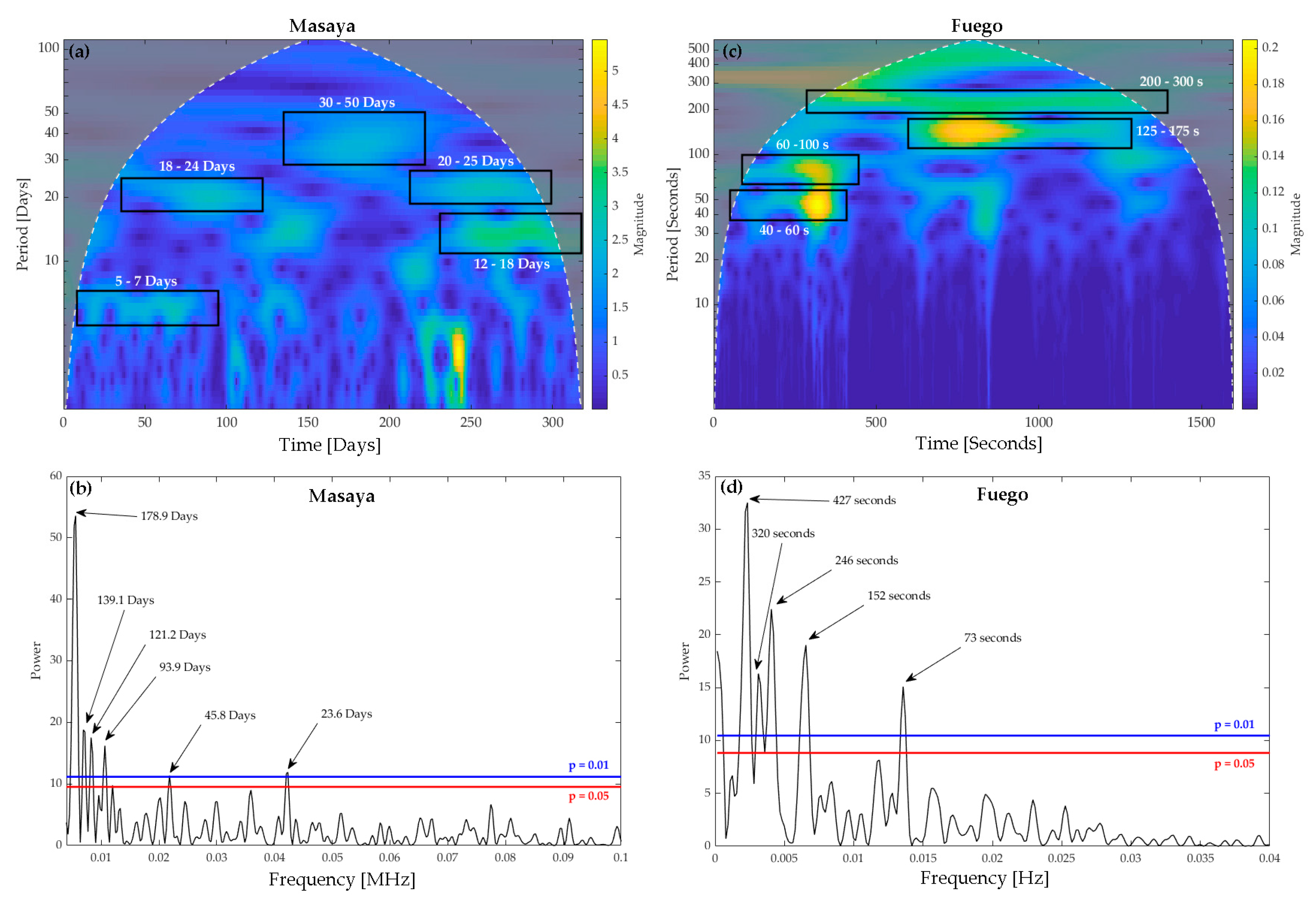
| Fuego | Basalt | 70–430 s | SO2 flux | [80], This Study |
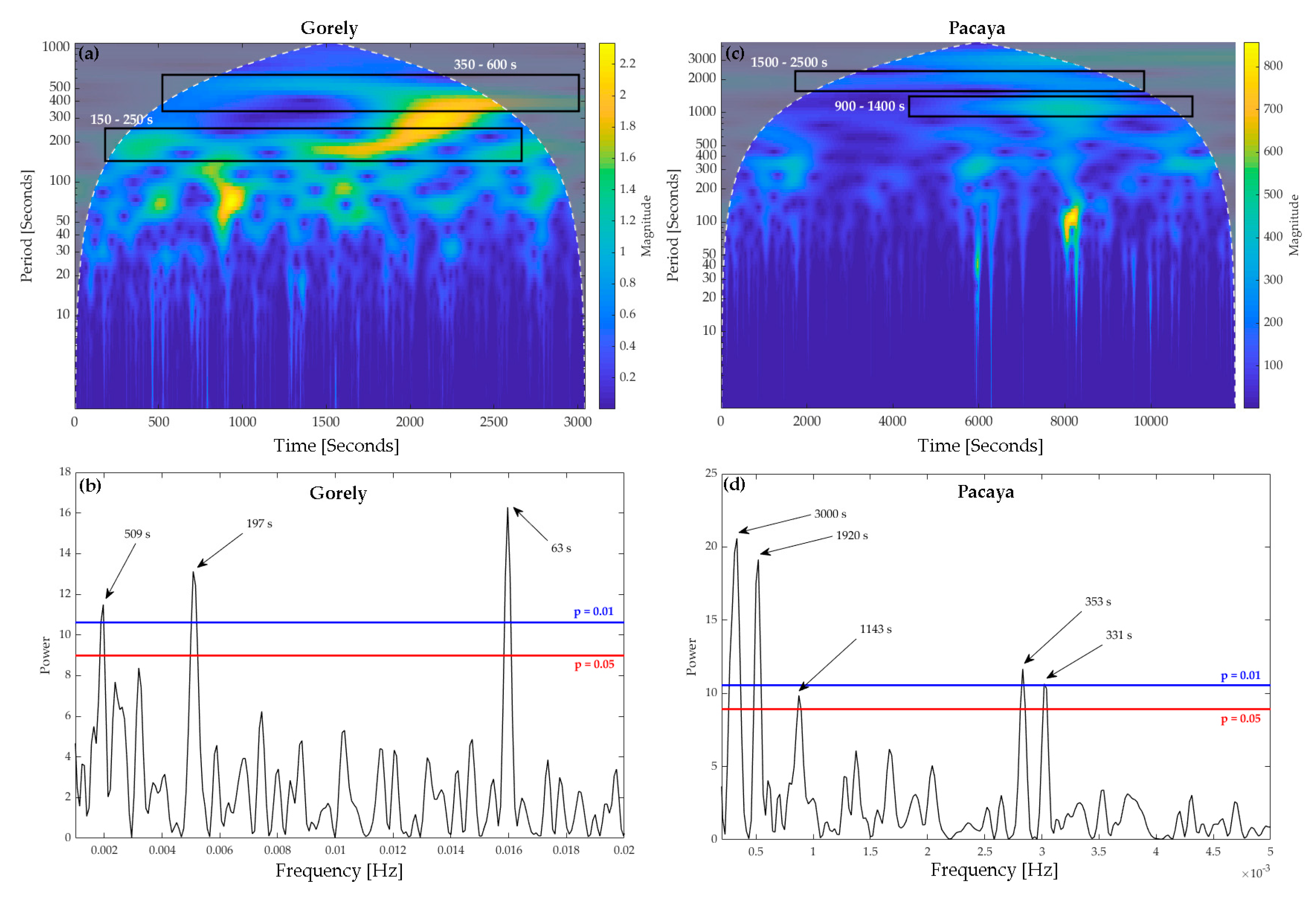
| Gorely | Basalt | 60–510 s | SO2 flux | [81], This Study |
| Kīlauea | Basalt | 1–3600 s 1.6–7.8 h 4 m–15.8 h | Gas Pistoning; different ranges represent different time periods. | [82,83,84,85] |
| Llaima | Basalt | 14 d | SO2 flux | [65] |
| Masaya | Basalt | 200–300 s 50–180 d | SO2 flux | [17], This Study |
| Mayon | Andesite/Basaltic-Andesite | 100–500 s 600–900 s 1200–1600 s 2000 s | H2O flux | [56] |
| Soufrière Hills | Andesite/Basaltic-Andesite | 30–50 d 100–340 d | SO2 flux | [21,66] |
| Pacaya | Basalt | 330–3000 s | SO2 flux | [86], This Study |
| Popocatépetl | Andesite/Basaltic-Andesite | 250, 330 s | SO2 flux | [18] |
| Sabancaya | Andesite/Basaltic-Andesite/Dacite | 240 s 120, 420 s | CO2/SO2 RatioSO2 flux | [26] |
| Stromboli | Basalt | ~1–5 s 5–40 m | Strombolian activity | [87,88] |
| Turrialba | Andesite/Basaltic-Andesite | 100 s 10–14 d | SO2 Flux | [89,90] |
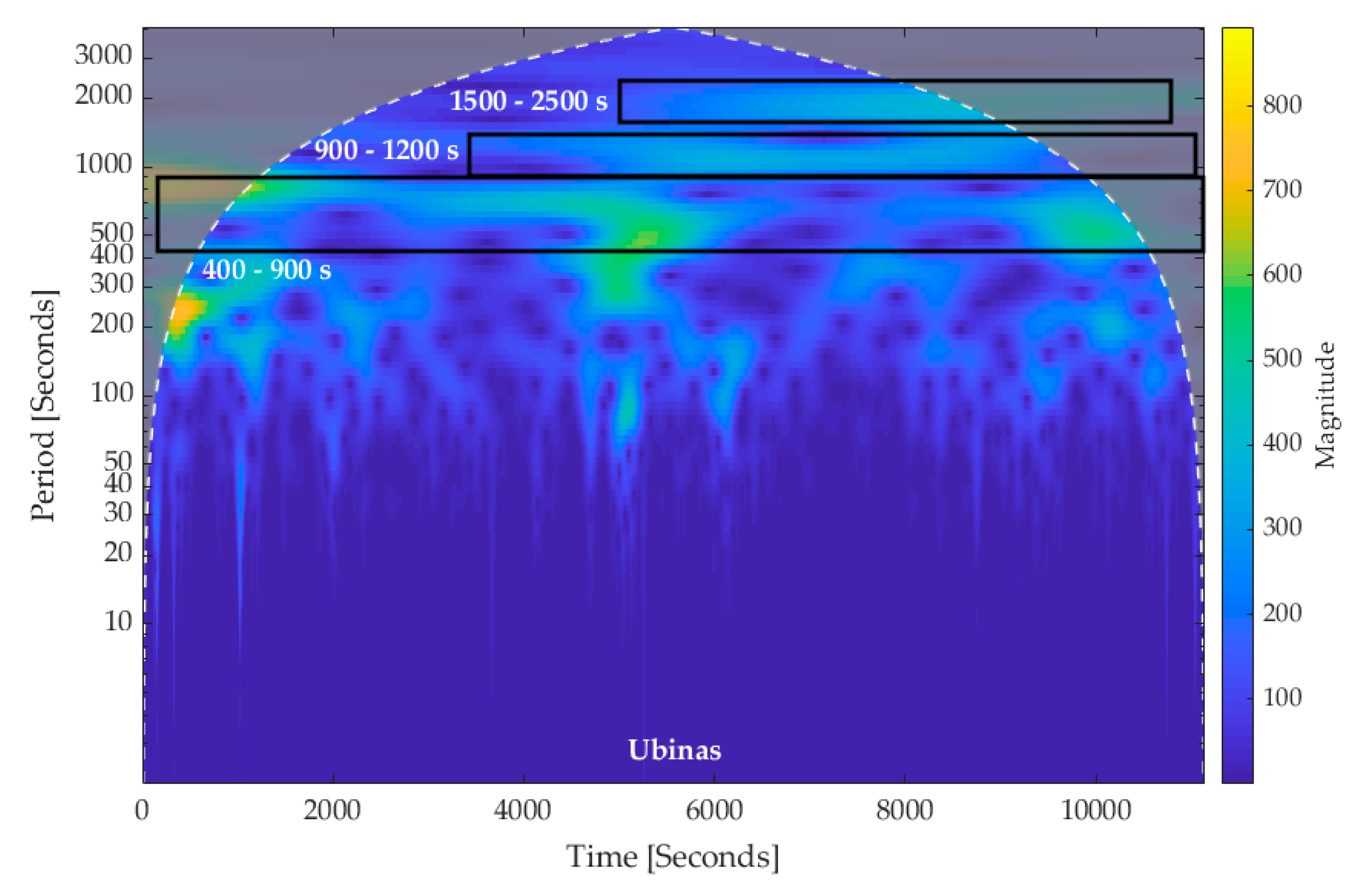
| Ubinas | Andesite/Basaltic-Andesite | 400–900 s 900–1200 s 1500–2500 s | SO2 Flux | [26], This Study |
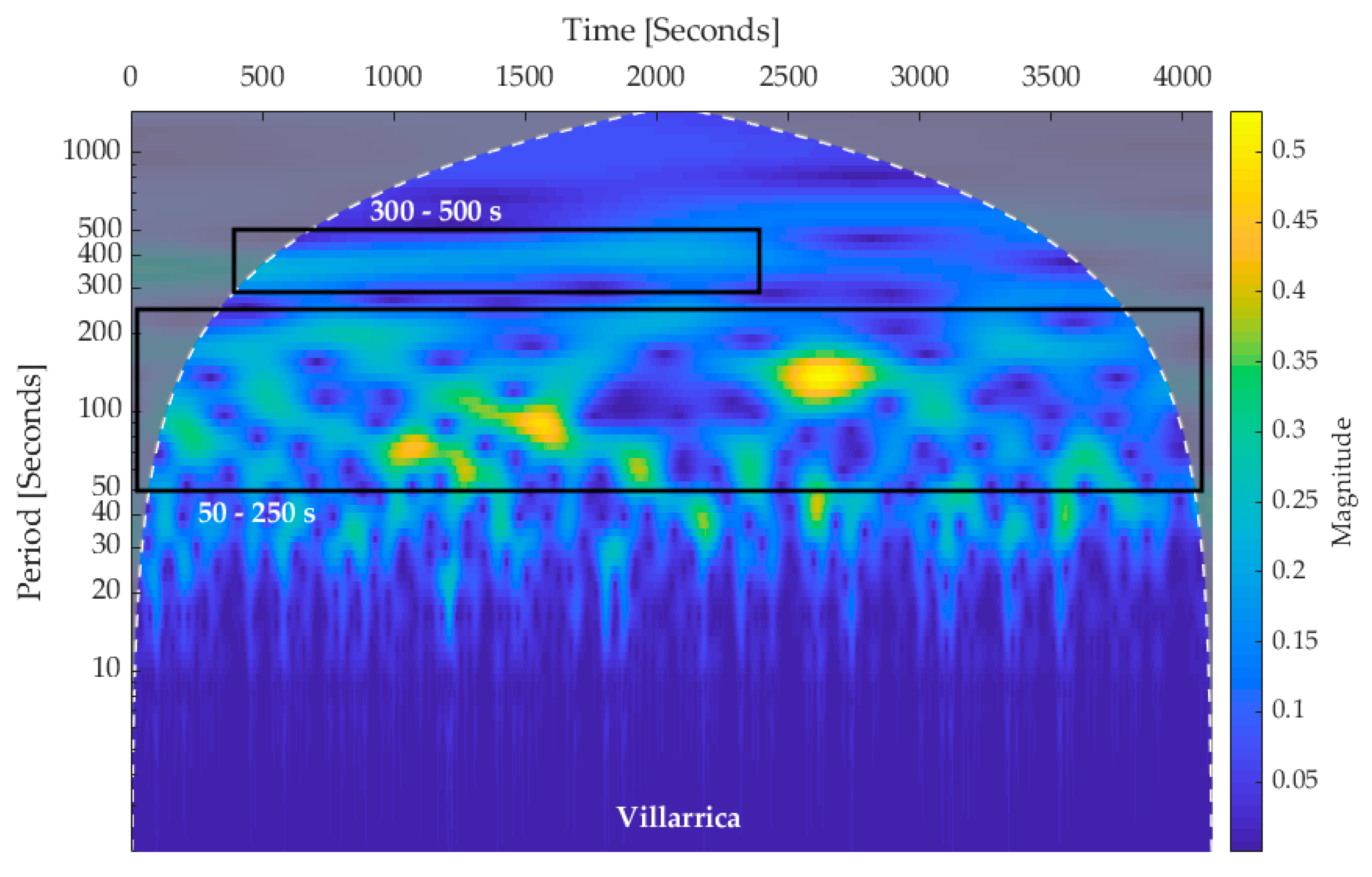
| Villarrica | Basalt | None 30–50 s 340–710 s 14 d | SO2 flux SO2 concentration | [19,53,65] |
| Yasur | Basalt | ~10 s–10 m | Strombolian activity | [29,91,92] |
| Category | Description | Dominant Range |
|---|---|---|
| C1 | Non-volcanic, atmospheric- or tidal- generated | Variable |
| C2 | Gas-driven, shallow process | Seconds to Hours |
| C3 | Shallow magma movement, in-conduit or shallow storage | Minutes to Days |
| C4 | Deep magmatic processes | Days to Months |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pering, T.D.; Ilanko, T.; Liu, E.J. Periodicity in Volcanic Gas Plumes: A Review and Analysis. Geosciences 2019, 9, 394. https://doi.org/10.3390/geosciences9090394
Pering TD, Ilanko T, Liu EJ. Periodicity in Volcanic Gas Plumes: A Review and Analysis. Geosciences. 2019; 9(9):394. https://doi.org/10.3390/geosciences9090394
Chicago/Turabian StylePering, Tom D., Tehnuka Ilanko, and Emma J. Liu. 2019. "Periodicity in Volcanic Gas Plumes: A Review and Analysis" Geosciences 9, no. 9: 394. https://doi.org/10.3390/geosciences9090394
APA StylePering, T. D., Ilanko, T., & Liu, E. J. (2019). Periodicity in Volcanic Gas Plumes: A Review and Analysis. Geosciences, 9(9), 394. https://doi.org/10.3390/geosciences9090394





