Method for Near-Real Time Estimation of Tsunami Sources Using Ocean Bottom Pressure Sensor Network (S-Net)
Abstract
1. Introduction
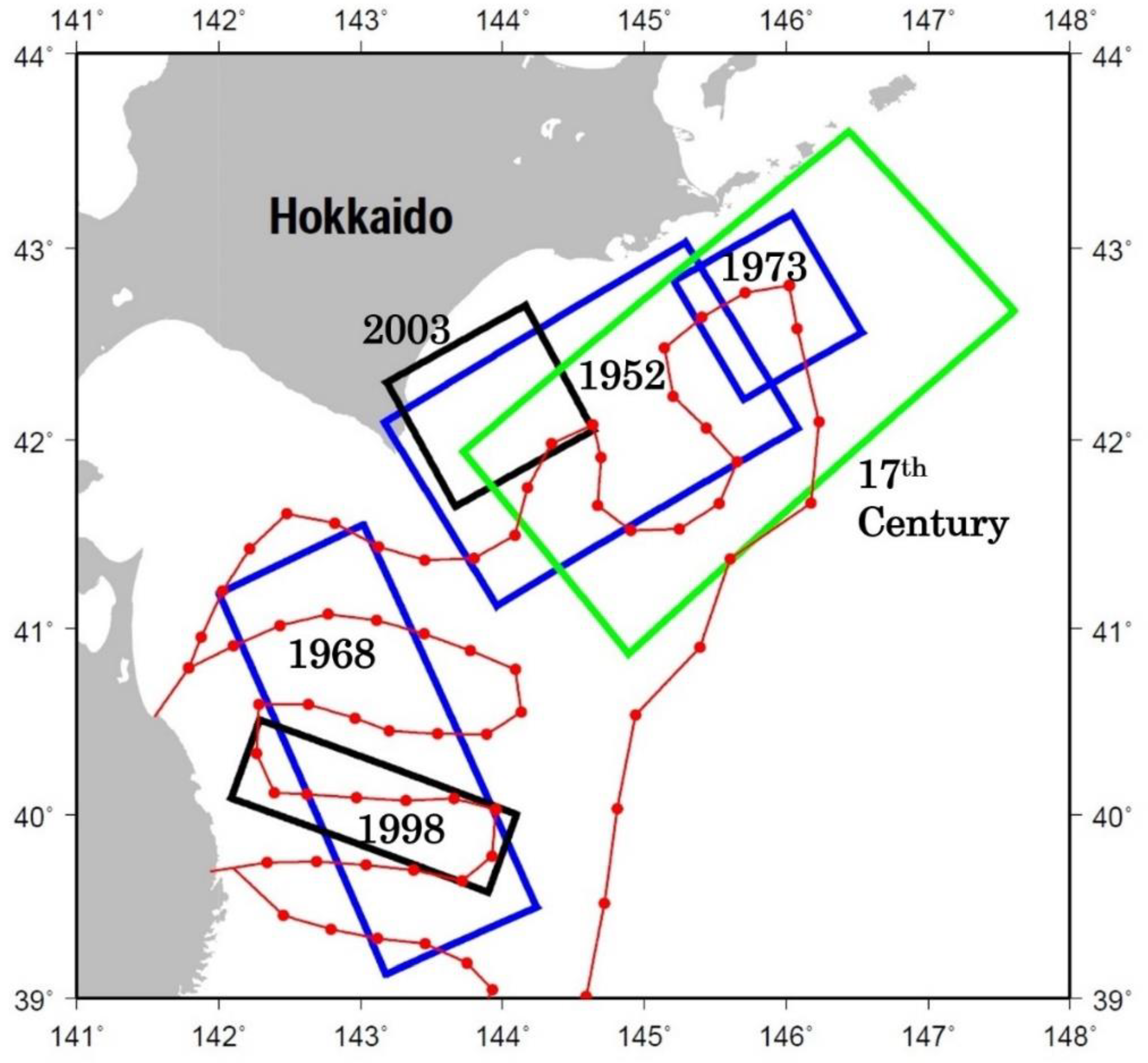
2. Great Earthquakes Generated Tsunamis along the Pacific Coast of Hokkaido
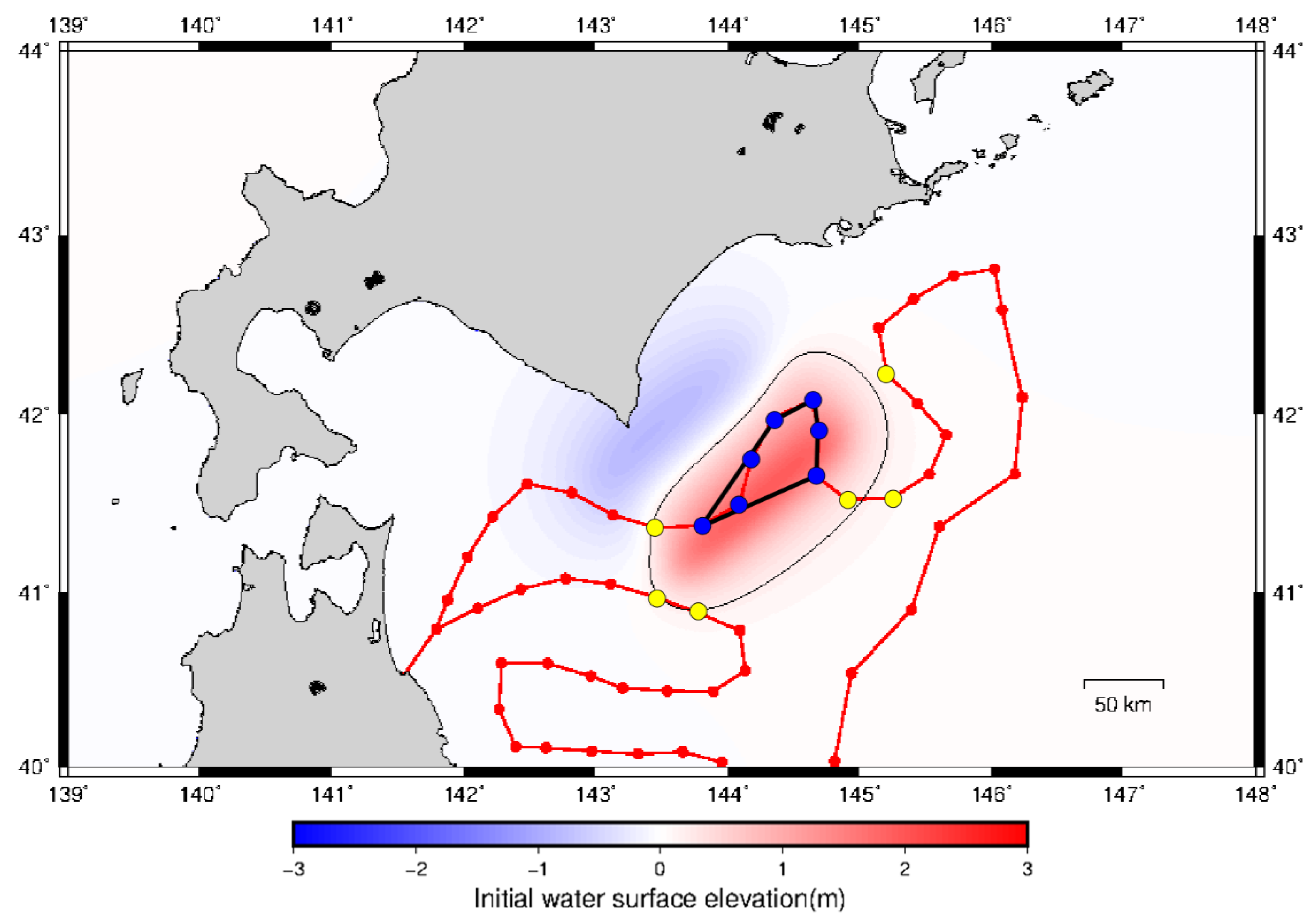
3. Fault Models
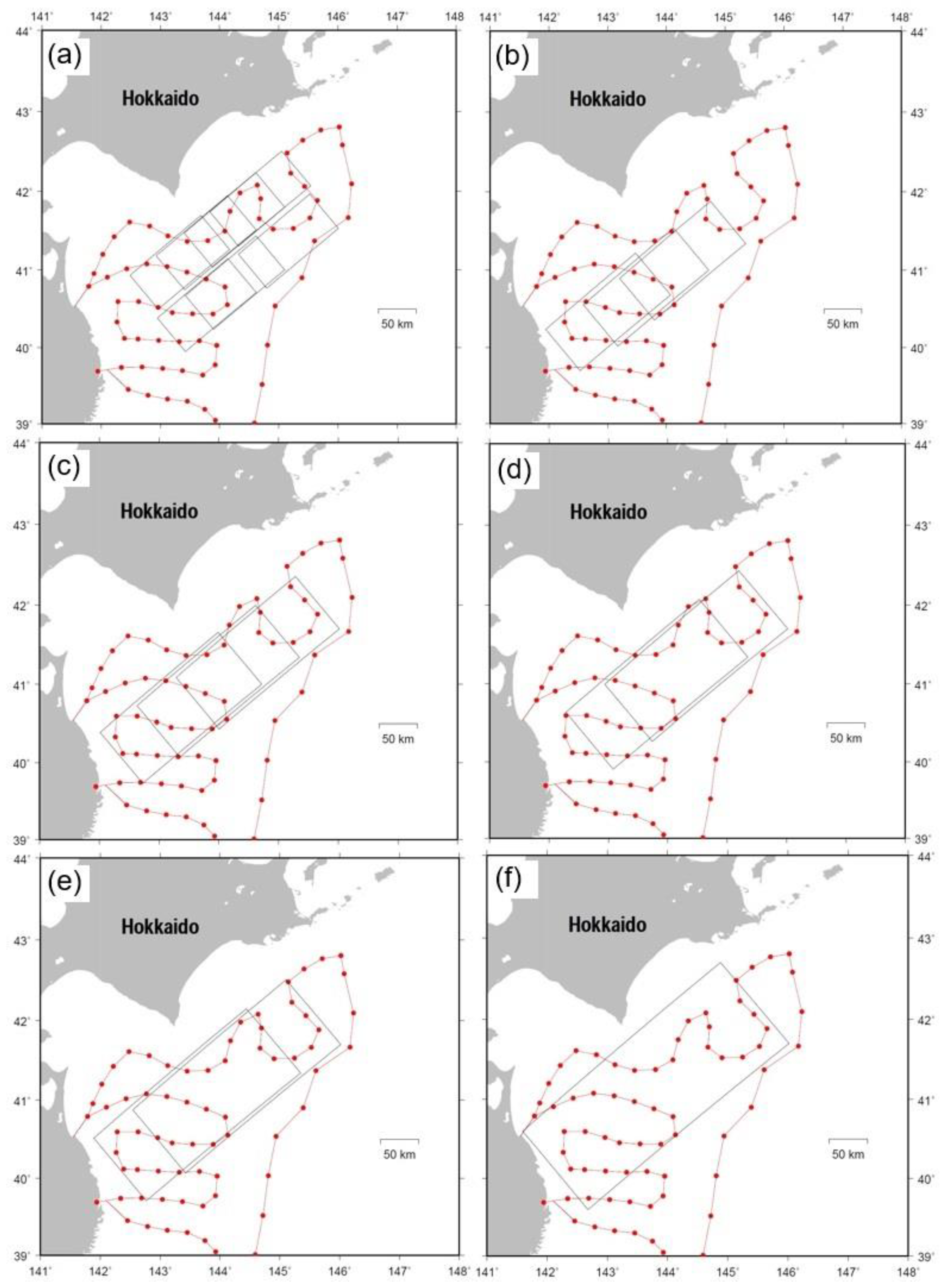
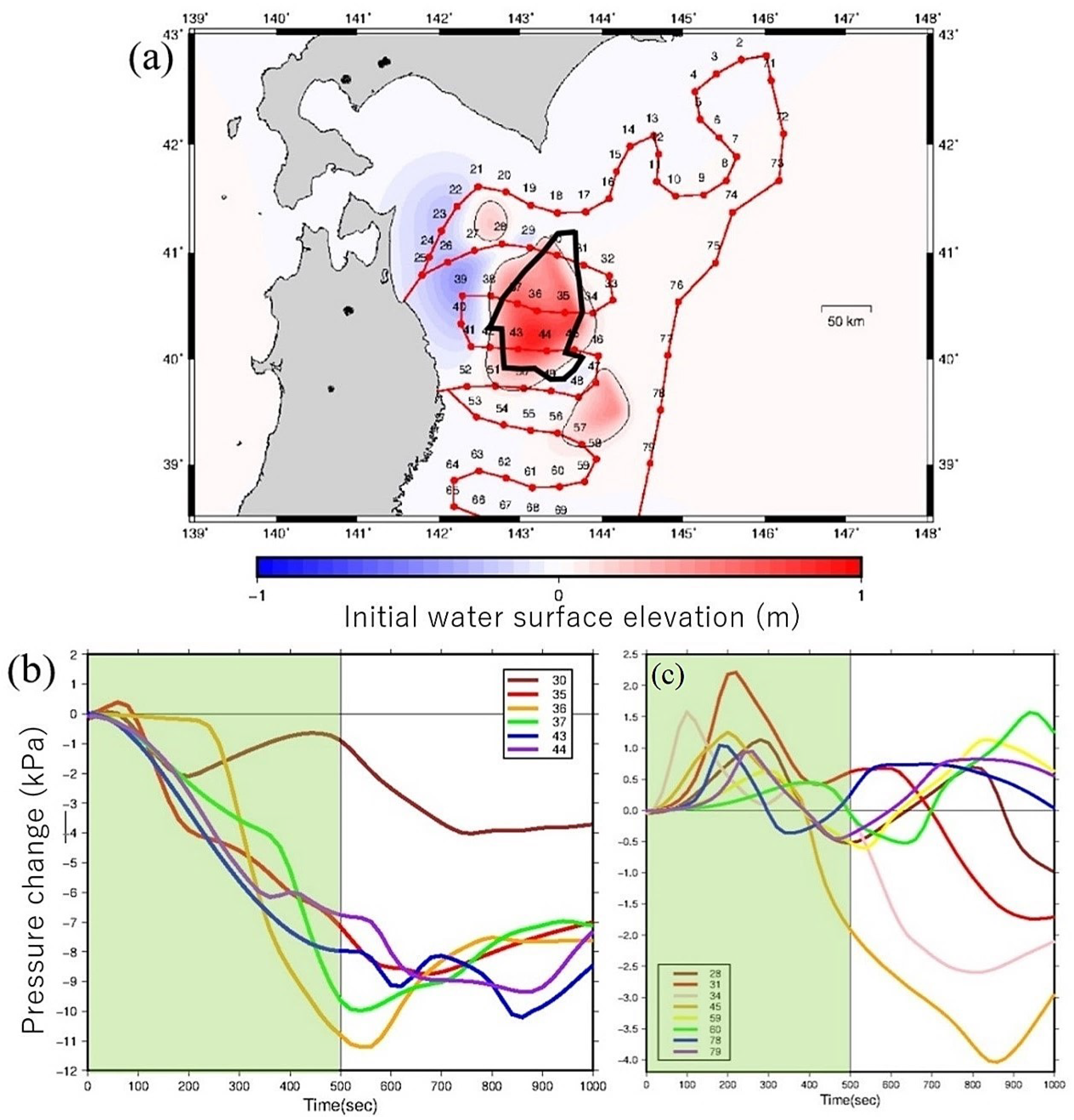
4. Tsunami Numerical Simulation
5. Development of Near-Real Time Tsunami Source Estimation Technique
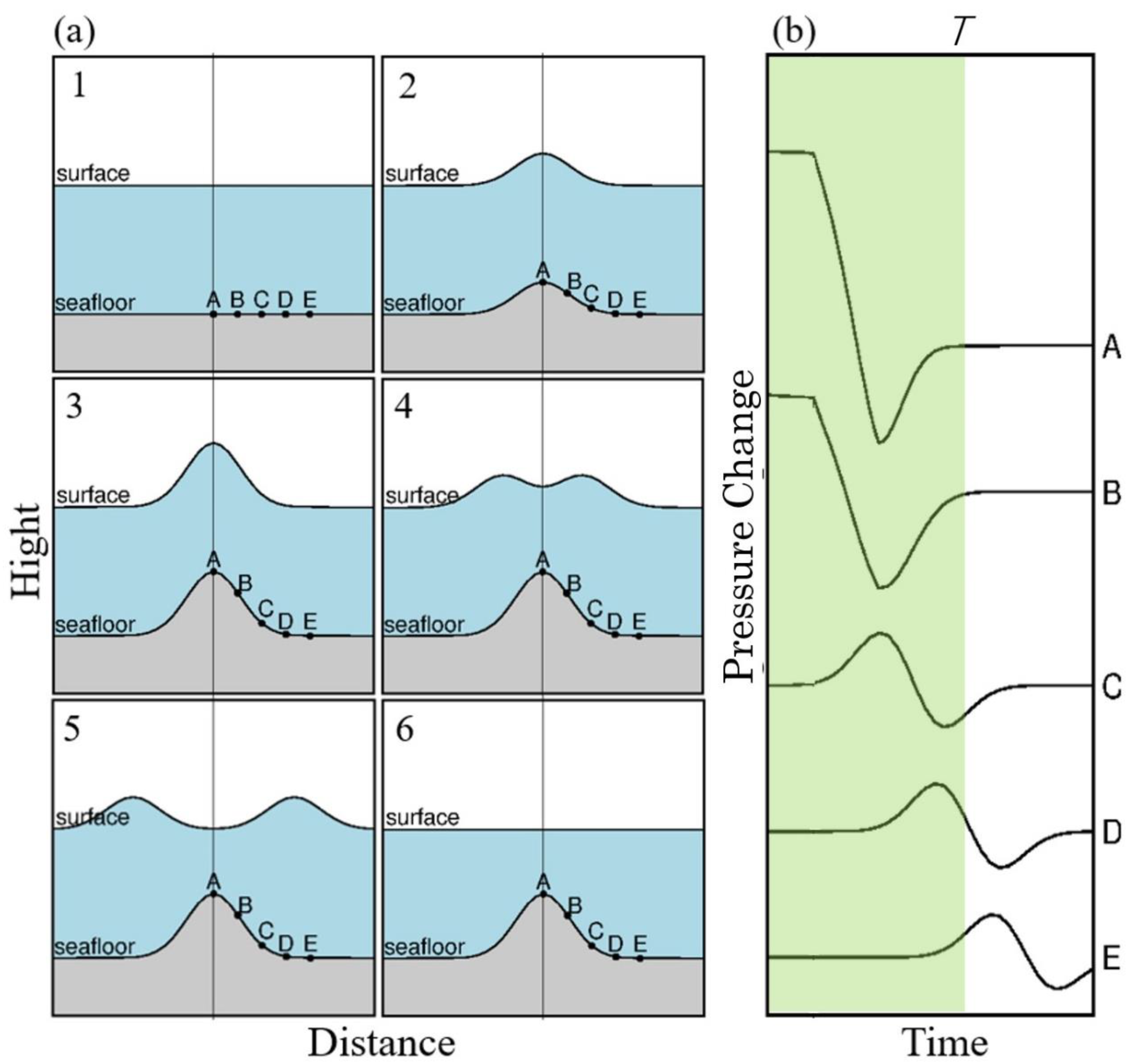
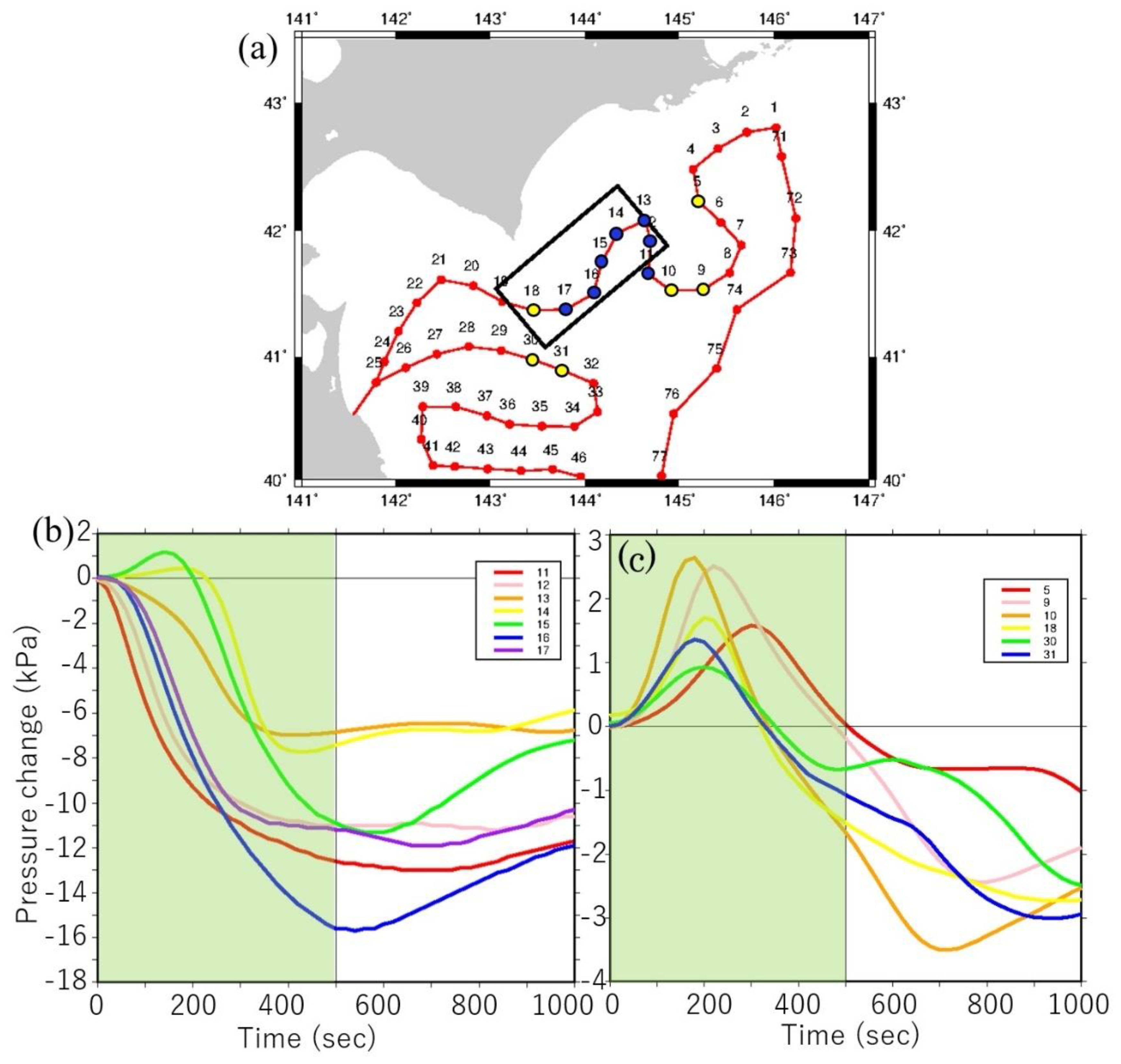
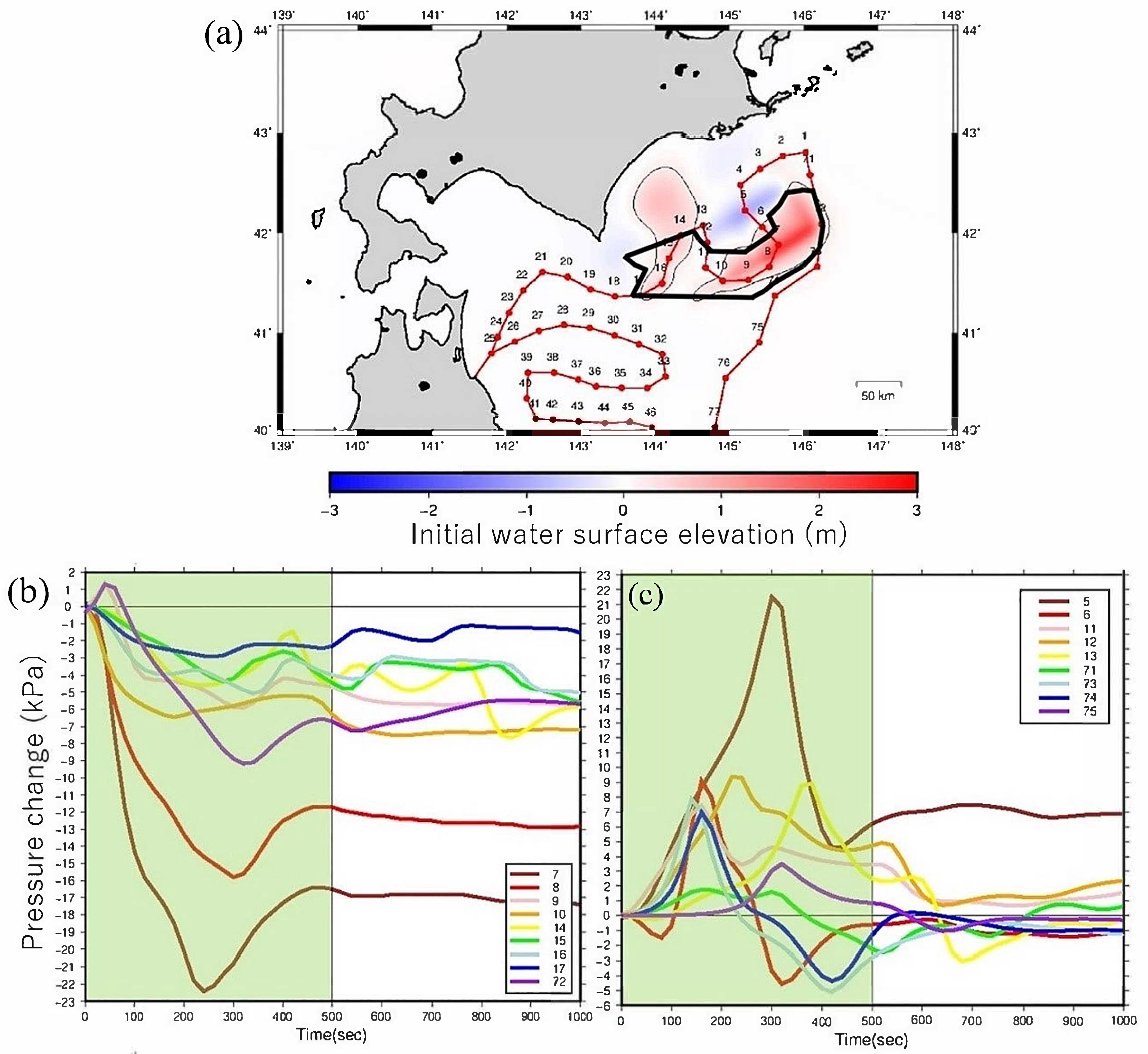
5.1. Classification Method for Pressure Waveforms Observed at the Ocean Bottom
5.2. Classification Results of Pressure Waveforms
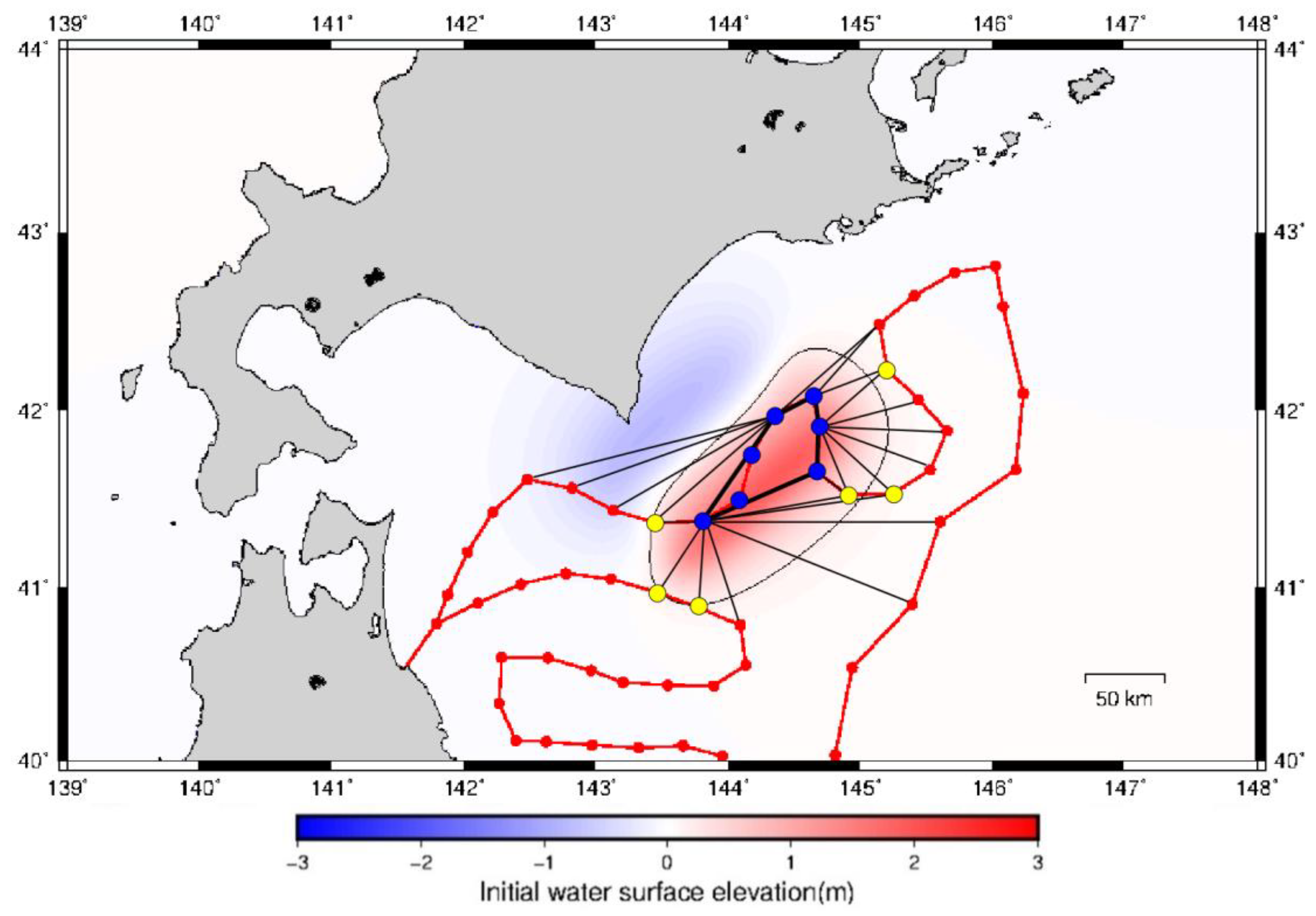
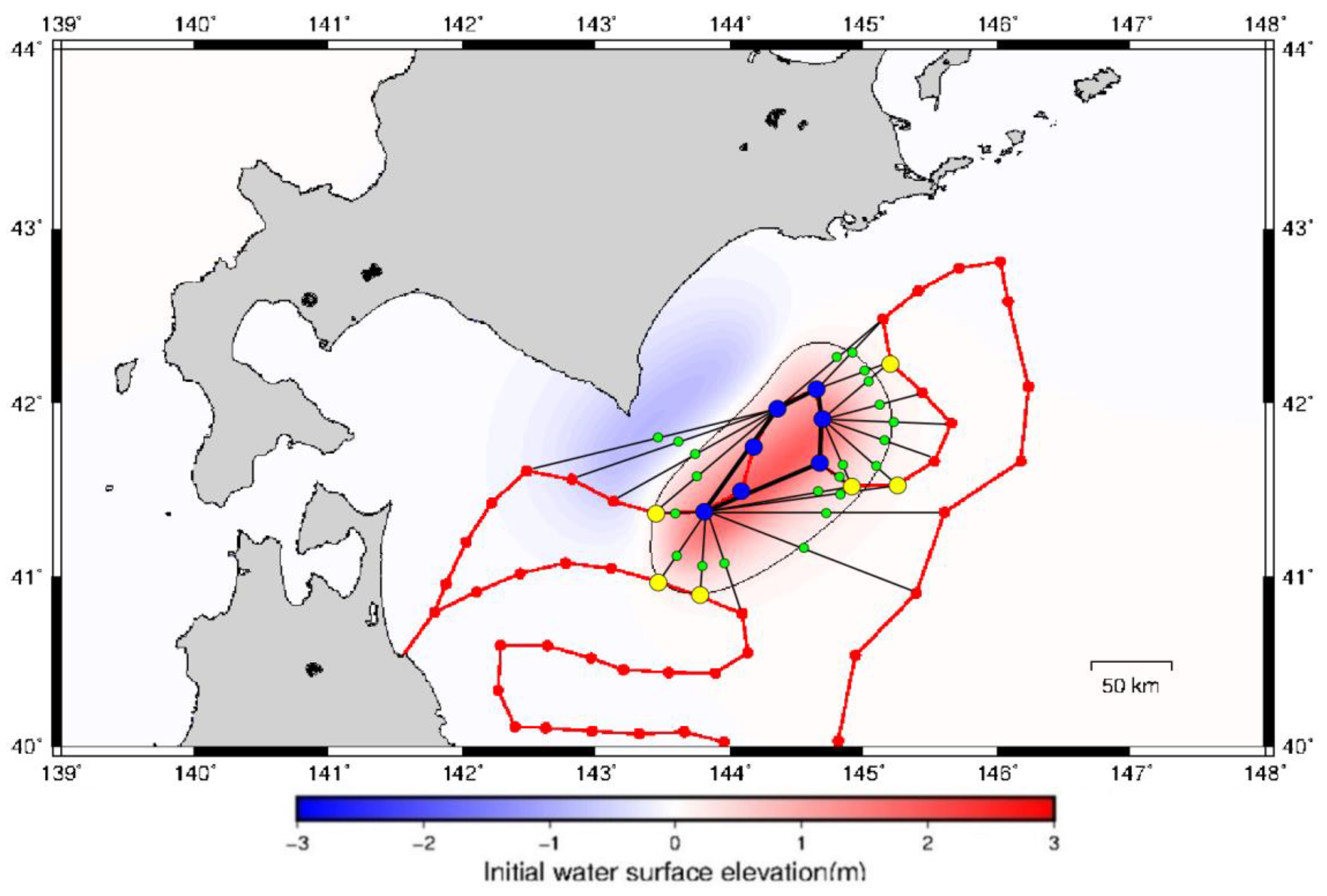
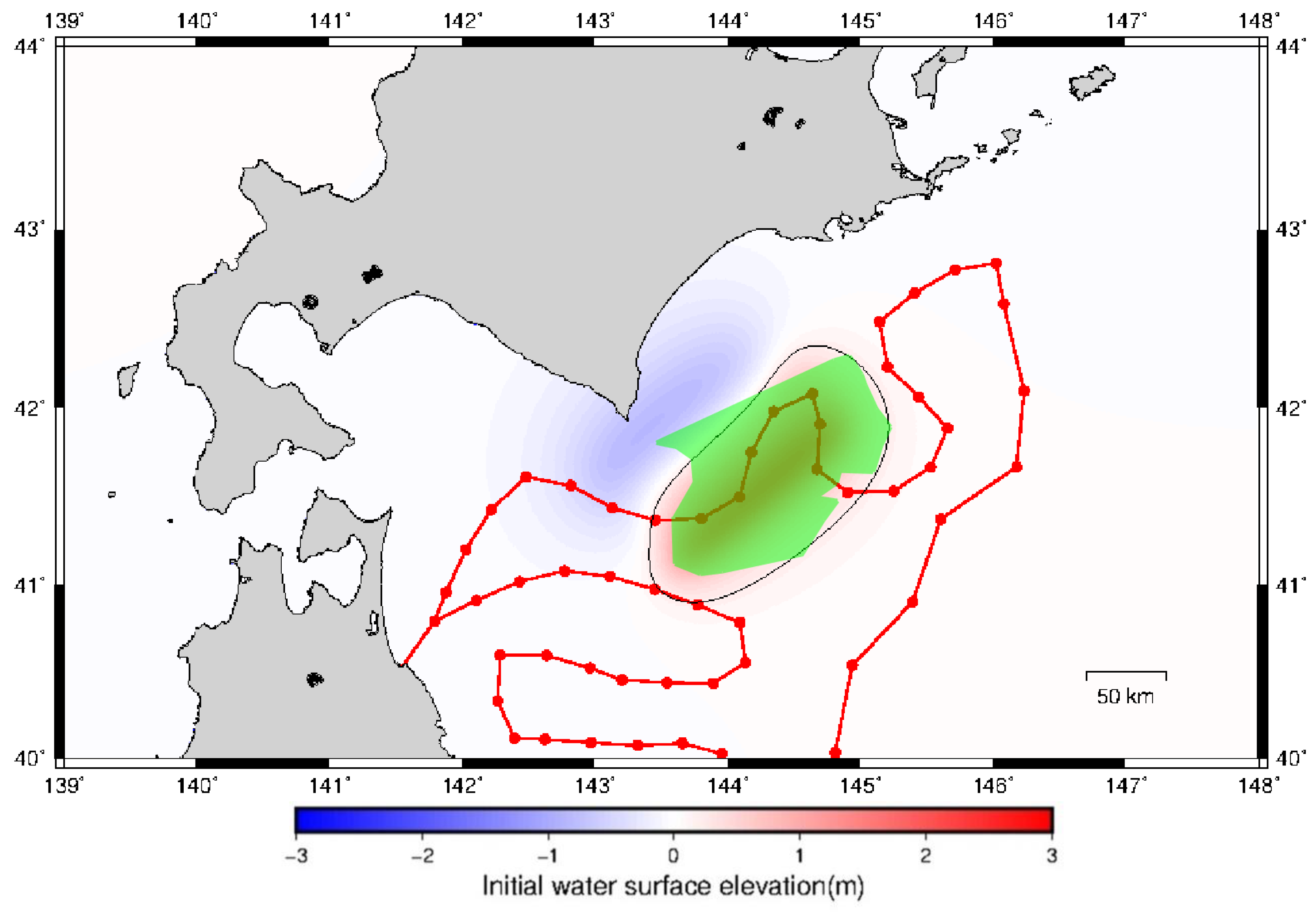
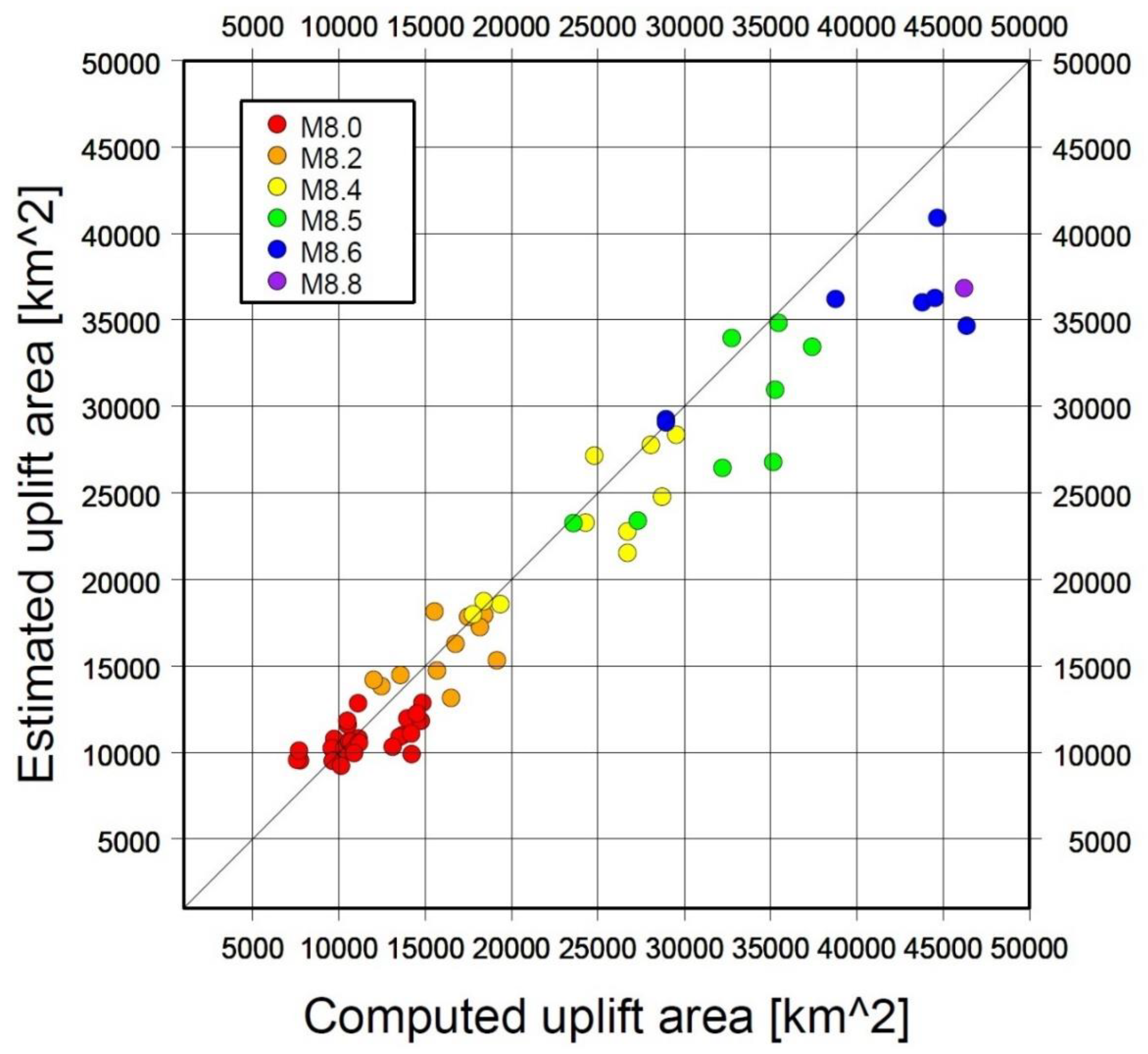
5.3. Estimation of Uplift Areas from Three Classification Types
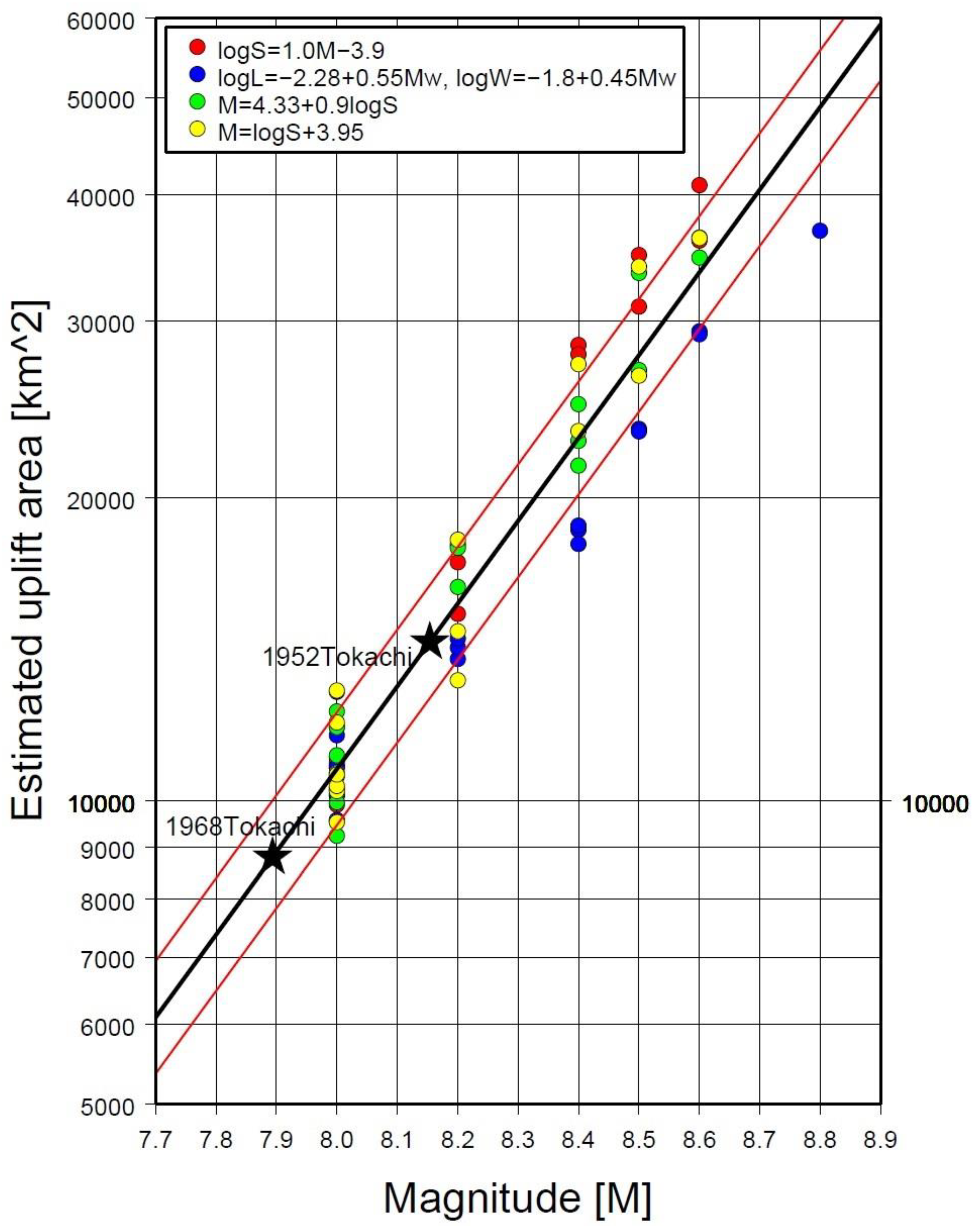
5.4. Estimation of Magnitudes from Uplift Areas
6. Validation of Tsunami Source Estimation for Previous Large Earthquakes
6.1. Case Study for the 1952 Tokachi-Oki Earthquake (Mw8.2)
6.2. Case Study for the 1968 Tokachi-Oki Earthquake (Mw8.1)
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Mori, N.; Takahashi, T. The 2011 Tohoku earthquake tsunami joint survey group Nationwide post event survey and analysis of the 2011 Tohoku earthquake tsunami. Coast. Eng. J. 2012, 54, 1250001. [Google Scholar] [CrossRef]
- Ozaki, T. Outline of the 2011 off the Pacific coast of Tohoku earthquake (Mw 9.0)—Tsunami warnings/advisories and observations. Earth Planets Space 2011, 63, 827–830. [Google Scholar] [CrossRef]
- The Fire and Disaster Management Agency. Damage Status of the 2011 off the Pacific Coast of Tohoku Earthquake (as of 7 March 2014). 2014. Available online: https://www.fdma.go.jp/disaster/higashinihon/assets/jishin149.pdf (accessed on 7 March 2014). (In Japanese).
- Kamigaichi, O. Tsunami forecasting and warning, in Extreme Environmental Events. In Complexity in Forecasting and Early Warning; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Uehira, K. Ocean Bottom Seismic and Tsunami Network along the Japan Trench. J. Soc. Instrum. Control Eng. 2014, 53, 477–481. (In Japanese) [Google Scholar] [CrossRef]
- Kanazawa, T. Japan Trench earthquake and tsunami monitoring network of cable-linked 150 ocean bottom observatories and its impact to earth disaster science. In Proceedings of the 2013 IEEE International Underwater Technology Symposium (UT), Tokyo, Japan, 5–8 March 2013; pp. 1–5. [Google Scholar]
- Tsushima, H.; Hino, R.; Fujimoto, H.; Tanioka, Y.; Imamura, F. Near-field tsunami forecasting from cabled ocean bottom pressure data. J. Geophys. Res. Space Phys. 2009, 114, 06309. [Google Scholar] [CrossRef]
- Tsushima, H.; Hino, R.; Tanioka, Y.; Imamura, F.; Fujimoto, H. Tsunami waveform inversion incorporating permanent seafloor deformation and its application to tsunami forecasting. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Yamamoto, N.; Aoi, S.; Hirata, K.; Suzuki, W.; Kunugi, T.; Nakamura, H. Multi-index method using offshore ocean-bottom pressure data for real-time tsunami forecast. Earth Planets Space 2016, 68, 57. [Google Scholar] [CrossRef]
- Maeda, T.; Obara, K.; Shinohara, M.; Kanazawa, T.; Uehira, K. Successive estimation of a tsunami wavefield without earthquake source data: A data assimilation approach toward real-time tsunami forecasting. Geophys. Res. Lett. 2015, 42, 7923–7932. [Google Scholar] [CrossRef]
- Tanioka, Y. Tsunami Simulation Method Assimilating Ocean Bottom Pressure Data near a Tsunami Source Region. Pageoph. Top. Vol. 2018, 175, 197–205. [Google Scholar] [CrossRef]
- Tanioka, Y.; Gusman, A.R. Near-field tsunami inundation forecast method assimilating ocean bottom pressure data: A synthetic test for the 2011 Tohoku-oki tsunami. Phys. Earth Planet. Inter. 2018, 283, 82–91. [Google Scholar] [CrossRef]
- Hirata, K.; Geist, E.; Satake, K.; Tanioka, Y.; Yamaki, S. Slip distribution of the 1952 Tokachi-Oki earthquake (M8.1) along the Kuril Trench deduced from tsunami waveform inversion. J. Geophys. Res. Space Phys. 2003, 108, 2196. [Google Scholar] [CrossRef]
- Satake, K. Inversion of tsunami waveforms for the estimation of heterogeneous fault motion of large submarine earthquakes: The 1968 Tokachi-oki and 1983 Japan Sea earthquakes. J. Geophys. Res. Space Phys. 1989, 94, 5627. [Google Scholar] [CrossRef]
- Tanioka, Y.; Satake, K.; Hirata, K. Recurrence of recent large earthquakes along the southernmost Kurile-Kamchatka subduction zone. In Volcanism and Subduction: The Kamchatka Region; Eichelberger, J., Gordeev, E., Izbekov, P., Kasahara, M., Lees, J., Eds.; American Geophysical Union: Washington, DC, USA, 2007; Volume 172, pp. 145–152. [Google Scholar]
- Tanioka, Y.; Ruff, L.; Satake, K. The Sanriku-Oki, Japan, Earthquake of 28 December, 1994 (Mw7.7): Rupture of a different asperity from a previous earthquake. Geophys. Res. Lett. 1996, 23, 1465–1468. [Google Scholar] [CrossRef]
- Tanioka, Y.; Hirata, K.; Hino, R.; Kanazawa, T. Slip distribution of the 2003 Tokachi-oki earthquake estimated from tsunami waveform inversion. Earth Planets Space 2004, 56, 373–376. [Google Scholar] [CrossRef]
- Tanioka, Y.; Nishimura, Y.; Hirakawa, K.; Imamura, F.; Abe, I.; Abe, Y.; Shindou, K.; Matsutomi, H.; Takahashi, T.; Imai, K.; et al. Tsunami run-up heights of the 2003 Tokachi-oki earthquake. Earth Planets Space 2004, 56, 359–365. [Google Scholar] [CrossRef]
- Nanayama, F.; Satake, K.; Furukawa, R.; Shimokawa, K.; Atwater, B.F.; Shigeno, K.; Yamaki, S. Unusually large earthquakes inferred from tsunami deposits along the Kuril trench. Nature 2003, 424, 660–663. [Google Scholar] [CrossRef] [PubMed]
- Hirakawa, K.; Nakamura, Y. Mega-Tsunamis since last 6500 years along the Pacific Coast of Hokkaido, Special Issue. Chikyu Mon. 2005, 49, 173–180. (In Japanese) [Google Scholar]
- Sawai, Y.; Kamataki, T.; Shishikura, M.; Nasu, H.; Okamura, Y.; Satake, K.; Thomson, K.H.; Matsumoto, D.; Fujii, Y.; Komatsubara, J.; et al. Aperiodic recurrence of geologically recorded tsunamis during the past 5500 years in eastern Hokkaido, Japan. J. Geophys. Res. 2009, 114, B01319. [Google Scholar] [CrossRef]
- Satake, K.; Nanayama, F.; Yamaki, S. Fault models of unusual tsunami in the 17th century along the Kuril trench. Earth Planets Space 2008, 60, 925–935. [Google Scholar] [CrossRef]
- Ioki, K.; Tanioka, Y. Re-estimated fault model of the 17th century great earthquake off Hokkaido using tsunami deposit data. Earth Planet. Sci. Lett. 2016, 433, 133–138. [Google Scholar] [CrossRef]
- Utsu, T.; Seki, A. Relation between the area of aftershock region and the energy of the Main Shock (in Japanese). Zisin J. Seismol. Soc. Japan 2nd Ser. 1955, 7, 233–240. [Google Scholar]
- Wells, L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Somerville, P.; Irikura, K.; Graves, R.; Sawada, S.; Wald, D.; Abrahamson, N.; Iwasaki, Y.; Kagawa, T.; Smith, N.; Kowada, A. Characterizing Crustal Earthquake Slip Models for the Prediction of Strong Ground Motion. Seism. Res. Lett. 1999, 70, 59–80. [Google Scholar] [CrossRef]
- Blaser, L.; Krüger, F.; Ohrnberger, M.; Scherbaum, F. Scaling Relations of Earthquake Source Parameter Estimates with Special Focus on Subduction Environment Scaling Relations of Earthquake Source Parameter Estimates with Focus on Subduction Environment. Bull. Seismol. Soc. Am. 2010, 100, 2914–2926. [Google Scholar] [CrossRef]
- Satake, K.; Hirata, K.; Yamaki, S.; Tanioka, Y. Re-estimation of tsunami source of the 1952 Tokachi-oki earthquake. Earth Planets Space 2006, 58, 535–542. [Google Scholar] [CrossRef]
- Kita, S.; Okada, T.; Hasegawa, A.; Nakajima, J.; Matsuzawa, T. Anomalous deepening of a seismic belt in the upper-plane of the double seismic zone in the Pacific slab beneath the Hokkaido corner: Possible evidence for thermal shielding caused by subducted forearc crust materials. Earth Planet. Sci. Lett. 2010, 290, 415–426. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Satake, K. Linear and nonlinear computations of the 1992 Nicaragua earthquake tsunami. Pure Appl. Geophys. 1995, 144, 455–470. [Google Scholar] [CrossRef]
- Tanioka, Y.; Satake, K. Tsunami generation by horizontal displacement of ocean bottom. Geophys. Res. Lett. 1996, 23, 861–864. [Google Scholar] [CrossRef]
- Saito, T.; Tsushima, H. Synthesizing ocean bottom pressure records including seismic wave and tsunami contributions: Toward realistic tests of monitoring systems. J. Geophys. Res. Solid Earth 2016, 121, 8175–8195. [Google Scholar] [CrossRef]
- Nosov, M.; Karpov, V.; Kolesov, S.; Sementsov, K.; Matsumoto, H.; Kaneda, Y. Relationship between pressure variations at the ocean bottom and the acceleration of its motion during a submarine earthquake. Earth Planets Space 2018, 70, 100. [Google Scholar] [CrossRef]
- Wallace, L.M.; Araki, E.; Saffer, D.; Wang, X.; Roesner, A.; Kopf, A.; Nakanishi, A.; Power, W.; Kobayashi, R.; Kinoshita, C.; et al. Near-field observations of an offshore M w 6.0 earthquake from an integrated seafloor and subseafloor monitoring network at the Nankai Trough, southwest Japan. J. Geophys. Res. Solid Earth 2016, 121, 8338–8351. [Google Scholar] [CrossRef]
- Kubota, T.; Suzuki, W.; Nakamura, T.; Chikasada, N.Y.; Aoi, S.; Takahashi, N.; Hino, R. Tsunami source inversion using time-derivative waveform of offshore pressure records to reduce effects of non-tsunami components. Geophys. J. Int. 2018, 215, 1200–1214. [Google Scholar] [CrossRef]
| Magnitude (M) | Length (km) | Width (km) | Latitude (°) | Longitude (°) | Depth (km) | Dip (°) | Slip (m) | Computed × 103 (km2) | Estimate × 103 (km2) |
|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 140 | 70 | 42.22 | 145.56 | 17.15 | 21 | 3.6 | 14.2 | 9.9 |
| 8.0 | 140 | 70 | 41.70 | 146.02 | 7.321 | 11 | 3.6 | 9.7 | 10.8 |
| 8.0 | 140 | 70 | 41.88 | 144.87 | 20.55 | 14 | 3.6 | 13.7 | 11.0 |
| 8.0 | 140 | 70 | 41.34 | 145.35 | 6.849 | 11 | 3.6 | 9.6 | 10.2 |
| 8.0 | 140 | 70 | 41.50 | 144.16 | 20.83 | 13 | 3.6 | 13.5 | 10.9 |
| 8.0 | 140 | 70 | 41.00 | 144.72 | 6.707 | 7 | 3.6 | 10.3 | 10.2 |
| 8.2 | 200 | 100 | 41.70 | 146.02 | 7.321 | 12.12 | 3.59 | 19.1 | 15.3 |
| 8.2 | 200 | 100 | 41.34 | 145.35 | 6.849 | 8.46 | 3.59 | 18.4 | 18.0 |
| 8.2 | 200 | 100 | 41.00 | 144.72 | 6.707 | 7.44 | 3.59 | 18.2 | 17.3 |
| 8.4 | 250 | 125 | 41.70 | 146.02 | 7.321 | 11.97 | 4.6 | 29.5 | 28.4 |
| 8.4 | 250 | 125 | 41.34 | 145.35 | 6.849 | 8.89 | 4.6 | 28.1 | 27.8 |
| 8.5 | 280 | 140 | 41.70 | 146.02 | 7.321 | 10.81 | 5.16 | 35.5 | 34.9 |
| 8.5 | 280 | 140 | 41.34 | 145.35 | 6.849 | 9.26 | 5.16 | 35.3 | 31.0 |
| 8.6 | 310 | 155 | 41.70 | 146.02 | 7.321 | 9.76 | 5.9 | 43.8 | 36.0 |
| 8.6 | 310 | 155 | 41.34 | 145.35 | 6.849 | 9.65 | 5.9 | 44.7 | 40.9 |
| Magnitude (M) | Length (km) | Width (km) | Latitude (°) | Longitude (°) | Depth (km) | Dip (°) | Slip (m) | Computed × 103 (km2) | Estimate × 103 (km2) |
|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 154 | 77 | 41.53 | 146.01 | 4.776 | 9.80 | 3.0 | 11.2 | 10.6 |
| 8.0 | 154 | 77 | 41.80 | 145.10 | 15.933 | 13.39 | 3.0 | 14.8 | 11.8 |
| 8.0 | 154 | 77 | 41.26 | 145.54 | 3.871 | 8.63 | 3.0 | 10.9 | 10.0 |
| 8.0 | 154 | 77 | 41.51 | 144.62 | 16.041 | 17.67 | 3.0 | 14.5 | 12.3 |
| 8.0 | 154 | 77 | 41.00 | 145.10 | 4.135 | 10.73 | 3.0 | 10.1 | 9.2 |
| 8.0 | 154 | 77 | 41.26 | 144.17 | 15.700 | 10.73 | 3.0 | 14.2 | 11.1 |
| 8.0 | 154 | 77 | 40.70 | 144.62 | 6.845 | 5.90 | 3.0 | 10.5 | 11.8 |
| 8.2 | 200 | 100 | 41.34 | 145.35 | 6.849 | 8.8 | 3.6 | 17.5 | 17.8 |
| 8.2 | 200 | 100 | 41.00 | 144.72 | 6.707 | 7.1 | 3.6 | 16.7 | 16.3 |
| 8.4 | 258 | 129 | 41.70 | 146.02 | 7.321 | 12.1 | 4.3 | 28.7 | 24.8 |
| 8.4 | 258 | 129 | 41.34 | 145.35 | 6.849 | 8.45 | 4.3 | 26.7 | 22.8 |
| 8.4 | 258 | 129 | 41.00 | 144.72 | 6.707 | 8.18 | 4.3 | 26.7 | 21.5 |
| 8.5 | 294 | 147 | 41.70 | 146.02 | 7.321 | 11.3 | 4.7 | 37.4 | 33.4 |
| 8.5 | 294 | 147 | 41.34 | 145.35 | 6.849 | 8.77 | 4.7 | 35.2 | 26.8 |
| 8.6 | 334 | 167 | 41.70 | 146.02 | 7.321 | 9.99 | 5.1 | 44.5 | 36.3 |
| 8.6 | 334 | 167 | 41.34 | 145.35 | 6.849 | 9.59 | 5.1 | 46.3 | 34.7 |
| Magnitude (M) | Length (km) | Width (km) | Latitude (°) | Longitude (°) | Depth (km) | Dip (°) | Slip (m) | Computed × 103 (km2) | Estimate × 103 (km2) |
|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 150 | 75 | 41.53 | 146.01 | 4.776 | 9.80 | 3.2 | 9.6 | 9.5 |
| 8.0 | 150 | 75 | 41.80 | 145.10 | 15.933 | 13.39 | 3.2 | 14.8 | 12.9 |
| 8.0 | 150 | 75 | 41.26 | 145.54 | 3.871 | 8.63 | 3.2 | 10.3 | 10.2 |
| 8.0 | 150 | 75 | 41.51 | 144.62 | 16.041 | 17.67 | 3.2 | 13.9 | 12.0 |
| 8.0 | 150 | 75 | 41.00 | 145.10 | 4.135 | 10.73 | 3.2 | 10.6 | 10.6 |
| 8.0 | 150 | 75 | 41.26 | 144.17 | 15.700 | 10.73 | 3.2 | 13.1 | 10.3 |
| 8.0 | 150 | 75 | 40.70 | 144.62 | 6.845 | 5.90 | 3.2 | 10.7 | 10.6 |
| 8.2 | 188 | 94 | 41.70 | 146.02 | 7.321 | 11.8 | 4.1 | 16.5 | 13.2 |
| 8.2 | 188 | 94 | 41.34 | 145.35 | 6.849 | 8.8 | 4.1 | 15.7 | 14.7 |
| 8.2 | 188 | 94 | 41.00 | 144.72 | 6.707 | 7.1 | 4.1 | 15.5 | 18.2 |
| 8.4 | 238 | 119 | 41.70 | 146.02 | 7.321 | 12.1 | 5.1 | 24.8 | 27.1 |
| 8.4 | 238 | 119 | 41.34 | 145.35 | 6.849 | 8.45 | 5.1 | 24.3 | 23.3 |
| 8.5 | 266 | 133 | 41.70 | 146.02 | 7.321 | 11.3 | 5.7 | 32.8 | 34.0 |
| 8.5 | 266 | 133 | 41.34 | 145.35 | 6.849 | 8.77 | 5.7 | 32.2 | 26.4 |
| 8.6 | 298 | 149 | 41.34 | 145.35 | 6.849 | 9.59 | 6.4 | 38.8 | 36.2 |
| Magnitude (M) | Length (km) | Width (km) | Latitude (°) | Longitude (°) | Depth (km) | Dip (°) | Slip (m) | Computed × 103 (km2) | Estimate × 103 (km2) |
|---|---|---|---|---|---|---|---|---|---|
| 8.0 | 132 | 63 | 42.07 | 145.54 | 15.229 | 17.10 | 4.3 | 11.1 | 10.8 |
| 8.0 | 132 | 63 | 41.53 | 146.01 | 4.776 | 9.80 | 4.3 | 7.7 | 9.6 |
| 8.0 | 132 | 63 | 41.80 | 145.10 | 15.933 | 13.39 | 4.3 | 10.5 | 11.6 |
| 8.0 | 132 | 63 | 41.51 | 144.62 | 16.041 | 17.67 | 4.3 | 11.1 | 12.8 |
| 8.0 | 132 | 63 | 41.00 | 145.10 | 4.135 | 10.73 | 4.3 | 7.6 | 9.6 |
| 8.0 | 132 | 63 | 41.26 | 144.17 | 15.700 | 10.73 | 4.3 | 10.5 | 10.1 |
| 8.0 | 132 | 63 | 40.70 | 144.62 | 6.845 | 5.90 | 4.3 | 7.7 | 10.1 |
| 8.2 | 170 | 78 | 41.34 | 145.35 | 6.849 | 8.90 | 5.4 | 12.5 | 13.8 |
| 8.2 | 170 | 78 | 41.00 | 144.72 | 6.707 | 6.82 | 5.4 | 12.0 | 14.2 |
| 8.2 | 170 | 78 | 40.68 | 144.07 | 11.614 | 7.97 | 5.4 | 13.6 | 14.5 |
| 8.4 | 219 | 95 | 41.70 | 146.02 | 7.321 | 11.62 | 6.9 | 19.3 | 18.6 |
| 8.4 | 219 | 95 | 41.34 | 145.35 | 6.849 | 8.12 | 6.9 | 18.4 | 18.8 |
| 8.4 | 219 | 95 | 41.00 | 144.72 | 6.707 | 6.75 | 6.9 | 17.8 | 18.0 |
| 8.5 | 248 | 106 | 41.70 | 146.02 | 7.321 | 11.70 | 7.7 | 27.3 | 23.4 |
| 8.5 | 248 | 106 | 41.34 | 145.35 | 6.849 | 8.11 | 7.7 | 23.6 | 23.3 |
| 8.6 | 282 | 117 | 41.70 | 146.02 | 7.321 | 10.56 | 8.7 | 28.9 | 29.3 |
| 8.6 | 282 | 117 | 41.34 | 145.35 | 6.849 | 9.80 | 8.7 | 28.9 | 29.1 |
| 8.8 | 363 | 145 | 41.70 | 146.02 | 7.321 | 12.37 | 10.8 | 46.2 | 36.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoue, M.; Tanioka, Y.; Yamanaka, Y. Method for Near-Real Time Estimation of Tsunami Sources Using Ocean Bottom Pressure Sensor Network (S-Net). Geosciences 2019, 9, 310. https://doi.org/10.3390/geosciences9070310
Inoue M, Tanioka Y, Yamanaka Y. Method for Near-Real Time Estimation of Tsunami Sources Using Ocean Bottom Pressure Sensor Network (S-Net). Geosciences. 2019; 9(7):310. https://doi.org/10.3390/geosciences9070310
Chicago/Turabian StyleInoue, Mayu, Yuichiro Tanioka, and Yusuke Yamanaka. 2019. "Method for Near-Real Time Estimation of Tsunami Sources Using Ocean Bottom Pressure Sensor Network (S-Net)" Geosciences 9, no. 7: 310. https://doi.org/10.3390/geosciences9070310
APA StyleInoue, M., Tanioka, Y., & Yamanaka, Y. (2019). Method for Near-Real Time Estimation of Tsunami Sources Using Ocean Bottom Pressure Sensor Network (S-Net). Geosciences, 9(7), 310. https://doi.org/10.3390/geosciences9070310





