Ecohydrological Behaviour of Mountain Beech Forest: Quantification of Stomatal Conductance Using Sap Flow Measurements
Abstract
:1. Introduction
- Quantifying stomatal conductance, gc, of the newly formed beech forest from a vegetative period to a deciduous period;
- Determining the patterns of the diurnal variation of stomatal conductance for different vegetation periods;
- Evaluating the impact of environmental factors on stomatal conductance.
2. Materials and Methods
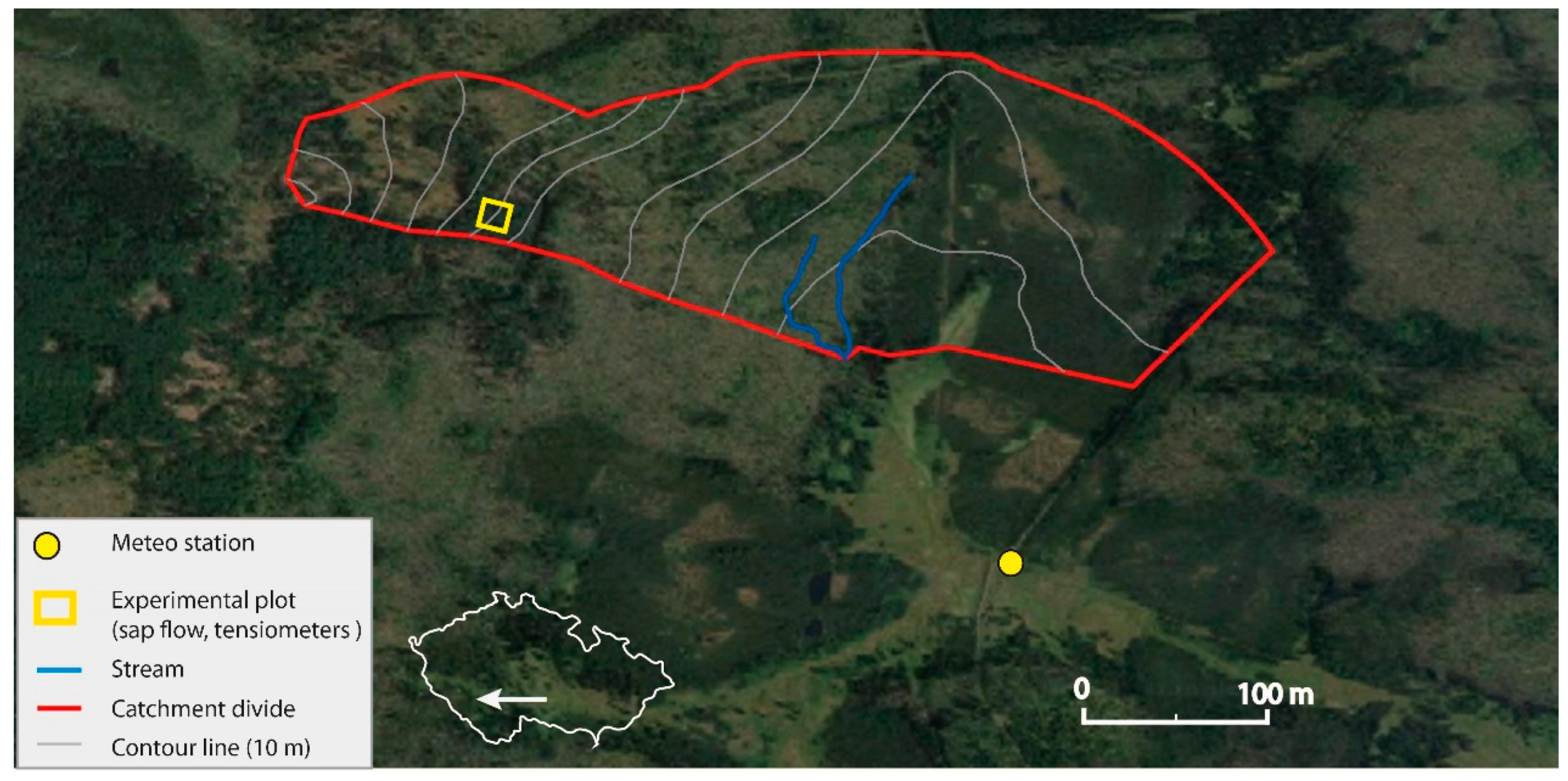
2.1. Study Site
- “Dead” forest stands (at locations with former spruce forests) with grass cover and rarely a solitary tree;
- Beech forests at locations of former mixed forests.
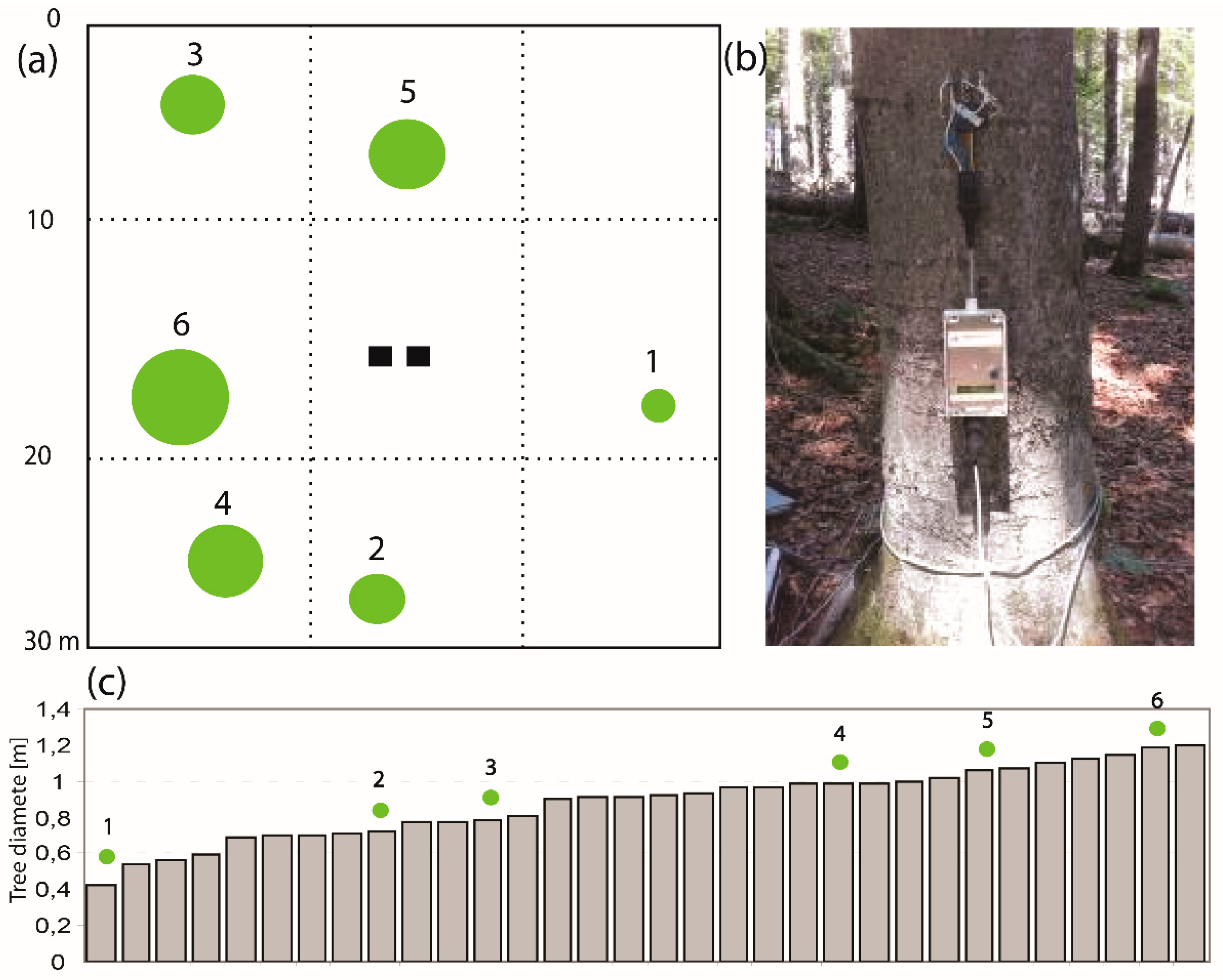
2.2. Experiment Instrumentation and Data
- Classified groups of the trunk DBH and calculated canopy conductance from sap flow for each group (step 10 cm);
- Calculated ratio of the number of trees per DBH group;
- Recalculated canopy conductance from groups to tree DBH.
2.3. Canopy Stomatal Conductance Calculation
3. Results
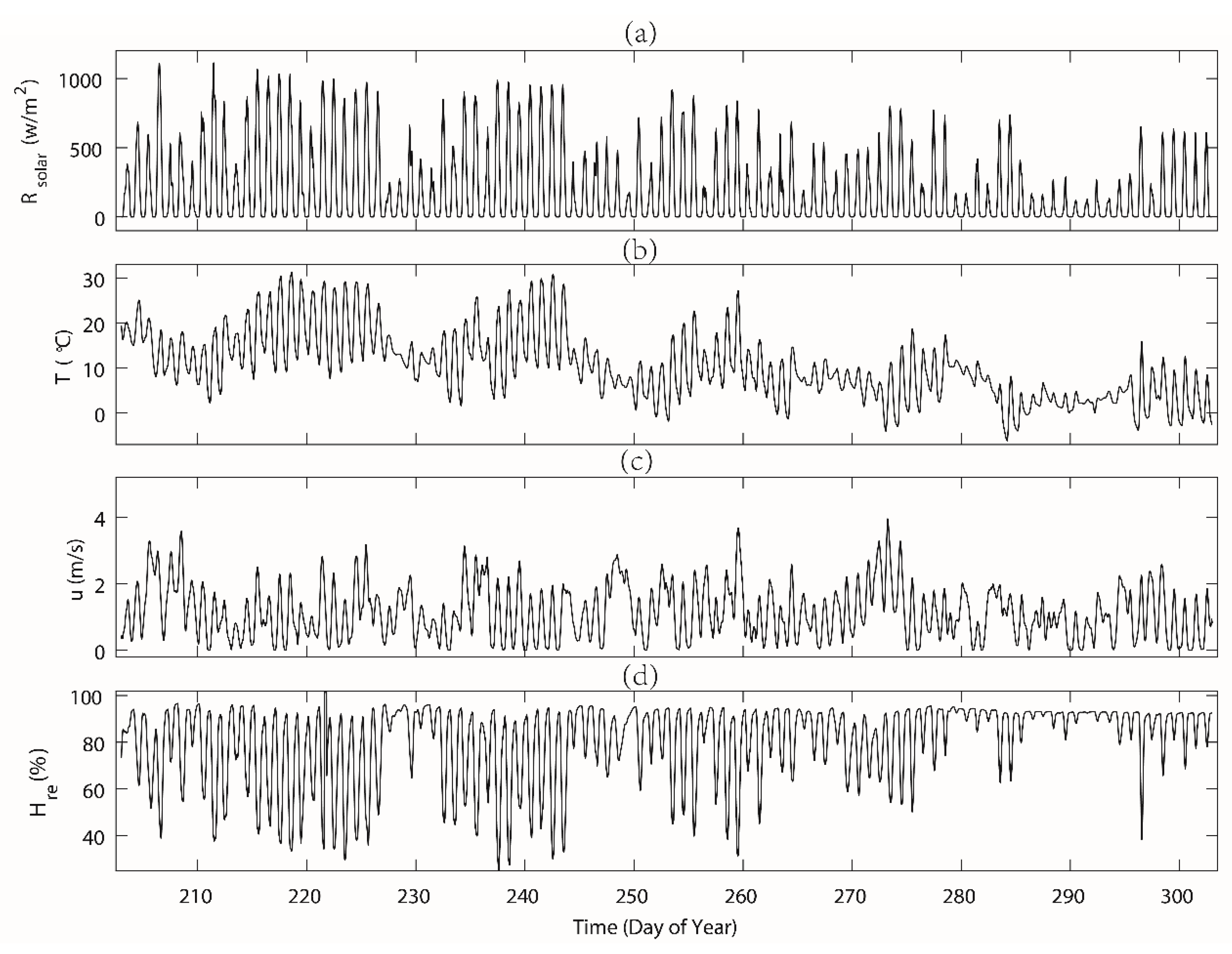
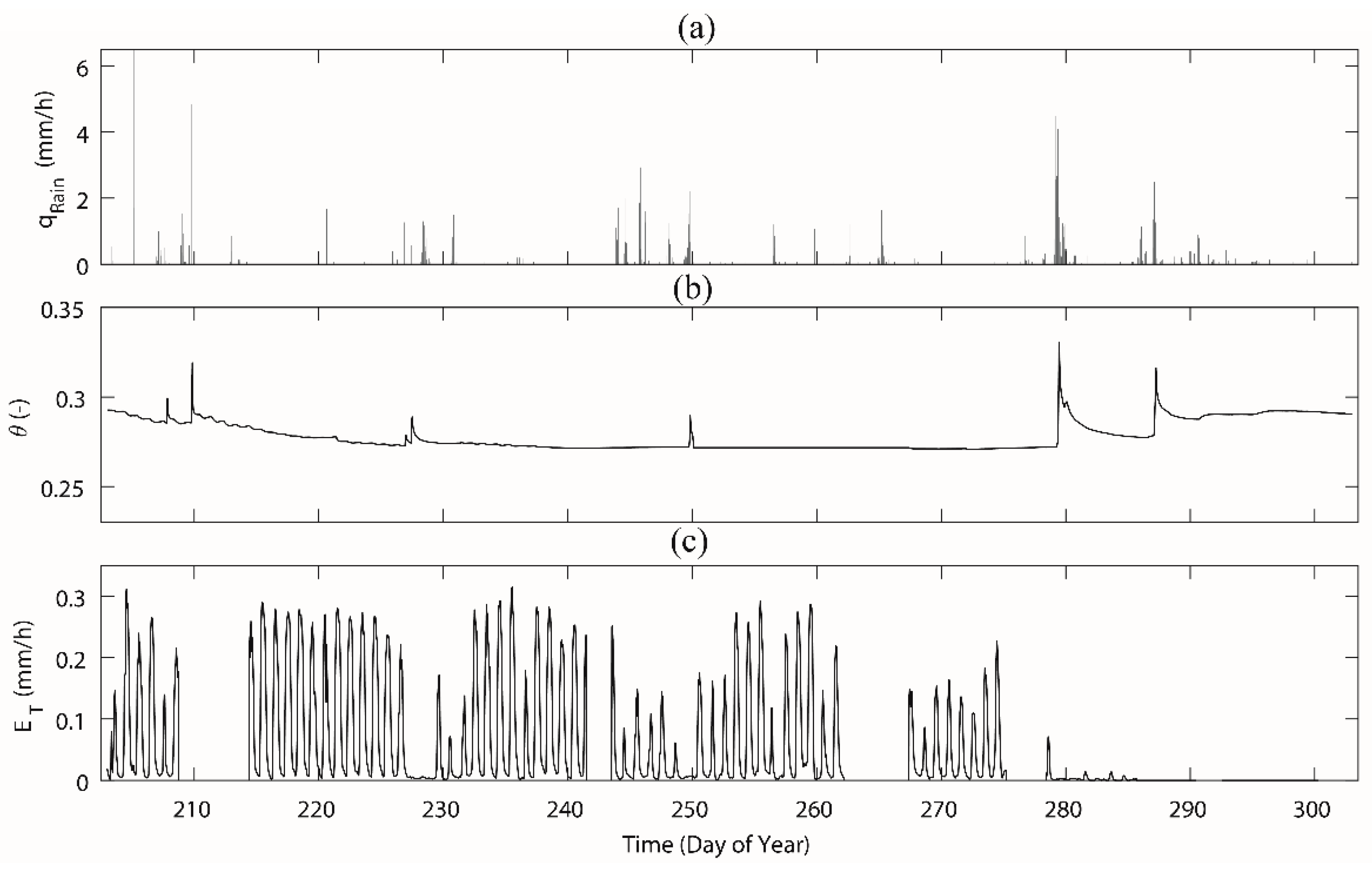
3.1. Meteorological Parameters, Soil Moisture and Sap Flow
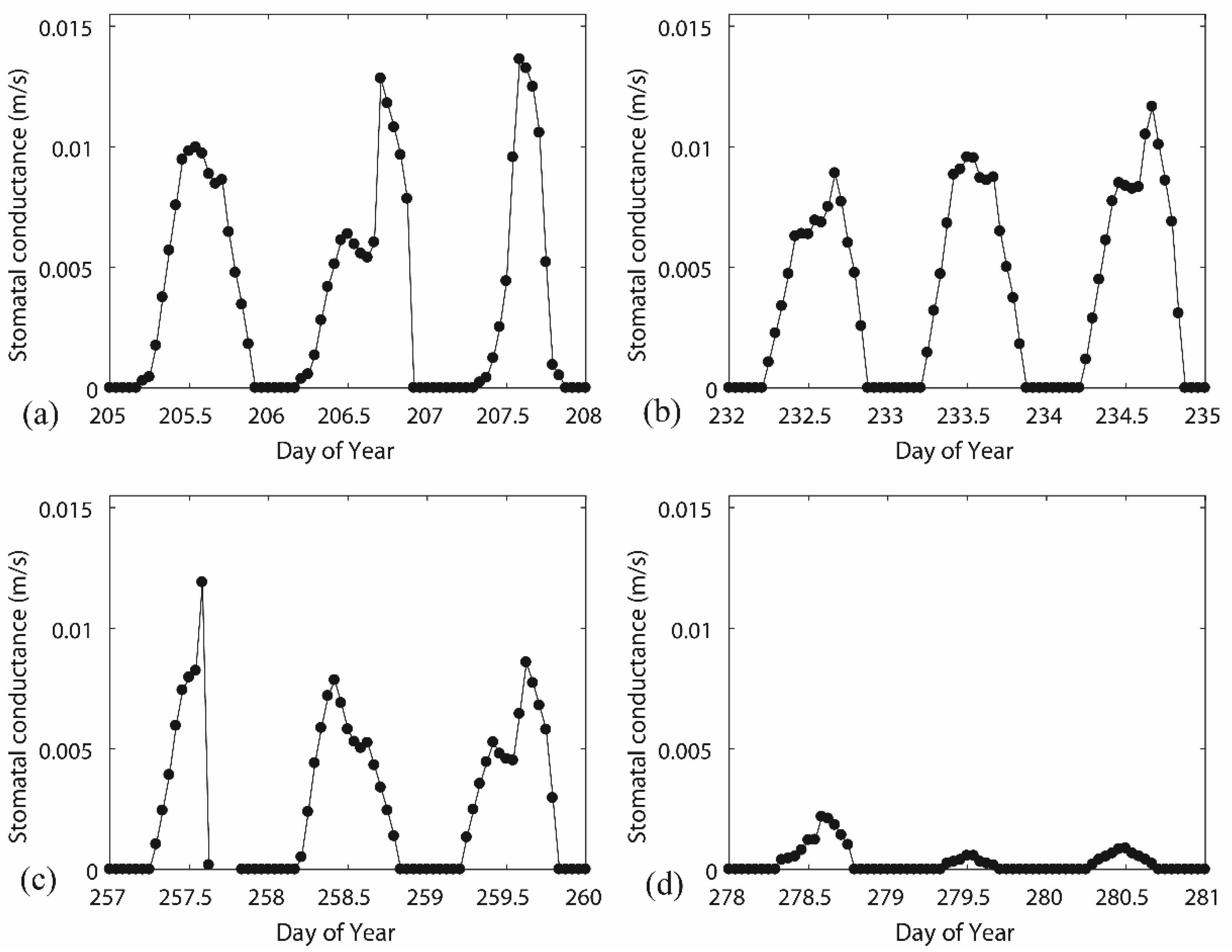
3.2. Diurnal Behaviours of Stomatal Conductance and Responses of Canopy Conductance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moreira, M.; Sternberg, L.; Martinelli, L.; Victoria, R.; Barbosa, E.; Bonates, L.; Nepstad, D. Contribution of transpiration to forest ambient vapour based on isotopic measurements. Chang. Boil. 1997, 3, 439–450. [Google Scholar] [CrossRef]
- Ewers, B.; Mackay, D.; Gower, S.; Ahl, D.; Burrows, S.; Samanta, S. Tree species effects on stand transpiration in northern Wisconsin. Water Resour. Res. 2002, 38, 8-1–8-11. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. Meteorol. 2014, 189, 115–117. [Google Scholar] [CrossRef]
- Buckley, T.N.; Mott, K.A. Modelling stomatal conductance in response to environmental factors. Plant Cell Environ. 2013, 36, 1691–1699. [Google Scholar] [CrossRef] [PubMed]
- Wehr, R.; Commane, R.; Munger, J.W.; McManus, J.B.; Nelson, D.D.; Zahniser, M.S.; Saleska, S.R.; Wofsy, S.C. Dynamics of canopy stomatal conductance, transpiration, and evaporation in a temperate deciduous forest, validated by carbonyl sulfide uptake. Biogeosciences 2017, 14, 389–401. [Google Scholar] [CrossRef] [Green Version]
- Rao, P.; Agaewal, S.K. Diurnal variation in leaf water potential, stomatal conductance, and irradiance of winter crop under different moisture levels. Boil. Plant. 1984, 26, 1–4. [Google Scholar] [CrossRef]
- Lin, Y.-S.; Medlyn, B.E.; Duursma, R.A.; Prentice, I.C.; Wang, H.; Baig, S.; Eamus, D.; De Dios, V.R.; Mitchell, P.; Ellsworth, D.S.; et al. Optimal stomatal behaviour around the world. Nat. Clim. Chang. 2015, 5, 459–464. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 4, 205–234. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-Fao Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Monteith, J. Evaporation and surface temperature. Q. J. Meteorol. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Iritz, Z.; Tourula, T.; Lindroth, A.; Heikinheimo, M. Simulation of willow short-rotation forest evaporation using a modified Shuttleworth-Wallace approach. Hydrol. Process. 2001, 15, 97–113. [Google Scholar] [CrossRef]
- Whitley, R.; Medlyn, B.; Zeppel, M.; Macinnis-Ng, C.; Eamus, D.; Macinnis-Ng, C. Comparing the Penman–Monteith equation and a modified Jarvis–Stewart model with an artificial neural network to estimate stand-scale transpiration and canopy conductance. J. Hydrol. 2009, 373, 256–266. [Google Scholar] [CrossRef]
- Guan, H.; Wilson, J.L. A hybrid dual-source model for potential evaporation and transpiration partitioning. J. Hydrol. 2009, 377, 405–416. [Google Scholar] [CrossRef]
- Damour, G.; Simonneau, T.; Cochard, H.; Urban, L. An overview of models of stomatal conductance at the leaf level. Plant Cell 2010, 33, 1419–1438. [Google Scholar] [CrossRef]
- Hernandez-Santana, V.; Fernández, J.; Rodriguez-Dominguez, C.; Romero, R.; Diaz-Espejo, A. The dynamics of radial sap flux density reflects changes in stomatal conductance in response to soil and air water deficit. Agric. Meteorol. 2016, 218, 92–101. [Google Scholar] [CrossRef]
- Čermák, J.; Cienciala, E.; Kucera, J.; Lindroth, A.; Bednárová, E. Individual variation of sap-flow rate in large pine and spruce trees and stand transpiration: A pilot study at the central NOPEX site. J. Hydrol. 1995, 168, 17–27. [Google Scholar] [CrossRef]
- Kučera, J.; Brito, P.; Jiménez, M.S.; Urban, J. Direct Penman–Monteith parameterization for estimating stomatal conductance and modeling sap flow. Trees 2017, 31, 873–885. [Google Scholar] [CrossRef]
- Köstner, B.M.M.; Schulze, E.-D.; Kelliher, F.M.; Hollinger, D.Y.; Byers, J.N.; Hunt, J.E.; McSeveny, T.M.; Meserth, R.; Weir, P.L. Transpiration and canopy conductance in a pristine broad-leaved forest of Nothofagus: An analysis of xylem sap flow and eddy correlation measurements. Oecologia 1992, 91, 350–359. [Google Scholar] [CrossRef] [PubMed]
- Naithani, K.J.; Ewers, B.E.; Pendall, E. Sap flux-scaled transpiration and stomatal conductance response to soil and atmospheric drought in a semi-arid sagebrush ecosystem. J. Hydrol. 2012, 464, 176–185. [Google Scholar] [CrossRef]
- Wang, H.; Guan, H.; Deng, Z.; Simmons, C.T. Optimization of canopy conductance models from concurrent measurements of sap flow and stem water potential on Drooping Sheoak in South Australia. Water Resour. 2014, 50, 6154–6167. [Google Scholar] [CrossRef] [Green Version]
- Granier, A.; Biron, P.; Lemoine, D. Water balance, transpiration and canopy conductance in two beech stands. Agric. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
- Roberts, J. The influence of physical and physiological characteristics of vegetation on their hydrological response. Hydrol. Process. 2000, 14, 2885–2901. [Google Scholar] [CrossRef]
- Vertessy, R.A.; Benyon, R.G.; O’Sullivan, S.K.; Gribben, P.R. Relationships between stem diameter, sapwood area, leaf area and transpiration in a young mountain ash forest. Tree Physiol. 1995, 15, 559–567. [Google Scholar] [CrossRef]
- Ewers, B.E.; Gower, S.T.; Wang, C.K.; Bond-Lamberty, B.; Bond-Lamberty, B.; Bond-Lamberty, B. Effects of stand age and tree species on canopy transpiration and average stomatal conductance of boreal forests. Plant Cell 2005, 28, 660–678. [Google Scholar] [CrossRef]
- Bernsteinová, J.; Bässler, C.; Zimmermann, L.; Langhammer, J.; Beudert, B. Changes in runoff in two neighbouring catchments in the Bohemian Forest related to climate and land cover changes. J. Hydrol. Hydromech. 2015, 63, 342–352. [Google Scholar] [CrossRef] [Green Version]
- Langhammer, J.; Su, Y.; Bernsteinová, J. Runoff Response to Climate Warming and Forest Disturbance in a Mid-Mountain Basin. Water 2015, 7, 3320–3342. [Google Scholar] [CrossRef]
- Su, Y.; Langhammer, J.; Jarsjö, J. Geochemical responses of forested catchments to bark beetle infestation: Evidence from high frequency in-stream electrical conductivity monitoring. J. Hydrol. 2017, 550, 635–649. [Google Scholar] [CrossRef]
- Oulehle, F.; Chuman, T.; Majer, V.; Hruška, J. Chemical recovery of acidified Bohemian lakes between 1984 and 2012: The role of acid deposition and bark beetle induced forest disturbance. Biogeochemistry 2013, 116, 83–101. [Google Scholar] [CrossRef]
- Tesař, M.; Šír, M.; Dvořák, I.J.; Lichner, Ľ. Influence of vegetative cover changes on the soil water regime in headwater regions in the Czech Republic. IHP/HWRP-Berichte 2004, 2, 57–72. [Google Scholar]
- Hais, M.; Kučera, T. Surface temperature change of spruce forest as a result of bark beetle attack: Remote sensing and GIS approach. Eur. J. 2008, 127, 327–336. [Google Scholar] [CrossRef]
- Wild, J.; Kopecký, M.; Svoboda, M.; Zenáhlíková, J.; Edwards-Jonášová, M.; Herben, T. Spatial patterns with memory: Tree regeneration after stand-replacing disturbance in Picea abies mountain forests. J. Veg. Sci. 2014, 25, 1327–1340. [Google Scholar] [CrossRef]
- Schipka, F.; Heimann, J.; Leuschner, C. Regional variation in canopy transpiration of Central European beech forests. Oecologia 2005, 143, 260–270. [Google Scholar] [CrossRef] [PubMed]
- Schume, H.; Hager, H.; Jost, G. Water and energy exchange above a mixed European Beech—Norway Spruce forest canopy: A comparison of eddy covariance against soil water depletion measurement. Theor. Appl. Climatol. 2005, 81, 87–100. [Google Scholar] [CrossRef]
- Střelcová, K.; Minďáš, J.; Škvarenina, J. Influence of tree transpiration on mass water balance of mixed mountain forests of the West Carpathians. Biologia 2006, 61, S305–S310. [Google Scholar] [CrossRef]
- Heil, K. Wasserhaushalt und Stoffumsatz in Fichten- (Picea abies (L.) Karst.) und Bucheno¨kosystemen (Fagus Sylvatica L.) der ho¨Heren Lagen des Bayerischen Waldes. Ph.D. Thesis, University of Munich, München, Germany, 1996. [Google Scholar]
- Čada, V.; Svoboda, M.; Janda, P. Dendrochronological reconstruction of the disturbance history and past development of the mountain Norway spruce in the Bohemian Forest, central Europe. Ecol. Manag. 2013, 295, 59–68. [Google Scholar] [CrossRef]
- Vlček, L.; Falátková, K.; Schneider, P. Identification of runoff formation with two dyes in a mid-latitude mountain headwater. Hydrol. Earth Sci. 2017, 21, 3025–3040. [Google Scholar] [Green Version]
- Van Genuchten, M.T.; Leij, F.; Yates, S. The Retc Code for Quantifying the Hydraulic Functions of Unsaturated Soils; US Salinity Laboratory: Riverside, CA, USA, 1991. [Google Scholar]
- Čermák, J.; Kučera, J.; Nadezhdina, N. Sap flow measurements with some thermodynamic methods, flow integration within trees and scaling up from sample trees to entire forest stands. Trees 2004, 18, 529–546. [Google Scholar] [CrossRef]
- Frazer, G.W.; Trofymow, J.A.; Lertzman, K.P. A Method for Estimating Canopy Openness, Effective Leaf Area Index, and Photosynthetically Active Photon Flux Density Using Hemispherical Photography and Computerized Image Analysis Techniques; Information Report BC-X-373; Pacific Forestry Centre, Natural Resources Canada: Victoria, BC, Canada, 1997; p. 73. [Google Scholar]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere, 4th ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Zhou, M.; Ishidaira, H.; Hapuarachchi, H.; Magome, J.; Kiem, A.; Takeuchi, K.; Kiem, A. Estimating potential evapotranspiration using Shuttleworth–Wallace model and NOAA-AVHRR NDVI data to feed a distributed hydrological model over the Mekong River basin. J. Hydrol. 2006, 327, 151–173. [Google Scholar] [CrossRef]
- Jarvis, P.G. The Interpretation of the Variations in Leaf Water Potential and Stomatal Conductance Found in Canopies in the Field. Philos. Trans. Soc. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Stewart, J. Modelling surface conductance of pine forest. Agric. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Xu, D.; Cai, J.; Li, F. Evapotranspiraton estimation based on scaling up from leaf stomatal conductance to canopy conductance. Agric. Meteorol. 2011, 151, 1086–1095. [Google Scholar] [CrossRef]
- Granier, A.; Ceschia, E.; Damesin, C.; Lebaube, S.; Le Dantec, V.; Lemoine, D.; Lucot, E.; Pontailler, J.Y.; Dufrêne, E.; Epron, D.; et al. The carbon balance of a young Beech forest. Funct. Ecol. 2000, 14, 312–325. [Google Scholar] [CrossRef]
- Magnani, F.; Leonardi, S.; Tognetti, R.; Grace, J.; Borghetti, M. Modelling the surface conductance of a broad-leaf canopy: Effects of partial decoupling from the atmosphere. Plant Cell 1998, 21, 867–879. [Google Scholar] [CrossRef]
- Zhang, L.; Brook, J.R.; Vet, R. A revised parameterization for gaseous dry deposition in air-quality models. Atmos. Chem. Phys. Discuss. 2003, 3, 2067–2082. [Google Scholar] [CrossRef] [Green Version]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis under Different Environmental Conditions. In Progress in Photosynthesis Research; Springer Nature: Basingstoke, UK, 1987; pp. 221–224. [Google Scholar]
- Gerosa, G.; Mereu, S.; Finco, A.; Marzuoli, R. Stomatal Conductance Modeling to Estimate the Evapotranspiration of Natural and Agricultural Ecosystems. In Evapotranspiration—Remote Sensing and Modeling; Irmak, A., Ed.; Inech: Rijeka, Croatia, 2012; pp. 403–420. [Google Scholar]
- Ge, Z.-M.; Zhou, X.; Kellomäki, S.; Peltola, H.; Wang, K.-Y. Climate, canopy conductance and leaf area development controls on evapotranspiration in a boreal coniferous forest over a 10-year period: A united model assessment. Ecol. Model. 2011, 222, 1626–1638. [Google Scholar] [CrossRef]
- Viterbo, P.; Beljaars, A.C.M. An Improved Land Surface Parameterization Scheme in the ECMWF Model and Its Validation. J. Clim. 1995, 8, 2716–2748. [Google Scholar] [CrossRef] [Green Version]
- Tiedtke, M. ECMWF Model Parameterisation of Sub-Grid Scale Processes; European Centre for Medium Range Weather Forecast: Reading, UK, 1979. [Google Scholar]
- Tateishi, M.; Kumagai, T.; Suyama, Y.; Hiura, T. Differences in transpiration characteristics of Japanese beech trees, Fagus crenata, in Japan. Tree Physiol. 2010, 30, 748–760. [Google Scholar] [CrossRef] [Green Version]
- Shao, W.; Su, Y.; Langhammer, J. Simulations of coupled non-isothermal soil moisture transport and evaporation fluxes in a forest area. J. Hydrol. Hydromech. 2017, 65, 410–425. [Google Scholar] [CrossRef] [Green Version]
- Köstner, B. Evaporation and transpiration from forests in Central Europe—Relevance of patch-level studies for spatial scaling. Theor. Appl. Clim. 2001, 76, 69–82. [Google Scholar]
- Williams, M.; Malhi, Y.; Nobre, A.D.; Rastetter, E.; Pereira, M.G.P. Seasonal variation in net carbon exchange and evapotranspiration in a Brazilian rain forest: A modelling analysis. Plant Cell Environ. 1998, 21, 953–968. [Google Scholar] [CrossRef]
- Herbst, M.; Eschenbach, C.; Kappen, L. Water use in neighbouring stands of beech (Fagus sylvatica L.) and black alder (Alnus glutinosa (L.) Gaertn.). Ann. For. Sci. 1999, 56, 107–120. [Google Scholar] [CrossRef]
- Körner, C. Humidity responses in forest trees: Precautions in thermal scanning surveys. Theor. Appl. Clim. 1985, 36, 83–98. [Google Scholar] [CrossRef]
- Harley, J.L. A Study of the Root System of the Beech in Woodland Soils, with Especial Reference to Mycorrhizal Infection. J. Ecol. 1940, 28, 107. [Google Scholar] [CrossRef]
- David, T.S.; Pinto, C.A.; Nadezhdina, N.; Kurz-Besson, C.; Henriques, M.O.; Quilhó, T.; Čermák, J.; Chaves, M.M.; Pereira, J.S.; David, J.S. Root functioning, tree water use and hydraulic redistribution in Quercus suber trees: A modeling approach based on root sap flow. Ecol. Manag. 2013, 307, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in Soil Evaporation Physics—A Review. Vadose Zone J. 2013, 12, 12. [Google Scholar] [CrossRef]
- Gerke, K.M.; Sidle, R.C.; Mallants, D. Preferential flow mechanisms identified from staining experiments in forested hillslopes. Hydrol. Process. 2015, 29, 4562–4578. [Google Scholar] [CrossRef]
- Granier, A.; Loustau, D. Measuring and modelling the transpiration of a maritime pine canopy from sap-flow data. Agric. Meteorol. 1994, 71, 61–81. [Google Scholar] [CrossRef]

| Period | Vegetative Period DOY203–272 | Deciduous Period DOY273–302 | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Mean | Min | Max | 5-y Average 2 | Mean | Min | Max | 5-y Average 2 |
| Air temperature [°C] | 13.3 | 6.1 | 31.3 | 15.7 | 4.6 | −6.2 | 18.7 | 6.7 |
| Solar radiation [W m−2] 1 | 685.7 | 177.8 | 1113.2 | 701.3 | 428.1 | 119.2/ | 801.4 | 456.2 |
| Wind speed [m s−1] | 1.2 | / | 3.7 | 1.2 | 1.1 | / | 3.9 | 1.2 |
| Relative humidity [%] | 77.3 | 25.2 | 122.9 | 79.4 | 87.1 | 38.3 | 95.9 | 82.5 |
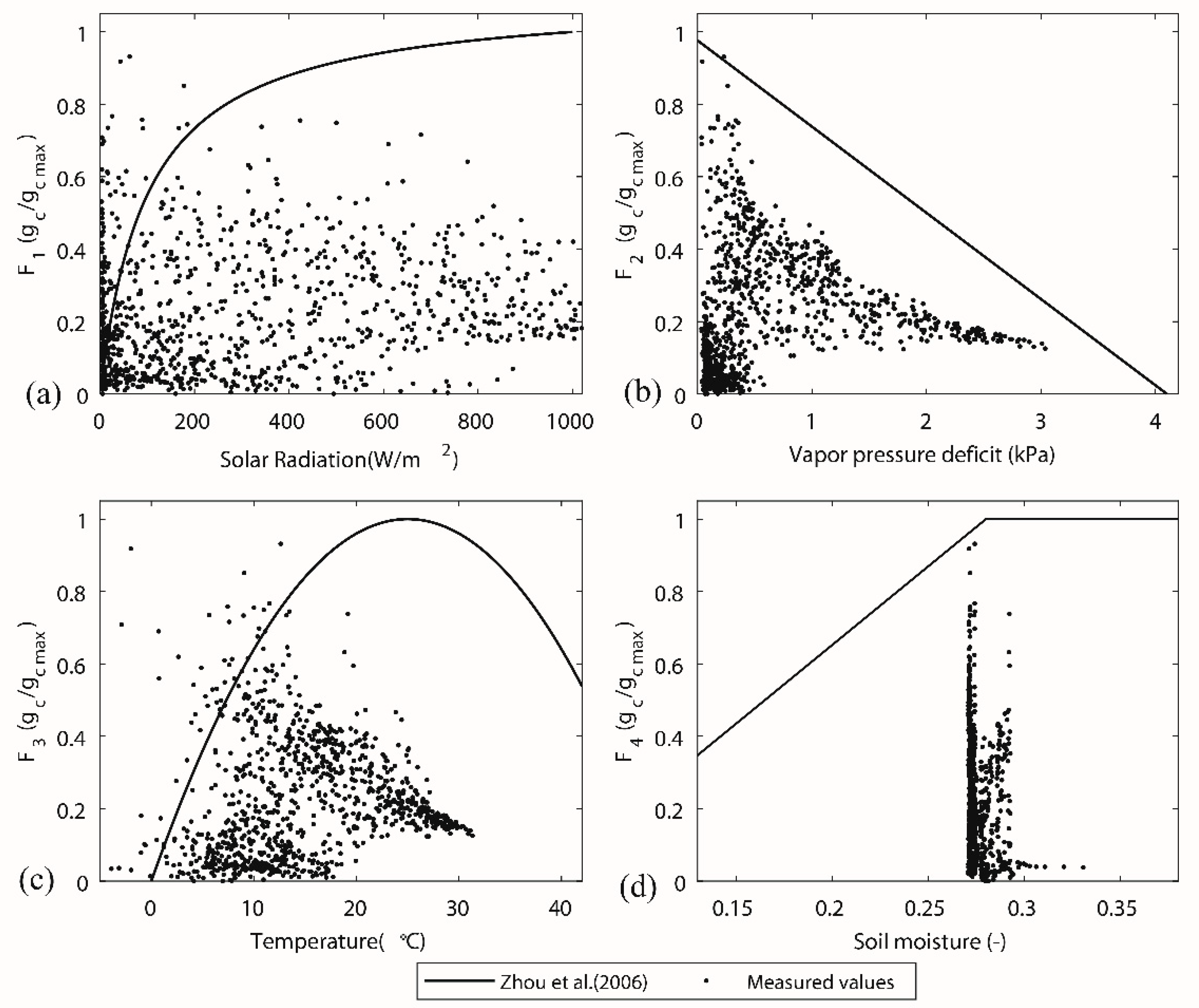
| Stress function (Typical Parameters) | Reference | Stress Function (Zhou et al. [42]’s Parameters) |
|---|---|---|
| 1 | [42,44,46] | . |
| 2 | [43,44] | . |
| 3 | [43,47,48] | 5 |
| 4 | [12,42] | . |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Shao, W.; Vlček, L.; Langhammer, J. Ecohydrological Behaviour of Mountain Beech Forest: Quantification of Stomatal Conductance Using Sap Flow Measurements. Geosciences 2019, 9, 243. https://doi.org/10.3390/geosciences9050243
Su Y, Shao W, Vlček L, Langhammer J. Ecohydrological Behaviour of Mountain Beech Forest: Quantification of Stomatal Conductance Using Sap Flow Measurements. Geosciences. 2019; 9(5):243. https://doi.org/10.3390/geosciences9050243
Chicago/Turabian StyleSu, Ye, Wei Shao, Lukáš Vlček, and Jakub Langhammer. 2019. "Ecohydrological Behaviour of Mountain Beech Forest: Quantification of Stomatal Conductance Using Sap Flow Measurements" Geosciences 9, no. 5: 243. https://doi.org/10.3390/geosciences9050243
APA StyleSu, Y., Shao, W., Vlček, L., & Langhammer, J. (2019). Ecohydrological Behaviour of Mountain Beech Forest: Quantification of Stomatal Conductance Using Sap Flow Measurements. Geosciences, 9(5), 243. https://doi.org/10.3390/geosciences9050243







