New Sensitivity Indices of a 2D Flood Inundation Model Using Gauss Quadrature Sampling
Abstract
1. Introduction
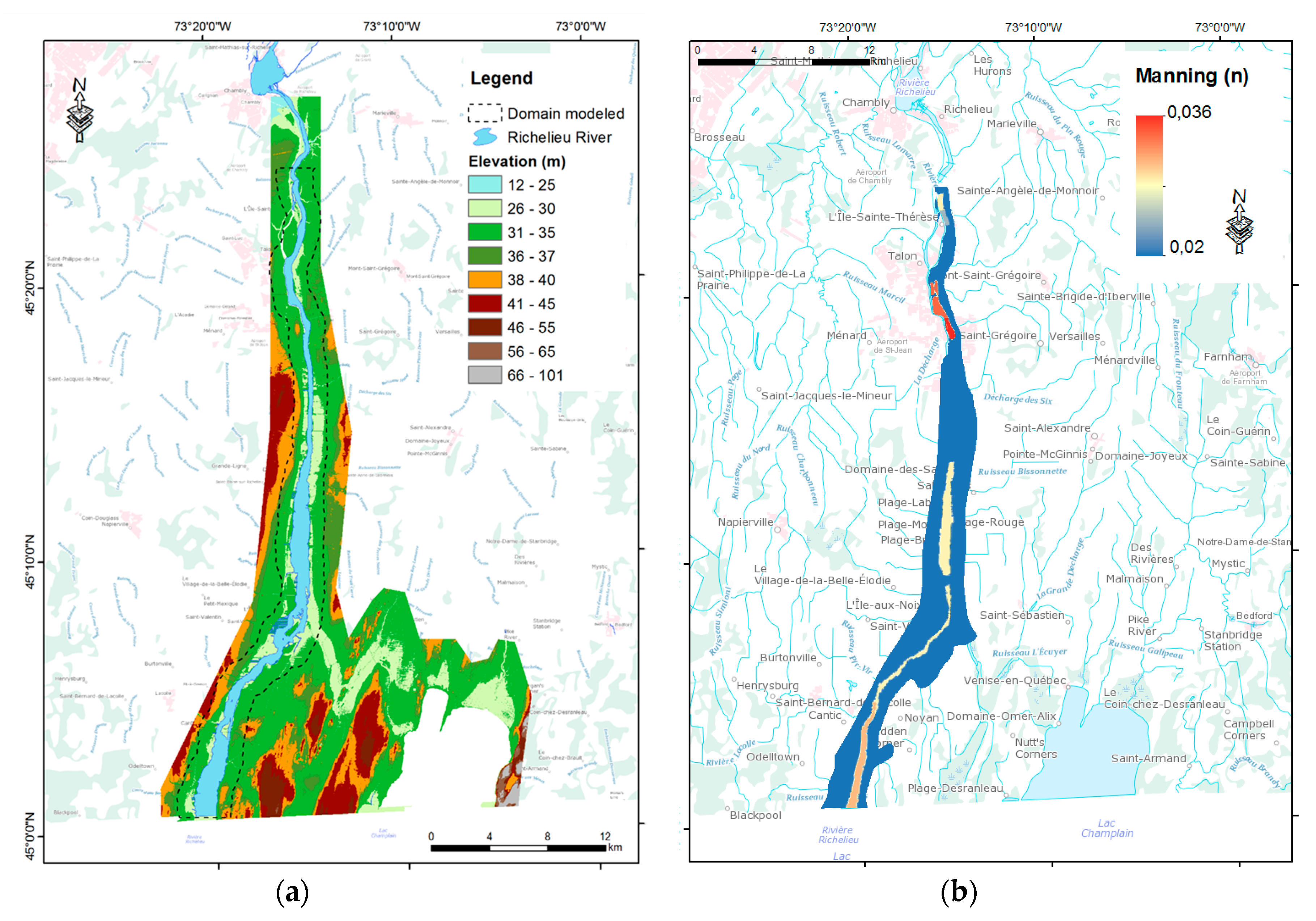
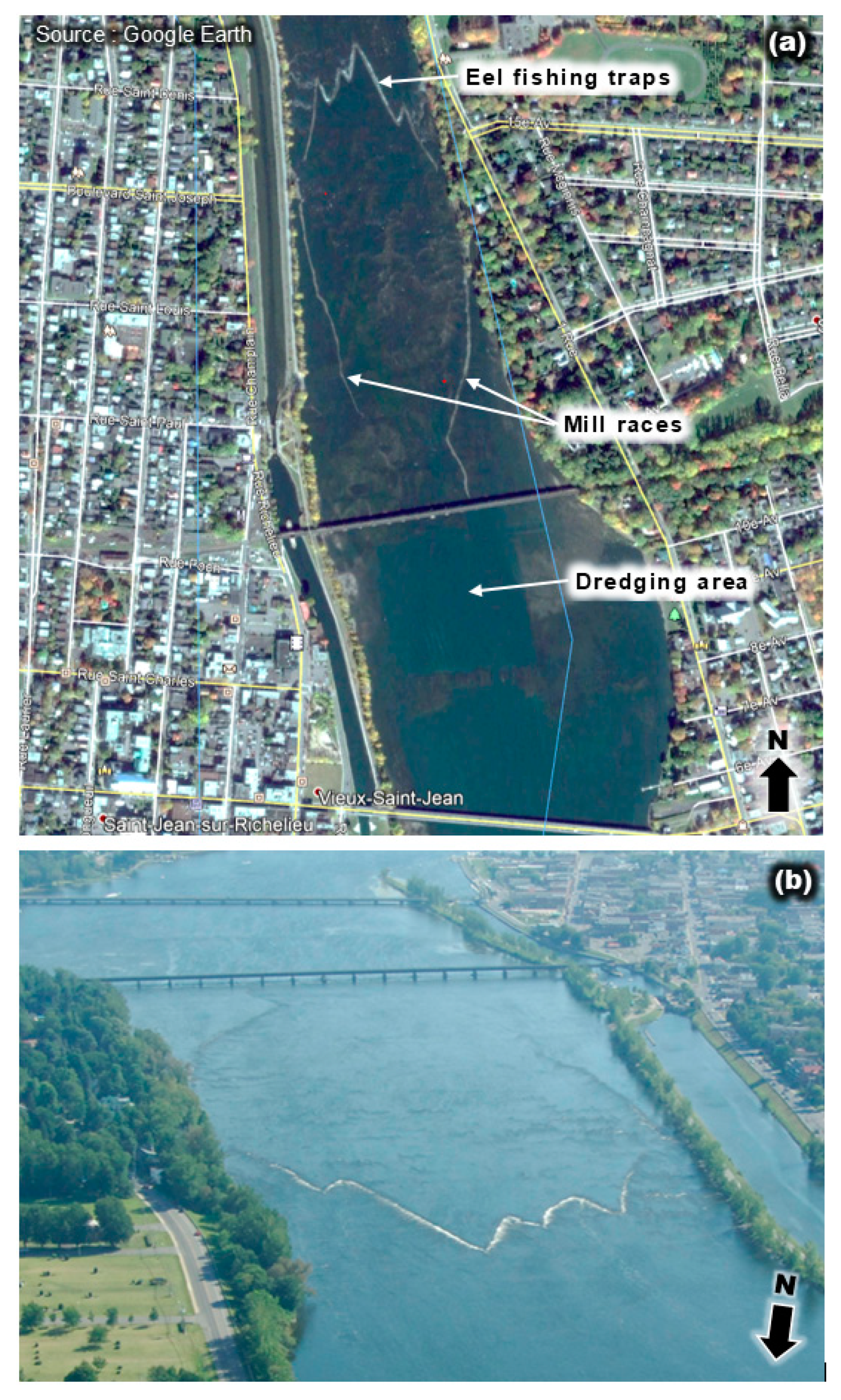
2. Hydraulic Model of Richelieu River
3. The Sensitivity Analysis Method
3.1. Derivative-Based Sensitivity Indices
3.2. Gaussian Quadrature Sampling
3.3. Settings of Input Variables
3.3.1. Flow Rate
3.3.2. Manning’s n Coefficient
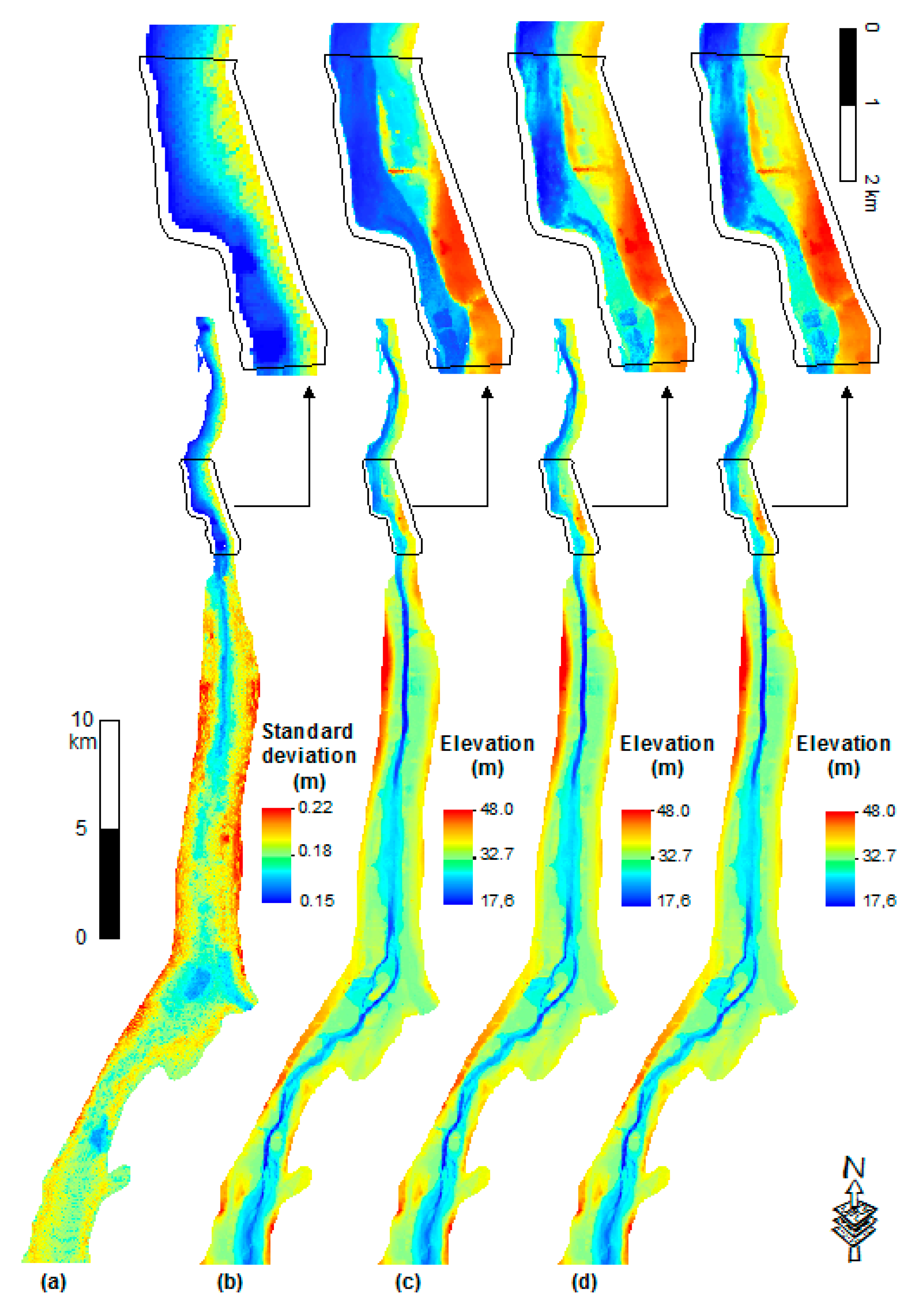
3.3.3. Topography
4. Results and Discussion
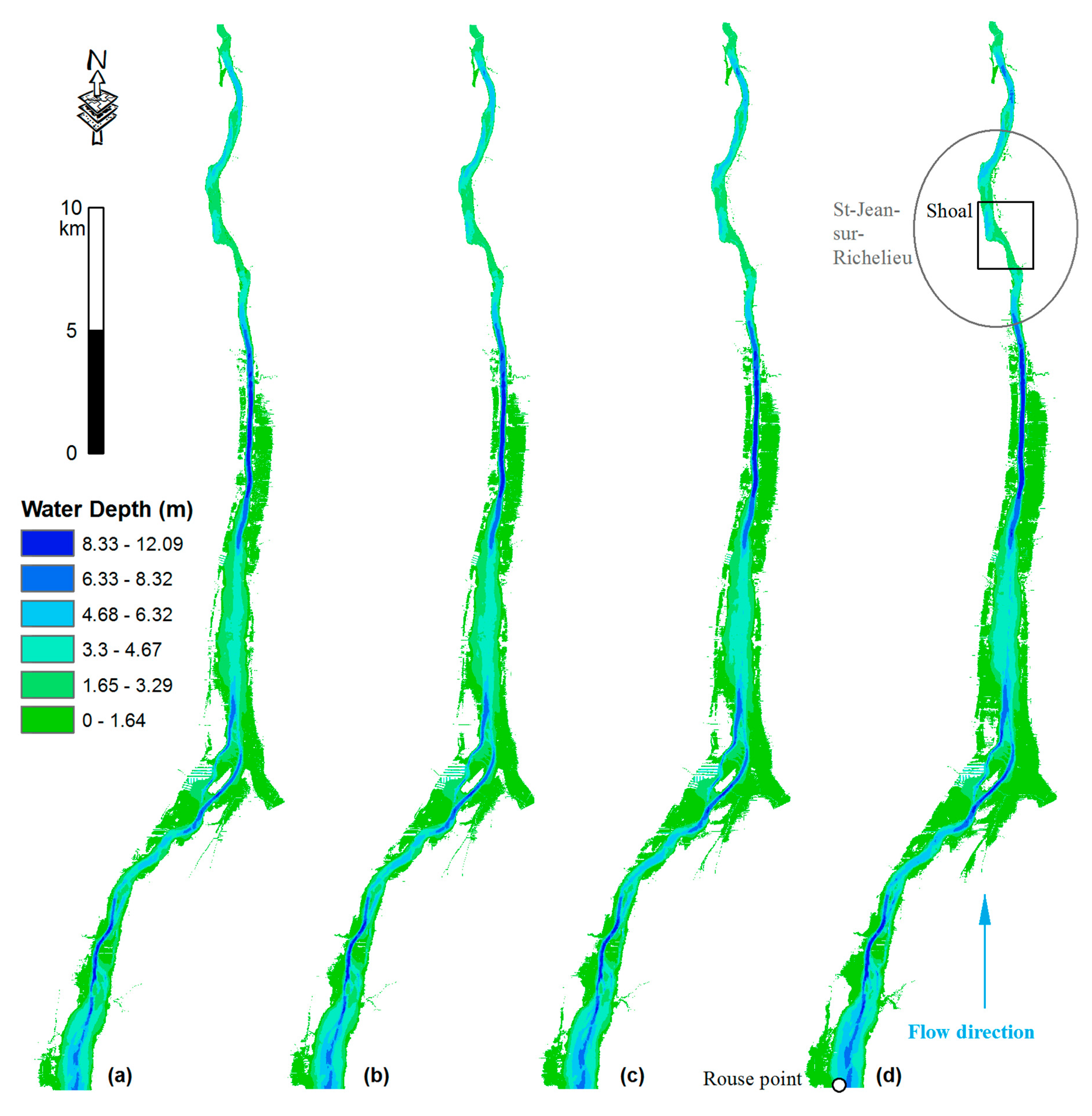
4.1. Water Depth Outputs
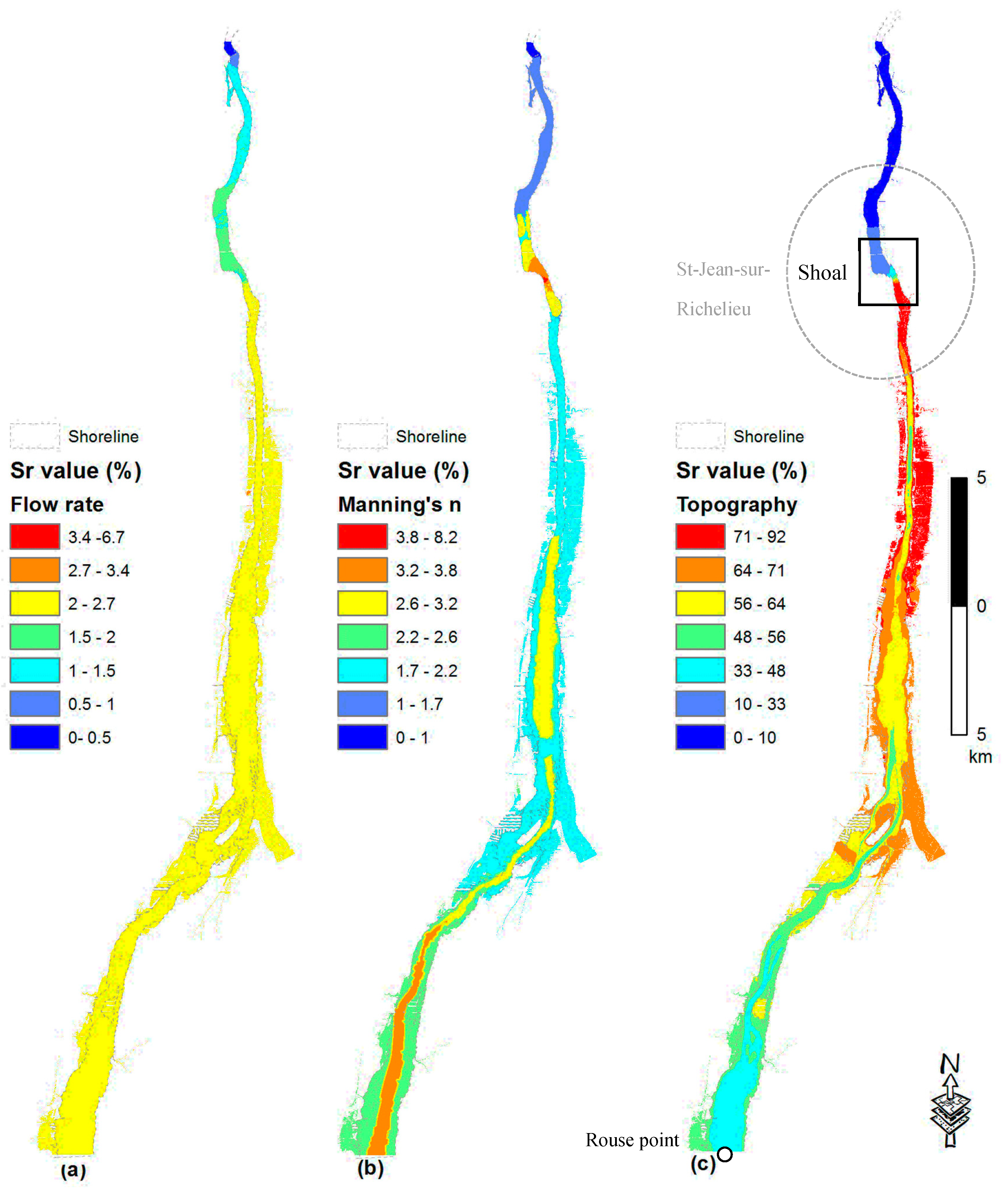
4.2. Results of Sensitivity Analysis
- (i)
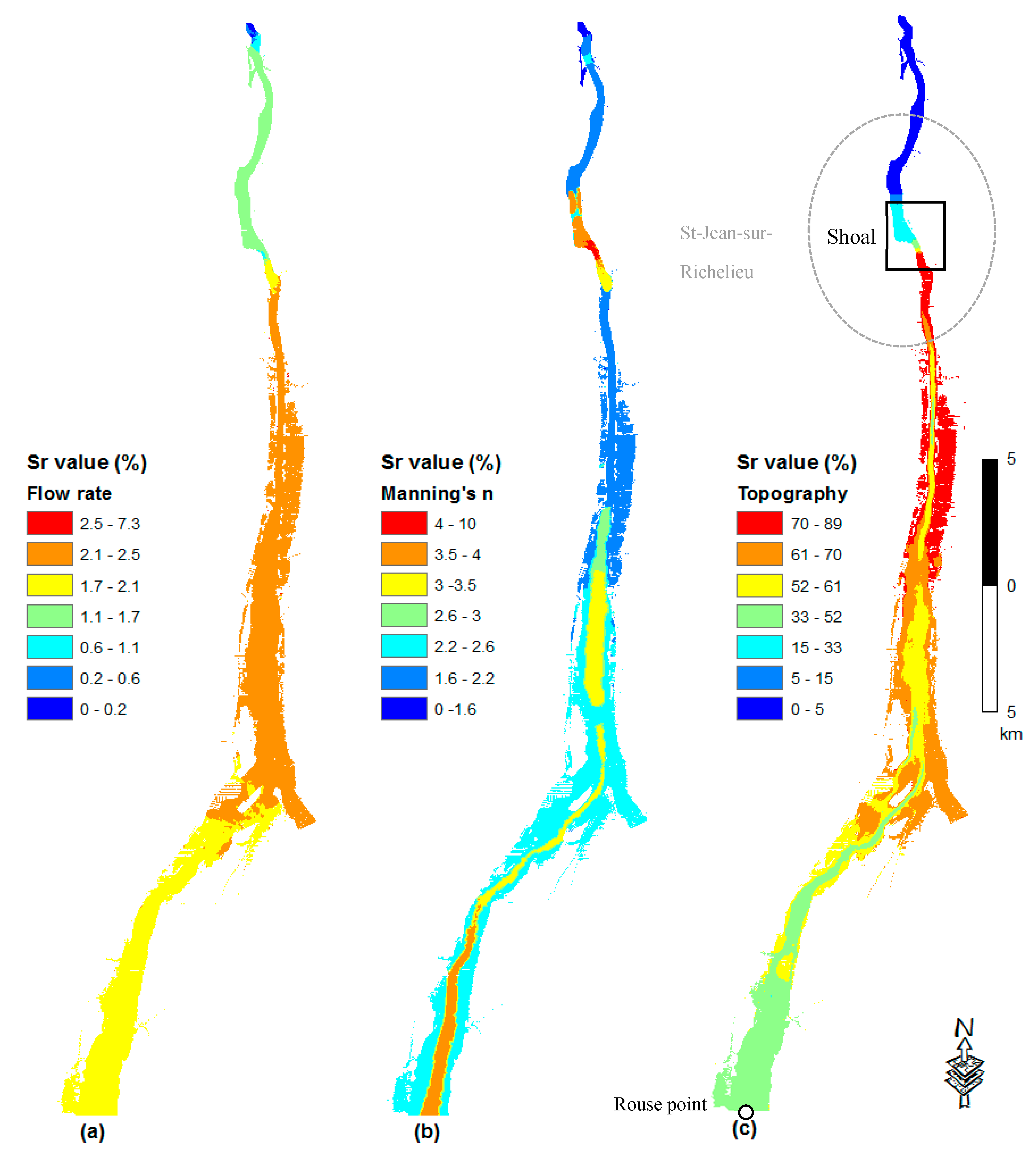
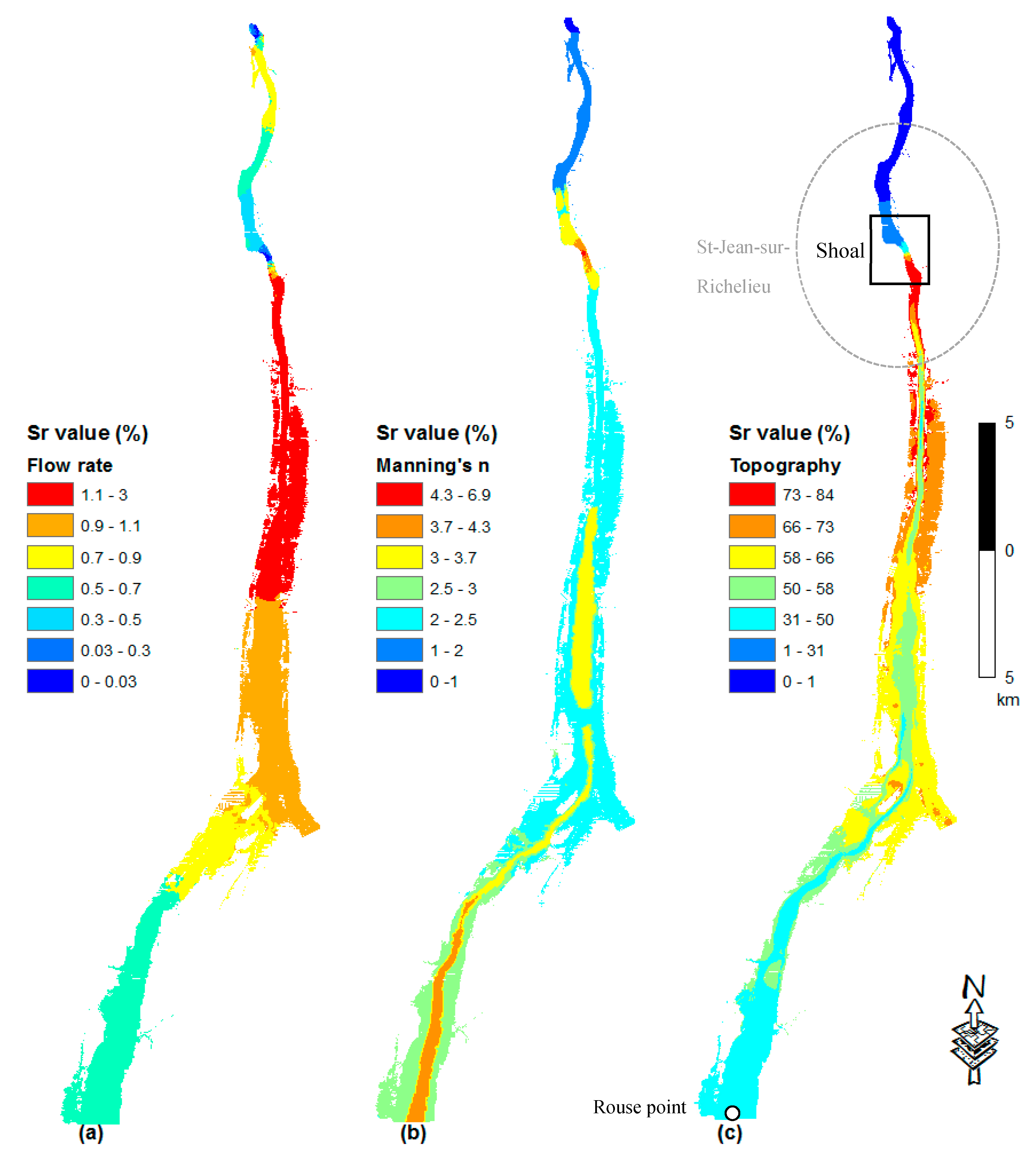
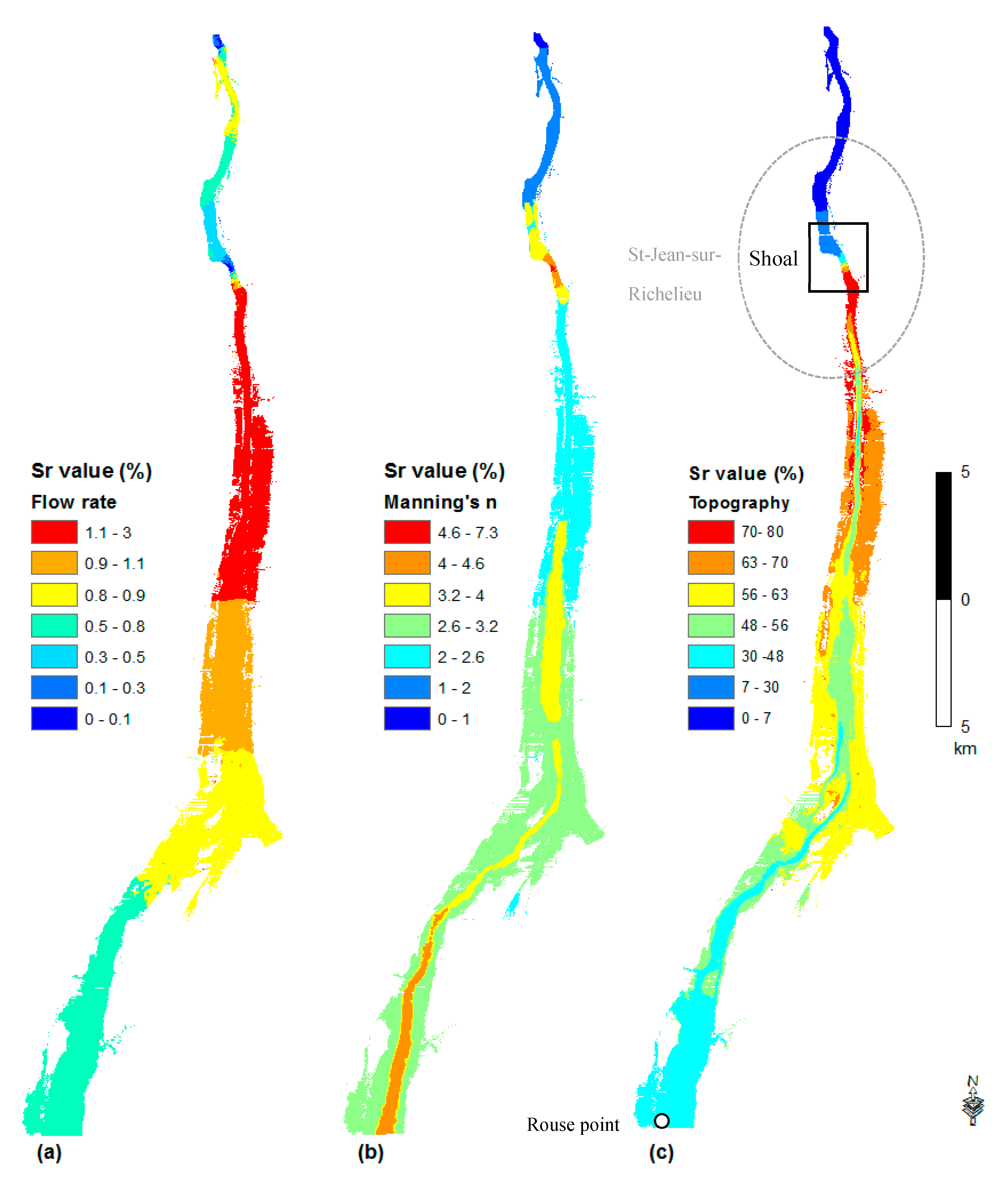
- The sensitivity index for the topography values are the highest, indicating highest impacts on the computed water depths, particularly just upstream of the shoal. At the same time, the Manning’s n coefficient and the flow rate have comparatively lower Sr values. The sensitivity index for the computed water depths, with respect to the topography is highest close to the Saint-Jean-sur-Richelieu shoal area, and decreases gradually further upstream (Figure 5c, Figure 6c, Figure 7c and Figure 8c). This observation suggests that upstream water depths are influenced by the shoal at Saint-Jean-sur-Richelieu, which exerts major control on the hydraulic system for all depth ranges and outflow rates from Lake Champlain;
- (ii)
- The sensitivity index for the flow rate, in each regime is lower in the upstream part and gradually increases in the downstream direction until the shoal, to drop again further downstream (Figure 5a, Figure 6a, Figure 7a and Figure 8a). Such spatial distribution of sensitivity indices for flow rates is most probably due to the influence of the upstream boundary at Rouses Point;
- (iii)
- On the other hand, the sensitivity index for Manning’s n coefficient, is higher for areas where high values of the coefficient were measured, especially in a steep slope and where the riverbed is composed of a coarser substrate (Figure 5b, Figure 6b, Figure 7b and Figure 8b). Among these areas, the rapids of Saint-Jean located at shoal are the most sensitive to the Manning’s n coefficient. Thus, the impact of Manning’s n coefficient on water depth predictions is rather local. This can be explained by the fact that higher Manning’s n coefficients increase the frictional force of the water flow in the channel, reducing the flow velocity and consequently increasing the water level so that more water spreads outside of the bank. In the upstream direction, the sensitivity index to Manning’s n coefficient decreases to compensate the increased flow rate. At the upstream end of the studied reach, Manning’s coefficient contributes more to the uncertainty of the model output than the flow rate (Figure 5b, Figure 6b, Figure 7b and Figure 8b).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cesare, M. First-order analysis of open-channel flow. J. Hydraul. Eng. 1991, 117, 242–247. [Google Scholar] [CrossRef]
- Neal, J.; Fewtrell, T.; Trigg, M. Parallelisation of storage cell flood models using OpenMP. Environ. Model. Softw. 2009, 24, 872–877. [Google Scholar] [CrossRef]
- Peña, F.; Nardi, F.J.H. Floodplain terrain analysis for coarse resolution 2D flood modeling. Dimensions 2018, 5, 52. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal, J.C.; Alfieri, L.; Freer, J. A high-resolution global flood hazard model. AGU 100 2015, 51, 7358–7381. [Google Scholar] [CrossRef] [PubMed]
- Sanders, B.F.; Schubert, J.E.; Detwiler, R.L. ParBreZo: A parallel, unstructured grid, godunov-type, shallow-water code for high-resolution flood inundation modeling at the regional scale. Adv. Water Resour. 2010, 33, 1456–1467. [Google Scholar] [CrossRef]
- Aronica, G.; Hankin, B.; Beven, K. Uncertainty and equifinality in calibrating distributed roughness coefficients in a flood propagation model with limited data. Adv. Water Resour. 1998, 22, 349–365. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.; Hunter, N.; Mason, D.; Cobby, D. Numerical Modelling of Floodplain Flow; John Wiley and Sons Ltd.: Chichester, UK, 2005. [Google Scholar]
- Crosetto, M.; Tarantola, S.; Saltelli, A. Sensitivity and uncertainty analysis in spatial modelling based on GIS. Agr. Ecosyst. Environ. 2000, 81, 71–79. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Montanari, G.A.; Lins, H.; Koutsoyiannis, D.; Brandimarte, L.; Blöschl, G. Flood fatalities in Africa: From diagnosis to mitigation. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- He, M.; Hogue, T.S.; Franz, K.J.; Margulis, S.A.; Vrugt, J.A. Characterizing parameter sensitivity and uncertainty for a snow model across hydroclimatic regimes. Adv. Water Resour. 2011, 34, 114–127. [Google Scholar] [CrossRef]
- Apel, H.; Merz, B.; Thieken, A.H. Quantification of uncertainties in flood risk assessments. JRBM 2008, 6, 149–162. [Google Scholar] [CrossRef]
- Apel, H.; Merz, B.; Thieken, A.H.; Blöschl, G. Flood risk assessment and associated uncertainty. Nat. Hazard. Earth Sys. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Alliau, D.; De Saint Seine, J.; Lang, M.; Sauquet, E.; Renard, B. Étude du risque d’inondation d’un site industriel par des crues extrêmes: De l’évaluation des valeurs extrêmes aux incertitudes hydrologiques et hydrauliques. HAL 2015, 2, 67–74. [Google Scholar] [CrossRef][Green Version]
- Hall, J.; Tarantola, S.; Bates, P.; Horritt, M. Distributed sensitivity analysis of flood inundation model calibration. J. Hydraul. Eng. 2005, 131, 117–126. [Google Scholar] [CrossRef]
- Jung, Y.; Merwade, V. Estimation of uncertainty propagation in flood inundation mapping using a 1-D hydraulic model. Hydrol. Process. 2015, 29, 624–640. [Google Scholar] [CrossRef]
- Nguyen, T.-M.; Richet, Y.; Balayn, P.; Bardet, L. Propagation des incertitudes dans les modeles hydrauliques 1D. Houille Blanche. 2015, 5, 55–62. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J.; Ratto, M.; Matgen, P. Multi-method global sensitivity analysis of flood inundation models. Adv. Water Resour. 2008, 31, 1–14. [Google Scholar] [CrossRef]
- Abily, M.; Bertrand, N.; Delestre, O.; Gourbesville, P.; Duluc, C.-M. Spatial Global Sensitivity Analysis of High. Resolution classified topographic data use in 2D urban flood modelling. Environ. Model. Softw. 2016, 77, 183–195. [Google Scholar] [CrossRef]
- Savage, J.T.S.; Pianosi, F.; Bates, P.; Freer, J.; Wagener, T. Quantifying the importance of spatial resolution and other factors through global sensitivity analysis of a flood inundation model. AGU100 2016, 52, 9146–9163. [Google Scholar]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Butler, M.P.; Reed, P.M.; Fisher-Vanden, K.; Keller, K.; Wagener, T. Identifying parametric controls and dependencies in integrated assessment models using global sensitivity analysis. Environ. Model. Softw. 2014, 59, 10–29. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Letcher, R.A.; Norton, J.P. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar] [CrossRef]
- Nguyen, T.; De Kok, J.; Titus, M. A new approach to testing an integrated water systems model using qualitative scenarios. Environ. Model. Softw. 2007, 22, 1557–1571. [Google Scholar] [CrossRef]
- Singh, R.; Wagener, T.; Crane, R.; Mann, M.; Ning, L. A vulnerability driven approach to identify adverse climate and land use change combinations for critical hydrologic indicator thresholds: Application to a watershed in Pennsylvania, USA. Water Resour. Res. 2014, 50, 3409–3427. [Google Scholar] [CrossRef]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.-B.; Pfister, L.; Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Apel, H.; Aronica, G.; Kreibich, H.; Thieken, A. Flood risk analyses—How detailed do we need to be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- Werner, M.; Blazkova, S.; Petr, J. Spatially distributed observations in constraining inundation modelling uncertainties. Hydrol. Process. 2005, 19, 3081–3096. [Google Scholar] [CrossRef]
- Horritt, M. Stochastic modelling of 1-D shallow water flows over uncertain topography. J. Comput. Phys. 2002, 180, 327–338. [Google Scholar] [CrossRef]
- Horritt, M. A linearized approach to flow resistance uncertainty in a 2-D finite volume model of flood flow. J. Hydrol. 2006, 316, 13–27. [Google Scholar] [CrossRef]
- Cobby, D.M.; Mason, D.C.; Horritt, M.S.; Bates, P.D. Two-dimensional hydraulic flood modelling using a finite-element mesh decomposed according to vegetation and topographic features derived from airborne scanning laser altimetry. Hydrol. Process. 2003, 17, 1979–2000. [Google Scholar] [CrossRef]
- Eilertsen, R.S.; Hansen, L. Morphology of river bed scours on a delta plain revealed by interferometric sonar. Geomorphology 2008, 94, 58–68. [Google Scholar] [CrossRef]
- Nicholas, A.; Mitchell, C. Numerical simulation of overbank processes in topographically complex floodplain environments. Hydrol. Process. 2003, 17, 727–746. [Google Scholar] [CrossRef]
- Woodhead, S.; Asselman, N.; Zech, Y.; Soares-Frazão, S.; Bates, P.; Kortenhaus, A. Evaluation of inundation models. FLOODsite Project Report T08-07-01. 2007. Available online: http://www.floodsite.net (accessed on 14 May 2019).
- Johnson, P.A. Uncertainty of hydraulic parameters. J. Hydraul. Eng. 1996, 122, 112–114. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Effects of rating-curve uncertainty on the calibration of numerical hydraulic models. In Proceedings of the First IAHR European Congress, Edinburgo, Scotland, 4 May 2010. [Google Scholar]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Norton, J. An introduction to sensitivity assessment of simulation models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Devenish, B.; Francis, P.; Johnson, B.; Sparks, R.; Thomson, D. Sensitivity analysis of dispersion modeling of volcanic ash from Eyjafjallajökull in May 2010. J. Geophy. Res. Atmos. 2012, 117, 1–21. [Google Scholar] [CrossRef]
- Paton, F.; Maier, H.; Dandy, G. Relative magnitudes of sources of uncertainty in assessing climate change impacts on water supply security for the southern Adelaide water supply system. Water Resour. Res. 2013, 49, 1643–1667. [Google Scholar] [CrossRef]
- Tung, Y.K.; Yen., B.C. Hydrosystems Engineering Uncertainty Analysis; American Society of Civil Engineers: New York, NY, USA, 2005. [Google Scholar]
- Kucherenko, S.; Tarantola, S.; Annoni, P. Estimation of global sensitivity indices for models with dependent variables. Comput. Phys. Commun. 2012, 183, 937–946. [Google Scholar] [CrossRef]
- Oakley, J.E.; O’Hagan, A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2004, 66, 751–769. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, J. Illustration of sampling-based methods for uncertainty and sensitivity analysis. Risk Anal. 2002, 22, 591–622. [Google Scholar] [CrossRef] [PubMed]
- Iman, R.L.; Helton, J.C. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal. 1988, 8, 71–90. [Google Scholar] [CrossRef]
- Storlie, C.B.; Swiler, L.P.; Helton, J.C.; Sallaberry, C.J. Implementation and evaluation of nonparametric regression procedures for sensitivity analysis of computationally demanding models. Reliab. Eng. Syst. Saf. 2009, 94, 1735–1763. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Tang, T.; Reed, P.; Wagener, T.; Van Werkhoven, K. Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation. Hydrol. Earth Syst. Sc. Discussions 2006, 3, 3333–3395. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Borgonovo, E.; Tarantola, S.; Plischke, E.; Morris, M. Transformations and invariance in the sensitivity analysis of computer experiments. J. Roy. Stat. Soc. Ser. B (Stat. Methodol.) 2014, 76, 925–947. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Kucherenko, S. Derivative based global sensitivity measures and their link with global sensitivity indices. Math. Comput. Simulat. 2009, 79, 3009–3017. [Google Scholar]
- Parajuli, P.B. SWAT Bacteria Sub-Model Evaluation And Application. Ph.D. Thesis, Kansas State University, Manhattan, KS, USA, January 2007. [Google Scholar]
- Chaubey, I.; Haan, C.; Salisbury, J.; Grunwald, S. Quantifying Model Output Uncertainty Due To Spatial Variability Of Rainfall. JAWRA 1999, 35, 1–11. [Google Scholar] [CrossRef]
- Khanal, S.; Parajuli, P.B. Sensitivity Analysis and Evaluation of Forest Biomass Production Potential Using SWAT Model. J. Sustain. Bioenerg. Systems 2014, 4, 136. [Google Scholar] [CrossRef]
- Riboust, P.; Brissette, F. Climate change impacts and uncertainties on spring flooding of Lake Champlain and the Richelieu River. JAWRA 2015, 51, 776–793. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Trombley, T.J.; Olson, S.A. Assessment of the spatial extent and height of flooding in Lake Champlain during May 2011, using satellite remote sensing and ground-based information. USGS 2014. [Google Scholar] [CrossRef]
- Secretan, Y. H2D2 Software. 2013. Available online: http://www.gre-ehn.ete.inrs.ca/H2D2/contenu_download (accessed on 14 May 2019).
- Boudreau, P.J.-F.; Cantin, A.; Bouchard, O.; Champoux, P.; Fiset, J.-M.; Fortin, N.; Guy Mori, J.T. Création d’un modèle hydraulique 2D de la rivière Richelieu entre Rouses Point et Sorel. Available online: https://legacyfiles.ijc.org/tinymce/uploaded/LCRRTWG/T%c3%a2che_2-3_Rivi%c3%a8re_Richelieu_2D_mod%c3%a9lisation_EC-SHN_FR.pdf (accessed on 14 October 2015).
- Youn, B.D.; Choi, K.K.; Du, L. Enriched Performance Measure Approach for Reliability-Based Design Optimization. AIAA J. 2005, 43, 874–884. [Google Scholar] [CrossRef]
- Larocque, M.; Banton, O. Determining parameter precision for modeling nitrate leaching: Inorganic fertilization in nordic climates. Soil Sci. Soc. Am. J. 1994, 58, 396–400. [Google Scholar] [CrossRef]
- Chokmani, K.; Viau, A.; Bourgeois, G. Analyse de l’incertitude de quatre modèles de phytoprotection relative à l’erreur des mesures des variables agrométéorologiques d’entrée. Agronomie. HAL 2001, 21, 147–167. [Google Scholar]
- Turanyi, T.; Rabitz, H. Local Methods. Sensitivity Analysis; Wiley: New York, NY, USA, 2000; pp. 81–99. [Google Scholar]
- Mitchell, A.R.; Griffiths, D.F. The Finite Difference Method In Partial Differential Equations; John Wiley: New York, NY, USA, 1980. [Google Scholar]
- Hill, M.; Tiedeman, C. Effective Calibration of Groundwater Models, with Analysis of Data, Sensitivities, Predictions, and Uncertainty; John Wiely: New York, NY, USA, 2007. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput.Simulat. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Babolian, E.; MasjedJamei, M.; Eslahchi, M. On numerical improvement of Gauss–Legendre quadrature rules. Appl. Math. Comput. 2005, 160, 779–789. [Google Scholar] [CrossRef]
- Dagde, K.K.; Akpa, J.G. Numerical Simulation of an Industrial Absorber for Dehydration of Natural Gas. Using Triethylene Glycol. J. Eng. 2014. [Google Scholar] [CrossRef][Green Version]
- Tørvi, H.; Hertzberg, T. Estimation of uncertainty in dynamic simulation results. Comput. Chem. Eng. 1997, 21, S181–S185. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: New York, NY, USA, 1964. [Google Scholar]
- Christian, J.T.; Baecher, G.B. Point-estimate method as numerical quadrature. J. Geotech. Geoenviron. 1999, 125, 779–786. [Google Scholar] [CrossRef]
- Stedinger, J.R. Confidence intervals for design events. J. Hydraul. Eng-Asce. 1983, 109, 13–27. [Google Scholar] [CrossRef]
- Pukelsheim, F. The three sigma rule: The American statistician. ASA 1994, 48, 88–91. [Google Scholar]
- Goncalves, J.; Oliveira, A. Accuracy analysis of DEMs derived from ASTER imagery. Intern. Arch. Photogramm. Remote Sens. 2004, 35, 168–172. [Google Scholar]
- Kornus, W.; Alamús, R.; Ruiz, A.; Talaya, J. Assessment of DEM accuracy derived from SPOT-5 high resolution stereoscopic imagery. Intern. Arch. Photogramm. Remote Sens. 2004, 35, 445–453. [Google Scholar]
- Di Baldassarre, G.; Claps, P. A hydraulic study on the applicability of flood rating curves. Hydrol. Res. 2011, 42, 10–19. [Google Scholar] [CrossRef]
- Wilson, M.; Atkinson, P. The use of elevation data in flood inundation modelling: A comparison of ERS interferometric SAR and combined contour and differential GPS data. Intern. J. River Basin Manag. 2005, 3, 3–20. [Google Scholar] [CrossRef]

| 759 | 39.4 | 690.75 | 827.24 |
| 824 | 36 | 761.64 | 886.35 |
| 936 | 33.7 | 877.62 | 994.37 |
| 1113 | 39.4 | 1044.75 | 1181.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oubennaceur, K.; Chokmani, K.; Nastev, M.; Gauthier, Y.; Poulin, J.; Tanguy, M.; Raymond, S.; Lhissou, R. New Sensitivity Indices of a 2D Flood Inundation Model Using Gauss Quadrature Sampling. Geosciences 2019, 9, 220. https://doi.org/10.3390/geosciences9050220
Oubennaceur K, Chokmani K, Nastev M, Gauthier Y, Poulin J, Tanguy M, Raymond S, Lhissou R. New Sensitivity Indices of a 2D Flood Inundation Model Using Gauss Quadrature Sampling. Geosciences. 2019; 9(5):220. https://doi.org/10.3390/geosciences9050220
Chicago/Turabian StyleOubennaceur, Khalid, Karem Chokmani, Miroslav Nastev, Yves Gauthier, Jimmy Poulin, Marion Tanguy, Sebastien Raymond, and Rachid Lhissou. 2019. "New Sensitivity Indices of a 2D Flood Inundation Model Using Gauss Quadrature Sampling" Geosciences 9, no. 5: 220. https://doi.org/10.3390/geosciences9050220
APA StyleOubennaceur, K., Chokmani, K., Nastev, M., Gauthier, Y., Poulin, J., Tanguy, M., Raymond, S., & Lhissou, R. (2019). New Sensitivity Indices of a 2D Flood Inundation Model Using Gauss Quadrature Sampling. Geosciences, 9(5), 220. https://doi.org/10.3390/geosciences9050220








