Machine Learning for Projecting Extreme Precipitation Intensity for Short Durations in a Changing Climate
Abstract
1. Introduction
2. Background
2.1. Intensity–Duration–Frequency Curves
2.2. Supervised Machine Learning
- Features. Feature (X) refers to the properties of the data that are known for the training dataset and projection datasets.
- Label. Label (Y) refers to the property that is only known for the training dataset and is unknown in the projection dataset. The goal is to predict the label for projection data using their features.
- Training phase. This is a procedure where a set of data is available, such that both features and labels are given for each data entry. The training phase takes these data entries as input and produces a compact description, namely the ML model, which describes the input–output relationship.
- Prediction phase. This is a procedure where a set of data, namely the testing data, is given but with features without labels only. The procedure also takes the model obtained above as input and outputs a label for each entry of the training data.
2.3. Spatial Downscaling
- Find a parameterized model to abstract the downscaling relationship between the global climate and local climate. The model is usually parameterized by a set of values.
- Use historical data to fit the model and find the parameters for the model. These parameters are assumed not to change over time. Perform bias correction to the results using methods like the Constructed Analogue method [43].
- Compute the local climate data using the model with fitted parameters and the future global climate.
3. Methods
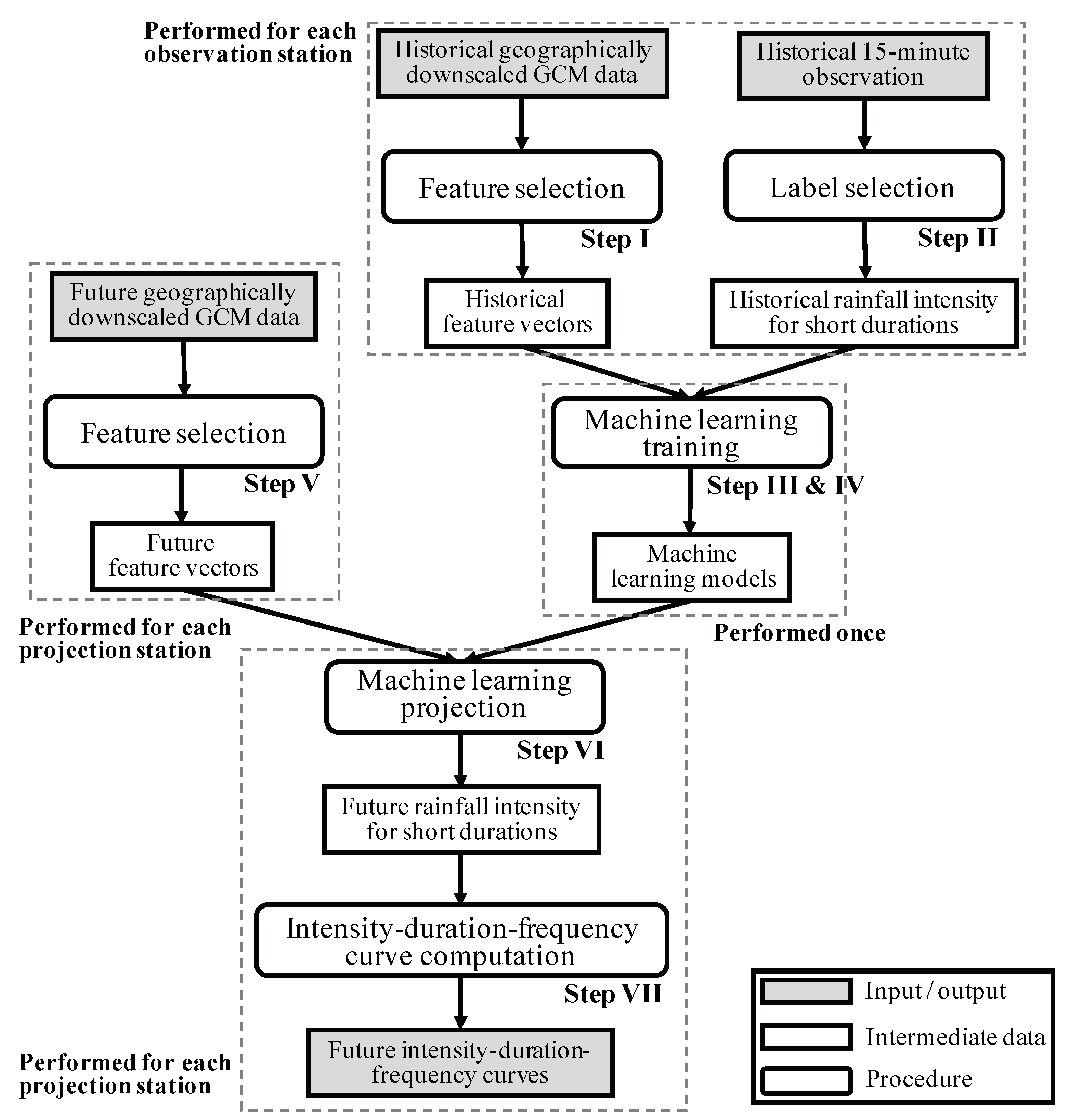
3.1. Overview
- Obtain some number of entries with both properties and targets. Taking these entries as the input, compute a description of the relationship between the entry properties and the targets.
- Make the assumption that the relationship between properties and targets holds for the projected entries.
- Use the above relationship as well as the properties for the projected entries, then compute the target value of the projected entries.
3.2. Detailed Steps
3.2.1. Step I: Historical Feature Selection
- 1.
- One-day and two-day precipitation intensities of the events with return periods of 2, 5, and 10 years.
- 2.
- Average daily precipitation.
- 3.
- Number of rainy days.
- 4.
- Top 20 heaviest daily precipitation amounts in descending order.
- 5.
- Number of days with a daily precipitation of more than 5, 10, 15, 20, 30, 40, 50, and 60 mm.
- 6.
- Altitude of the location. This was obtained from the National Oceanic and Atmospheric Administration Climate Data Online (NOAA CDO).
- 7.
- The coordinates of the location, that is, latitude and longitude.
- 8.
- Climate division of the location. Since there are 344 climate divisions for the contiguous US [48], this feature had a value from 1 to 344. The use of climate division is to reinforce the geographic proximity between stations.
3.2.2. Step II: Label Selection
3.2.3. Step III: Model Selection
3.2.4. Step IV: Future Feature Selection
3.2.5. Step V: Model Training
3.2.6. Step VI: Machine-Learning Projection
3.2.7. Step VII: IDF Curve Reconstruction
3.3. Validation
3.3.1. k-Fold Cross Validation
- Collect data from n stations. For a station, the data contains the downscaled GCM simulations of daily precipitation data and locally observed precipitation data with better resolution.
- Partition n stations of data into k disjoint and equal-sized sets, namely . Repeat the following step (step 3) k times.
- In the i-th repetition, use the i-th dataset as the test data (namely ), and the remaining data are used as training data (namely, ). Use the training data to train a machine learning model as described in the previous section and apply it to compute an IDF curve for stations in . Calculate the error based on the local precipitation testing data.
- Find the average of all errors in all k iterations above.
3.3.2. Validation of IDF Curves
4. Analysis and Results
4.1. Data and Model Selection
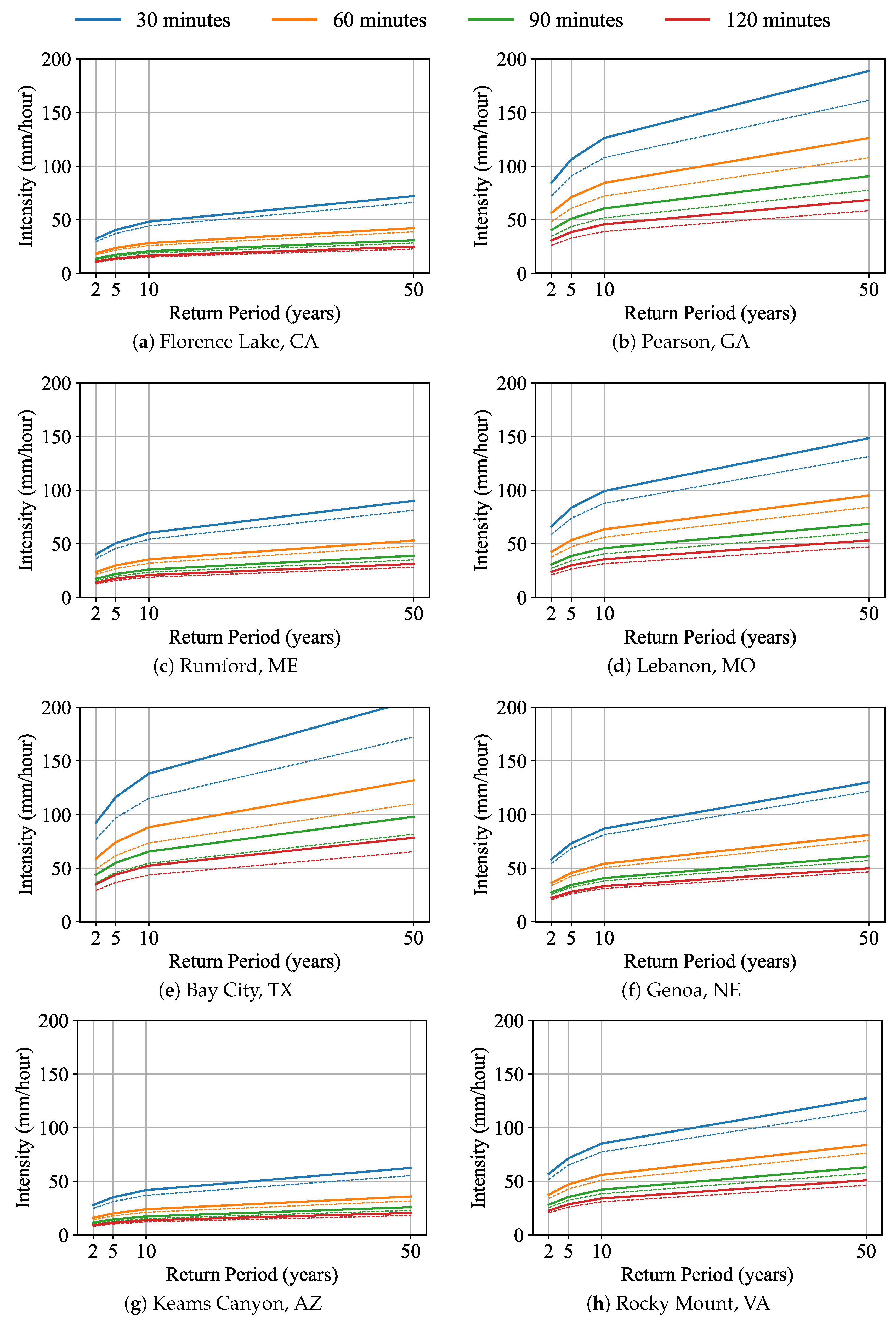
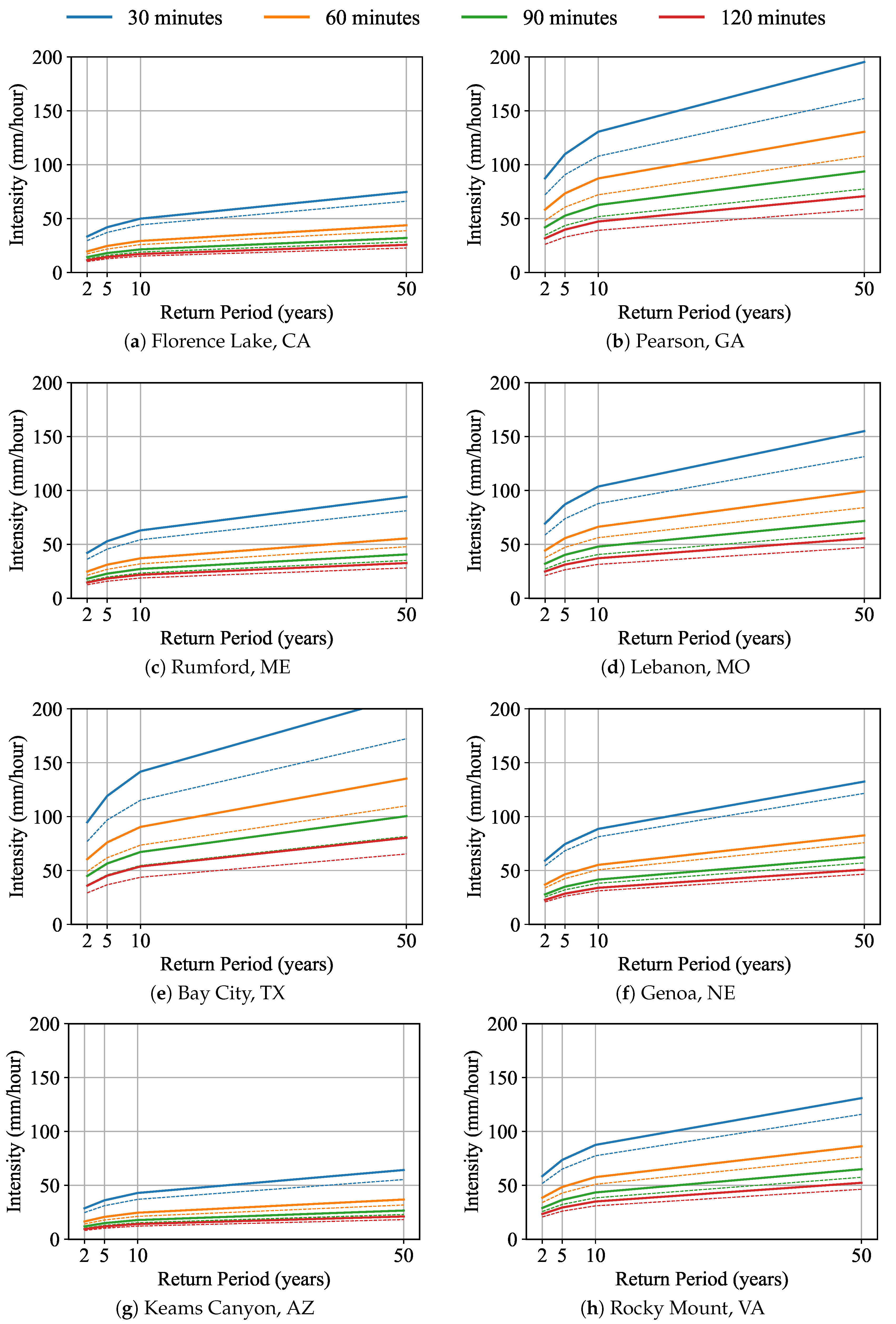
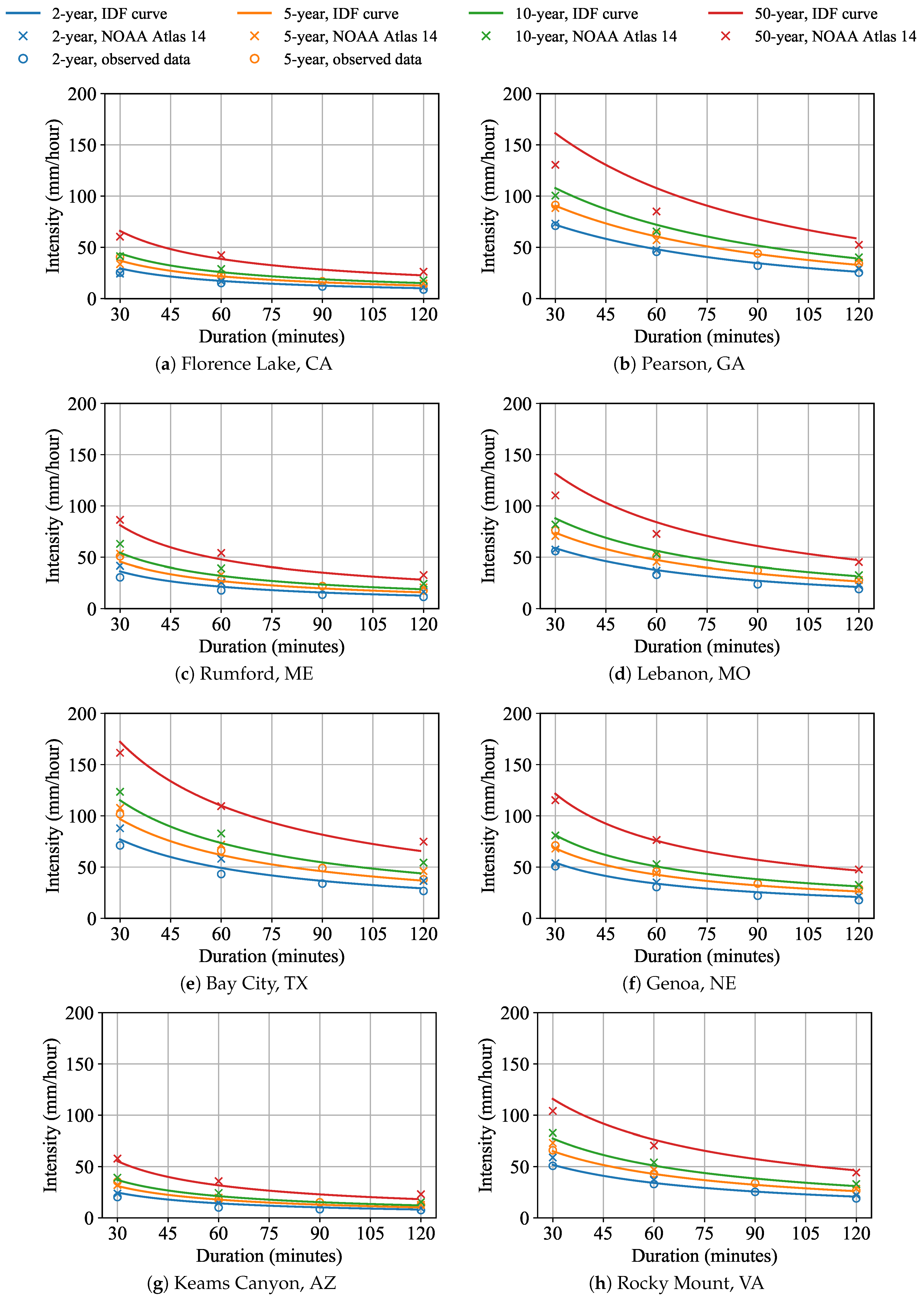
4.2. Validation and Historical IDF Curves
- The ∘-shape data points represent precipitation intensity extracted from the historical data from NOAA CDO, with intensities of 30, 60, 90, and 120 min and return periods of 2 and 5 years.
- The solid lines are IDF curves fitted based on the above observed data using Equation (3). This equation was used for all return periods, and four IDF curves were plotted for return periods of 2, 5, 10, and 50 years.
- The ×-shape data points represent the precipitation intensity obtained from NOAA Atlas 14.
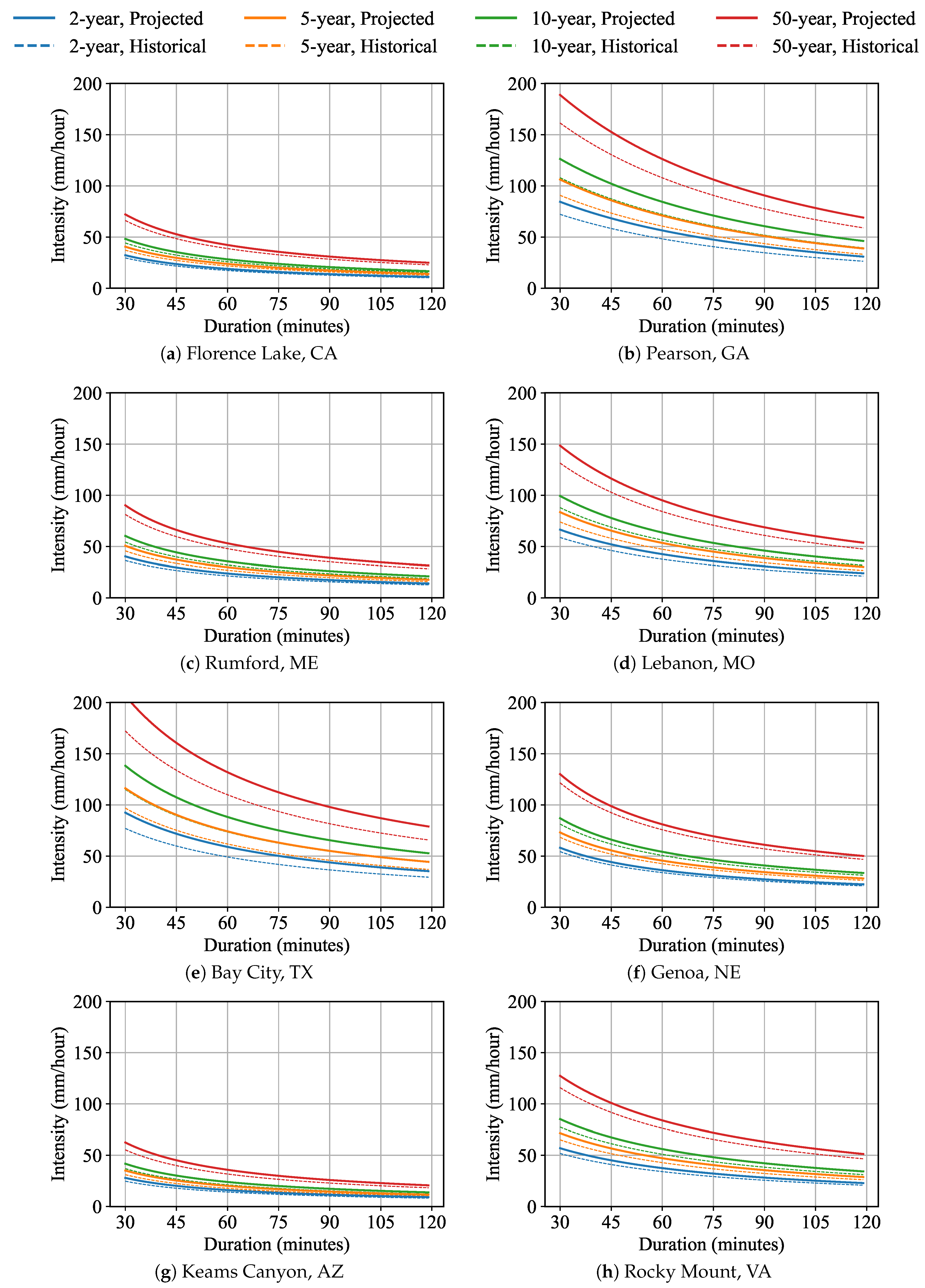
4.3. Projection Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Frequency Analysis on Precipitation Intensity
| Station | Location | State | NRMSE | NMAE |
|---|---|---|---|---|
| 010140 | ALBERTA | AL | 0.109 | 0.077 |
| 034839 | MILLWOOD DAM | AR | 0.122 | 0.11 |
| 026119 | ORACLE 2 SE | AZ | 0.057 | 0.051 |
| 048025 | SAWYERS BAR RANGER STATION | CA | 0.145 | 0.117 |
| 052790 | EVERGREEN | CO | 0.111 | 0.104 |
| 066942 | ROCKVILLE | CT | 0.09 | 0.077 |
| 076410 | NEWARK UNIVERSITY FARM | DE | 0.142 | 0.12 |
| 083538 | GRACEVILLE 1 SW | FL | 0.067 | 0.062 |
| 093312 | FARGO | GA | 0.133 | 0.117 |
| 510055 | AHUIMANU LOOP | HI | 0.061 | 0.053 |
| 130608 | BELLEVUE L AND D 12 | IA | 0.087 | 0.075 |
| 114355 | ILLINOIS CITY DAM 16 | IL | 0.064 | 0.06 |
| 120830 | BLUFFTON 6 N | IN | 0.149 | 0.128 |
| 146024 | ONAGA 12 SSW | KS | 0.049 | 0.04 |
| 153929 | HODGENVILLE LINCOLN | KY | 0.169 | 0.12 |
| 161411 | CALHOUN RES STATION | LA | 0.144 | 0.134 |
| 190998 | BUFFUMVILLE LAKE | MA | 0.182 | 0.174 |
| 180700 | BELTSVILLE | MD | 0.11 | 0.078 |
| 170273 | AUGUSTA | ME | 0.048 | 0.039 |
| 200662 | BELLAIRE | MI | 0.06 | 0.054 |
| 218323 | TRACY | MN | 0.111 | 0.107 |
| 230204 | APPLETON CITY | MO | 0.076 | 0.065 |
| 227276 | RALEIGH 6 N | MS | 0.052 | 0.045 |
| 311241 | BURLINGTON | NC | 0.126 | 0.118 |
| 325993 | MINOT EXPERIMENT STATION | ND | 0.048 | 0.044 |
| 250075 | ALBION 7 W | NE | 0.107 | 0.089 |
| 273182 | FRANKLIN FALLS DAM | NH | 0.085 | 0.075 |
| 281351 | CAPE MAY 2 NW | NJ | 0.155 | 0.141 |
| 292700 | EAGLE NEST | NM | 0.215 | 0.207 |
| 264698 | LOVELOCK | NV | 0.2 | 0.193 |
| 309442 | WHITNEY POINT DAM | NY | 0.058 | 0.049 |
| 332272 | DOVER DAM | OH | 0.103 | 0.097 |
| 340179 | ALTUS IRIG RES STATION | OK | 0.07 | 0.062 |
| 369367 | WAYNESBURG 1 E | PA | 0.136 | 0.126 |
| 375215 | NEWPORT ROSE | RI | 0.209 | 0.208 |
| 383468 | GEORGETOWN 2 E | SC | 0.158 | 0.146 |
| 391452 | CARPENTER 4 NNE | SD | 0.066 | 0.06 |
| 406170 | MONTEREY | TN | 0.157 | 0.129 |
| 414679 | JUSTIN | TX | 0.105 | 0.077 |
| 420086 | ALTON | UT | 0.14 | 0.123 |
| 446475 | PAINTER 2 W | VA | 0.108 | 0.1 |
| 433914 | HIGHGATE FALLS | VT | 0.101 | 0.09 |
| 473038 | GENOA DAM 8 | WI | 0.049 | 0.044 |
| 463238 | FREEMANSBURG 5 NE | WV | 0.096 | 0.074 |
| Average | 0.110 | 0.097 |
References
- U.S. Global Change Research Program (USGCRP). Impacts, Risks, and Adaptation in the United States: Fourth National Climate Assessment, Volume II; USGCRP: Washington, DC, USA, 2018. [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Global warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Ali, H.; Mishra, V. Increase in Subdaily Precipitation Extremes in India Under 1.5 and 2.0° Warming Worlds. Geophys. Res. Lett. 2018, 45, 6972–6982. [Google Scholar] [CrossRef]
- Newby, M.; Franks, S.W.; White, C.J. Estimating urban flood risk-uncertainty in design criteria. Proc. Int. Assoc. Hydrol. Sci. 2015, 370, 3–7. [Google Scholar] [CrossRef][Green Version]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef]
- Krishnamurthy, L.; Vecchi, G.A.; Yang, X.; van der Wiel, K.; Balaji, V.; Kapnick, S.B.; Jia, L.; Zeng, F.; Paffendorf, K.; Underwood, S. Causes and probability of occurrence of extreme precipitation events like Chennai 2015. J. Clim. 2018. [Google Scholar] [CrossRef]
- Nogal, M.; O’Connor, A.; Martinez-Pastor, B.; Caulfield, B. Novel probabilistic resilience assessment framework of transportation networks against extreme weather events. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 04017004. [Google Scholar] [CrossRef]
- Tabari, H.; Willems, P. Anomalous Extreme Rainfall Variability Over Europe—Interaction between Climate Variability and Climate Change. In New Trends in Urban Drainage Modelling; Mannina, G., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 375–379. [Google Scholar]
- Mailhot, A.; Duchesne, S. Design criteria of urban drainage infrastructures under climate change. J. Water Resour. Plan. Manag. 2009, 136, 201–208. [Google Scholar] [CrossRef]
- Committee, A.S. Flood Resistant Design and Construction; Technical Report; American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Kilgore, R.T.; Herrmann, G.R.; Thomas, W.O., Jr.; Thompson, D.B. Highways in the River Environment- Floodplains, Extreme Events, Risk, and Resilience; Technical Report; Federal Highway Administration: Washington, DC, USA, 2016. [Google Scholar]
- Saini, A.; Tien, I. Impacts of climate change on the assessment of long-term structural reliability. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 04017003. [Google Scholar] [CrossRef]
- Huard, D.; Mailhot, A.; Duchesne, S. Bayesian estimation of intensity–duration–frequency curves and of the return period associated to a given rainfall event. Stoch. Environ. Res. Risk Assess. 2010, 24, 337–347. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D. Intensity-duration-frequency curves from scaling representations of rainfall. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- DeGaetano, A.T.; Castellano, C.M. Future projections of extreme precipitation intensity-duration-frequency curves for climate adaptation planning in New York State. Clim. Serv. 2017, 5, 23–35. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Nazemi, A.; Elshorbagy, A. Quantile-based downscaling of precipitation using genetic programming: Application to IDF curves in Saskatoon. J. Hydrol. Eng. 2013, 19, 943–955. [Google Scholar] [CrossRef]
- Herath, H.; Sarukkalige, P.R.; Nguyen, V. Downscaling approach to develop future sub-daily IDF relations for Canberra Airport Region, Australia. Proc. Int. Assoc. Hydrol. Sci. 2015, 369, 147–155. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, A. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef]
- Mailhot, A.; Duchesne, S.; Caya, D.; Talbot, G. Assessment of future change in intensity–duration–frequency (IDF) curves for Southern Quebec using the Canadian Regional Climate Model (CRCM). J. Hydrol. 2007, 347, 197–210. [Google Scholar] [CrossRef]
- Wang, X.; Huang, G.; Liu, J. Projected increases in intensity and frequency of rainfall extremes through a regional climate modeling approach. J. Geophys. Res. Atmos. 2014, 119, 13–271. [Google Scholar] [CrossRef]
- De Paola, F.; Giugni, M.; Topa, M.E.; Bucchignani, E. Intensity-Duration-Frequency (IDF) rainfall curves, for data series and climate projection in African cities. SpringerPlus 2014, 3, 133. [Google Scholar] [CrossRef] [PubMed]
- Haerter, J.; Berg, P.; Hagemann, S. Heavy rain intensity distributions on varying time scales and at different temperatures. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- NASA. The NASA Earth Exchange—OpenNex2018. 2018. Available online: https://nex.nasa.gov/OpenNEX (accessed on 15 February 2019).
- Vandal, T.; Kodra, E.; Ganguly, A.R. Intercomparison of machine learning methods for statistical downscaling: The case of daily and extreme precipitation. Theor. Appl. Climatol. 2017, 1–14. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Wherry, S.A. Statistical downscaling of precipitation using machine learning with optimal predictor selection. J. Hydrol. Eng. 2010, 16, 650–664. [Google Scholar] [CrossRef]
- Anandhi, A.; Srinivas, V.; Nanjundiah, R.S.; Nagesh Kumar, D. Downscaling precipitation to river basin in India for IPCC SRES scenarios using support vector machine. Int. J. Climatol. 2008, 28, 401–420. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Tfwala, C.; van Rensburg, L.; Schall, R.; Mosia, S.; Dlamini, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Clim. Risk Manag. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K. Scaling model of a rainfall intensity-duration-frequency relationship. Hydrol. Process. 2006, 20, 3747–3757. [Google Scholar] [CrossRef]
- Blanchet, J.; Ceresetti, D.; Molinié, G.; Creutin, J.D. A regional GEV scale-invariant framework for Intensity–Duration–Frequency analysis. J. Hydrol. 2016, 540, 82–95. [Google Scholar] [CrossRef]
- Das, S. Distribution selection for hydrologic frequency analysis using subsampling method. IOP Conf. Ser. Earth Environ. Sci. 2016, 39, 012059. [Google Scholar] [CrossRef]
- Hidalgo-Muñoz, J.M.; Argüeso, D.; Calandria-Hernández, D.; Gámiz-Fortis, S.; Esteban-Parra, M.; Castro-Díez, Y. Extreme Value Analysis of Precipitation Series in the South of Iberian Peninsula; Universidad de Granada: Granada, Spain, 2010; Available online: https://ams.confex.com/ams/pdfpapers/159994.pdf (accessed on 9 May 2019).
- Sherman, C.W. Frequency and intensity of excessive rainfalls at Boston, Massachusetts. Trans. Am. Soc. Civ. Eng. 1931, 95, 951–960. [Google Scholar]
- Chow, V.T. Hydrologic Determination of Waterway Areas for the Design of Drainage Structures in Small Drainage Basins; Technical Report; University of Illinois at Urbana Champaign, College of Engineering, Engineering Experiment Station: Champaign County, IL, USA, 1962. [Google Scholar]
- Bernard, M.M. Formulas for rainfall intensities of long duration. Trans. Am. Soc. Civ. Eng. 1932, 96, 592–606. [Google Scholar]
- Singh, V.P.; Zhang, L. IDF curves using the Frank Archimedean copula. J. Hydrol. Eng. 2007, 12, 651–662. [Google Scholar] [CrossRef]
- Jain, A.; Pandey, R. Progressive improvements in basic Intensity-Duration-Frequency curves deriving approaches: A review. Int. Res. J. Eng. Technol. 2017, 4, 1739–1743. [Google Scholar]
- Dar, A.Q.; Maqbool, H.; Raazia, S. An empirical formula to estimate rainfall intensity in Kupwara region of Kashmir valley, J and K, India. In Proceedings of the 4th International Conference on Advancements in Engineering & Technology (ICAET-2016), Newark, NJ, USA, 11 May 2016; Volume 57. [Google Scholar]
- Foresti, L.; Pozdnoukhov, A.; Tuia, D.; Kanevski, M. Extreme precipitation modelling using geostatistics and machine learning algorithms. In geoENV VII–Geostatistics for Environmental Applications; Springer: Berlin, Germany, 2010; pp. 41–52. [Google Scholar]
- Xue, Y.; Vasic, R.; Janjic, Z.; Mesinger, F.; Mitchell, K.E. Assessment of dynamic downscaling of the continental US regional climate using the Eta/SSiB regional climate model. J. Clim. 2007, 20, 4172–4193. [Google Scholar] [CrossRef]
- Denis, B.; Laprise, R.; Caya, D.; Côté, J. Downscaling ability of one-way nested regional climate models: The Big-Brother Experiment. Clim. Dyn. 2002, 18, 627–646. [Google Scholar]
- Laprise, R. Resolved scales and nonlinear interactions in limited-area models. J. Atmos. Sci. 2003, 60, 768–779. [Google Scholar] [CrossRef]
- Maurer, E.P. The utility of daily large-scale climate data in the assessment of climate change impacts on daily streamflow in California. Hydrol. Earth Syst. Sci. 2010, 14, 1125–1138. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Brown, T.J. A comparison of statistical downscaling methods suited for wildfire applications. Int. J. Climatol. 2012, 32, 772–780. [Google Scholar] [CrossRef]
- Pierce, D.W.; Cayan, D.R.; Thrasher, B.L. Statistical downscaling using localized constructed analogs (LOCA). J. Hydrometeorol. 2014, 15, 2558–2585. [Google Scholar] [CrossRef]
- Pierce, D.; Cayan, D. Downscaling humidity with localized constructed analogs (LOCA) over the conterminous united states. Clim. Dyn. 2016, 47, 411–431. [Google Scholar] [CrossRef]
- Bao, Y.; Wen, X. Projection of China’s near-and long-term climate in a new high-resolution daily downscaled dataset NEX-GDDP. J. Meteorol. Res. 2017, 31, 236–249. [Google Scholar] [CrossRef]
- NOAA. Climate Division. 2016. Available online: https://www.ncdc.noaa.gov/monitoring-references/maps/us-climate-divisions.php (accessed on 15 February 2019).
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Caesar, J. Global land-based datasets for monitoring climatic extremes. Bull. Am. Meteorol. Soc. 2013, 94, 997–1006. [Google Scholar] [CrossRef]
- Tripathi, S.; Govindaraju, R.S. On selection of kernel parametes in relevance vector machines for hydrologic applications. Stoch. Environ. Res. Risk Assess. 2007, 21, 747–764. [Google Scholar] [CrossRef]
- NOAA. NOAA Atlas 14. 2017. Available online: https://hdsc.nws.noaa.gov/hdsc/pfds/ (accessed on 27 March 2019).
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- NOAA. Climate Data Online. 2016. Available online: http://www.ncdc.noaa.gov/cdo-web/ (accessed on 15 February 2019).
- NASA. The NASA Earth Exchange Global Daily Downscaled Projections. 2019. Available online: https://nex.nasa.gov/nex/projects/1356 (accessed on 15 February 2019).

| Method | Known Property | Known Target | Projection Property | Projection Target |
|---|---|---|---|---|
| Machine Learning | Train data features | Train data label | Test data features | Test data label |
| Statistical downscaling | Historical GCM data | Historical downscaled data | Future GCM data | downscaled GCM data |
| Temporal downscaling | Historical GCM daily data | Historical 15-min intensity | Future GCM daily data | Future 15-min intensity |
| Station ID | Name | State | Latitude | Longitude |
|---|---|---|---|---|
| COOP:043093 | Florence Lake | California | 37.27389 | −118.97333 |
| COOP:096879 | Pearson | Georgia | 31.2928 | −82.8422 |
| COOP:177325 | Rumford | Maine | 44.53083 | −70.53722 |
| COOP:234825 | Lebanon | Missouri | 37.68502 | −92.69388 |
| COOP:410569 | Bay City | Texas | 28.9798 | −95.9749 |
| COOP:253185 | Genoa | Nebraska | 41.4513 | −97.7644 |
| COOP:024586 | Keams Canyon | Arizona | 35.8109 | −110.1932 |
| COOP:447338 | Rocky Mount | Virginia | 36.9769 | −79.8961 |
| Duration (minutes) | Return Period (year) | CA | GA | ME | MO | TX | AZ | NE | VA |
|---|---|---|---|---|---|---|---|---|---|
| 30 | 2 | 21% | −1% | −12% | 2% | −12% | 3% | 0% | −12% |
| 30 | 5 | 10% | 2% | −14% | 4% | −10% | −2% | 0% | −10% |
| 30 | 10 | 6% | 7% | −13% | 7% | −6% | −5% | 0% | −6% |
| 30 | 50 | 9% | 23% | −5% | 19% | 6% | −4% | 5% | 11% |
| 60 | 2 | 1% | 1% | −16% | 2% | −15% | −3% | −3% | −7% |
| 60 | 5 | −7% | 6% | −18% | 4% | −14% | −9% | −3% | −8% |
| 60 | 10 | −10% | 10% | −18% | 5% | −11% | −12% | −4% | −5% |
| 60 | 50 | −8% | 26% | −11% | 15% | 0% | −11% | 0% | 8% |
| 120 | 2 | −8% | −10% | −23% | −6% | −19% | −14% | −3% | −7% |
| 120 | 5 | −14% | −6% | −23% | −5% | −20% | −19% | −4% | −8% |
| 120 | 10 | −15% | −2% | −22% | −3% | −19% | −21% | −4% | −6% |
| 120 | 50 | −13% | 11% | −13% | 4% | −12% | −21% | −2% | 4% |
| CA | GA | ME | MO | TX | AZ | NE | VA | |
|---|---|---|---|---|---|---|---|---|
| NRMSE | 0.117 | 0.121 | 0.170 | 0.085 | 0.137 | 0.033 | 0.127 | 0.084 |
| NMAE | 0.107 | 0.092 | 0.163 | 0.068 | 0.124 | 0.028 | 0.108 | 0.081 |
| Location | CA | GA | ME | MO | TX | AZ | NE | VA |
|---|---|---|---|---|---|---|---|---|
| Ratio of Increase (2040–2069) | 9% | 17% | 11% | 13% | 20% | 13% | 7% | 10% |
| Ratio of Increase (2070–2099) | 13% | 21% | 16% | 18% | 23% | 16% | 9% | 13% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Ayyub, B.M. Machine Learning for Projecting Extreme Precipitation Intensity for Short Durations in a Changing Climate. Geosciences 2019, 9, 209. https://doi.org/10.3390/geosciences9050209
Hu H, Ayyub BM. Machine Learning for Projecting Extreme Precipitation Intensity for Short Durations in a Changing Climate. Geosciences. 2019; 9(5):209. https://doi.org/10.3390/geosciences9050209
Chicago/Turabian StyleHu, Huiling, and Bilal M. Ayyub. 2019. "Machine Learning for Projecting Extreme Precipitation Intensity for Short Durations in a Changing Climate" Geosciences 9, no. 5: 209. https://doi.org/10.3390/geosciences9050209
APA StyleHu, H., & Ayyub, B. M. (2019). Machine Learning for Projecting Extreme Precipitation Intensity for Short Durations in a Changing Climate. Geosciences, 9(5), 209. https://doi.org/10.3390/geosciences9050209





