Changing Impacts of North Atlantic Tropical Cyclones on Extreme Precipitation Distribution across the Mid-Atlantic United States
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Statistical Methods
2.2.1. Data
2.2.2. Quantile Regression
2.2.3. Generalized Extreme Value Distribution
2.3. Identification of TC-induced Precipitation
3. Results
3.1. Spatial Pattern of TC-induced Top 10 Wettest Days
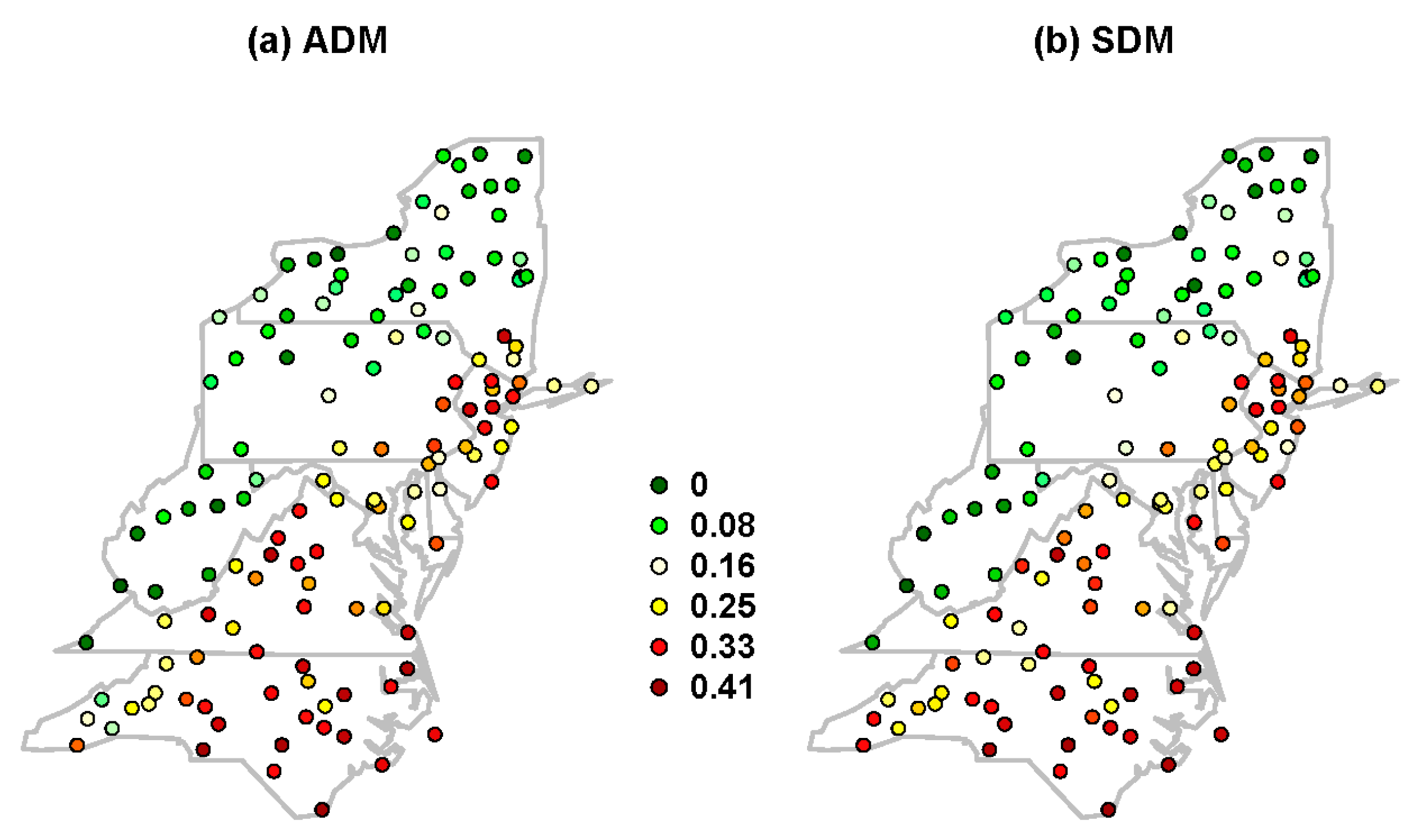
3.2. Spatial Distribution of the Frequency of TC-induced Extreme Precipitation in ADM and SDM
3.3. Probability of Exceedance Based on GEV Distribution
3.4. Trends of the Top 10 TC-Induced Wettest Days
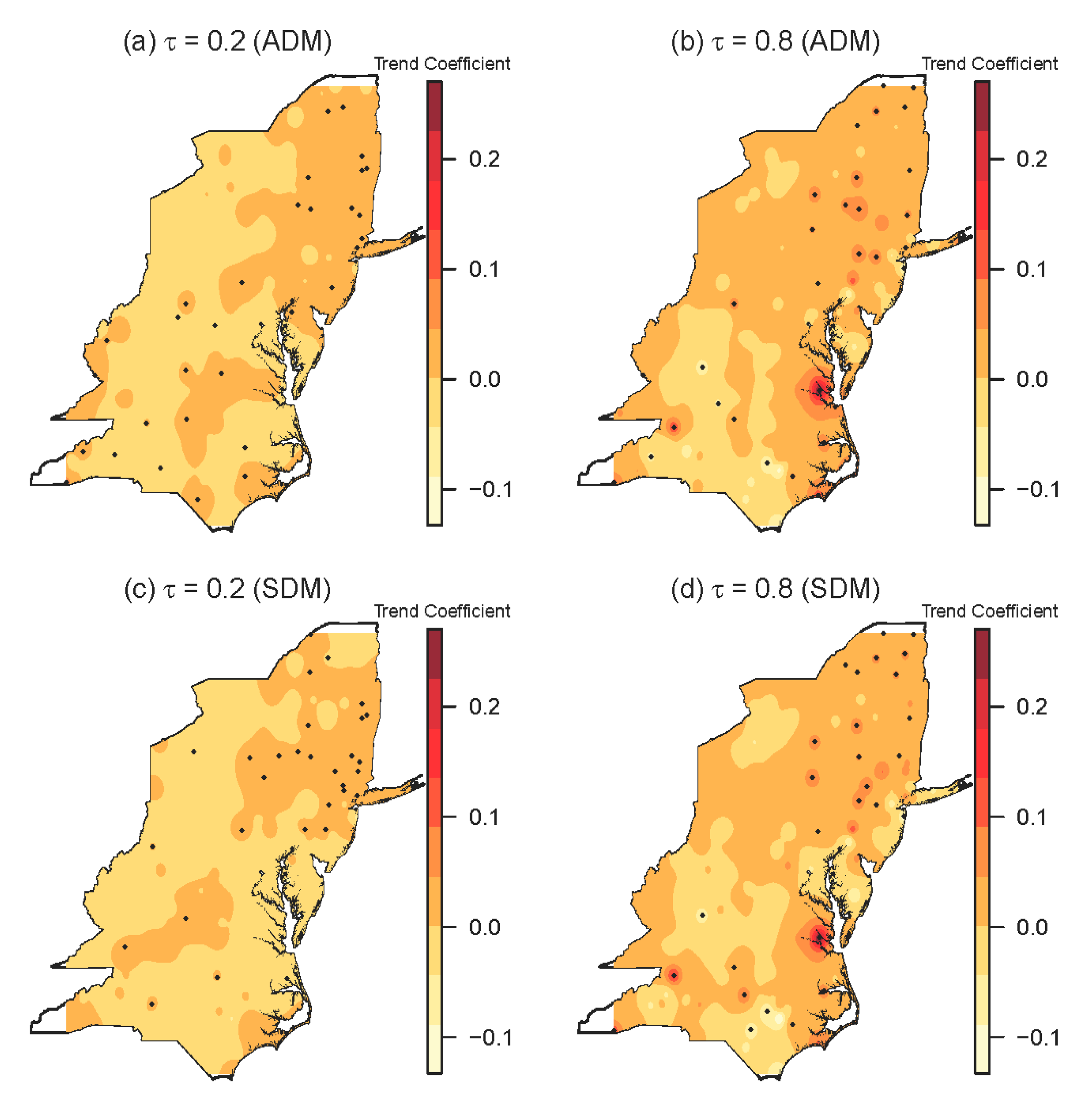
3.5. Spatial Patterns of Lower and Upper-Quantile Trends for ADM and SDM
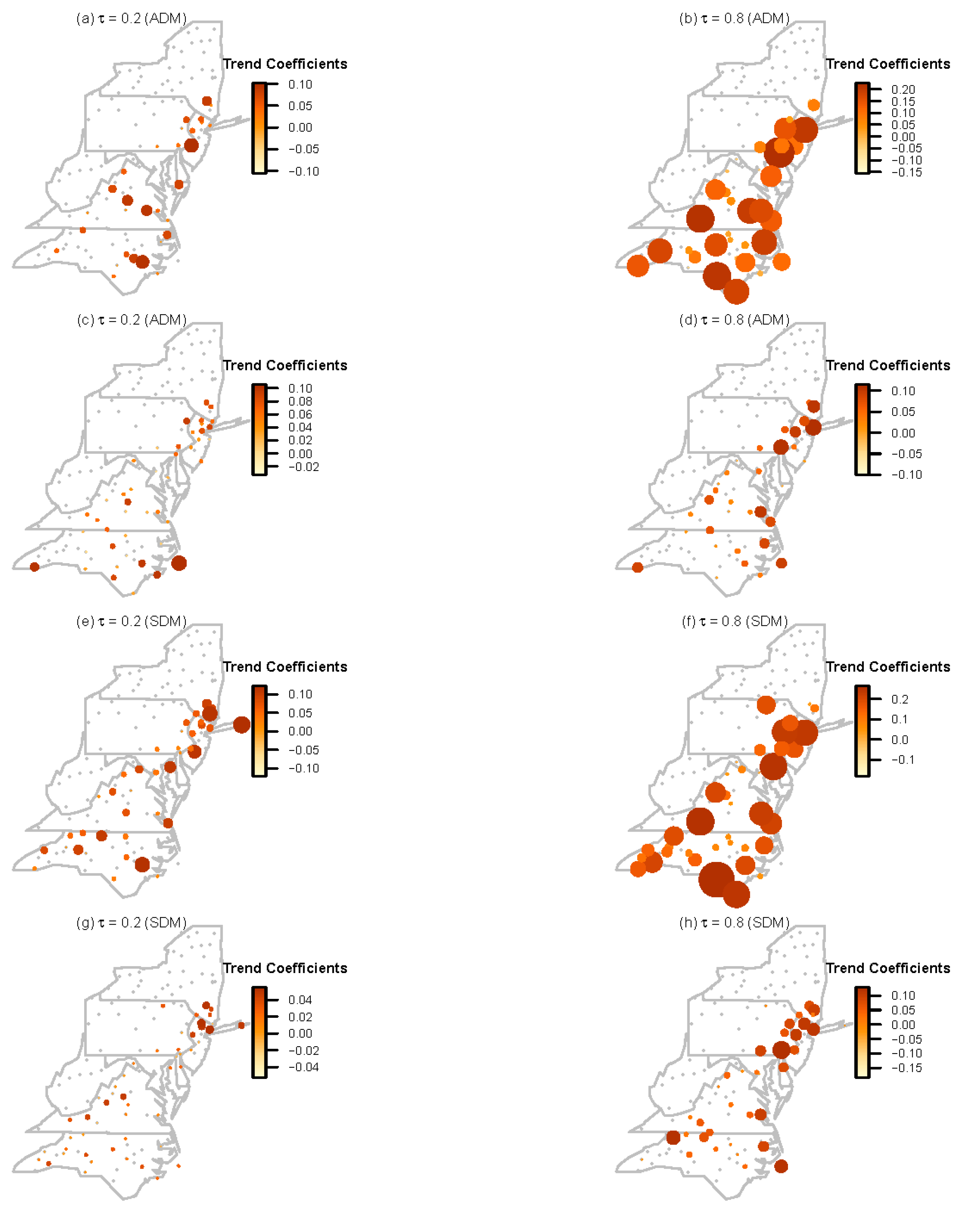
3.6. Contribution of TCs in the Distribution of ADM and SDM
4. Summary and Conclusions
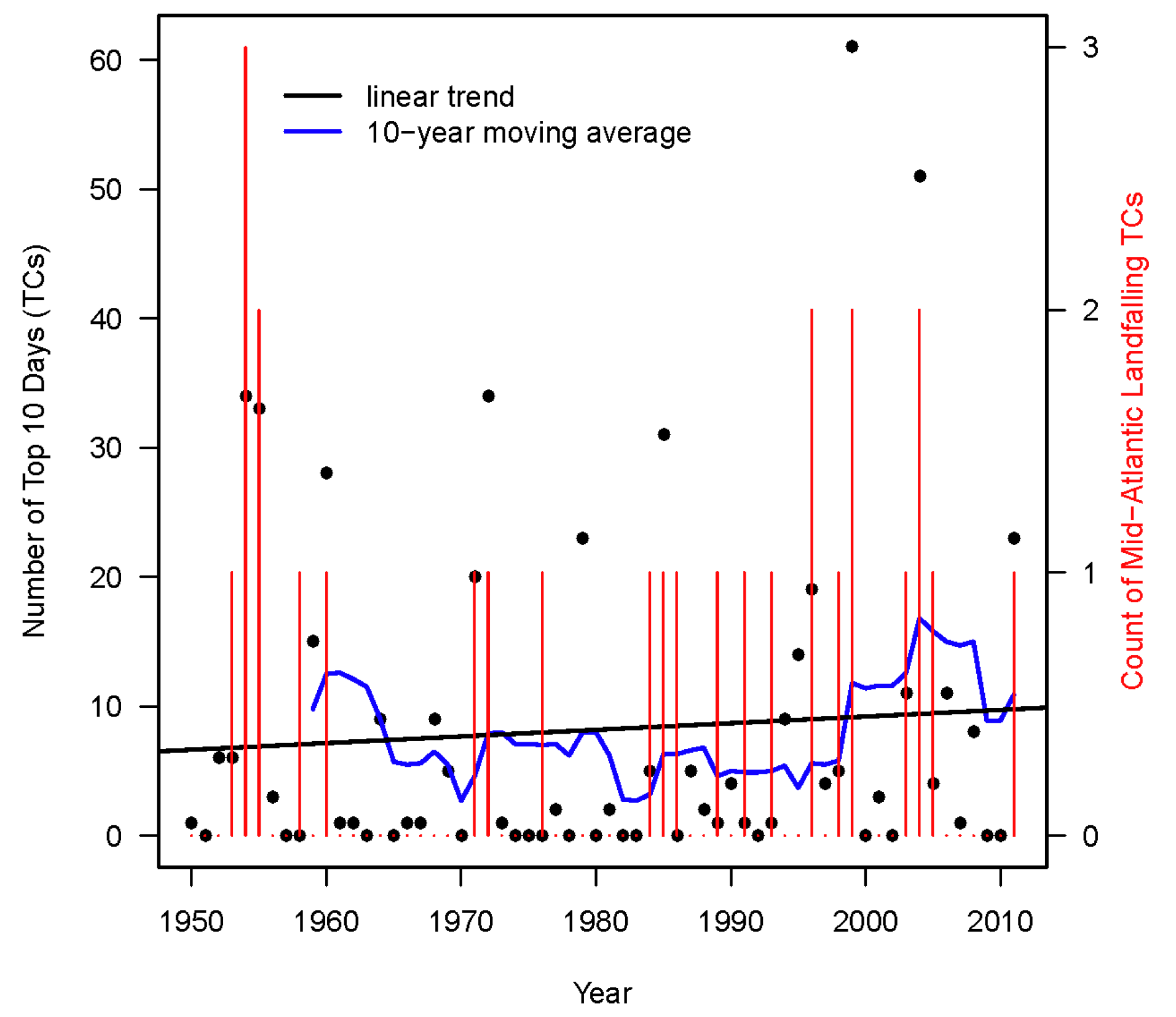
- Analysis of the top 10 wettest days shows that for the coastal stations, a higher percentage of top 10 wettest days is caused by TCs as compared to inland stations (Figure 1). Similarly, an analysis of the temporal changes in the counts of the top 10 TC-induced wettest days across all stations using the 10-year moving average shows that there has been an increase in the number of TC-induced heavy precipitation events during the post-1990 period (Figure 4).
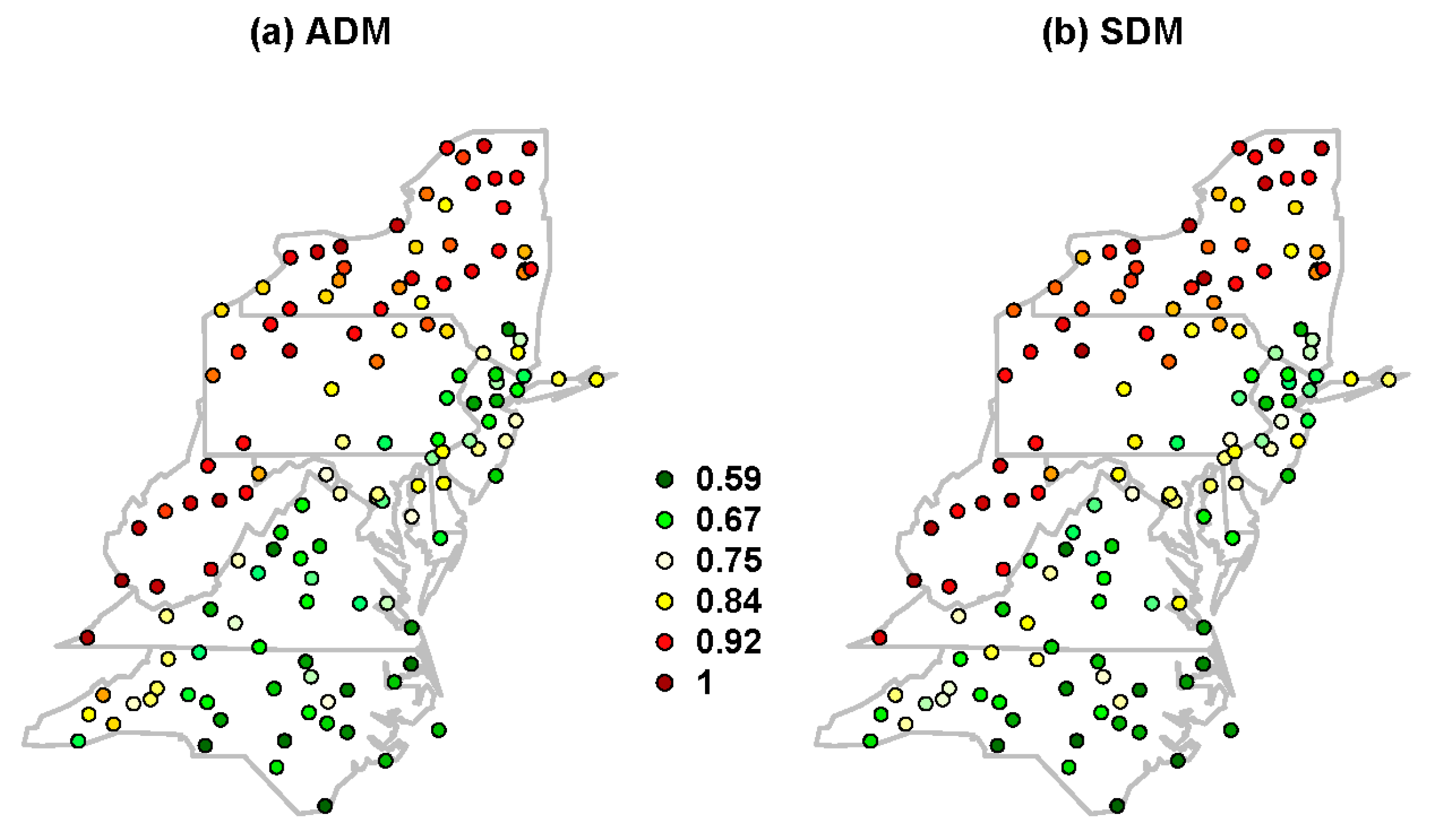
- Analysis of the spatial distribution of the frequency of TC-induced extreme precipitation in ADM and SDM shows that the values of frequency are higher for coastal sites and lower for inland sites. Stations along Virginia and North Carolina have comparatively higher values of the frequency (Figure 2).
- Analysis of the spatial pattern of the lower and upper-quantile trends of the ADM and SDM revealed an overall positive trend in the southern region of the study area for both the lower and upper quantiles. Additionally, upper-quantile trends have greater magnitudes in most of the sites as compared with the lower quantile trends, indicating that the rates of changes in the upper quantile have greatly strengthened (Figure 5).
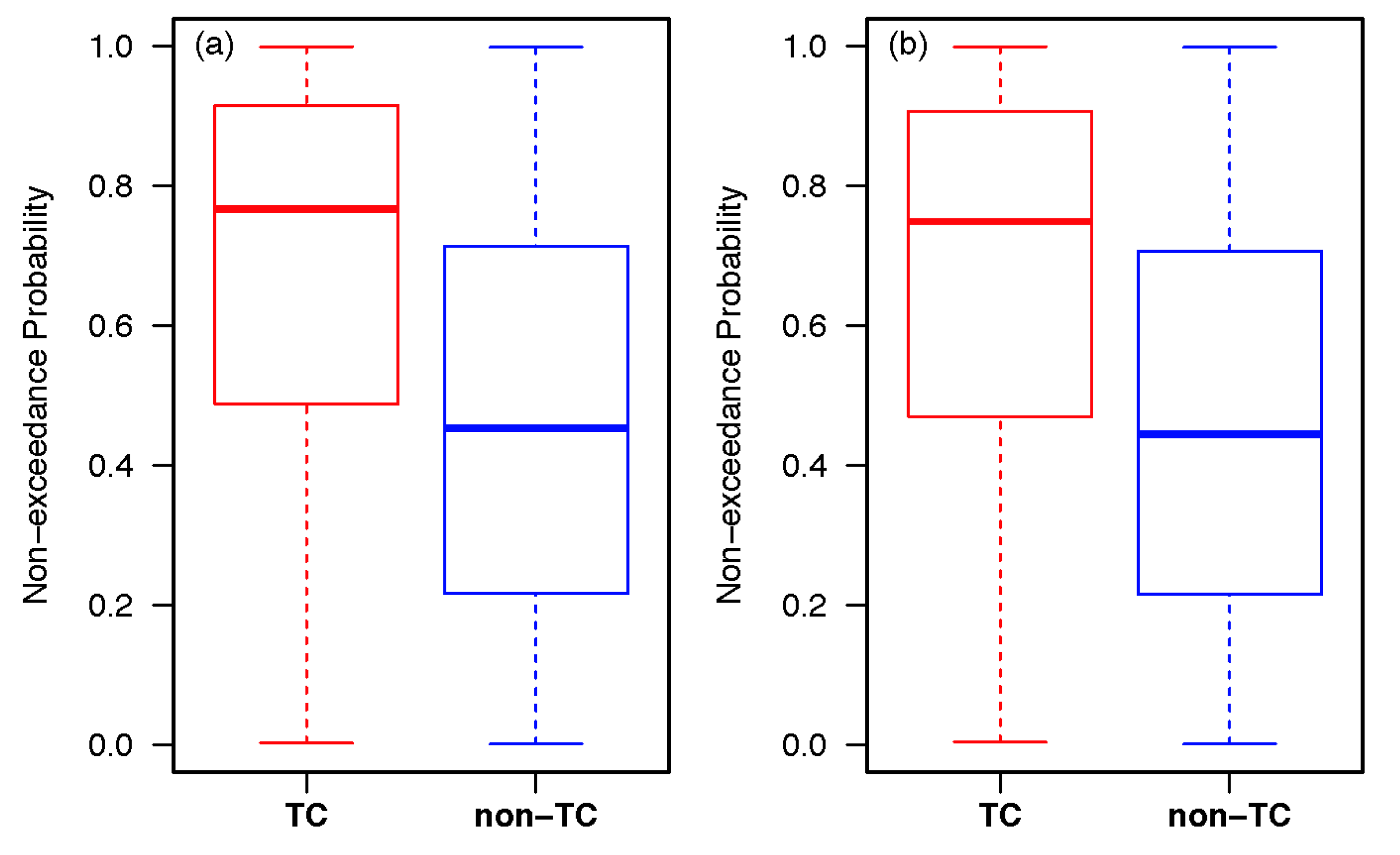
- Analysis of the impact of TCs in the distribution of extreme precipitation shows that trends have larger magnitudes in most of the sites for TC precipitation series as compared with the non-TC precipitation series for both the lower and upper quantiles. However, the highest trends are observed in the upper quantile for TC time series indicating that TC precipitation is contributing more to the changes in the upper tails of the extreme precipitation distribution as compared to the non-TC precipitation (Figure 6). This is a key finding of this manuscript.
Funding
Conflicts of Interest
Appendix A
References
- Changnon, S.A. Assessment of flood losses in the United States. J. Contemp. Water Res. Educ. 2008, 138, 38–44. [Google Scholar] [CrossRef]
- Lin, N.; Smith, J.A.; Villarini, G.; Marchok, T.P.; Baeck, M.L. Modeling extreme rainfall, winds, and surge from Hurricane Isabel (2003). Weather Forecast. 2010, 25, 1342–1361. [Google Scholar] [CrossRef]
- Rappaport, E.N. Loss of life in the United States associated with recent Atlantic tropical cyclones. Bull. Am. Meteorol. Soc. 2000, 81, 2065–2073. [Google Scholar] [CrossRef]
- Rappaport, E.N. Fatalities in the United States from Atlantic tropical cyclones: New data and interpretation. Bull. Am. Meteorol. Soc. 2014, 95, 341–346. [Google Scholar] [CrossRef]
- Villarini, G.; Goska, R.; Smith, J.A.; Vecchi, G.A. North Atlantic tropical cyclones and US flooding. Bull. Am. Meteorol. Soc. 2014, 95, 1381–1388. [Google Scholar] [CrossRef]
- Klotzbach, P.; Bowen, S.G.; Pielke, R.; Bell, M. Continental United States Hurricane Landfall Frequency and Associated Damage: Observations and Future Risks. Bull. Amer. Meteor. Soc. 2018. [Google Scholar] [CrossRef]
- Douglas, E.; Jacobs, J.; Hayhoe, K.; Silka, L.; Daniel, J.; Collins, M.; Wake, C. Progress and challenges in incorporating climate change information into transportation research and design. J. Infrastruct. Syst. 2017, 23, 04017018. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Easterling, D.R.; Kristovich, D.A.; Gleason, B.; Stoecker, L.; Smith, R. Recent increases in US heavy precipitation associated with tropical cyclones. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Barlow, M. Influence of hurricane-related activity on North American extreme precipitation. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Keim, B.D.; Robbins, K.D. Occurrence dates of North Atlantic tropical storms and hurricanes: 2005 in perspective. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Bove, M.C.; O’Brien, J.J.; Eisner, J.B.; Landsea, C.W.; Niu, X. Effect of El Niño on US landfalling hurricanes, revisited. Bull. Am. Meteorol. Soc. 1998, 79, 2477–2482. [Google Scholar] [CrossRef]
- Nogueira, R.C.; Keim, B.D. Annual volume and area variations in tropical cyclone rainfall over the eastern United States. J. Clim. 2010, 23, 4363–4374. [Google Scholar] [CrossRef]
- Landsea, C.W.; Pielke Jr, R.A.; Mestas-Nunez, A.M.; Knaff, J.A. Atlantic basin hurricanes: Indices of climatic changes. Clim. Change 1999, 42, 89–129. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.-R. Changes in tropical cyclone number and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed]
- Emanuel, K.A. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 326, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Klotzbach, P.J. Trends in global tropical cyclone activity over the past twenty years (1986–2005). Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Elsner, J.B.; Kossin, J.P.; Jagger, T.H. The increasing intensity of the strongest tropical cyclones. Nature 2008, 455, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, J.M.; Grundstein, A.; Mote, T.L. Quantifying the contribution of tropical cyclones to extreme rainfall along the coastal southeastern United States. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Lau, K.M.; Zhou, Y.P.; Wu, H.T. Have tropical cyclones been feeding more extreme rainfall? J. Geophys. Res.: Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Knight, D.B.; Davis, R.E. Contribution of tropical cyclones to extreme rainfall events in the southeastern United States. J. Geophys. Res.: Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R.; Easterling, D.R.; Sun, B.; Lawrimore, J.H. Contemporary changes of the hydrological cycle over the contiguous United States: Trends derived from in situ observations. J. Hydrometeorol. 2004, 5, 64–85. [Google Scholar] [CrossRef]
- Zhu, L.; Quiring, S.M. Variations in tropical cyclone precipitation in Texas (1950 to 2009). J. Geophys. Res. Atmos. 2013, 118, 3085–3096. [Google Scholar] [CrossRef]
- Agel, L.; Barlow, M.; Qian, J.H.; Colby, F.; Douglas, E.; Eichler, T. Climatology of daily precipitation and extreme precipitation events in the northeast United States. J. Hydrometeorol. 2015, 16, 2537–2557. [Google Scholar] [CrossRef]
- Interagency Committee on Water Data (IACWD) (1982) Guidelines for Determining Flood Flow Frequency: Bulletin 17-B. Available online: https://www.fema.gov/media-library-data/20130726-1553-20490-9670/dl_flow.pdf (accessed on 8 May 2019).
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; Cambridge University Press: Cambridge, UK, 2012; p. 582. [Google Scholar]
- Koenker, R. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Koenker, R.; Quantreg: Quantile Regression. R package version 5.05. R Foundation, for Statistical Computing: Vienna) 2013. Available online: http://CRAN.R-project.org/package=quantreg (accessed on 8 May 2019).
- Dhakal, N.; Tharu, B. Spatiotemporal trends in daily precipitation extremes and their connection with North Atlantic tropical cyclones for the Southeastern United States. Int. J. Climatol. 2018. [Google Scholar] [CrossRef]
- Ying, M.; Chen, B.; Wu, G. Climate trends in tropical cyclone-induced wind and precipitation over mainland China. Geophys. Res. Lett. 2011, 38, L01702. [Google Scholar] [CrossRef]
- Hernandez; Ayala, J.J.; Matyas, C.J. Spatial distribution of tropical cyclone rainfall and its contribution to the climatology of Puerto Rico. Phys. Geogr. 2017, 39, 1–20. [Google Scholar] [CrossRef]
- National Climate Assessment. US Global Change Research Program. Available online: http://nca2014.globalchange.gov/ (accessed on 27 January 2019).
- Polsky, C.; Allard, J.; Crane, R.; Yarnal, B. The Mid-Atlantic Region and its climate: Past, present, and future. Clim. Res. 2000, 4, 161–173. [Google Scholar] [CrossRef]
- Easterling, D.R.; Peterson, T.C.; Karl, T.R. On the development and use of homogenized climate datasets. J. Clim. 1996, 9, 1429–1434. [Google Scholar] [CrossRef]
- Jarvinen, B.R.; Neumann, C.J.; Davis, M.A.S. A Tropical Cyclone Data Tape for the North Atlantic Basin, 1886–1983: Contents, Limitations, and Uses; NOAA Tech. Memo., NWS NHC: Miami, FL, USA, 1984.
- Barbosa, S.M. Quantile trends in Baltic sea level. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/ CRC (Monographs on Statistics & Applied Probability): London, UK, 1994. [Google Scholar]
- Galvao, A.F.; Montes-Rojas, G. On bootstrap inference for quantile regression panel data: A monte carlo study. Econometrics 2015, 3, 654–666. [Google Scholar] [CrossRef]
- Fan, L.; Chen, D. Trends in extreme precipitation indices across China detected using quantile regression. Atmos. Sci. Lett. 2016, 17, 400–406. [Google Scholar] [CrossRef]
- Tan, X.; Shao, D. Precipitation trends and teleconnections identified using quantile regressions over Xinjiang, China. Int. J. Climatol. 2017, 37, 1510–1525. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- DeGaetano, A.T. Time-dependent changes in extreme-precipitation return-period amounts in the continental United States. J. Appl. Meteorol. Climatol. 2009, 48, 2086–2099. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W. Estimating extremes in transient climate change simulations. J. Clim. 2005, 18, 1156–1173. [Google Scholar] [CrossRef]
- Smith, R.L.; Naylor, J.C. A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Appl. Stat. 1987, 36, 358–369. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Changes in extreme precipitation in Texas. J. Geophys. Res.: Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Cry, G.W. Effects of Tropical Cyclone Rainfall on the Distribution of Precipitation over the Eastern and Southern United States; Professional Paper 1; United States Department of Commerce, Environmental Sciences Services Administration: Rockville, MD, USA, 1967; p. 67. [Google Scholar]
- Englehart, P.J.; Douglas, A.V. The role of eastern North Pacific tropical storms in the rainfall climatology of western Mexico. Int. J.Climatol. 2001, 21, 1357–1370. [Google Scholar] [CrossRef]
- Nogueira, R.C.; Keim, B.D.; Brown, D.P.; Robbins, K.D. Variability of rainfall from tropical cyclones in the eastern USA and its association to the AMO and ENSO. Theor. Appl. Climatol. 2013, 112, 273–283. [Google Scholar] [CrossRef]
- Rodgers, E.B.; Adler, R.F.; Pierce, H.F. Contribution of tropical cyclones to the North Pacific climatological rainfall as observed from satellites. J.Appl. Meteorol. 2000, 39, 1658–1678. [Google Scholar] [CrossRef]
- Rodgers, E.B.; Adler, R.F.; Pierce, H.F. Contribution of tropical cyclones to the North Atlantic climatological rainfall as observed from satellites. J.Appl. Meteorol. 2001, 40, 1785–1800. [Google Scholar] [CrossRef]
- Jiang, H.; Zipser, E.J. Contribution of tropical cyclones to the global precipitation from eight seasons of TRMM data: Regional, seasonal, and interannual variations. J. Clim. 2010, 23, 1526–1543. [Google Scholar] [CrossRef]
- Wright, D.B.; Knutson, T.R.; Smith, J.A. Regional climate model projections of rainfall from US landfalling tropical cyclones. Clim. Dyn. 2015, 45, 3365–3379. [Google Scholar] [CrossRef]
- Hirschboeck, K.K. Climate and floods. Natl. Water Summ. 1988, 89, 67–88. [Google Scholar]
- Son, C.; Lee, T.; Kwon, H.H. Integrating nonstationary behaviors of typhoon and non-typhoon extreme rainfall events in East Asia. Sci. Rep. 2017, 7, 5097. [Google Scholar] [CrossRef]
- Rossi, F.; Fiorentino, M.; Versace, P. Two-component extreme value distribution for flood frequency analysis. Water Resour. Res. 1984, 20, 847–856. [Google Scholar] [CrossRef]
- Waylen, P.; Woo, M.K. Prediction of annual floods generated by mixed processes. Water Resour. Res. 1982, 18, 1283–1286. [Google Scholar] [CrossRef]
- Walsh, K.J.E.; McBride, J.L.; Klotzbach, P.J.; Balachandran, S.; Camargo, S.J.; Holland, G.; Knutson, T.R.; Kossin, J.P.; Lee, T.-C.; Sobel, A.; et al. Tropical cyclones and climate change. WIREs Clim. Change 2016, 7, 65–89. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhakal, N. Changing Impacts of North Atlantic Tropical Cyclones on Extreme Precipitation Distribution across the Mid-Atlantic United States. Geosciences 2019, 9, 207. https://doi.org/10.3390/geosciences9050207
Dhakal N. Changing Impacts of North Atlantic Tropical Cyclones on Extreme Precipitation Distribution across the Mid-Atlantic United States. Geosciences. 2019; 9(5):207. https://doi.org/10.3390/geosciences9050207
Chicago/Turabian StyleDhakal, Nirajan. 2019. "Changing Impacts of North Atlantic Tropical Cyclones on Extreme Precipitation Distribution across the Mid-Atlantic United States" Geosciences 9, no. 5: 207. https://doi.org/10.3390/geosciences9050207
APA StyleDhakal, N. (2019). Changing Impacts of North Atlantic Tropical Cyclones on Extreme Precipitation Distribution across the Mid-Atlantic United States. Geosciences, 9(5), 207. https://doi.org/10.3390/geosciences9050207




