Assessment of CO2 Injectivity During Sequestration in Depleted Gas Reservoirs
Abstract
1. Introduction
2. CO Storage in a Depleted Gas Reservoir
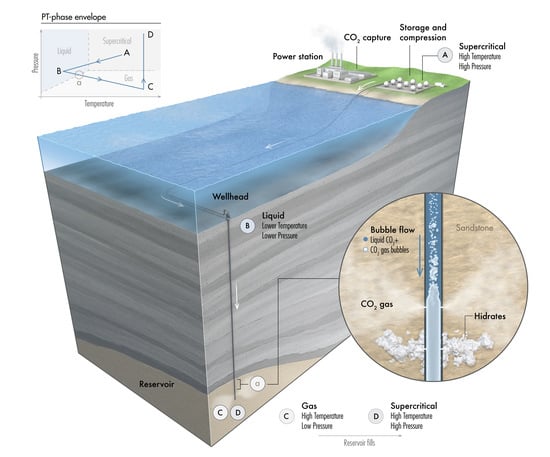
3. CO Transport Journey
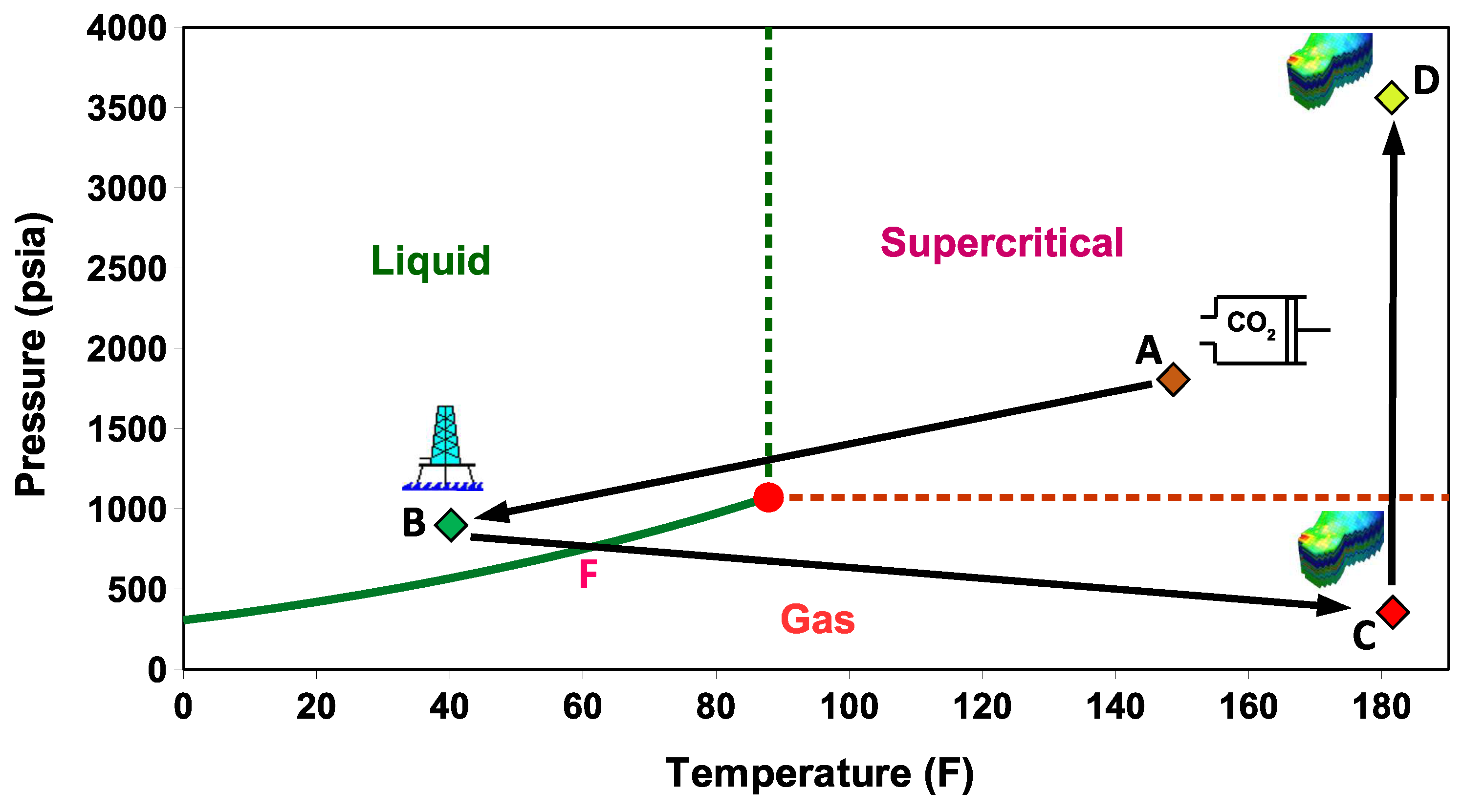
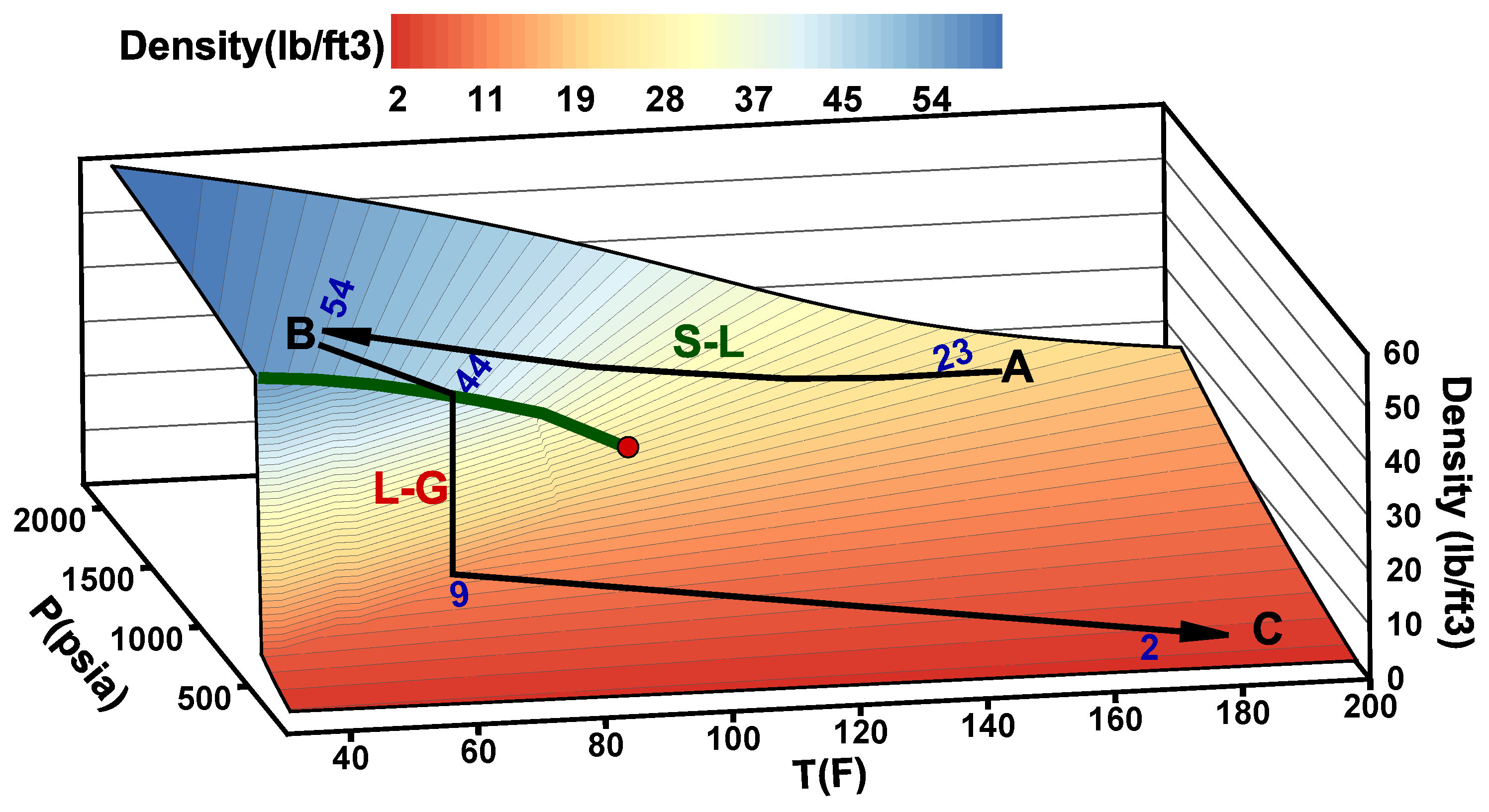
- Stage A: CO is captured, dehydrated, and compressed at the onshore power plant. The required delivery pressure at the compressor depends on the desired injection rate at the wellhead, the pipeline tubing diameter, and the corresponding pressure drop between the compression site and the subsurface reservoir. The pressure drop is expected to vary during the reservoir filling process, as will be discussed later. To maintain efficiency in pipeline transportation, CO must be transported and injected in the dense state. Transporting CO in the gas state is inefficient. Stage A in Figure 2 corresponds to one scenario where the pressure and temperature of CO delivered from a multistage compression unit at the onshore facility is about A = (1550 psia, 150 F).
- Stage B: This stage corresponds to the arrival conditions of CO at the wellhead. The pressure drop within the 140 km pipeline (AB) is about 550 psia, and the CO temperature is expected to adjust to the seawater temperature. The seawater temperature fluctuates between 40 F in the winter and 60F in the summer. Within that temperature range, CO is in the liquid state (Figure 2). Stage B in Figure 2 corresponds to a scenario where the pressure and temperature of CO at the wellhead is B = (1000 psia, 40 F).
- Stage C: This stage corresponds to the reservoir pressure and temperature conditions before the CO injection begins. Therefore, stage C in Figure 2 corresponds to the current reservoir conditions of C = (200 psia, 182 F). We note the liquid-to-gas (L–G) phase transition that occurs as a result of the pressure and temperature change from the surface to the reservoir. Point L–G denotes the flash point of CO. Depending on the flow and thermal conditions, the transition to a gas state may occur within the well tubing or the near-wellbore formation. Additional details are provided in the next section.
- Stage D: This stage represents the expected pressure and temperature conditions after the reservoir has been filled up with CO. We assume 100% voidage replacement, and therefore, the final pressure is expected to roughly equal the initial reservoir pressure. With no perturbation to the average reservoir temperature, stage D in Figure 2 corresponds to a supercritical state of CO at D = (3500 psia, 182 F).
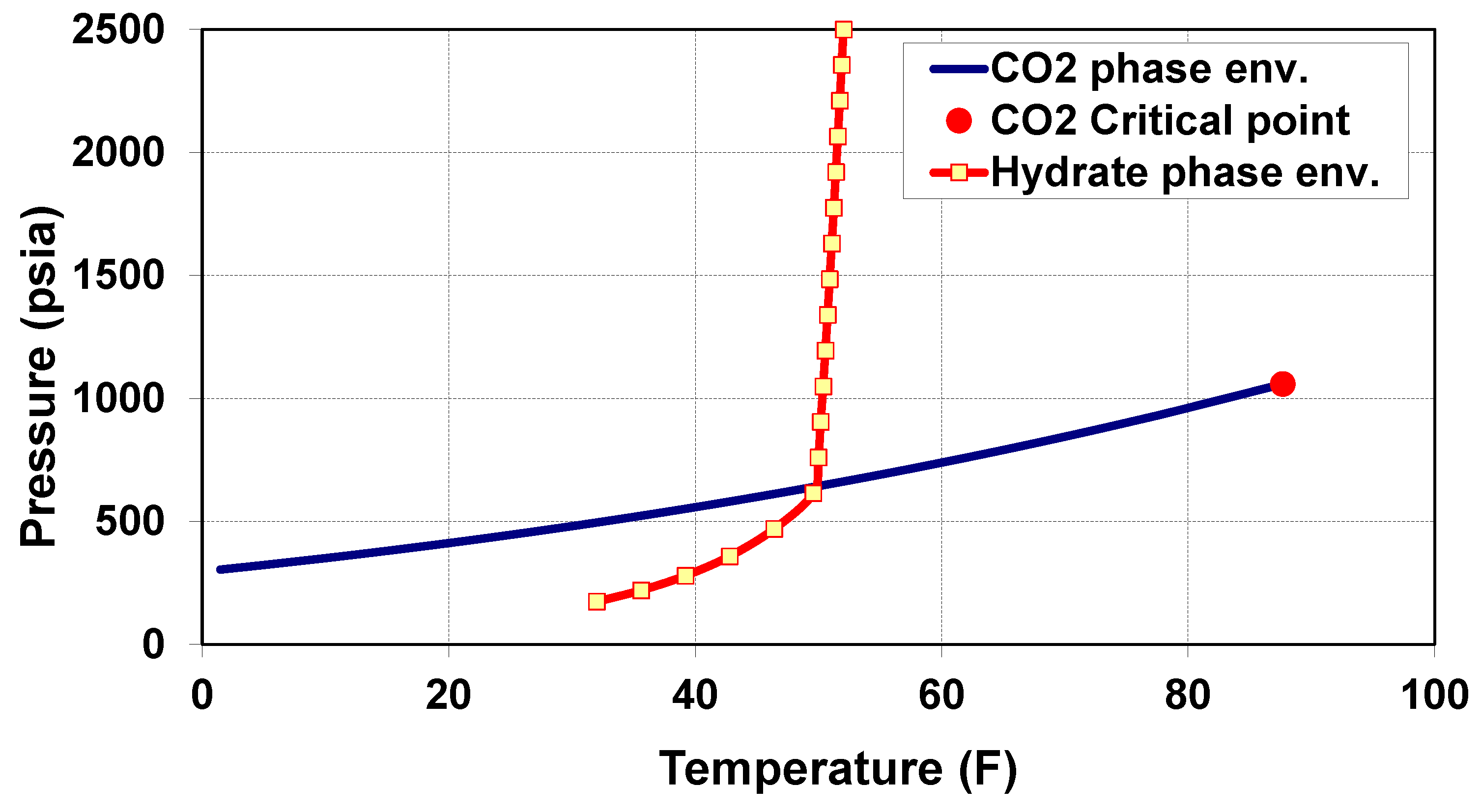
4. CO Thermodynamic Phase Behavior in the Wellbore
- Scenario 1—CO vaporization within the well tubing: If CO vaporizes within the well tubing and is not completely dry (i.e., water is present), then hydrates may form within the tubing [27]. On the other hand, if water is absent, as expected, no hydrates will form inside the tubing. However, the risk of hydrate formation due to vaporization within the well tubing will remain relevant within the reservoir as the cooled gaseous CO hits wet sand near the wellbore.
- Scenario 2—CO vaporization across the perforations: CO vaporization across the well perforations or within 1–2 feet of the wellbore could be the worst scenario. Cooling would be more localized, possibly causing hydrates or even dry ice to form across the perforations, resulting in a loss of injectivity.
- Scenario 3—CO vaporization within the reservoir: CO vaporization within the reservoir formation, away from the wellbore, is less problematic since hydrate formation is unlikely to result in complete plugging. Nevertheless, this scenario may cause partial loss of injectivity.
5. Decoupled Approach
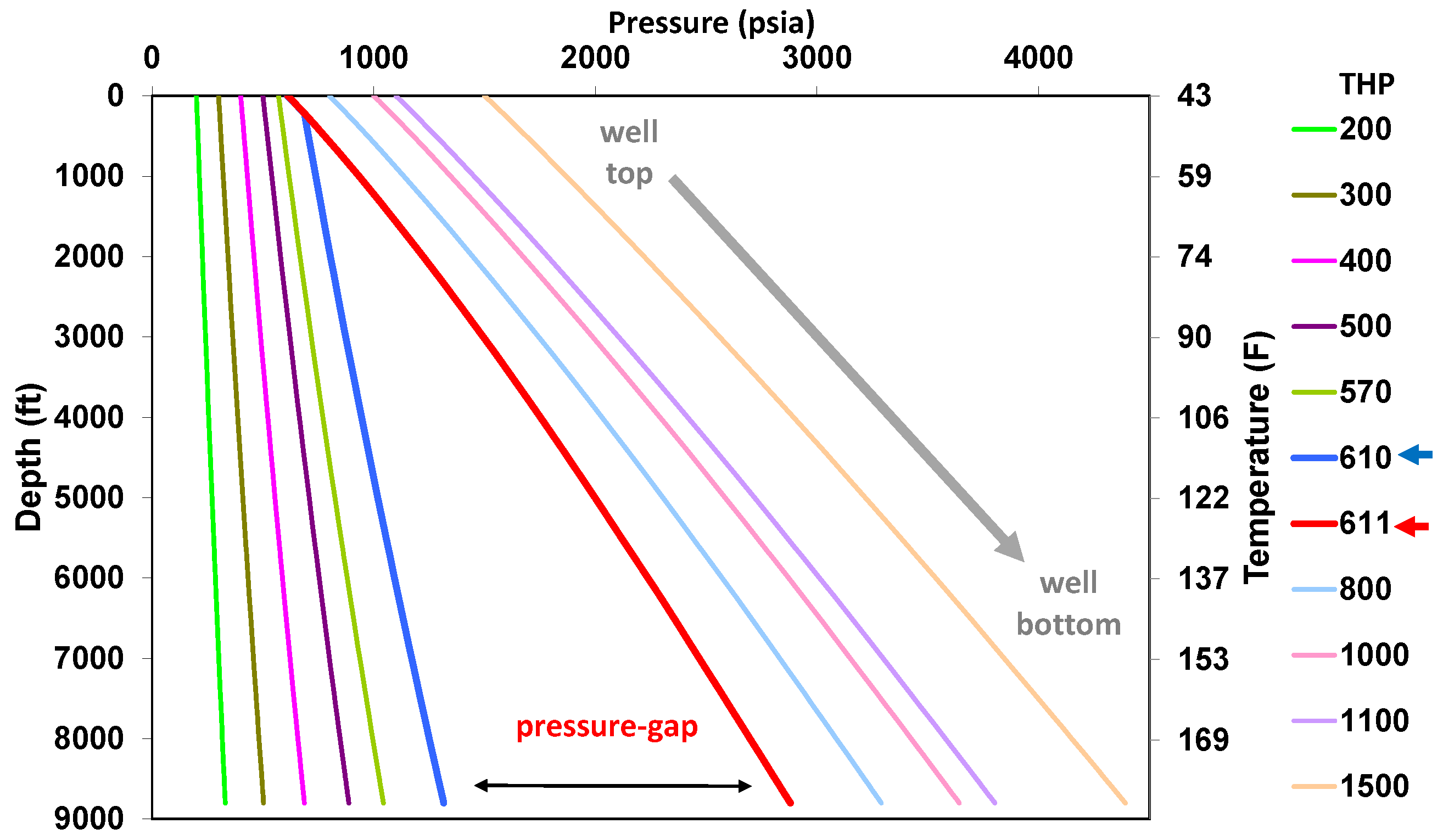
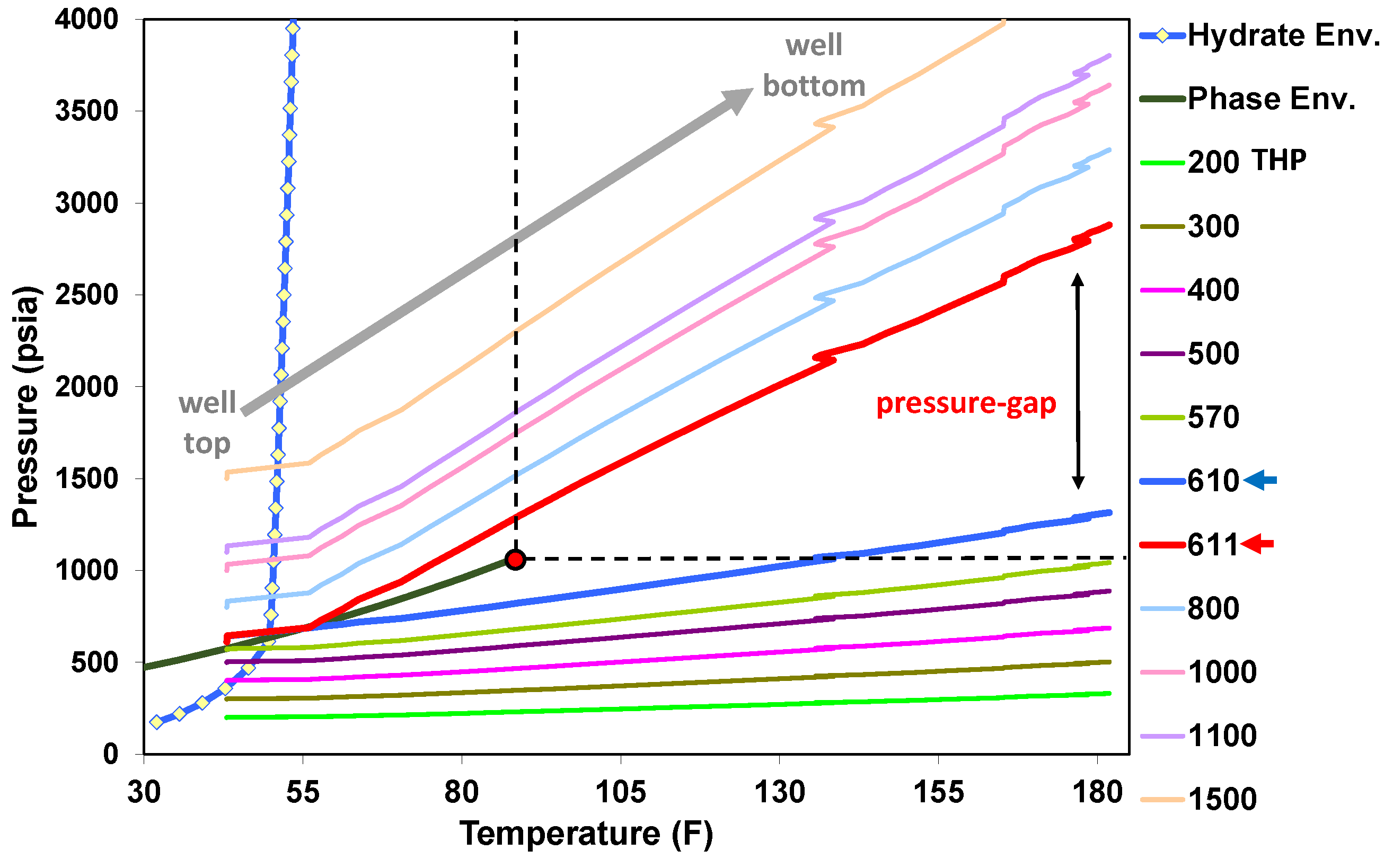
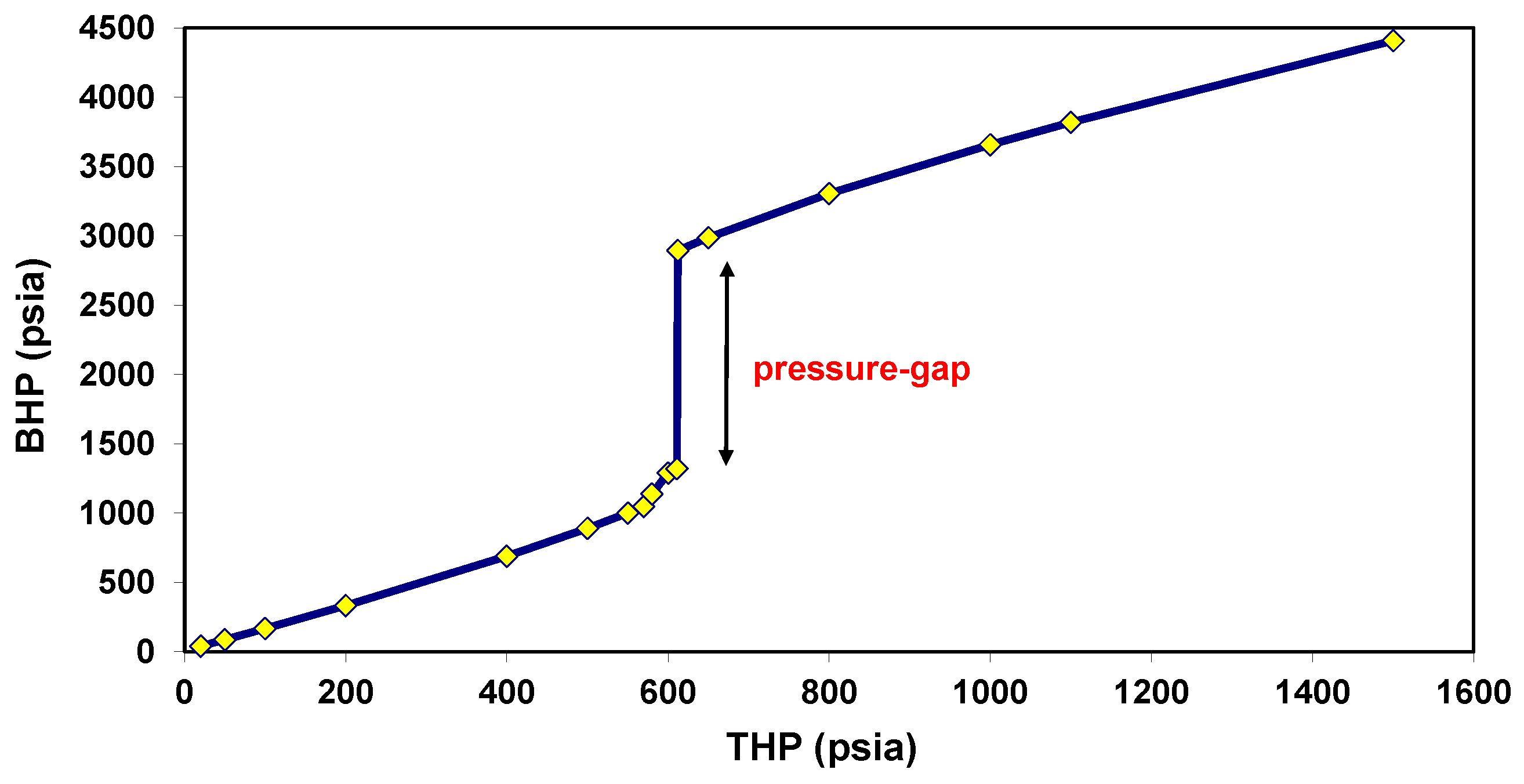
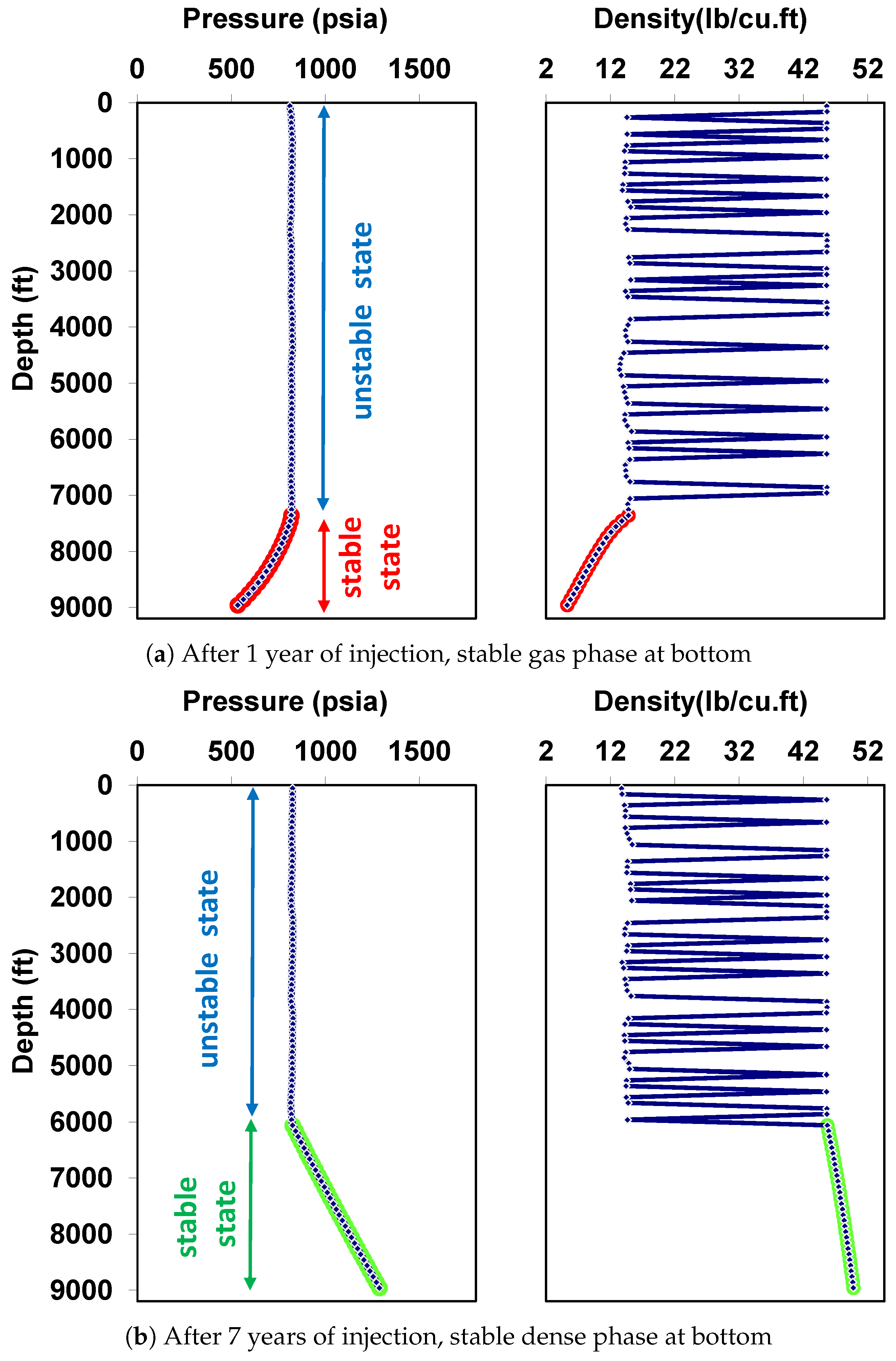
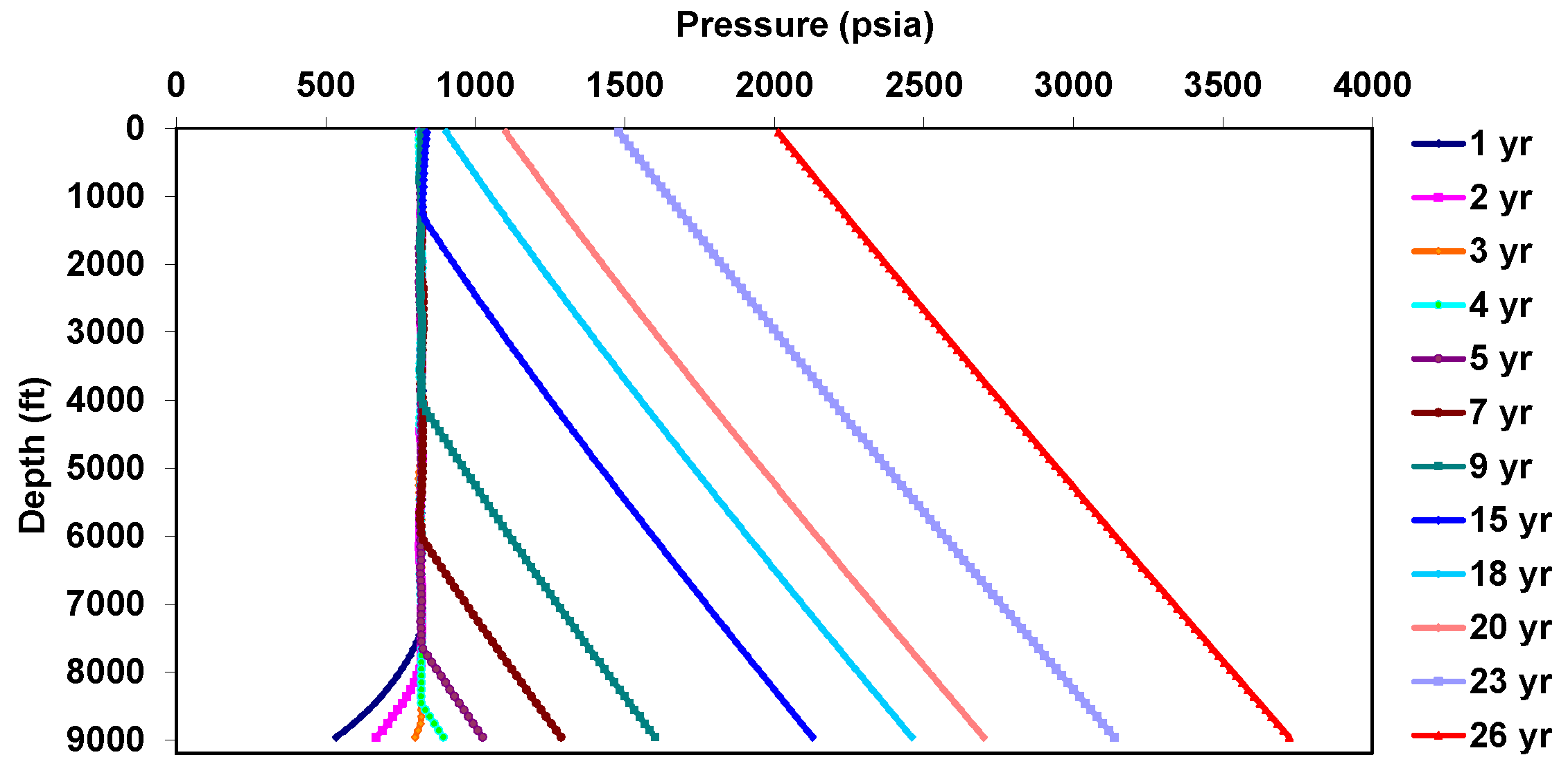
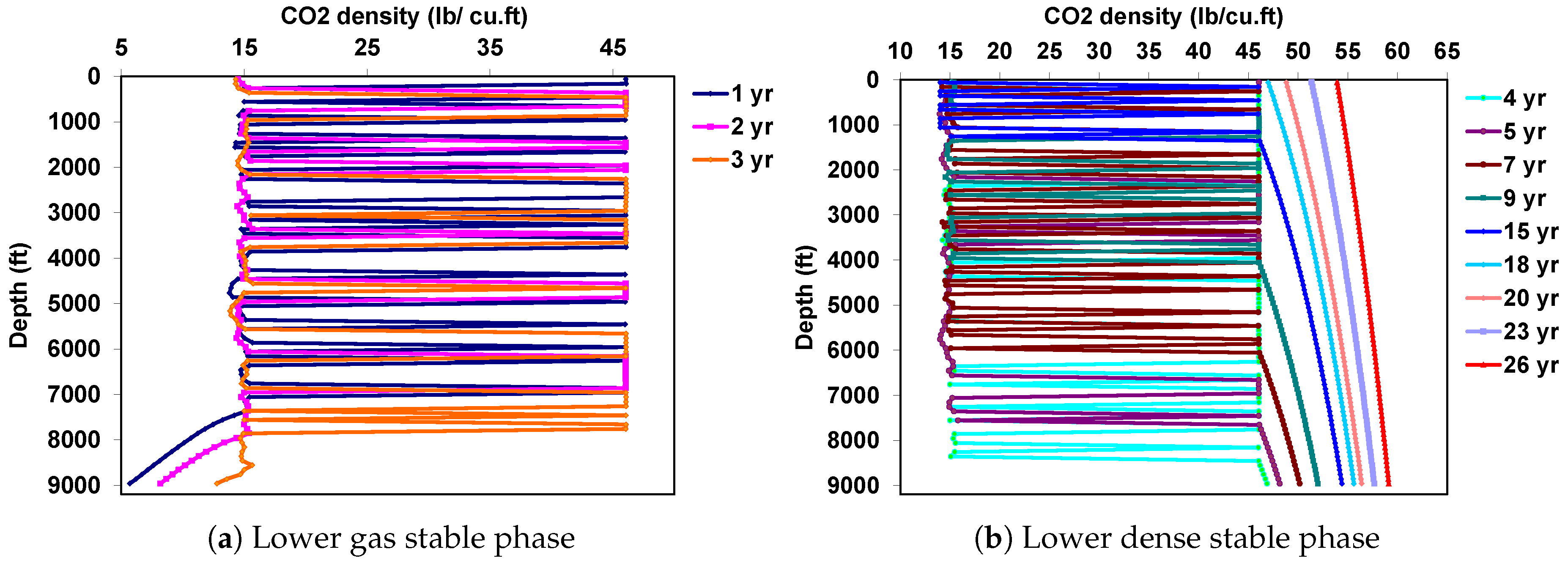
5.1. Behavior under Static Conditions
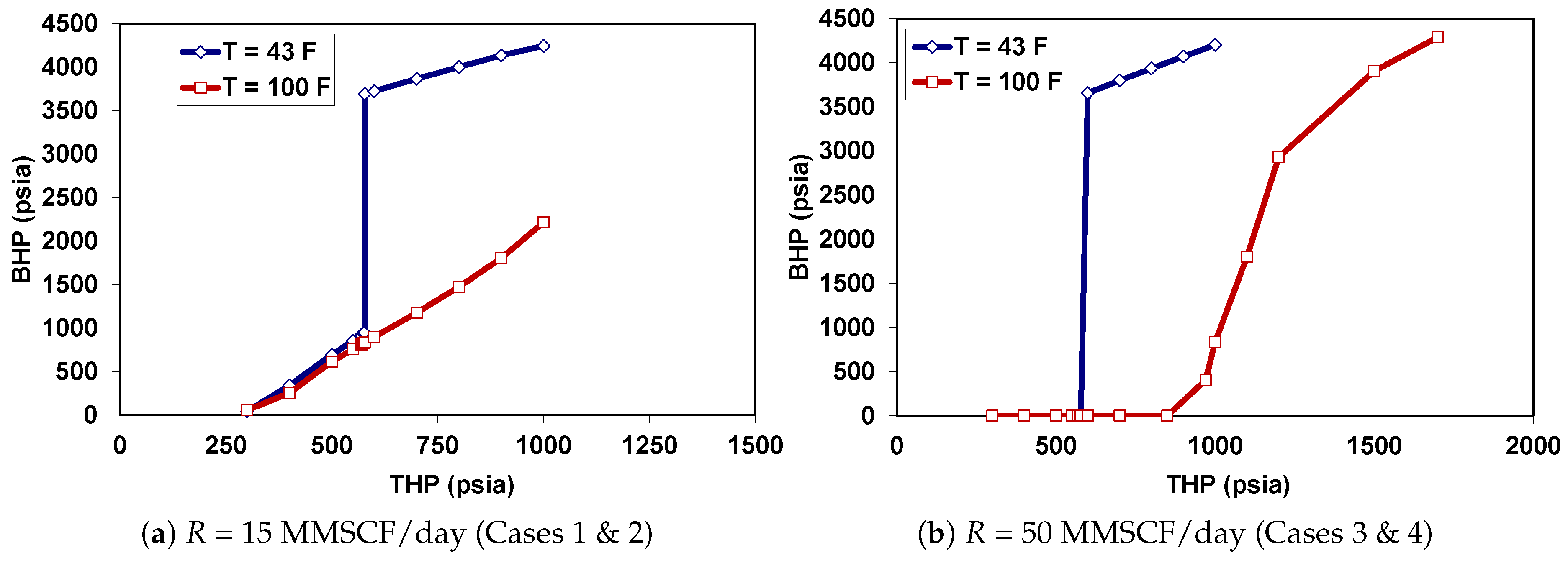
5.2. Behavior under Dynamic Conditions
| Case | Injection Rate (MMSCF/day) * | (F) |
| 1 | 15 | 43 |
| 2 | 15 | 100 |
| 3 | 50 | 43 |
| 4 | 50 | 100 |
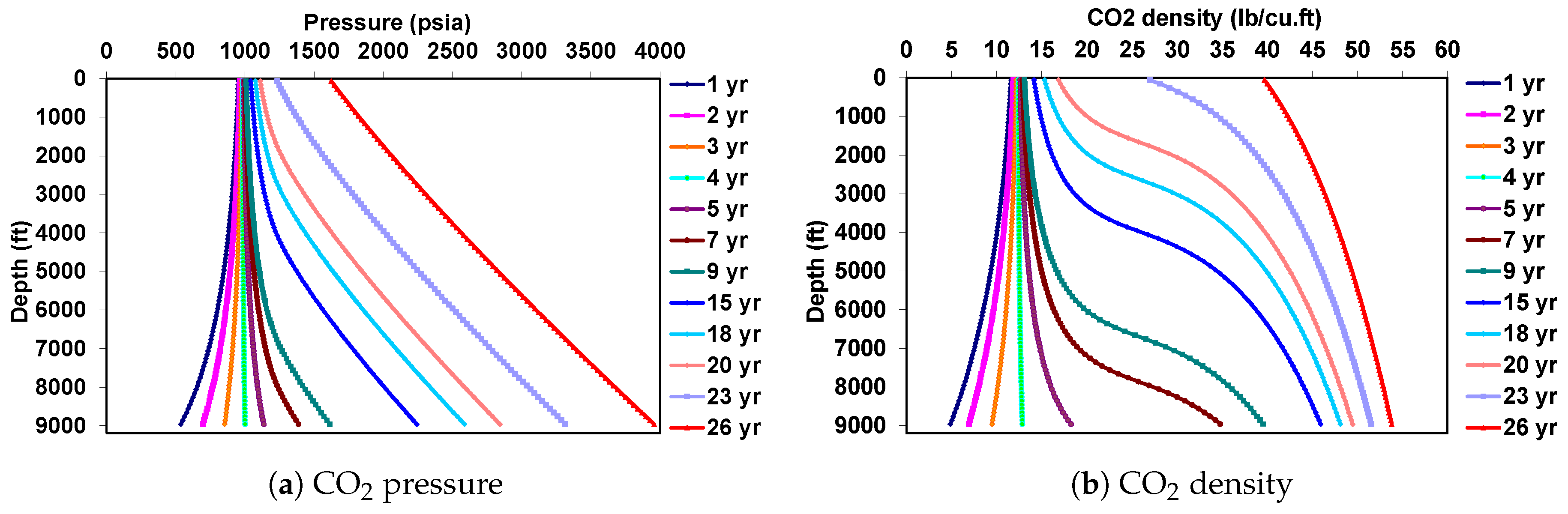
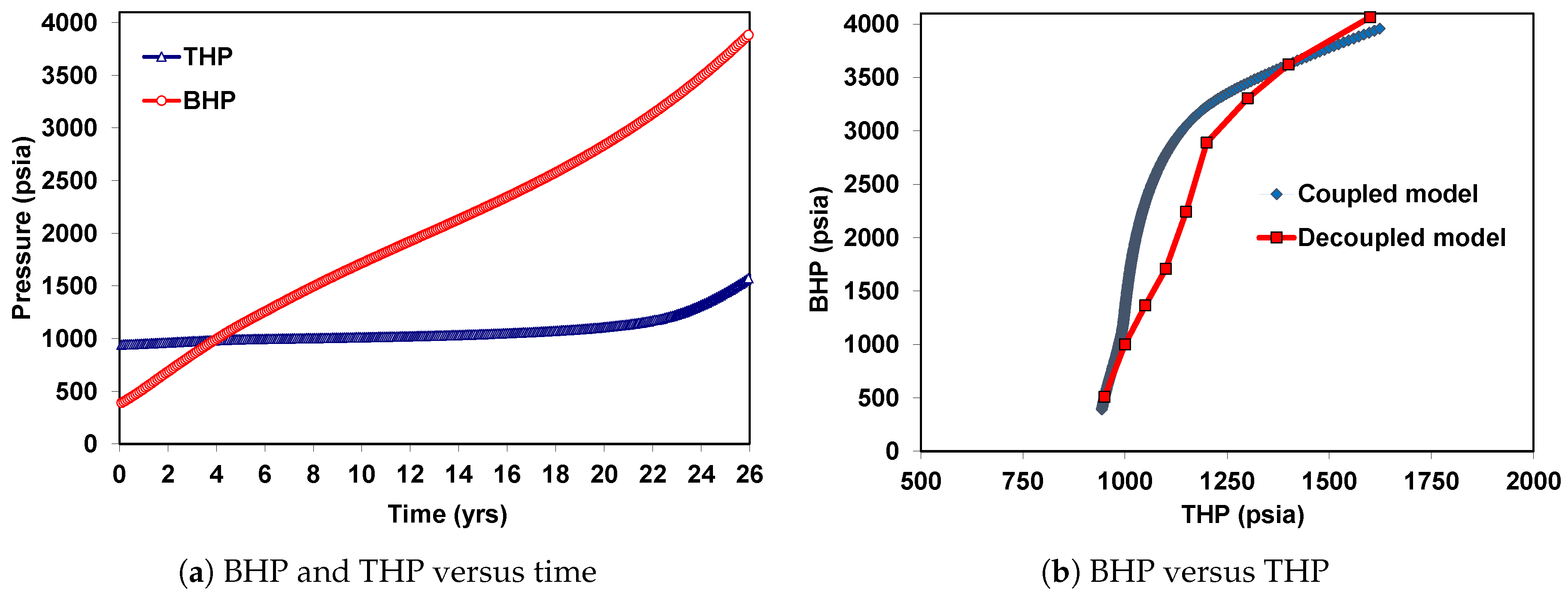
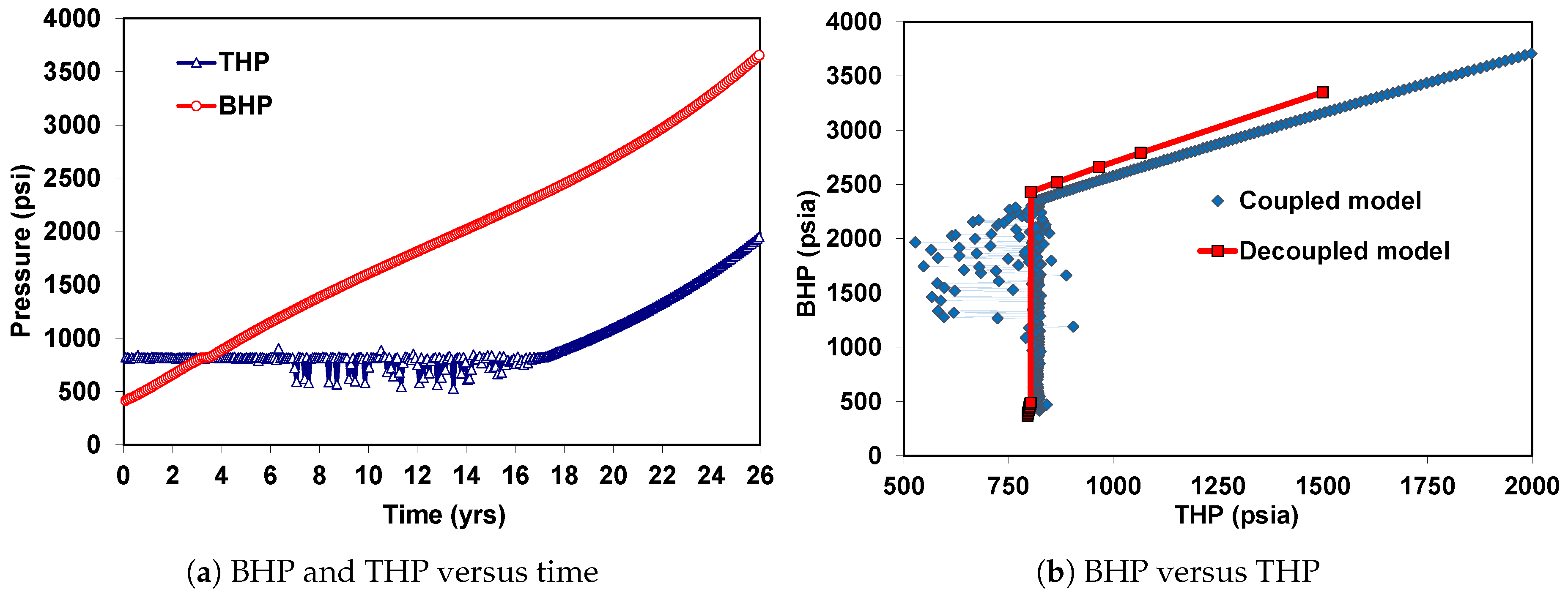
6. Coupled Approach
6.1. Case 1: Injection of CO in the Supercritical State
6.2. Case 2: Injection of CO in the Liquid State
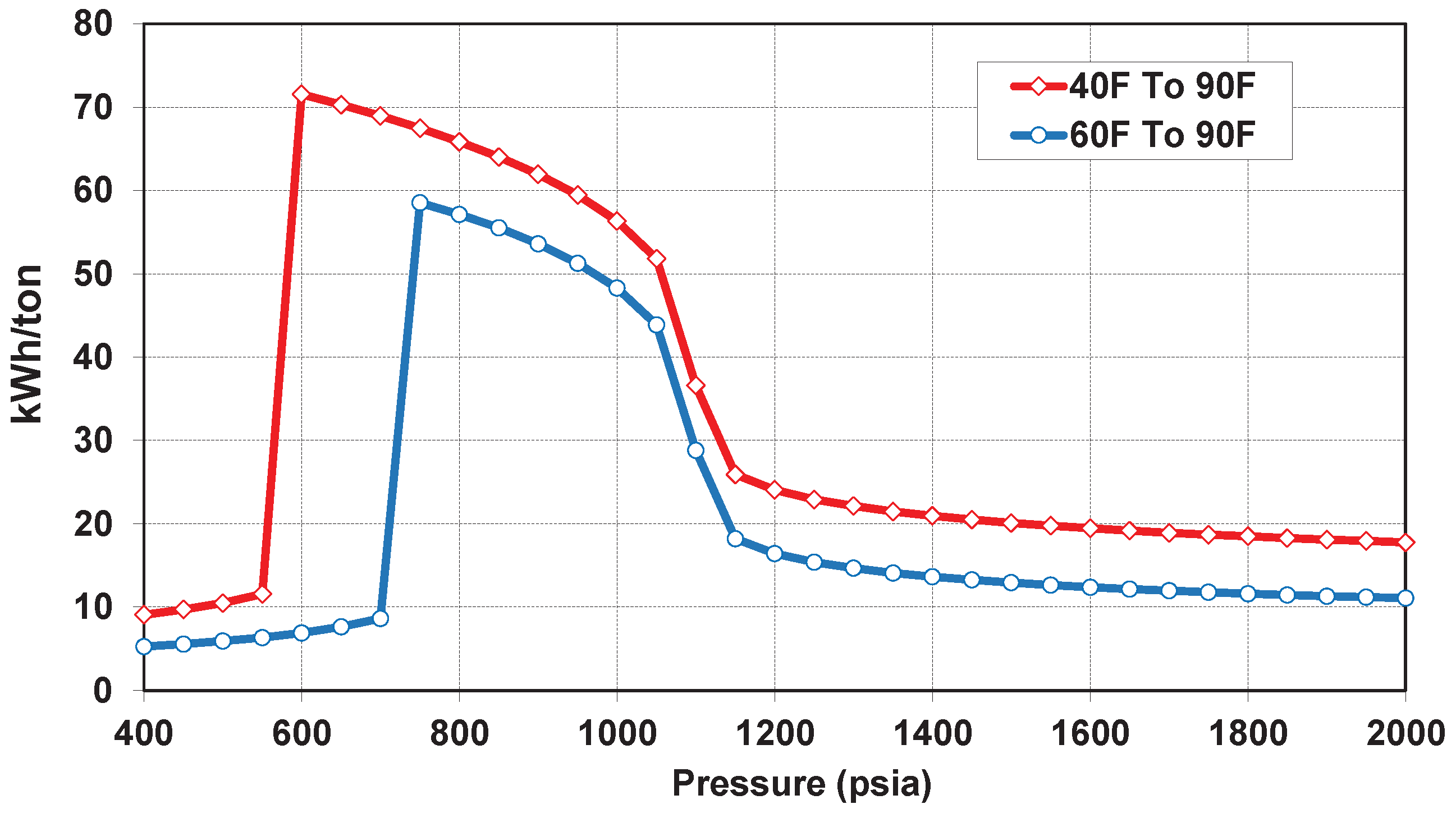
7. CO Heating
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; p. 1535. [Google Scholar]
- Rose, S.K.; Richels, R.; Blanford, G.; Rutherford, T. The Paris Agreement and next steps in limiting global warming. Clim. Chang. 2017, 142, 255–270. [Google Scholar] [CrossRef]
- Cook, J.; Oreskes, N.; Doran, P.T.; Anderegg, W.R.L.; Verheggen, B.; Maibach, E.W.; Carlton, J.S.; Lewandowsky, S.; Skuce, A.G.; Green, S.A.; et al. Consensus on consensus: A synthesis of consensus estimates on human-caused global warming. Environ. Res. Lett. 2016, 11, 048002. [Google Scholar] [CrossRef]
- Verheggen, B.; Strengers, B.; Cook, J.; van Dorland, R.; Vringer, K.; Peters, J.; Visser, H.; Meyer, L. Scientists’ Views about Attribution of Global Warming. Environ. Sci. Technol. 2014, 48, 8963–8971. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.S. Determinants of carbon dioxide emissions: Empirical evidence from 69 countries. Appl. Energy 2011, 88, 376–382. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Mitigation of Climate Change: Working Group III Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2015. [Google Scholar]
- IEA. 20 Years of Carbon Capture and Storage Accelerating Future Deployment; IEA: Paris, France, 2016. [Google Scholar] [CrossRef]
- Godec, M.; Kuuskraa, V.; Van Leeuwen, T.; Melzer, L.S.; Wildgust, N. CO2 Storage in Depleted Oil Fields: The Worldwide Potential for Carbon Dioxide Enhanced Oil Recovery. Energy Procedia 2011, 4, 2162–2169. [Google Scholar] [CrossRef]
- Bruhn, T.; Naims, H.; Olfe-Kräutlein, B. Separating the debate on CO2 utilisation from carbon capture and storage. Environ. Sci. Policy 2016, 60, 38–43. [Google Scholar] [CrossRef]
- Rogelj, J.; den Elzen, M.; Hohne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Chaeffer, R.S.; Ha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 degrees C. Nature 2016, 534, 631–639. [Google Scholar]
- Ladbrook, B.; Smith, N.; Pershad, H.; Harland, K.; Slater, S.; Holloway, S.; Kirk, K. CO2 Storage in Depleted Gas Fields. IEA Technical Report. 2009. Available online: https://hub.globalccsinstitute.com/sites/default/files/publications/95786/co2-storage-depleted-gas-fields.pdf (accessed on 24 April 2019).
- Koide, H.; Tazaki, Y.; Noguchi, Y.; Iijima, M.; Ito, K.; Shindo, Y. Underground-Storage of Carbon-Dioxide in Depleted Natural-Gas Reservoirs and in Useless Aquifers. Eng. Geol. 1993, 34, 175–179. [Google Scholar] [CrossRef]
- Winter, E.M.; Bergman, P.D. Availability of Depleted Oil and Gas-Reservoirs for Disposal of Carbon-Dioxide in the United-States. Energy Convers. Manag. 1993, 34, 1177–1187. [Google Scholar] [CrossRef]
- Gunter, W.; Wong, S.; Cheel, D.; Sjostrom, G. Large CO2 Sinks: Their role in the mitigation of greenhouse gases from an international, national (Canadian) and provincial (Alberta) perspective. Appl. Energy 1998, 61, 209–227. [Google Scholar] [CrossRef]
- Seo, J.G.; Mamora, D.D. Experimental and Simulation Studies of Sequestration of Supercritical Carbon Dioxide in Depleted Gas Reservoirs. In Proceedings of the Exploration and Production Environmental Conference, San Antonio, TX, USA, 10–12 March 2003. [Google Scholar] [CrossRef]
- Oldenburg, C.M.; Benson, S.M. CO2 Injection for Enhanced Gas Production and Carbon Sequestration. In Proceedings of the SPE International Petroleum Conference and Exhibition in Mexico, Villahermosa, Mexico, 10–12 February 2002. [Google Scholar] [CrossRef]
- Clemens, T.; Wit, K. CO2 Enhanced Gas Recovery Studied for an Example Gas Reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar] [CrossRef]
- Holloway, S.; Vanderstraaten, R. The Joule-Ii Project the Underground Disposal of Carbon-Dioxide. Energy Convers. Manag. 1995, 36, 519–522. [Google Scholar] [CrossRef]
- Holloway, S. An overview of the Joule II project the underground disposal of carbon dioxide. Energy Convers. Manag. 1996, 37, 1149–1154. [Google Scholar] [CrossRef]
- Li, Z.W.; Dong, M.Z.; Li, S.L.; Huang, S. CO2 sequestration in depleted oil and gas reservoirs—Caprock characterization and storage capacity. Energy Convers. Manag. 2006, 47, 1372–1382. [Google Scholar] [CrossRef]
- Naylor, M.; Wilkinson, M.; Haszeldine, R.S. Calculation of CO2 column heights in depleted gas fields from known pre-production gas column heights. Mar. Pet. Geol. 2011, 28, 1083–1093. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.R.; Intergovernmental Panel on Climate Change. Climate Change 2014 Impacts Adaptation, and Vulnerability: Working Group II Contribution to the Fifth Assessment Report of The Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2015. [Google Scholar]
- Jiang, X. A review of physical modelling and numerical simulation of long-term geological storage of CO2. Appl. Energy 2011, 88, 3557–3566. [Google Scholar] [CrossRef]
- Welkenhuysen, K.; Rupert, J.; Compernolle, T.; Ramirez, A.; Swennen, R.; Piessens, K. Considering economic and geological uncertainty in the simulation of realistic investment decisions for CO2-EOR projects in the North Sea. Appl. Energy 2017, 185, 745–761. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Santamarina, J.C. CO2 breakthrough-Caprock sealing efficiency and integrity for carbon geological storage. Int. J. Greenhouse Gas Control 2017, 66, 218–229. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, Y.; Bielicki, J.; Amooie, M.A.; Zhang, M.; Yang, C.; Zou, Y.; Ampomah, W.; Xiao, T.; Jia, W.; et al. Heterogeneity-assisted carbon dioxide storage in marine sediments. Appl. Energy 2018, 225, 876–883. [Google Scholar] [CrossRef]
- Maloney, D.R.; Briceno, M. Experimental Investigation of Cooling Effects Resulting from Injecting High Pressure Liquid or Supercritical CO2 into a Low Pressure Gas Reservoir. Petrophysics 2009, 50, 335–344. [Google Scholar]
- Hoteit, H. Modeling the Injectivity-Gap Problem in the Wellbore during CO2 Injection into Low Pressure Reservoirs. In Mathematical & Computational Issues in the Geosciences; SIAM: Long Beach, CA, USA, 2011. [Google Scholar]
- Shell. Storage Development Plan. 2015. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/531016/DECC_Ready_-_KKD_11.128_Storage_Development_Plan.pdf (accessed on 24 April 2019).
- Klotz, I.M.; Rosenberg, R.M. Chemical Thermodynamics: Basic Theory and Methods, 5th ed.; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Tabor, D. Gases, Liquids and Solids: And Other States of Matter, 3rd ed.; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Jenkins, C.R.; Cook, P.J.; Ennis-King, J.; Undershultz, J.; Boreham, C.; Dance, T.; de Caritat, P.; Etheridge, D.M.; Freifeld, B.M.; Hortle, A.; et al. Safe storage and effective monitoring of CO2 in depleted gas fields. Proc. Natl. Acad. Sci. USA 2012, 109, E35–E41. [Google Scholar] [CrossRef]
- Porse, S.L.; Wade, S.; Hovorka, S.D. Can we Treat CO2 Well Blowouts like Routine Plumbing Problems? A Study of the Incidence, Impact, and Perception of Loss of Well Control. Energy Procedia 2014, 63, 7149–7161. [Google Scholar] [CrossRef]
- Skinner, L. CO2 Blowouts: An Emerging Problem. World Oil 2003, 1, 224. [Google Scholar]
- Xu, Q.J.; Weir, G.F.; Paterson, L.; Black, I.; Sharma, S. A CO2-Rich Gas Well Test and Analyses. In Proceedings of the Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 30 October–1 November 2007. [Google Scholar] [CrossRef]
- Oldenburg, C.M. Joule-Thomson cooling due to CO2 injection into natural gas reservoirs. Energy Convers. Manag. 2007, 48, 1808–1815. [Google Scholar] [CrossRef]
- Mathias, S.A.; Gluyas, J.G.; Oldenburg, C.M.; Tsang, C.F. Analytical solution for Joule-Thomson cooling during CO2 geo-sequestration in depleted oil and gas reservoirs. Int. J. Greenhouse Gas Control 2010, 4, 806–810. [Google Scholar] [CrossRef]
- Ziabakhsh-Ganji, Z.; Kooi, H. Sensitivity of Joule-Thomson cooling to impure CO2 injection in depleted gas reservoirs. Appl. Energy 2014, 113, 434–451. [Google Scholar] [CrossRef]
- Hughes, D.S. Carbon storage in depleted gas fields: Key challenges. Greenhouse Gas Control Technol. 2009, 1, 3007–3014. [Google Scholar] [CrossRef]
- Galic, H.; Cawley, S.J.; Bishop, S.R.; Gas, F.; Todman, S. CO2 Injection Into Depleted Gas Reservoirs. In Proceedings of the Offshore Europe, Aberdeen, UK, 8–11 September 2009. [Google Scholar] [CrossRef]
- Lake, L. Petroleum Engineering Handbook: Indexes and Standards; Society of Petroleum Engineers: Richardson, TX, USA, 2007. [Google Scholar]
- Michelsen, M.L. Calculation of Hydrate Fugacities. Chem. Eng. Sci. 1991, 46, 1192–1193. [Google Scholar] [CrossRef]
- Munck, J.; Skjoldjorgensen, S.; Rasmussen, P. Computations of the Formation of Gas Hydrates. Chem. Eng. Sci. 1988, 43, 2661–2672. [Google Scholar] [CrossRef]
- Firoozabadi, A. Thermodynamics of Hydrocarbon Reservoirs; McGraw-Hill: New York, NY, USA, 1999; p. 355. [Google Scholar]

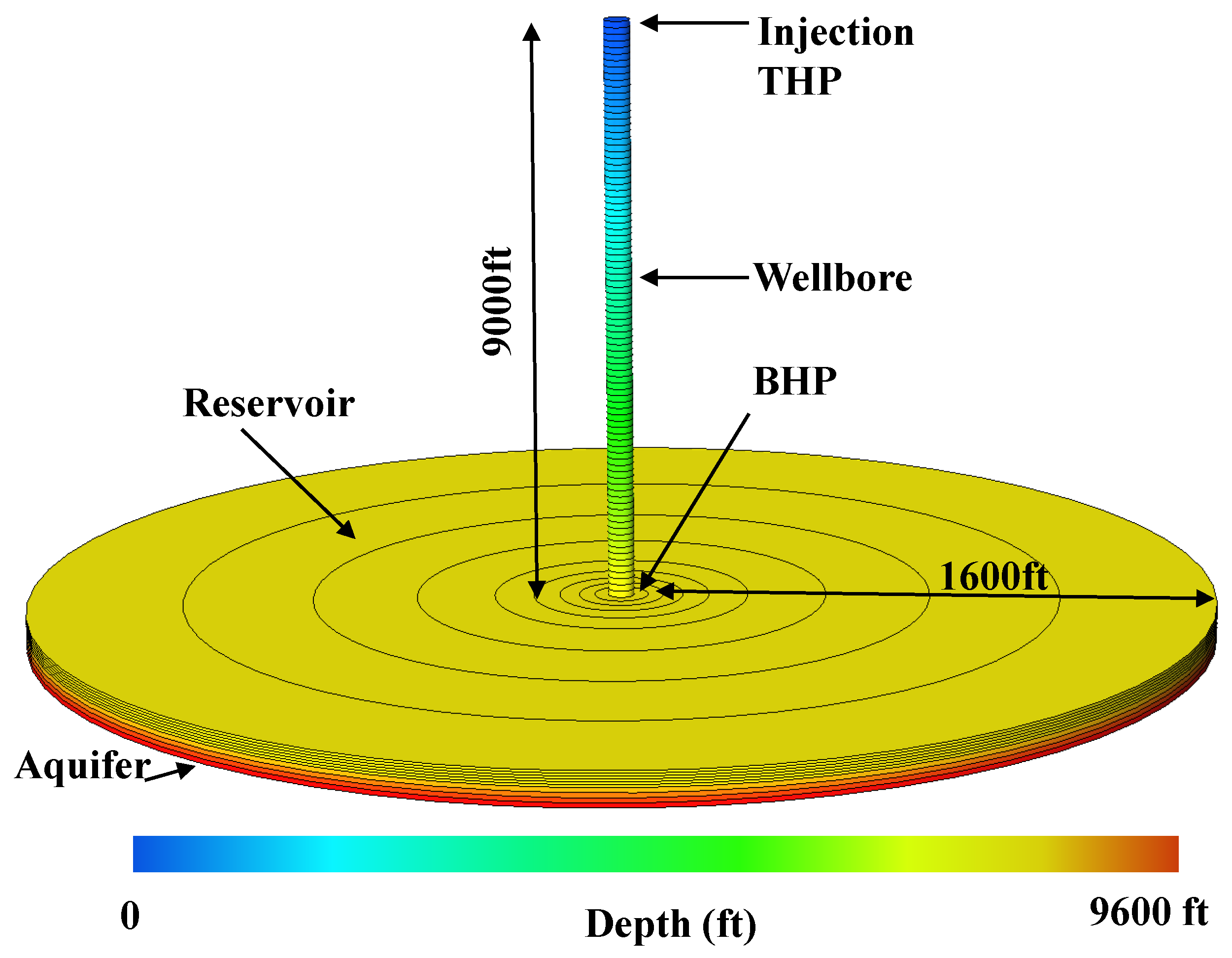

| Well true vertical depth, TVD (ft) | 9000 |
| Well tubing diameter, OD (in) | 5.5 |
| Surface temperature range (F) | 43–60 |
| Reservoir pressure (psia) | 200 |
| Reservoir temperature (F) | 182 |
| Geothermal gradient (F/1000 ft) | 15.7 |
| Injection rate (MMSCF/day) | 15–50 |
| CO mole fraction | 1 |
| Critical temperature, (F) | 87.7 |
| Critical pressure, (psia) | 1070 |
| Critical volume, (ft/lb-mol) | 1.5 |
| Volume shift, (ft/lb-mol) | −0.1 |
| Acentric factor (–) | 0.24 |
| Molecular weight (g/mol) | 44.01 |
| Parachor (–) | 78 |
| Reservoir depth (ft) | 9000 |
| Reservoir thickness (ft) | 250 |
| Reservoir radial size (ft) | 1600 |
| Aquifer thickness (ft) | 300 |
| Radial permeability (mDarcy) | 300 |
| Vertical permeability (mDarcy) | 30 |
| Porosity (fraction) | 0.2 |
| Connate water saturation (–) | 0.2 |
| Reservoir temperature (F) | 182 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoteit, H.; Fahs, M.; Soltanian, M.R. Assessment of CO2 Injectivity During Sequestration in Depleted Gas Reservoirs. Geosciences 2019, 9, 199. https://doi.org/10.3390/geosciences9050199
Hoteit H, Fahs M, Soltanian MR. Assessment of CO2 Injectivity During Sequestration in Depleted Gas Reservoirs. Geosciences. 2019; 9(5):199. https://doi.org/10.3390/geosciences9050199
Chicago/Turabian StyleHoteit, Hussein, Marwan Fahs, and Mohamad Reza Soltanian. 2019. "Assessment of CO2 Injectivity During Sequestration in Depleted Gas Reservoirs" Geosciences 9, no. 5: 199. https://doi.org/10.3390/geosciences9050199
APA StyleHoteit, H., Fahs, M., & Soltanian, M. R. (2019). Assessment of CO2 Injectivity During Sequestration in Depleted Gas Reservoirs. Geosciences, 9(5), 199. https://doi.org/10.3390/geosciences9050199