Sources and Impacts of Bottom Slope Uncertainty on Estimation of Seafloor Backscatter from Swath Sonars
Abstract
:1. Introduction
2. Materials and Methods
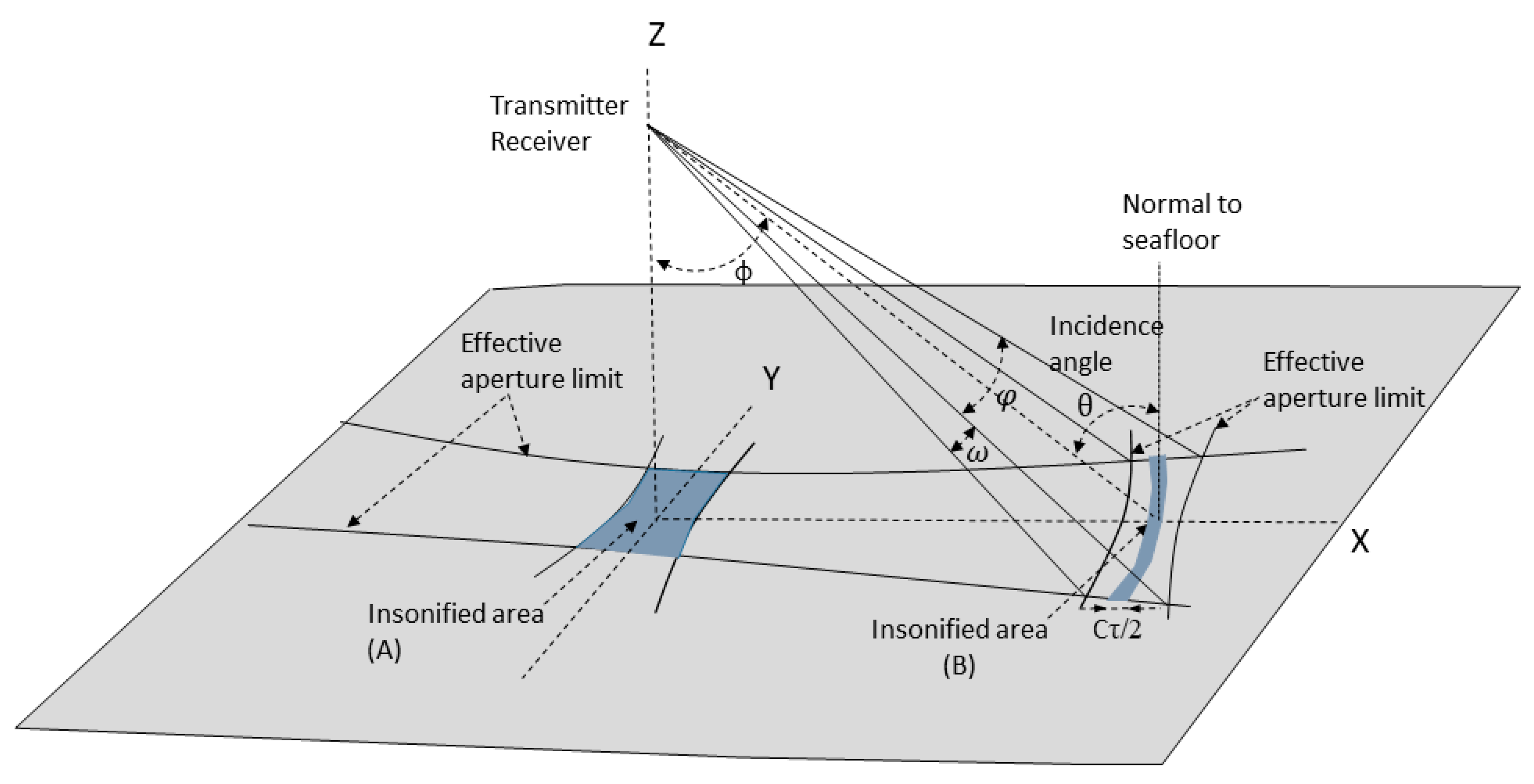
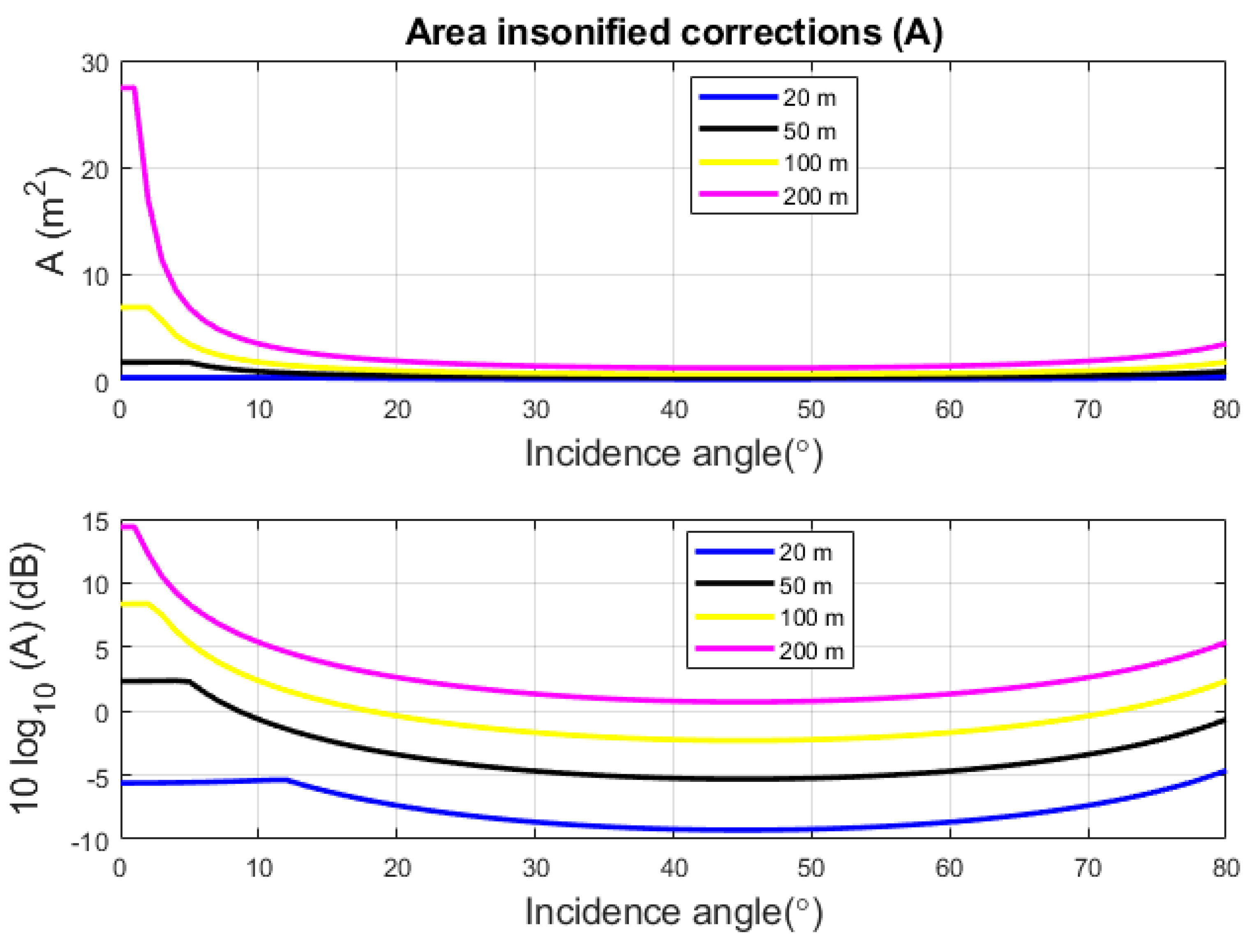
2.1. Area Insonified Correction
2.2. Seafloor Incidence Angle Correction
2.3. Estimation of Seafloor Slope and Its Uncertainty
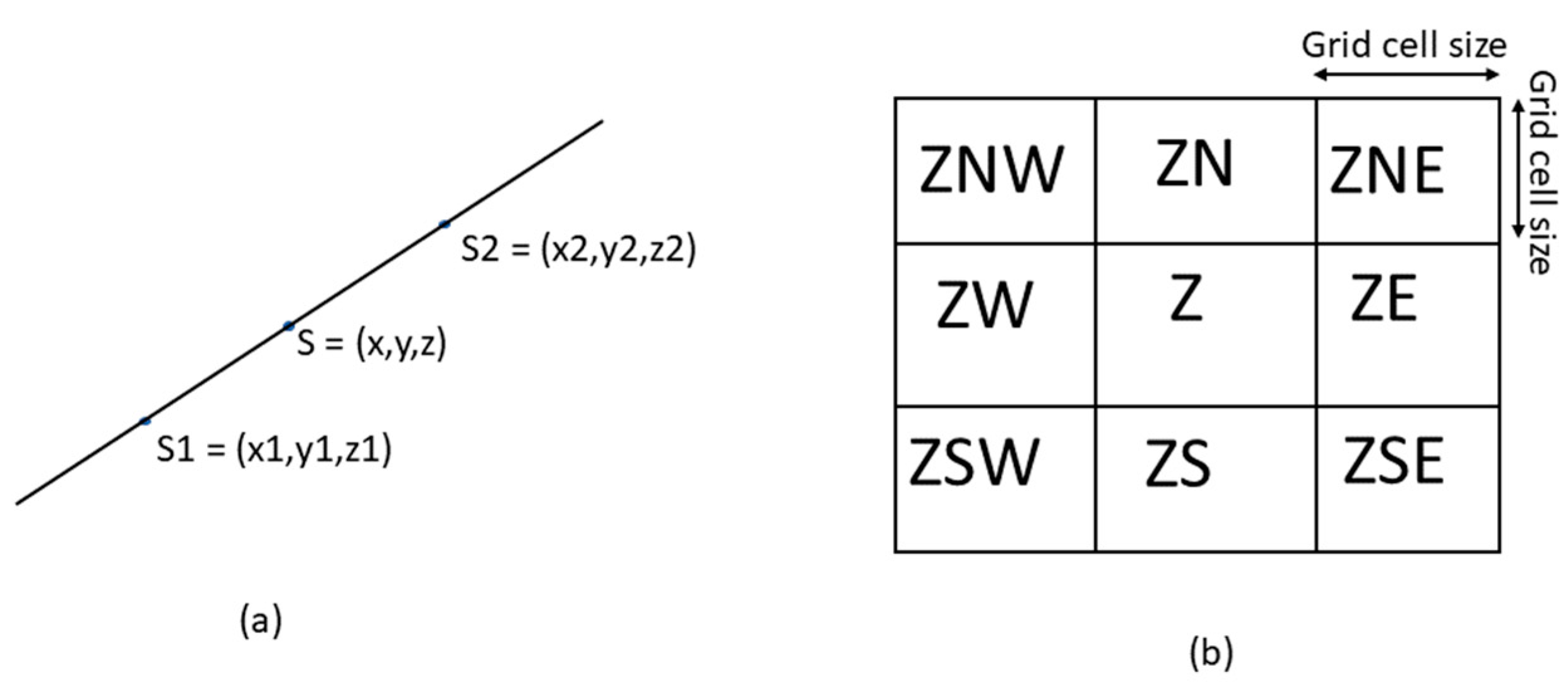
2.3.1. Directional Slope (Along-Track and Across-Track from Reference Grid)
2.3.2. Estimation of Slope Uncertainty
2.4. Multibeam Sonar Test Dataset
MBES Bathymetric Data Processing
3. Results
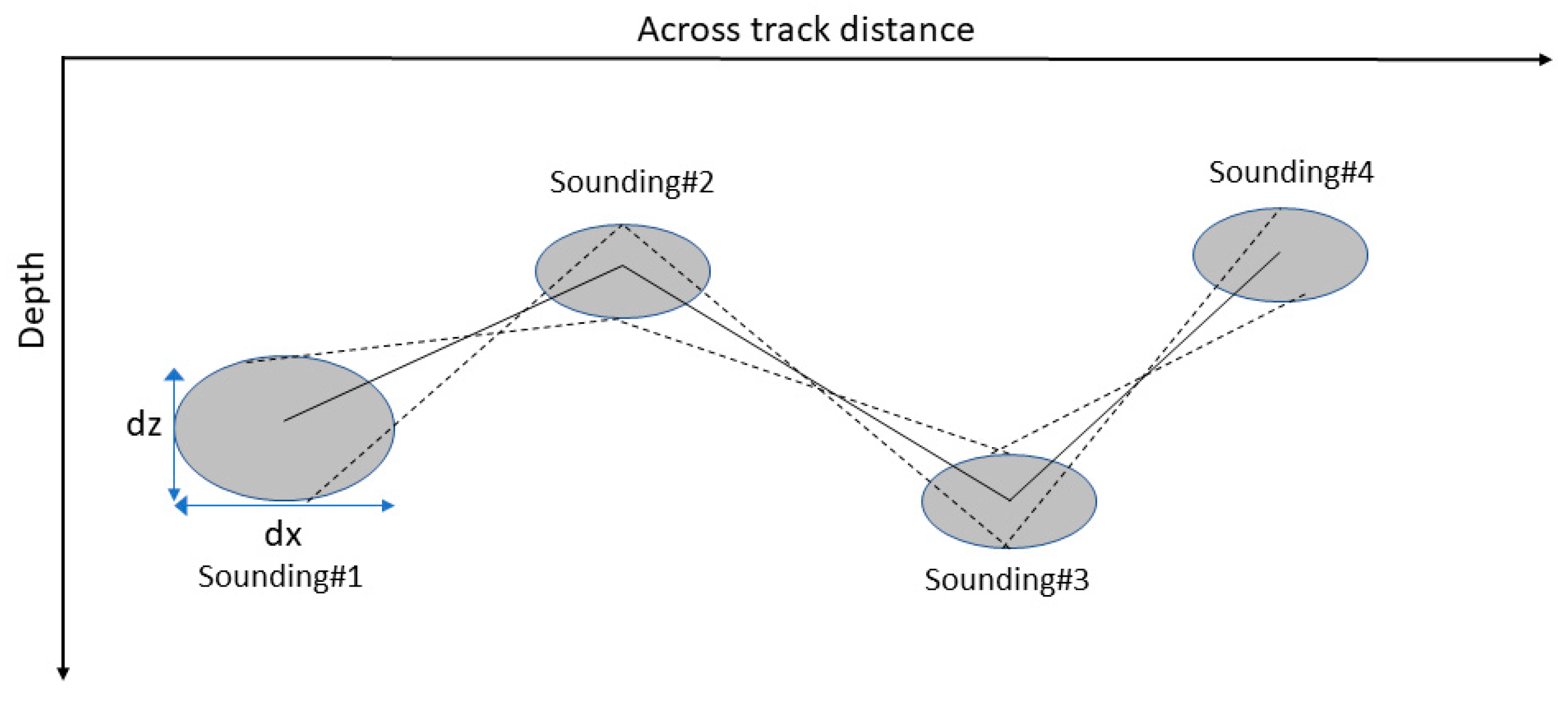
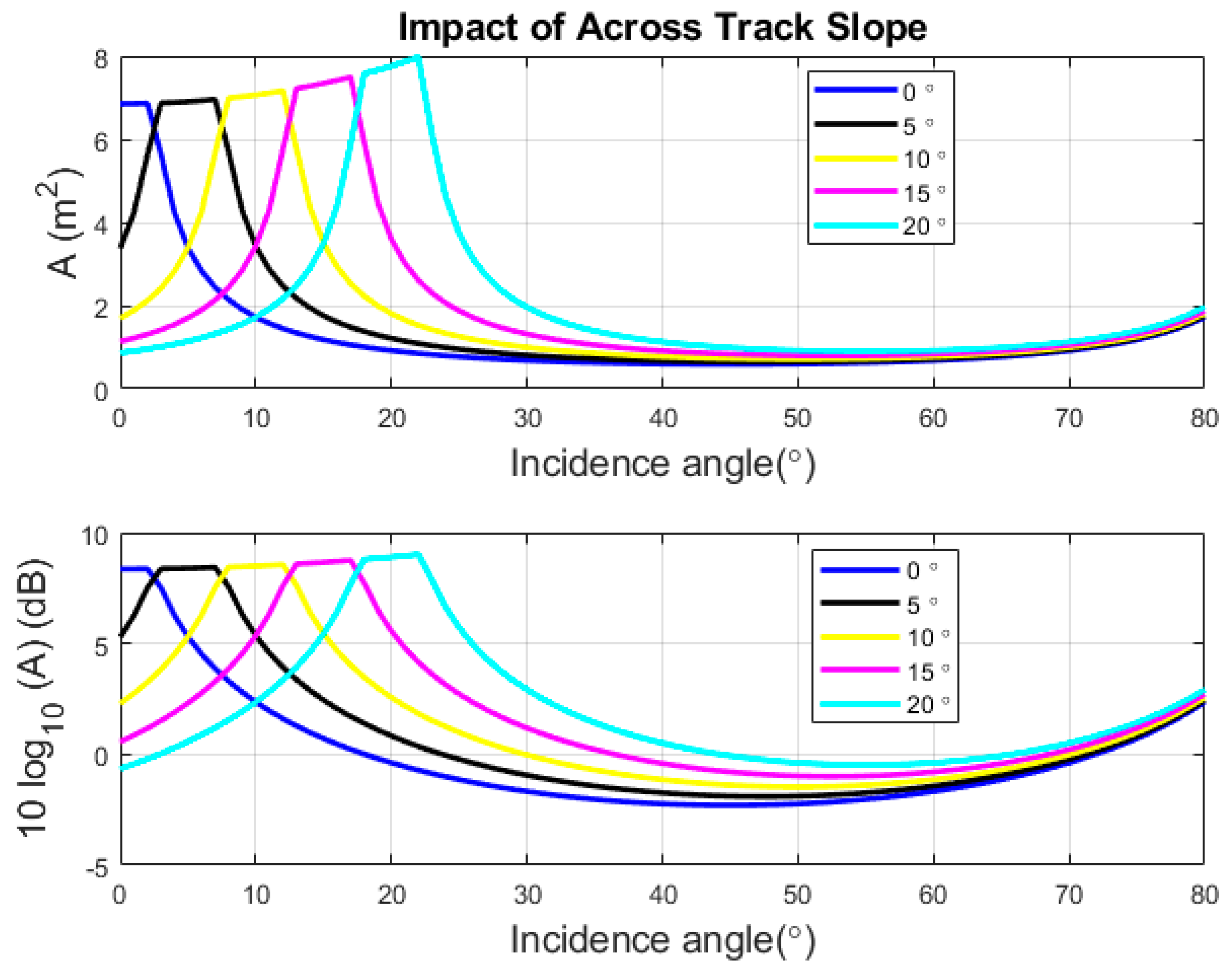
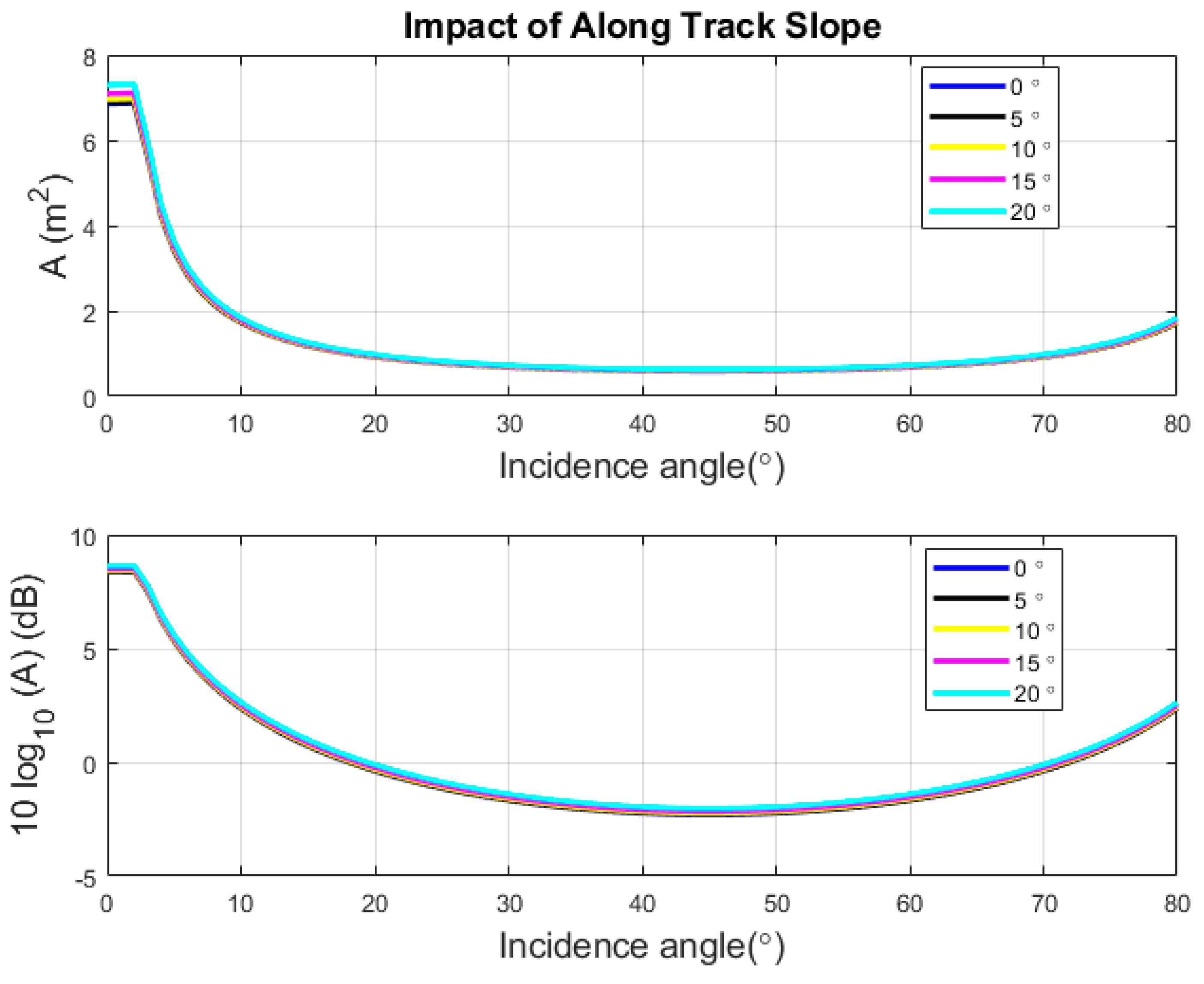
3.1. Slope Impact on the Footprint Extent
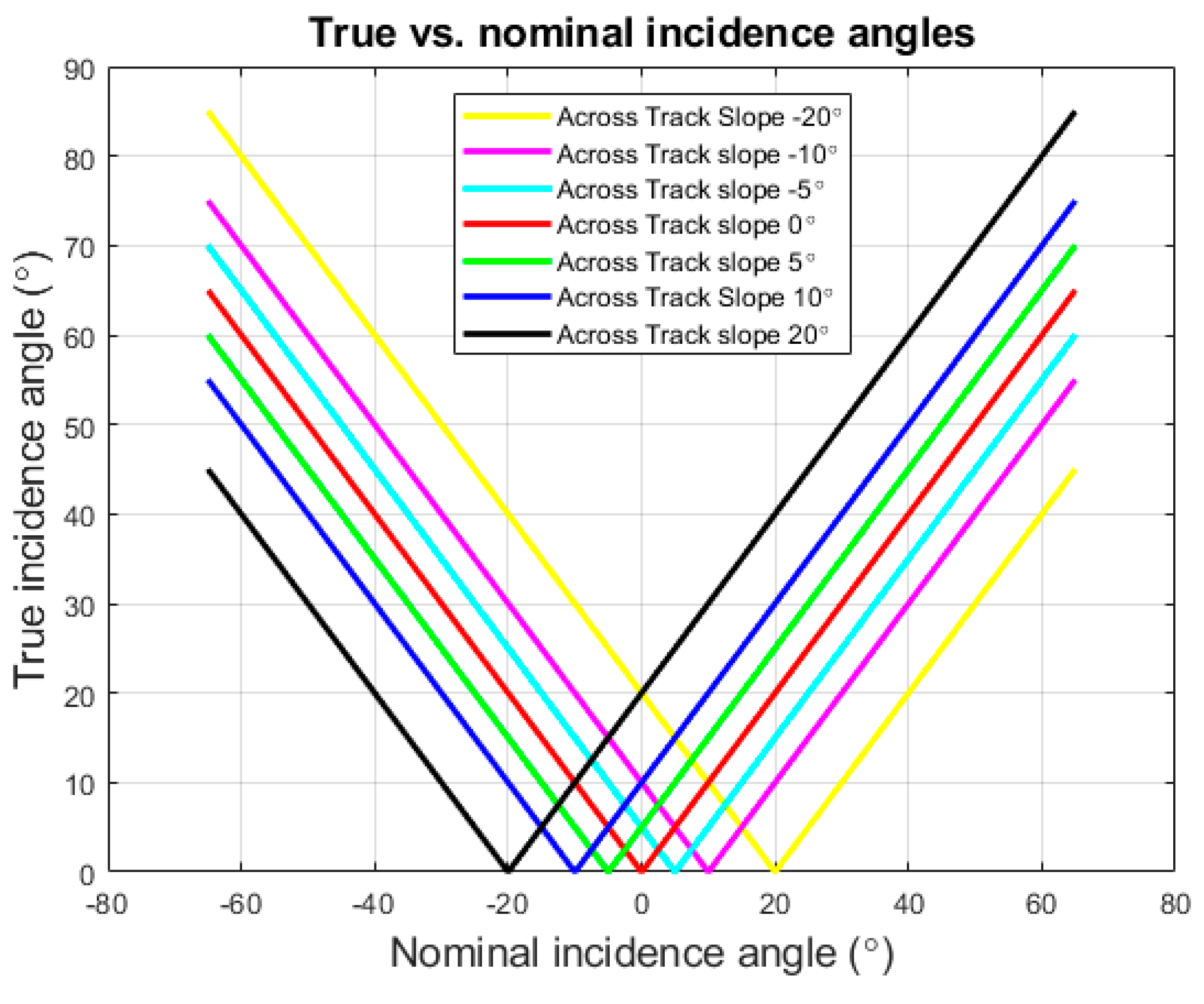
3.2. Seafloor Slope Impact on Incidence Angle
3.3. Scale Dependent Slope Estimation Uncertainty
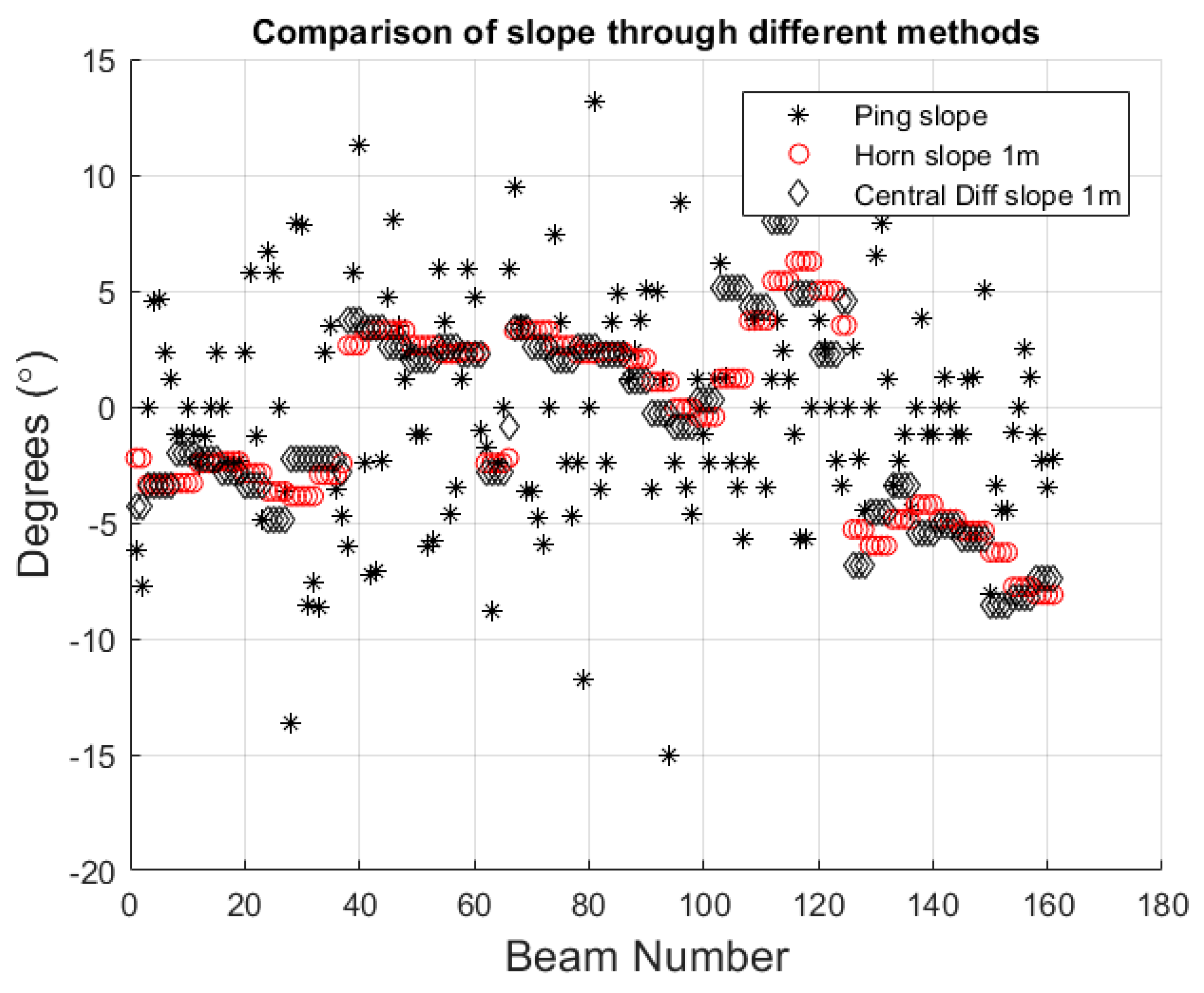
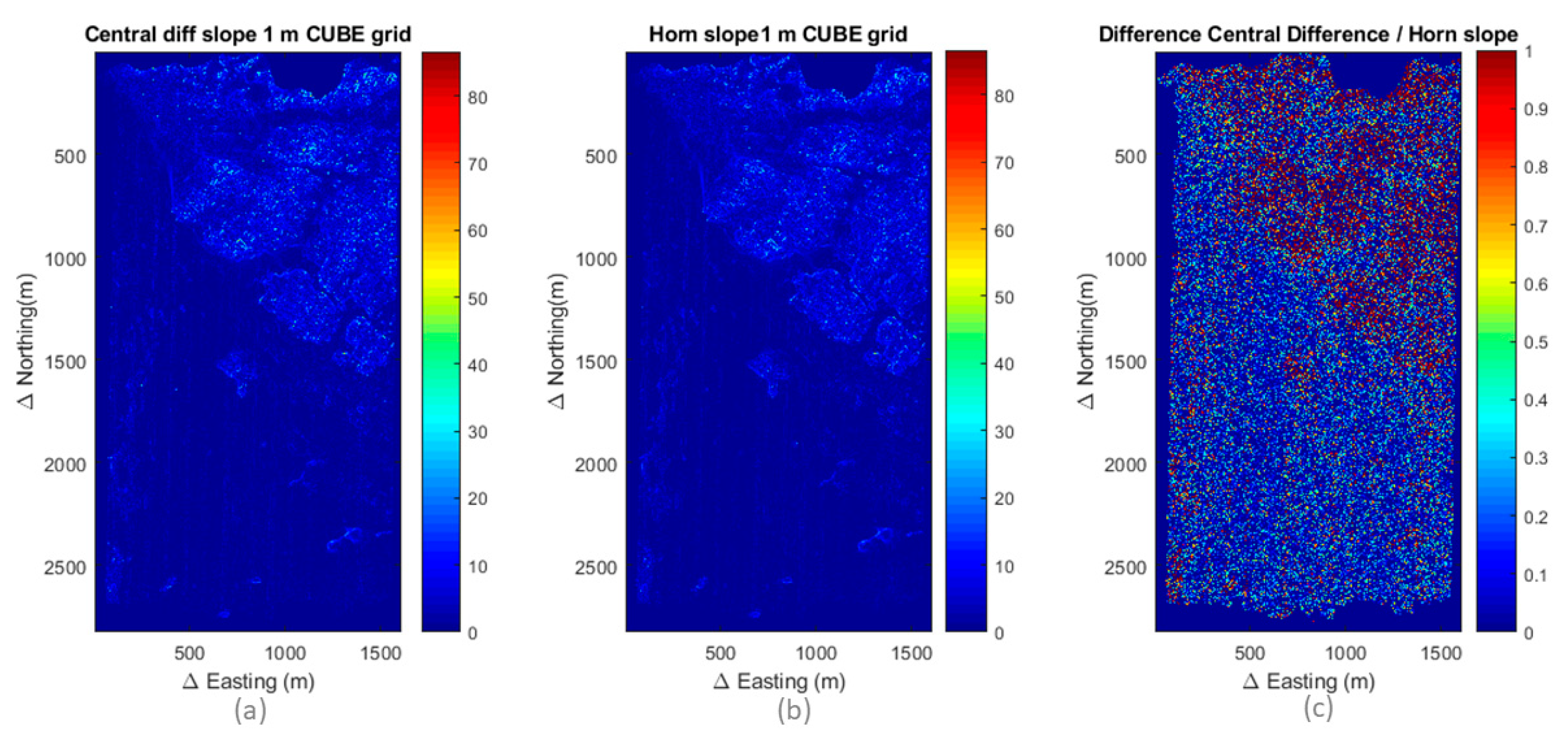
3.4. Uncertainty Due to the Slope Estimation Method
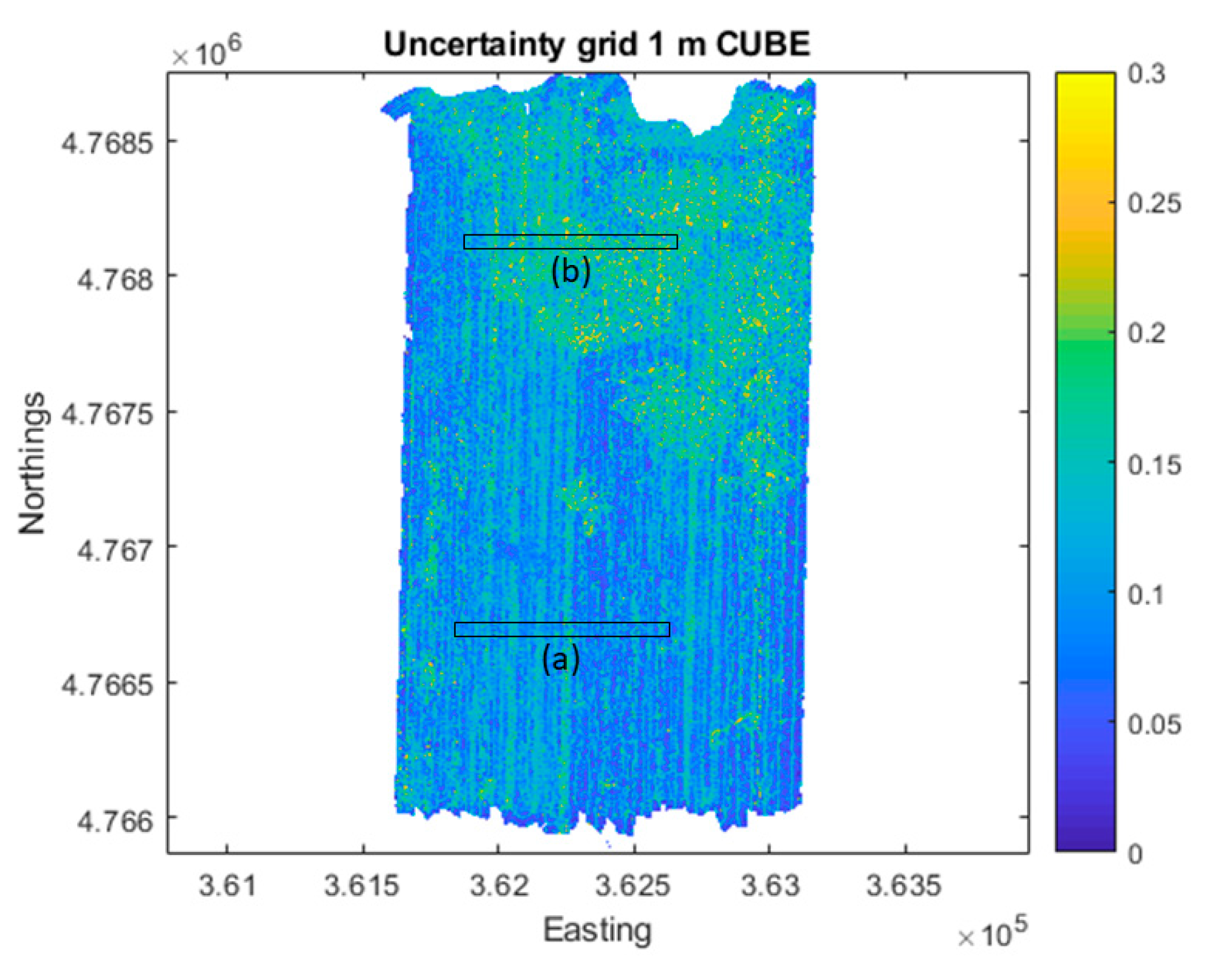
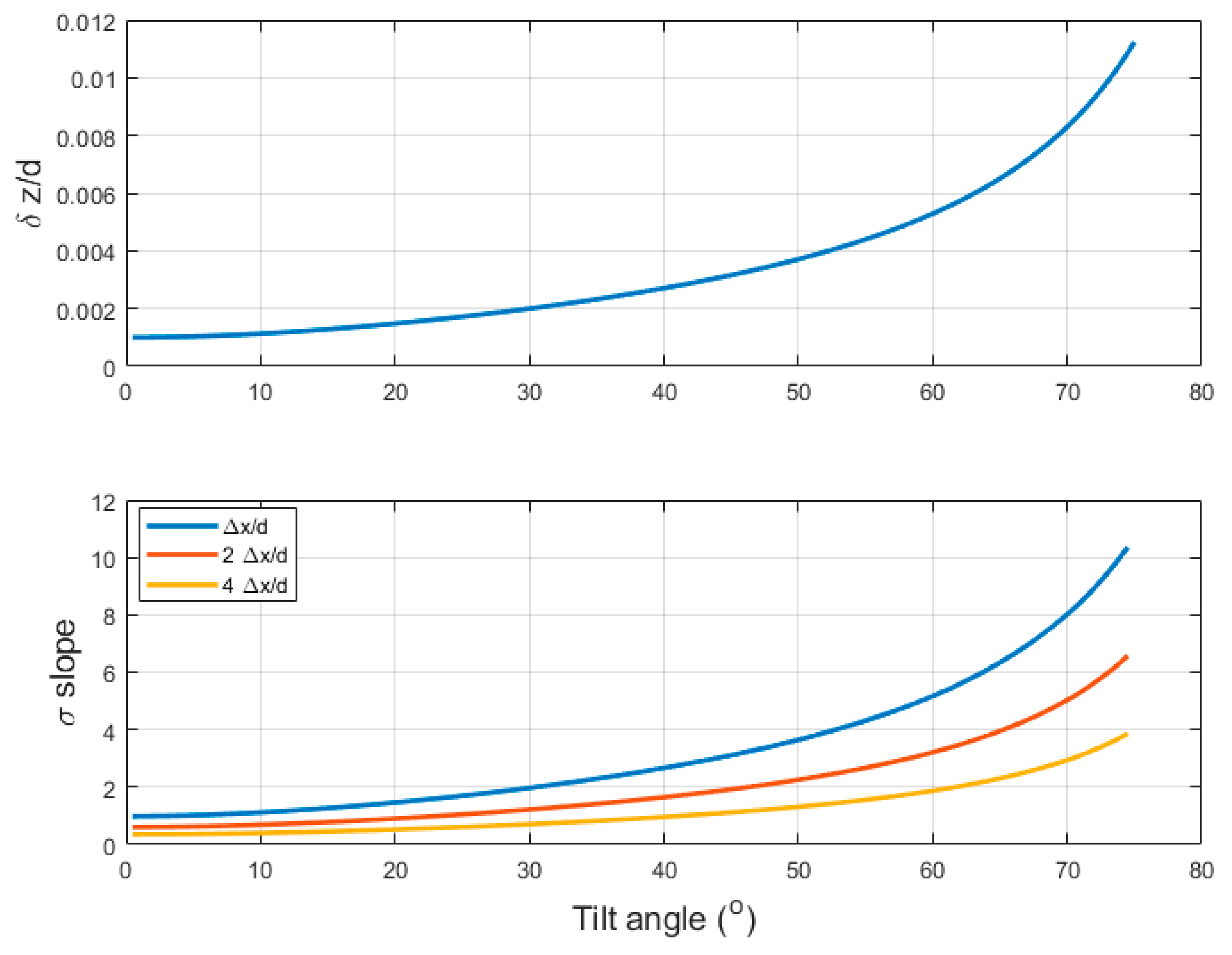
3.5. Propagation of Depth Uncertainty to Slope Uncertainty
3.6. Impact of Unresolved Seafloor Slope on Backscatter Ensemble Average
3.7. Practical Impact of Slope Scale on Incidence Angle and Processed Backscatter Results
4. Discussion
4.1. Summary of Uncertainty Components of Seafloor Backscatter Measurements Related to Seafloor Slope
4.1.1. Approaches to Using Bathymetry for Slope Estimation
4.1.2. Impact of Spatial Scale
4.1.3. Impact of Bathymetric Uncertainty
4.1.4. Slope Uncertainty vs. Grid Resolution and Computation Approach
5. Conclusions
Funding
Disclaimer
Acknowledgments
Conflicts of Interest
References
- Hughes Clarke, J.E.; Mayer, L.A.; Wells, D.E. Shallow-water imaging multibeam sonars: A new tool for investigating seafloor processes in the coastal zone and on the continental shelf. Mar. Geophys. Res. 1996, 18, 607–629. [Google Scholar] [CrossRef]
- Mayer, L.A. Frontiers in Seafloor Mapping and Visualization. Mar. Geophys. Res. 2006, 27, 7–17. [Google Scholar] [CrossRef]
- ICES. Acoustic Seabed Classification of Marine Physical and Biological Landscapes; ICES Cooperative Research Report No. 286; ICES: Copenhagen, Denmark, 2007; p. 185. ISBN 87-7482-058-3. [Google Scholar]
- Lucieer, V.; Roche, M.; Degrendele, K.; Malik, M.; Dolan, M.; Lamarche, G. User expectations for multibeam echo sounders backscatter strength data-looking back into the future. Mar. Geophys. Res. 2018, 39, 23–40. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Gopal, S. The Accuracy of Spatial Databases; Taylor & Francis: New York, NY, USA, 1989; ISBN 978-0-85066-847-6. [Google Scholar]
- Kiiveri, H.T. Assessing, representing and transmitting positional uncertainty in maps. Int. J. Geogr. Inf. Sci. 1997, 11, 33–52. [Google Scholar] [CrossRef]
- Congalton, R. Quantifying Spatial Uncertainty in Natural Resources: Theory and Applications for GIS and Remote Sensing, 1st ed.; Mowrer, H.T., Congalton, R.G., Eds.; CRC Press: Chelsea, MI, USA, 2000; ISBN 978-1-57504-131-5. [Google Scholar]
- Zhang, J.; Goodchild, M.F. Uncertainty in Geographical Information; CRC Press: Chelsea, MI, USA, 2002; ISBN 978-0-203-47132-6. [Google Scholar]
- Malik, M.; Lurton, X.; Mayer, L. A framework to quantify uncertainties of seafloor backscatter from swath mapping echosounders. Mar. Geophys. Res. 2018, 39, 151–168. [Google Scholar] [CrossRef]
- Hare, R.; Godin, A.; Mayer, L.A. Accuracy Estimation of Canadian Swath (Multibeam) and Sweep (Multitransducer) Sounding Systems; Canadian Hydrographic Service Internal Report: Ottawa, ON, Canada, 1995. [Google Scholar]
- Calder, B.R.; Mayer, L.A. Automatic processing of high-rate, high-density multibeam echosounder data. Geochem. Geophys. Geosystems 2003, 4. [Google Scholar] [CrossRef] [Green Version]
- Lamarche, G.; Lurton, X. Recommendations for improved and coherent acquisition and processing of backscatter data from seafloor-mapping sonars. Mar. Geophys. Res. 2018, 39, 5–22. [Google Scholar] [CrossRef]
- Stephens, D.; Diesing, M. A Comparison of Supervised Classification Methods for the Prediction of Substrate Type Using Multibeam Acoustic and Legacy Grain-Size Data. PLOS ONE 2014, 9, e93950. [Google Scholar] [CrossRef]
- Kloser, R.J.; Penrose, J.D.; Butler, A.J. Multi-beam backscatter measurements used to infer seabed habitats. Cont. Shelf Res. 2010, 30, 1772–1782. [Google Scholar] [CrossRef]
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; Peninsula Pub: Los Altos, CA, USA, 1996; ISBN 978-0-932146-62-5. [Google Scholar]
- Jackson, D.R.; Richardson, M.D. High-Frequency Seafloor Acoustics; Springer Science & Business Media: New York, NY, USA, 2007; ISBN 978-0-387-34154-5. [Google Scholar]
- Lurton, X. An Introduction to Underwater Acoustics: Principles and Applications, 2nd ed.; Springer-Verlag: Berlin, Germany, 2010; ISBN 978-3-540-78480-7. [Google Scholar]
- Lurton, X.; Lamarche, G. Backscatter Measurements by Seafloor-Mapping Sonars. Guidelines and Recommendations. Geohab Report. 2015. Available online: http://geohab.org/wp-content/uploads/2014/05/BSWGREPORT-MAY2015.pdf (accessed on 17 April 2019).
- Amiri-Simkooei, A.; Snellen, M.; Simons, D.G. Riverbed sediment classification using multi-beam echo-sounder backscatter data. J. Acoust. Soc. Am. 2009, 126, 1724–1738. [Google Scholar] [CrossRef]
- Neteler, M.; Mitasova, H. Open Source GIS: A GRASS GIS Approach, 3rd ed.; Springer US: New York, NY, USA, 2008; ISBN 978-0-387-35767-6. [Google Scholar]
- Dolan, M.F.J.; Lucieer, V.L. Variation and Uncertainty in Bathymetric Slope Calculations Using Geographic Information Systems. Mar. Geod. 2014, 37, 187–219. [Google Scholar] [CrossRef]
- Horn, B.K.P. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef] [Green Version]
- Lucieer, V.; Huang, Z.; Siwabessy, J. Analyzing Uncertainty in Multibeam Bathymetric Data and the Impact on Derived Seafloor Attributes. Mar. Geod. 2016, 39, 32–52. [Google Scholar] [CrossRef]
- Jones, K.H. A comparison of algorithms used to compute hill slope as a property of the DEM. Comput. Geosci. 1998, 24, 315–323. [Google Scholar] [CrossRef]
- Goulden, T.; Hopkinson, C.; Jamieson, R.; Sterling, S. Sensitivity of DEM, slope, aspect and watershed attributes to LiDAR measurement uncertainty. Remote Sens. Environ. 2016, 179, 23–35. [Google Scholar] [CrossRef]
- Kongsberg Inc. EM 3002 Product Description (855-164771/Rev.E/20.06.2006). Available online: http://www.bkmarine.no/index_htm_files/EM%203002%20Product%20description.pdf (accessed on 19 April 2019).
- QIMERA 1.6.0; Quality Positioning Services BV (QPS): Zeist, The Netherlands, 2018.
- FMGT—Fledermaus Geocoder Toolbox 7.8.0; Quality Positioning Services BV (QPS): Zeist, The Netherlands, 2018.
- ARC MAP 10.3; Environmental Systems Research Institute—ESRI: Redlands, CA, USA, 2014.
- Lamarche, G.; Lurton, X.; Verdier, A.-L.; Augustin, J.-M. Quantitative characterisation of seafloor substrate and bedforms using advanced processing of multibeam backscatter—Application to Cook Strait, New Zealand. Cont. Shelf Res. 2011, 31, S93–S109. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mukherjee, S.; Bhardwaj, A.; Mukhopadhyay, A.; Garg, R.D.; Hazra, S. Accuracy of Cartosat-1 DEM and its derived attribute at multiple scale representation. J. Earth Syst. Sci. 2015, 124, 487–495. [Google Scholar] [CrossRef]
- Buscombe, D.; Grams, P.E.; Kaplinski, M.A. Compositional Signatures in Acoustic Backscatter Over Vegetated and Unvegetated Mixed Sand-Gravel Riverbeds. J. Geophys. Res. Earth Surf. 2017, 122, 1771–1793. [Google Scholar] [CrossRef] [Green Version]
- IHO Standards for Hydrographic Surveys, 5th ed.; Special Publication No. 44; International Hydrographic Office: Monaco, 2008.
- Marks, K.M.; Smith, W.H.F. An uncertainty model for deep ocean single beam and multibeam echo sounder data. Mar. Geophys. Res. 2008, 29, 239–250. [Google Scholar] [CrossRef]
- Rice, G.; Greenaway, S. NOAA Ship Fairweather Launch 2017 SAT | Multibeam Advisory Committee. Available online: http://mac.unols.org/reports/noaa-ship-fairweather-launch-2017-sat (accessed on 20 March 2019).
- Beaudoin, J.; Johnson, P.; Lurton, X.; Augustin, J.M. SAT and Trial Cruise of the Acoustical Sensors Onboard R/V Falkor. Available online: http://mac.unols.org/sites/mac.unols.org/files/20120904_Falkor_EM710_EM302_report.pdf (accessed on 19 March 2019).
- Dark, S.J.; Bram, D. The modifiable areal unit problem (MAUP) in physical geography. Prog. Phys. Geogr. 2007, 31, 471–479. [Google Scholar] [CrossRef]
- Chang, K.; Tsai, B. The Effect of DEM Resolution on Slope and Aspect Mapping. Cartogr. Geogr. Inf. Syst. 1991, 18, 69. [Google Scholar] [CrossRef]

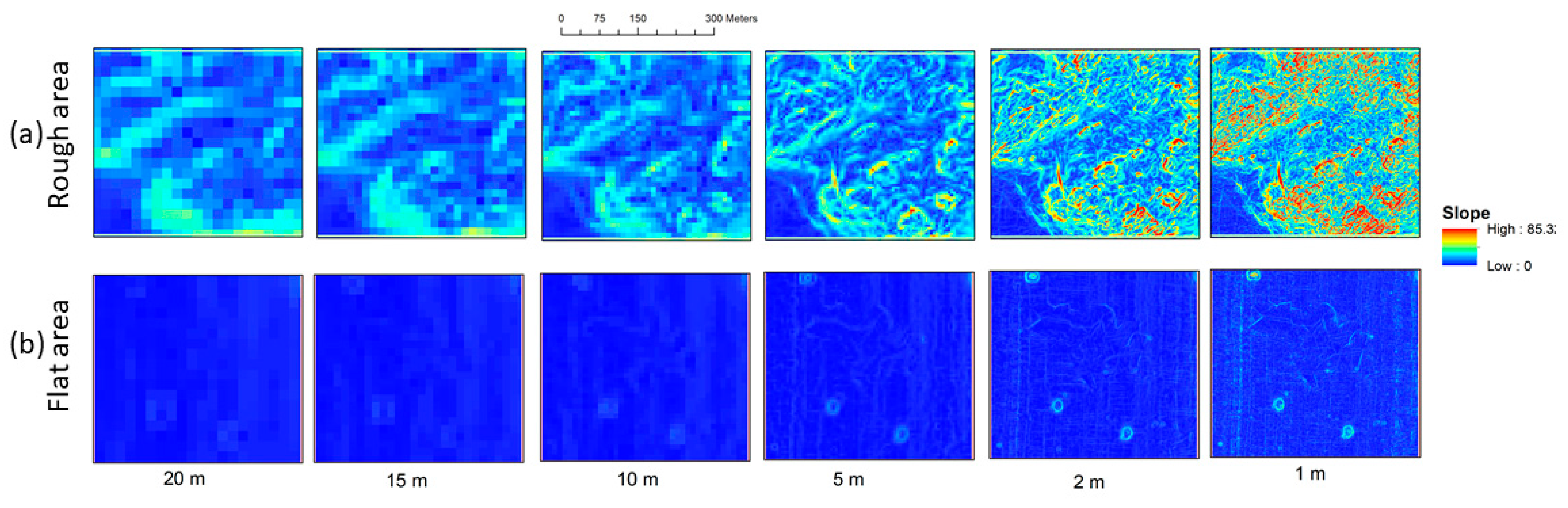
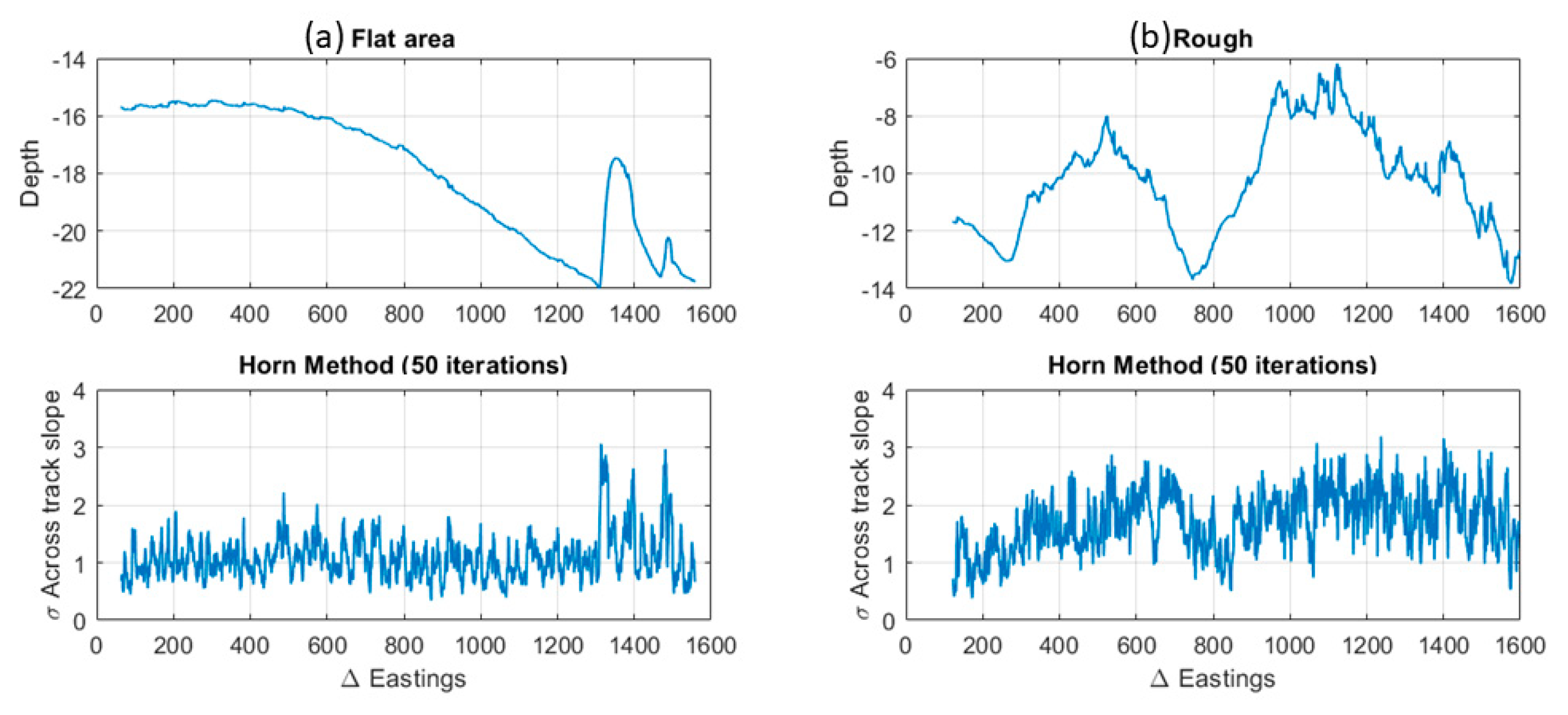
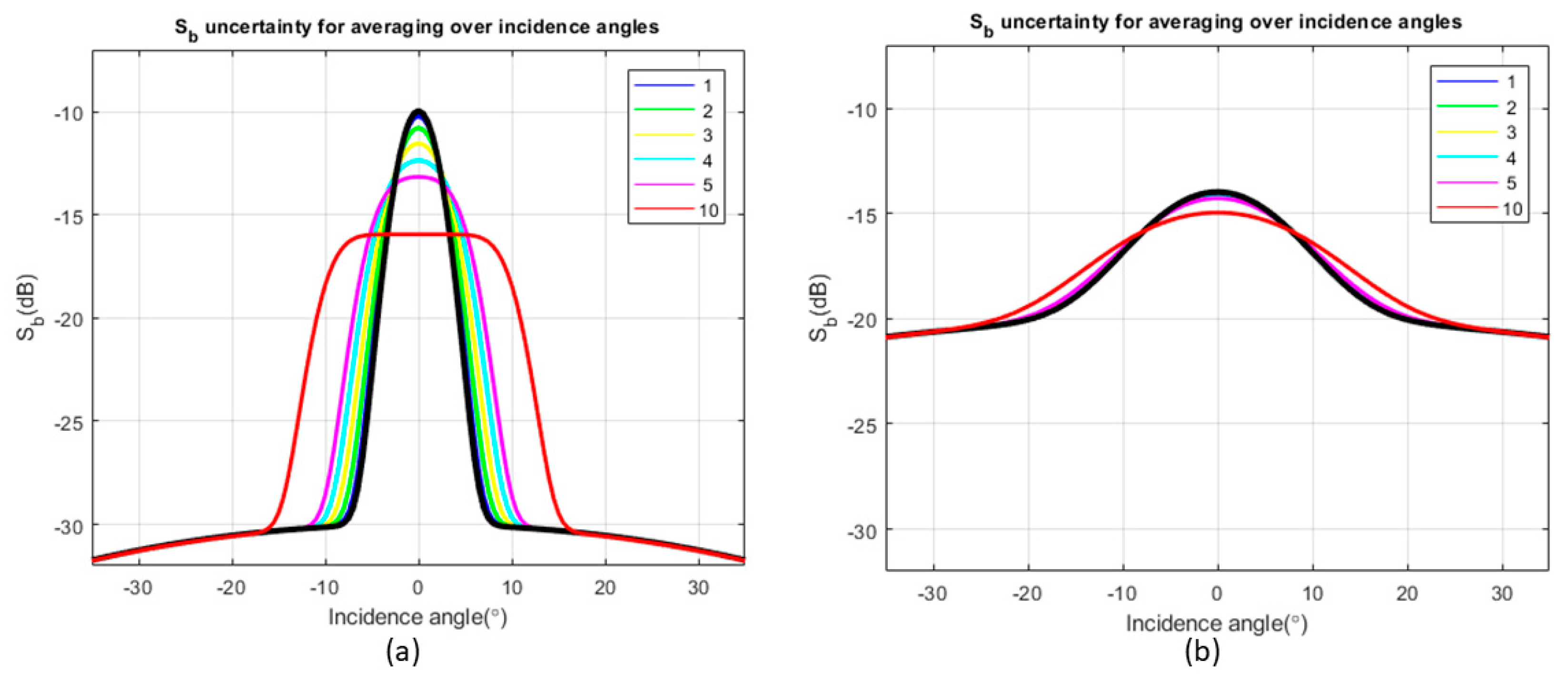
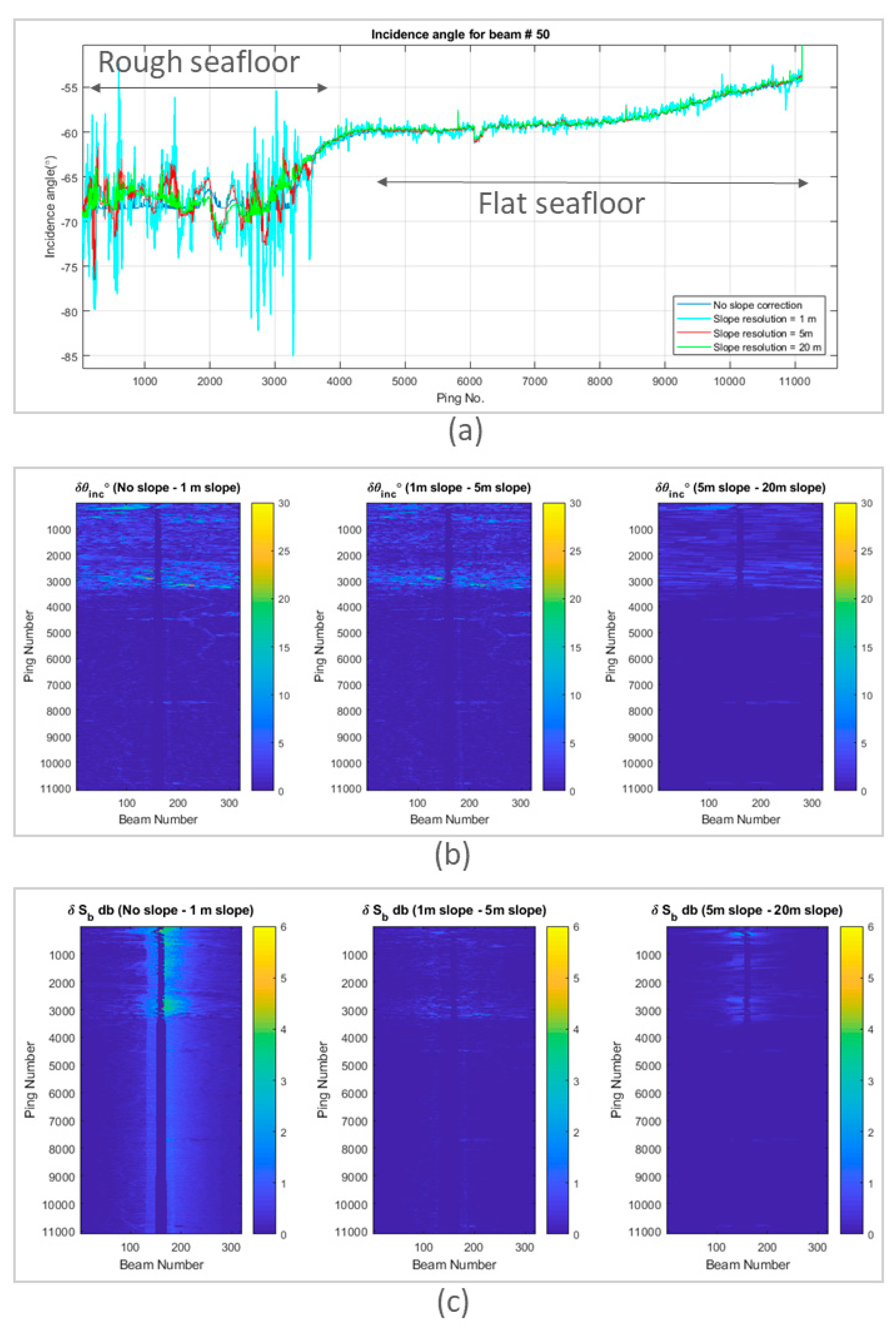
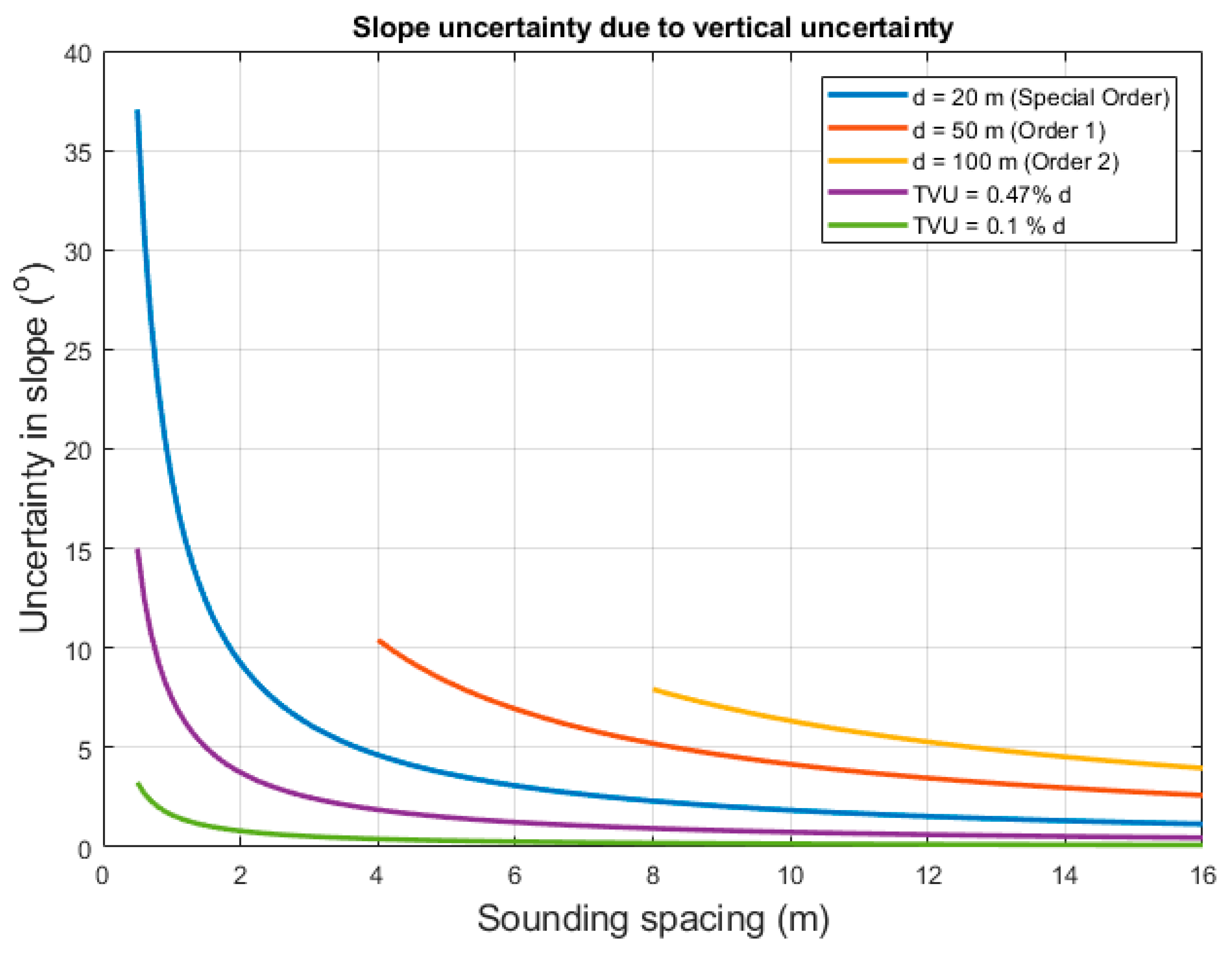
| Grid Cell Size | MIN | MAX | RANGE | MEAN | STD | |
|---|---|---|---|---|---|---|
| Flat area | 20 | 0.02 | 1.02 | 0.99 | 0.24 | 0.14 |
| Flat area | 15 | 0.00 | 1.22 | 1.22 | 0.26 | 0.16 |
| Flat area | 10 | 0.01 | 1.84 | 1.84 | 0.28 | 0.18 |
| Flat area | 5 | 0.00 | 3.44 | 3.44 | 0.35 | 0.29 |
| Flat area | 1 | 0.00 | 16.70 | 16.70 | 0.78 | 0.64 |
| Rough area | 20 | 0.06 | 6.48 | 6.42 | 2.10 | 1.30 |
| Rough area | 15 | 0.05 | 7.33 | 7.28 | 2.24 | 1.33 |
| Rough area | 10 | 0.02 | 17.24 | 17.22 | 3.32 | 2.14 |
| Rough area | 5 | 0.03 | 29.98 | 29.95 | 4.51 | 3.18 |
| Rough area | 1 | 0.00 | 45.07 | 45.07 | 5.74 | 4.39 |
| Across Track Beam Spacing (m) | Across Track Backscatter Footprint | |||||
|---|---|---|---|---|---|---|
| Equiangular | Equidistant | |||||
| Depth (m) | 0° | 45° | 60° | All angles | Near Nadir | Oblique Angles |
| 10 | 0.26 | 0.53 | 1.09 | 0.26 | 0.26 | 0.11 |
| 20 | 0.52 | 1.06 | 2.19 | 0.53 | 0.52 | 0.11 |
| 50 | 1.30 | 2.68 | 5.48 | 1.34 | 1.30 | 0.11 |
| 100 | 2.61 | 5.37 | 10.97 | 2.68 | 2.61 | 0.11 |
| 200 | 5.23 | 10.75 | 21.94 | 5.36 | 5.23 | 0.11 |
| Negligible (N) | Small (S) | Moderate (M) | High (H) | Prohibitive (P) | |
|---|---|---|---|---|---|
| Area correction (dB) | 0.01 to 0.1 | 0.1 to 1 | 1 to 3 | 3 to 6 | Beyond 6 |
| Incidence angle (°) | 0.01 to 0.1 | 0.1 to 1 | 1 to 3 | 3 to 6 | Beyond 6 |
| Seafloor Slope Uncertainty Source | Magnitude of Uncertainty in Area Insonified and Incidence Angle | Possible Quality Improvement |
|---|---|---|
| Flat seafloor assumption (seafloor slope completely ignored) | N to P depending on topography | Use bathymetry in slope compensation |
| Inappropriate scale of seafloor slope computation (beam bathymetry vs. grid at lower resolution) | M to H depending on large scale topography | Use of highest available resolution bathymetry |
| Unresolved seafloor slope | N to M depending on small scale topography | Average backscatter values inside angular bins |
| Bathymetry uncertainty | S to M depending on bathymetric uncertainty and magnitude of seafloor slope | - |
| Seafloor slope algorithm based on bathymetry grid | N to S | - |
| Water Depth (d) | a | b (% d) | ||
|---|---|---|---|---|
| Special Order | 20 m | 0.25 | 0.0075 (0.75) | 0.29 |
| Order 1 | 50 m | 0.5 | 0.013 (1.3) | 0.82 |
| Order 2 | 100 m | 1 | 0.023 (2.3) | 2.50 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, M. Sources and Impacts of Bottom Slope Uncertainty on Estimation of Seafloor Backscatter from Swath Sonars. Geosciences 2019, 9, 183. https://doi.org/10.3390/geosciences9040183
Malik M. Sources and Impacts of Bottom Slope Uncertainty on Estimation of Seafloor Backscatter from Swath Sonars. Geosciences. 2019; 9(4):183. https://doi.org/10.3390/geosciences9040183
Chicago/Turabian StyleMalik, Mashkoor. 2019. "Sources and Impacts of Bottom Slope Uncertainty on Estimation of Seafloor Backscatter from Swath Sonars" Geosciences 9, no. 4: 183. https://doi.org/10.3390/geosciences9040183
APA StyleMalik, M. (2019). Sources and Impacts of Bottom Slope Uncertainty on Estimation of Seafloor Backscatter from Swath Sonars. Geosciences, 9(4), 183. https://doi.org/10.3390/geosciences9040183





