Finite Element Simulations of an Elasto-Viscoplastic Model for Clay
Abstract
:1. Introduction
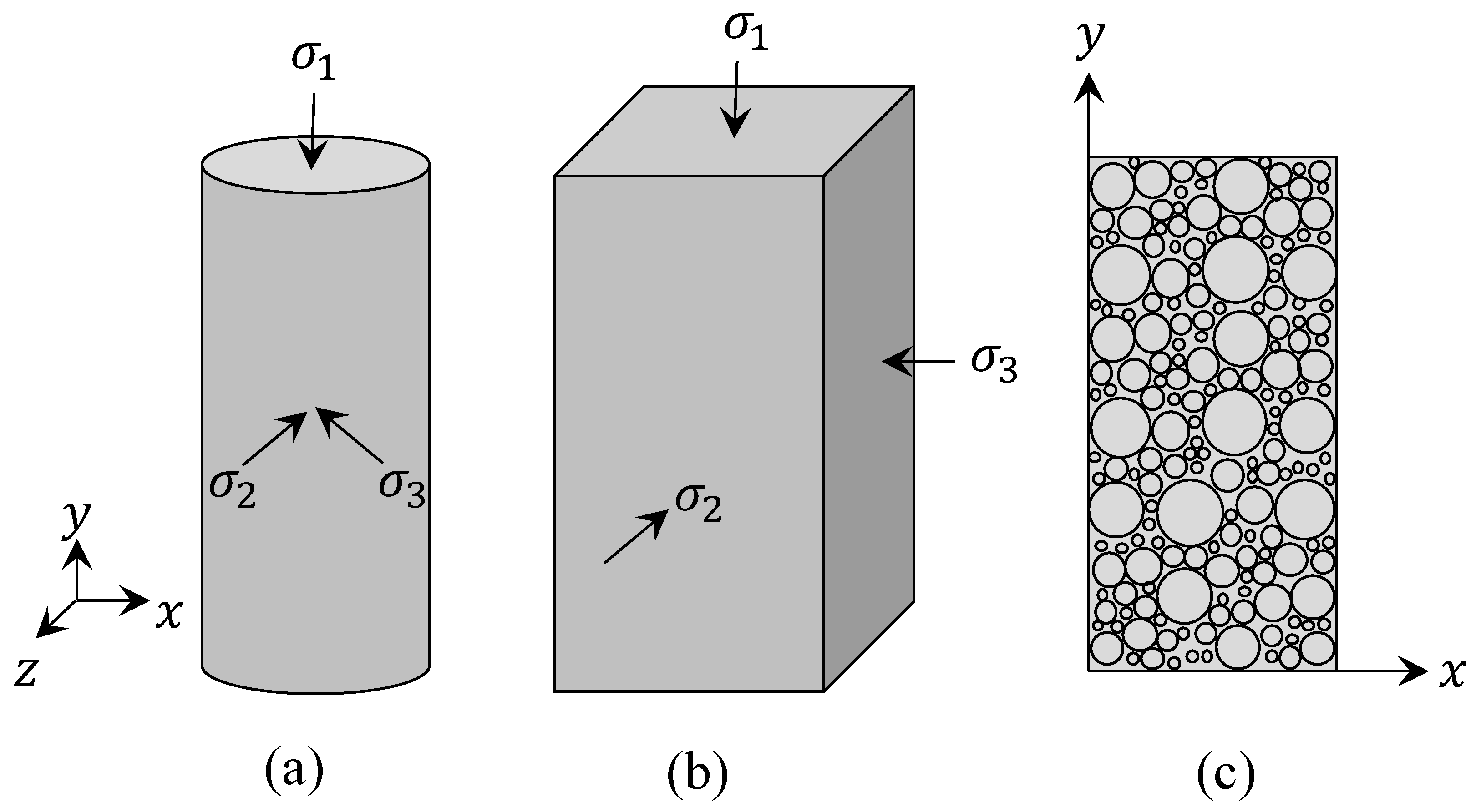
2. Basic Equations
3. Constitutive Modeling
3.1. Fluid Component and the Interaction Forces
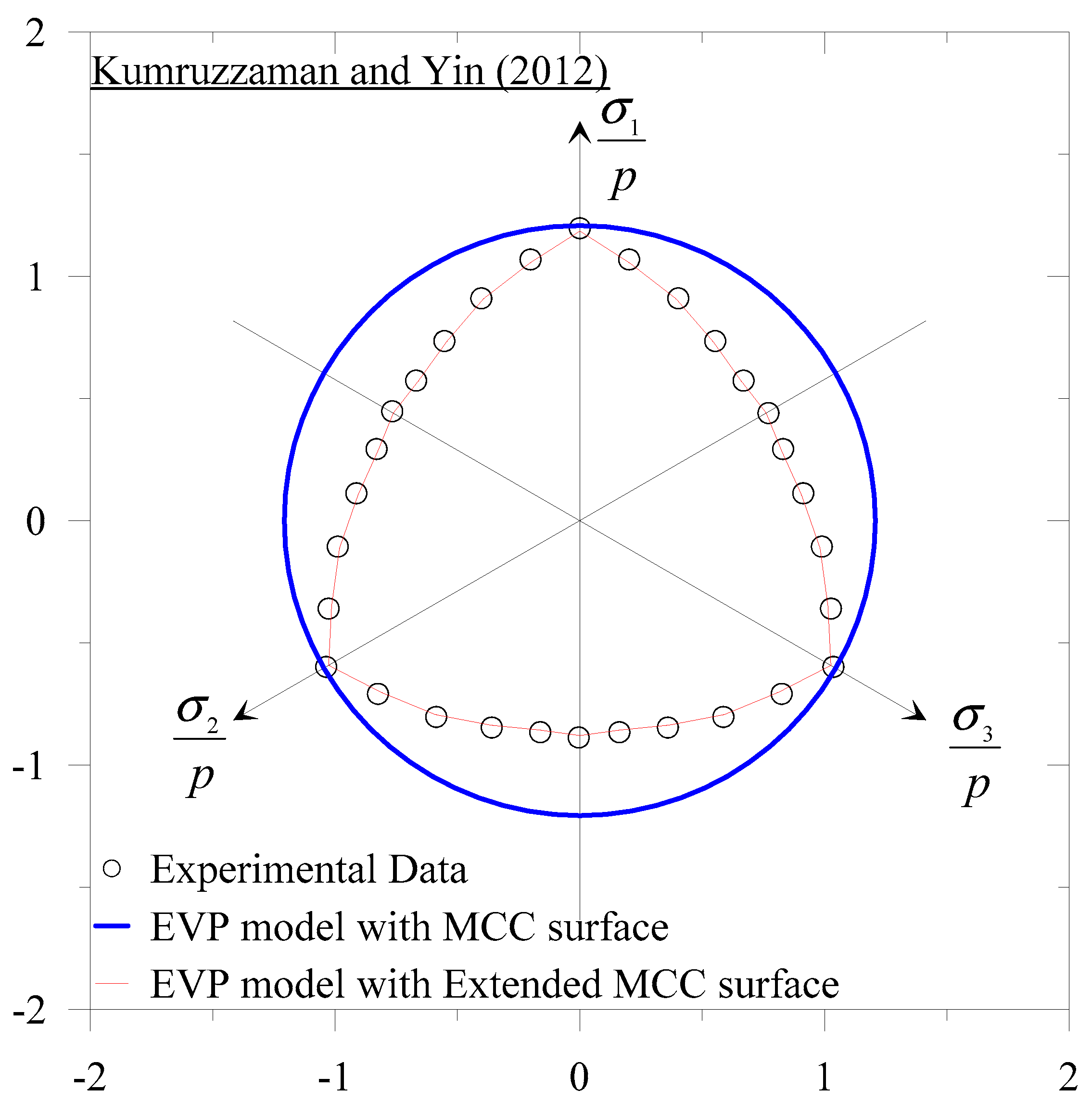
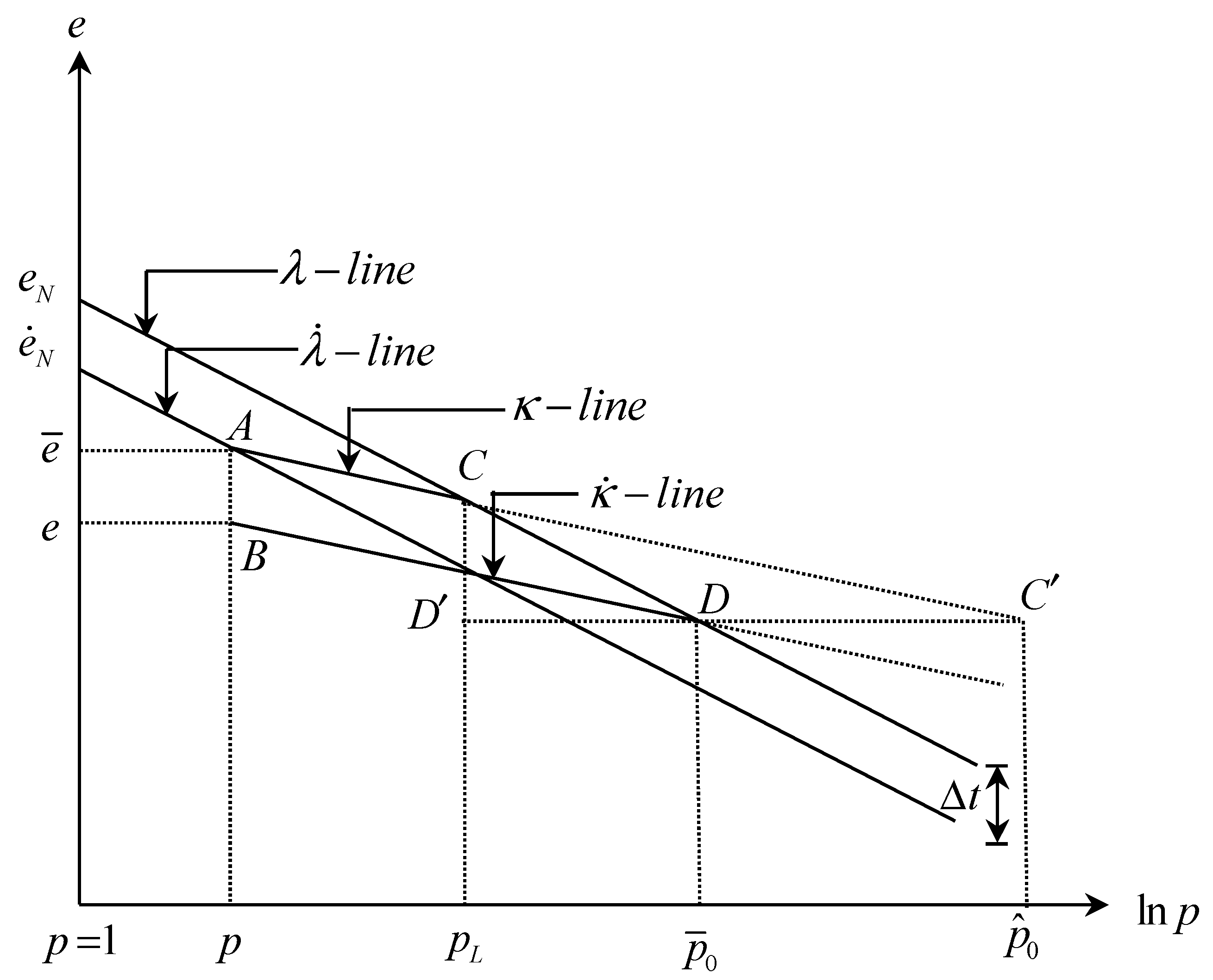
3.2. Solid Component
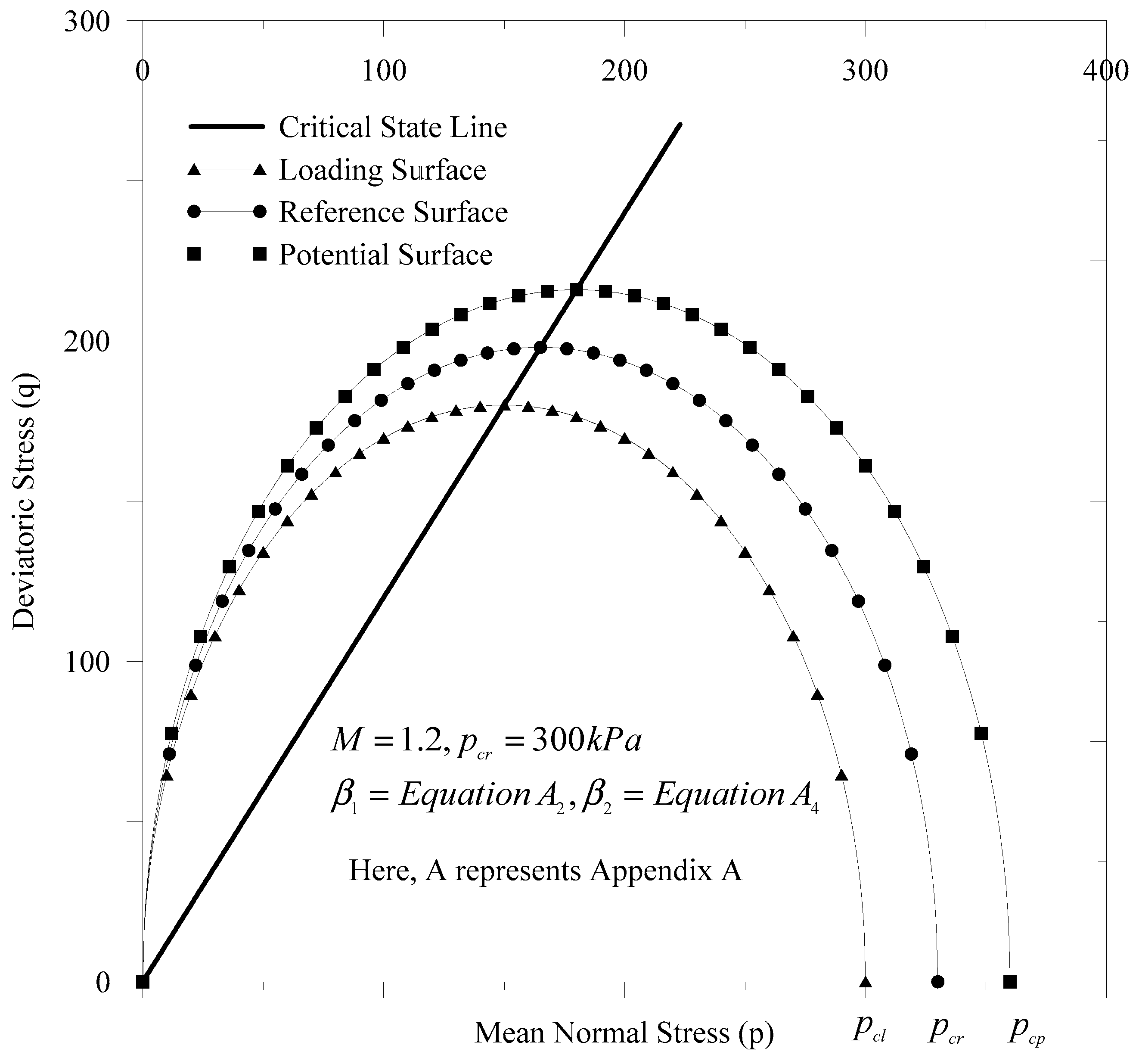
3.3. Model Parameters
3.4. Summary of the Basic Equations and the Assumptions Used in the Code
4. Finite Element Solutions
Weak Form Formulation
5. Model Verification and Discussion
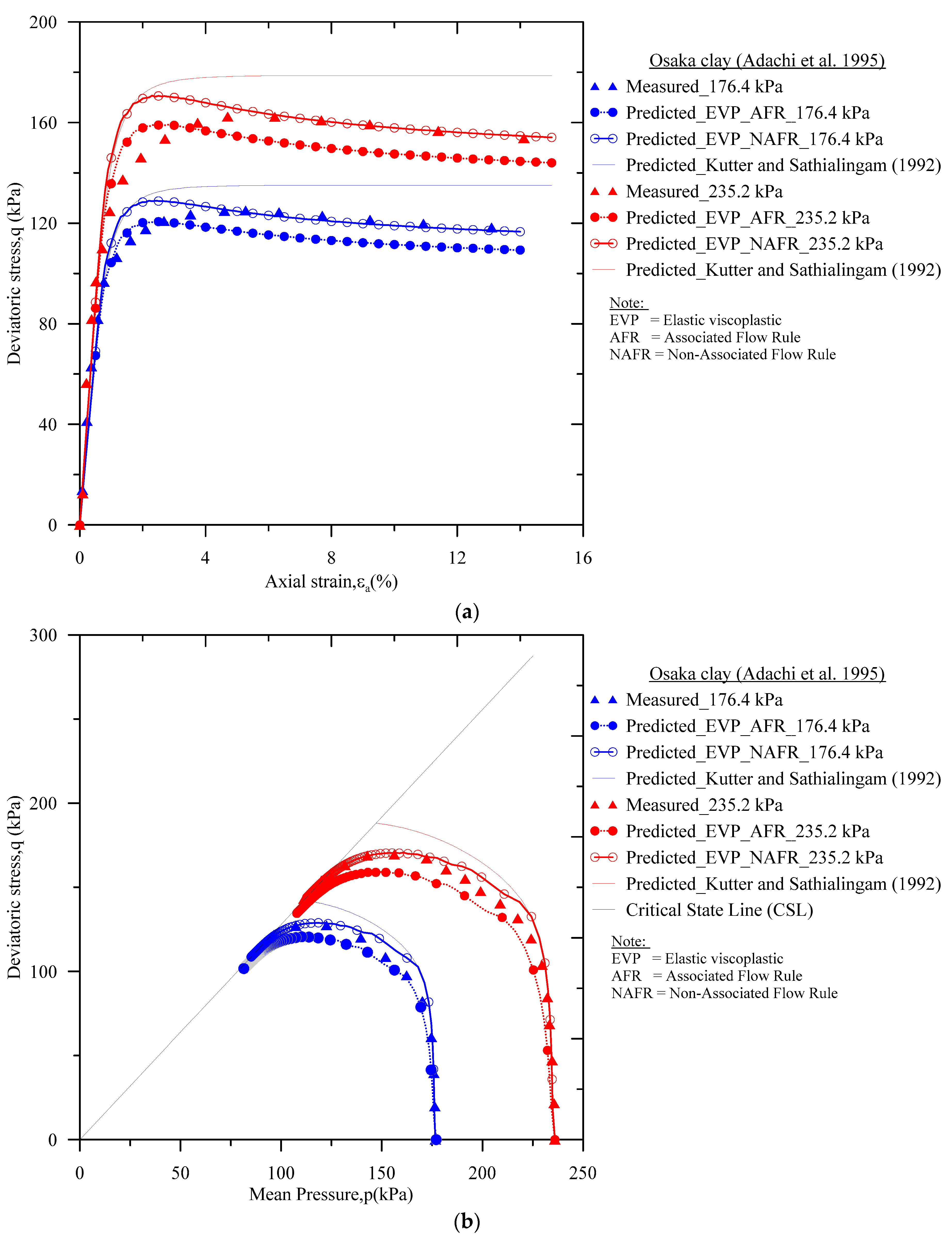
5.1. Simulation of the Undrained Triaxial Test on the Osaka Clay
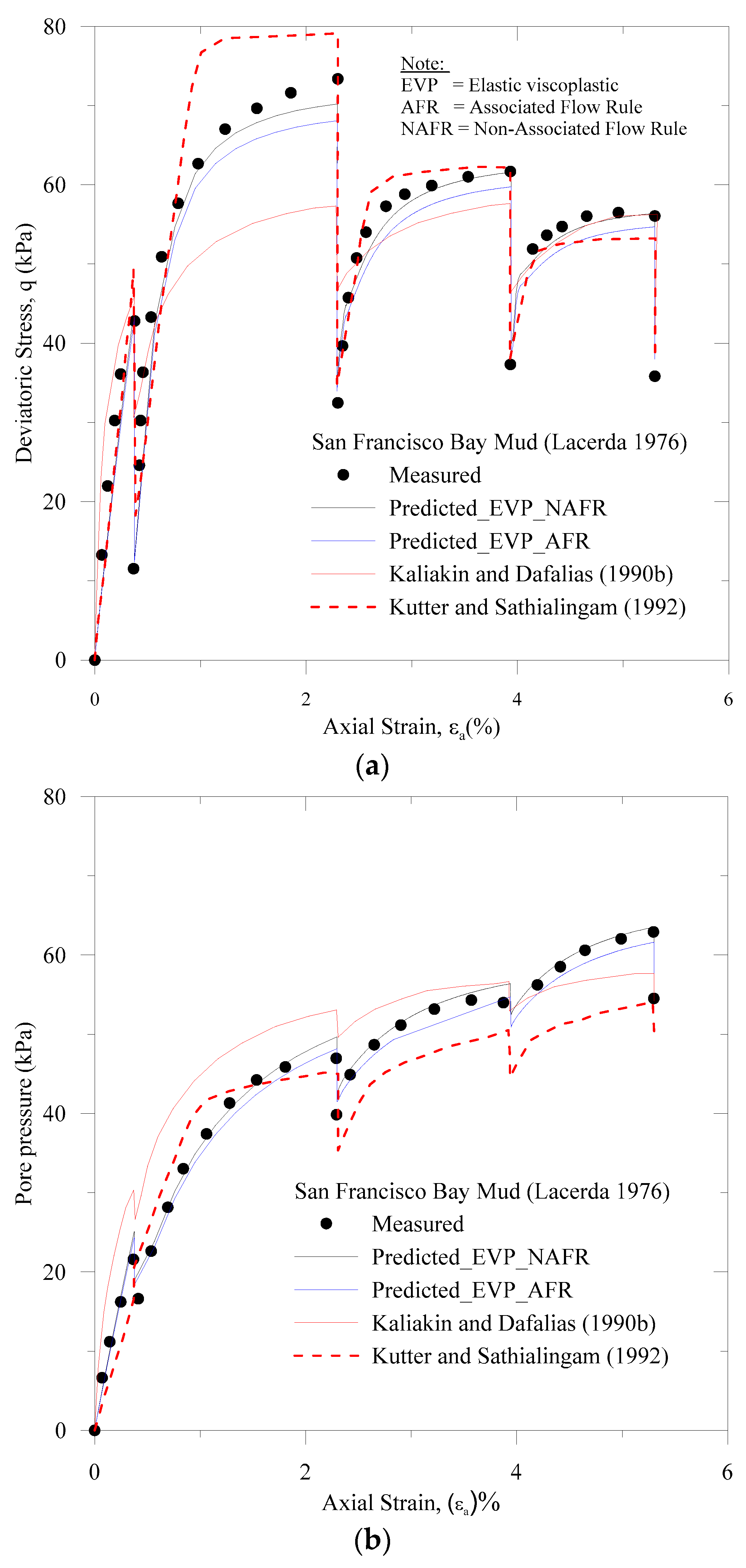
5.2. Simulation of the Undrained Triaxial Stress Relaxation Test on the San Francisco Bay Mud Clay
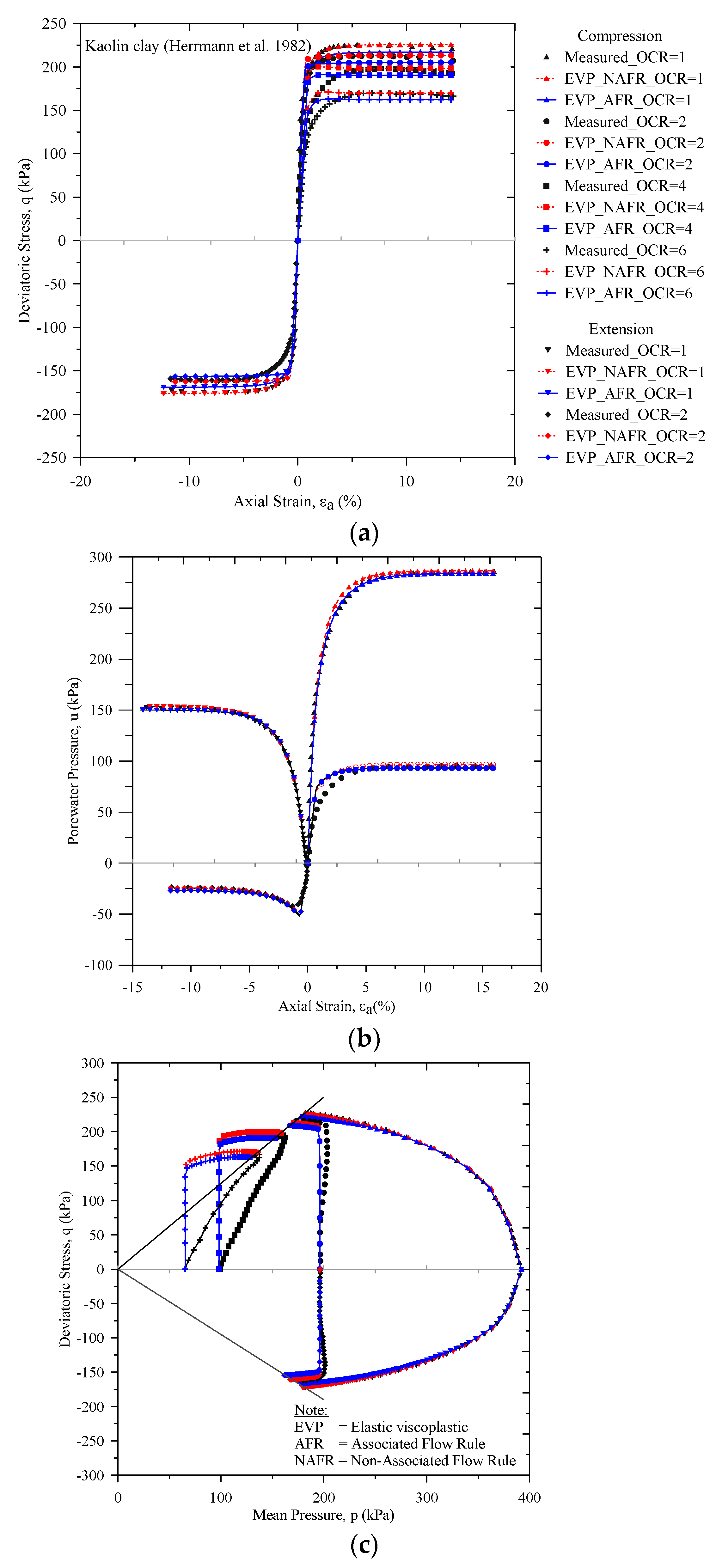
5.3. Simulation of the Consolidated Undrained Triaxial Tests on the Kaolin Clay
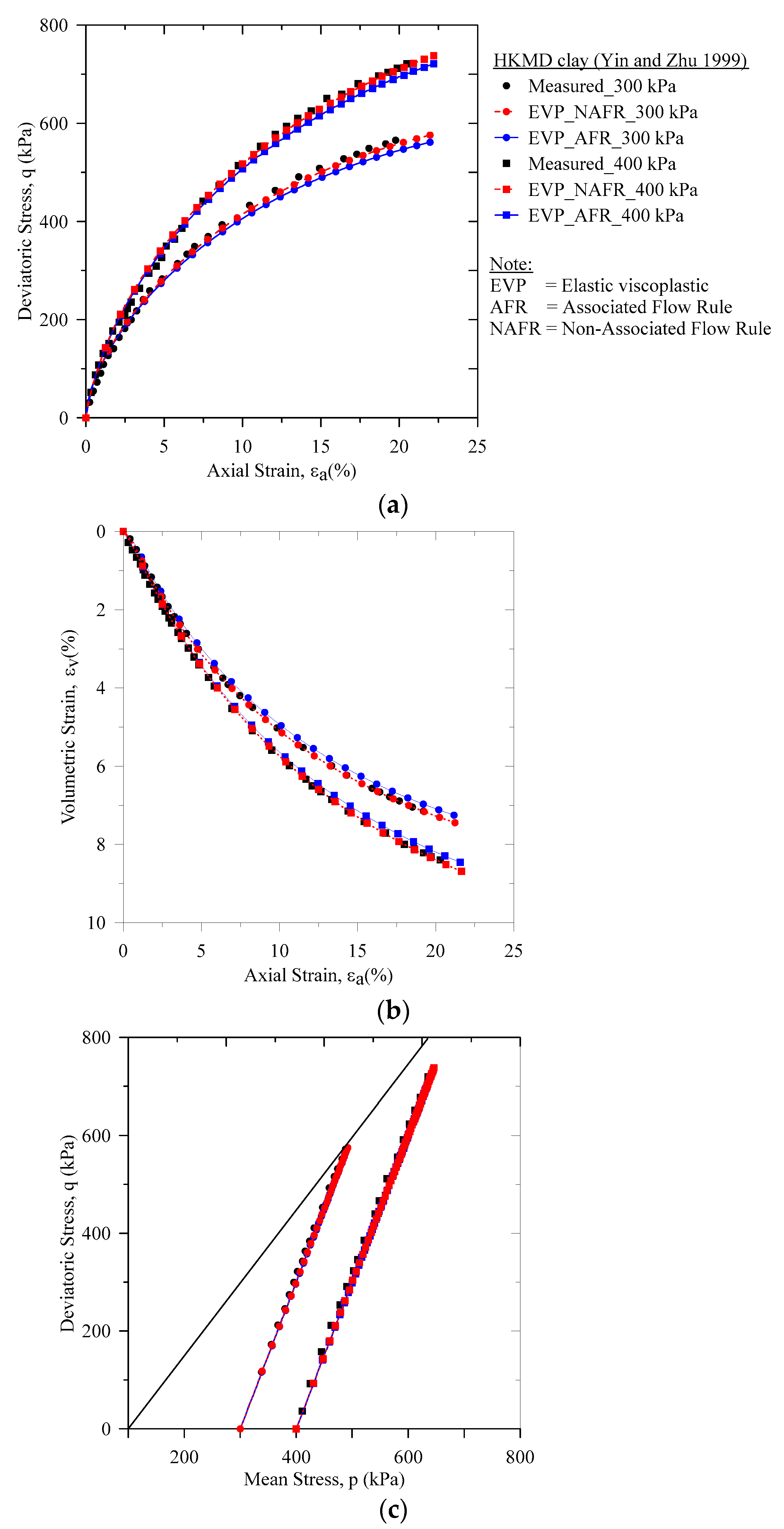
5.4. Simulation of the Consolidated Drained Tests on the Hong Kong Marine Deposit Clay
6. Perturbation Analysis
7. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Image Parameters
Appendix B. Derivation of the Rate Sensitivity Function
Appendix C. Derivation of the Viscoplastic Strain Rate
Appendix D. Derivation of the Gradient Matrix
References
- Saito, M.; Uezawa, H. Failure of soil due to creep. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering (ICSMFE), Paris, France, 17–22 July 1961; Volume 1, pp. 315–318. [Google Scholar]
- Muller-Salzburg, L. The Rock Slide in the Vaiont Valley; Springer: Wien, Germany, 1964. [Google Scholar]
- Rowe, P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 269, 500–527. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Barden, L. Consolidation of Clay with Non-linear Viscosity. Géotechnique 1965, 15, 345–362. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Lloret, A. Precompression design for secondary settlement reduction. Geotechnique 2000, 50, 645–656. [Google Scholar] [CrossRef]
- Potts, D.M.; Zdravkovic, L. Finite Element Analysis in Geotechnical Engineering: Theory; Thomas Telford: London, UK, 1999. [Google Scholar]
- Owen, D.R.J.; Hinton, E. Finite Elements in Plasticity: Theory and Practice; Pineridge Press Limited: Swansea, UK, 1980. [Google Scholar]
- Desai, C.; Siriwardane, H.J. Constitutive Laws For Engineering Materials; Prentice-Hall: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Chaboche, J.L. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Bendetto, H.D.; Enomoto, T.; Kawabe, S.; Kongkitkul, W. Various viscosity types of geomaterials in shear and their mathematical expression. Soils Found. 2008, 48, 41–60. [Google Scholar] [CrossRef]
- Liingaard, M.; Augustesen, A.; Lade, P. Characterization of Models for Time-Dependent Behavior of Soils. Int. J. Geomech. 2004, 4, 157–177. [Google Scholar] [CrossRef]
- Singh, A.; Mitchell, J.K. General Stress-strain-time Function for Soils. J. Soil Mech. Found. Div ASCE 1968, 94, 21–46. [Google Scholar]
- Feda, J. Creep of Soils: And Related Phenomena (Developments in Geotechnical Engineering), 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Adachi, T.; Okano, M. A constitutive equation for normally consolidated clay. Soils Found. 1974, 14, 55–73. [Google Scholar] [CrossRef]
- Sekiguchi, H. Macrometric Approaches-Static-Intricsically Time Dependent Constitutive Laws of Soils. In Proceedings of the 11th ICFMFE, San Francisco, CA, USA, 29–31 March 2019; pp. 66–98. [Google Scholar]
- Sekiguchi, H. Rheological Characteristics of Clays. In Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering, Tokyo, Japan, 10–15 July 1977; pp. 289–292. [Google Scholar]
- Dafalias, Y.F.; Herrmann, L.R. Bounding surface formulation of soil plasticity. In Soil Mechanics-Transient and Cyclic Loads; Pande, G.N., Zienkiewicz, O.C., Eds.; Wiley: Chichester, UK, 1982; pp. 253–282. [Google Scholar]
- Borja, R.I.; Kavazanjian, J.E. A constitutive model for the stress-strain&-time behaviour of ‘wet’ clays. Geotechnique 1985, 35, 283–298. [Google Scholar]
- Perzyna, P. Constitutive equations for rate-sensitive plastic materials. Q. Appl. Math. 1963, 20, 321–331. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Burland, J.B. On the generalized stress-strain behavior of wet clay. In Engineering Plasticity; Heyman, J., Leckie, F.A., Eds.; Cambridge University Press: Cambridge, UK, 1968; pp. 535–609. [Google Scholar]
- Islam, M.N.; Gnanendran, C.T. Elastic-Viscoplastic Model for Clays: Development, Validation, and Application. J. Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Carter, J.P.; Balaam, N.P. AFENA User’s Manual. Version 5.0; Center for Geotechnical Research, University of Sydney: Sydney, Australia, 1995. [Google Scholar]
- Atkin, R.J.; Craine, R.E. Continuum theories of mixtures: Basic theory and historical development. Q. J. Mech. Appl. Math. 1976, 29, 209–244. [Google Scholar] [CrossRef]
- Bowen, R.M. Theory of Mixtures, Part I. In Continuum Physics III; Eringen, A., Ed.; Academic Press: Cambridge, MA, USA, 1976; pp. 2–127. [Google Scholar]
- Truesdell, C. Rational Thermodynamics, 2nd ed.; Springer: New York, NY, USA, 1984. [Google Scholar]
- Rajagopal, K.R. On a hierarchy of approximate models for flows of incompressible fluids through porous solids. Math. Models Methods Appl. Sci. 2007, 17, 215–252. [Google Scholar] [CrossRef]
- Martins-Costa, M.L.; Sampaio, R.; da Gama, R.M.S. Modelling and simulation of energy transfer in a saturated flow through a porous medium. Appl. Math. Model. 1992, 16, 589–597. [Google Scholar] [CrossRef]
- Oka, F.; Kimoto, S. Computational Modeling of Multiphase Geomaterials; CRC Press: London, UK, 2013. [Google Scholar]
- Massoudi, M. On the importance of material frame-indifference and lift forces in multiphase flows. Chem. Eng. Sci. 2002, 57, 3687–3701. [Google Scholar] [CrossRef]
- Massoudi, M. Constitutive relations for the interaction force in multicomponent particulate flows. Int. J. Non-Linear Mech. 2003, 38, 313–336. [Google Scholar] [CrossRef]
- Williams, W.O. Constitutive equations for flow of an incompressible viscous fluid through a porous medium. Q. Appl. Math. 1978, 36, 255–267. [Google Scholar] [CrossRef]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Davis, R.O.; Selvadurai, A.P.S. Plasticity and Geomechanics; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Schofield, A.N.; Wroth, P. Critical State Soil Mechanics; McGrawHill: London, UK, 1968. [Google Scholar]
- Matsuoka, H.; Sun, D.A. The SMP Concept-Based 3D Constitutive Models for Geomaterials; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Phillips, A.; Sierakowski, R.L. On the concept of the yield surface. Acta Mech. 1965, 1, 29–35. [Google Scholar] [CrossRef]
- Habib, P. Influence of the variation of the average principal stress upon the shearing strength of soils. In Proceedings of the 3rd International Conference on Soil Mechanics and Foundation Engineering, Zurich, Switzerland, 16–27 August 1953; pp. 131–136. [Google Scholar]
- Bjerrum, L. Engineering geology of Norwegian normally consolidated marine clays as related to settlements of buildings. Geotechnique 1967, 17, 81–118. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and non-associated visco-plasticity and plasticity in soil mechanics. Geotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Maranini, E.; Yamaguchi, T. A non-associated viscoplastic model for the behaviour of granite in triaxial compression. Mech. Mater. 2001, 33, 283–293. [Google Scholar] [CrossRef]
- Kutter, B.L.; Sathialingam, N. Elastic-viscoplastic modelling of the rate-dependent behaviour of clays. Géotechnique 1992, 42, 427–441. [Google Scholar] [CrossRef]
- Hickman, R.J.; Gutierrez, M.S. Formulation of a three-dimensional rate-dependent constitutive model for chalk and porous rocks. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 583–605. [Google Scholar] [CrossRef]
- Cristescu, N.D. Nonassociated elastic/viscoplastic constitutive equations for sand. Int. J. Plast. 1991, 7, 41–64. [Google Scholar] [CrossRef]
- Florea, D. Nonassociated elastic/viscoplastic model for bituminous concrete. Int. J. Eng. Sci. 1994, 32, 87–93. [Google Scholar] [CrossRef]
- Jin, J.; Cristescu, N.D. An elastic/viscoplastic model for transient creep of rock salt. Int. J. Plast. 1998, 14, 85–107. [Google Scholar] [CrossRef]
- Augustesen, A.; Liingaard, M.; Lade, P. Evaluation of Time-Dependent Behavior of Soils. Int. J. Geomech. 2004, 4, 137–156. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Introduction to Modeling of Transport Phenomena in Porous Media; Kluwer Academic Publishers: London, UK, 1990; Volume 4. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Galerkin, B.G. Series solution of some problems of elastic equilibrium of rods and plates (in Russian). Vestn. Inzh. Tech. 1915, 19, 897–908. [Google Scholar]
- Koutromanos, I. Fundamentals of Finite Element Analysis: Linear Finite Element Analysis; John Wiley and Sons: Noida, India, 2018. [Google Scholar]
- Kanchi, M.B.; Zienkiewicz, O.C.; Owen, D.R.J. The visco-plastic approach to problems of plasticity and creep involving geometric non-linear effects. Int. J. Numer. Methods Eng. 1978, 12, 169–181. [Google Scholar] [CrossRef]
- Adachi, T.; Oka, F.; Hirata, T.; Hashimoto, T.; Nagaya, J.; Mimura, M.; Pradhan, T.B.S. Stress–strain behavior and yielding characteristics of Eastern Osaka clay. Soil Found. 1995, 35, 1–13. [Google Scholar] [CrossRef]
- Lacerda, W.A. Stress-Relaxation and Creep Effects on Soil Deformation. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1976. [Google Scholar]
- Herrmann, L.R.; Shen, C.K.; Jafroudi, S.; DeNatale, J.S.; Dafalias, Y.F. A Verification Study for the Bounding Surface Plasticity Model for Cohesive Soils; Final Report to the Civil Engineering Laboratory; Naval Construction Battalion Center: Port Hueneme, CA, USA, 1982. [Google Scholar]
- Yin, J.H.; Zhu, J.G. Measured and predicted time-dependent stress-strain behaviour of Hong Kong marine deposits. Can. Geotech. J. 1999, 36, 760–766. [Google Scholar] [CrossRef]
- Jiang, J.; Ling, H.I.; Kaliakin, V.N. An Associative and Non-Associative Anisotropic Bounding Surface Model for Clay. J. Appl. Mech. 2012, 79, 031010. [Google Scholar] [CrossRef]
- Whittle, A.; Kavvadas, M. Formulation of MIT-E3 Constitutive Model for Overconsolidated Clays. J. Geotech. Eng. 1994, 120, 173–198. [Google Scholar] [CrossRef]
- Kaliakin, V.N.; Dafalias, Y.F. Verification of the Elastoplastic-Viscopalstic Bounding Surface Model for Cohesive Soils. Soils Found. 1990, 30, 25–36. [Google Scholar] [CrossRef]
- Hashiguchi, K.; Ueno, M. Elastoplastic constitutive laws of granular materials. In Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering (ICFSME), Session 9, Tokyo, Japan, 10–15 July 1977; pp. 73–82. [Google Scholar]
- Lade, P.V. Triaxial Testing of Soils; Chapter 2; John Wiley & Sons: Chichester, UK, 2016; p. 88. [Google Scholar]
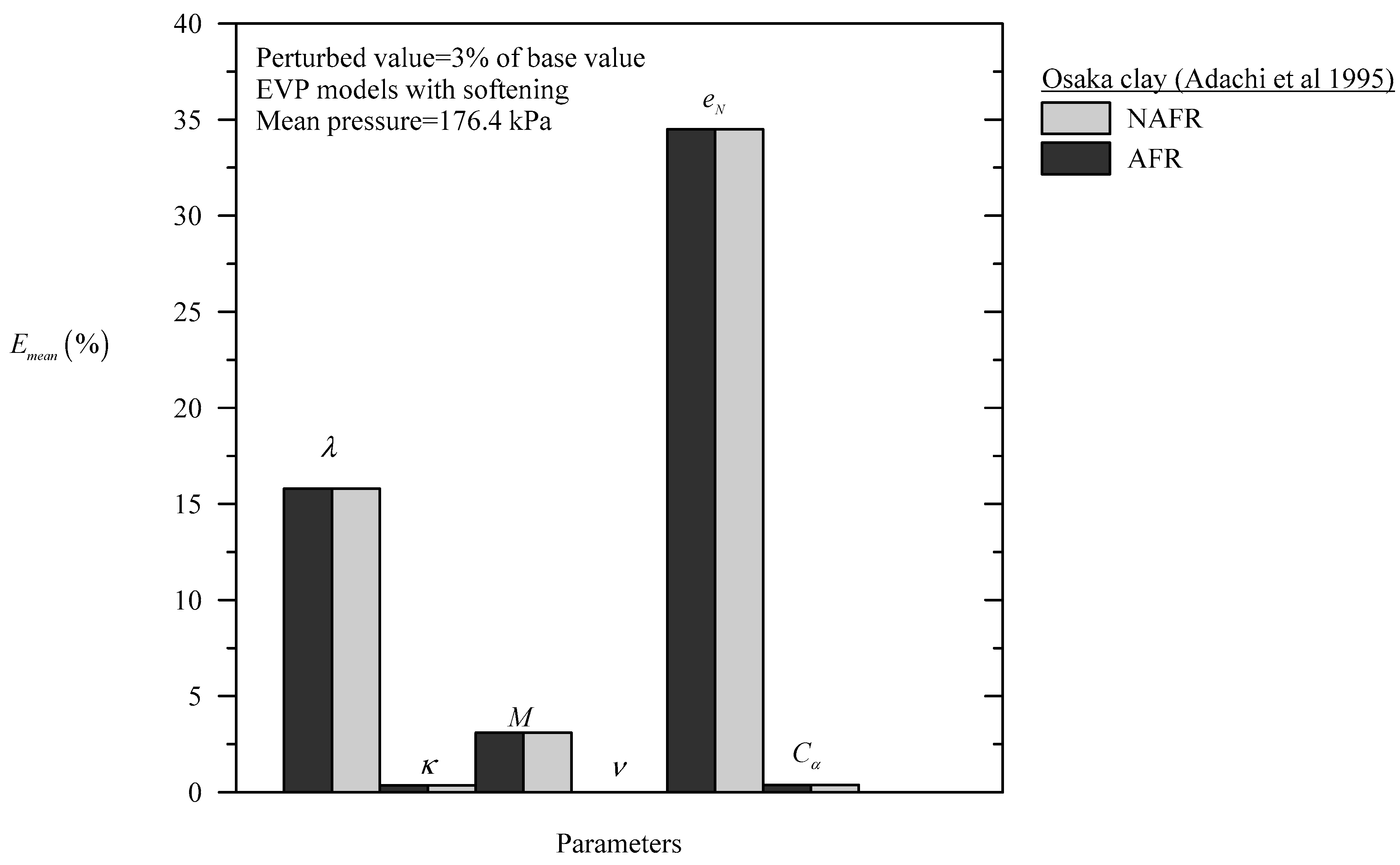
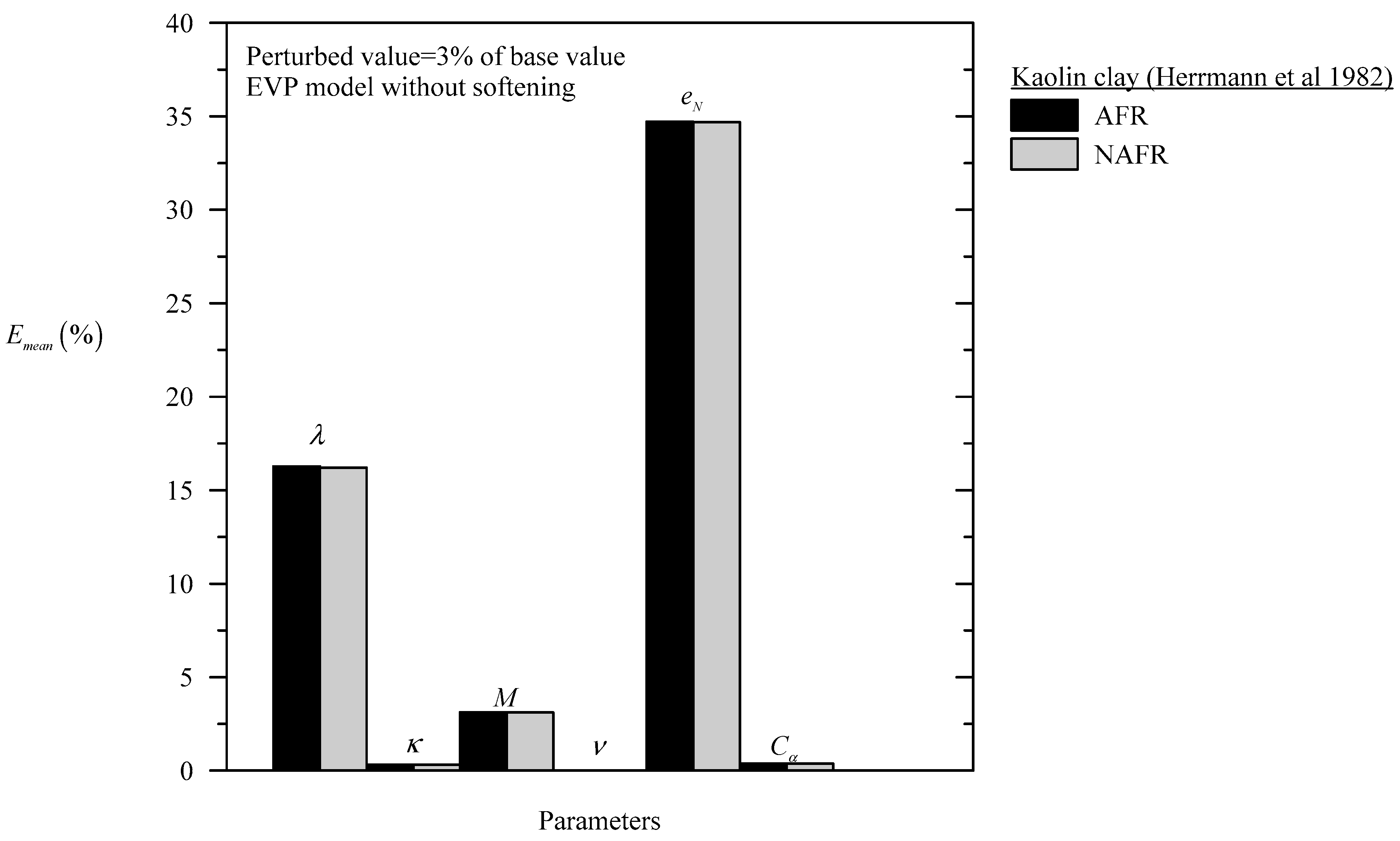
| Model | Material | Parameter | CSSM | Surface Shape |
|---|---|---|---|---|
| Model in this paper | Clay | 6 | Yes | NC |
| Zienkiewicz et al. [40] | Clay | 9 | Yes | NC |
| Kutter and Sathialingam [42] | Clay | 7 | Yes | C |
| Hickman and Gutierrez [43] | Chalk | 10 | Yes | NC |
| Cristescu [44] | Sand | 15 | No | C |
| Florea [45] | Concrete | 15 | No | C |
| Jin and Cristescu [46] | Rock | 32 | No | C |
| Maranini and Yamaguchi [41] | Granite | 44 | No | C |
| Equations | Unknown Variables | |||
|---|---|---|---|---|
| Name | Reference | Number | Variables | Number |
| Mass balance | Equation (54) | 1 | 1 | |
| Equilibrium | Equation (49) | 3 | 6 | |
| Stress–strain | Equation (37) | 6 | 6 | |
| Strain–displacement | Equation (7) | 6 | 3 | |
| Total equation | 16 | Total unknowns | 16 | |
| Parameters | Osaka Clay [53] | SFBM Clay [54] | Kaolin Clay [55] | HKMD Clay [56] |
|---|---|---|---|---|
| 0.36 | 0.37 | 0.15 | 0.20 | |
| 0.047 | 0.054 | 0.018 | 0.045 | |
| 1.28 | 1.40 | 1.25 | 1.26 | |
| — | — | 0.95 | 0.89 | |
| 0.3 | G = 23520 kPa | 0.30 | 0.30 | |
| 3.54 | 3.17 | 1.51 | 2.18 | |
| 0.0327 | 0.053 | 0.014 | 0.106 |
| Phase | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Test | Shear | Rel. | Shear | Rel. | Shear | Rel. | Shear | Rel. |
| 1.5 | 0 | 1.5 | 0 | 0.0162 | 0 | 0.00081 | 0 | |
| Time | 0.25 | 3070 | 1.28 | 1320 | 101.24 | 2700 | 1679 | 8370 |
| 0-0.38 | 0.38 | 0.38-2.3 | 2.3 | 2.3-3.94 | 3.94 | 3.94-5.3 | 5.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.N.; Gnanendran, C.T.; Massoudi, M. Finite Element Simulations of an Elasto-Viscoplastic Model for Clay. Geosciences 2019, 9, 145. https://doi.org/10.3390/geosciences9030145
Islam MN, Gnanendran CT, Massoudi M. Finite Element Simulations of an Elasto-Viscoplastic Model for Clay. Geosciences. 2019; 9(3):145. https://doi.org/10.3390/geosciences9030145
Chicago/Turabian StyleIslam, Mohammad N., Carthigesu T. Gnanendran, and Mehrdad Massoudi. 2019. "Finite Element Simulations of an Elasto-Viscoplastic Model for Clay" Geosciences 9, no. 3: 145. https://doi.org/10.3390/geosciences9030145
APA StyleIslam, M. N., Gnanendran, C. T., & Massoudi, M. (2019). Finite Element Simulations of an Elasto-Viscoplastic Model for Clay. Geosciences, 9(3), 145. https://doi.org/10.3390/geosciences9030145






