Estimating Residential Property Values on the Basis of Clustering and Geostatistics
Abstract
1. Introduction
2. Methods
2.1. The Two-Stage Model, General Assumptions
2.2. The Choice of Representative Attributes and Updating of Transaction Prices
- X1, X2, …, Xn—all property attributes taken into account at the market (including the time of the transaction);
- —individual property prices at the market; and
- 1, 2, …, n—regression coefficient of variable c with respect to variable X.
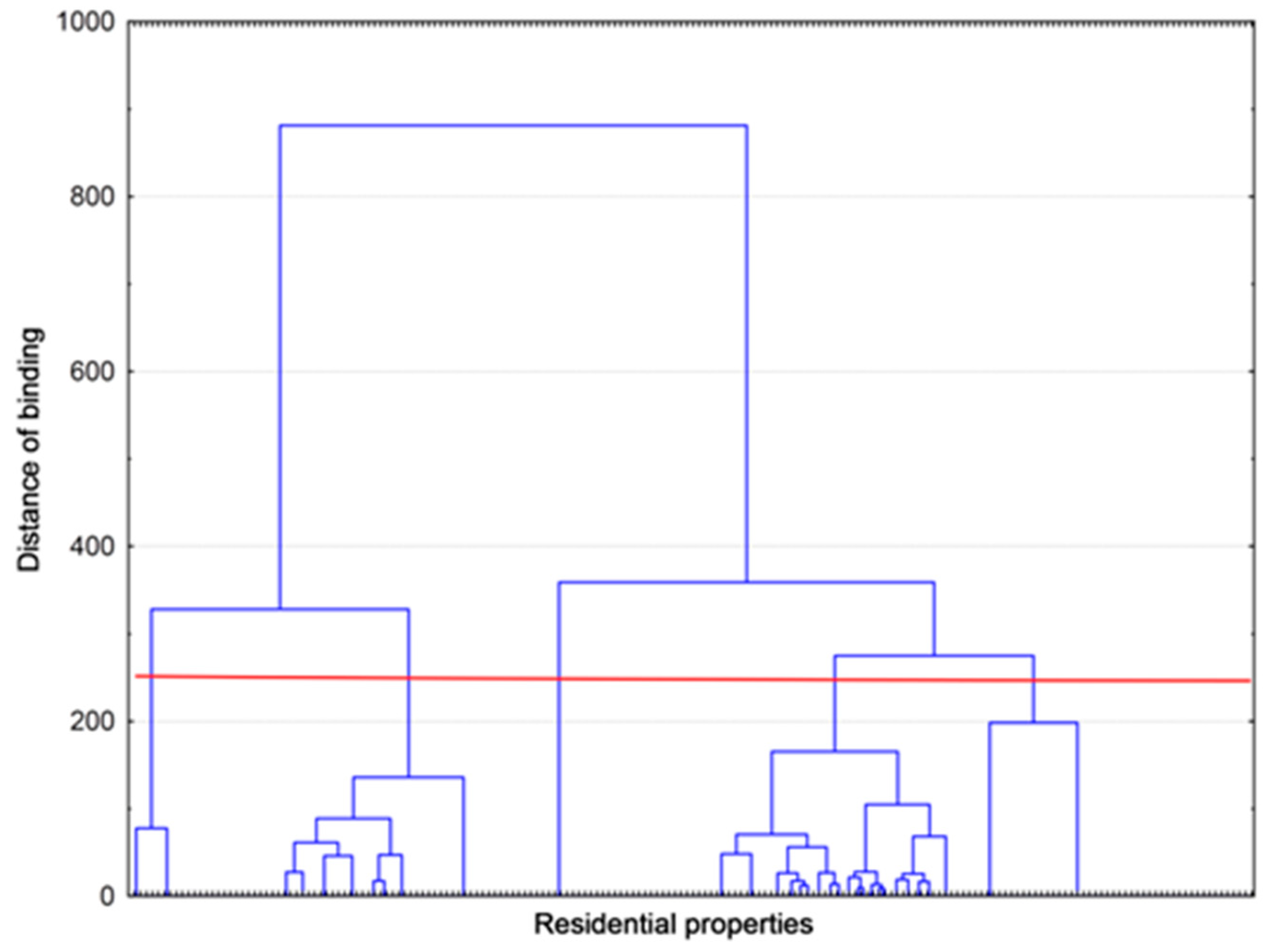
2.3. Clustering—Spatially Insensitive Model
2.4. Interpolation of Property Values Employing the Ordinary Kriging Method—Pure Spatial Model
- wi—is the weighting factor assigned to a single observation;
- Zi—is the value of the parameter being studied at a single point, and;
- n—is the amount of data taken into account when estimating the value of the parameter.
2.5. Assessing the Accuracy of the Estimate
- —difference between the estimated value and the observed value for the time period τ.
3. Experimental Investigation
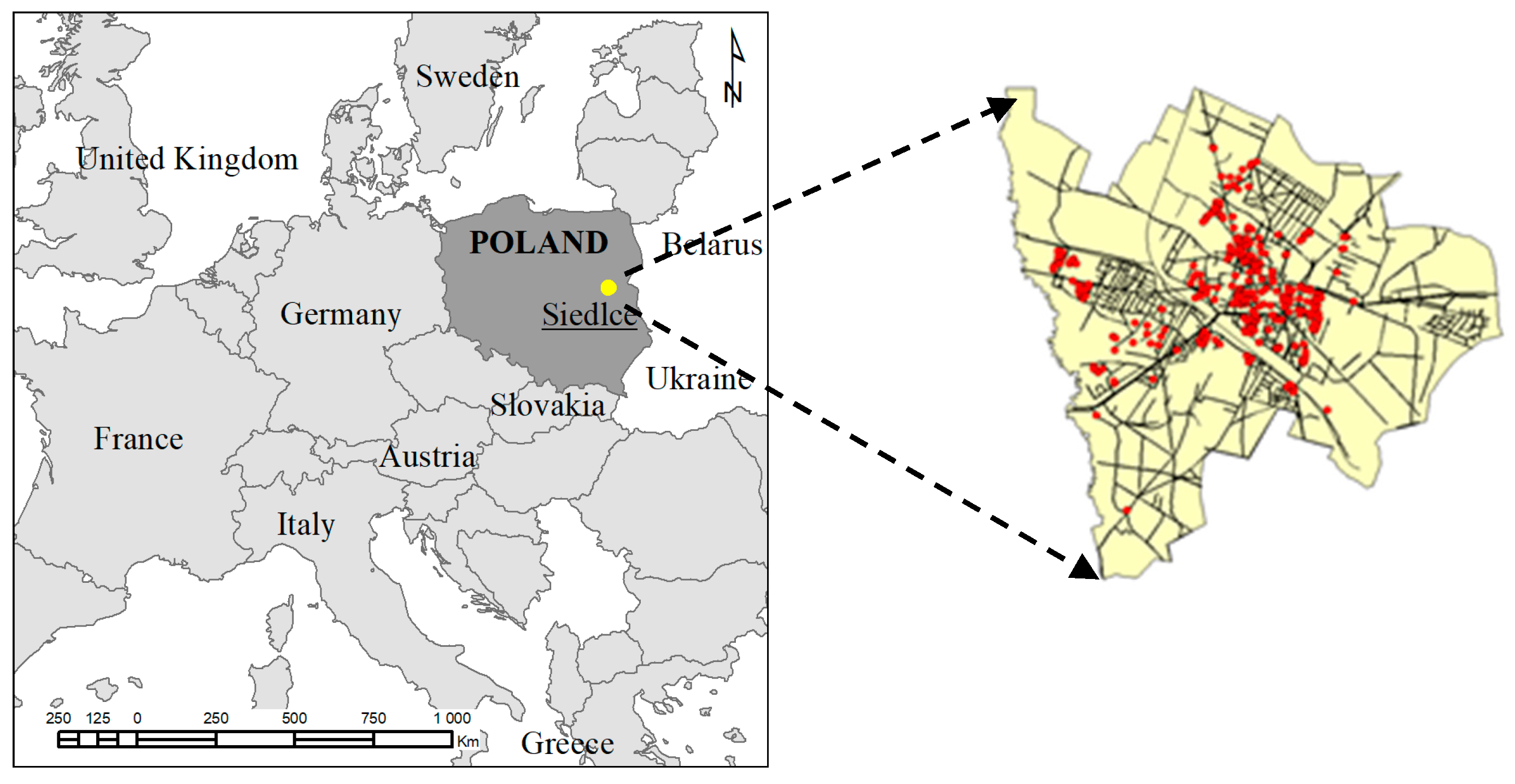
3.1. Study Area and Data
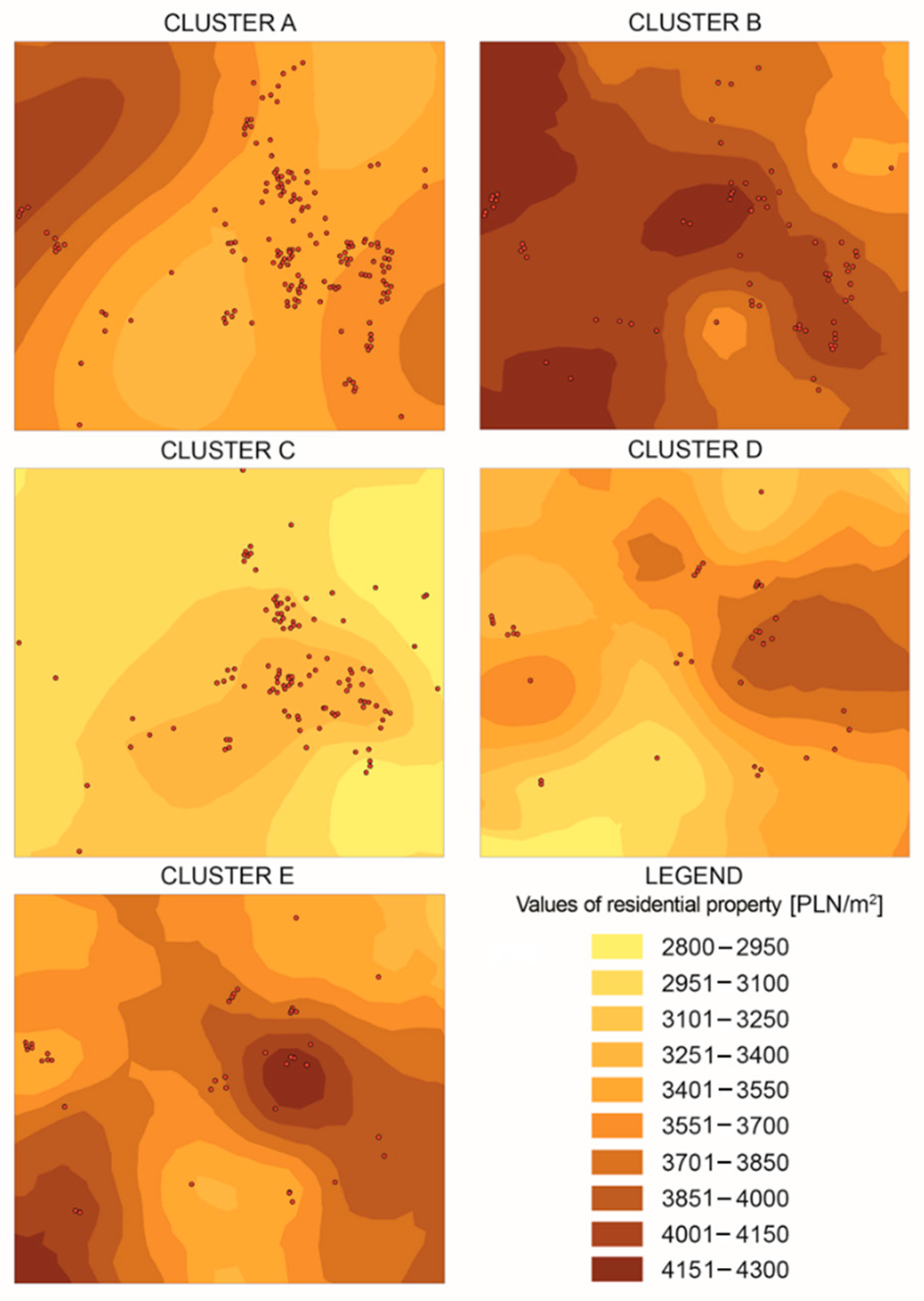
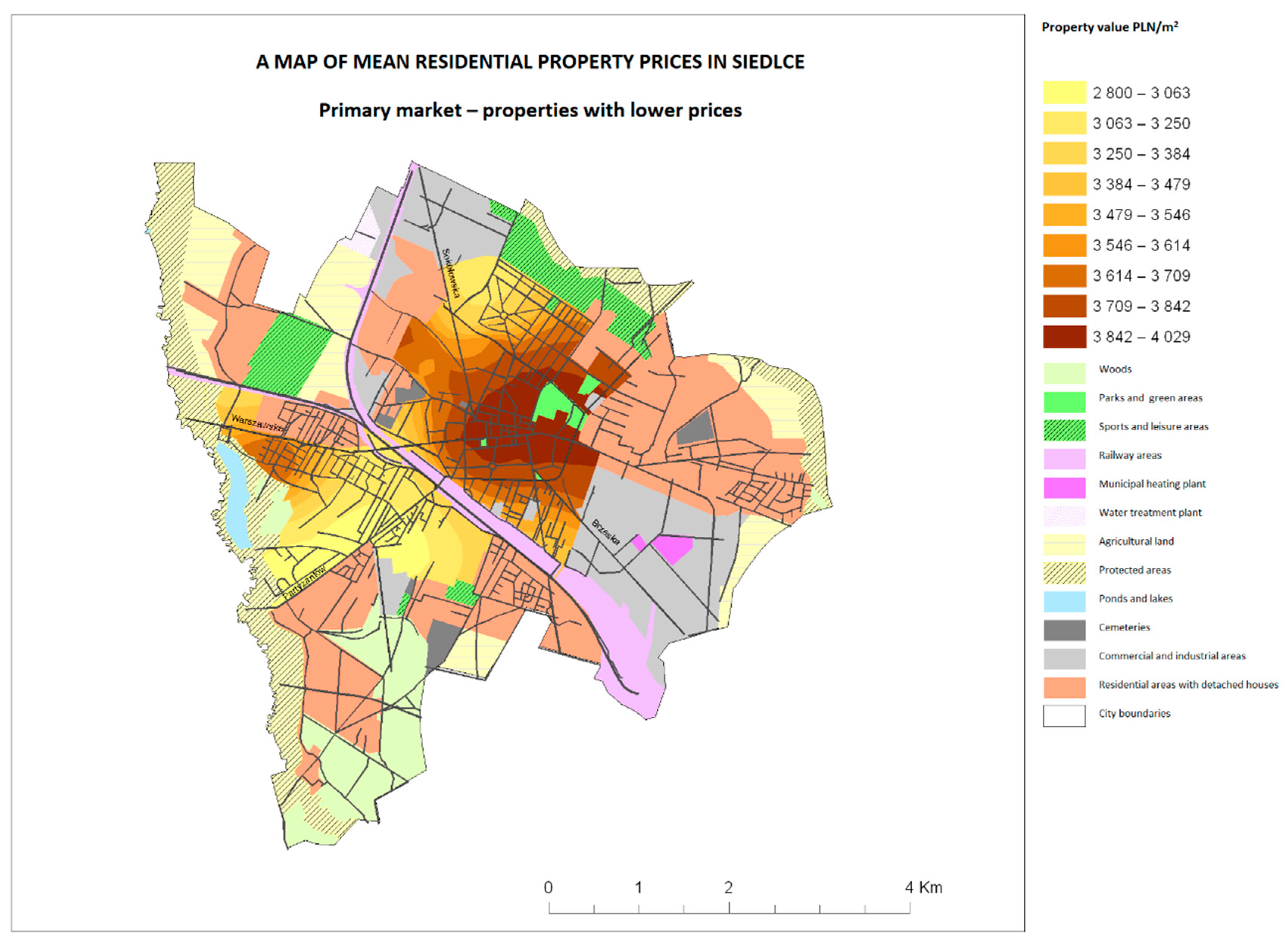
3.2. Results
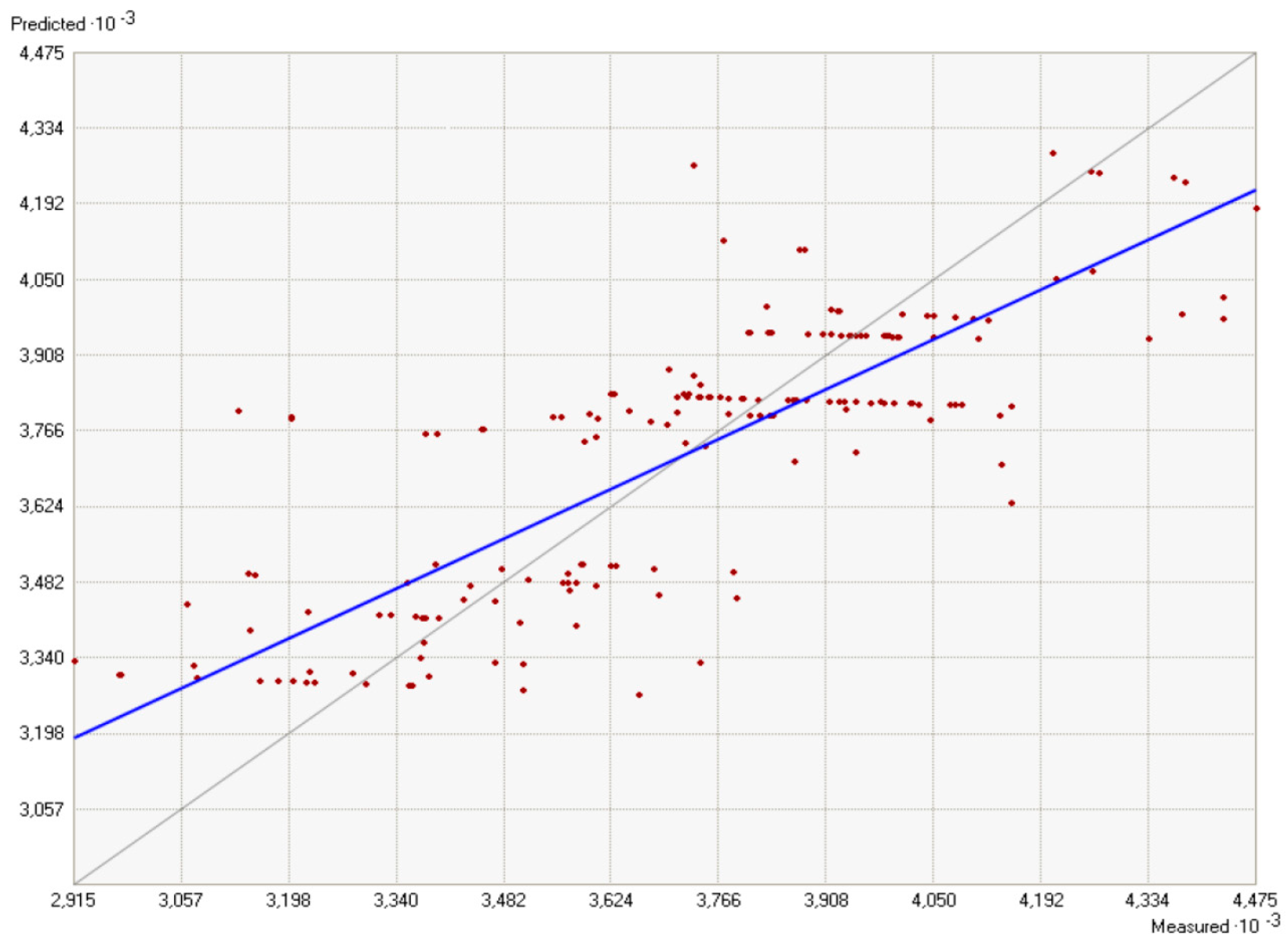
4. Discussion
5. Summary and Conclusions
Funding
Conflicts of Interest
References
- Kontrimas, V.; Verikas, A. The mass appraisal of the real estate by computational intelligence. Appl. Soft Comput. 2011, 11, 443–448. [Google Scholar] [CrossRef]
- Linne, M.R.; Kane, S.M.; Dell, G. A Guide to Appraisal Valuation; Appraisal Institute: Chicago, IL, USA, 2000. [Google Scholar]
- Bielecka, E.; Calka, B. Taxonomy of real estate properties with the use of k-means method. In Proceedings of the 14th International Multidiscipli-nary Scientific GeoConference SGEM 2014, Albena, Bulgaria, 17–26 June 2014. [Google Scholar]
- Ciuna, M.; Milazzo, L.; Salvo, F. A Mass Appraisal Model Based on Market Segment Parameters. Buildings 2017, 7, 34. [Google Scholar] [CrossRef]
- Maleta, M.; Calka, B. Examining spatial autocorrelation of real estate features using moran statistics. In Proceedings of the 15th International Multidisciplinary Scientific GeoConference SGEM, Albena, Bulgaria, 18–24 June 2015. [Google Scholar]
- Maleta, M.; Mościcka, A. Selection and significance evaluation of agricultural parcels determinants. Geod. Cartogr. 2018, 67, 239–253. [Google Scholar] [CrossRef]
- Maclennan, D.; Tu, Y. Economic perspectives on the structure of local housing systems. Hous. Stud. 1996, 11, 387–406. [Google Scholar] [CrossRef]
- Pi-ying, L. Analysis of mass appraisal model. In Proceedings of the 23rd Pan Pacyfic Congress of Appraisal, Valuers and Consumers, San Francisko, CA, USA, 16–19 September 2006. [Google Scholar]
- Cebula, R.J. The hedonic pricing model applied to the housing market of the City of Savannah and Its Savannah Historic Landmark District. Rev. Reg. Stud. 2009, 39, 9–22. [Google Scholar]
- Canavarro, C.; Caridad, J.M.; Ceular, N. Hedonic Methodologies in the Real Estates Valuation. 2010. Available online: http://repositorio.ipcb.pt/handle/10400.11/412 (accessed on 3 January 2019).
- Monson, M. Valuation using hedonic pricing model. Cornell Real Estate Rev. 2009, 7, 62–73. [Google Scholar]
- Stevens, B.H. Location theory and programming models: The Von Thünen case. Pap. Reg. Sci. 1968, 21, 19–34. [Google Scholar] [CrossRef]
- Cellmer, R.; Belej, M.; Zrobek, S.; Kovac, M.S. Urban land value maps—A methodological approach. Geod. Vestn. 2014, 58, 535–551. [Google Scholar] [CrossRef]
- Basu, S.; Thibodeau, T. Analysis of spatial autocorrelation in house prices. J. Real Estate Financ. Econ. 1998, 17, 61–85. [Google Scholar] [CrossRef]
- Gillen, K.; Thibodeau, T.G.; Wachter, S. Anisotropic autocorrelation in house prices. J. Real Estate Financ. Econ. 2001, 23, 5–30. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Ecker, M.D.; Knight, J.R.; Sirmans, C.F. The Dynamics of Location in Home Price. J. Real Estate Financ. Econ. 2004, 29, 149–166. [Google Scholar] [CrossRef]
- Tu, Y.; Sun, H.; Yu, S. Spatial autocorrelations and urban housing market segmentation. J. Real Estate Financ. Econ. 2007, 34, 385–406. [Google Scholar] [CrossRef]
- Chica-Olmo, J.; Cano-Guervos, R.; Chica-Olmo, M. A coregionalized model to predict housing prices. Urban Geogr. 2013, 34, 395–412. [Google Scholar] [CrossRef]
- Giannopoulou, M.; Vamvatsikos, V.; Lykostratis, K. A Process for Defining Relations between Urban Integration and Residential Market Prices. Procedia—Soc. Behav. Sci. 2016, 223, 153–159. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Song, Y.; Wen, H. Spatial Spillover of House Prices: An Empirical Study of the Yangtze Delta Urban Agglomeration in China. Sustainability 2019, 11, 544. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, X.; Zhou, M.; Song, Y.; Luo, X.; Kuang, B. Complex spatial morphology of urban housing price based on digital elevation model: A case study of Wuhan city, China. Sustainability 2019, 11, 348. [Google Scholar] [CrossRef]
- Palma, M.; Cappello, C.; De Iaco, S.; Pellegrino, D. The residential real estate market in Italy: A spatio-temporal analysis. Qual. Quant. 2018, 53, 1–22. [Google Scholar] [CrossRef]
- Renigier-Biłozor, M.; Janowski, A.; Walacik, M. Geoscience Methods in Real Estate Market Analyses Subjectivity Decrease. Geosciences 2019, 9, 130. [Google Scholar] [CrossRef]
- Cichociński, P. An attempt to apply geostatistical methods to real estate valuation. Ann. Geomat. 2009, VII, 17–24. [Google Scholar]
- Colakovic, M.; Vucetic, D. Possibility of Using GIS and Geostatistic for Modelling the Influence of Location on the Value of Residential Properties. 2012. Available online: http://www.fig.net/pub/fig2012 (accessed on 4 January 2019).
- McCluskey, W.; Davis, P.; Haran, M.; McCord, M.; McIlhatton, D. The potential of artificial neural networks in mass appraisal: The case revisited. J. Financ. Manag. Prop. Constr. 2012, 17, 274–292. [Google Scholar] [CrossRef]
- Worzala, E.; Lenk, M.; Silva, A. An exploration of neural networks and its application to Real estate valuation. J. Real Estate Res. 1995, 10, 185–202. [Google Scholar]
- Peterson, P.S.; Flanagan, A.B. Neural network hedonic pricing models in mass real eestate appraisal. J. Real Estate Res. (JRER) 2015. Available online: http://ssrn.com/abstract=1086702 (accessed on 3 January 2019).
- Wong, S.K.; Yiu, C.Y.; Chau, K.W. Trading volume-induced spatial autocorrelation in real estate prices. J. Real Estate Financ. Econ. 2013, 46, 596–608. [Google Scholar] [CrossRef]
- Cellmer, R. The possibilities and limitations of geostatistical methods in real estate market analyses. Real Estate Manag. Valuat. 2014, 22, 54–62. [Google Scholar] [CrossRef]
- Gall, J. Future of value maps in European context. In Proceedings of the XXIII FIG Congress, TS-17 Land Value Maps and Taxation, Munich, Germany, 8–13 October 2006. [Google Scholar]
- Sayce, S.; Vickers, T.; Morad, M.; Connellan, O. Value map the next utility. In Proceedings of the XXIII FIG Congress, TS-17 Land Value Maps and Taxation, Munich, Germany, 8–13 October 2006. [Google Scholar]
- Źróbek, S.; Cellmer, R.; Kuryj, J. Land value map as a source of information about local real estate market. Geodezja 2005, 11, 63–74. [Google Scholar]
- Batt, H.W. Tax regimes that don’t invite corruption. Int. J. Transdiscipl. Res. 2012, 6, 65–82. [Google Scholar]
- Amster, D. Housing Prices. Map 194. Available online: http://www.worldmapper.org/posters/worldmapper_map194_ver5.pdf (accessed on 4 January 2015).
- Sosnowska, M.; Karsznia, I. Methodology for mapping the average transaction prices of residential premises using GIS. Pol. Cartogr. Rev. 2016, 48, 161–171. [Google Scholar] [CrossRef]
- Medynska-Gulij, B. Cartographic sign as a core of multimedia map prepared by non-cartographers in free map services. Geod. Cartogr. 2014, 63, 55–64. [Google Scholar] [CrossRef]
- Medynska-Gulij, B. How the black line, dash and dot created the rules of cartographic design 400 years ago. Cartogr. J. 2013, 50, 356–368. [Google Scholar] [CrossRef]
- Calka, B.; Cahan, B. Interactive map of refugee movement in Europe. Geod. Cartogr. 2016, 65, 139–148. [Google Scholar] [CrossRef]
- Calka, B. Comparing continuity and compactness of choropleth map classes. Geod. Cartogr. 2018, 67, 21–34. [Google Scholar] [CrossRef]
- Horbiński, T.; Medyńska-Gulij, B. Geovisualisation as a process of creating complementary visualisations: Static two-dimensional, surface three-dimensional, and interactive. Geod. Cartogr. 2017, 66, 45–58. [Google Scholar] [CrossRef]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Meyer, T.H. The Discontinuous Nature of Kriging Interpolation for Digital Terrain Modelling. Cartogr. Geogr. Inf. Sci. 2004. [Google Scholar] [CrossRef]
- Jimenez-Martinez, N.; Ramirez, M.; Diaz-Hernandez, R.; Rodriguez-Gomez, G. Fluvial Transport Model from Spatial Distribution Analysis of Libyan Desert Glass Mass on the Great Sand Sea (Southwest Egypt): Clues to Primary Glass Distribution. Geosciences 2015, 5, 95–116. [Google Scholar] [CrossRef]
- Bielecka, E. The possibility of use the spatial data stored in state geodetic and cartographic resource for state property management. J. Pol. Real Estate Sci. Soc. 2012, 20, 19–30. (In Polish) [Google Scholar]
- Maleta, M. Methods for Determining the Impact of the Temporal Trend in the Valuation of Land Property. Real Estate Manag. Valuat. 2013, 21. [Google Scholar] [CrossRef]
- Czaja, J. Methods of Estimating of the Market Value and Cadastral Value of the Properties; KOMP-SYSTEM: Kraków, Poland, 2001. [Google Scholar]
- Barańska, A.; Michalik, S. Variants of Modeling Dwelling Market Value. Real Estate Manag. Valuat. 2014, 22, 28–35. [Google Scholar] [CrossRef]
- Vattani, A. K-means requires exponentially many iterations even in the plane. Discret. Comput. Geom. 2011, 45, 596–616. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Bielecka, E.; Bober, A. Reliability analysis of interpolation methods in travel time maps-the case of Warsaw. Geod. Vestn. 2013, 57, 299–312. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Dickinson, H.O. Von Thünen’s Economics. Econ. J. 1969, 79, 894–902. [Google Scholar] [CrossRef]
| Statistics | Values |
|---|---|
| Number of properties | 1873 |
| Minimum price | 2518 |
| Maximum price | 4830 |
| Average price (arithmetical) | 3577 |
| Standard deviation | 470 |
| Asymmetry coefficient (skewness) | 0.0621 |
| Kurtosis | −0.5300 |
| First quartile | 3237 |
| Median | 3575 |
| Third quartile (PLN) | 3887 |
| Shapiro–Wilk test | W = 0.99217; p = 0.0000 |
| Name of Attribute | Domains of Attributes | Rank | Cramer’s Correlation Coefficient (p-Value) |
|---|---|---|---|
| Type of market | primary | 1 | 0.28 (0.000) |
| secondary | 2 | ||
| Standard of the flat | high | 1 | 0.62 (0.000) |
| average | 2 | ||
| low | 3 | ||
| Year of construction | since 2001 | 1 | 0.23 (0.000) |
| 1985–2000 | 2 | ||
| older | 3 | ||
| Story | first floor | 1 | 0.18 (0.000) |
| middle floor | 2 | ||
| ground and top floors | 3 |
| Attribute | Cluster A | Cluster B | Cluster C | Cluster D | Cluster E |
|---|---|---|---|---|---|
| Type of market | secondary | secondary | secondary | primary | primary |
| Standard of the property | average | high | low | average | high |
| Year of construction | before 2006 | after 1990 | before 1990 | after 2006 | after 2006 |
| Story | middle | middle | top | middle or top | middle |
| Average price (PLN/m2) | 3671 | 3906 | 3195 | 3510 | 3790 |
| Number of properties | 441 | 199 | 307 | 668 | 258 |
| Descriptive Statistics | Cluster A | Cluster B | Cluster C | Cluster D | Cluster E |
|---|---|---|---|---|---|
| Number of properties | 441 | 199 | 307 | 668 | 258 |
| Minimum value (PLN) | 2582 | 2747 | 2518 | 2560 | 2807 |
| Maximum value (PLN) | 4830 | 4764 | 4370 | 4655 | 4691 |
| Arithmetic mean (PLN) | 3671 | 3906 | 3195 | 3510 | 3790 |
| Standard deviation (PLN) | 496 | 499 | 410 | 350 | 388 |
| Asymmetry coefficient (skewness) | 0.1283 | −0.5856 | 0.5865 | −0.3654 | −0.2630 |
| Kurtosis | −0.8164 | −0.6665 | −0.1457 | 0.1811 | −0.5209 |
| First quartile (PLN) | 3303 | 3570 | 2851 | 3292 | 3506 |
| Median (PLN) | 3624 | 4020 | 3167 | 3559 | 3829 |
| Third quartile (PLN) | 4070 | 4282 | 3433 | 3764 | 4072 |
| Shapiro–Wilk test | W = 0.98046 p = 0.00001 | W = 0.94194 p = 0.00000 | W = 0.96287 p = 0.00000 | W = 0.98091 p = 0.00000 | W = 0.98621 p = 0.01388 |
| Cluster A | Cluster B | Cluster C | Cluster D | Cluster E | |
|---|---|---|---|---|---|
| Lag size (m) | 360 | 164 | 98 | 184 | 180 |
| Number of steps | 12 | 12 | 12 | 12 | 12 |
| Smooth factor | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| ME (PLN) | −0.22 | 2.19 | 3.59 | 1.44 | 2.68 |
| RMSE (PLN) | 342.71 | 310.21 | 318.69 | 194.53 | 218.34 |
| MSSR | 1.016 | 0.917 | 1.009 | 0.935 | 0.920 |
| Statistics | Cluster A | Cluster B | Cluster C | Cluster D | Cluster E |
|---|---|---|---|---|---|
| Number of points in test sample | 34 | 18 | 24 | 46 | 20 |
| MAE (PLN) | 346 | 263 | 246 | 302 | 165 |
| MAPE (%) | 9.5 | 6.3 | 7.8 | 8.5 | 4.5 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calka, B. Estimating Residential Property Values on the Basis of Clustering and Geostatistics. Geosciences 2019, 9, 143. https://doi.org/10.3390/geosciences9030143
Calka B. Estimating Residential Property Values on the Basis of Clustering and Geostatistics. Geosciences. 2019; 9(3):143. https://doi.org/10.3390/geosciences9030143
Chicago/Turabian StyleCalka, Beata. 2019. "Estimating Residential Property Values on the Basis of Clustering and Geostatistics" Geosciences 9, no. 3: 143. https://doi.org/10.3390/geosciences9030143
APA StyleCalka, B. (2019). Estimating Residential Property Values on the Basis of Clustering and Geostatistics. Geosciences, 9(3), 143. https://doi.org/10.3390/geosciences9030143





