Automated Classification of Terrestrial Images: The Contribution to the Remote Sensing of Snow Cover
Abstract
1. Introduction
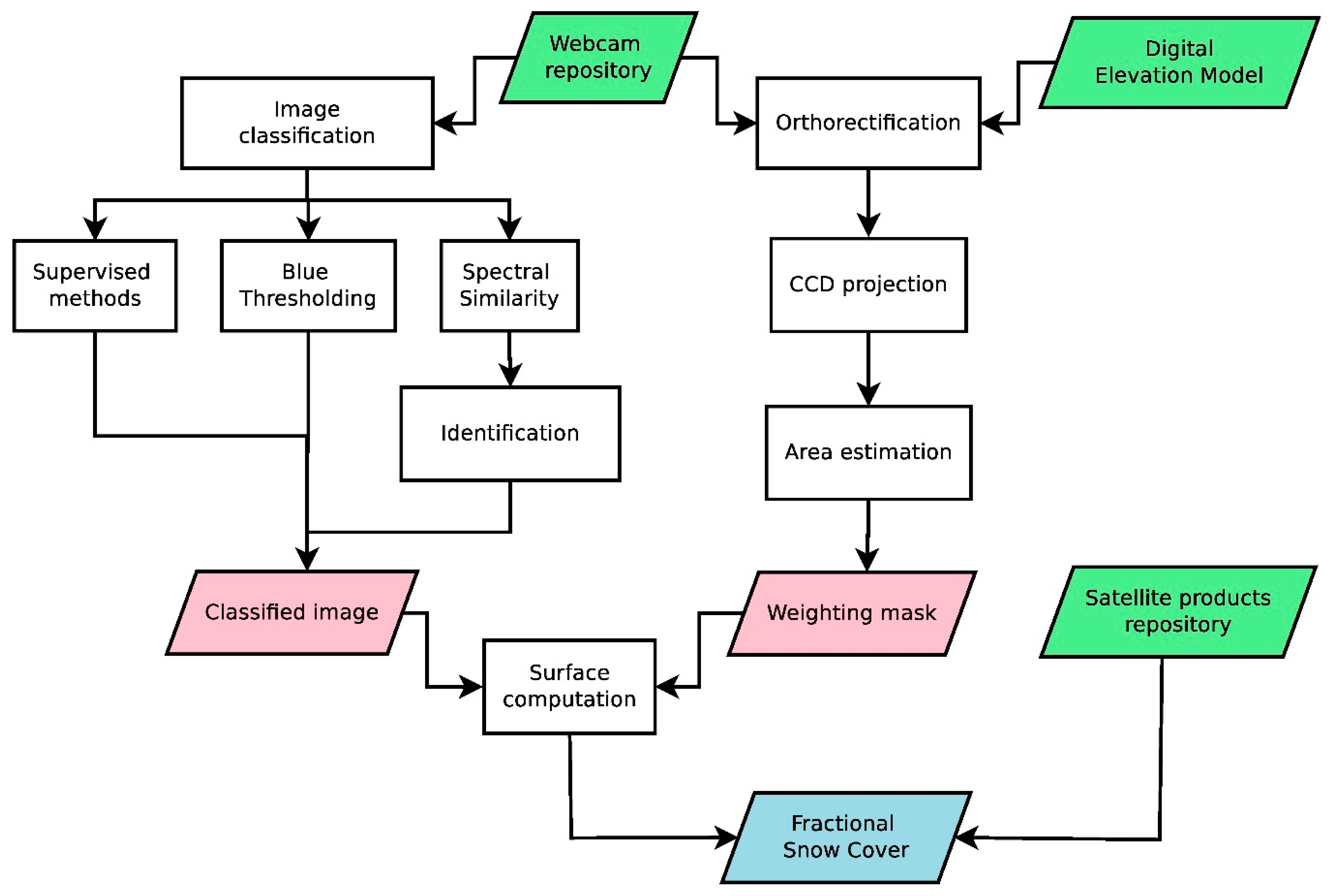
2. Methods
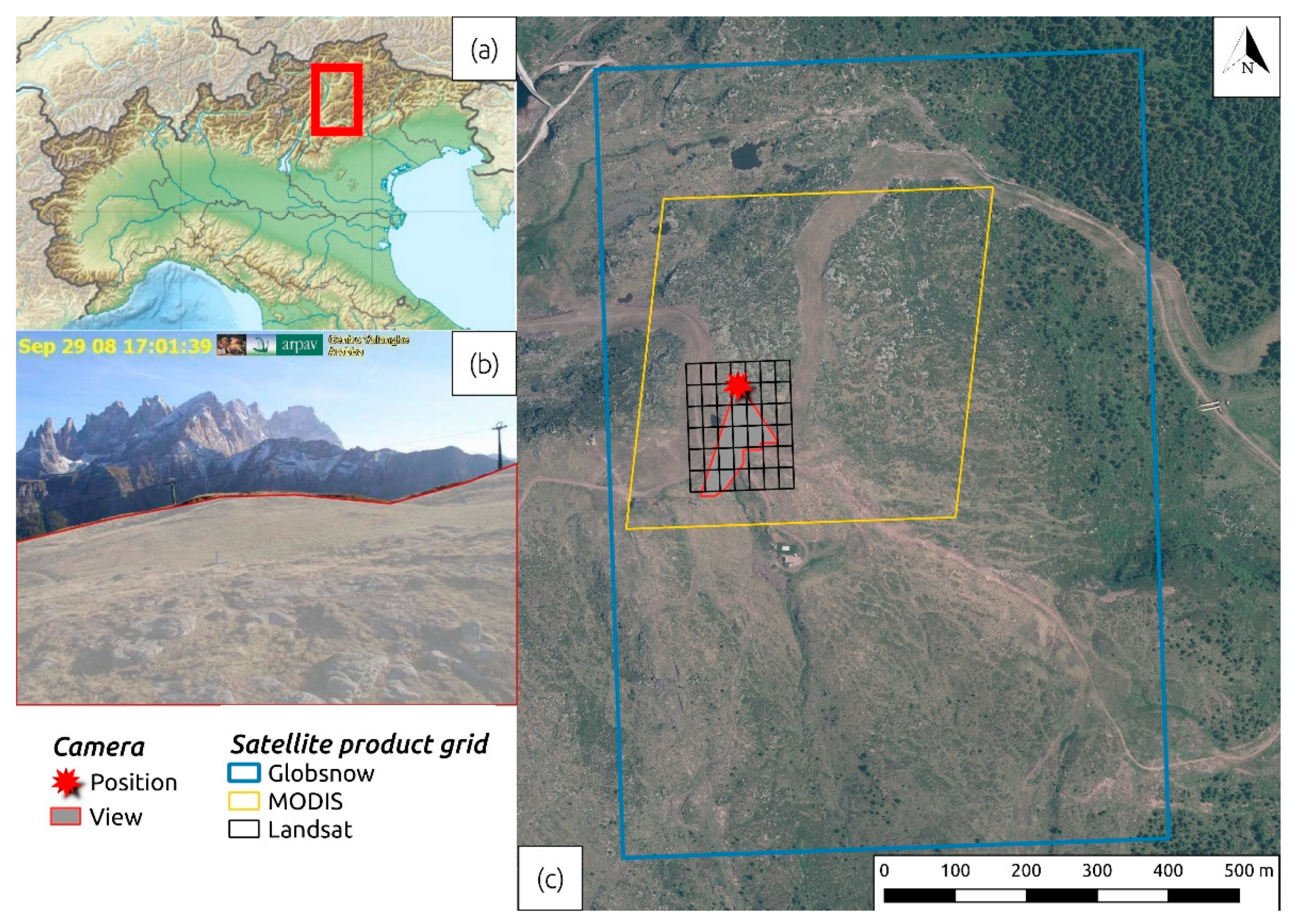
2.1. Study Area
2.2. Camera Setup
2.3. Terrestrial Image Classification
2.3.1. Supervised Methods
2.3.2. Blue Thresholding
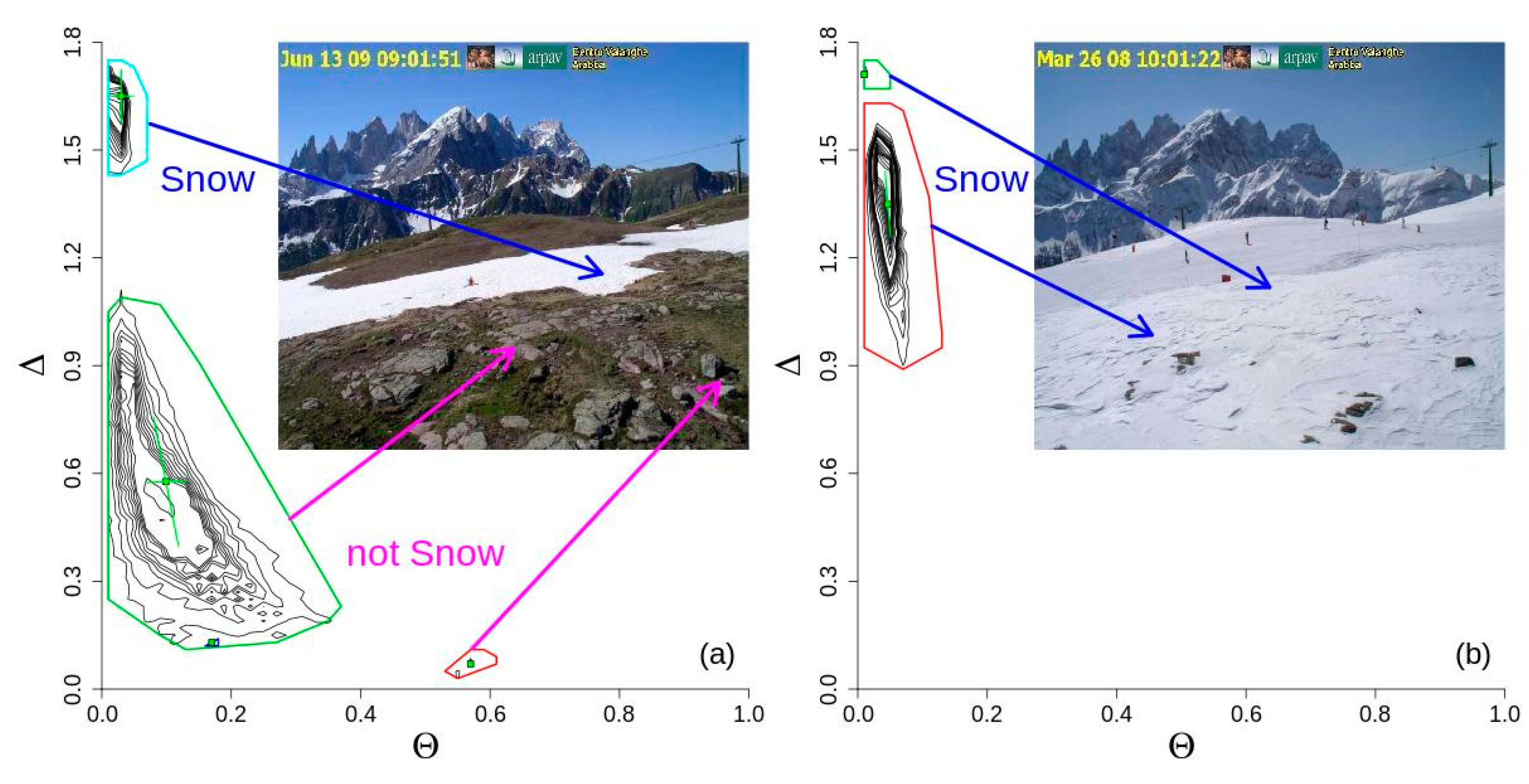
2.3.3. Spectral Similarity
2.4. Orthorectification
2.5. Satellite Snow Products
2.5.1. Optical Remote Sensing with High Spatial Resolution
2.5.2. Optical Remote Sensing with Intermediate Spatial Resolution
2.5.3. Optical Remote Sensing with Low Spatial Resolution
2.6. Statistical Analysis
3. Results
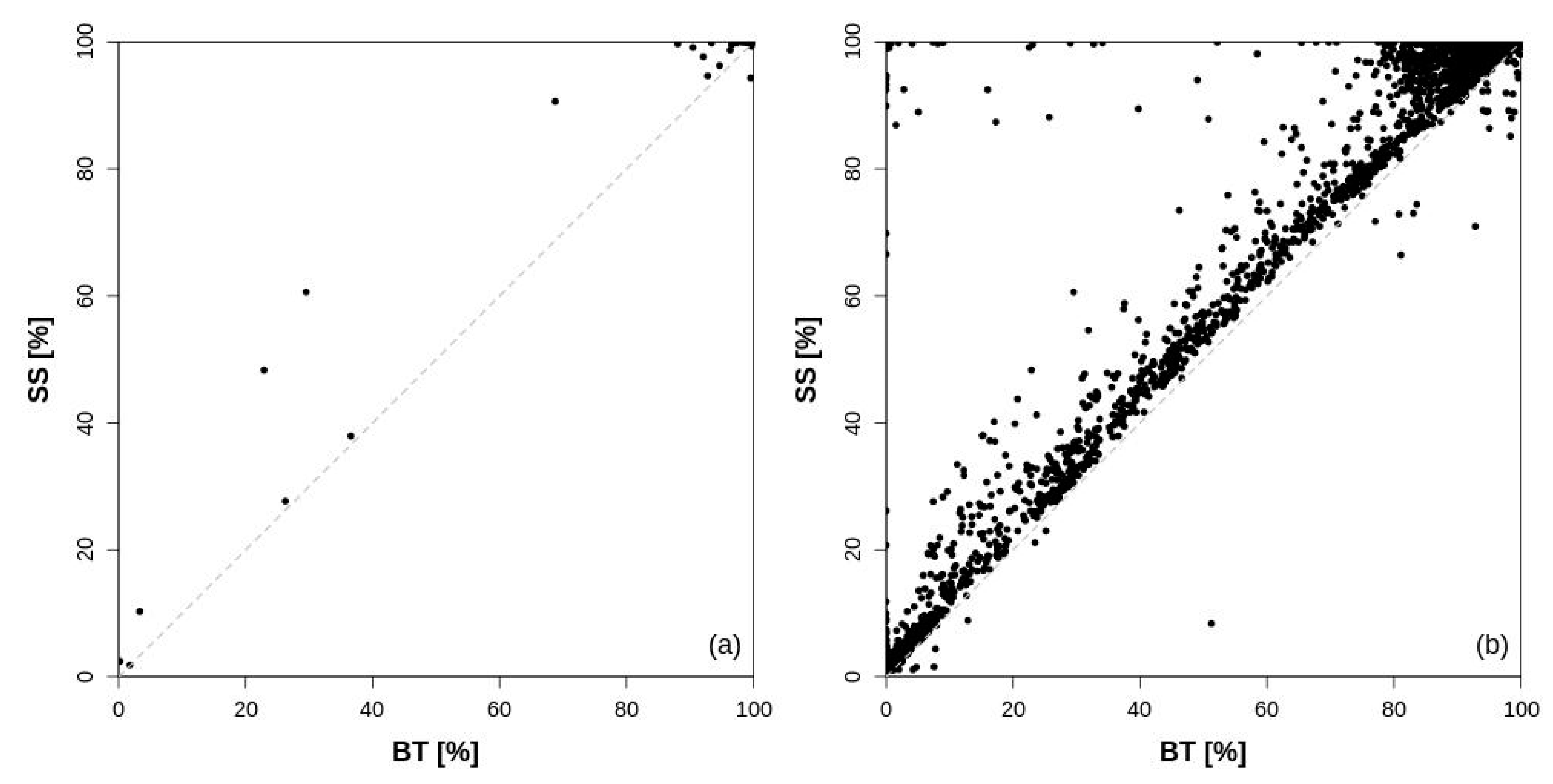
3.1. Comparison between Supervised and Automated Classifiers
3.2. Comparison between Automated Classifiers
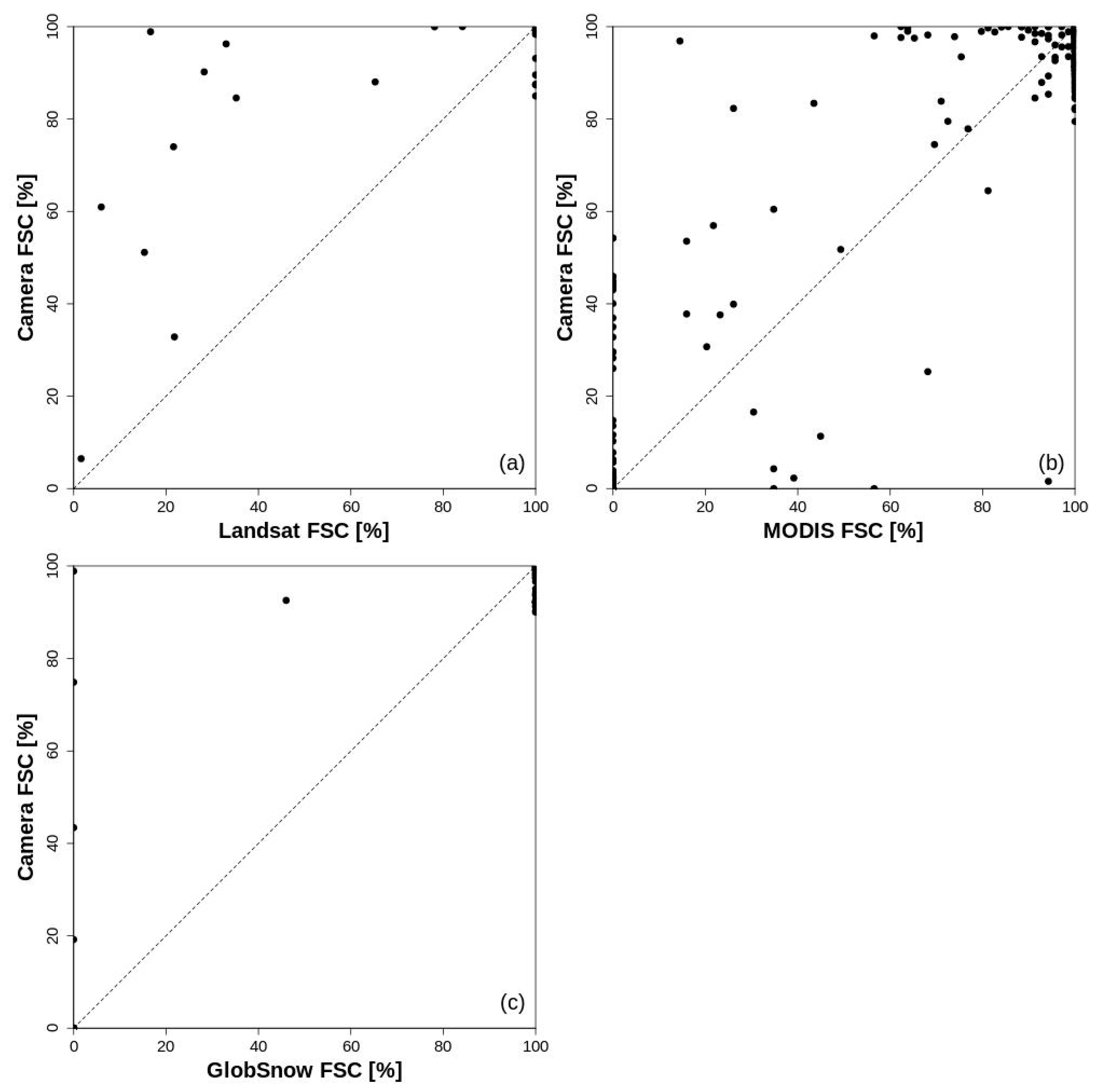
3.3. Comparison between FSC Estimations Obtained by Terrestrial Photography and Remote Sensing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Beniston, M.; Farinotti, D.; Stoffel, M.; Andreassen, L.M.; Coppola, E.; Eckert, N.; Fantini, A.; Giacona, F.; Hauck, C.; Huss, M.; et al. The European mountain cryosphere: A review of its current state, trends, and future challenges. Cryosphere 2018, 12, 759–794. [Google Scholar] [CrossRef]
- Helmert, J.; Şensoy Şorman, A.; Alvarado Montero, R.; De Michele, C.; de Rosnay, P.; Dumont, M.; Finger, D.; Lange, M.; Picard, G.; Potopová, V.; et al. Review of Snow Data Assimilation Methods for Hydrological, Land Surface, Meteorological and Climate Models: Results from a COST HarmoSnow Survey. Geosciences 2018, 8, 489. [Google Scholar] [CrossRef]
- Pirazzini, R.; Leppänen, L.; Picard, G.; Lopez-Moreno, J.I.; Marty, C.; Macelloni, G.; Kontu, A.; von Lerber, A.; Tanis, C.M.; Schneebeli, M.; et al. European In-Situ Snow Measurements: Practices and Purposes. Sensors 2018, 18, 2016. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow–A review of available methods. Int. J. Remote Sens. 2011, 33, 4094–4134. [Google Scholar] [CrossRef]
- Dozier, J.; Green, R.O.; Nolin, A.W.; Painter, T.H. Interpretation of snow properties from imaging spectrometry. Remote Sens. Environ. 2009, 113, 525–537. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R. Updating a land surface model with MODIS-derived snow cover. J. Hydrometeorol. 2004, 5, 1064–1075. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow-covered area and grain size from imaging spectrometer data. Remote Sens. Environ. 2009, 113, 868–879. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Development of the Aqua MODIS NDSI fractional snow cover algorithm and validation results. IEEE Trans. Geosci. Remote 2006, 44, 1747–1756. [Google Scholar] [CrossRef]
- Yin, D.; Cao, X.; Chen, X.; Shao, Y.; Chen, J. Comparison of automatic thresholding methods for snow-cover mapping using Landsat TM imagery. Int. J. Remote Sens. 2013, 34, 6529–6538. [Google Scholar] [CrossRef]
- Härer, S.; Bernhardt, M.; Siebers, M.; Schulz, K. On the need for a time- and location-dependent estimation of the NDSI threshold value for reducing existing uncertainties in snow cover maps at different scales. Cryosphere 2018, 12, 1629–1642. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/[Terra/Aqua] Snow Cover Daily L3 Global 500m Grid, Version 6. NASA National Snow and Ice Data Center Distributed Active Archive Center. Available online: https://nsidc.org/data/modis/data_summaries (accessed on 1 October 2018).
- Solberg, R.; Amlien, J.; Koren, H. A Review of Optical Snow Cover Algorithms. Norwegian Computing Center Note, SAMBA/40/06. 2006. Available online: https://www.nr.no/directdownload/4400/Solberg_-_A_review_of_optical_snow_algorithms.pdf (accessed on 1 October 2018).
- Metsämäki, S.; Pulliainen, J.; Salminen, M.; Luojus, K.; Wiesmann, A.; Solberg, R.; Böttcher, K.; Hiltunen, M.; Ripper, E. Introduction to GlobSnow Snow Extent products with considerations for accuracy assessment. Remote Sens. Environ. 2015, 156, 96–108. [Google Scholar] [CrossRef]
- Arslan, A.N.; Tanis, C.M.; Metsämäki, S.; Aurela, M.; Böttcher, K.; Linkosalmi, M.; Peltoniemi, M. Automated Webcam Monitoring of Fractional Snow Cover in Northern Boreal Conditions. Geosciences 2017, 7, 55. [Google Scholar] [CrossRef]
- Kepski, D.; Luks, B.; Migała, K.; Wawrzyniak, T.; Westermann, S.; Wojtuń, B. Terrestrial Remote Sensing of Snowmelt in a Diverse High-Arctic Tundra Environment Using Time-Lapse Imagery. Remote Sens. 2017, 9, 733. [Google Scholar] [CrossRef]
- Bradley, E.S.; Clarke, K.C. Outdoor Webcams as Geospatial Sensor Networks: Challenges, Issues and Opportunities. Cartogr. Geogr. Inf. Sci. 2011, 38, 3–19. [Google Scholar] [CrossRef]
- Fedorov, R.; Camerada, A.; Fraternali, P.; Tagliasacchi, M. Estimating snow cover from publicly available images. IEEE Trans. Multimed. 2016, 18, 1187–1200. [Google Scholar] [CrossRef]
- Parajka, J.; Haas, P.; Kirnbauer, R.; Jansa, J.R.; Blöschl, G. Potential of time-lapse photography of snow for hydrological purposes at the small catchment scale. Hydrol. Process. 2012, 26, 3327–3337. [Google Scholar] [CrossRef]
- Härer, S.; Bernhardt, M.; Corripio, J.G.; Schulz, K. PRACTISE–Photo Rectification and ClassificaTIon SoftwarE (V.1.0). Geosci. Model Dev. 2013, 6, 837–848. [Google Scholar] [CrossRef]
- Tanis, C.M.; Peltoniemi, M.; Linkosalmi, M.; Aurela, M.; Böttcher, K.; Manninen, T.; Arslan, A.N. A system for Acquisition, Processing and Visualization of Image Time Series from Multiple Camera Networks. Data 2018, 3, 23. [Google Scholar] [CrossRef]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 4th ed.; Pearson Series in Geographic Information Science; Pearson: Glenview, IL, USA, 2015; pp. 1–544. ISBN 013405816X. [Google Scholar]
- Valt, M.; Cianfarra, P. Recent snow cover variability in the Italian Alps. Cold Reg. Sci. Tech. 2010, 64, 146–157. [Google Scholar] [CrossRef]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Richards, J.A.; Jia, X. Remote Sensing Digital Image Analysis: An Introduction, 4th ed.; Springer: Berlin, Germany, 2005; pp. 1–494. ISBN 3540251286. [Google Scholar]
- Salvatori, R.; Plini, P.; Giusto, M.; Valt, M.; Salzano, R.; Montagnoli, M.; Cagnati, A.; Crepaz, G.; Sigismondi, D. Snow cover monitoring with images from digital camera systems. Ital. J. Remote Sens. 2011, 43, 137–145. [Google Scholar] [CrossRef]
- Härer, S.; Bernhardt, M.; Schulz, K. PRACTISE–Photo Rectification and ClassificaTIon SoftwarE (V.2.1). Geosci. Model Dev. 2016, 9, 307–321. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)-Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; ver. 3.4.4; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 1 October 2018).
- Vincent, L.; Soille, P. Watersheds in Digital Spaces: An Efficient Algorithm Based on Immersion Simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Seo, J.; Chae, S.; Shim, J.; Kim, D.; Cheong, C.; Han, T. Fast Contour-Tracing Algorithm Based on a Pixel-Following Method for Image Sensors. Sensors 2016, 16, 353. [Google Scholar] [CrossRef] [PubMed]
- Corripio, J.G. Snow surface albedo estimation using terrestrial photography. Int. J. Remote Sens. 2004, 25, 5705–5729. [Google Scholar] [CrossRef]
- Regione del Veneto. Modello Digitale del Terreno dell’Intero Territorio Regionale con Celle di 5 Metri di Lato. 2006. Available online: http://idt.regione.veneto.it/app/metacatalog ID: C0103024_DTM5 (accessed on 1 October 2018).
- Giuliani, G.; Chatenoux, B.; De Bono, A.; Rodila, D.; Richard, J.; Allenbach, K.; Dao, H.; Peduzzi, P. Building an Earth Observations Data Cube: Lessons learned from the Swiss Data Cube (SDC) on generating Analysis Ready Data (ARD). Big Earth Data 2017, 1, 100–117. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Barsi, J.A.; Lee, K.; Kvaran, G.; Markham, B.L.; Pedelty, J.A. The Spectral Response of the Landsat-8 Operational Land Imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef]
- Metsämäki, S.; Mattila, O.P.; Pulliainen, J.; Niemi, K.; Luojus, K.; Böttcher, K. An optical reflectance model-based method for fractional snow cover mapping applicable to continental scale. Remote Sens. Environ. 2012, 123, 508–521. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; pp. 1–177. ISBN 978142005. [Google Scholar]
| Overall Accuracy (%) | ||||
|---|---|---|---|---|
| MA | ML | MD | PD | |
| BT | 96.9 | 96.8 | 97.9 | 97.8 |
| SS | 97.9 | 98.5 | 99.2 | 98.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salzano, R.; Salvatori, R.; Valt, M.; Giuliani, G.; Chatenoux, B.; Ioppi, L. Automated Classification of Terrestrial Images: The Contribution to the Remote Sensing of Snow Cover. Geosciences 2019, 9, 97. https://doi.org/10.3390/geosciences9020097
Salzano R, Salvatori R, Valt M, Giuliani G, Chatenoux B, Ioppi L. Automated Classification of Terrestrial Images: The Contribution to the Remote Sensing of Snow Cover. Geosciences. 2019; 9(2):97. https://doi.org/10.3390/geosciences9020097
Chicago/Turabian StyleSalzano, Roberto, Rosamaria Salvatori, Mauro Valt, Gregory Giuliani, Bruno Chatenoux, and Luca Ioppi. 2019. "Automated Classification of Terrestrial Images: The Contribution to the Remote Sensing of Snow Cover" Geosciences 9, no. 2: 97. https://doi.org/10.3390/geosciences9020097
APA StyleSalzano, R., Salvatori, R., Valt, M., Giuliani, G., Chatenoux, B., & Ioppi, L. (2019). Automated Classification of Terrestrial Images: The Contribution to the Remote Sensing of Snow Cover. Geosciences, 9(2), 97. https://doi.org/10.3390/geosciences9020097







