Discriminating Wet Snow and Firn for Alpine Glaciers Using Sentinel-1 Data: A Case Study at Rofental, Austria
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
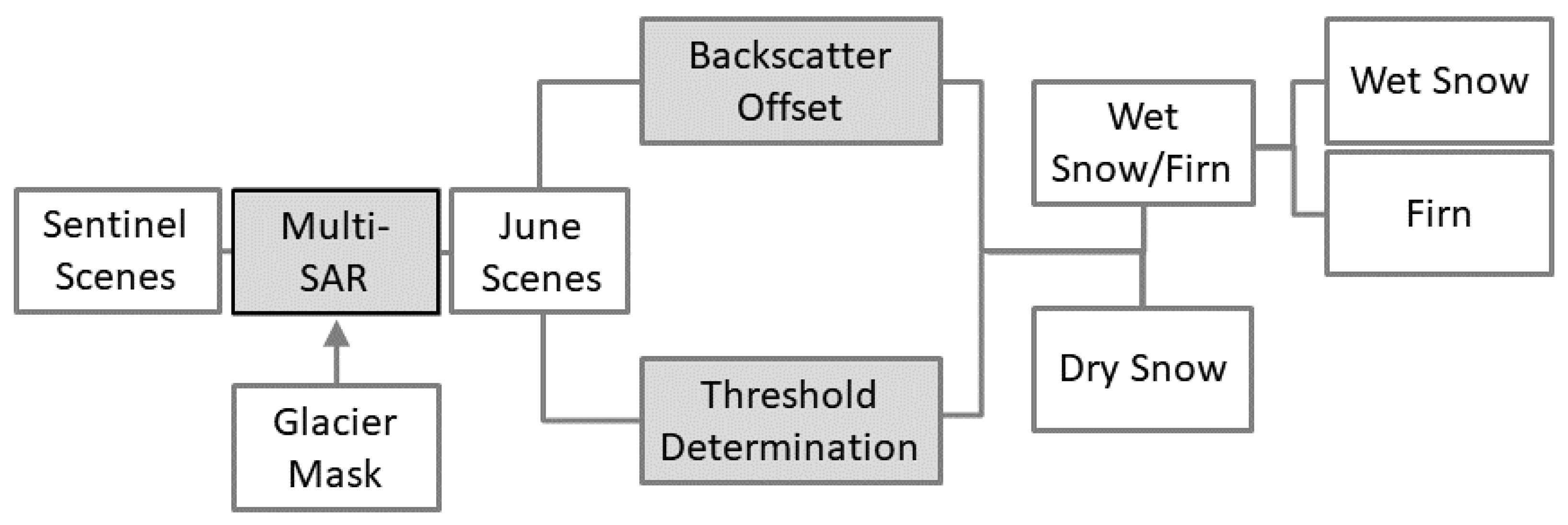
2.2. SAR Data Workflow
2.2.1. Multi-SAR-System
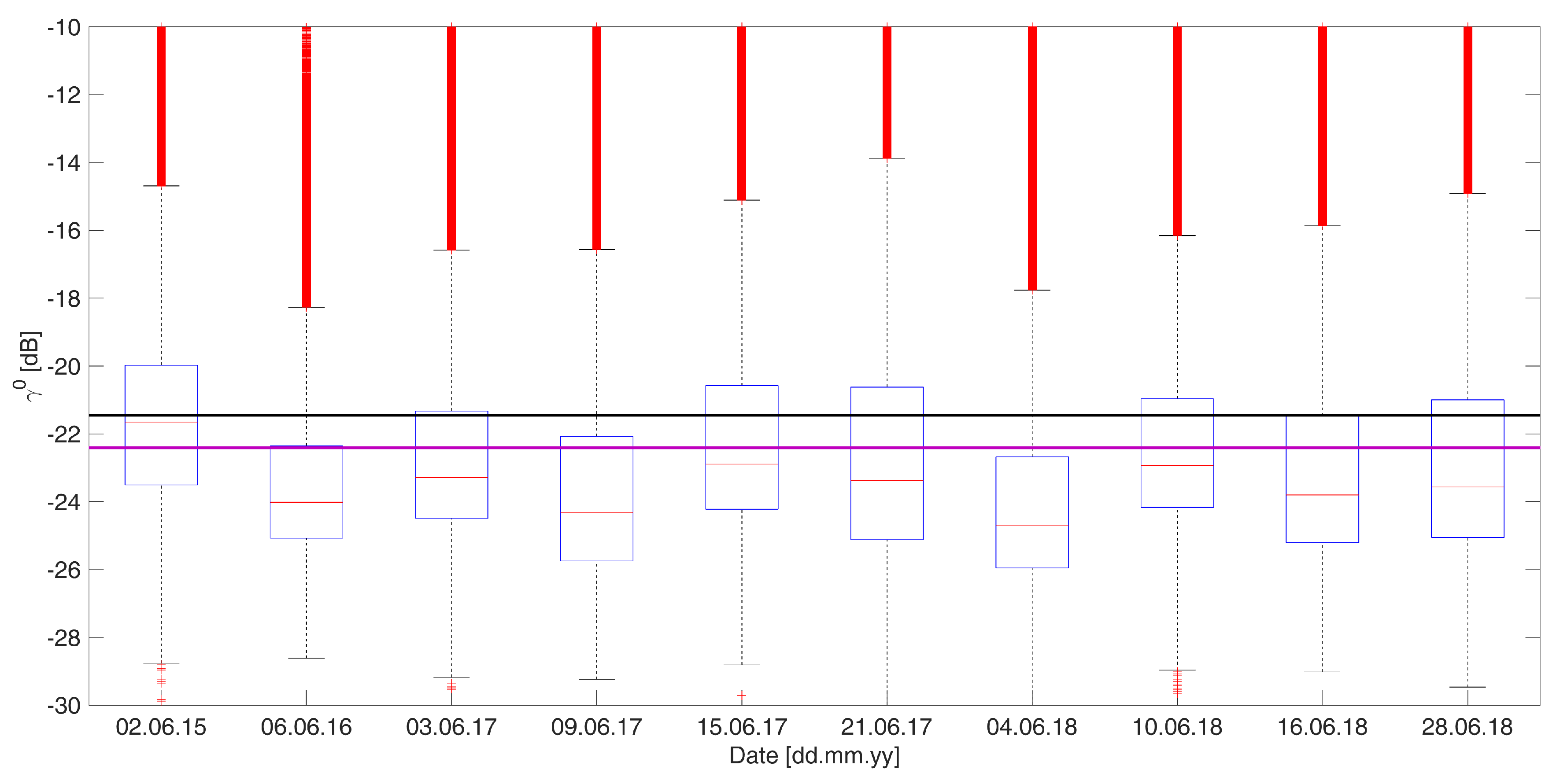
2.2.2. Backscatter Variability of Wet Snow Scenes
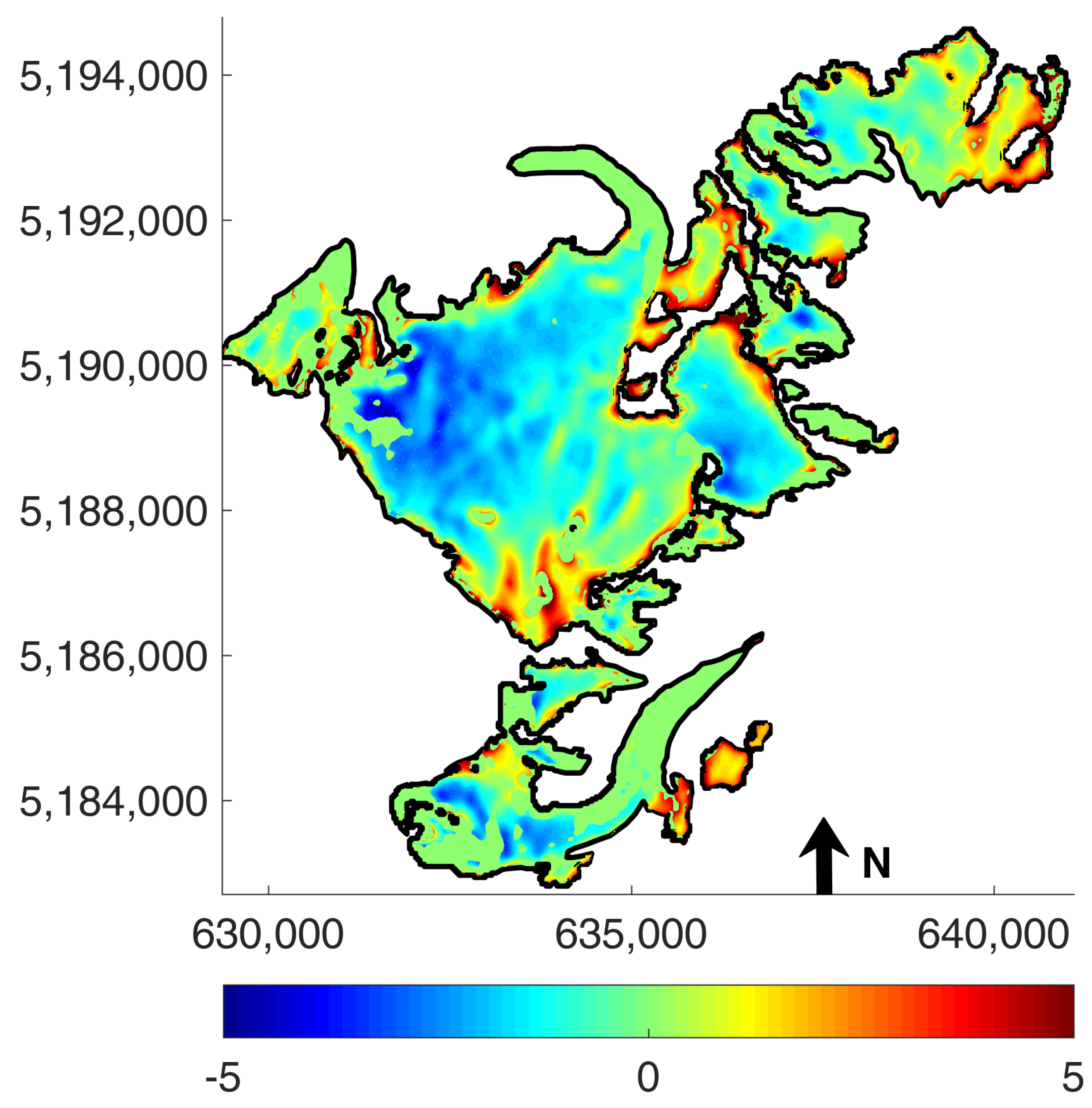
2.2.3. Correction of Systematic Backscatter Offsets
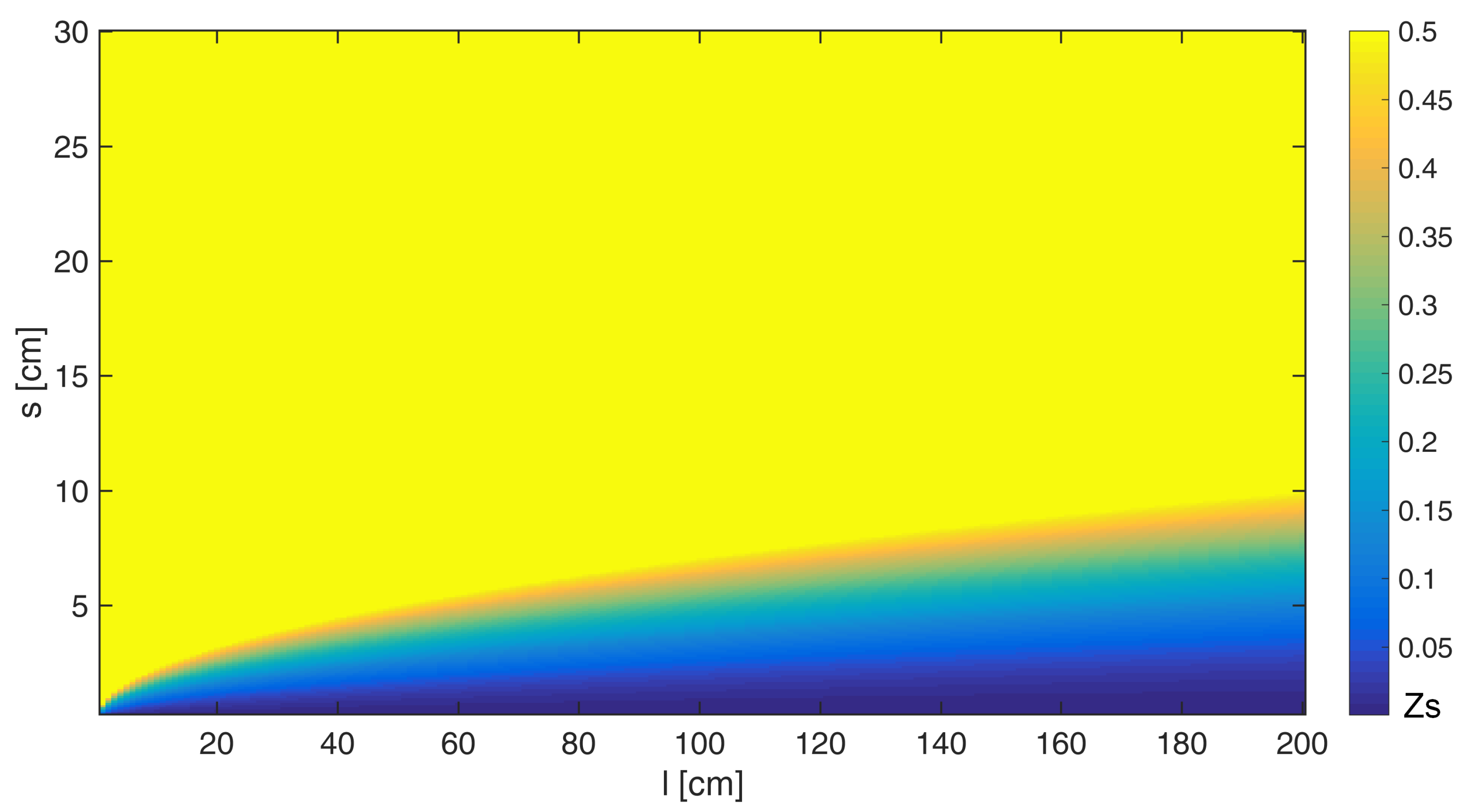
2.2.4. Threshold Determination
2.3. Processing of Optical and Near-Infrared Remote Sensing Data
2.4. Annual Minimum Wet Snow Covered Area Extent
3. Results
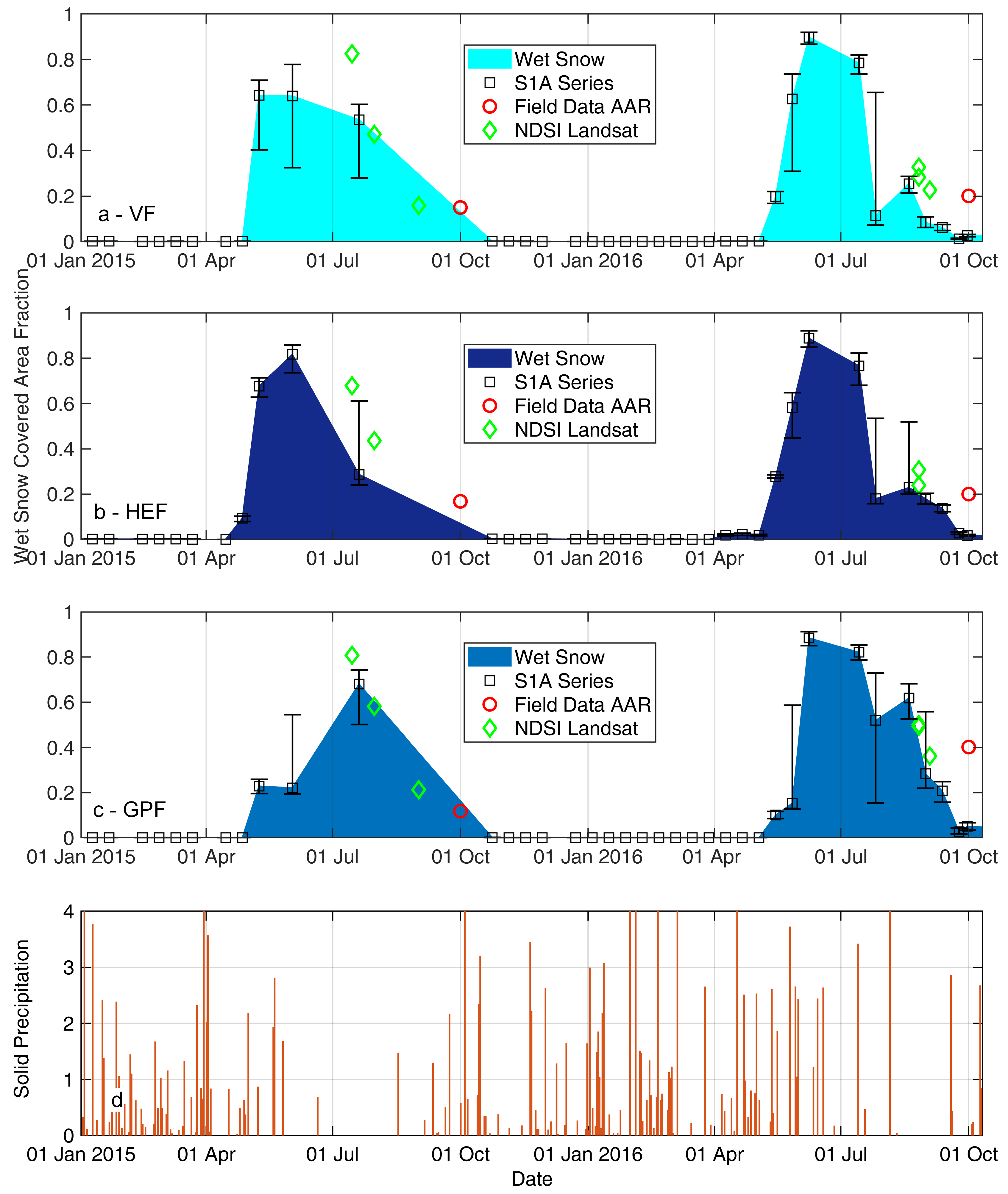
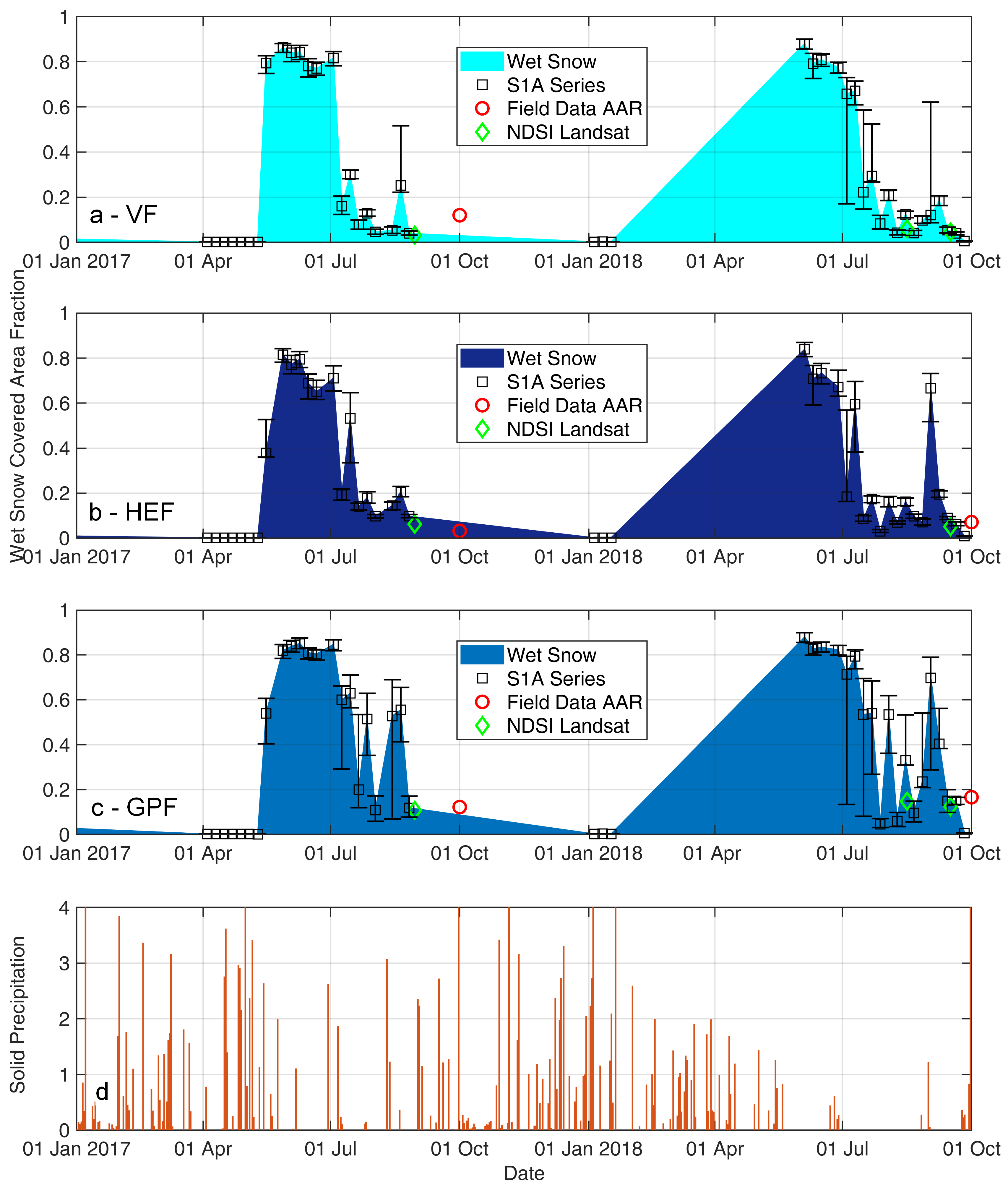
3.1. Wet Snow Covered Area Extent
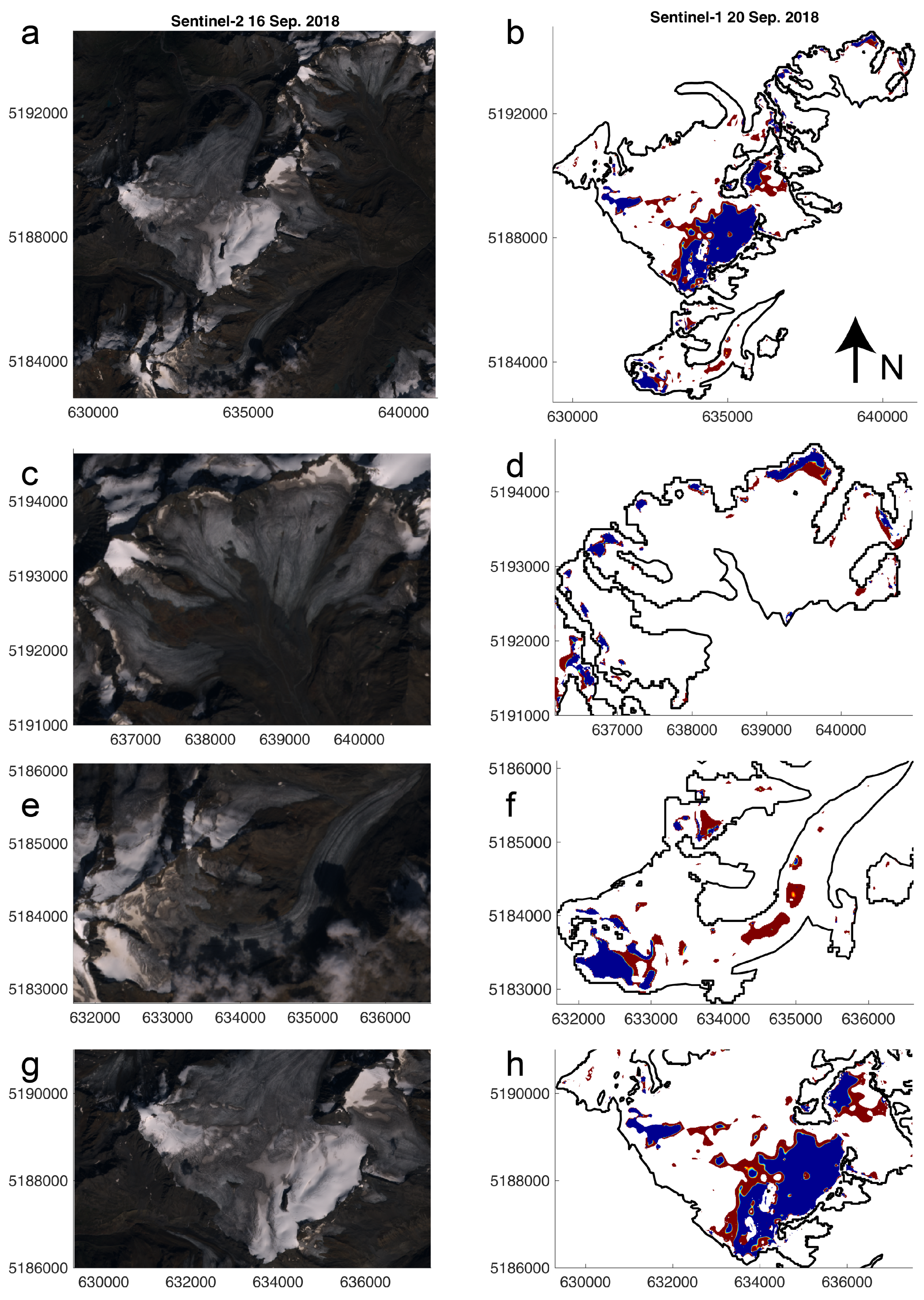
3.2. Discriminating Firn and Wet Snow
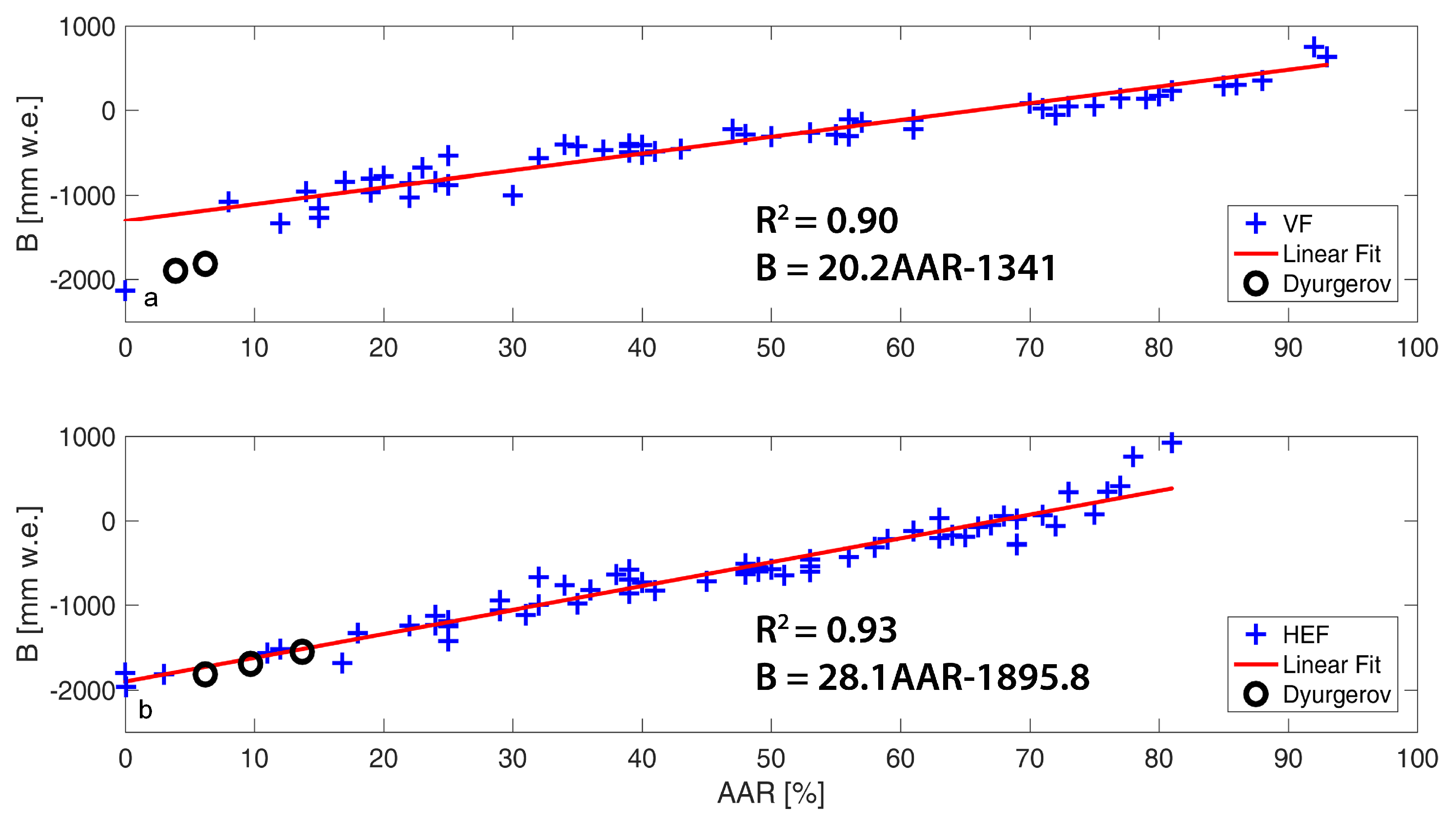
3.3. From Minimum Wet Snow Extent to Mass Balances
4. Discussion
4.1. Uncertainty Analysis and Limitations
4.2. Discrimination of Wet Snow and Firn
4.3. SAR Data for Application in Seasonal Mass Balance Estimates
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AAR | Accumulation Area Ratio |
| AOI | Area Of Interest |
| B | Mass Balance |
| CV | Coefficient of Variation |
| DEM | Digital Elevation Model |
| GPF | AOI Gepatschferner |
| GY | Glaciological Year |
| HEF | AOI Hintereisferner |
| NDSI | Normalized Difference Snow Index |
| NESZ | Noise Equivalent sigma-0 |
| RMS | Root Mean Square |
| S1 | Sentinel-1 |
| S1A | Sentinel-1A |
| SAR | Synthetic Aperture Radar |
| SCE | Snow Cover Extent |
| SRTM | Shuttle Radar Topography Mission |
| USGS | United States Geological Survey |
| UTC | Universal Time Coordinated |
| UTM | Universal Transverse Mercator |
| VF | AOI Vernagtferner |
| VH | Vertical polarisation transmit and Horizontal polarisation receive |
| VV | Vertical polarisation transmit and Vertical polarisation receive |
| WGS | World Geodetic System |
| WSCAF | Wet Snow Covered Area Fraction |
Appendix A
| S1 | S1 | S1 | S1 |
|---|---|---|---|
| 9 January 2015 | 21 January 2015 | 14 February 2015 | 26 February 2015 |
| 10 March 2015 | 22 March 2015 | 15 April 2015 | 27 April 2015 |
| 9 May 2015 | 21 May 2015 | 02 June 2015 | 20 July 2015 |
| 24 October 2015 | 05 November 2015 | 17 November 2015 | 29 November 2015 |
| 23 December 2015 | 04 January 2016 | 16 January 2016 | 28 January 2016 |
| 9 February 2016 | 21 February 2016 | 04 March 2016 | 16 March 2016 |
| 28 March 2016 | 09 April 2016 | 21 April 2016 | 03 May 2016 |
| 15 May 2016 | 27 May 2016 | 08 June 2016 | 14 July 2016 |
| 26 July 2016 | 19 August 2016 | 31 August 2016 | 12 September 2016 |
| 24 September 2016 | 30 September 2016 | 4 April 2017 | 10 April 2017 |
| 16 April 2017 | 22 April 2017 | 28 April 2017 | 4 May 2017 |
| 10 May 2017 | 16 May 2017 | 28 May 2017 | 3 June 2017 |
| 9 June 2017 | 15 June 2017 | 21 June 2017 | 3 July 2017 |
| 9 July 2017 | 15 July 2017 | 21 June 2017 | 27 July 2017 |
| 2 August 2017 | 14 August 2017 | 20 August 2017 | 26 August 2017 |
| 5 January 2018 | 11 January 2018 | 17 January 2018 | 4 June 2018 |
| 10 June 2018 | 16 June 2018 | 28 June 2018 | 4 July 2018 |
| 10 July 2018 | 16 July 2018 | 22 July 2018 | 28 July 2018 |
| 3 August 2018 | 09 August 2018 | 15 August 2018 | 21 August 2018 |
| 27 August 2018 | 2 Sept. 2018 | 8 September 2018 | 14 September 2018 |
| 20 September 2018 | 26 September 2018 | 2 October 2018 |

References
- Zemp, M.; Thibert, E.; Huss, M.; Stumm, D.; Rolstad Denby, C.; Nuth, C.; Nussbaumer, S.U.; Moholdt, G.; Mercer, A.; Mayer, C.; et al. Reanalysing glacier mass balance measurement series. Cryosphere 2013, 7, 1227–1245. [Google Scholar] [CrossRef]
- WGMS. Global Glacier Change Bulletin No. 1 (2012–2013); ICSU(WDS)/IUGG(IACS)/UNEP/UNESCO/WMO; World Glacier Monitoring Service: Zurich, Switzerland, 2015. [Google Scholar]
- Benn, D.I.; Evans, D.J.A. Glaciers & Glaciation; Arnold: London, UK, 2006. [Google Scholar]
- Nagler, T.; Rott, H. Retrieval of wet snow by means of multitemporal SAR data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 754–765. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. The value of MODIS snow cover data in validating and calibrating conceptual hydrologic models. J. Hydrol. 2008, 358, 240–258. [Google Scholar] [CrossRef]
- de Ruyter Wildt, M.S.; Oerlemans, J.; Björnsson, H. A method for monitoring glacier mass balance using satellite albedo measurements: Application to Vatnajökull, Iceland. J. Glaciol. 2002, 48, 267–278. [Google Scholar] [CrossRef]
- Cogley, J.G.; Hock, R.; Rasmussen, L.A.; Arendt, A.A.; Bauder, A.; Braithwaite, R.J.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L.; et al. Glossary of Glacier Mass Balance and Related Terms. IHP-VII Technical Documents in Hydrology No. 86; IACS Contribution No. 2; UNESCO-IHP: Paris, France, 2011; p. 114. [Google Scholar]
- Adam, S.; Pietroniro, A.; Brugman, M. Glacier snow line mapping using ERS-1 SAR imagery. Remote Sens. Environ. 1997, 61, 46–54. [Google Scholar] [CrossRef]
- Nagler, T.; Rott, H.; Ripper, E.; Bippus, G.; Hetzenecker, M. Advancements for Snowmelt Monitoring by Means of Sentinel-1 SAR. Remote Sens. 2016, 8, 348. [Google Scholar] [CrossRef]
- Heilig, A.; Mitterer, C.; Schmid, L.; Wever, N.; Schweizer, J.; Marshall, H.P.; Eisen, O. Seasonal and diurnal cycles of liquid water in snow-Measurements and modeling. J. Geophys. Res. Earth Surf. 2015, 120, 2139–2154. [Google Scholar] [CrossRef]
- Baghdadi, N.; Gauthier, Y.; Bernier, M. Capability of Multitemporal ERS-1 SAR Data for Wet-Snow Mapping. Remote Sens. Environ. 1997, 60, 174–186. [Google Scholar] [CrossRef]
- König, M.; Winther, J.G.; Isaksson, E. Measuring snow and glacier ice properties from satellite. Rev. Geophys. 2001, 39, 1–27. [Google Scholar] [CrossRef]
- Jaenicke, J.; Mayer, C.; Scharrer, K.; Münzer, U.; Gudmundsson, Á. The use of remote-sensing data for mass-balance studies at Mýrdalsjökull ice cap, Iceland. J. Glaciol. 2006, 52, 565–573. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Tian, B.s.; Chen, Q.; Liu, J.L.; Zhang, R. Classification and snow line detection for glacial areas using the polarimetric SAR image. Remote Sens. Environ. 2011, 115, 1721–1732. [Google Scholar] [CrossRef]
- Brown, I.A. Synthetic Aperture Radar Measurements of a Retreating Firn Line on a Temperate Icecap. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 153–160. [Google Scholar] [CrossRef]
- Barry, R.G.; Gan, T.Y. The Global Cryosphere: Past, Present, and Future; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Huss, M.; Sold, L.; Hoelzle, M.; Stokvis, M.; Salzmann, N.; Farinotti, D.; Zemp, M. Towards remote monitoring of sub-seasonal glacier mass balance. Ann. Glaciol. 2013, 54, 75–83. [Google Scholar] [CrossRef]
- Lambrecht, A.; Kuhn, M. Glacier changes in the Austrian Alps during the last three decades, derived from the new Austrian glacier inventory. Ann. Glaciol. 2007, 46, 177–184. [Google Scholar] [CrossRef]
- Sentinel-1Team. Sentinel-1 User Handbook; European Space Agency: Frascati, Italy, 2013. [Google Scholar]
- Braun, L.; Reinwarth, O.; Weber, M. Der Vernagtferner als Objekt der Gletscherforschung. Zeitschrift f. Gletscherkunde und Glazialgeologie 2011, 45/46, 85–104. [Google Scholar]
- Geodesy; Glaciology. Kenngrößen des Massenhaushaltes des Vernagtferners für den Zeitraum 1964 bis 2015. Available online: http://glaziologie.de/massbal/index.html (accessed on 9 January 2017).
- WGMS. WGMS Fluctuations of Glaciers Browser. Available online: http://wgms.ch/fogbrowser/ (accessed on 9 January 2017).
- Oestrem, G.; Stanley, A. Glacier Mass Balance Measurements: A Manual for Field and Office Work; NHRI Science Report 4; National Hydrology Research Institute: Ottawa, ON, Canada, 1969. [Google Scholar]
- Zemp, M.; Hoelzle, M.; Haeberli, W. Six decades of glacier mass-balance observations: A review of the worldwide monitoring network. Ann. Glaciol. 2009, 50, 101–111. [Google Scholar] [CrossRef]
- Jansson, P. Effect of Uncertainties in Measured Variables on the Calculated Mass Balance of storglaciaren. Geogr. Ann. Ser. A Phys. Geogr. 1999, 81, 633–642. [Google Scholar] [CrossRef]
- Funk, M.; Morelli, R.; Stahel, W. Mass balance of Griesgletscher 1961–1994: Different methods of determination. Zeitschrift f. Gletscherkunde und Glazialgeologie 1997, 33, 41–55. [Google Scholar]
- Small, D. Flattening Gamma: Radiometric Terrain Correction for SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Schmitt, A.; Wendleder, A.; Hinz, S. The Kennaugh element framework for multi-scale, multi-polarized, multi-temporal and multi-frequency SAR image preparation. ISPRS J. Photogramm. Remote Sens. 2015, 102, 122–139. [Google Scholar] [CrossRef]
- Bertram, A.; Wendleder, A.; Schmitt, A.; Huber, M. Long-term Monitoring of water dynamics in the Sahel region using the Multi-SAR-System. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI, 313–320. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Dozier, J. Spectral signature of alpine snow cover from the landsat thematic mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 1995, 54, 127–140. [Google Scholar] [CrossRef]
- Singh, V.P.; Singh, P.; Haritashya, U.K. (Eds.) Encyclopedia of Snow, Ice and Glaciers; Encyclopedia of Earth Sciences Series; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- ESA—Sentinel Online. Level-2A Algorithm Overview. 2018. Available online: https://earth.esa.int/web/sentinel/technical-guides/sentinel-2-msi/level-2a/algorithm (accessed on 6 December 2018).
- Oerlemans, J.; Klok, E.J. Effect of summer snowfall on glacier mass balance. Ann. Glaciol. 2004, 38, 97–100. [Google Scholar] [CrossRef]
- Charalampidis, C.; Fischer, A.; Kuhn, M.; Lambrecht, A.; Mayer, C.; Thomaidis, K.; Weber, M. Mass-Budget Anomalies and Geometry Signals of Three Austrian Glaciers. Front. Earth Sci. 2018, 6, 205. [Google Scholar] [CrossRef]
- Dyurgerov, M.; Meier, M.F.; Bahr, D.B. A new index of glacier area change: A tool for glacier monitoring. J. Glaciol. 2009, 55, 710–716. [Google Scholar] [CrossRef]
- Mattia, F.; Le Toan, T.; Souyris, J.C.; de Carolis, C.; Floury, N.; Posa, F.; Pasquariello, N.G. The effect of surface roughness on multifrequency polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 954–966. [Google Scholar] [CrossRef]
- Deroin, J.P.; Company, A.; Simonin, A. An empirical model for interpreting the relationship between backscattering and arid land surface roughness as seen with the SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 86–92. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N. A new soil roughness parameter for the modelling of radar backscattering over bare soil. Remote Sens. Environ. 2014, 152, 62–73. [Google Scholar] [CrossRef]
- Drolon, V.; Maisongrande, P.; Berthier, E.; Swinnen, E.; Huss, M. Monitoring of seasonal glacier mass balance over the European Alps using low-resolution optical satellite images. J. Glaciol. 2016, 62, 912–927. [Google Scholar] [CrossRef]
- Floricioiu, D.; Rott, H. Seasonal and short-term variability of multifrequency, polarimetric radar backscatter of Alpine terrain from SIR-C/X-SAR and AIRSAR data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2634–2648. [Google Scholar] [CrossRef]
Sample Availability: S1 and S2 data can be downloaded from the respective webpages of Copernicus Services, Landsat data can be obtained through GLOVIS USGS. Processed S1 results are available from the authors on request. |

| Glacier Name | Elevation [m a.s.l.] | Exposition | Size [km] |
|---|---|---|---|
| Gepatschferner | 2180–3507 | NW–NE | 16.6 |
| Guslarferner gr. | 2842–3479 | NE–SE | 1.4 |
| Guslarferner mi. | 2928–3317 | NE | 0.5 |
| Hintereisferner | 2484–3711 | E–NE | 7.5 |
| Hintereiswände | 3091–3428 | SE | 0.5 |
| Kesselwandferner | 2792–3492 | NE–SE | 3.8 |
| Rofenberg E | 2937–3173 | NW | 0.1 |
| Rofenberg W | 2885–3268 | NW | 0.4 |
| Vernagelwandferner N | 3003–3267 | E | 0.3 |
| Vernaglwandferner S | 2942–3429 | SE | 0.6 |
| Vernagtferner | 2828–3621 | SE–W | 8.3 |
| Weissseeferner | 2608–3502 | N–NE | 2.6 |
| Parameters | S1 |
|---|---|
| Band | C |
| Repeat Pass | 12 d, 6 d |
| Polarization | VV, VH |
| Orbit Ascending | 15, 117 (46, 37) |
| Orbit Descending | 168 (39) |
| Acquisition Time | 05:30 D/ 17:10 A |
| Acquisition Period | 01/2015–10/2018 |
| NESZ | −22 dB |
| Number Scenes | 82 |
| Platform | Orbit | Date | VH | VV |
|---|---|---|---|---|
| S1 | 168 | 2 June 2015 | 0.14 | 0.24 |
| S1 | 168 | 8 June 2016 | 0.10 | 0.20 |
| S1 | 168 | 3 June 2017 | 0.13 | 0.25 |
| S1 | 168 | 9 June 2017 | 0.13 | 0.26 |
| S1 | 168 | 15 June 2017 | 0.14 | – |
| S1 | 168 | 21 June 2017 | 0.15 | – |
| S1 | 168 | 4 June 2018 | 0.13 | – |
| S1 | 168 | 10 June 2018 | 0.14 | – |
| S1 | 168 | 16 June 2018 | 0.15 | – |
| S1 | 168 | 28 June 2018 | 0.15 | – |
| S1 | 117 | 10 June 2015 | 0.13 | 0.26 |
| S1 | 117 | 22 June 2015 | 0.21 | 0.44 |
| S1 | 117 | 3 June 2015 | 0.10 | 0.17 |
| S1 | 15 | 15 June 2015 | 0.11 | 0.20 |
| S1 | 15 | 27 June 2015 | 0.11 | 0.18 |
| VF | HEF | |||
|---|---|---|---|---|
| GY | Field Data | S1 | Field Data | S1 |
| 2015/16 | 20.0 | 6.2 (12 Sep.) | 20.0 | 13.7 |
| 2016/17 | 12.0 | 3.9 (26 Aug.) | 3.2 | 9.7 |
| 2017/18 | – | 3.9 (20 Sep.) | 7.1 | 6.2 |
| VF | HEF | |||||||
|---|---|---|---|---|---|---|---|---|
| GY | Field Data | Linear Fit | Dyu | Dyu EAlps | Field Data | Linear Fit | Dyu | Dyu EAlps |
| 2015/16 | −781 | −1216 | −1814 | −1406 | −1263 | −1511 | −1547 | −1223 |
| 2016/17 | −1335 | −1262 | −1896 | −1463 | −1826 | −1623 | −1689 | −1321 |
| 2017/18 | – | −1262 | −1896 | −1463 | −1963 | −1722 | −1814 | −1406 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heilig, A.; Wendleder, A.; Schmitt, A.; Mayer, C. Discriminating Wet Snow and Firn for Alpine Glaciers Using Sentinel-1 Data: A Case Study at Rofental, Austria. Geosciences 2019, 9, 69. https://doi.org/10.3390/geosciences9020069
Heilig A, Wendleder A, Schmitt A, Mayer C. Discriminating Wet Snow and Firn for Alpine Glaciers Using Sentinel-1 Data: A Case Study at Rofental, Austria. Geosciences. 2019; 9(2):69. https://doi.org/10.3390/geosciences9020069
Chicago/Turabian StyleHeilig, Achim, Anna Wendleder, Andreas Schmitt, and Christoph Mayer. 2019. "Discriminating Wet Snow and Firn for Alpine Glaciers Using Sentinel-1 Data: A Case Study at Rofental, Austria" Geosciences 9, no. 2: 69. https://doi.org/10.3390/geosciences9020069
APA StyleHeilig, A., Wendleder, A., Schmitt, A., & Mayer, C. (2019). Discriminating Wet Snow and Firn for Alpine Glaciers Using Sentinel-1 Data: A Case Study at Rofental, Austria. Geosciences, 9(2), 69. https://doi.org/10.3390/geosciences9020069




