Abstract
Comparing nearby areas with contrasted seismicity distributions like the French Variscan Armorican Massif (AM) and the surrounding intracratonic Paris Basin (PB) can help deciphering which parameters control the occurrence or absence of diffuse, intraplate seismicity. In this paper, we examine how lithosphere temperature, fluid pressure, and frictional strength variations, combined with horizontal and bending stresses, may condition brittle, ductile or elastic behaviours of the crust in the AM and PB. We compute yield stress envelopes (YSE) and lithospheric flexure across a 1000 km-long SW–NE profile crossing the AM and PB approximately parallel to the direction of the minimum horizontal stress. Flexural models slightly better fit measured Bouguer gravity data if we apply two vertical loads on the AM and PB, with values (positive downward) ranging between −3 and −2.1012, and between 4 and 6.1012 N·m−2, respectively, depending on the chosen crustal composition. Our results evidence that whatever the crustal composition, bending stresses and heat flow variations alone are not sufficient to explain the difference in seismogenic behaviour between the AM and the PB. Variations in friction coefficient, in the range of standard values, are not totally satisfying either, since they do not restrain the brittle crustal thickness in the PB to less than 10 km, which is still large enough to be the locus of shallow earthquakes. Oppositely, increasing the cohesion from 10 to 80 MPa has a stronger effect on the thickness of the brittle upper crust, decreasing it from 10 to 15 km beneath the AM to 0–5 km beneath the PB. This suggests that the Mesozoic sedimentary pile can act as a sticky layer holding together basement rocks of the PB, which is equivalent to an increase in cohesion, and protects them from failure.
1. Introduction
Understanding the origin of seismicity in slow deforming areas requires both to decipher the stresses at the origin of earthquakes (far-field stresses due to tectonic plate motions, local stresses due to erosion, sedimentation and flexure, deep-seated processes, or any combination of these) and to characterize the mechanical response of the lithosphere to these stresses. Several hypotheses have been proposed to explain the origin of seismicity in slow deforming areas, among which are the viscoelastic behaviour of a weak lower crust responding to stress perturbations [1], stress concentration due to lithosphere heterogeneities [2], stress perturbation due to glacio-isostatic effects [3], thermal weakening of the lithosphere [4,5], or fluid flow in fault zones [6].
A classic example of enigmatic intraplate seismicity is the New Madrid Seismic Zone (NMSZ) in Central USA, where several large magnitude earthquakes (Mw > 7) have occurred, though GPS velocities depict almost no relative horizontal motions across this zone [1,5,7,8]. The Charlevoix Seismic Zone (CSZ) in Eastern Canada is another example of intraplate seismicity with almost no detectable horizontal strain [2,4,9]. With much lower magnitudes, West and Central France are also prone to diffuse intraplate seismicity, in the Variscan Armorican Massif and Central Massif (AM and CM, respectively) [10,11]. In these areas, GPS velocities also evidence null relative horizontal motions [12]. All these areas also have in common that the seismicity is at least partially localized on inherited basement faults: The Cambrian Reelfoot Rift in the NMSZ [13,14], Precambrian to Early Paleozoic faults in the CSZ [2], and Variscan strike-slip shear zones in the AM and CM [11,15], suggesting that damage zones associated with these old faults are still weaker than the surrounding crustal domains.
Understanding why there are earthquakes in a given region could also be addressed by determining why there are no earthquakes in surrounding areas, because the number of parameters (geology, heat flow, far field or local stresses) that really differ between an active seismic zone and its immediate surroundings ought to be limited. In this paper, we focus on the contrasted seismicity distribution between the French Armorican Massif and the surrounding intracratonic Paris Basin (PB). We examine how lithosphere temperature, fluid pressure, and friction coefficient variations, combined with horizontal and bending stresses, may condition brittle or elastic behaviours of the upper crust.
2. Geologic Setting
The AM and CM are outcropping remnants of the Paleozoic Variscan belt [16]. They are made of an assemblage of Proterozoic and Early Paleozoic metamorphic rocks of various origins: Sediments, granites, mafic, and ultramafic slivers, intruded by syn- and post-orogenic granites and overlain by late Carboniferous late- and post-orogenic basins. In the Armorican massif, the most visible Variscan structures are major Devonian to Carboniferous strike-slip crustal structures like the South Armorican Shear zone [17]. In contrast, Variscan structures of the Central Massif and in the PB are mostly flat-lying, slightly folded lower crustal thrusts, except for some late Carboniferous strike-slip faults [18].
East of the AM and North of the CM, the ~400 km-wide, almost circular Paris Basin is a large intracratonic basin that developed between the Permian and the late Cenozoic [19,20]. Mesozoic sediments of the PB lie with an angular unconformity over Variscan structures of the AM and CM. To the East, these sediments are slightly tilted westwards, because of the Late Cenozoic uplift of the Vosges–Black Forest bulge [21]. The maximum thickness of Mesozoic and Paleozoic sediments is found near Paris and reaches approximately 3.5 km [20]. No major faults are visible at the surface in the PB, except the Bray–Vittel fault which is a reactivated Variscan structure (Figure 1).
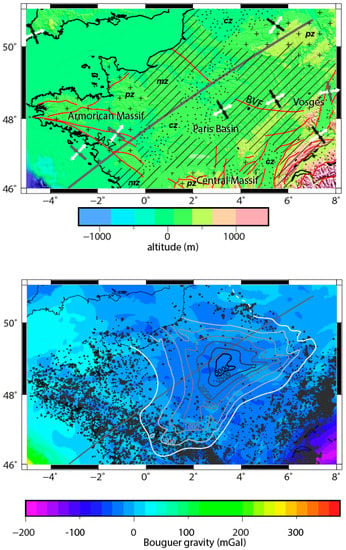
Figure 1.
Top: Topography, simplified geologic setting and main faults of the Armorican Massif and Paris Basin. Plus symbols, oblique lines, and dots indicate outcropping Palaeozoic basement (pz), and Mesozoic (mz) and Cenozoic (cz) sediments, respectively. Thick grey line corresponds to the modelled profile, and red lines indicate main faults: BVF = Bray–Vittel fault. SASZ = South Armorican Shear Zone. Horizontal stress directions (white = 3; gray = 2; black = 1) are after [24], [26] and [28]. Bottom: Bouguer gravity (Bureau Gravimétrique International Database), seismicity [23], and isopachs of the Paris Basin in meters (Bureau des Recherches Géologiques et Minières, Geological map of France scale 1:1,000,000). Solid line corresponds to the modelled profile.
Seismicity in the Armorican massif [22,23] has a diffuse character compared to interplate seismicity (Figure 1). Some earthquake epicentres seem to cluster close to major Variscan structures, but many others cannot be attributed to any identified fault trace. Seismicity is abundant in the southern part of the Armorican Massif and on the northern border of the Central Massif. Some earthquakes occur between these two areas, at the southern extremity of the Paris basin, suggesting that active structures of these two massifs somehow connect to each other beneath the Mesozoic sediments of the basin. There is a striking difference in the epicentre density distribution between the PB and the two crystalline massifs, with much less earthquakes in the PB. Moreover, the density of earthquakes decreases rapidly with the thickness of Mesozoic–Cenozoic sediments overlying the Variscan basement (Figure 2). The same pattern is observed further south in the Aquitaine basin [23].
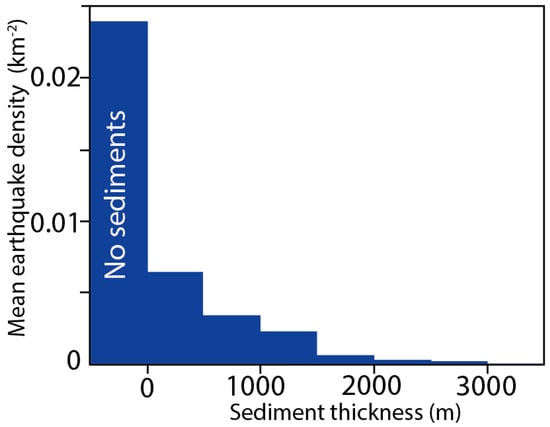
Figure 2.
Mean earthquake density (km−2) as a function of overlying Mesozoic and Cenozoic sediment thickness in the area corresponding to Figure 1. The left column corresponds to areas of outcropping basement, i.e., without sediments.
Focal depths available in the seismicity catalogue [23] are probably not well constrained, owing to the low magnitude of most seismic events (≤3.0). According to [24], most hypocentres in the AM and CM are located between 0 and 10 km, i.e., in the upper crust. Earthquake focal mechanisms depict mostly normal or normal-oblique faulting [25] and the resulting stress field shows a minimum extensional stress trending ~NE–SW in the AM and PB, while the stress regime varies from extensional in the AM to strike-slip in the PB (Figure 1) [24,26,27].
However, according to [28], in the CM and AM the relative magnitudes of σ1 and σ2 are similar so there is no large difference, in terms of stress magnitudes, between the two stress regimes. The Bouguer gravity anomaly is typical of a stable continental lithosphere in a passive margin setting, with moderately negative values in the continental domain (−60 to −80 mGal) increasing to strongly positive ones (>150 mGal) in the oceanic domain (SW). Some short-wavelength negative and positive Bouguer anomalies in the AM and PB probably reflect density variations in the crust [11] (Figure 1).
3. What Can Explain the Contrasted Seismicity Distribution between PB and AM?
The main physical parameters that can increase or decrease the abundance of seismicity in a given area are the geotherm; crustal composition; orientation and friction coefficient of inherited structures; magnitude of horizontal stresses; and bending stresses due to flexure, cohesion, and pore fluid pressure in the crust. In the PB, AM, and CM, potential sources of horizontal stress are the Pyrenees, the Alps, and the Atlantic mid-oceanic ridge [29]. As there is no major actively deforming boundary between the AM, PB, and CM, we assume that the lithospheric stress does not change much between these regions. Surface heat flow is rather low in the AM and in the northern part of the PB (40–70 mW·m−2) and increases to more than 110 mW·m−2 southwards, towards the CM [30]. Thus, there is no striking correlation between surface heat flow and the density of earthquakes.
Except for the presence or absence of Meso-Cenozoic sediments (mainly limestones, chalk, and sandstones), there is no reason either to suppose that the crustal composition or structure differs between the PB and the AM in a way that is sufficient to explain the large difference in seismicity distribution. On the other hand, the clear drop in earthquake density with the increasing thickness of sediments in the PB suggest that the latter play a role either directly or indirectly (i) by protecting underlying basement faults from alteration and subsequent development of low-friction gouge fault minerals; (ii) because basement faults are at larger temperatures (60–100 °C), hence more prone to re-crystallisation and healing beneath the basin than when they outcrop at the surface; or (iii) because the pile of consolidated and almost undeformed Meso-Cenozoic sediments act as a sticky patch on the more intensely fractured basement, increasing its effective cohesion and preventing it from failure.
4. Method
We computed the yield stress envelopes (YSE) and lithospheric flexure across a 1000 km-long SW–NE profile crossing the AM and PB approximately parallel to the direction of the minimum horizontal stress, i.e., parallel to the extension direction [27]. Surface heat flow data along the profile were extracted from an interpolated grid of heat flow measurements [30]. Temperatures on the left part of the profile, in the offshore domain, were extrapolated since we do not have surface heat flow measurements.
The 2D geotherm along the profile was computed using the steady-state heat equation and assuming only vertical heat conduction (Figure 3):
with k the thermal conductivity (assumed constant), hr the characteristic depth of radiogenic heat production in the crust, and P0(x) = hrρH0(x) is the surface heat flux coming from radiogenic heat production in the crust (see Table 1 for values and units). We assume that the heat flux coming from the mantle (Qm) at the base of the crust is constant, so we can estimate the variation of the heat production from the surface heat flux Q0:

Figure 3.
2D temperature model (in °C) from surface heat flow data along the profile [30].

Table 1.
List of parameters used in this study and their corresponding units and values.
4.1. Brittle Domains
The transition from elastic to brittle behaviour obeys the Mohr–Coulomb rupture criterion:
where τ is the tangential stress on a given plane, σn is the normal stress, μ is the friction coefficient and C0 is the cohesion. If we consider a medium with no weak faults, the friction coefficient is ~0.6 [31]. We also tested a friction coefficient of 0.3 in the crust, which simulates the presence of weaker faults. The differential brittle yielding stress σ1-σ3 is computed using the Mohr circle construction, such as
with the angle between the normal to the potential slip plane and σ1. For a compressional stress regime, σ3 is vertical and equal to the overburden pressure, whereas for an extensional stress regime σ1 equals the overburden pressure. Pore fluid pressure favours brittle deformation by reducing the normal stress applied to the slip plane. We assume two end-member cases with either a dry crust (i.e., with no fluid pressure) or a “wet” crust with hydrostatic fluid pressure. We do not consider overpressured fluids the AM as there is no cap-rock lying upon basement aquifers that could help building-up fluid overpressure. We also consider a wet crust (i.e., hydrostatic fluid pressure) in the PB as, even if most aquifers are contained within the sedimentary layers, it is unlikely that the basement is completely dry.
4.2. Ductile Domains
The transition from elastic to ductile behaviour is computed using a temperature and stress-dependent dislocation creep power law:
where is the strain rate (assumed constant and equal to 1e−17s−1), n is a power law exponent, H is the creep activation energy, R is the gas constant, σ1-σ3 is the differential yielding stress, and T is the temperature in Kelvins (Table 1). We used a dry olivine rheology for the upper mantle, and either diorite or diabase rheologies for the crust [32,33]. The YSE is the contour of the minimum yielding stress, i.e., the differential stress which conditions the transition between elastic and either brittle or ductile behaviours at each depth. It is then used to compute the effective elastic thickness (EET) of the lithosphere.
4.3. Effective Elastic Thickness and Flexure
We consider as pertaining to elastic crust and mantle lids the domains where the yielding stress (either in ductile or brittle domains) is larger than a threshold of 20 MPa [34]. If the crust and mantle are mechanically coupled (i.e., there is no weak ductile lower crust), EET is simply the sum of the crust and mantle elastic layer thicknesses, hcrust and hmantle, respectively. If there is a mechanical decoupling between the upper crust and upper mantle, then
The effective elastic thickness is then used to compute the flexural rigidity D and solve the 1D flexure equation using a 1D finite element model:
where E and ν are Young’s modulus and Poisson ratio, ρm and ρf are the mantle and infill (water offshore and air onshore) densities, w is the plate deflection, and q is the vertical load applied to the plate. The latter comprises both the present-day positive topography load and possible additional forces due either to dynamic processes in the mantle, erosion at the surface, or to buried loads in the lithosphere. Plate deflection cause bending stresses σb that modify the thickness of the elastic layers, hence the effective elastic thickness. In addition, horizontal stresses σh applied to the lithosphere also alter the YSE and modify EET [34]. The resulting differential stress resolved on the lithosphere is σd = min(|YSE|, |σh + σb|). We iteratively compute EET and w until the model converges towards a stable solution, while imposing null deflection at both plate extremities. The Moho deflection is then used to compute a synthetic Bouguer gravity anomaly (assuming a crustal density ρc), which is then corrected for the sediment infill of the PB and compared to Bouguer gravity data.
5. Results
Whatever the chosen crustal composition, we find that flexural models slightly better fit Bouguer gravity data if we apply two vertical loads (positive downward), at x = 400 km and x = 750 km, with magnitudes ranging between −3 and −2.1012, and between 4 and 6.1012 N·m−2, respectively, depending on the chosen crustal composition (Figure 4 and Figure 5). The first load could correspond to isostatic uplift of the AM in response to erosion or post-glacial adjustment, which has already been suggested as a possible source of stresses in the AM [3]. The second one might correspond to a buried load beneath the deepest part of the sedimentary basin, which may explain why this basin experienced subsidence. A positive value of 5.1012 N·m−2 corresponds for example to a positive density perturbation of 100 kg·m−3 on a 1 km × 1 km × 5 km crustal block. In the following models, we keep these loads in order to insure a good fit to gravity data (see Discussion). Moreover, as bending stresses due to flexure modify the yield stress envelopes, it is important to test whether these additional loads, although small, could explain the seismogenic behaviour of the AM and PB.
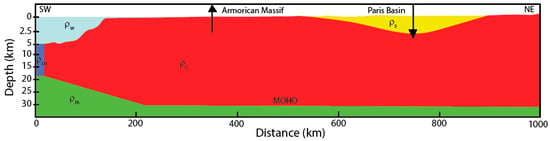
Figure 4.
Crust geometry, densities and forces used to compute plate deflection and the synthetic Bouguer gravity on the selected profile (see Table 1 for details).
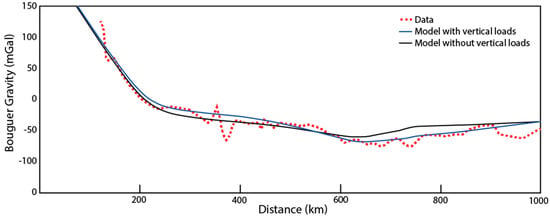
Figure 5.
Observed (open red dots) and modelled (solid lines) Bouguer gravity along the profile for a model without additional line loads (i.e., with only elastic compensation of the topographic load, in black) and with line loads applied at km 400 and 750 (in blue).
Flexural models with a strong continental crust (dry diabase), a friction coefficient of 0.6, a cohesion of 10 MPa, and no horizontal stresses predict that the continental crust behaves elastically along the largest part of the profile, except in places where bending stresses are large enough to reach the yielding stress of the ductile lower crust. The elastic cores of the crust and upper mantle are coupled except around the points where bending stresses are the highest, which causes drastic drops in EET from > 80 km (coupled case) to 25 km (decoupled case) along the profile (Figure 6). In this first model, differential stresses are much too low to cause any permanent deformation in the lithosphere.
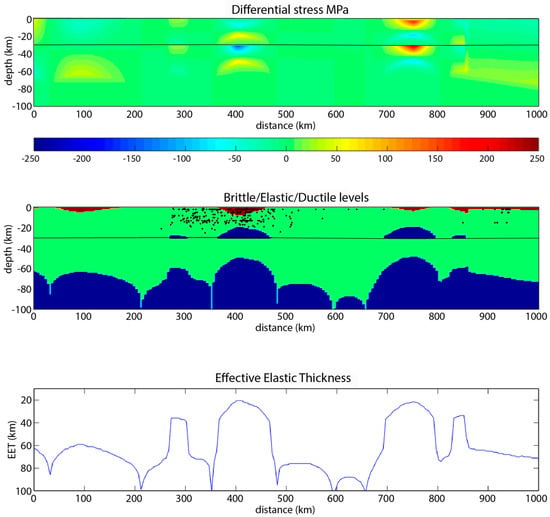
Figure 6.
Model with a diabase crustal composition and no horizontal extensional stress. Top = differential stress (bending stresses due to the topographic load and applied vertical forces); Middle = predicted brittle (brown), elastic (green), or ductile (blue) areas. Solid dots are projected earthquake hypocentres on a 30 km wide swath. Bottom = computed effective elastic thickness along the profile (increasing downwards). Left side corresponds to the SW extremity of the profile. Thin solid line indicates the Moho.
If a horizontal extensional stress of 150 MPa is added, all the uppermost crust falls in the brittle field and there is no striking difference between the rheological layering of the AM and PB (Figure 7). Compared to the previous test, in this case the elastic crustal and mechanical layers are always mechanically decoupled, so that EET varies between 20 km and 35 km.
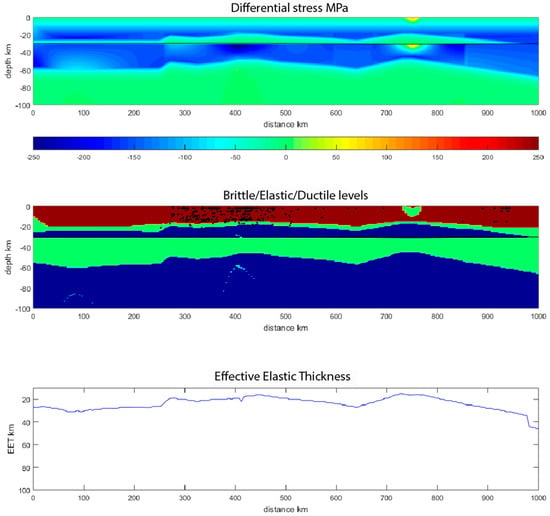
Figure 7.
Same legend as Figure 6 but with a horizontal extensional stress of 150 MPa.
If we use a weaker crust rheology (diorite) with a hydrostatic pore fluid pressure and a reduced friction coefficient of 0.3, we obtain results that are not satisfying: Without horizontal extension, there is only a very thin (0–3 km) and discontinuous brittle crustal layer, then a ~10 km-thick elastic lid, below which the crust behaves as a weak ~20 km-thick ductile layer. The EET varies between 20 and 30 km, with some higher peaks where plate curvature is null (Figure 8). The extremely thin (or inexistent) brittle crust and the thick ductile lower crust predicted by this model are difficult to reconcile with the abundance of earthquakes in the AM. Moreover, there is still no visible difference in the mechanical behaviour of the crust between the AM and the PB.
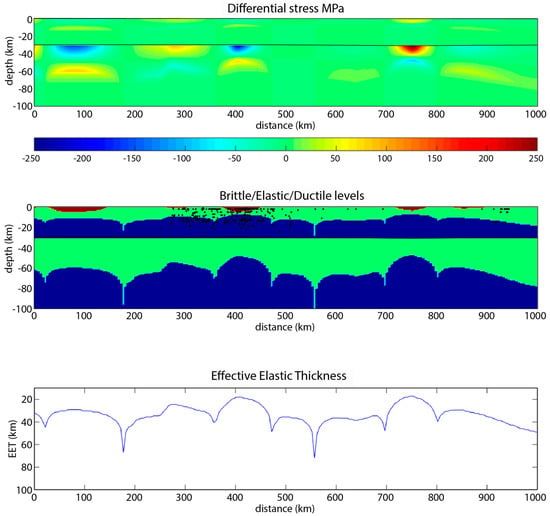
Figure 8.
Model with a diorite crustal composition and no horizontal extensional stress. Same legend as Figure 6.
For the same crustal rheology and with a low horizontal extensional stress of 50 MPa, a thicker and more continuous part of the uppermost crust (~10 km) falls in the brittle field, the crustal elastic lid is reduced to less than 2 km, and the rest of the crust is weak and ductile. Moreover, here again there is no difference of crustal mechanical behaviour between the AM and the PB (Figure 9).
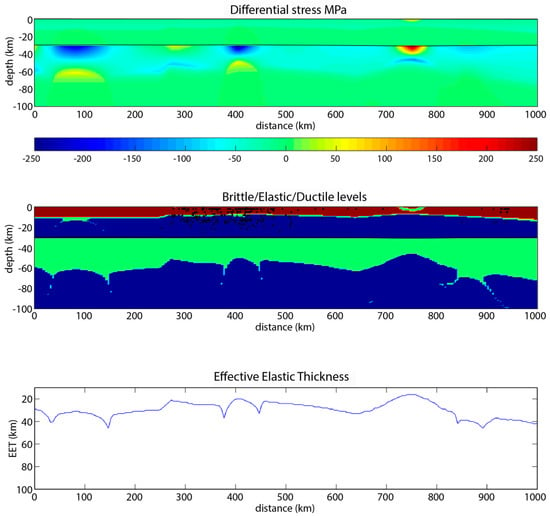
Figure 9.
Same legend as Figure 8 but with a horizontal extensional stress of 50 MPa.
This first set of models evidence that if we keep a constant crustal rheology along the profile, neither bending stresses nor heat flow variations can explain the contrasted seismogenic behaviour between the AM and PB. We then consider two different crustal domains. Multiple tests allow us to determine that, overall, a “strong” crust composition (diabase) better suits than a weak (diorite) one for the whole profile. In a next series of models, we test the possibility of a different friction coefficient and/or a different cohesion between the left part of the profile (from 0 to 540 km), which corresponds to the Armorican Massif domain, and the right part of the profile, corresponding to the Paris Basin. We keep a constant horizontal extensional stress of 100 MPa and a hydrostatic fluid pressure for the whole profile. Varying the friction coefficient allows us to simulate the effect of different material properties in the crust (due to variable alteration or recrystallization of inherited fractures for instance), whereas the cohesion is modified in order to simulate the presence or absence of a sticky patch of consolidated sediments overlying the basement.
In the model with two different friction coefficients of 0.3 and 0.7 for the AM and PB, respectively, the thickness of the brittle crust decreases from ~20–25 to 10–12 km between the left and right parts of the profile (Figure 10). In the right part of the profile (corresponding to the PB) the elastic crust is much thicker than on the left part (>20 km) but the brittle crust is thick enough to be the locus of numerous shallow earthquakes, which is not consistent with observations. As the crust and mantle are always decoupled, the EET varies between 20 and 40 km. Finally, if we assume a change in cohesion (10 to 80 MPa) between the left and right parts of the profile without changing the friction coefficient (0.6), we can adequately reduce the brittle crustal thickness to 0–5 km and increase the thickness of the crustal elastic lid in the PB (Figure 11), while the AM crust is characterized by three approximately equal brittle, elastic and ductile layers. In this model, we obtain a large contrast in the thickness of the brittle crust between the AM and PB, which seems more consistent with earthquake distribution. The effective elastic thickness varies between 20 and 40 km and the crust and uppermost mantle are decoupled.
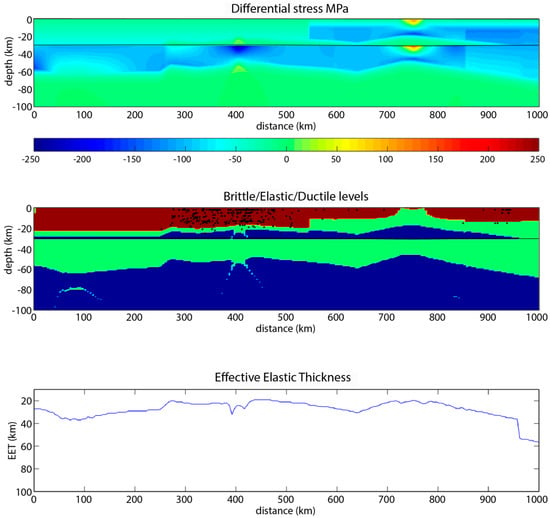
Figure 10.
Model with a diabase crust, an extensional stress of 100 MPa and two different domains: Hydrostatic fluid pressure and a friction coefficient of 0.3 up to km 540, and the same fluid pressure and a friction coefficient of 0.7 right of km 540 (cohesion is constant and equal to 10 MPa). Same legend as Figure 6.
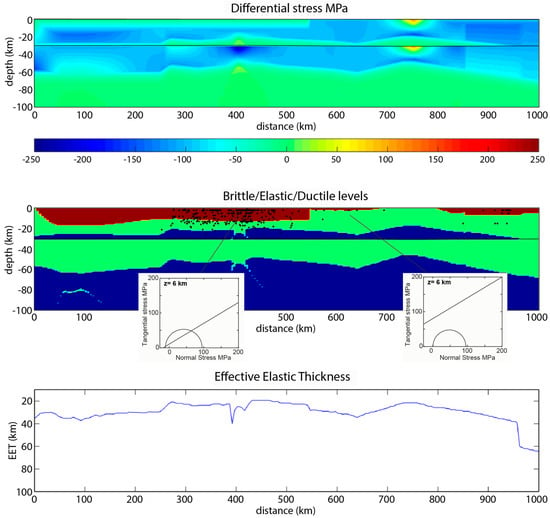
Figure 11.
Model with a diabase crust, an extensional stress of 100 MPa and two different domains: Hydrostatic fluid pressure and a cohesion of 10 MPa up to km 540, and the same fluid pressure but a cohesion of 80 MPa right of km 540 (friction coefficient is constant and equal to 0.6). Same legend as Figure 6. Insets show two Mohr diagrams corresponding to the AM and PB stresses at a depth of 6 km but with two different cohesions of 10 and 80 MPa, respectively.
6. Discussion and Conclusions
Our results evidence that whatever the chosen crustal composition, bending stresses and heat flow variations alone are not sufficient to explain the difference in seismogenic behaviour between the AM and the PB. Variations in friction coefficient between AM and PB, in the range of tested values (0.3 to 0.7, respectively) are not totally satisfying since they do not restrain the brittle crustal thickness in the PB to less than 10 km, which is still large enough to be the locus of shallow earthquakes. As a friction coefficient of 0.7 is in the upper range of values commonly inferred for intact crustal rocks, we doubt that a much larger (i.e., >0.8) value could realistically be used. In fact, a friction coefficient of 0.9 still increases the thickness of the elastic lid, but it does not sufficiently reduce the thickness of the brittle crust in the PB to explain the lack of earthquakes. Oppositely, increasing the cohesion from 10 to 80 MPa has a stronger effect of the thickness of the brittle upper crust, decreasing it from 10 to 15 km beneath the AM to less 0–5 km beneath the PB. A cohesion of 80 MPa is in the upper bound of expected values for strong, cohesive rocks [35]. Our results therefore suggest that the unfaulted Meso-Cenozoic sedimentary pile acts as a sticky layer holding together the faulted basement rocks of the PB. This is equivalent to an increase in cohesion (Figure 12). Mechanical coupling in the PB between basement rocks and the overlying sedimentary pile has already been proposed [36] and strengthens this interpretation.
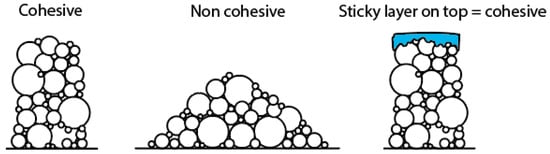
Figure 12.
Schematic interpretation of the “sticky layer” effect due to the presence of poorly fractured, consolidated sediments on the top of Variscan basement rocks in the PB.
Another outcome of our models is the use of negative and positive vertical loads on the central parts of the AM and PB, respectively. Since the fit to Bouguer gravity data is only slightly better with these line loads than without (Figure 5), we cannot claim that they are absolutely necessary. Flexural models with the same setting as Figure 11 but without line loads produce a large contrast in brittle crustal thickness between the AM and PB. Still, it was important to estimate the maximum magnitude of these vertical loads and our study suggests that they cannot be responsible for the contrasted seismicity distribution between the AM and PB. However, they can explain, for instance, (i) the long-term subsidence of the PB; (ii) the relative uplift of the AM [37]; and (iii) the supposed activity of the reverse Bray fault north of the PB [38].
Our thermal model with a constant heat conductivity could also be questioned, in particular because of the presence of low conductivity Triassic evaporites in the PB [20]. Indeed, temperatures computed with a thin (1 km) low-conductivity (0.5 W·m−1·K−1) layer are up to 100 K larger than in our model. As a result, ductile-elastic transitions in the crust and mantle beneath the PB are uplifted by 7 and 9 km, respectively. However, this thermal blanketing has no effect on the depth of brittle-elastic transitions, which is not temperature dependent, hence on the brittle behaviour of the crust.
Unlike in previously published studies [39,40], we cannot use here the depth distribution of earthquakes to better constrain the crust rheology. Due to the low magnitude of events and relative looseness of the seismic network, we can only assume that most earthquakes are contained within the first ~10–15 km of the crust.
The differences in the seismic behaviours between the AM and the PB come from the pile of the sedimentary layers on top of the PB. We here show that these sediments may act as a sticky patch, which is equivalent to an increase in cohesion. This strength increase prevents the occurrence of seismicity as long as there are no stress perturbations. However, it does not mean that the fault state is far from failure. Indeed, transient perturbations of local stress, fault strength, or fluid pressure may generate earthquakes in those area [41], as seen in, e.g., the Oklahoma state where a small fluid pressure increase lead to large earthquakes and cascading seismicity [42].
Author Contributions
Methodology, C.P.; writing—original draft preparation, C.P.; writing—review and editing, L.d.B., G.D. and Y.M.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to two anonymous reviewers for their comments on the first version of this manuscript, and to Anthony Mémin for his support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kenner, S.J.; Segall, P. A mechanical model for intraplate earthquakes: Application to the new madrid seismic zone. Science 2000, 289, 2329–2333. [Google Scholar] [CrossRef] [PubMed]
- Baird, A.F.; Mckinnon, S.D.; Godin, L. Stress channelling and partitioning of seismicity in the Charlevoix seismic zone, Quebec, Canada. Geophys. J. Int. 2009, 179, 559–568. [Google Scholar] [CrossRef]
- Van Vliet-Lanoe, B.; Bonnet, S.; Hallegouet, B.; Laurent, M. Neotectonic and seismic activity in the Armorican and Cornubian massifs: Regional stress field with glacio-isostatic influence? J. Geodyn. 1997, 24, 219–239. [Google Scholar] [CrossRef]
- Lamontagne, M.; Ranalli, G. Thermal and rheological constraints on the ea distribution in the Charlevoix, Canada, intraplate seismic zone. Tectonophysics 1996, 257, 55–69. [Google Scholar] [CrossRef]
- Liu, L.; Zoback, M.D. Lithospheric strength and intraplate seismicity in the New Madrid seismic zone. Tectonophysics 1997, 16, 585–595. [Google Scholar] [CrossRef]
- Audin, L.; Avouac, J.; Flouzat, M.; Plantet, J. Fluid-driven seismicity in a stable tectonic context: The Remiremont fault zone, Vosges, France. Geophys. Res. Lett. 2002, 29, 2–5. [Google Scholar] [CrossRef]
- Newman, A.V.; Stein, S.; Newman, A.; Stein, S.; Weber, J.; Engeln, J.; Mao, A.; Dixon, T. Slow deformation and lower seismic hazard at the new madrid seismic zone. Science 1999, 284, 619–621. [Google Scholar] [CrossRef]
- Tuttle, M.P.; Schweig, E.S.; Sims, J.D.; Lafferty, R.H.; Wolf, L.W.; Haynes, M.L. The Earthquake Potential of the New Madrid Seismic Zone. Bull. Seismol. Soc. Am. 2002, 92, 2080–2089. [Google Scholar] [CrossRef]
- Lambert, A.; Kurt, R.D.; Bower, D.R.; Anglin, F.M. Twelve years of geophysical research in the Charlevoix seismic zone. Tectonophysics 1988, 156, 193–224. [Google Scholar]
- Mazabraud, Y.; Béthoux, N.; Delouis, B. Is earthquake activity along the French Atlantic margin favoured by local rheological contrasts? C. R. Geosci. 2013, 345, 373–382. [Google Scholar] [CrossRef]
- Mazabraud, Y.; Bethoux, N. Characterisation of the seismological pattern in a slowly deforming intraplate region: Central and western France. Tectonophysics 2005, 409, 175–192. [Google Scholar] [CrossRef]
- Nocquet, J.-M.; Calais, E.; Altamimi, Z.; Sillard, P.; Boucher, C. Intraplate deformation in Western Europe deduced from an analysis of the International Terrestrial Reference Frame 1997 ITRF97 velocity field Intraplate deformation in western Europe deduced from an analysis of the International Terrestrial Reference. J. Geophys. Res. Atmos. 2001, 1997, 11239–11258. [Google Scholar] [CrossRef]
- Braile, L.W.; Keller, G.R.; Hinze, W.J.; Lidiak, E.G. An ancient rift complex and its relation to contemporary seismicity in the New Madrid Seismic Zone. Tectonics 1982, 1, 225–237. [Google Scholar] [CrossRef]
- Hildenbrand, T.G.; Hendricks, J.D. Geophysical Setting of the Reelfoot Rift and Relations Between Rift Structures and the New Madrid Seismic Zone; U.S. geological survey professional paper, United States Government Printing Office: Washington, WA, USA, 1995. [Google Scholar]
- Perrot, J.; Arroucau, P.; Guilbert, J.; Mazabraud, Y.; Rolet, J.; Mocquet, A.; Mousseau, M.; Matias, L. Analysis of the Mw 4.3 Lorient earthquake sequence: A multidisciplinary approach to the geodynamics of the Armorican Massif, westernmost France. Geophys. J. Int. 2005, 162, 935–950. [Google Scholar] [CrossRef]
- Matte, P. Accretionary history and crustal evolution of the Variscan belt in Western Europe. Tectonophysics 1991, 196, 309–337. [Google Scholar] [CrossRef]
- Berthé, D.; Choukroune, P.; Jegouzo, P. Orthogneiss, mylonite and non coaxial deformation of granites: The example of the South Armorican Shear Zone. J. Struct. Geol. 1979, 1, 31–42. [Google Scholar] [CrossRef]
- Burg, J.P.; Leyreloup, A.; Marchand, J.; Matte, P. Inverted metamorphic zonation and large-scale thrusting in the Variscan Belt: An example in the French Massif Central. Geol. Soc. Lond. Spec. Publ. 1984, 14, 47–61. [Google Scholar] [CrossRef]
- Brunet, M.-F.; Le Pichon, X. Subsidence of the Paris Basin. J. Geophys. Res. 1982, 87, 8547–8560. [Google Scholar] [CrossRef]
- Guillocheau, F.; Robin, C.; Allemand, P.; Bourquin, S.; Brault, N.; Dromart, G.; Friedenberg, R.; Garcia, J.; Gaulier, J.; Gaumet, F.; et al. Meso-Cenozoic geodynamic evolution of the Paris Basin: 3D stratigraphic constraints. Geodin. Acta 2000, 13, 189–245. [Google Scholar] [CrossRef]
- Ziegler, P.A.; Dèzes, P. Cenozoic uplift of variscan massifs in the alpine foreland: Timing and controlling mechanisms. Glob Planet. Chang. 2007, 58, 237–269. [Google Scholar] [CrossRef]
- Cara, M.; Cansi, Y.; Schlupp, A. SI-Hex: A new catalogue of instrumental seismicity in metropolitan France. SI-Hex: A new catalogue of instrumental seismicity for metropolitan France. Bull. Soc. Geol. Fr. 2015, 186, 3–19. [Google Scholar] [CrossRef]
- Manchuel, K.; Traversa, P.; Baumont, D.; Cara, M.; Nayman, E.; Durouchoux, C. The French seismic CATalogue (FCAT-17). Bull. Earthq. Eng. 2018, 16, 2227–2251. [Google Scholar] [CrossRef]
- Amorèse, D.; Walker, A.; Lagarde, J.-L.; Santoire, J.-P.; Volant, P.; Font, M.; Amore, D.; Lecornu, M. New seismotectonic data from an intraplate region: Focal mechanisms in the Armorican Massif (northwestern France). Geophys. J. Int. 2000, 143, 837–846. [Google Scholar] [CrossRef]
- Cornet, F.H.; Burlet, D. Stress field determinations in France by hydraulic tests in boreholes. J. Geophys. Res. 1992, 97, 829–849. [Google Scholar] [CrossRef]
- Heidbach, O.; Custodio, S.; Kingdon, A.; Mariucci, M.T.; Montone, P.; Müller, B.; Pierdominici, S.; Rajabi, M.; Reinecker, J.; Reiter, K.; et al. Stress Map of the Mediterranean and Central Europe. GFZ Data Serv. 2016. [Google Scholar] [CrossRef]
- Mazabraud, Y.; Béthoux, N.; Guilbert, J.; Bellier, O. Evidence for short-scale stress field variations within intraplate central-western France. Geophys. J. Int. 2005, 160, 161–178. [Google Scholar] [CrossRef]
- Delouis, B.; Haessler, H.; Cisternas, A.; Rivera, L. Stress tensor determination in France and neighbouring regions. Tectonophysics 1993, 221, 413–437. [Google Scholar] [CrossRef]
- Rocher, M.; Cushing, M.; Lemeille, F.; Baize, S. Stress induced by the Mio-Pliocene Alpine collision in northern France. Bull. Soc. Geol. Fr. 2005, 176, 319–328. [Google Scholar] [CrossRef]
- Lucazeau, F.; Vasseur, G. Heat flow density data from France and surrounding margins. Tectonophysics 1989, 164, 251–258. [Google Scholar] [CrossRef]
- Byerlee, J. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Carter, L.; Tsenn, C. Flow properties of continental lithosphere. Tectonophysics 1987, 136, 27–63. [Google Scholar] [CrossRef]
- Kirby, S.H.; Kronenberg, A.K. Rheology of the lithosphere: Selected topics. Rev. Geophys. 1987, 25, 1219–1244. [Google Scholar] [CrossRef]
- Burov, E.B.; Diament, M. The effective elastic thickness (Te) of continental lithosphere: What does it really mean? J. Geophys. Res. 1995, 100, 3905–3927. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics, 2nd ed.; Wiley: New York, NY, USA, 1989; p. 562. [Google Scholar]
- Gunzburger, Y.; Magnenet, V. Tectonophysics stress inversion and basement-cover stress transmission across weak layers in the Paris basin, France. Tectonophysics 2014, 617, 44–57. [Google Scholar] [CrossRef]
- Bonnet, S.; Guillocheau, F.; Brun, J.P. Large-scale relief development related to quaternary tectonic uplift of a Proterozoic-Paleozoic basement: The Armorican Massif, France. J. Geophys. Res. 2000, 105, 19273–19288. [Google Scholar] [CrossRef]
- Baize, S.; Cushing, E.M.; Lemeille, F.; Jomard, H. Updated seismotectonic zoning scheme of Metropolitan France, with reference to geologic and seismotectonic data. Bull. Soc. Geol. Fr. 2013, 184, 225–259. [Google Scholar] [CrossRef]
- Albaric, J.; Déverchère, J.; Petit, C.; Perrot, J.; Le Gall, B. Crustal rheology and depth distribution of earthquakes: Insights from the central and southern East African Rift System. Tectonophysics 2009, 468, 28–41. [Google Scholar] [CrossRef]
- Déverchère, J.; Petit, C.; Gileva, N.; Radziminovitch, N.; Melnikova, V.; San’Kov, V. Depth distribution of earthquakes in the Baikal rift system and its implications for the rheology of the lithosphere. Geophys. J. Int. 2001, 146, 714–730. [Google Scholar] [CrossRef]
- Calais, E.; Camelbeeck, T.; Stein, S.; Liu, M.; Craig, T.J. A new paradigm for large earthquakes in stable continental plate interiors. Geophys. Res. Lett. 2016, 43, 10621–10637. [Google Scholar] [CrossRef]
- Schoenball, M.; Ellsworth, W. A systematic assessment of the spatiotemporal evolution of fault activation through induced seismicity in Oklahoma and Southern Kansas. J. Geophys. Res. Solid Earth 2017, 122, 189–206. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).