Constrained Full Waveform Inversion for Borehole Multicomponent Seismic Data
Abstract
1. Introduction
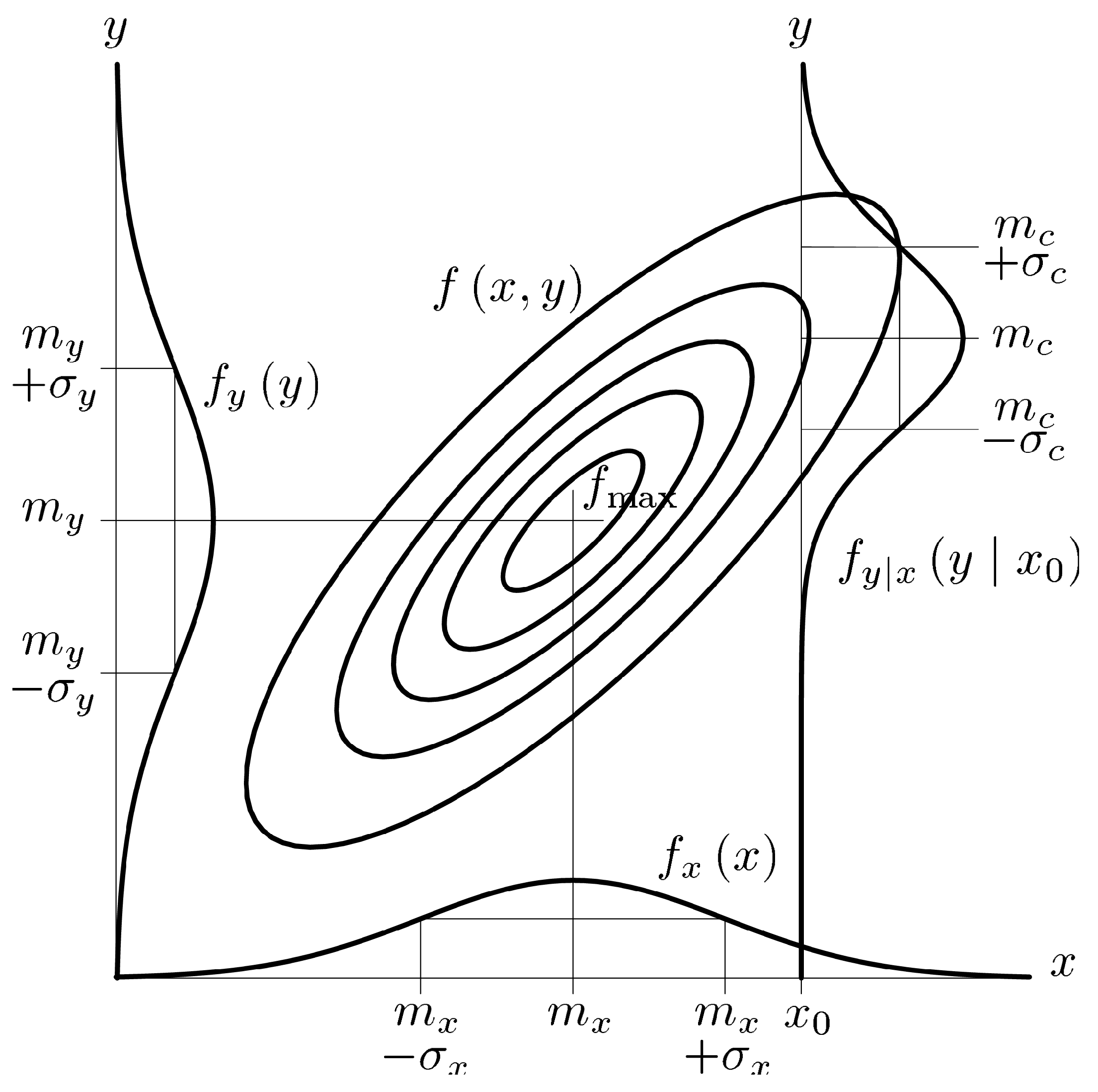
2. Constrained Least Squares Inversion
- is the perturbation in the vicinity of the current model ,
- are the data residuals for the model ,
- is the difference between the current model and the a priori model
- is the linear function tangent to at the model ,
- is the function mapping the model space into the data space
- is the covariance matrix on the data space.
- is the covariance matrix on the model space (defining the Gaussian a priori probability density).
3. Constraints on the Data Space
3.1. Cross-Correlations and Polarization
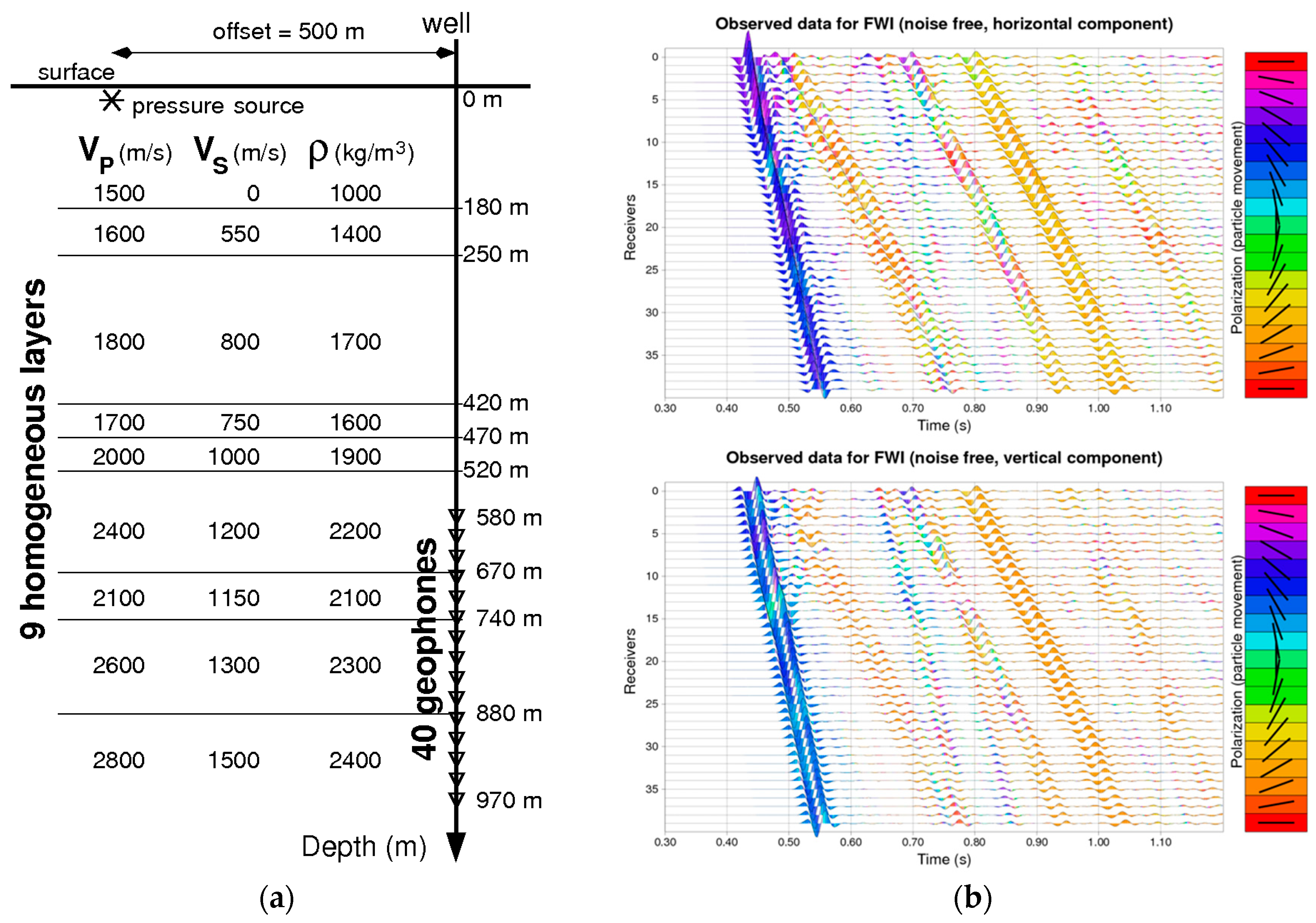
3.2. An Offset VSP Synthetic Example
4. Constraints on the Model Space
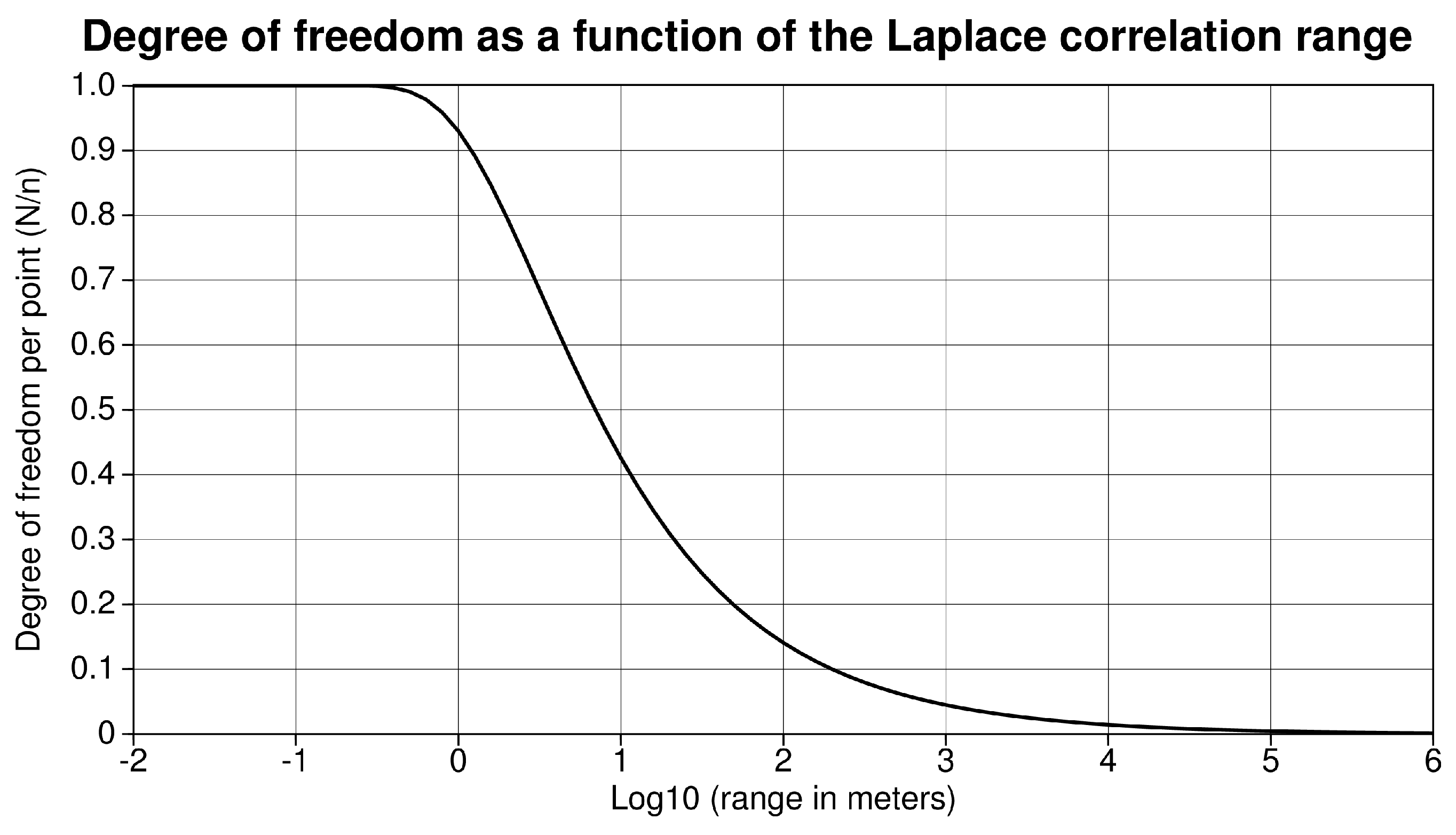
4.1. Quantification of Number of Degrees of Freedom
4.1.1. General Case
4.1.2. Spatial Correlation on the Model Space
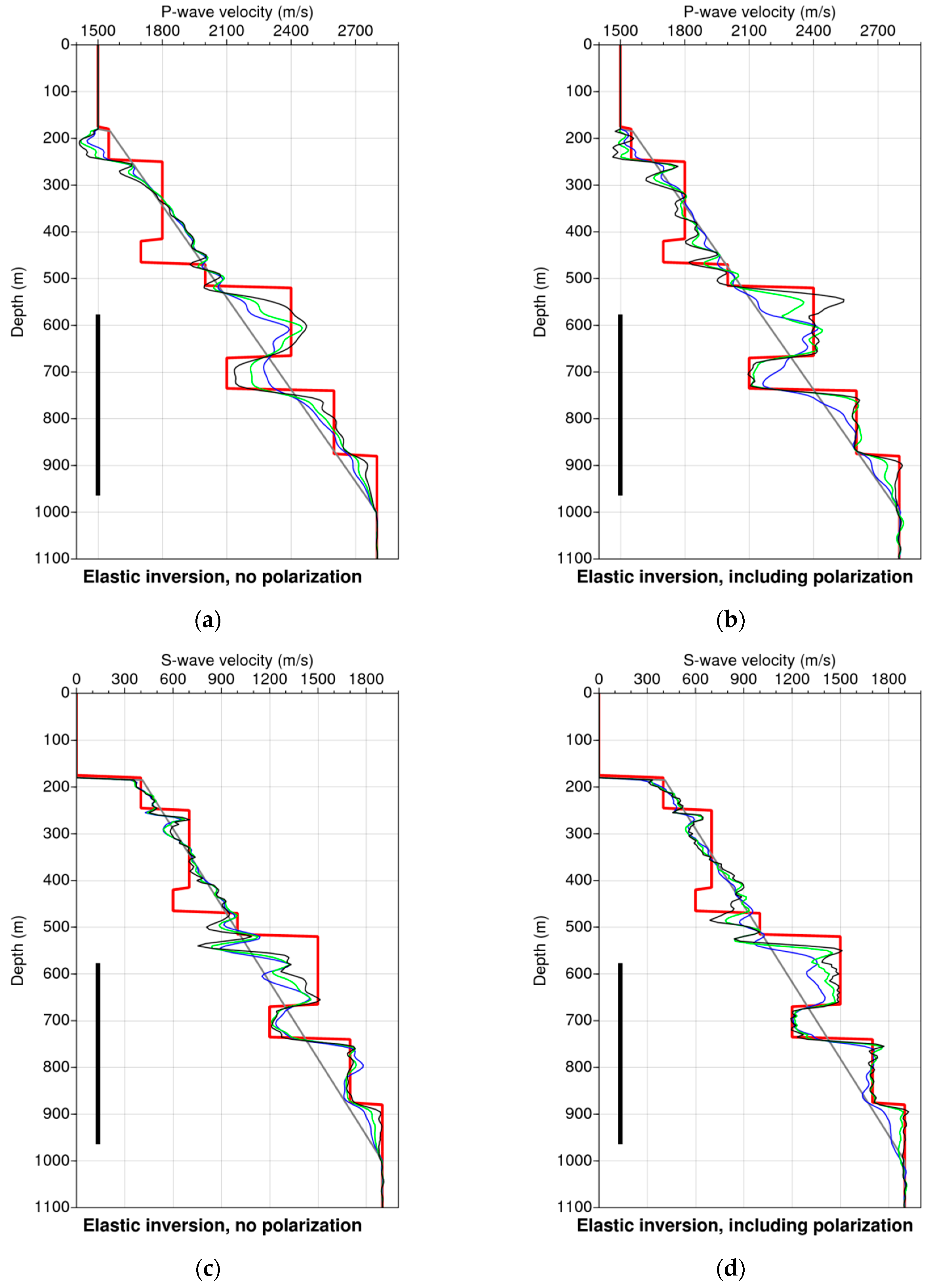
4.2. Seismic Crosswell Numerical Experiment Example
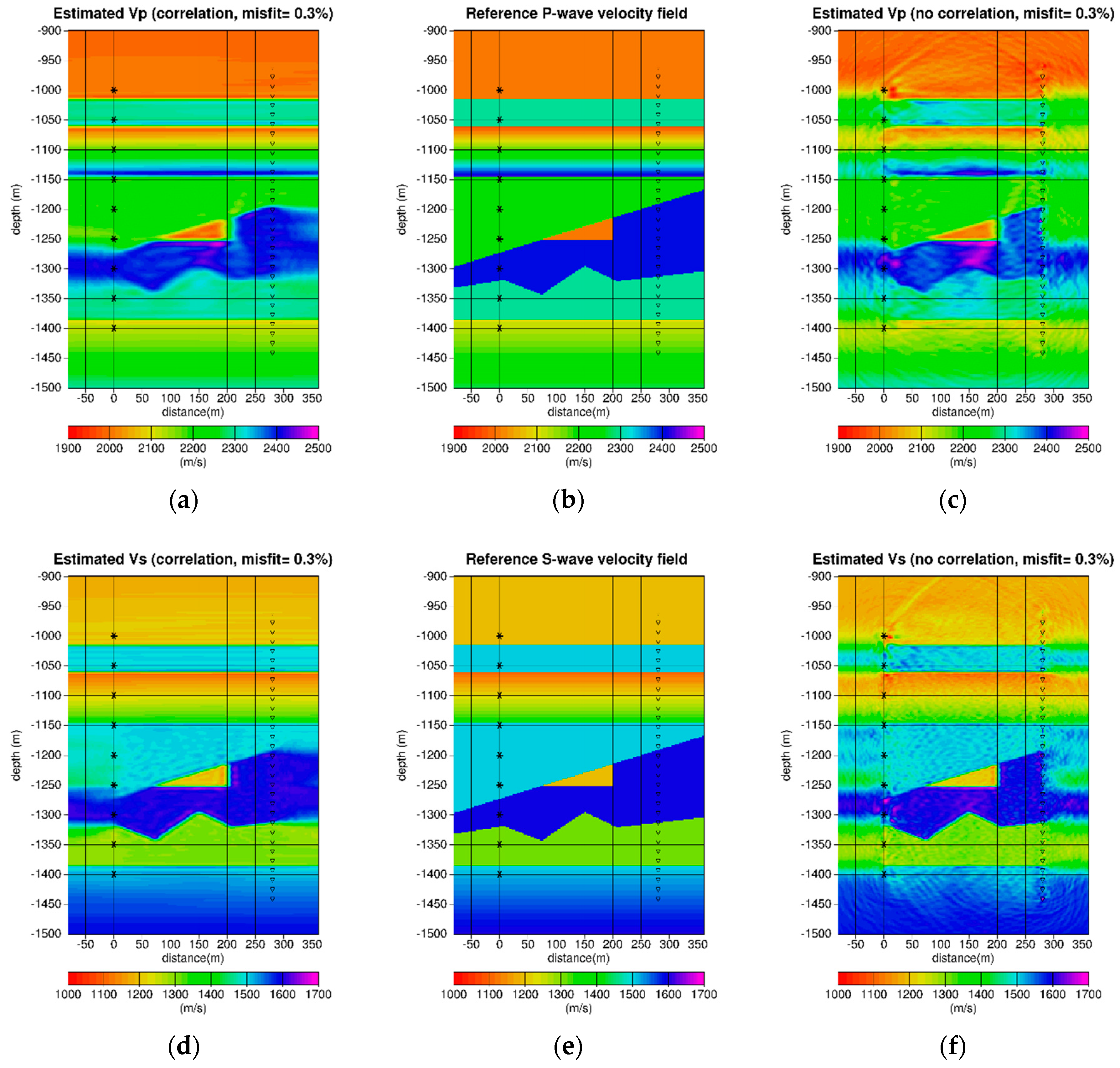
4.2.1. Description of the Crosswell Experiment and Observed Data
4.2.2. Multiscale Constrained Inversion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Generalities
Appendix A.2. Sequential Simulation
Appendix A.3. The Simulation Technique
Appendix A.4. Interpretation of the Decomposition of the Covariance Matrix
Appendix A.5. The Decomposition of the Correlation Matrix
Appendix B
References
- Virieux, J.; Operto, S. An overview of full waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Menke, W. Geophysical Data Analysis: Discrete Inverse Theory; Academic Press, Inc.: Orlando, FL, USA, 1984. [Google Scholar]
- Tarantola, A. Inverse Problem Theory: Methods for Data Fitting and Model Parameter Estimation: Discrete Inverse Theory; Elsevier Science Publ. Co., Inc.: New York, NY, USA, 1987. [Google Scholar]
- Tikhonov, A.; Arsenin, V. Solution of Ill-Posed Problems; Winston: Washington, DC, USA, 1977. [Google Scholar]
- Operto, S.; Virieux, J.; Dessa, X.; Pascal, G. Crustal imaging from multifold ocean bottom seismometers data by frequency-domain full-waveform tomography: Application to the eastern Nankai trough. J. Geophys. Res. 2006, 111, B09306. [Google Scholar] [CrossRef]
- Guitton, A.; Ayeni, G.; Gonzales, G. A preconditioning scheme for full waveform inversion. In SEG Technical Program Expanded Abstracts 2010; Society of Exploration Geophysicists: Tulsa, OK, USA, 2010; pp. 1008–1012. [Google Scholar] [CrossRef]
- Guitton, A. A blocky regularization scheme for full waveform inversion. In SEG Technical Program Expanded Abstracts 2011; Society of Exploration Geophysicists: Tulsa, OK, USA, 2011; pp. 2418–2422. [Google Scholar] [CrossRef]
- Abubakar, A.; Hu, W.; Habashy, T.M.; van den Berg, P.M. Application of the finite-difference contrast-source inversion algorithm to seismic full-waveform data. Geophysics 2009, 74, WCC47–WCC58. [Google Scholar] [CrossRef]
- Herrmann, F.J.; Erlangga, Y.A.; Lin, T.T.Y. Compressive simultaneous full-waveform simulation. Geophysics 2009, 74, A35–A40. [Google Scholar] [CrossRef]
- Loris, I.; Douma, H.; Nolet, G.; Daubechies, I.; Regone, C. Nonlinear regularization techniques for seismic tomography. J. Comput. Phys. 2010, 229, 890–905. [Google Scholar] [CrossRef]
- Asnaashari, A.; Brossier, R.; Garambois, S.; Audebert, F.; Thore, P.; Virieux, J. Regularized seismic Full-waveform inversion with prior model information. Geophysics 2013, 78, R25–R36. [Google Scholar] [CrossRef]
- Asnaashari, A.; Brossier, R.; Garambois, S.; Audebert, F.; Thore, P.; Virieux, J. Time-lapse seismic imaging using regularized full-waveform inversion with a prior model: Which strategy? Geophys. Prospect. 2015, 63, 78–98. [Google Scholar] [CrossRef]
- Polak, E.; Ribière, G. Note sur la convergence de directions conjuguée. Rev. Fr. Inform. Rech. Oper. 3e Année 1969, 16, 35–43. [Google Scholar]
- Crase, E. Robust Elastic Nonlinear Inversion of Seismic Waveform Data. Ph.D. Thesis, University of Houston, Houston, TX, USA, 1989. [Google Scholar]
- Jurkevics, A. Polarization analysis of the three component array data. Bull. Seismol. Soc. Am. 1988, 78, 1725–1743. [Google Scholar]
- Virieux, J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]
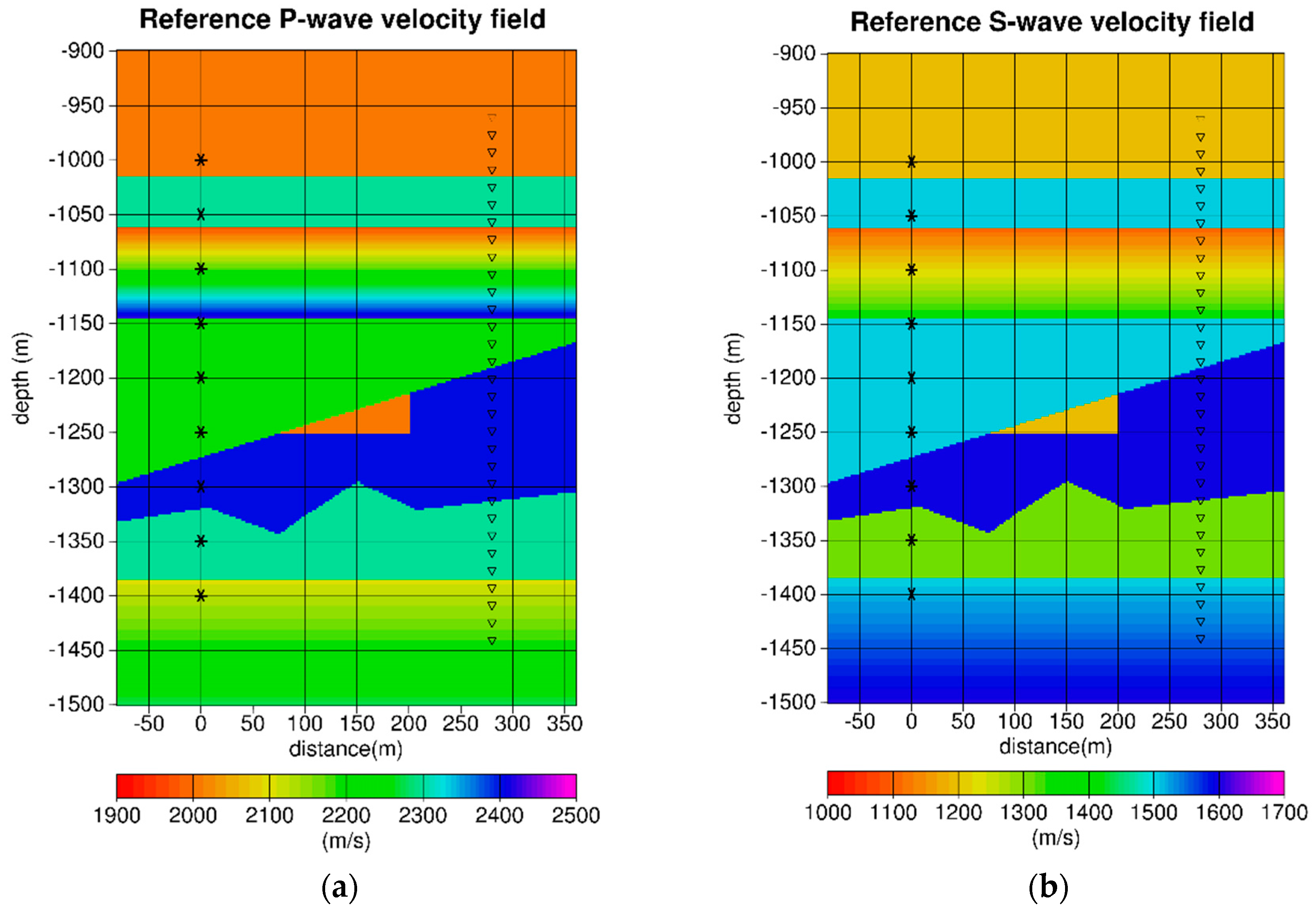
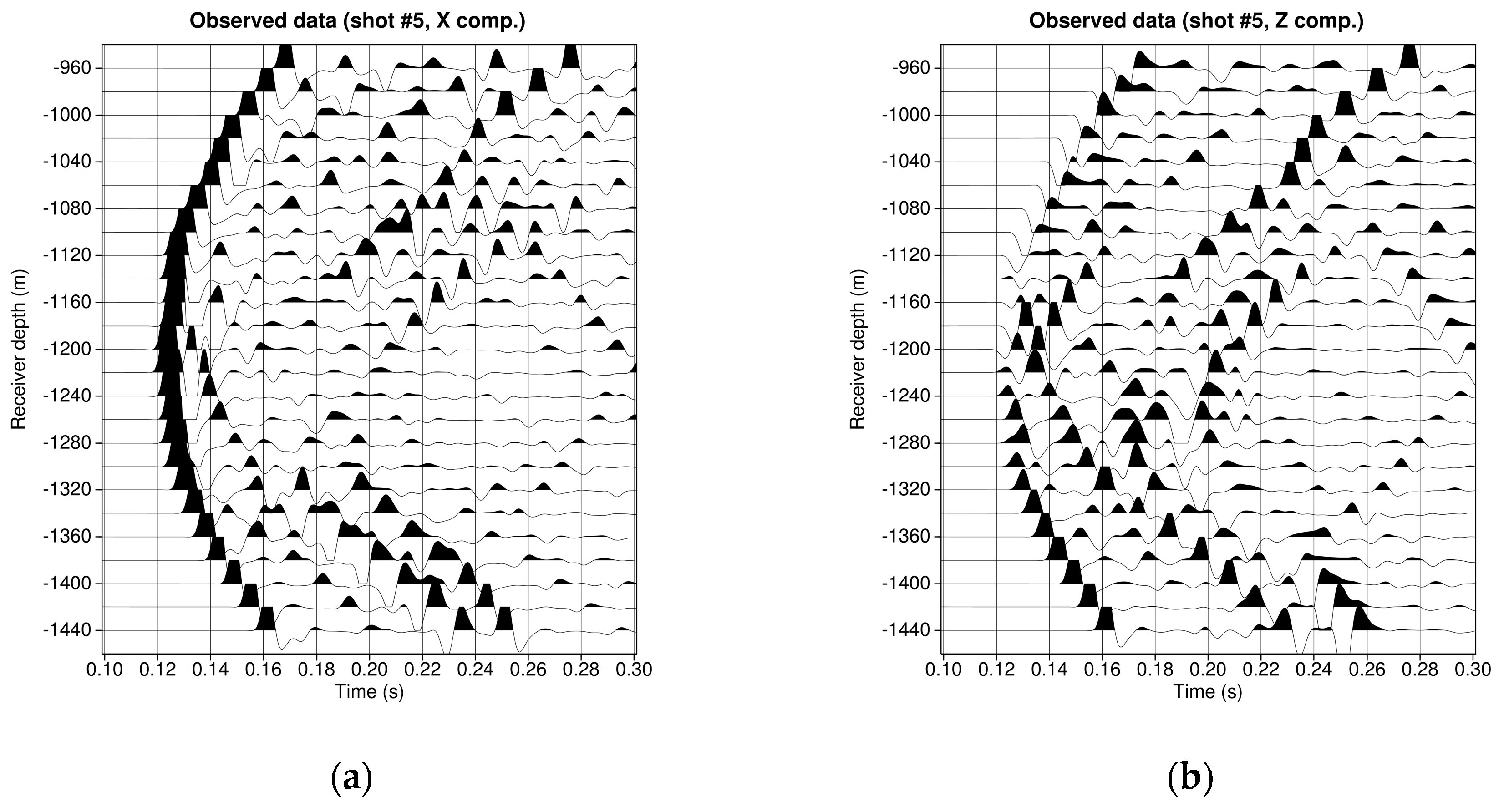
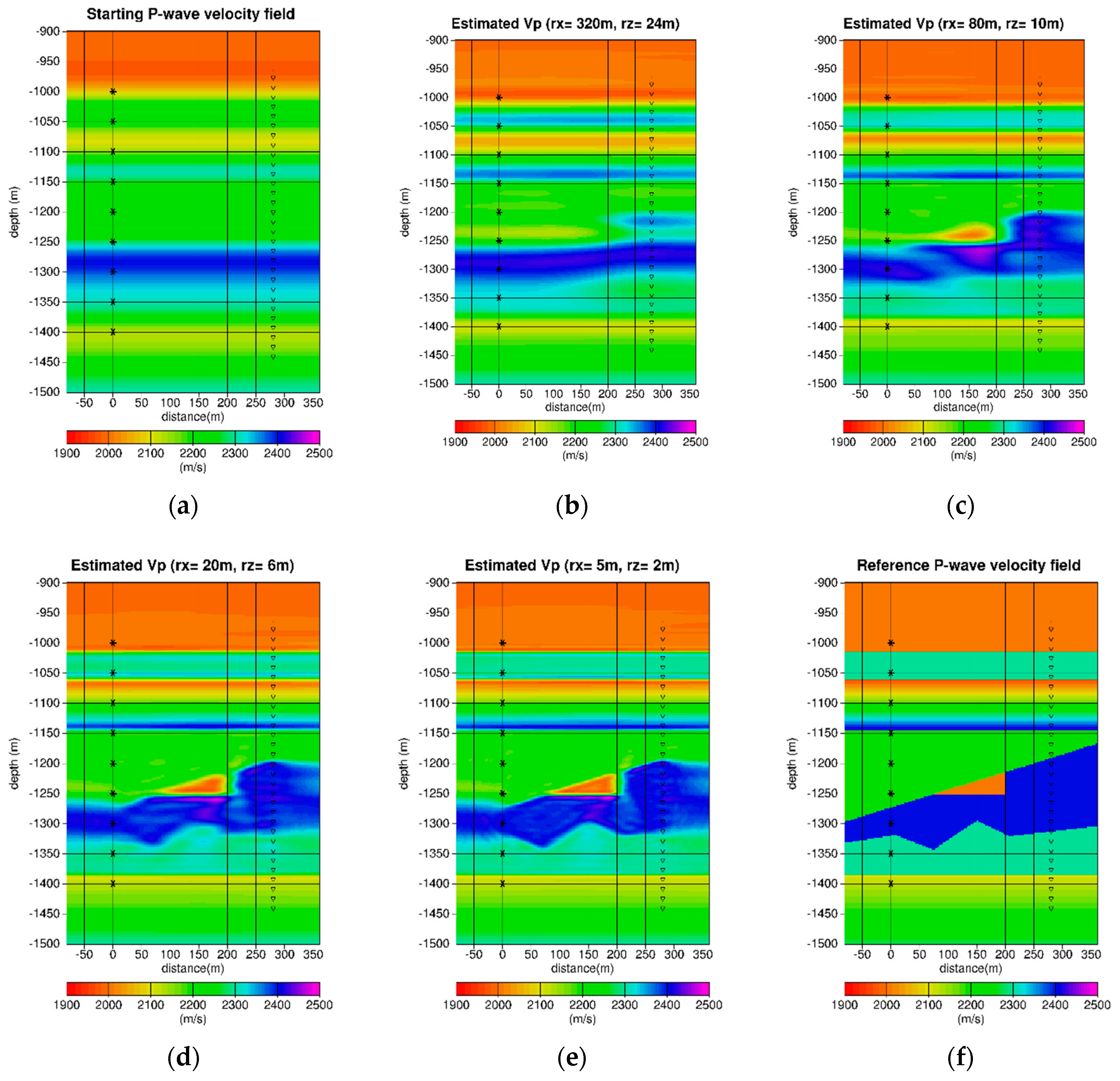
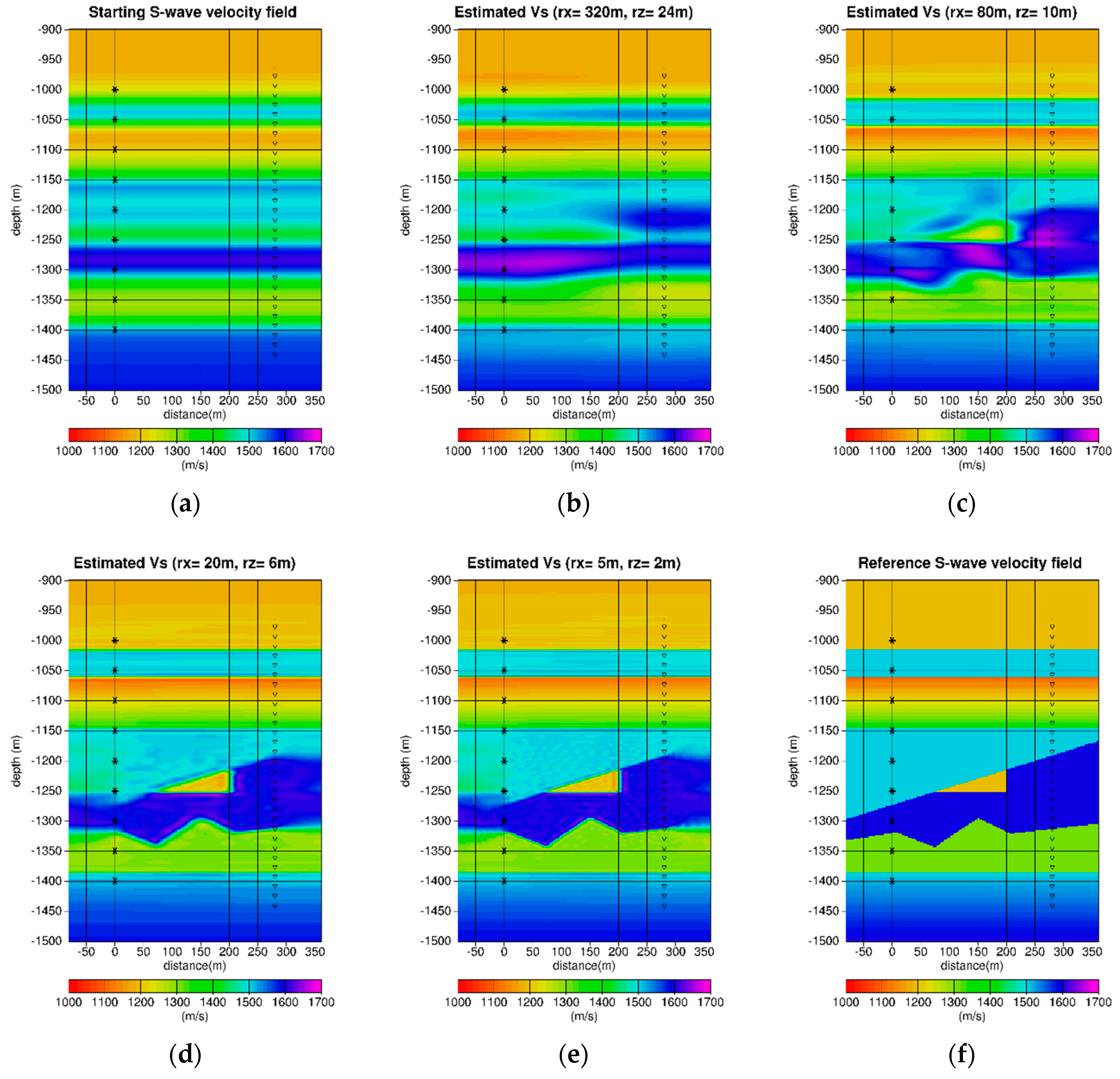
| Depth (m) | Region Type | Number of Vertical Points |
|---|---|---|
| 800–1120 | Quasi 1D | 161 |
| 1120–1180 | Transition | 29 |
| 1180–1340 | 2D | 81 |
| 1340–1400 | Transition | 29 |
| 1400–1600 | Quasi 1D | 101 |
| Region Type | Correlation Ranges (m) | Inversion Scale (b) | Inversion Scale (c) | Inversion Scale (d) | Inversion Scale (e) |
|---|---|---|---|---|---|
| Quasi 1D | (1000, 24) | (1000, 10) | (1000, 6) | (1000, 2) | |
| 2D | (320, 24) | (80, 10) | (20, 6) | (5, 2) |
| Inversion Parameters | Inversion Scale (b) | Inversion Scale (c) | Inversion Scale (d) | Inversion Scale (e) |
|---|---|---|---|---|
| Initial Misfit | 45.5% | 27.9% | 6.55% | 0.81% |
| Final Misfit | 27.9% | 6.55% | 0.81% | 0.14% |
| Iteration # | 30 | 30 | 50 | 50 |
| Region Type | Inversion Scale (b) | Inversion Scale (c) | Inversion Scale (d) | Inversion Scale (e) |
|---|---|---|---|---|
| Quasi 1D | 1919 | 2812 | 3416 | 4554 |
| Transition | 267 | 468 | 622 | 857 |
| 2D | 1022 | 2922 | 6792 | 15,725 |
| All | 3208 | 6202 | 10,830 | 21,136 |
| DoF/point | 2.8% | 5.5% | 9.6% | 18.8% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charara, M.; Barnes, C. Constrained Full Waveform Inversion for Borehole Multicomponent Seismic Data. Geosciences 2019, 9, 45. https://doi.org/10.3390/geosciences9010045
Charara M, Barnes C. Constrained Full Waveform Inversion for Borehole Multicomponent Seismic Data. Geosciences. 2019; 9(1):45. https://doi.org/10.3390/geosciences9010045
Chicago/Turabian StyleCharara, Marwan, and Christophe Barnes. 2019. "Constrained Full Waveform Inversion for Borehole Multicomponent Seismic Data" Geosciences 9, no. 1: 45. https://doi.org/10.3390/geosciences9010045
APA StyleCharara, M., & Barnes, C. (2019). Constrained Full Waveform Inversion for Borehole Multicomponent Seismic Data. Geosciences, 9(1), 45. https://doi.org/10.3390/geosciences9010045





