Abstract
Sparse spikes deconvolution is one of the oldest inverse problems, which is a stylized version of recovery in seismic imaging. The goal of sparse spike deconvolution is to recover an approximation of a given noisy measurement . Since the convolution destroys many low and high frequencies, this requires some prior information to regularize the inverse problem. In this paper, the authors continue to study the problem of searching for positions and amplitudes of the reflection coefficients of the medium (SP&ARCM). In previous research, the authors proposed a practical algorithm for solving the inverse problem of obtaining geological information from the seismic trace, which was named . In the current paper, the authors improved the method of the algorithm and applied it to the real (non-synthetic) data. Firstly, the authors considered the matrix approach and Differential Evolution approach to the SP&ARCM problem and showed that their efficiency is limited in the case. Secondly, the authors showed that the course to improve the lays in the direction of optimization with sequential regularization. The authors presented calculations for the accuracy of the for that case and experimental results of the convergence. The authors also considered different initialization parameters of the optimization process from the point of the acceleration of the convergence. Finally, the authors carried out successful approbation of the algorithm on synthetic and real data. Further practical development of the algorithm will be aimed at increasing the robustness of its operation, as well as in application in more complex models of real seismic data. The practical value of the research is to increase the resolving power of the wave field by reducing the contribution of interference, which gives new information for seismic-geological modeling.
1. Introduction
The amplitudes of the seismic trace vary depending on the effect of geological factors of the medium on the trajectory of the passage of elastic waves. The main aim of seismic exploration is to obtain geological properties of sub-surface from reflected seismic data. However, the possibilities of interpretation are limited by the finite frequency spectrum of the reflected seismic signal. The limitation of the frequency band leads to a non-zero time length of wavelets, which causes the interference of reflected signals. Thus, many techniques have been developed to remove the wavelet from reflected signals, to increase the resolution of seismic data.
The common way to increase the resolution of seismic data is spike deconvolution. It was developed in 1973 by Clearbout and Muir [1]; they proposed to use L1 minimization to recover reflectivity. The other way is sparse spectral inversion of reflected data with using matching pursuit (MP), orthogonal matching pursuit (OMP) or basis pursuit (BP) decomposition. The authors of research [2] used a spectral inversion algorithm to perform thin-bed reflectivity inversion. Zhang and Castagna [3] used BP to decompose a seismic trace into a superposition of reflectivity patterns observed from a well.
Yuan in [4] showed two types of different spectral sparse reflection spikes inversion methods, including stochastic spectral inversion based on global optimum algorithms, such as particle swarm optimization algorithm and an ant colony optimization algorithm. In addition, Yuan et al. [5] demonstrated a spectral sparse Bayesian inversion method that focused on showing that sparse spikes inversion can identify thin layers and recover the information outside the frequency band of seismic data.
The authors of this paper have already investigated inversion methods using optimization methods with regularization in the work of Krasnov et al. [6]. However, we found it necessary to explore other methods more carefully to find out areas of improvements and finally handle testing of A0 on the data of the real seismic field.
Let us consider the problem of identifying environmental factors that form a seismic trace. It should be remembered that, as a result of processing field measurements, many seismic traces are obtained with a coordinate reference to the surface. A separate seismic trace represents a vector of amplitudes. Such vector can be defined as , where N is vector dimension. Amplitude of the vector T shall be called amplitude of the seismic trace in -dimension. Dimension will be also called samples. Let us consider the formulation of the problem of searching for positions and amplitudes of the reflection coefficients of the medium (SP&ARCM) with the help of linear operators. For simplicity, suppose that the seismic trace is formed as a result of passing the model signal W through two separating planes (reflection planes) with reflection coefficients , with samples numbers , , respectively. The amplitude vector of such a seismic trace can be calculated by Equation (1):
According to book [7] by a model signal we mean a Ricker wavelet with a certain frequency f and a center in a sample number . The wavelet is also a vector of amplitudes and is defined in the same space as the seismic trace. The amplitude of the wavelet with center at in j-sample will be marked as . Then, Equation (1) for a seismic trace can be represented as a sum of amplitudes of wavelets with corresponding reflection coefficients (2):
An example of the graphical view of the seismic trace given by Equation (2) is shown in Figure 1.
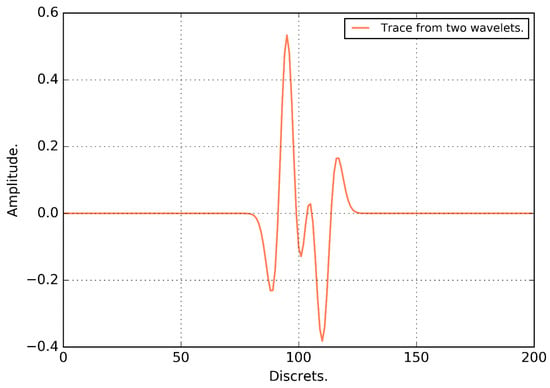
Figure 1.
Synthetic seismic trace.
In the general case with K reflecting coefficients, Equation (2) can be represented in form (3):
The expression in brackets of Equation (3) can be rewritten in matrix form. Then, the vector will be the result of the matrix product of the amplitude matrix , where on the vector of reflection coefficients , where Label (4):
We define for the matrix of amplitudes of wavelets and for the amplitude vector of the reflecting coefficients. Then, Equation (4) takes the form of the product of the matrix and the vector (5):
In this practical problem, we know the vector of the seismic trace T and matrix , but remains to be found. This problem has only one solution if matrix is not a singular.
Assertion 1.
The determinant of matrix for a model signal with the form of the Ricker wavelet when .
Assertion 1 can be proved with the help of numerical methods. The equation describing Ricker wavelet amplitude is provided in Label (6):
For Hz and wavelet frequency Hz, we calculate where for . Such interval change N corresponds to the most common durations of seismic traces from 1 to 4 s. Therefore, the matrix when will be singular and the rank of the matrix will always be less than its size N (Figure 2).
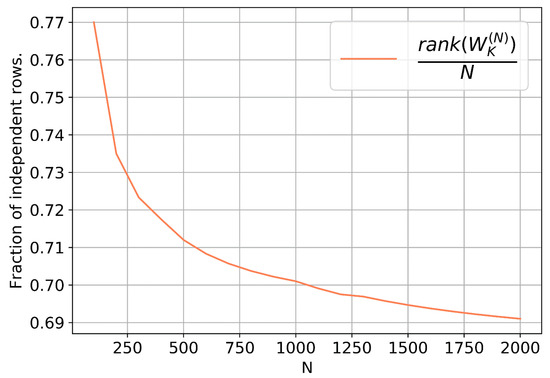
Figure 2.
Dependence of the proportion of linearly independent rows on the size of the matrix .
According to the initial conditions of the problem , or in other words, the number of reflecting planes in the path of the model signal is less than the dimension of the vector of the seismic trace. Thus, the dependence shown in Figure 2 reflects the upper limit on K.
Normally, there are significantly fewer reflections than samples are encountered in the signal path: condition is met.
Under the condition , the task of searching for positions and amplitudes of the reflection coefficients becomes invalid. In this formulation, this task of SP&ARCM has many solutions and introducing a criterion that will determine the best solution is required. Let us consider the approach to the solution of the SP&ARCM problem with the help of a search and successive approximations. One of the options for solving the problem of finding positions and amplitudes of reflection coefficients for a seismic trace T is to minimize the error function of a seismic trace reconstruction over a set of reflection coefficients and solving an optimization problem to find the minimum of the error function:
Let us consider variational optimization algorithms. To search through all the possible combinations N for K, it is required to first calculate variants, but since K is unknown, we need to consider for all the cases where k in . Therefore, the use of variational optimization algorithms in this case requires significant computing power. It should be noted that, in practice, not only is it necessary to process more than one route, but also the so-called cube of seismic trails containing on the average around traces.
Let us consider a slightly different formulation of the optimization problem. The error function is not necessarily convex and may have local minima. Therefore, it is advisable to use a class of optimization algorithms that allows for direct global optimization. One example of this class of optimization algorithms is the algorithm of “Differential Evolution” (DE) [8].
DE is a universal algorithm and at present there are several of its effective software implementations, with open source. The error function for optimization can be based on the calculation of the standard deviation (RMSE) reconstructed from the reflection coefficients of the trace and the original trace T.
For setting the boundary conditions for optimization, there are several options, depending on the strategy for finding the optimal number of positions and amplitudes of the reflection coefficients. For characteristic seismic lengths, the N vector T dimension will be 500–2000.
The computational complexity of the DE algorithm grows nonlinearly with increasing dimension of the optimized vector as [9]. Therefore, the problem of finding the minimum of the error function on the entire space of the seismic trace vector, as well as the variational optimization algorithms, can require considerable computing power. The vector of the variable X which DE uses to operate to solve the posed problem consists of K positions and K amplitudes of the reflection coefficients. Thus, the dimension of the vector is . For N, the range from 500 to 2000, taking into account the above-mentioned average upper limit above K, we get .
The estimation of the limiting accuracy of the DE in the problem under consideration can be made by means of a partial “looking into the future”. We can provide the value K for optimization which in fact we do not really know, thus simplifying optimization even before searching precisely for the K reflection coefficients. In this case, we can vary K from 1 to and relate to the error function obtained as a result of convergence. Figure 3 shows the dependence of the error of recovery of a seismic trace on the number of reflecting planes for such a simplified formulation of the problem.
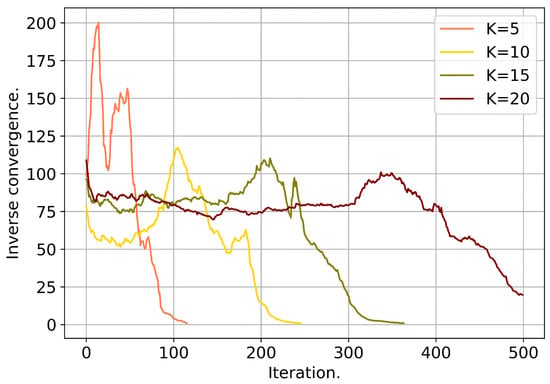
Figure 3.
Dependencies of inverse convergence for a seismic trace with for a different number of reflecting coefficients K.
Figure 4 shows the model trace, reflection coefficients and the reconstructed trace. The function is RMSE is used as the function . The error at this iteration is large enough to significantly affect the difference between model and reconstructed seismic traces.
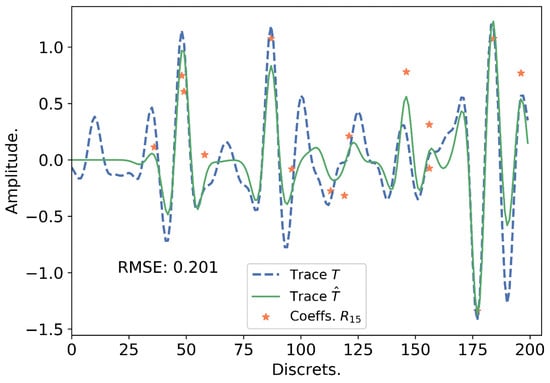
Figure 4.
Intermediate iteration of the DE for a seismic trace with .
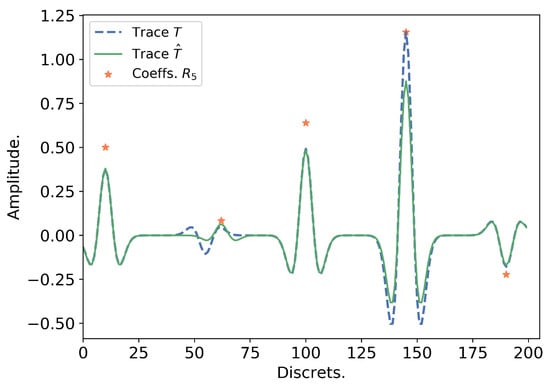
Figure 5.
Intermediate iteration of the DE for a seismic trace with .
While comparing Figure 4 and Figure 5, we can note that, for (Figure 5), there aren’t as many iterations remaining to perform the optimization and four out of five reflection coefficients are already at the desired positions and eventually only need selecting optimum amplitudes. The second (to the left) reflection coefficient is not yet in its place, and the first coefficient on the left already corresponds to the model coefficient both in position and amplitude. For (Figure 4), the optimization task looks much more complicated and requires many more iterations in order to complete it.
The stochastic nature of the DE algorithm allows us to solve a wide range of engineering problems, but has no connection with the physical processes from the subject domain considered in this article. The main physical limitations are the low density of the reflecting planes and the limitation on the values of the reflecting coefficients. A specific optimization algorithm that takes into account these physical constraints will benefit in speed from more universal optimization algorithms.
To use this advantage, we need to implement an algorithm that takes into account physical limitations for seismic traces in the process of minimizing the error functional. A rational approach will also be to use modern approaches to optimization from the field of machine learning. For example, we can use the adaptive step for a more accurate approach to a minimum or dropout some values of the vector for “popping out” from local minima. The optimization algorithm resulting from these developments is called by the authors.
2. What Is Special about the Algorithm
Let’s look at the equation of a seismic trace as a parametric distribution of amplitudes. With this approach, the trace T will always have N parameters :
where is the distribution function given by the parameters . Then, the task of the SP&ARCM is to find those featuring the distance between the distribution and T which is less than a certain predetermined value . Note that the function is known to us:
In Equation (9), is a vector defined by Equation (6), and is a scalar. Since the values can be either positive or negative, we get a limitation on the possibility of using distance functions based on cross entropy. Therefore, the authors applied proximity to the cosine metric: :
The distance between and T is equal to . Now the optimization problem can be written in the following way:
The problem (11) can be solved numerically by iterative selection of . To accelerate convergence, the authors used an analogy with the idea of an expectation–maximization (EM) algorithm [10]. At the E-step, we minimize , on the M-step maximize :
E–step:
M–step:
In order to account for the physical limitations of seismic traces in the algorithm , the authors apply the approach of sequential regularization. For this purpose, the term fining for the violation of the physical principles for the formation of a seismic trace is introduced into the functional (11). Since there are several physical restrictions, a separate regularizing term is created for each of them. In order to match to the condition for the sparsity of the reflection coefficients, one of the regularizers became norm , which penalizes the number of non-zero .
Each regularizing term enters the functional with its own hyper-parameters , so adjusting the values allows you to control the optimization process depending on the specificity of the seismic field. The equation of the functional with regularizing terms is provided in Label (14):
Adjustment of regularization coefficients to a specific seismic field is made before the optimization process and the search for the function global minimum.
In Figure 6, we can see the dependencies of the fitting curve (F) from different values of regularizing terms ().
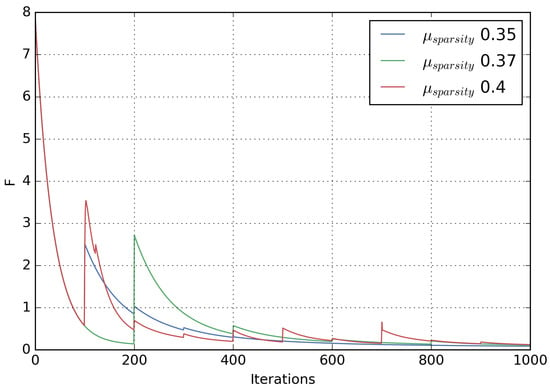
Figure 6.
The fitting curves (F) for different values of regularizing terms ().
The limiting estimate of the accuracy of the algorithm A0 was made on a synthetic trace with one single reflecting plane. Figure 7 shows the dependence for different degrees of mismatches T and .
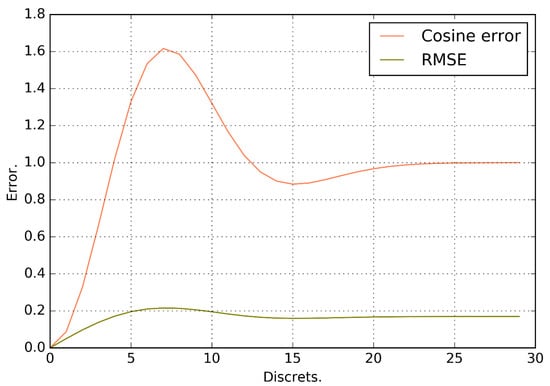
Figure 7.
Dependence of the error (distance) between vectors and for the case with one reflecting plane.
As a consequence of the fact that the degree of discrepancy is a sample, the minimum is 0.087. For comparison, Figure 7 shows the RMSE error between T and . The minimum RMSE value is 0.05. Note that the cosine measure is more sensitive to the differences between T and . This is why the authors chose the cosine measure as a measure of the difference between T and .
Another distinctive feature A0 is the initialization. For the initial step of the iterative process of selecting distribution parameters, the authors considered various initialization options: random numbers, similarity of T and zeros parameters.
The criterion for choosing an initialization option is the rate of convergence of the optimization process. From the information point of view, the best approximation to the result is the initialization based on the similarity of the seismic trace T. With this approach, each distribution parameter receives a value of the corresponding amplitude with a similarity coefficient. The problem of initialization based on similarity T is redundancy.
The solution of the problem of the SP&ARCM should have a number of non-zero parameters substantially less than N. To solve the problem of obtaining a high-resolution rarefaction , in , a regularization based on the -norm is introduced, which allows to nullify (zero) the parameters of the expansion.
The complete workflow of the former version on the A0 algorithms was described in [6]. In addition, the comparison of the performance features of the A0 to the OMP was studied.
3. Example of A0 Applied to Seismic Tasks
At the first stage, the authors use an acoustic model of the well for testing of the algorithm. Sonic log and density log along the well were used to create the model. Based on these measurements, the acoustic impedance curve was calculated, which was later converted to the reflection coefficients. The reflection coefficients were convolved with a seismic signal to obtain the wave field. The signal estimation was performed based on the frequency spectrum of available seismic survey data in the area of the well under study. The obtained model of wave field was used to reconstruct the reflection coefficients based on the algorithm via the Ricker wavelet library.
The result of the algorithm is shown in Figure 8. As can be seen from the comparison, there is a high degree of correlation between the real and the reconstructed curve of reflection coefficients (the correlation coefficient is higher than 0.93).
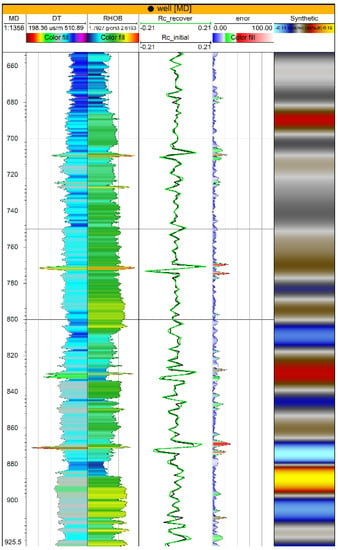
Figure 8.
The result of the application of the algorithm A0 on the acoustic model of the well: DT is the curve of the acoustic logging; RHOB—density curve; Rc initial—reflection coefficient curve; Rc recover—restored curve of reflection coefficients; error—relative error values (color settings: blue—error less than 10%, green—error 10–20%, red—error more than 20%); Synthetic is a model wave field.
The estimation of the relative mean square error along the well is about 4.25%. Therefore, it can be argued that, according to the results of testing the algorithm on the well data, there is a high accuracy of recovering the reflection coefficients from the wave field. It should be noted that the application of the algorithm does not require the availability of a priori information about the geological environment.
Further research was divided into two parts.
The first part of the study pursues the problem of determining the stability of the solution of the A0 algorithm at varying degrees of consistency of the seismic signal and the wavelets of the library, which is used to restore the reflection coefficients. Next, several acoustic models were calculated from the available well data using various wavelets (Figure 9):
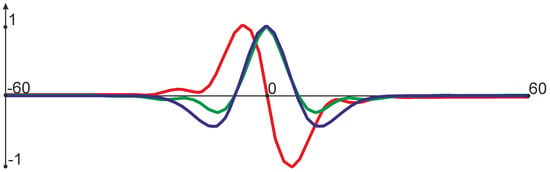
Figure 9.
Wavelets used for the formation of acoustic models in the well: blue—Ricker wavelet with a dominant frequency of 30 Hz (model 1); green—statistical pulse from seismic data (model 2); red—statistical pulse with a phase rotation of 90 degrees (model 3).
- model 1—using the Ricker wavelet with a dominant frequency of 30 Hz,
- model 2—using a wavelet estimated from the seismic data spectrum,
- model 3—using a wavelet estimated from the spectrum of seismic data, with the addition of phase rotation of 90 degrees.
The obtained models are characterized by varying levels of consistency between the seismic signal and the wavelets of the library. In the case of model 1, a complete coincidence of the signal and wavelets is observed, for model 2, the phase characteristics remain consistent, and the frequency spectra of the signals differ; in model 3, the trace and library signals differ both in frequency characteristics and in phase spectra. Such configuration of the experiment allows for assessing the generalization of the algorithm A0 in different models more completely.
For all three models of the wave field within the A0 algorithm, the library constructed from Ricker wavelets is used. The results of the reconstruction of the reflectance trace are given in Table 1.

Table 1.
The results of the experiment with different models.
The results of the comparison of the performance of the A0 algorithm for different models show well-built operation with frequency differences between the seismic signal and the library wavelet (model 2); however, if there are differences in phase characteristics between the wavelets, the model recovery accuracy drops significantly (model 3). Therefore, for the correct application of the A0 algorithm, it is necessary to perform matching between the seismic signal and the library wavelet, which can be done using filtering tools.
The second part of the study was intended at determining the endurance of the A0 algorithm to the noise. Gaussian noises with different amplitudes were incorporated into the wave field along the well. The resulting model was applied to the input of the A0 algorithm for the recovery of the reflection coefficients. The results of the comparison of the obtained models of reflection coefficients are given in Table 2 and Figure 10.

Table 2.
The results of the experiment with noise.
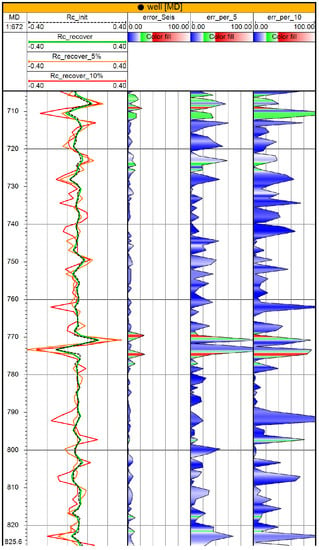
Figure 10.
The result of applying the A0 algorithm on the wave field along a well with different fractions of the noises: Rc init is the reflection coefficient curve; Rc recover—the restored curve of the reflection coefficients without noise; Rc recover 5%—the restored curve of reflection coefficients at a noise content of 5%; Rc recover 10%—restored curve of reflection coefficients at a noise content of 10%; error Seis, error per 5, error per 10—the corresponding relative mean square error curves (color settings: blue—error less than 10%, green—error 10–20%, red—error more than 20%).
As can be seen from the comparison, even with significant noise content (5–10% of the maximum amplitude), the A0 algorithm allows us to evaluate the reflection coefficients model. It should be noted that the fraction of noise was determined relative to the maximum amplitude along the entire trace. For the correct estimation of the fraction of the noise component, the average difference between the amplitudes of the trace and the maximum value, which was about 0.2, was estimated. Therefore, 5% of the noise from the maximum amplitude on average leads to a change in amplitudes by 25%. This fact explains the observed loss of algorithm accuracy when adding a random additive noise.
The possibility of practical use of the A0 algorithm is shown on a simplified three-dimensional model of the geological environment.
The main practical use of the algorithm in the context of seismic prospecting is possible for solving problems of wave field interpretation: refinement of structural features and forecasting of geological properties.
The task of structural interpretation is to trace the reflecting boundaries in the studied territory with a view to subsequently predicting the depth of occurrence of geological objects. Thus, the main task is to separate the individual reflecting boundaries of acoustically contrasting objects and layers. In this case, because of the non-zero duration of the seismic signal, the resolution of the wave field arises, which is that the reflections from closely located boundaries interfere with each other. Interference leads to the inability to separate two reflecting boundaries, the distance between which is less than wavelength. In this case, the algorithm allows for reducing the interference effect, thereby increasing the resolution of the wave field.
The task of dynamic interpretation is to forecast the geological structure of the target objects by changing the dynamic characteristics of the wave field. In the framework of this problem, the algorithm allows us to use the values of the coefficients obtained and to proceed to a relative estimate of the acoustic impedance.
Within the framework of the study, a three-dimensional synthetic model of acoustic impedance is considered as a practical case. To form the model, seven contrasting isotropic layers were used in which was placed a channel system with differing acoustic properties from the enclosing strata (Figure 11). The width of the channels is 250 m; the thickness varies from 0 to 30 m.
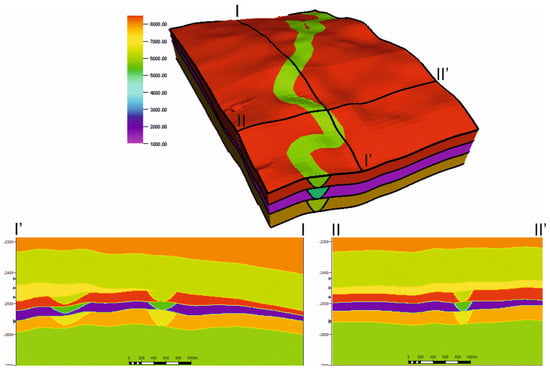
Figure 11.
(top) picture is the acoustic impedance model for three layers; (below) cuts along the lines I-I’ and II-II’.
The model was used to obtain a synthetic wave field by convolving reflection coefficients from a model with a Ricker wavelet (Figure 12).

Figure 12.
Seismic sections along the lines I-I’ and II-II’, obtained as a result of modeling.
The resulting wave field was applied to the input of the algorithm for solving the inverse problem, which consisted in restoring the reflection coefficient model for the available seismic traces. At the output of the algorithm, a cube of reflection coefficients was obtained. Figure 13 shows the comparison of obtained reflection coefficients with the model that was known a priori.
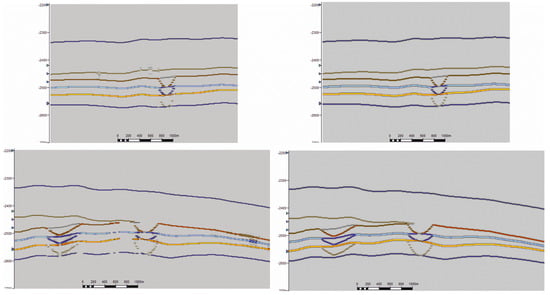
Figure 13.
(left), cuts of the reflection coefficients along the lines I-I’ and II-II’, obtained as a result of applying the algorithm; (right) the model sections of the reflection coefficients.
Comparison of the reflection coefficient sections allows us to establish a high degree of similarity between reflection coefficients reconstructed from the seismic trace using the algorithm and the original reflection coefficients incorporated in the model (Figure 14). It should be noted that, in places that the ambiguous operation of the algorithm is observed, expressed in the “skipping” of the coefficient or the appearance of the zone of “blurring” of the boundary. However, in the areas of wedging of seams, for example, in the channel edge zone, where interference appears, the algorithm manages to reconstruct the model correctly.
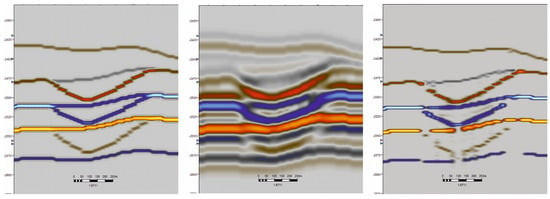
Figure 14.
(left): model section of the reflection coefficients, (center): model wave field; (right): the result of the algorithm .
At the end of testing, the developed algorithm was applied to real seismic data. Comparison of the results shows an increase in the wave field resolution, which makes it possible to reduce the uncertainty of interpretation (Figure 15).

Figure 15.
(left): the seismic section with reflective coefficients in well, (right): the result of the algorithm work.
The practical value of the obtained data is to increase the resolving power of the wave field by reducing the contribution of interference, which provides new information for seismic-geological modeling.
4. Conclusions
In this study, the authors continued to study the capabilities of their previously proposed algorithm [6] for identifying medium (environmental) factors forming the seismic trace. The authors have formulated the problem of finding the position and amplitude of the reflecting coefficients of the medium (SP&ARCM) using linear operators. This approach made it possible to obtain a top restriction on the number of reflecting planes for the path in ≈ of N.
Next, the authors considered the possibilities of applying global optimization for the solution of the SP&ARCM problem using the Differential Evolution (DE) algorithm. The study of the statement of the problem and the preliminary experiments have shown the limited application of the DE to the solution of the problem of SP&ARCM. In particular, this restriction is due to growing as computational complexity. Nevertheless, in the case of depleted seismic traces, the DE algorithm allows achieving the required accuracy quite quickly.
The main advantages of the algorithm are embedded in it by design and consist in increasing the specialization in comparison with the universal optimization algorithms. Increasing specialization is achieved by introducing sequential regularization, a discrete loss function, and initialization based on the similarity of the result. All these features make applicable to a wide range of operational tasks.
The novelty of this research is constituted in further exam and study of the possibilities of unique optimization algorithms, taking into account the features of the stable formulation of the problem.
The practical significance and value of this research are constituted in the successful application to solve the problems of restoring the seismic-geological model of the medium that in essence is the interpretation of the wave field.
As shown in the study, practical application of the algorithm is possible to increase the resolution of data, as well as to obtain additional information on the structure of the medium.
Author Contributions
Conceptualization, A.B. and F.K.; methodology, A.B.; software, F.K.; validation, A.B., F.K.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SP&ARCM | Searching for Positions and Amplitudes of the Reflection Coefficients of the Medium |
| OMP | Orthogonal Matching Pursuit |
| DE | Differential Evolution |
| BP | Basic Pursuit |
| MP | Matching Pursuit |
| RMSE | Root Mean Square Error |
References
- Claerbout, J.F.; Muir, F. Robust modeling with erratic data. Geophysics 1973, 38, 826–844. [Google Scholar] [CrossRef]
- Chopra, S.; Castagna, J.; Portniaguine, O. Thin-Bed Reflectivity Inversion; Society of Exploration Geophysicists: Tulsa, OK, USA, 2006; pp. 2057–2061. [Google Scholar]
- Zhang, R.; Castagna, J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition. Geophysics 2011, 76, R147–R158. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, S.; Tian, N. Swarm intelligence optimization and its application in geophysical data inversion. Appl. Geophys. 2009, 6, 166–174. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, S. Spectral sparse Bayesian learning reflectivity inversion. Geophys. Prospect. 2013, 61, 735–746. [Google Scholar] [CrossRef]
- Krasnov, F.; Howeverorin, A.; Andrei, M. Reconstruction of medium reflectivity coefficients based on seismic data through machine learning. St. Petersburg State Polytech. Univ. J. Comput. Sci. Telecommun. Control Syst. 2018, 11, 18–31. [Google Scholar]
- Yilmaz, Ö. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data; Society of Exploration Geophysicists: Tulsa, OK, USA, 2001. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Neal, R.M.; Hinton, G.E. A View of the EM Algorithm That Justifies Incremental, Sparse, and Other Variants; Springer: Dordrecht, The Netherlands, 1998; pp. 355–368. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).