Kriging with a Small Number of Data Points Supported by Jack-Knifing, a Case Study in the Sava Depression (Northern Croatia)
Abstract
1. Introduction
1.1. Basic Equations of the Applied (Geo-)Statistical Techniques/Methods
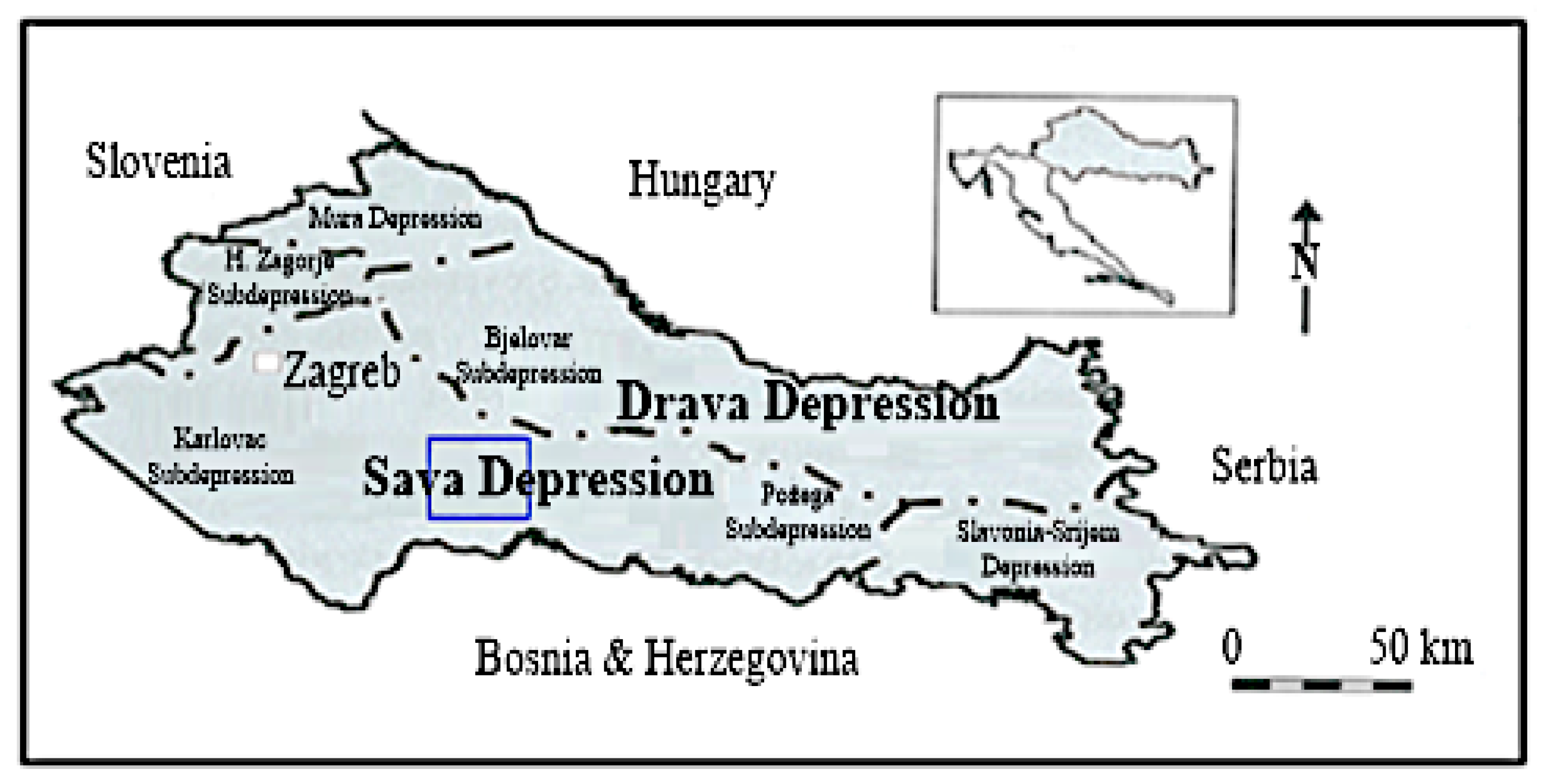
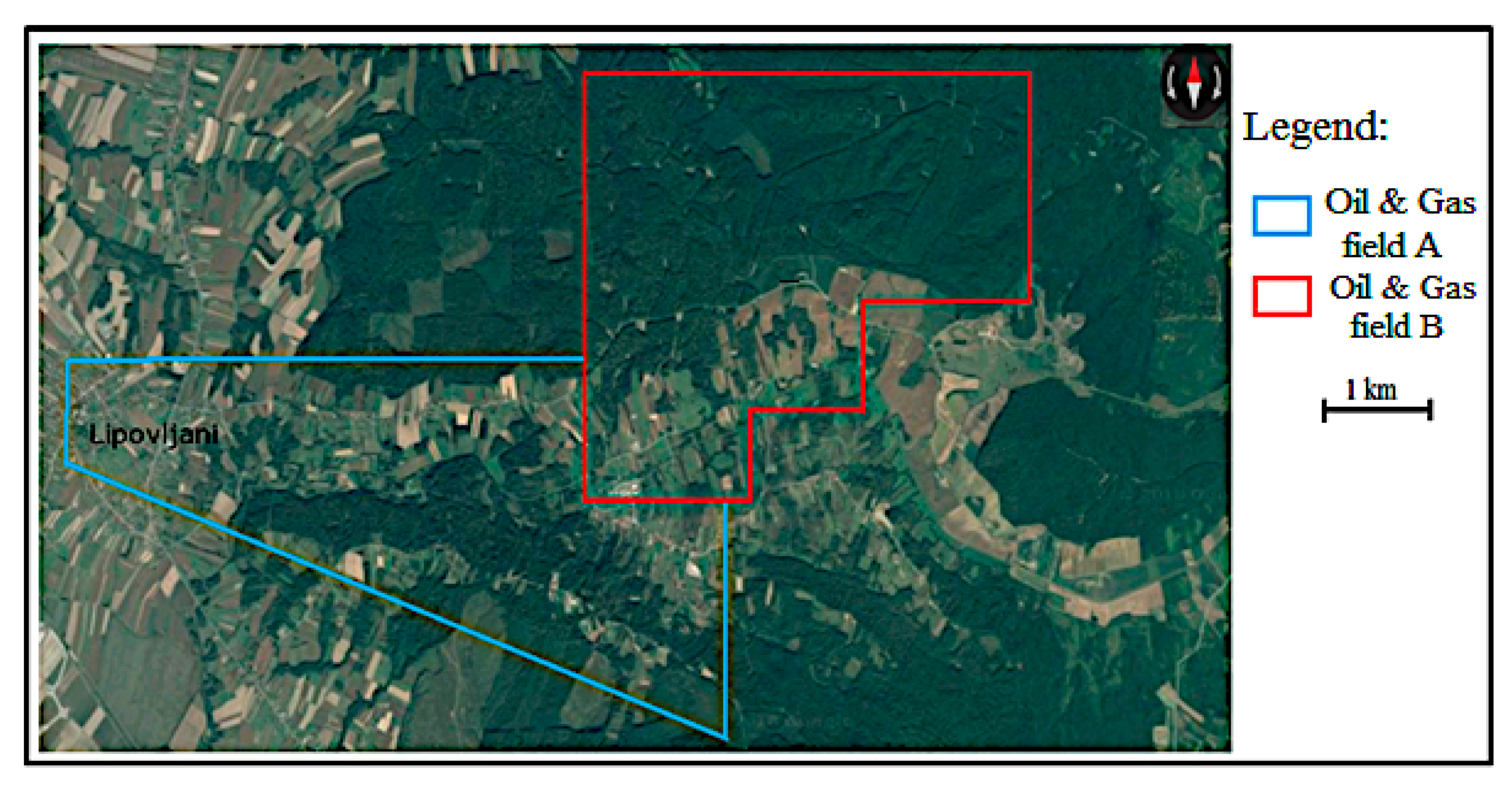
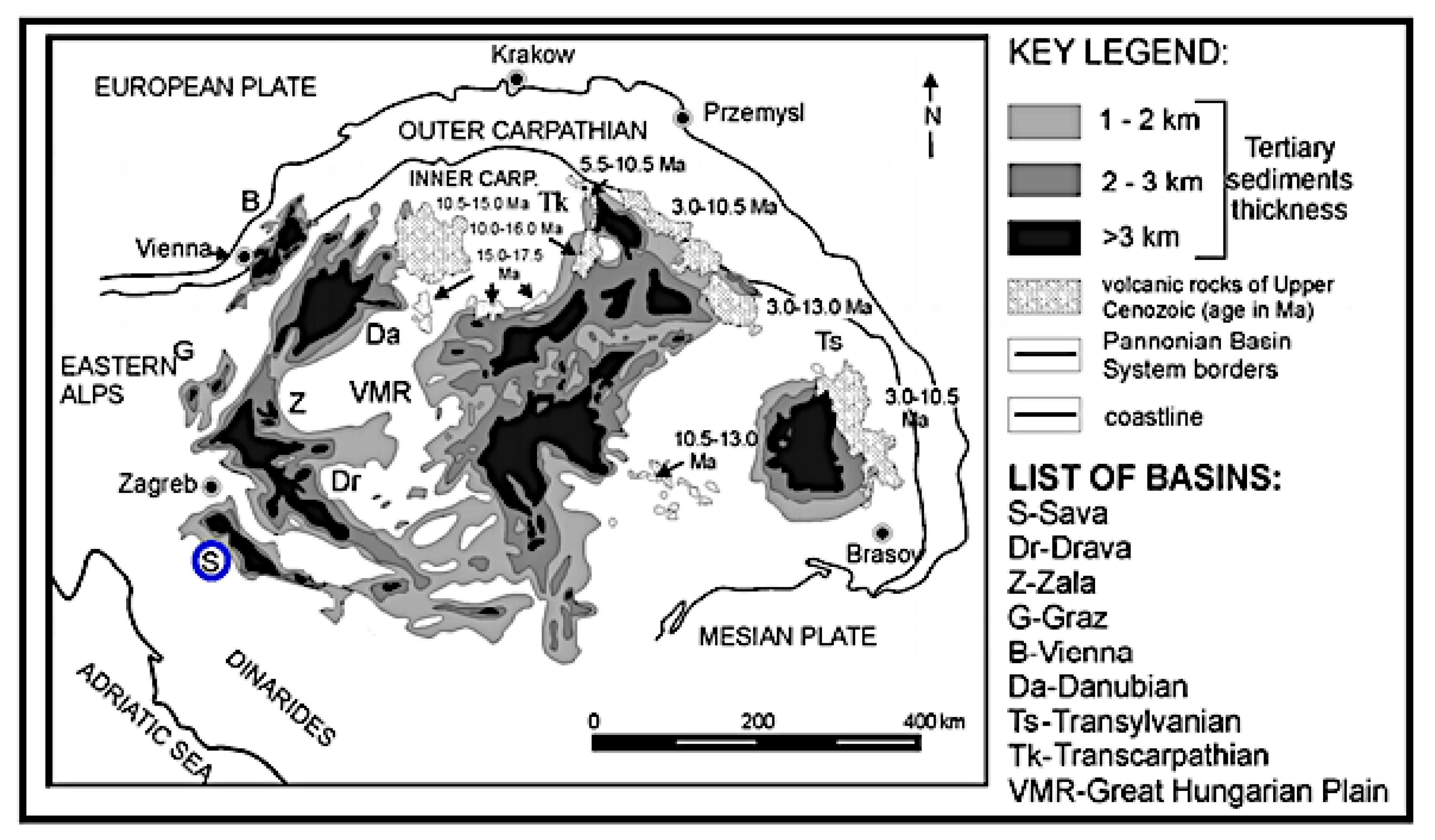
1.2. Geographical Locations of the Analyzed Hydrocarbon Fields (Northern Croatia)
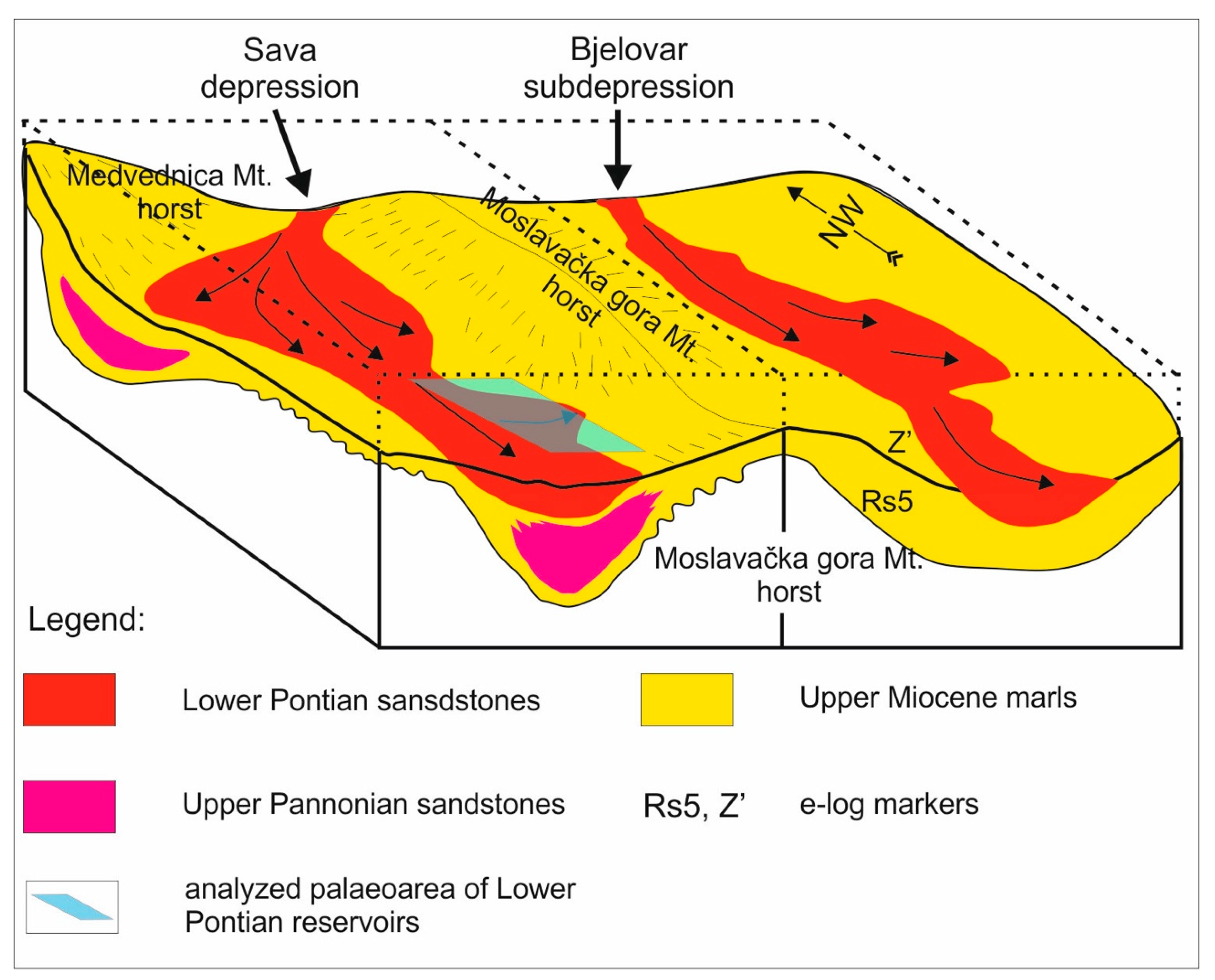
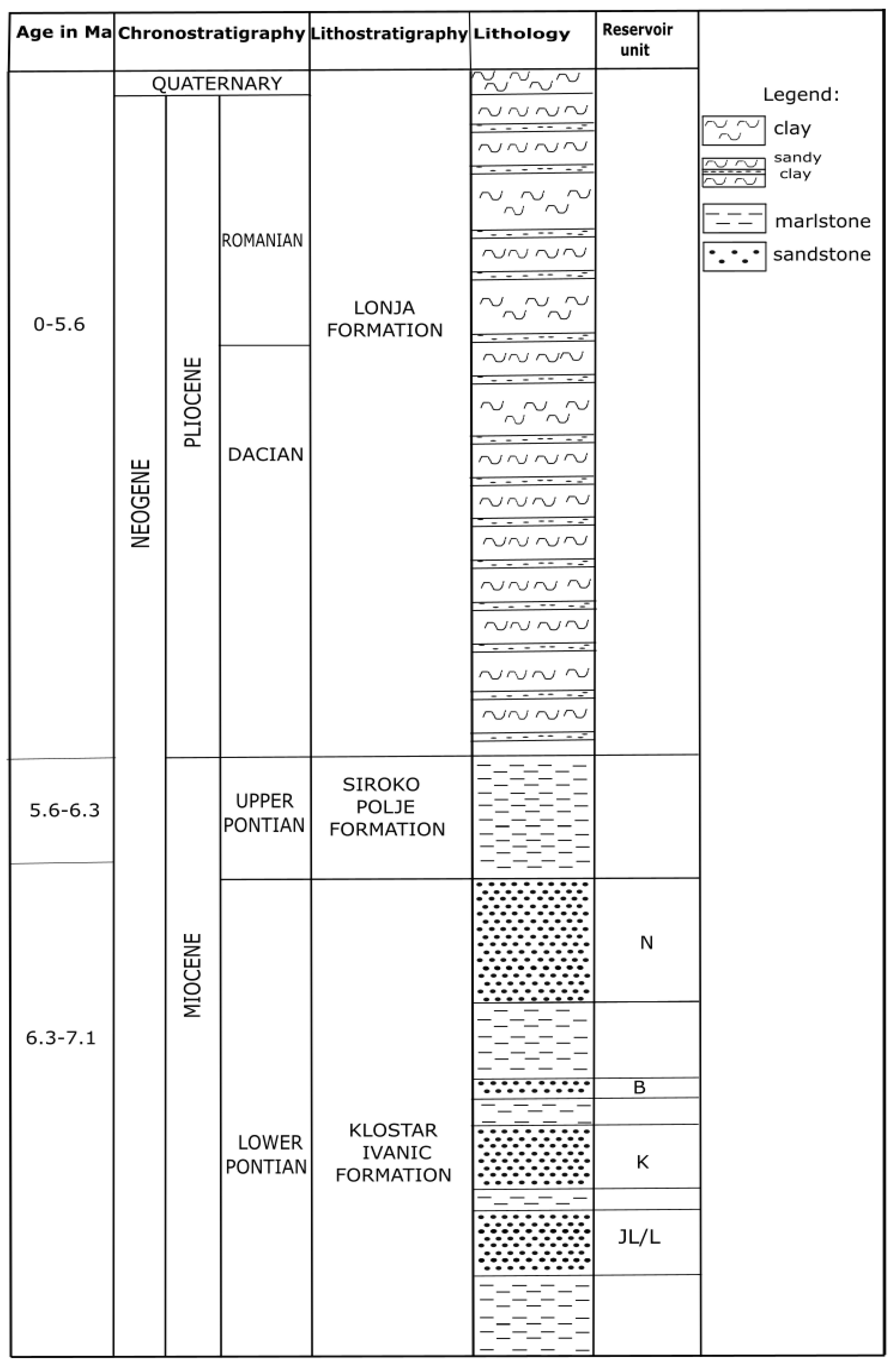
2. Geological History of the Western Part of the Sava Depression
3. Results
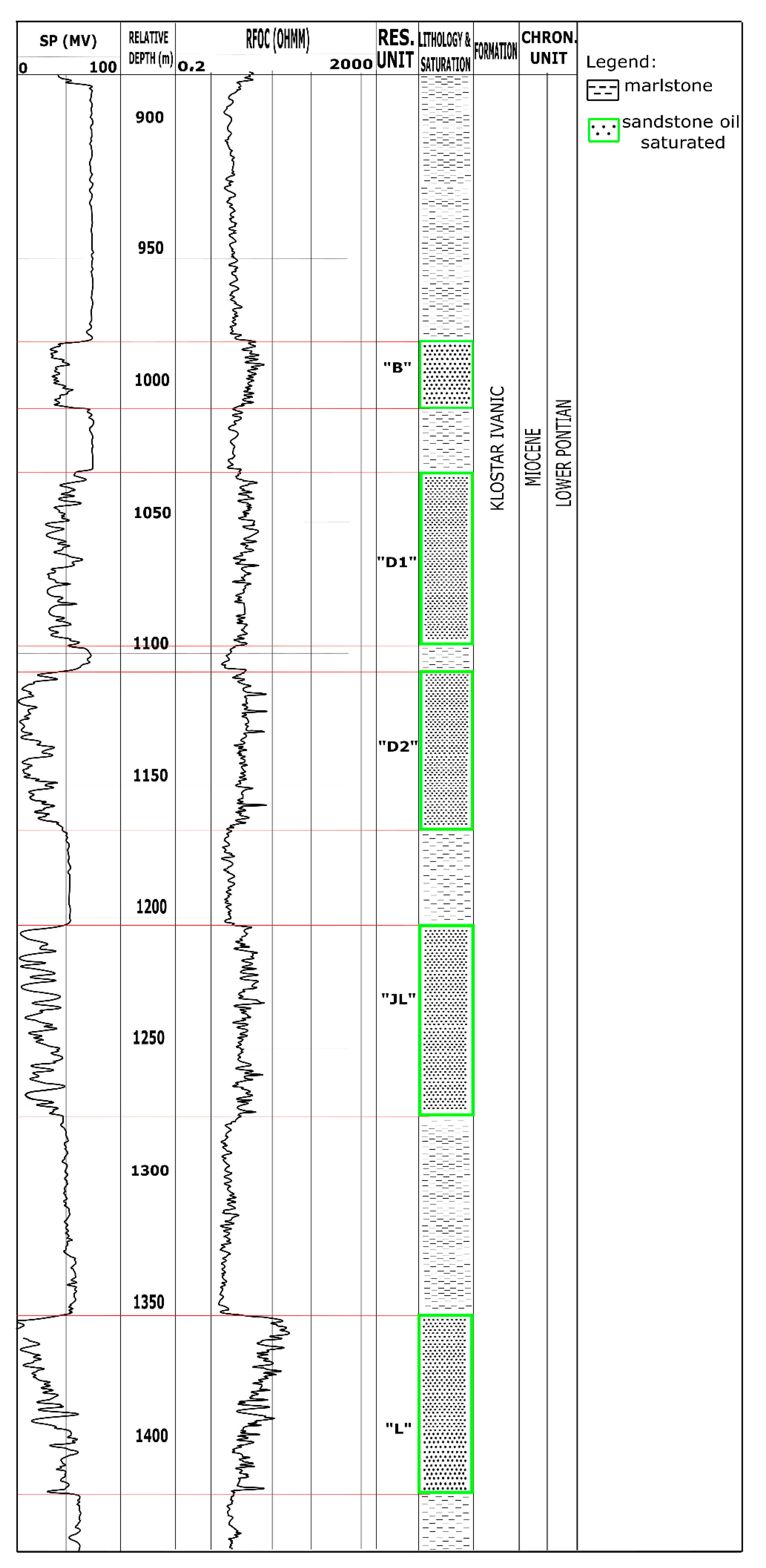
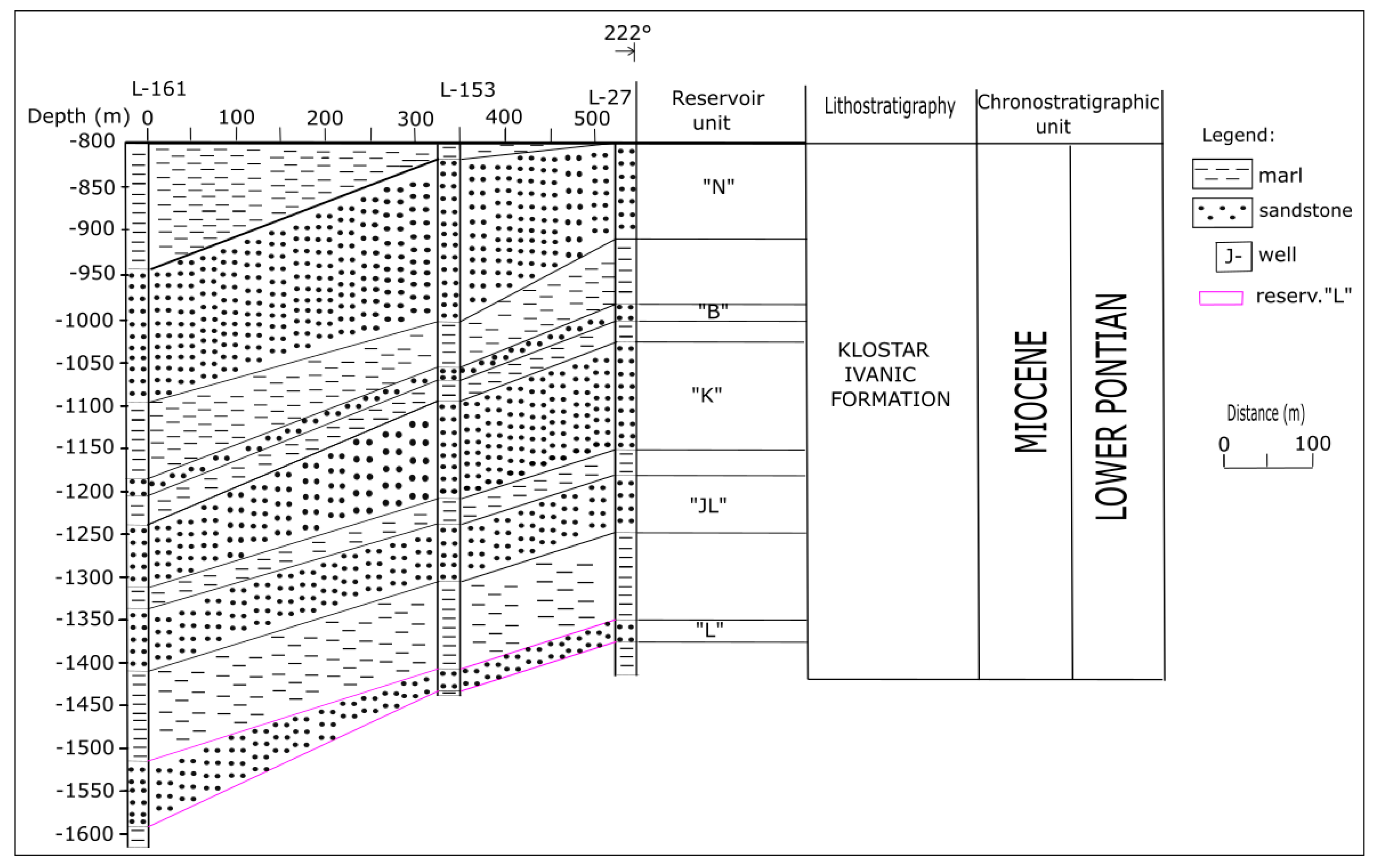
3.1. The Field “A”, Reservoir “L”
3.1.1. Reservoir Type
3.1.2. Granulometry, Porosity, Saturation and Permeability of Sandstones
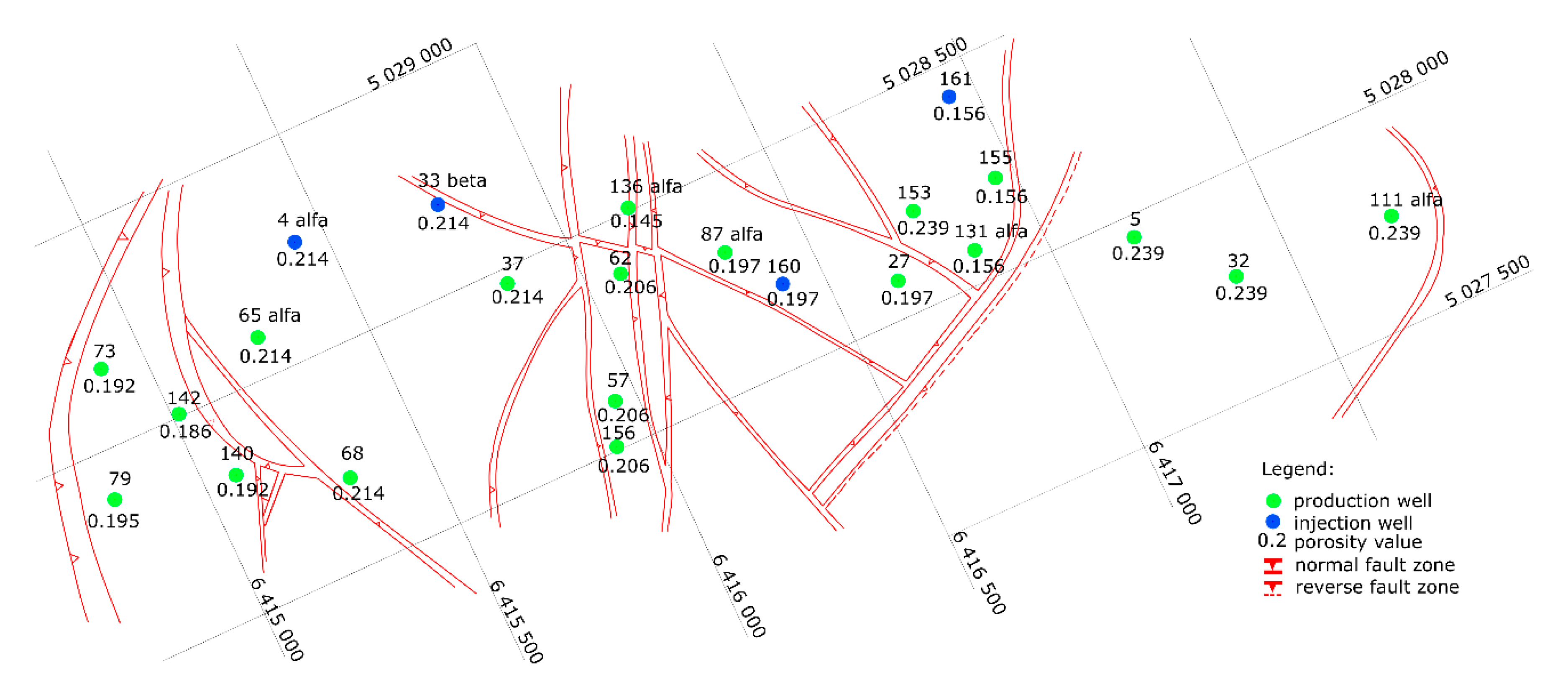
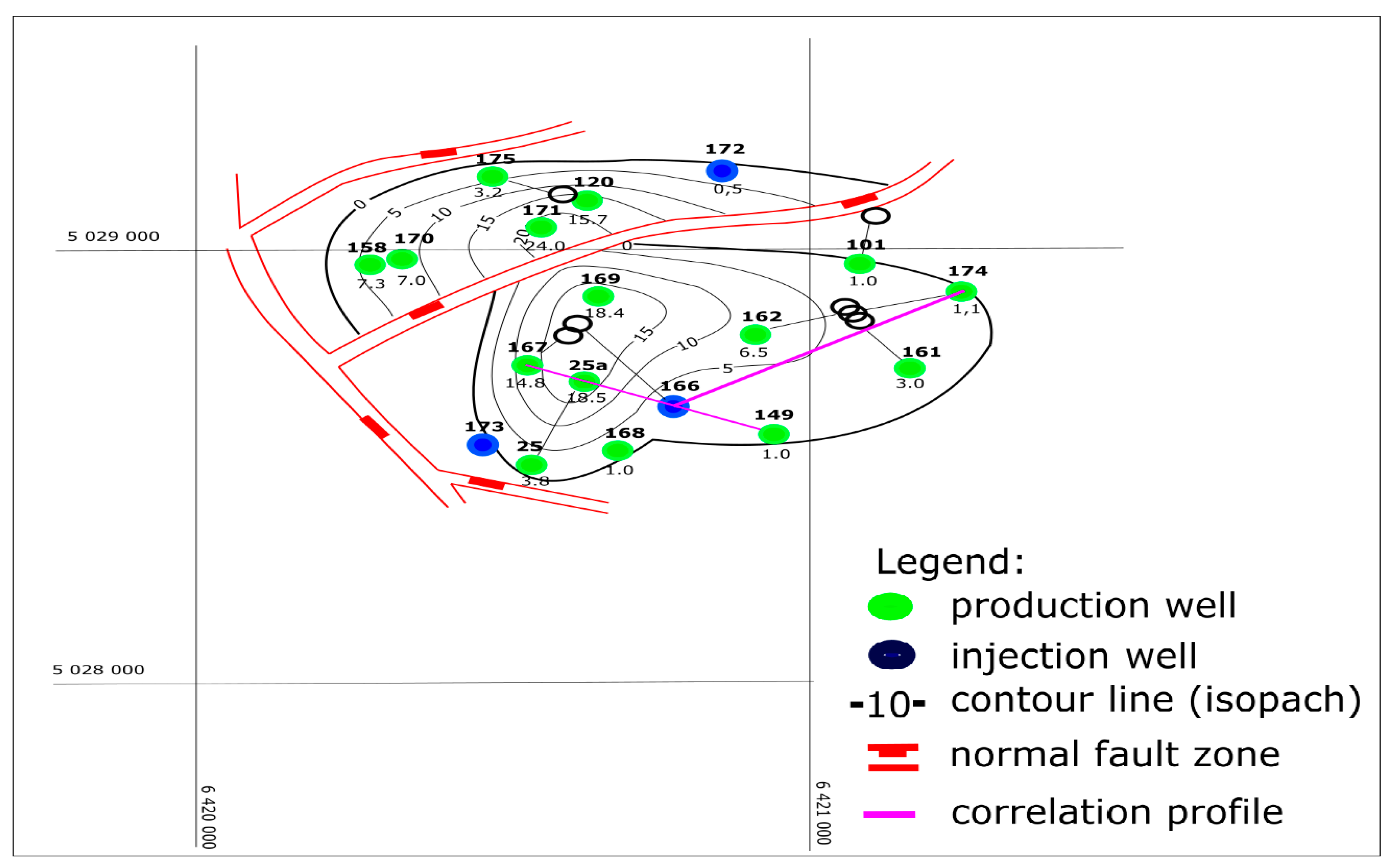
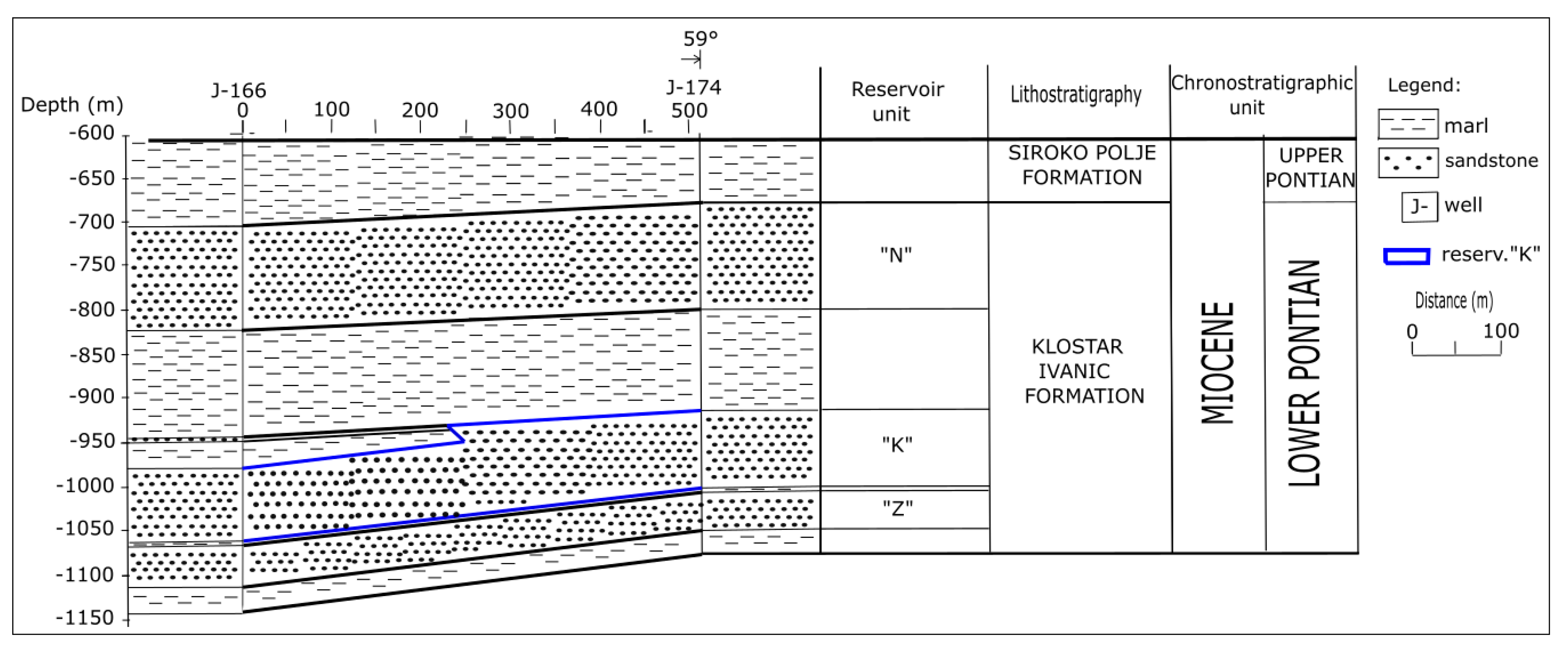
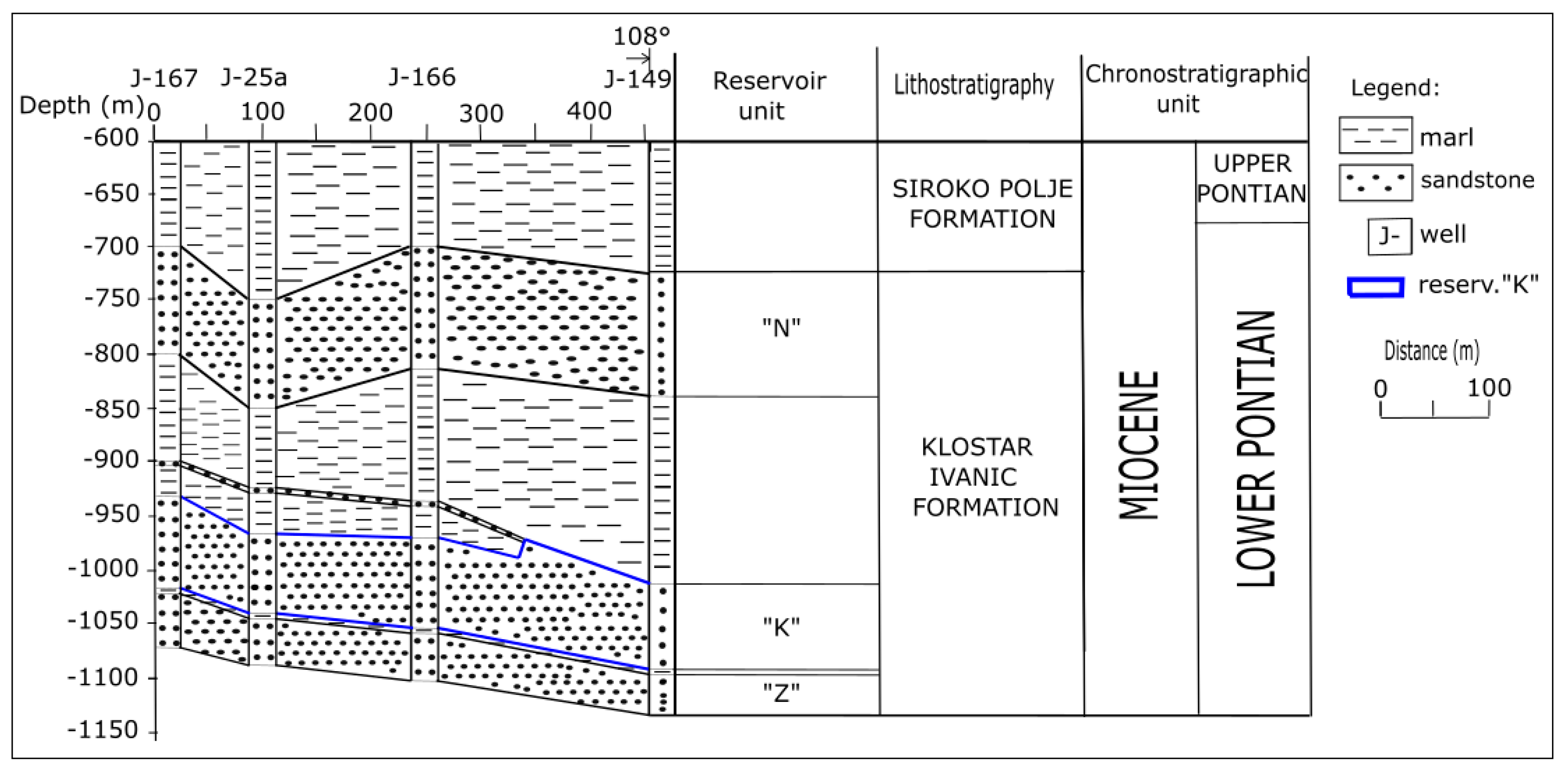
3.1.3. Structural Settings
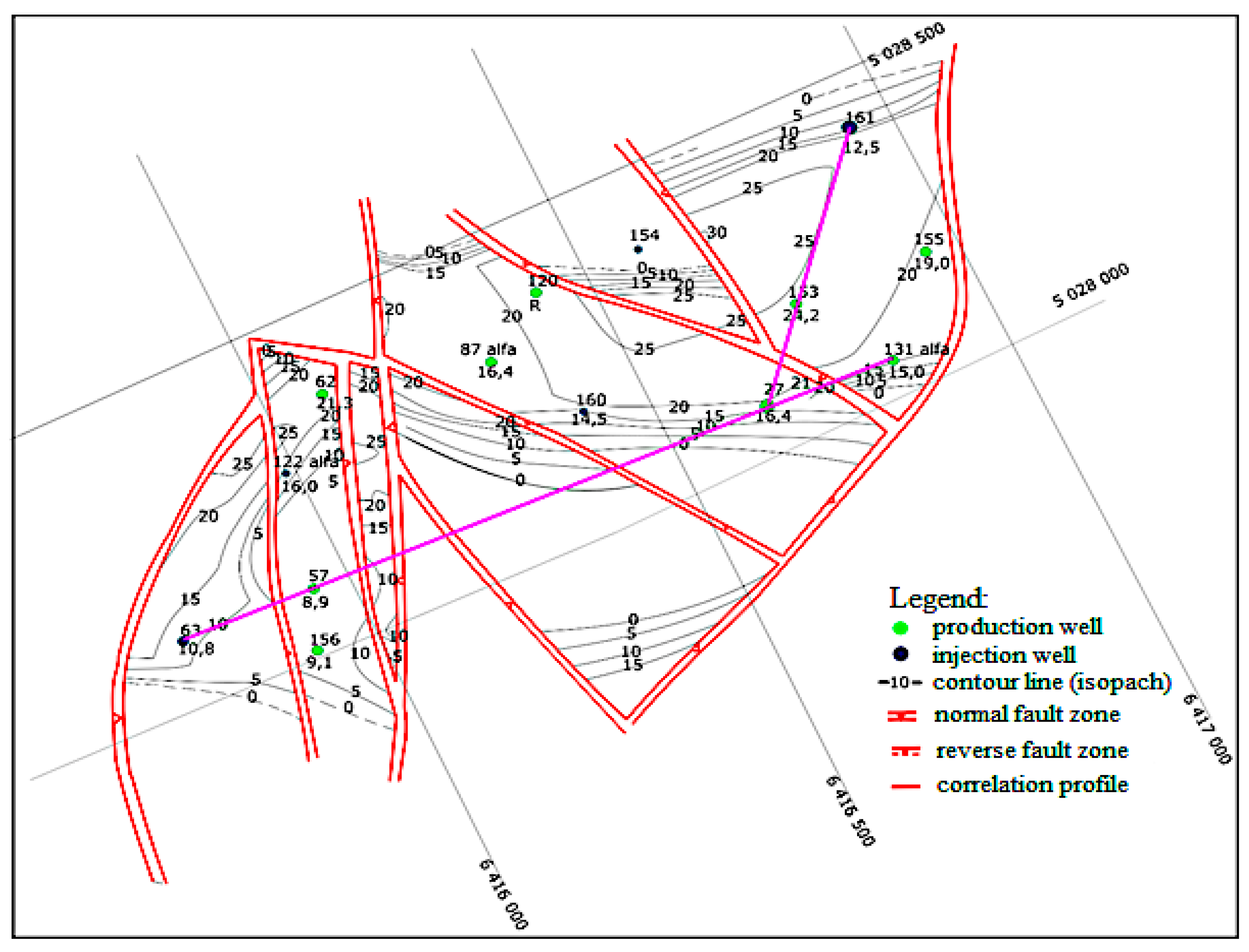
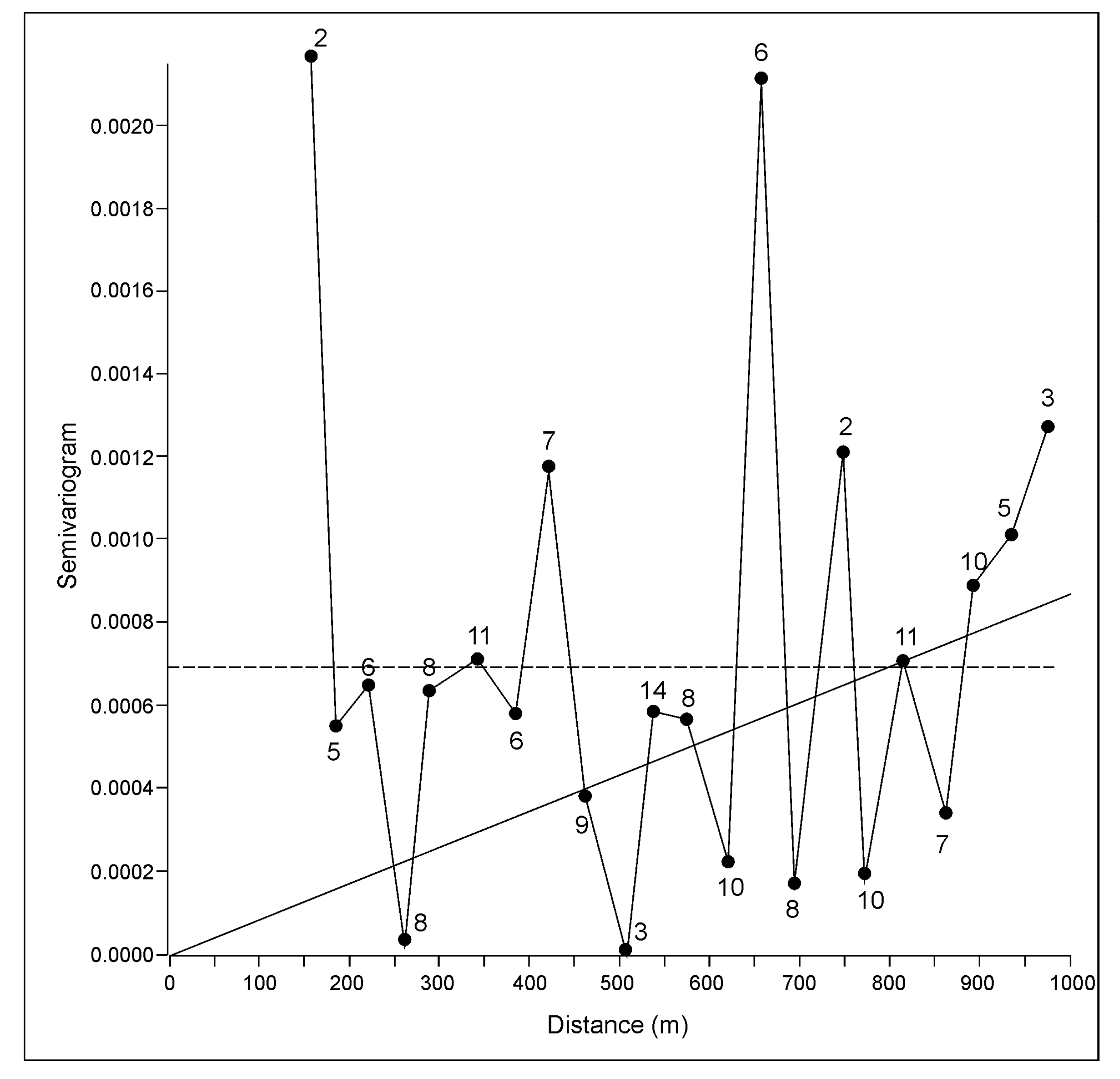
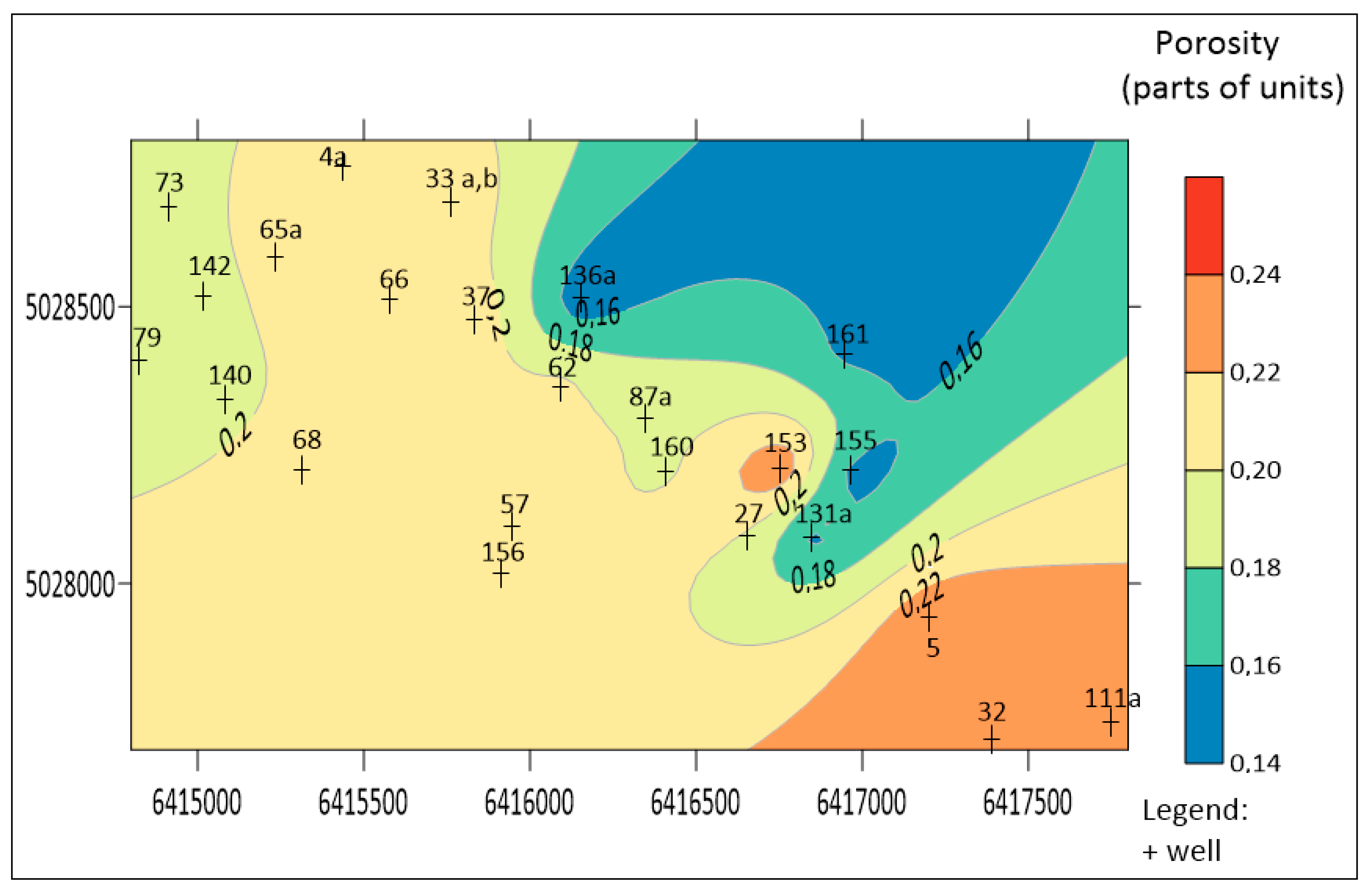
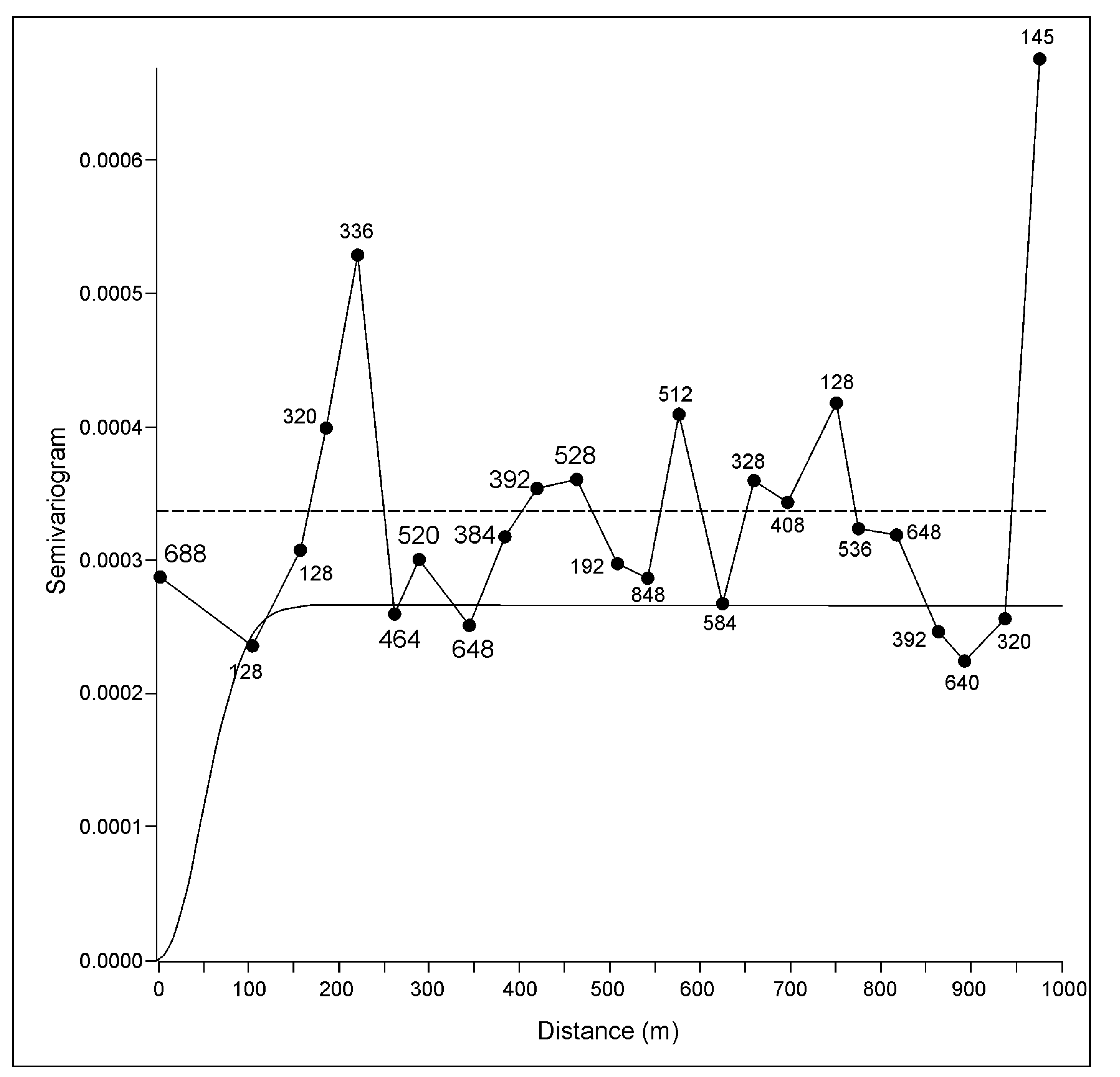
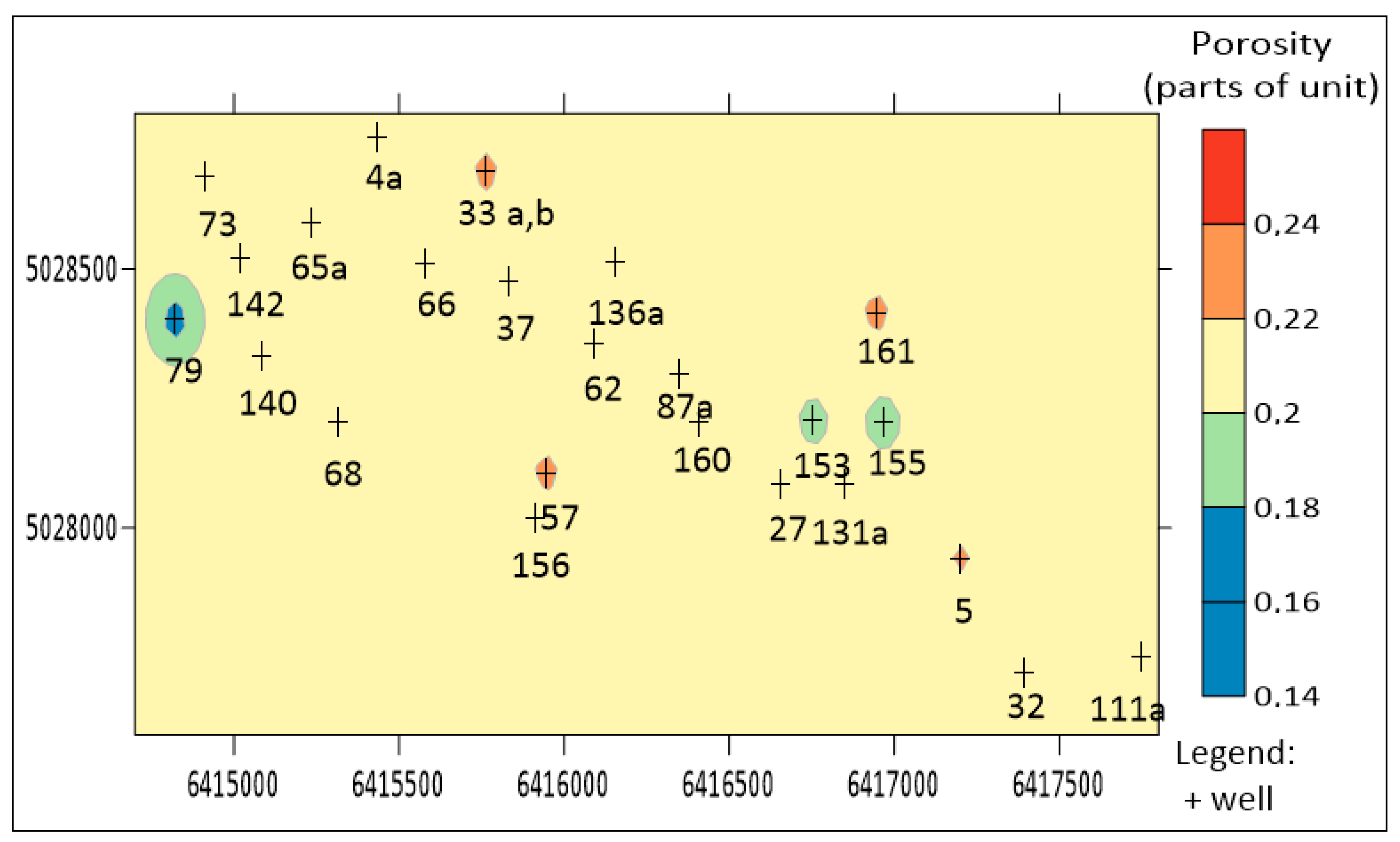
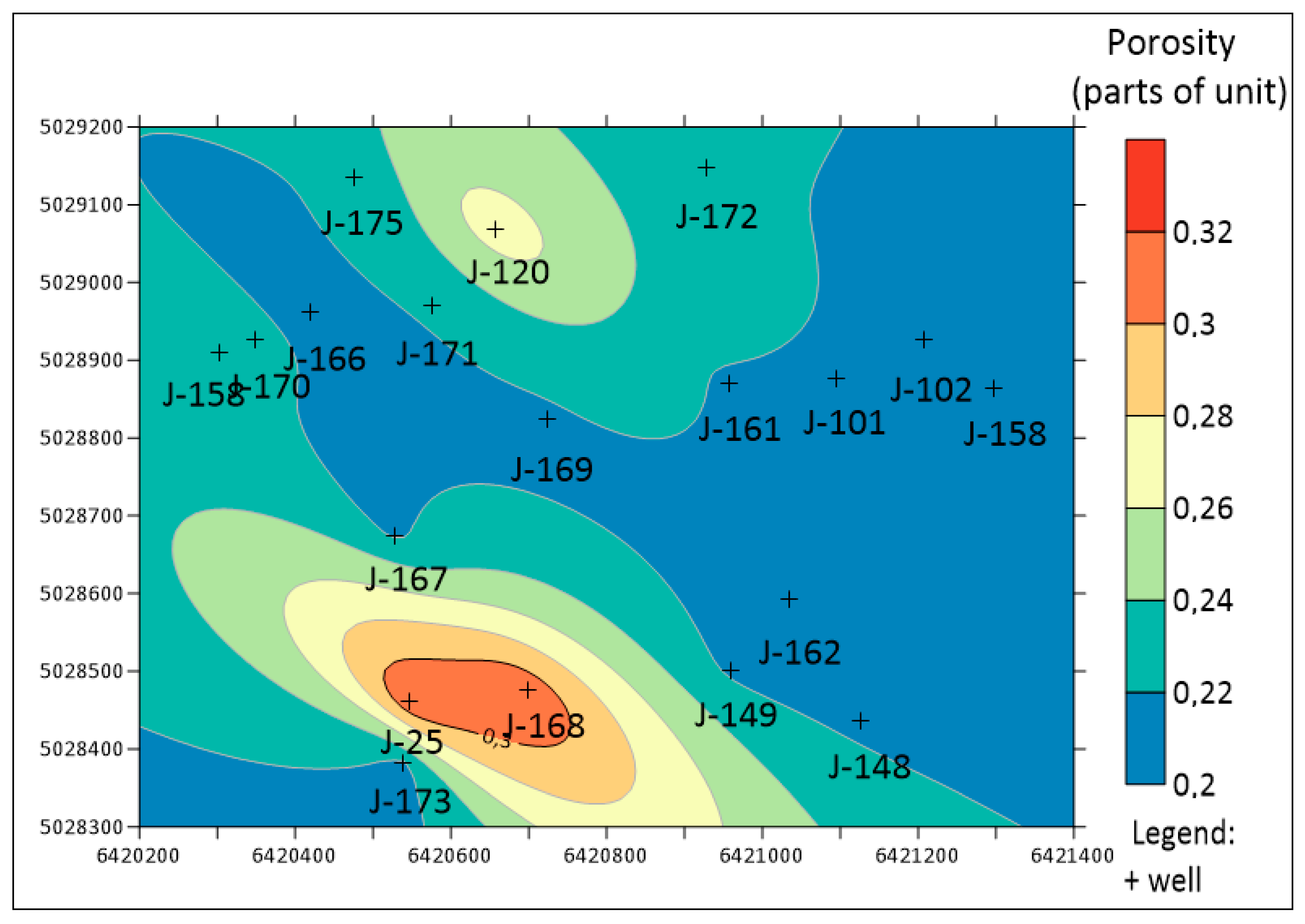
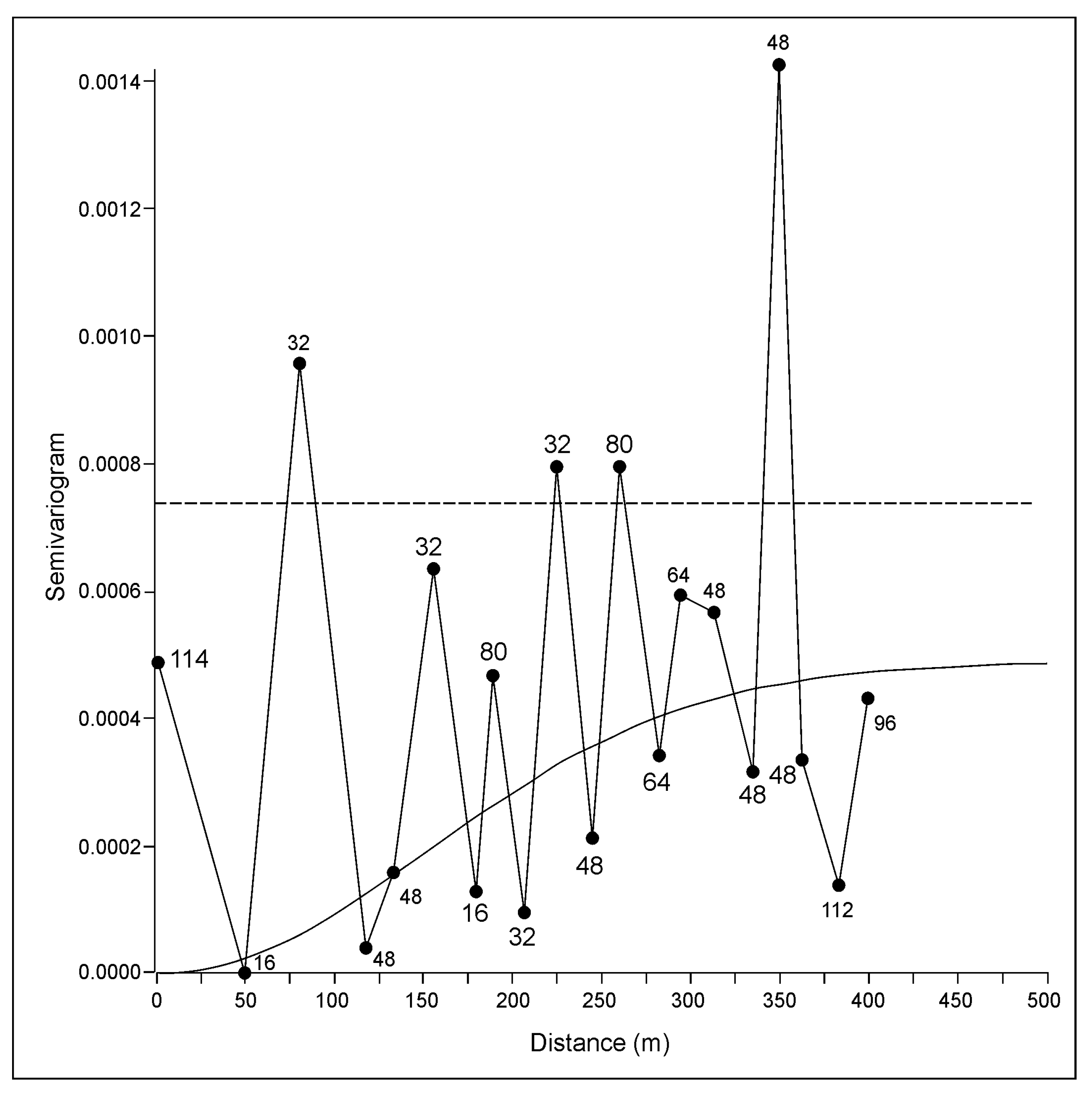
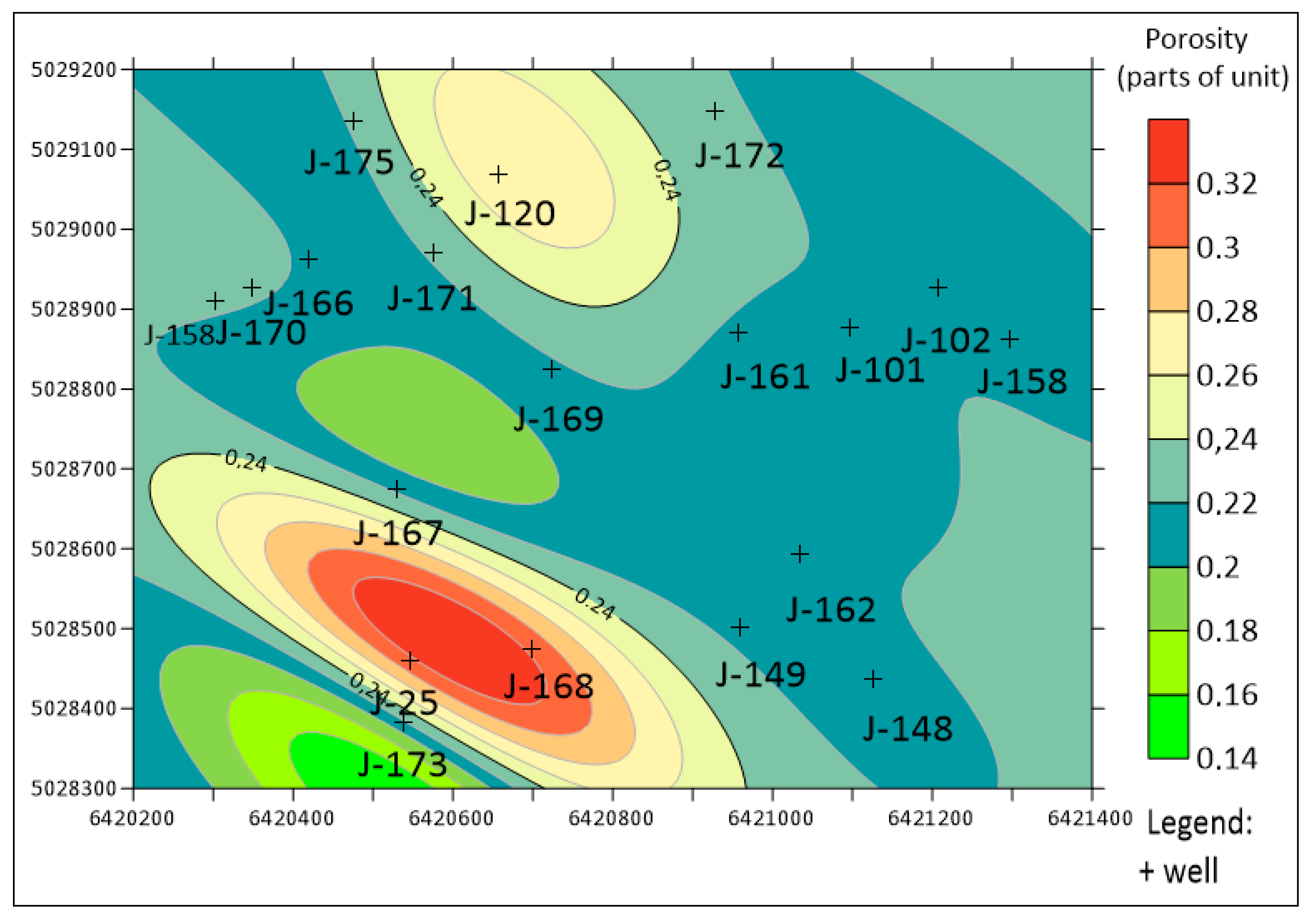
3.1.4. Variogram Analysis and Ordinary Kriging of Porosity
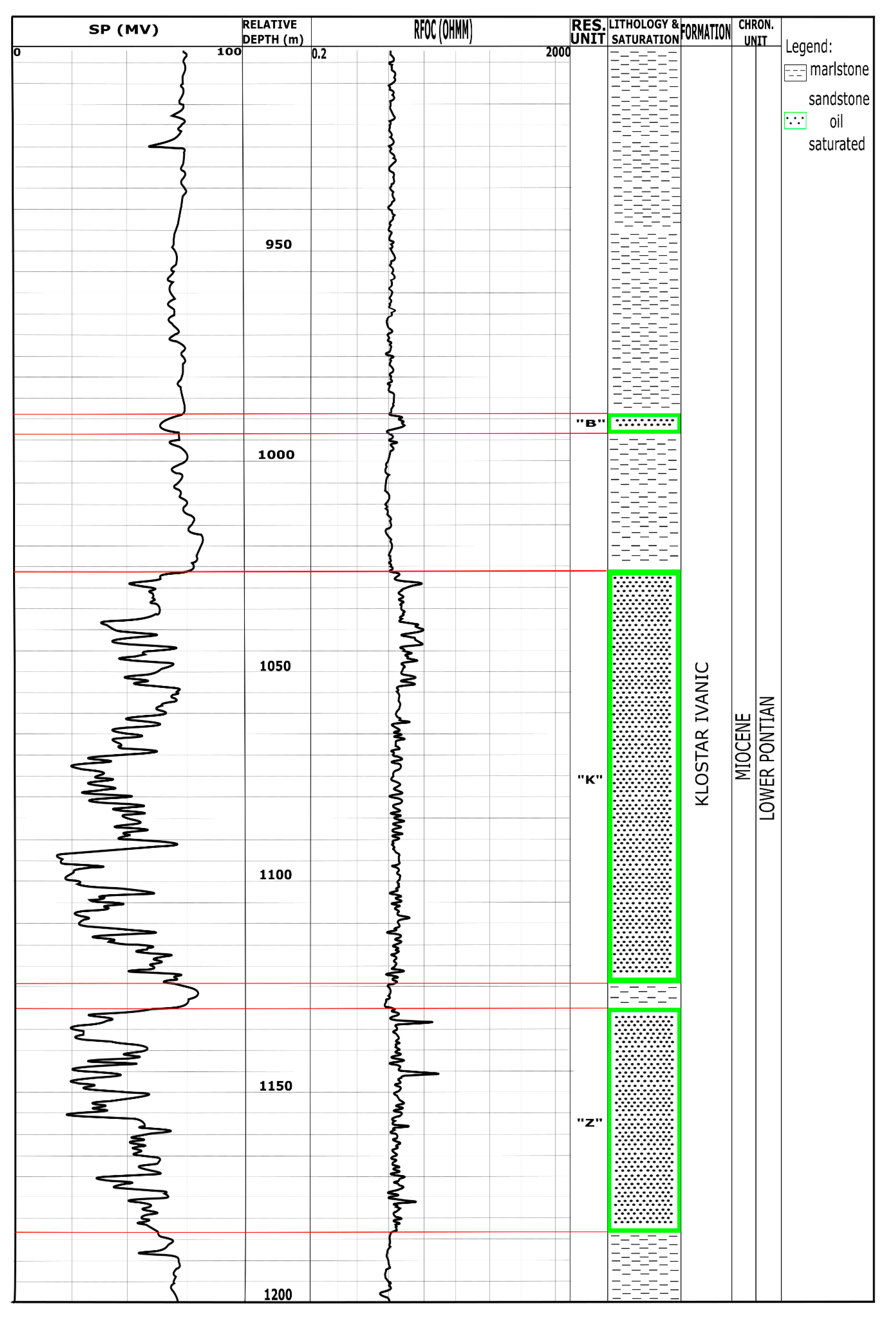
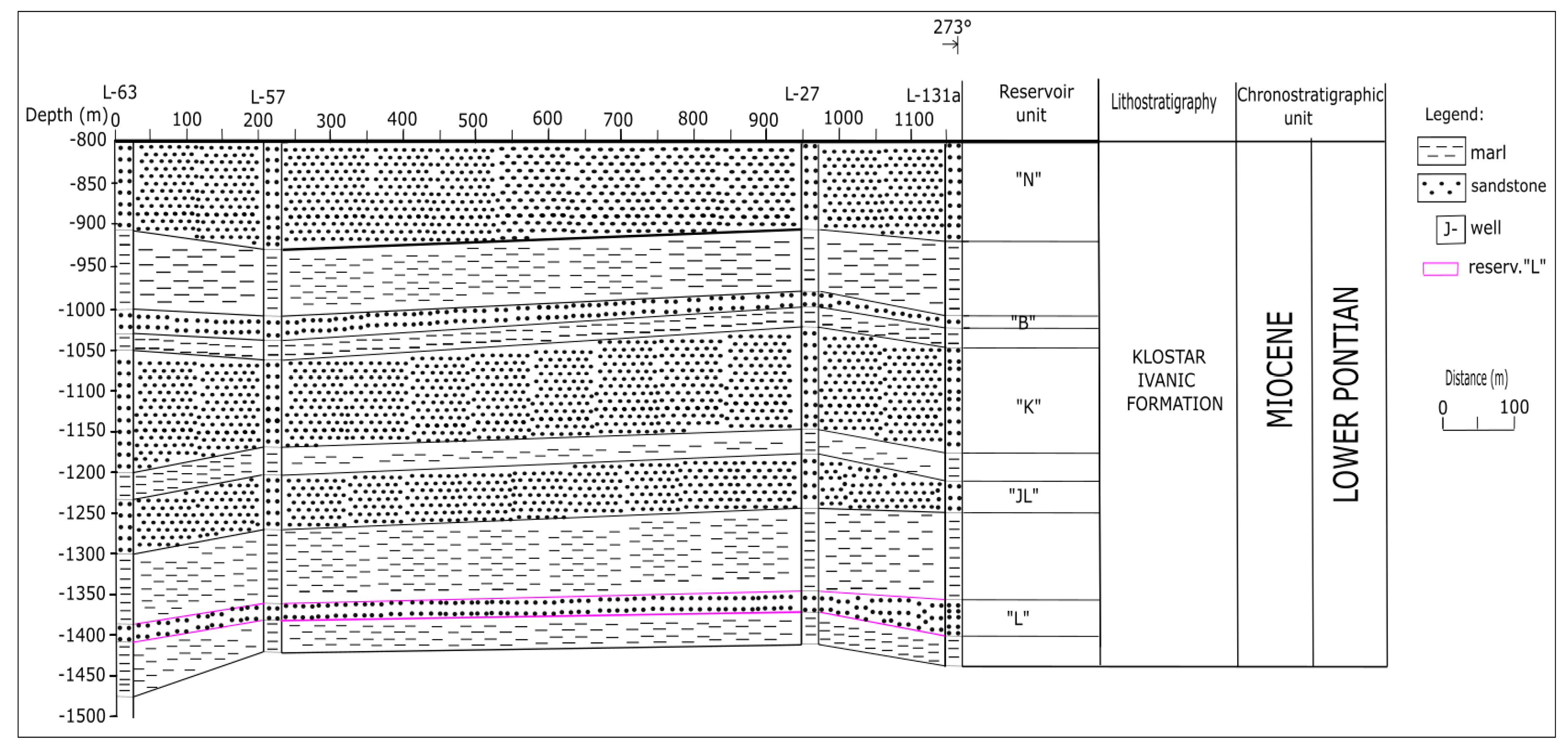
3.2. The Field “B”, Reservoir “K”, Hydrodynamic Unit “K1”
3.2.1. Reservoir Type
3.2.2. Granulometry, Porosity, Saturation and Permeability of Sandstones
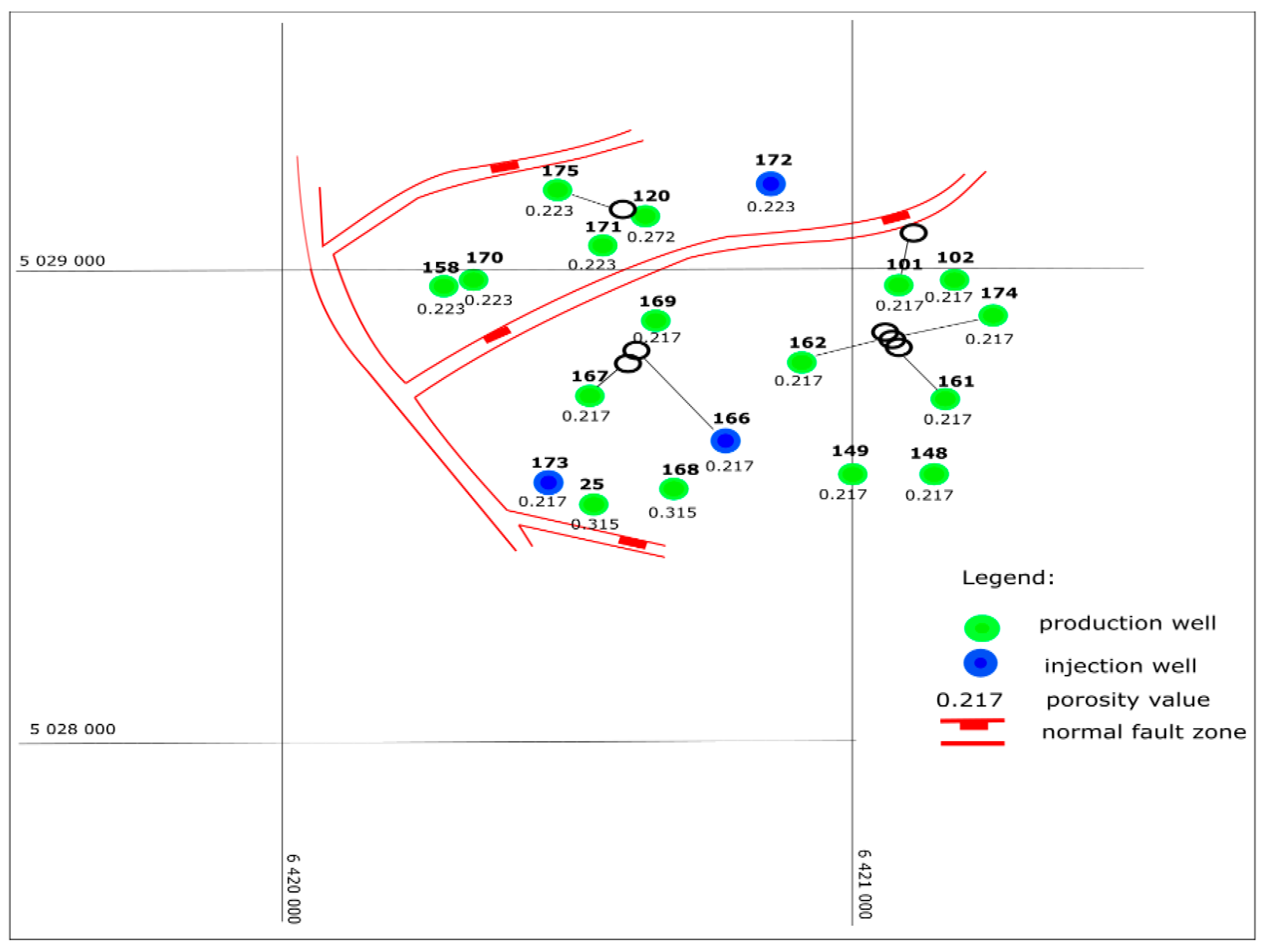
3.2.3. Structural Settings
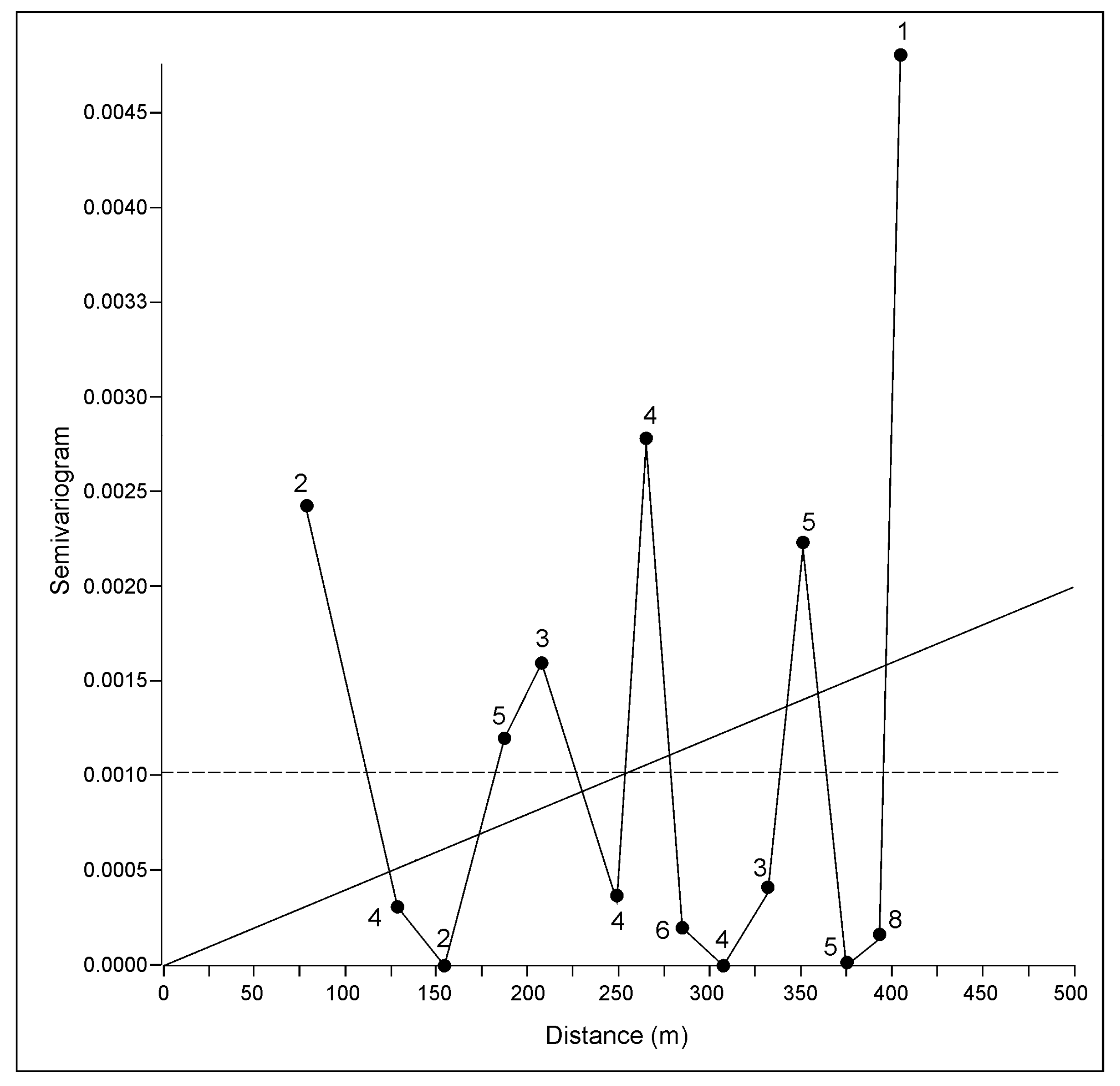
3.2.4. Variogram Analysis and Ordinary Kriging of Porosity
4. Discussion and Conclusions
- (1)
- When experimental semivariograms are described with large uncertainties it is recommended that the variogram is repeated using jack-knifed resampling, and followed by the kriging interpolation.
- (2)
- Any map from the set of “old” or “new” data/semivariograms firstly needs to be visually checked. If effects such as “bulls-eye” or “butterfly” shapes are numerous, the map needs to be eliminated.
- (3)
- If both kriged maps (based on original and jack-knifed datasets) are visually (geologically) acceptable, the selection can be done based on cross-validation values.
- (4)
- For small data sets (less than 15 data points) it is also recommended to interpolate with inverse distance weighting and compare both with ordinary kriging (OK) and inverse distance weighting (IDW) results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Malvić, T.; Velić, J.; Peh, Z. Qualitative-Quantitative Analyses of the Influence of Depth and Lithological Composition on Lower Pontian Sandstone Porosity in the Central Part of Bjelovar Sag (Croatia). Geol. Croat. 2015, 58, 73–85. [Google Scholar]
- Malvić, T. Production of a porosity Map by Kriging in Sandstone Reservoirs, Case study from the Sava Depression. Kartografija i Geoinf. 2008, 9, 12–19. [Google Scholar]
- Malvić, T.; Bastaić, B. Reducing variogram uncertainties using the “jack-knifing” method, a case study of the Stari Gradac—Barcs-Nyugat field. Bull. Hung. Geol. Soc. 2008, 138, 165–174. [Google Scholar]
- Malvić, T. Stochastical approach in deterministic calculation of geological risk—Theory and example. Nafta 2009, 60, 658–662. [Google Scholar]
- Malvić, T.; Balić, D. Linearnost i Lagrangeov linearni multiplikator u jednadžbama običnoga kriginga (Linearity and Lagrange Linear Multiplicator in the Equations of Ordinary Kriging). Nafta 2009, 60, 31–43. [Google Scholar]
- Novak Zelenika, K.; Malvić, T. Procjena sekvencijskim Gaussovim simulacijama ležišnih varijabli pješčenjačkog donjopontskoga ležišta nafte, polje Kloštar, Savska depresija, Hrvatska (Estimations by sequential Gaussian simulations of reservoir variables in Early Pontian oil reservoir, Kloštar Field, Sava Depression, Croatia). In Proceedings of the 4. Croatian Geological Congress with International Participation, Šibenik, Croatia, 14–15 October 2010; Horvat, M., Ed.; Croatian Geological Institute: Sachsova, Zagreb, 2010; pp. 263–264. [Google Scholar]
- Malvić, T. Kriging, cokriging or stohastical simulations, and the choice between deterministic or sequential approaches. Geol. Croat. 2008, 61, 37–47. [Google Scholar]
- Novak Zelenika, K.; Malvić, T.; Geiger, J. Mapping of the Late Miocene sandstone facies using indicator kriging. Nafta 2010, 61, 225–233. [Google Scholar]
- Novak Zelenika, K.; Malvić, T. Stochastic simulations of dependent geological variables in sandstone reservoirs of Neogene age: A case study of Kloštar Field, Sava Depression. Geol. Croat. 2011, 64, 173–183. [Google Scholar] [CrossRef]
- Novak Zelenika, K. Deterministički i stohastički geološki modeli gornjomiocenskih pješčenjačkih ležišta u naftno-plinskom polju Kloštar (Deterministic and Stochastic Geological Models of Upeer Miocene Sandstone Reservoirs at the Kloštar Oil and Gas Field). Ph.D. Thesis, Faculty of Mining, Geology and Petroleum, University of Zagreb, Zagreb, Croatia, 2012. [Google Scholar]
- Malvić, T. History of geostatistical analyses performed in the Croatian part of the Pannonian Basin System. Nafta 2012, 63, 223–235. [Google Scholar]
- Husanović, E.; Malvić, T. Review of deterministic geostatistical mapping methods in Croatian hydrocarbon reservoirs and advantages of such approach. Nafta 2014, 65, 57–63. [Google Scholar]
- Novak Zelenika, K.; Malvić, T. Utvrđivanje sekvencijskim indikatorskim metodama slabopropusnih litofacijesa kao vrste nekonvencionalnih ležišta ugljikovodika na primjeru polja Kloštar (Determination of Low Permeable Lithofacies, as Type of Unconventional Hydrocarbon Reservoirs, Using Sequential Indicator Methods, Case Study from the Kloštar Field). Rudarsko-geološko-naftni zbornik (Min.-Geol.-Pet. Eng. Bull.) 2014, 28, 23–38. [Google Scholar]
- Malvić, T.; Velić, J. Stochastically improved methodology for probability of success (POS) calculation in hydrocarbon systems. RMZ-Mater. Geoenviron. 2015, 62, 149–155. [Google Scholar]
- Novak Mavar, K. Modeliranje površinskoga transporta i geološki aspekti skladištenja ugljikova dioksida u neogenska pješčenjačka ležišta Sjeverne Hrvatske na primjeru polja Ivanić (Surface Transportation Modelling and Geological Aspects of Carbon-Dioxide Storage into Northern Croatian Neogene Sandstone Reservoirs, Case Study Ivanić Field). Ph.D. Thesis, Faculty of Mining, Geology and Petroleum, University of Zagreb, Zagreb, Croatia, 2015. [Google Scholar]
- Špelić, M.; Malvić, T.; Saraf, V.; Zalović, M. Remapping of depth of e-log markers between Neogene basement and Lower/Upper Pannonian border in the Bjelovar Subdepression. J. Maps 2016, 12, 45–52. [Google Scholar] [CrossRef]
- Mesić Kiš, I. Odabir interpolacijskog algoritma primjerenog za kartiranje naftno-plinskog polja Šandrovac (Selection of interpolation algorithm appropriate for mapping of oil and gas Šandrovac Field). In Proceedings of the Symposium PhD Students of Science, Zagreb, Croatia, 26 February 2016; Primožić, I., Hranilović, D., Eds.; Faculty of Science, University of Zagreb: Zagreb, Croatia, 2016; p. 64. [Google Scholar]
- Mesić Kiš, I. Kartiranje i reinterpretacija geološke povijesti Bjelovarske subdepresije univerzalnim krigiranjem te novi opći metodološki algoritmi za kartiranje sličnih prostora (Mapping and Reinterpretation of the Geological Evolution of the Bjelovar Subdepression by Universal Kriging and New General Methodological Algorithms for Mapping in Similar Areas). Ph.D. Thesis, Faculty of Science, University of Zagreb, Zagreb, Croatia, 2017. [Google Scholar]
- Malvić, T. Stochastics—Advantages and uncertainties for subsurface geological mapping and volumetric or probability calculations. Mater. Geoenviron. 2018, 65, 9–19. [Google Scholar] [CrossRef]
- Ivšinović, J. Deep mapping of hydrocarbon reservoirs in the case of a small number of data on the example of the Lower Pontian reservoirs of the western part of Sava Depression. In Proceedings of the 2nd Croatian Congress on Geomathematics and Geological Terminology, Zagreb, Croatia, 6 October 2018; Malvić, T., Velić, J., Rajić, R., Eds.; Faculty of Mining, Geology and Petroleum, University of Zagreb: Zagreb, Croatia, 2018; pp. 59–65. [Google Scholar]
- Gringarten, E.; Deutsch, C.V. Methodology for Variogram Interpretation and Modeling for Improved Reservoir Characterization. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. SPE-56654-MS. [Google Scholar] [CrossRef]
- Gringarten, E.; Deutsch, C.V. Teacher’s Aide Variogram Interpretation and Modeling. Math. Geol. 2001, 33, 507–534. [Google Scholar] [CrossRef]
- Journel, A.G.; Alabert, F.G. New Method for Reservoir Mapping. J. Pet. Technol. 1990, 40, 7. [Google Scholar] [CrossRef]
- Wenlong, X.; Tran, T.T.; Srivastava, R.M.; Journel, A.G. Integrating seismic Data in Reservoir Modeling: The Collocated Cokriging Alternative. Proc. SPE 1992, 24742, 833–842. [Google Scholar]
- Al-Mudhafar, W.J. Integrating Core Porosity and Well Logging Interpretations for Multivariate Permeability Modeling through Ordinary Kriging and Co-Kriging Algorithms. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. OTC-28764-MS. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Bayesian kriging for reproducing reservoir heterogeneity in a tidal depositional environment of a sandstone formation. J. Appl. Geophys. 2019, 160, 84–102. [Google Scholar] [CrossRef]
- Ortiz, J.C.; Deutsch, C.V. Calculation of Uncertainty in the Variogram. Math. Geol. 2002, 34, 169–183. [Google Scholar] [CrossRef]
- Olea, R.A.; Pardo-Iguzquiza, E. Generalized Bootstrap Method for Assessment of Uncertainty in Semivariogram Inference. Math. Geosci. 2011, 43, 203–228. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978; 600p. [Google Scholar]
- Hohn, M.E. Geostatistics and Petroleum Geology; Van Nostrand Reinhold: New York, NY, USA, 1988; 400p. [Google Scholar]
- Liebhold, A.M.; Rossi, R.E.; Kemp, W.P. Geostatistics and Geographic Information System in Applied Insect Ecology. Ann. Rev. Entomol. 1993, 38, 303–327. [Google Scholar] [CrossRef]
- Velić, J.; Malvić, T.; Cvetković, M. Geologija i istraživanje ležišta ugljikovodika (Geology and Exploration of Hydrocarbon Reservoirs); Faculty of Mining, Geology and Petroleum Zagreb, University of Zagreb: Zagreb, Croatia, 2015; p. 144. ISBN 978-953-6923-28-1. [Google Scholar]
- Malvić, T. Review of Miocene shallow marine and lacustrine depositional environments in Northern Croatia. Geol. Q. 2012, 56, 493–504. [Google Scholar] [CrossRef]
- Royden, L.H. Late Cenozoic tectonics of the Pannonian Basin System. AAPG 1988, 45, 27–48. [Google Scholar]
- Pavelić, D.; Kovačić, M. Sedimentology and stratigraphy of the Neogene rift-type North Croatian Basin (Pannonian Basin System, Croatia): A review. Mar. Pet. Geol. 2018, 91, 455–469. [Google Scholar] [CrossRef]
- Malvić, T.; Velić, J. Neogene Tectonics in Croatian Part of the Pannonian Basin and Reflectance in Hydrocarbon Accumulations. In New Frontiers in Tectonic Research: At the Midst of Plate Convergence; Schattner, U., Ed.; InTech: Rijeka, Croatia, 2011; pp. 215–238. ISBN 978-953-307-594-5. [Google Scholar]
- Vrbanac, B.; Velić, J.; Malvić, T. Sedimentation of deep-water turbidites in main and marginal basins in the SW part of the Pannonian Basin. Geol. Carpath. 2010, 61, 55–69. [Google Scholar] [CrossRef]
- Brod, I.O. Geological Terminology in Classification of Oil and Gas Accumulation. AAPG Bull. 1945, 29, 1738–1755. [Google Scholar]
- Malvić, T.; Vrbanac, B. Geostatistički pojmovnik (Geostatistical Glossary). Hrvatski Matematički Elektronički Časopis 2013, 23, 7–56. [Google Scholar]
- Wu, C.F.J. Jackknife, Bootstrap and Other Resampling Methods in Regression Analysis. Ann. Stat. 1986, 14, 1261–1295. [Google Scholar] [CrossRef]
- Shao, J. Jackknifing in generalized linear models. Ann. Stat. 1992, 44, 673–686. [Google Scholar] [CrossRef]
- McIntosh, A.I. The Jackknife Estimation Method, Cornell University Library. 2016. Available online: https://arxiv.org/abs/1606.00497 (accessed on 20 November 2018).
- Wojciech, M. Kriging Method Optimization for the Process of DTM Creation Based on Huge Data Sets Obtained from MBESs. Geosciences 2018, 8, 433. [Google Scholar] [CrossRef]

| Well | Md | So | Sk | Sand (%) | Coarse Silt (%) | Clay (%) | CaCO3 with Gran. (%) | CaCO3 (%) | No. of Data |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.095 | 1.697 | 0.831 | 71.5 | 21 | 7.5 | 30.6 | 3 | |
| 57 | 0.282 | 1.640 | 1.087 | 63 | 47 | 26.8 | 22.3 | 3 | |
| 83 | 0.068 | 1.581 | 0.938 | 53 | 42 | 5 | 29 | 25 | 28 |
| 91 | 0.074 | 1.558 | 0.935 | 59 | 38 | 3 | 31.8 | 23 | |
| 92 | 0.063 | 1.546 | 1.02 | 54 | 44 | 2 | 29 | 6 | |
| 145 | 0.081 | 2.31 | 0.683 | 59.5 | 37.5 | 3 | 26.5 | 6 | |
| 153 | 0.066 | 2.135 | 0.786 | 50 | 47.7 | 2.3 | 26.5 | 11 |
| Well | Md | So | Sk | Sand (%) | Coarse Silt (%) | Clay (%) | CaCO3 with Gran. (%) | CaCO3 (%) |
|---|---|---|---|---|---|---|---|---|
| 25 | 0.071 | 1.560 | 1.239 | 56 | 44 | 0 | 30.1 | 14 |
| 31 | 0.101 | 1.430 | 0.980 | 76 | 24 | 0 | 28.4 | 4 |
| 33 | 0.099 | 1.660 | 1.100 | 75 | 25 | 0 | 35.4 | 1 |
| 45 | 0.094 | 1.496 | 1.445 | 85 | 15 | 0 | 28.8 | 1 |
| 55 | 0.094 | 1.461 | 1.172 | 77 | 23 | 0 | 27.6 | 41 |
| 57 | 0.037 | 1.564 | 1.251 | 28 | 72 | 0 | 20.4 | 2 |
| 59 | 0.095 | 1.460 | 1.150 | 79 | 21 | 0 | 27.0 | 15 |
| 68 | 0.098 | 1.530 | 1.300 | 53 | 21 | 0 | 28.7 | 1 |
| 120 | 0.065 | 1.167 | 1.044 | 72 | 47 | 0 | 31.2 | 18 |
| Field/Reservoir | OK (Original Semivariogram) | OK (Jack-Knifed Semivariogram) | Recommendation |
|---|---|---|---|
| “A”/“L” | 0.000676 (linear) | 0.000420 (exponential) | OK with original semivariogram or IDW. The effect of “bull-eyes” eliminated the jack-knifed approach. |
| “B”/“K1” | 0.001320 (linear) | 0.000970 (Gaussian) | OK with jack-knifed semivariogram |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Kriging with a Small Number of Data Points Supported by Jack-Knifing, a Case Study in the Sava Depression (Northern Croatia). Geosciences 2019, 9, 36. https://doi.org/10.3390/geosciences9010036
Malvić T, Ivšinović J, Velić J, Rajić R. Kriging with a Small Number of Data Points Supported by Jack-Knifing, a Case Study in the Sava Depression (Northern Croatia). Geosciences. 2019; 9(1):36. https://doi.org/10.3390/geosciences9010036
Chicago/Turabian StyleMalvić, Tomislav, Josip Ivšinović, Josipa Velić, and Rajna Rajić. 2019. "Kriging with a Small Number of Data Points Supported by Jack-Knifing, a Case Study in the Sava Depression (Northern Croatia)" Geosciences 9, no. 1: 36. https://doi.org/10.3390/geosciences9010036
APA StyleMalvić, T., Ivšinović, J., Velić, J., & Rajić, R. (2019). Kriging with a Small Number of Data Points Supported by Jack-Knifing, a Case Study in the Sava Depression (Northern Croatia). Geosciences, 9(1), 36. https://doi.org/10.3390/geosciences9010036






