Re-Aeration on Stepped Spillways with Special Consideration of Entrained and Entrapped Air
Abstract
1. Introduction
2. Background
2.1. Gas Diffusion
2.2. Mass Transfer Coefficient
2.3. Specific Air-Water Interface
3. Methodology
3.1. General Comments (Data Base)
3.2. Air-Water Flow Measurements
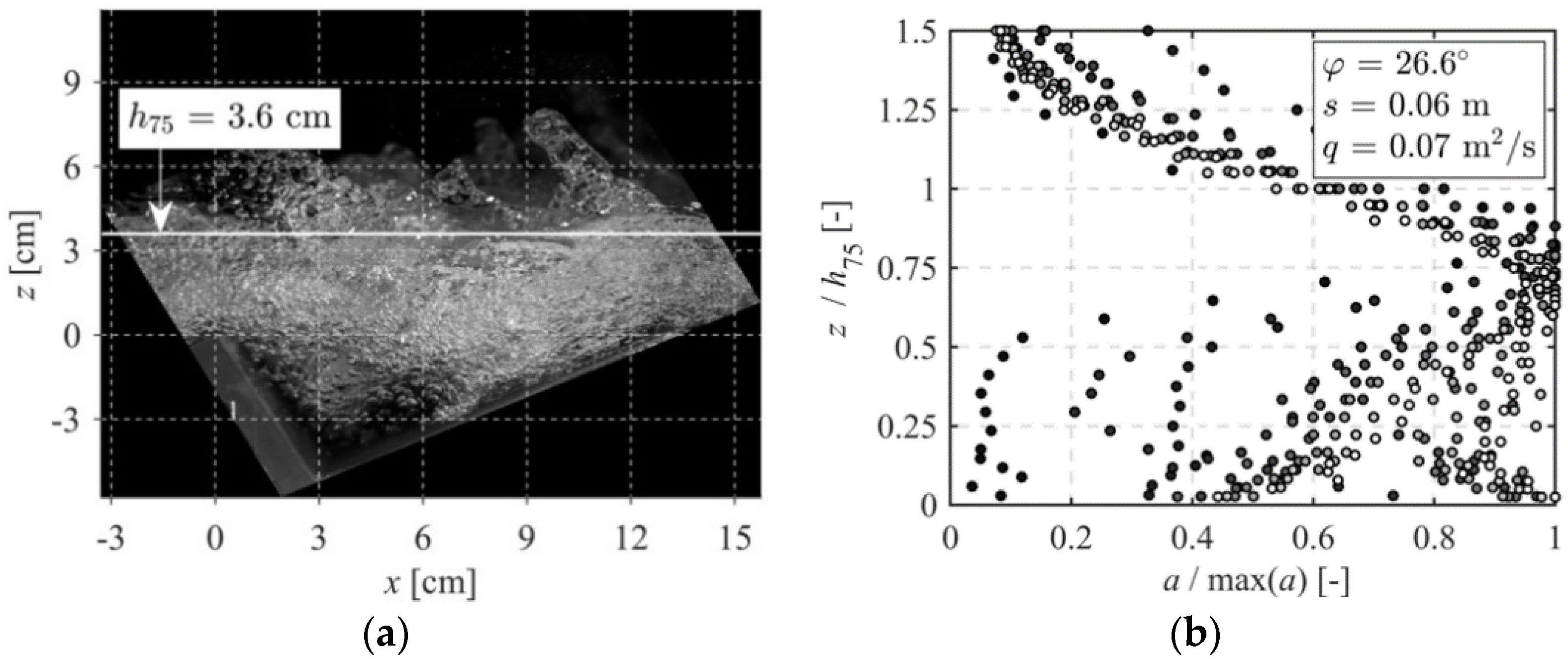
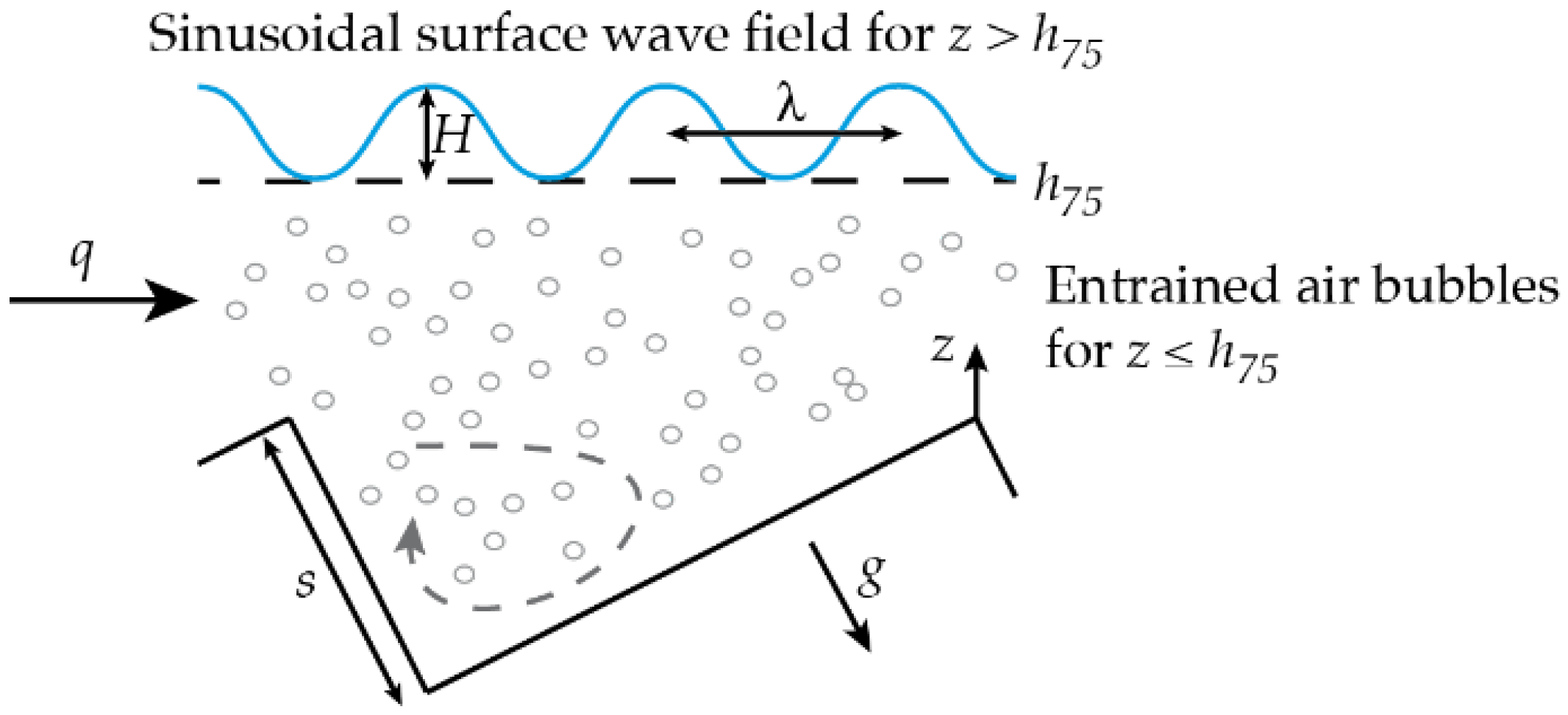
3.3. Surface Wave Characterization
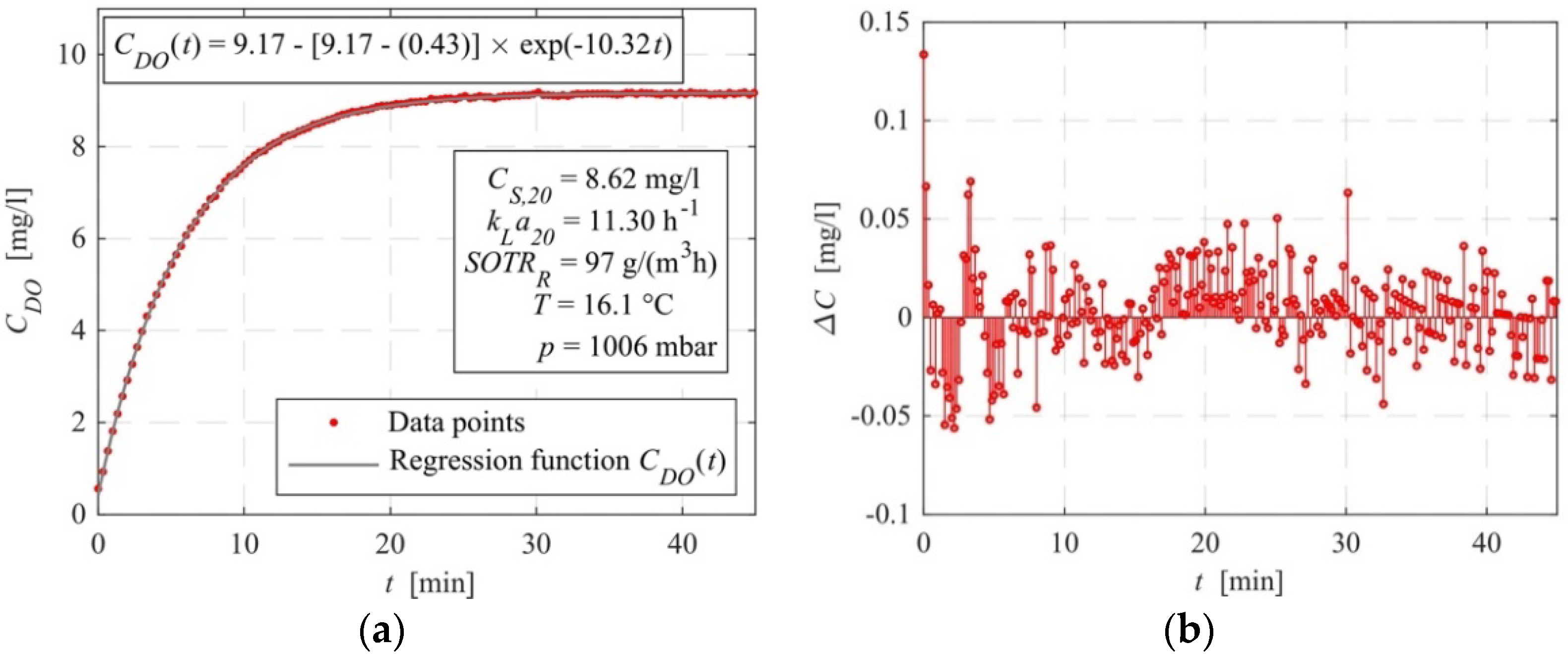
3.4. Dissolved Oxygen Measurements
4. Results
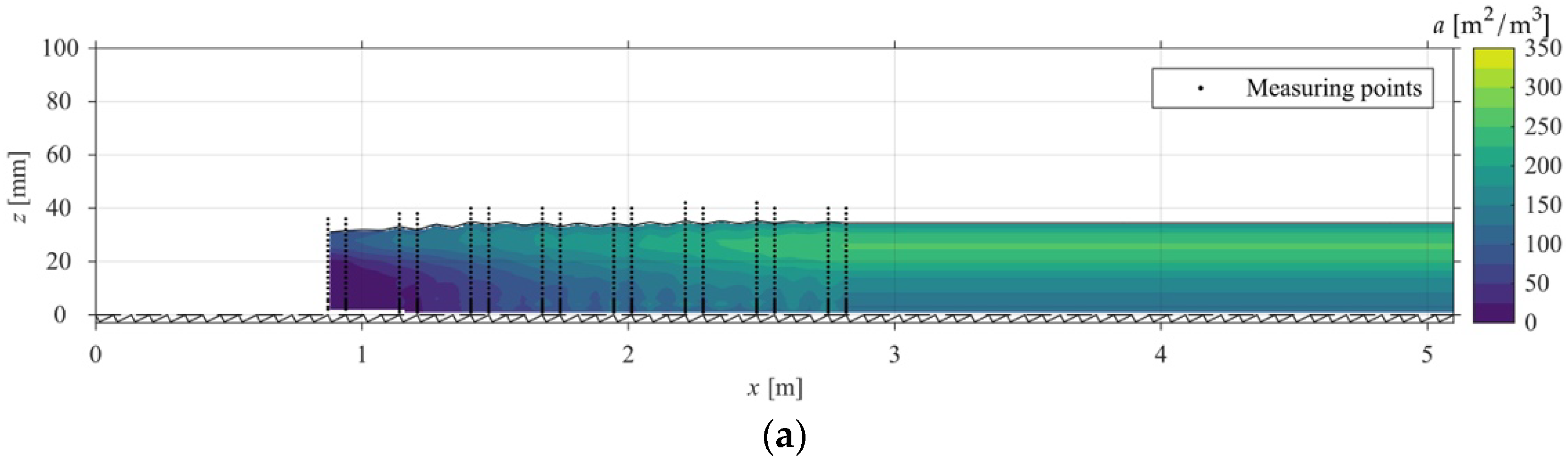
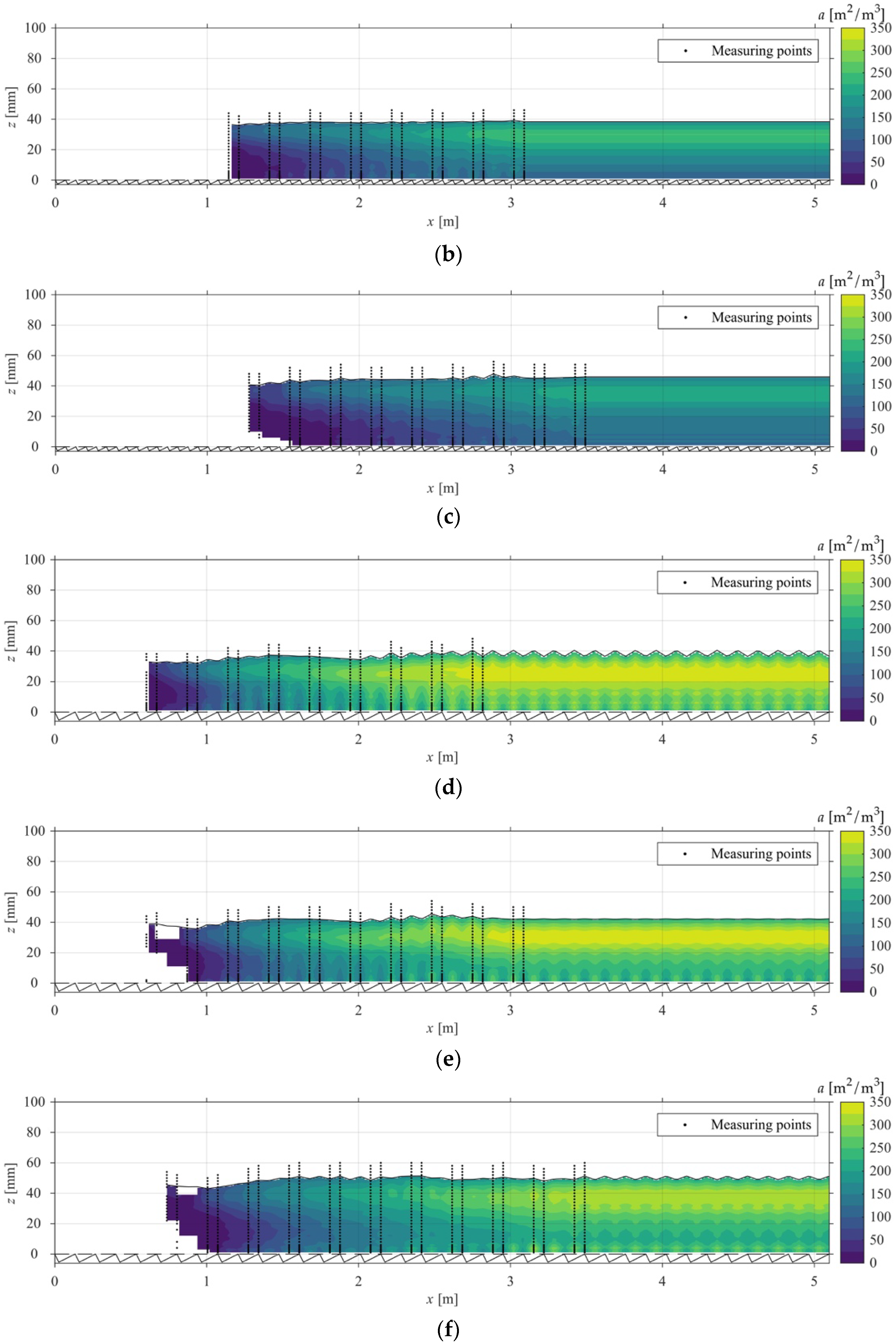
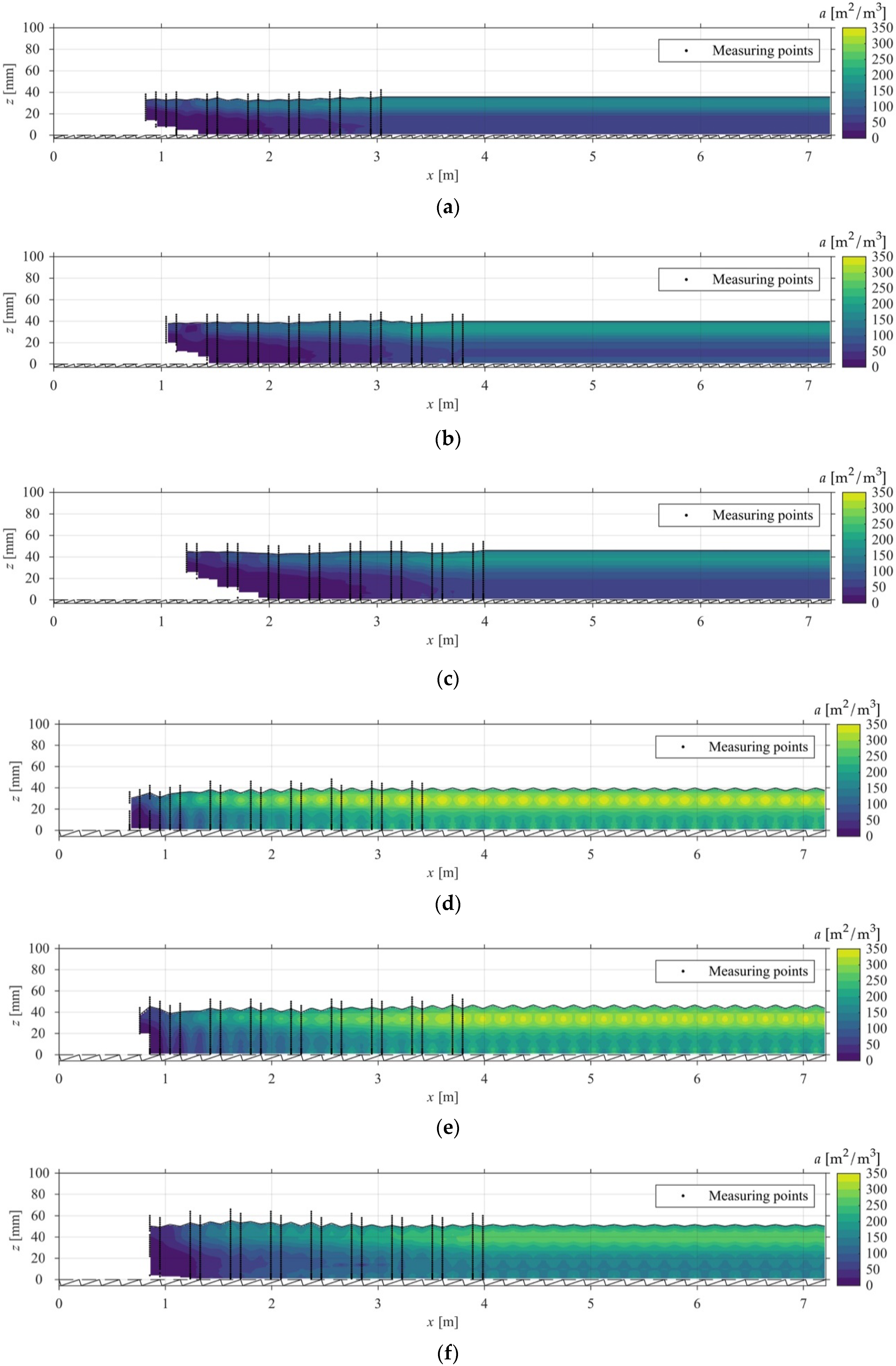
4.1. Specific Air-Water Interface
4.2. Re-Aeration Perfomance
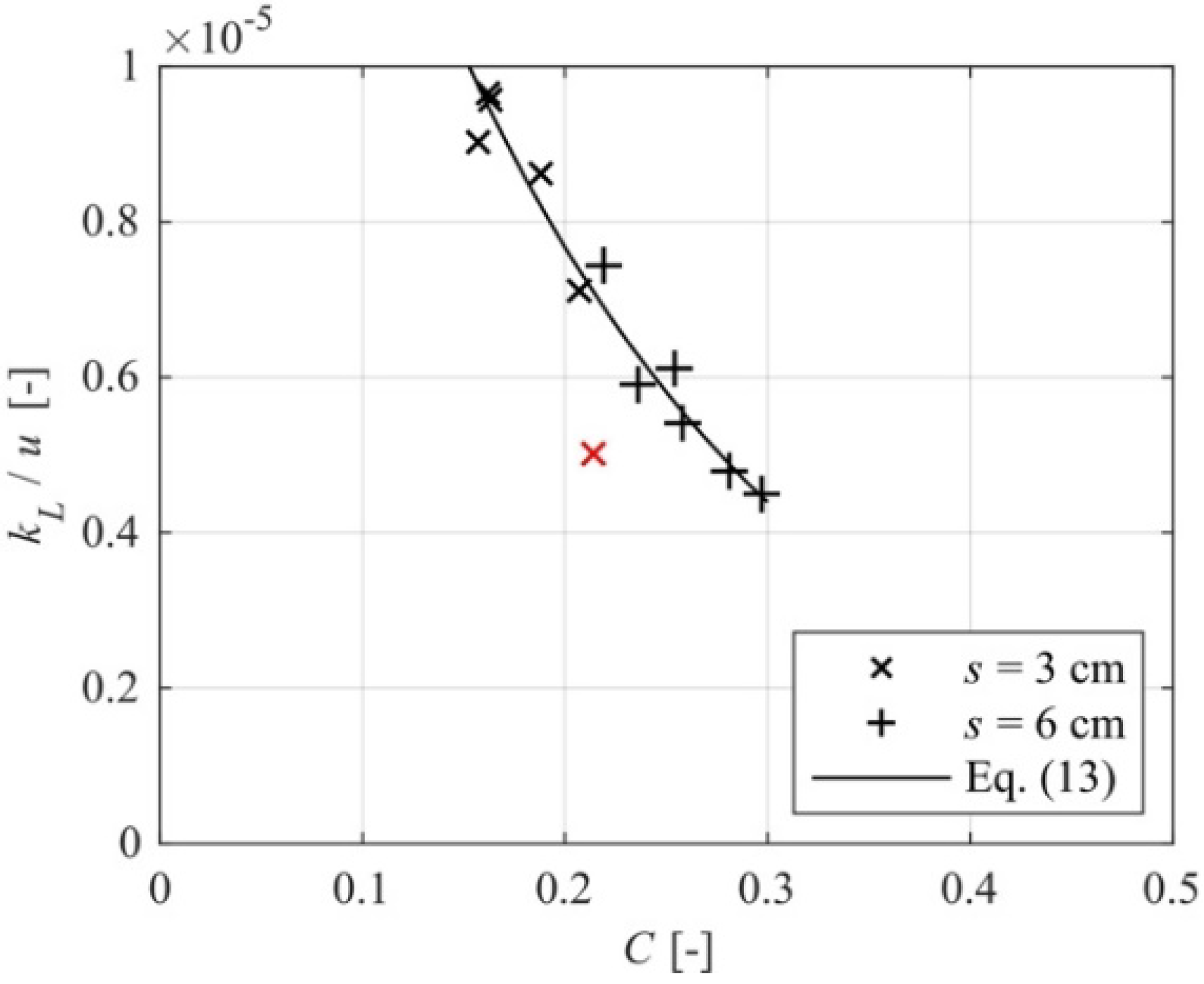
4.3. Mass Transfer Velocity
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Assumption of a Three-Dimensional, Sinusoidal Surface Wave Field
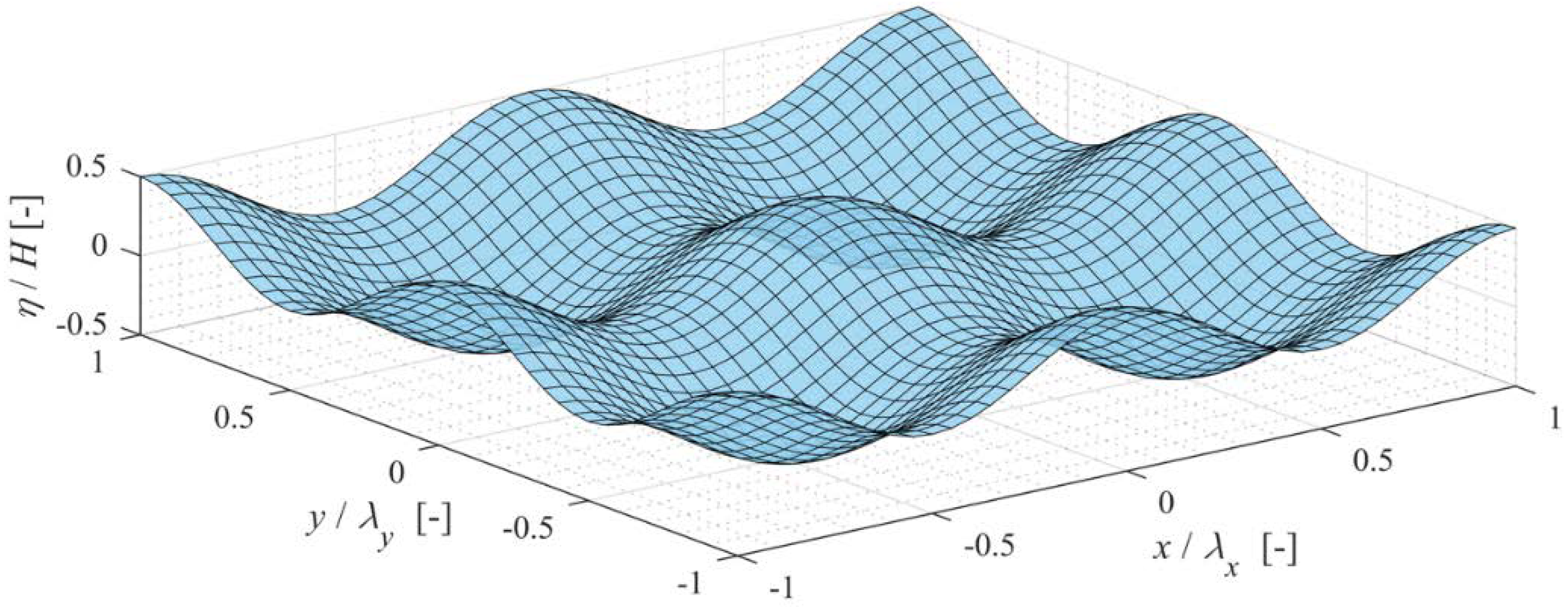
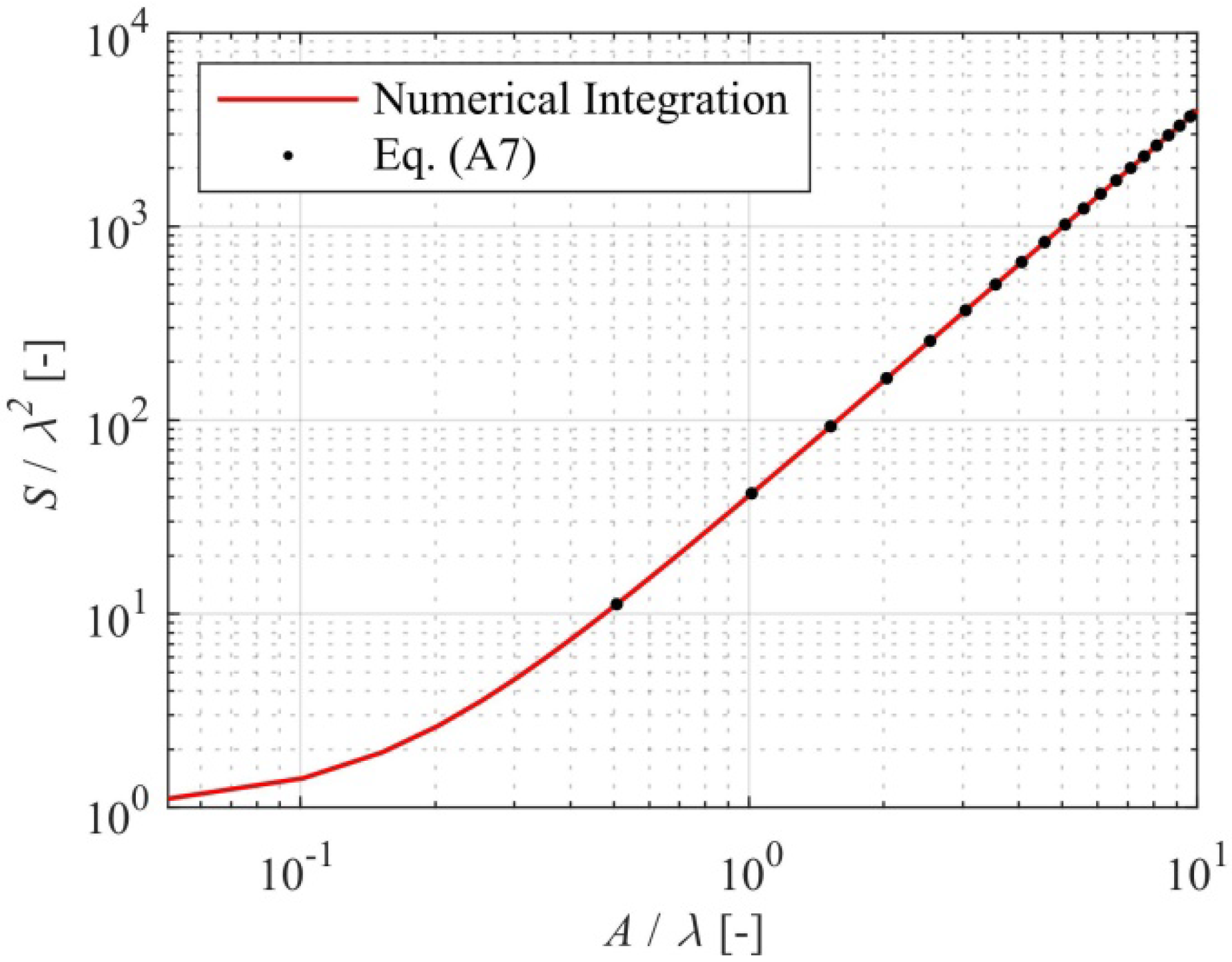
References
- Chanson, H.; Bung, D.B.; Matos, J. Stepped spillways and cascades. In Energy Dissipation in Hydraulic Structures; Chanson, H., Ed.; CRC Press: Leiden, The Netherlands, 2015; pp. 45–64. ISBN 978-1-138-02755-8. [Google Scholar]
- Valero, D.; Bung, D.B. Development of the interfacial air layer in the non-aerated region of high-velocity spillway flows. Instabilities growth, entrapped air and influence on the self-aeration onset. Int. J. Multiph. Flow 2016, 100, 66–74. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B. Reformulating self-aeration in hydraulic structures: Turbulent growth of free surface perturbations leading to air entrainment. Int. J. Multiph. Flow 2018, 100, 127–142. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Stepped Chutes and Spillways; A. A. Balkema: Lisse, The Nethererlands, 2002; ISBN 9058093522. [Google Scholar]
- Gameson, A.L.H. Weirs and Aeration of Rivers. J. Inst. Water Eng. 1957, 11, 477–490. [Google Scholar]
- Tebbutt, T.H.Y. Some studies on reaeration in cascades. Water Res. 1972, 6, 297–304. [Google Scholar] [CrossRef]
- Tebbutt, T.H.Y.; Essery, L.T.S.; Rasaratnam, S.K. Reaeration performance of stepped cascades. J. Inst. Water Eng. 1977, 31, 285–297. [Google Scholar]
- Avery, S.T.; Novak, P. Oxygen transfer at hydraulic structures. J. Hydraulics Div. 1978, 104, 1521–1540. [Google Scholar]
- Essery, I.T.S.; Tebutt, T.H.Y.; Rasaratnam, S.K. Design of Spillways for Re-Aeration of Polluted Waters; Construction Industry Research and Information Association (CIRIA): Birmingham, UK, 1978; ISBN 978-0860171102. [Google Scholar]
- Toombes, L.; Chanson, H. Air–water mass transfer on a stepped waterway. J. Environ. Eng. 2005, 131, 1377–1386. [Google Scholar] [CrossRef]
- Baylar, A.; Emiroglu, M.E.; Bagatur, T. An experimental investigation of aeration performance in stepped spillways. Water Environ. J. 2006, 20, 35–42. [Google Scholar] [CrossRef]
- Erpicum, S.; Lodomez, M.; Savatier, J.; Archambeau, P.; Dewals, B.; Pirotton, M. Physical modeling of an aerating stepped spillway. In Hydraulic Structures and Water System Management, Proceedings of the 6th IAHR International Symposium on Hydraulic Structures, Portland, OR, USA, 27–30 June 2016; Crookston, B., Tullis, B.P., Eds.; Utah State University: Logan, UT, USA, 2016; pp. 608–617. ISBN 978-1-884575-75-4. [Google Scholar] [CrossRef]
- Bung, D.B. Non-intrusive detection of air–water surface roughness in self-aerated chute flows. J. Hydraulic Res. 2013, 51, 322–329. [Google Scholar] [CrossRef]
- Killen, J.M. The Surface Characteristics of Self-Aerated Flow in Steep Channels. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1968. [Google Scholar]
- Wilhelms, S.C.; Gulliver, J.S. Bubbles and waves description of self-aerated spillway flow. J. Hydraulic Res. 2005, 43, 522–531. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 1997; ISBN 0 521 29846 0. [Google Scholar]
- Lewis, W.K.; Whitman, W.G. Principles of Gas Absorption. J. Ind. Eng. Chem. 1924, 16, 1215–1220. [Google Scholar] [CrossRef]
- Westrich, B.; Haag, I. Modellgestützte Optimierung des Einsatzes Finanzieller Mittel Zur Verbesserung des Sauerstoffhaushalts Im Neckar; Technical Report; University of Stuttgart: Stuttgart, Germany, 2002. [Google Scholar]
- Higbie, R. The rate of absorption of a pure gas into a still liquid during a short time exposure. Trans. Am. Inst. Chem. Eng. 1935, 31, 365–389. [Google Scholar]
- Danckwerts, P.V. Significance of liquid-film coefficients in gas absorption. J. Ind. Eng. Chem. 1951, 43, 1460–1467. [Google Scholar] [CrossRef]
- Fortescue, G.E.; Pearson, J.R.A. On Gas Absorption into a Turbulent Liquid. Chem. Eng. Sci. 1967, 22, 1163–1176. [Google Scholar] [CrossRef]
- Lamont, J.C.; Scott, D.S. An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE 1970, 16, 513–519. [Google Scholar] [CrossRef]
- Moog, D.B.; Jirka, G.H. Macro-roughness effects on stream reaeration. In Hydraulic Engineering ’94, Proceedings of the 1994 ASCE Conference, Buffalo, NY, USA, 1–5 August 1994; Cotroneo, G.V., Rumer, R.R., Eds.; American Society of Civil Engineers: Reston, VA, USA, 1994; pp. 994–998. [Google Scholar]
- Gualtieri, C.; Gualtieri, P. Turbulence-based models for gas transfer analysis with channel shape factor influence. Environ. Fluid Mech. 2004, 4, 249–271. [Google Scholar] [CrossRef]
- Jun, K.S.; Jain, S.C. Oxygen transfer in bubbly turbulent shear flow. J. Hydraulic Eng. 1993, 119, 21–36. [Google Scholar] [CrossRef]
- Kawase, Y.; Moo-Young, M. Correlations for liquid-phase mass transfer coefficients in bubble column reactors with newtonian and non-newtonian fluids. Can. J. Chem. Eng. 1992, 70, 48–54. [Google Scholar] [CrossRef]
- Demars, B.O.L.; Manson, R.J. Temperature dependence of stream aeration coefficients and the effect of water turbulence: A critical review. Water Res. 2013, 47, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Chanson, H. Measuring air-water interface area in supercritical open channel flows. Water Res. 1997, 31, 1414–1420. [Google Scholar] [CrossRef]
- Toombes, L. Experimental Study of Air-Water Flow Properties on Low-Gradient Stepped Cascades. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2002. [Google Scholar]
- Toombes, L.; Chanson, H. Air-Water Flow and Gas Transfer at Aeration Cascades: A Comparative Study of Smooth and Stepped Chutes. In International Workshop on Hydraulics of Stepped Spillways (IAHR); Minor, H.-E., Hager, W.H., Eds.; A.A. Balkema: Zurich, Switzerland, 2000; pp. S77–S84. [Google Scholar]
- Cain, P. Measurements within Self-Aerated Flow on a Large Spillway. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1978. [Google Scholar]
- Chanson, H. Study of Air Entrainment and Aeration Devices on Spillway Model. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1988. [Google Scholar]
- Pegram, G.G.S.; Officer, A.K.; Mottram, S.R. Hydraulics of skimming flow on modeled stepped spillways. J. Hydraulic Eng. 1999, 125, 500–510. [Google Scholar] [CrossRef]
- André, S. High Velocity Aerated Flows on Stepped Chutes with Macro-Roughness Elements. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2004. [Google Scholar]
- Pfister, M.; Hager, W.H. Self-entrainment of air in stepped spillways. Int. J. Multiph. Flow 2011, 37, 99–107. [Google Scholar] [CrossRef]
- Bung, D.B.; Valero, D. Optical flow estimation in aerated flows. J. Hydraulic Res. 2016, 575–580. [Google Scholar] [CrossRef]
- Bung, D.B. Zur Selbstbelüfteten Gerinneströmung Auf Kaskaden Mit Gemässigter Neigung; Shaker: Aachen, Germany, 2009; ISBN 978-3-8322-8382-7. [Google Scholar]
- Schlenkhoff, A.; Bung, D.B. Prediction of the oxygen transfer in self-aerated skimming flow on embankment stepped spillways. In Proceedings of the 33rd IAHR World Congress “Water Engineering for a Sustainable Environment”, Vancouver, BC, Canada, 9–14 August 2009. [Google Scholar]
- Bung, D.B. Fließcharakteristik und Sauerstoffeintrag bei selbstbelüfteten Gerinneströmungen auf Kaskaden mit gemäßigter Neigung. Österreichische Wasser- und Abfallwirtschaft 2011, 63, 76–81. [Google Scholar] [CrossRef]
- Bung, D.B. Developing flow in skimming flow regime on embankment stepped spillways. J. Hydraulic Res. 2011, 49, 639–648. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Hydraulic design of stepped spillways. J. Hydraulic Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Chanson, H.; Toombes, L. Hydraulics of stepped chutes: The transition flow. J. Hydraulic Res. 2004 42, 43–54. [CrossRef]
- Yasuda, Y.; Ohtsu, I. Flow Resistance of Skimming Flows in Stepped Channels. In Hydraulic Engineering for Sustainable Water Resources Management at the Turn of the Millenium, Proceedings of the 28th IAHR World Congress, Graz, Austria, 22–27 August 1999; Technical University Graz: Graz, Austria, 1999. [Google Scholar]
- Bung, D.B. Sensitivity of phase detection techniques in aerated chute flows to hydraulic design parameters. In Proceedings of the 2nd IAHR Europe Congress, Munich, Germany, 27–29 June 2012. [Google Scholar]
- Chanson, H. Air-water flow measurements with intrusive, phase-detection probes: Can we improve their interpretation? J. Hydraulic Eng. 2002, 128, 252–255. [Google Scholar] [CrossRef]
- Bung, D.B. Air-water surface roughness in self-aerated stepped spillway flows. In Proceedings of the 35th IAHR World Congress, Chengdu, China, 8–13 September 2013. [Google Scholar]
- American Society of Civil Engineers. Measurement of Oxygen Transfer in Clean Water; American Society of Civil Engineers: Reston, VA, USA, 2007. [Google Scholar]
- Boes, R.M.; Hager, W.H. Two-phase flow characteristics of stepped spillways. J. Hydraulic Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Scale effects in microscopic air-water flow properties in high-velocity free-surface flows. Exp. Therm. Fluid Sci. 2017 83, 19–36. [CrossRef]
| Slope 1:2 | Slope 1:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step Height [cm] | 3 | 6 | 3 | 6 | ||||||||
| Discharge [m2/s] | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 |
| λ [cm] | 6.1 (1.6) | 7.5 (1.4) | 8.9 (2.3) | 7.1 (1.7) | 7.3 (1.4) | 6.6 (1.8) | 6.7 (1.3) | 5.9 (1.2) | 7.1 (1.9) | 5.9 (1.3) | 5.7 (1.1) | 6.6 (1.6) |
| H [cm] | 1.4 (0.6) | 1.3 (0.8) | 1.3 (0.6) | 2.6 (1.0) | 2.0 (1.3) | 2.1 (1.1) | 1.3 (0.8) | 1.3 (0.5) | 1.2 (0.7) | 3.9 (1.4) | 3.1 (1.2) | 2.9 (1.2) |
| Slope 1:2 | Slope 1:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step Height [cm] | 3 | 6 | 3 | 6 | ||||||||
| Discharge [m2/s] | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 |
| Entrained air bubbles Aent [m2] (Equation (11)) | 7.37 | 7.31 | 6.93 | 12.67 | 12.60 | 13.21 | 5.65 | 7.05 | 6.89 | 17.58 | 18.32 | 16.06 |
| Air-water mixture surface [m2] (Equation (A7)) | 1.95 | 1.58 | 1.34 | 3.24 | 2.29 | 2.58 | 2.55 | 2.62 | 2.06 | 10.67 | 7.88 | 5.71 |
| Atot [m2] | 9.32 | 8.89 | 8.27 | 15.91 | 14.89 | 15.79 | 8.20 | 9.67 | 8.95 | 28.25 | 26.20 | 21.77 |
| Slope 1:2 | Slope 1:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step Height [cm] | 3 | 6 | 3 | 6 | ||||||||
| Discharge [m2/s] | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 |
| atot [m2/m3] | 150 | 132 | 106 | 197 | 190 | 177 | 91 | 98 | 81 | 223 | 196 | 153 |
| Slope 1:2 | Slope 1:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step Height [cm] | 3 | 6 | 3 | 6 | ||||||||
| Discharge [m2/s] | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 |
| kLa20 [1/h] | (6.71) 6.85 (7.04) | (9.27) 9.32 (9.41) | (9.39) 9.76 (10.13) | (8.51) 8.73 (8.87) | (11.61) 11.68 (11.81) | (10.53) 11.11 (11.49) | (6.56) 7.54 (11.33) | (8.14) 8.87 (11.33) | (9.74) 10.17 (11.33) | (7.74) 8.60 (11.33) | (9.40) 10.08 (11.33) | (10.92) 11.47 (11.89) |
| CS,20 [mg/L] | (8.44) 8.61 (8.77) | (8.57) 8.68 (8.78) | (8.60) 8.70 (8.70) | (8.46) 8.63 (8.80) | (8.54) 8.67 (8.79) | (8.61) 8.75 (8.95) | (8.29) 8.43 (8.61) | (8.39) 8.48 (8.61) | (8.41) 8.48 (8.61) | (8.26) 8.42 (8.61) | (8.31) 8.43 (8.61) | (8.34) 8.53 (8.86) |
| Slope 1:2 | Slope 1:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step Height [cm] | 3 | 6 | 3 | 6 | ||||||||
| Discharge [m2/s] | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 | 0.07 | 0.09 | 0.11 |
| kL [cm/h] | 4.6 | 7.1 | 9.2 | 4.4 | 6.1 | 6.3 | 8.3 | 9.1 | 12.6 | 3.9 | 5.1 | 7.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bung, D.B.; Valero, D. Re-Aeration on Stepped Spillways with Special Consideration of Entrained and Entrapped Air. Geosciences 2018, 8, 333. https://doi.org/10.3390/geosciences8090333
Bung DB, Valero D. Re-Aeration on Stepped Spillways with Special Consideration of Entrained and Entrapped Air. Geosciences. 2018; 8(9):333. https://doi.org/10.3390/geosciences8090333
Chicago/Turabian StyleBung, Daniel B., and Daniel Valero. 2018. "Re-Aeration on Stepped Spillways with Special Consideration of Entrained and Entrapped Air" Geosciences 8, no. 9: 333. https://doi.org/10.3390/geosciences8090333
APA StyleBung, D. B., & Valero, D. (2018). Re-Aeration on Stepped Spillways with Special Consideration of Entrained and Entrapped Air. Geosciences, 8(9), 333. https://doi.org/10.3390/geosciences8090333





