Decorrelation of GRACE Time Variable Gravity Field Solutions Using Full Covariance Information
Abstract
1. Introduction
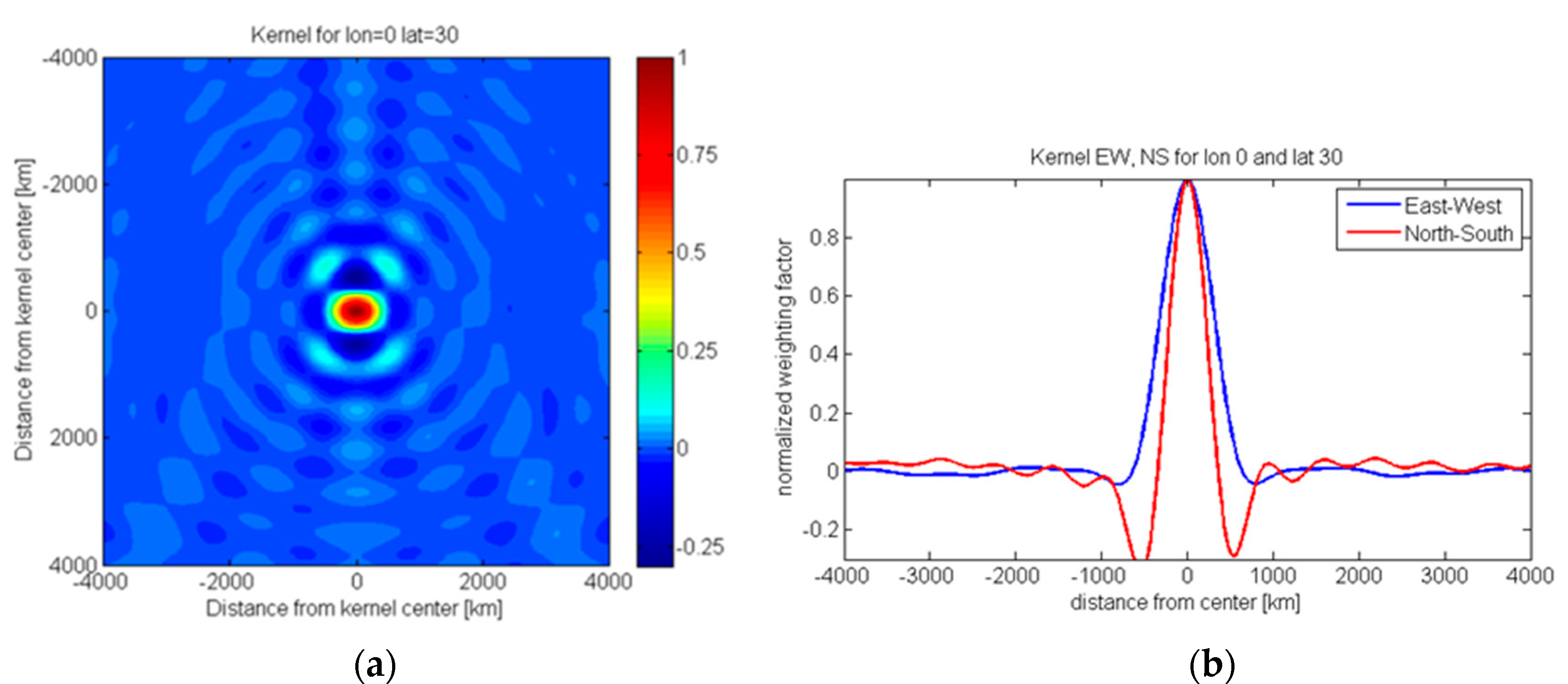
2. Decorrelation Strategy and Setup of Experiments
3. Results from Closed-Loop Simulations
3.1. The Closed-Loop Simulation Environment
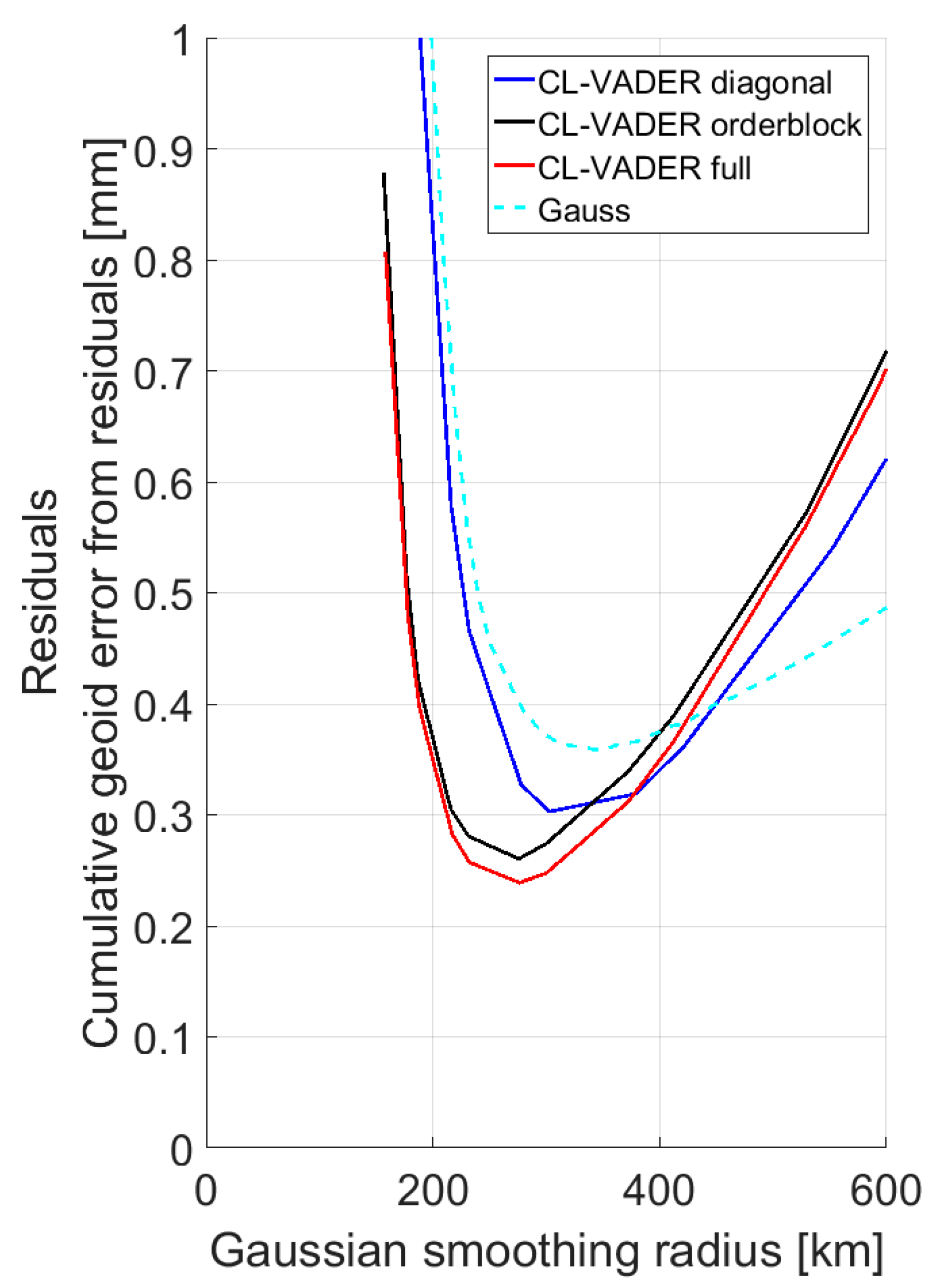
3.2. Determination of a Favorable Filter Design
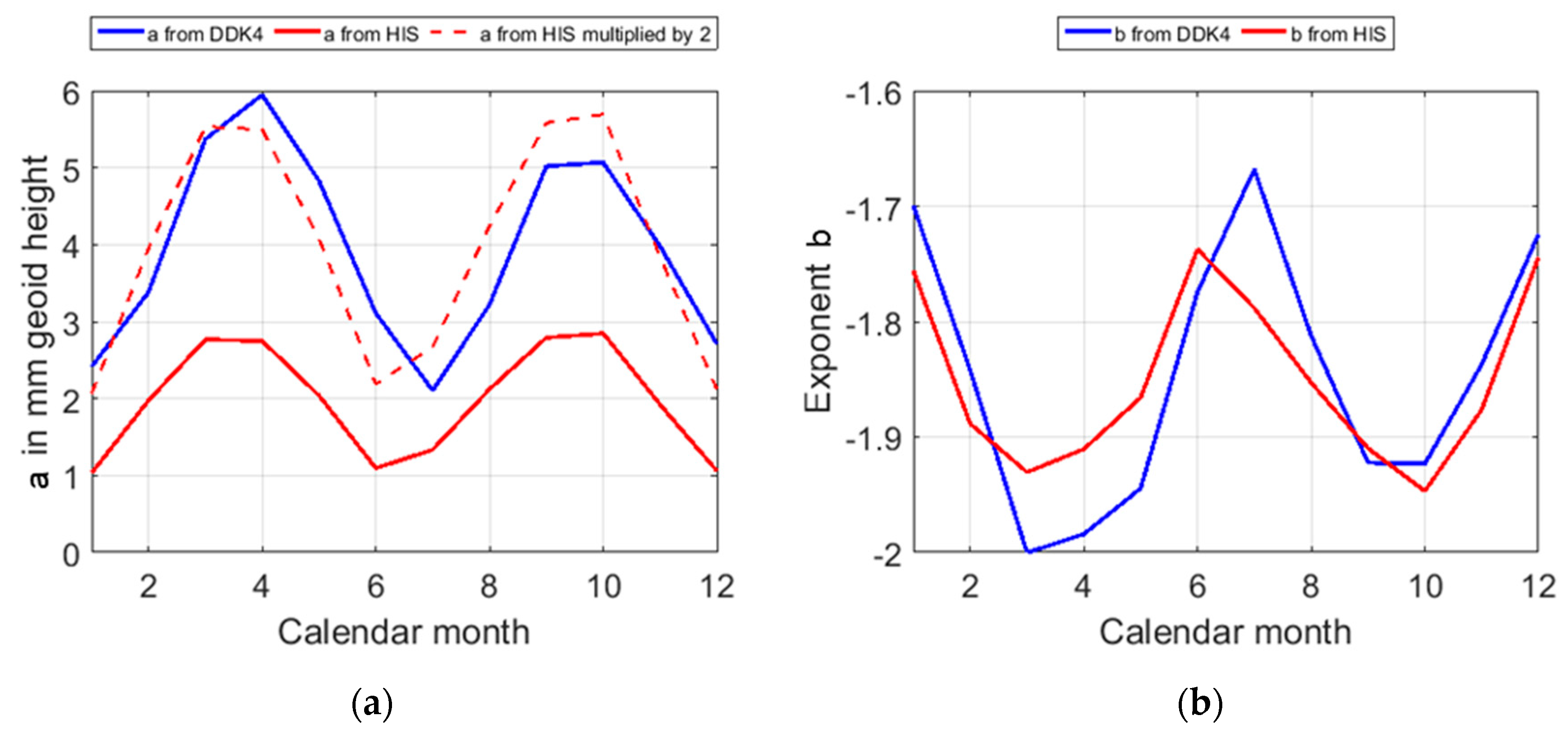
4. Impact of Post-Processing Methods on the Phase of Seasonal Signals with the Closed-Loop Environment
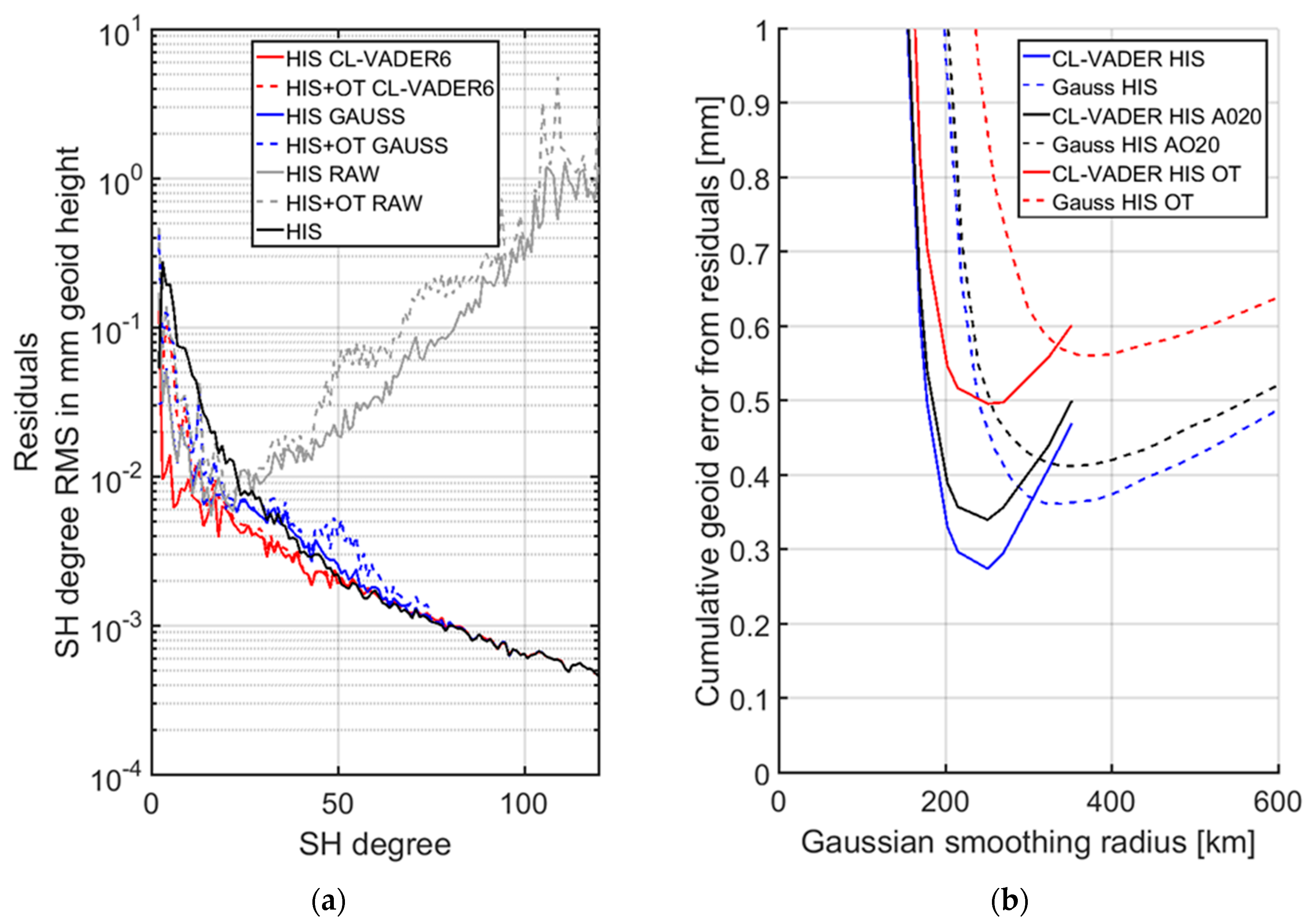
5. Application to Real Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Rgigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Shepherd, A.; Ivins, E.R.; Geruo, A.; Barletta, V.R.; Bentley, M.J.; Bettadpur, S.; Briggs, K.H.; Bromwich, D.H.; Forsberg, R.; Galin, N.; et al. A reconciled estimate of ice-sheet mass balance. Science 2012, 338, 1183–1189. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar] [CrossRef]
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36, L18401. [Google Scholar] [CrossRef]
- Kusche, J. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 2007, 81, 733–749. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Klees, R.; Revtova, E.A.; Gunter, B.C.; Ditmar, P.; Oudman, E.; Winsemius, H.C.; Savenije, H.H.G. The design of an optimal filter for monthly GRACE gravity models. Geophys. J. Int. 2008, 175, 417–432. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Zehentner, N.; Klinger, B.; Kvas, A. ITSG-Grace2014: A new GRACE gravity field release computed in Graz. In Proceedings of the GRACE Science Team Meeting 2014, Potsdam, Germany, 29 September–1 October 2014. [Google Scholar]
- ITSG-Grace2016-Monthly and Daily Gravity Field Solutions from GRACE. GFZ Data Services. Available online: https://graz.pure.elsevier.com/en/publications/itsg-grace2016-monthly-and-daily-gravity-field-solutions-from-gra (accessed on 22 August 2018).
- Kruizinga, A. CSR Release-05 GRACE Level-2 Data Products. Available online: http://www2.csr.utexas.edu/grace/RL05.html (accessed on 22 August 2018).
- Dahle, C. Release Notes for GFZ GRACE Level-2 Products—Version RL05. GFZ Potsdam. Available online: http://isdc.gfz-potsdam.de/index.php?name=UpDownload&req=getit&lid=574 (accessed on 22 August 2018).
- Horvath, A.G. Retrieving geophysical signals from current and future satellite gravity missions. Ph.D. Thesis, Technische Universität München, München, Gremany, 2017. [Google Scholar]
- Devaraju, B. Understanding Filtering on the Sphere. Experiences from Filtering GRACE Data; Technische Universität München: München, Gremany, 2015. [Google Scholar]
- Chen, J.L.; Wilson, C.R.; Famiglietti, J.S.; Rodell, M. Spatial sensitivity of the Gravity Recovery and Climate Experiment (GRACE) time-variable gravity observations. J. Geophys. Res. 2005, 110, B08408. [Google Scholar] [CrossRef]
- Rietbroek, R. (Institute of Geodesy and Geoinformation, University of Bonn, Bonn, Germany). Personal communication, 2015.
- Murböck, M.; Pail, R.; Daras, I.; Gruber, T. Optimal orbits for temporal gravity recovery regarding temporal aliasing. J. Geod. 2004, 88, 113–126. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Forootan, E.; Klemann, V.; Kusche, J.; Sasgen, I. Supplement to: The Updated ESA Earth System Model for Gravity Mission Simulation Studies. Available online: http://dataservices.gfz-potsdam.de/panmetaworks/showshort.php?id=escidoc:502893 (accessed on 29 August 2018).
- Schrama, E.J.O.; Wouters, B.; Lavallée, D.A. Signal and noise in Gravity Recovery and Climate Experiment (GRACE) observed surface mass variations. J. Geophys. Res. 2007, 112, B08407. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Forootan, E.; Dahle, C.; Mayer- Gürr, T.; Kusche, J.; Flechtner, F. Modeling of present-day atmosphere and ocean non-tidal de-aliasing errors for future gravity mission simulations. J. Geod. 2016, 90, 423–436. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dynamics 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Savcenko, R.; Bosch, W. EOT08a—Empirical Ocean Tide Model from Multi-Mission Satellite Altimetry. Available online: ftp://ftp.sirgas.org/pub/EOT08a/doc/EOTO8a.pdf (accessed on 22 August 2018).
- Zehentner, N.; Mayer-Gürr, T. Precise orbit determination based on raw GPS measurements. J. Geod. 2016, 90, 275–286. [Google Scholar] [CrossRef]
- Sasgen, I.; Martinec, Z.; Fleming, K. Wiener optimal filtering of GRACE data. Stud. Geophys. Geod. 2006, 50, 499–508. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Forootan, E.; Klemann, V.; Kusche, J.; Sasgen, I. The updated ESA Earth System Model for future gravity mission simulation studies. J. Geod. 2015, 89, 505–513. [Google Scholar] [CrossRef]
- Liu, X.; Ditmar, P.; Siemes, C.; Revtova, E.; Klees, R.; Riva, R.; Zhao, Q. DEOS Mass Transport model (DMT-1) based on GRACE satellite data: Methodology and validation. Geophys. J. Int. 2010, 181, 769–788. [Google Scholar] [CrossRef]
- Devaraju, B.; Sneeuw, N. On the Spatial Resolution of Homogeneous Isotropic Filters on the Sphere. In VIII Hotine-Marussi Symposium on Mathematical Geodesy; Sneeuw, N., Novák, P., Crespi, M., Sansò, F., Eds.; Springer: Cham, Switzerland, 2015; Volume 142. [Google Scholar]
- Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L.; Kusche, J. Does GRACE see the terrestrial water cycle “intensifying”? J. Geophys. Res. Atmos. 2016, 121, 733–745. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Fekete, B.M.; Meybeck, M.; Lammers, R.B. Global system of rivers: Its role in organizing continental land mass and defining land-to-ocean linkages. Glob. Biogeochem. Cycles 2000, 14, 599–621. [Google Scholar] [CrossRef]
- Vishwakarma, D.B.; Devaraju, B.; Sneeuw, N. Minimizing the effects of filtering on catchment scale GRACE solutions. Water Resour. Res. 2006, 52, 5868–5890. [Google Scholar] [CrossRef]
- The Combined Satellite-Only Global Gravity Field Model GOCO02S. EGU General Assembly 2011. Available online: http://www.meetingorganizer.copernicus.org/EGU2011/EGU2011-10571.pdf (accessed on 22 August 2018).
- Zwally, H.J.; Giovinetto, M.B. Overview and Assessment of Antarctic Ice-Sheet Mass Balance Estimates: 1992–2009. Surv. Geophys. 2011, 32, 351–376. [Google Scholar] [CrossRef]

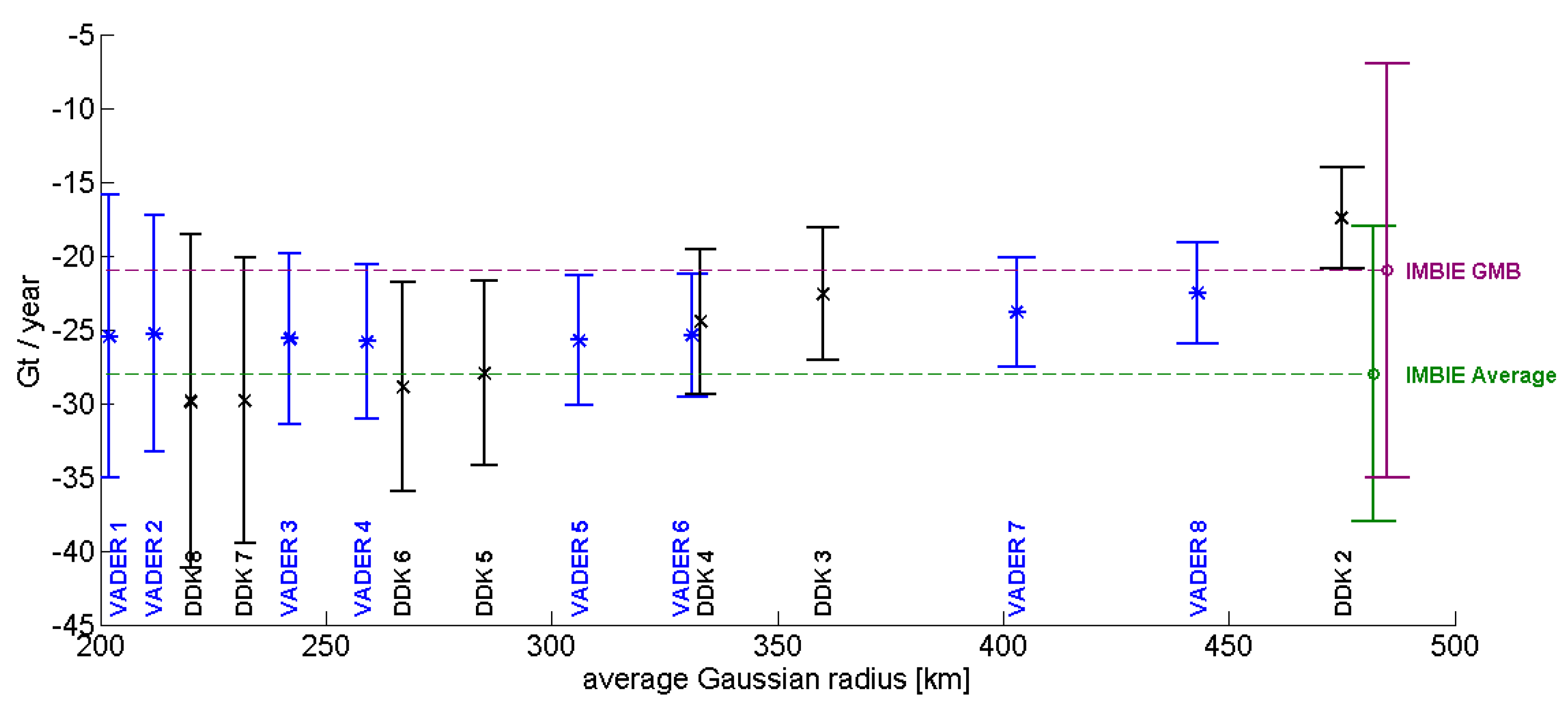
| DDK | Mean Gaussian Radius (km) | VADER (α) | |
|---|---|---|---|
| 7 | 232 | ||
| 6 | 267 | 254 | 0.1 |
| 5 | 285 | 287 | 0.5 |
| 4 | 333 | 335 | 1 |
| 3 | 360 | 436 | 5 |
| 2 | 475 | 492 | 10 |
| All Values mm Geoid | Median | Min | Max |
|---|---|---|---|
| S&W 250 km | 0.40 | 0.23 | 4.38 |
| Gauss 350 km | 0.36 | 0.22 | 6.75 |
| VADER M static N static (272 km) | 0.27 | 0.19 | 6.84 |
| VADER M variable N static (274 km) | 0.27 | 0.18 | 7.14 |
| VADER M static N variable (280 km) | 0.23 | 0.17 | 0.44 |
| VADER M variable N variable (276 km) | 0.24 | 0.17 | 0.43 |
| River | VADER | VADER Med. | S&W | Gauss |
|---|---|---|---|---|
| Parana | 8.7 (−0.7) | 9.4 (−0.5) | 13.5 (−4.8) | 12.1 (−0.1) |
| Mississippi | 1.4 (<0.1) | 1.4 (<0.1) | 3.3 (<0.1) | 1.8 (<0.1) |
| Amazon | 1.9 (−0.7) | 1.8 (−0.6) | 3.1 (−1.9) | 7.4 (−1.5) |
| Ganges | 8.0 (2.5) | 8.3 (2.5) | 29.8 (5.8) | 26.5 (5.9) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horvath, A.; Murböck, M.; Pail, R.; Horwath, M. Decorrelation of GRACE Time Variable Gravity Field Solutions Using Full Covariance Information. Geosciences 2018, 8, 323. https://doi.org/10.3390/geosciences8090323
Horvath A, Murböck M, Pail R, Horwath M. Decorrelation of GRACE Time Variable Gravity Field Solutions Using Full Covariance Information. Geosciences. 2018; 8(9):323. https://doi.org/10.3390/geosciences8090323
Chicago/Turabian StyleHorvath, Alexander, Michael Murböck, Roland Pail, and Martin Horwath. 2018. "Decorrelation of GRACE Time Variable Gravity Field Solutions Using Full Covariance Information" Geosciences 8, no. 9: 323. https://doi.org/10.3390/geosciences8090323
APA StyleHorvath, A., Murböck, M., Pail, R., & Horwath, M. (2018). Decorrelation of GRACE Time Variable Gravity Field Solutions Using Full Covariance Information. Geosciences, 8(9), 323. https://doi.org/10.3390/geosciences8090323





