Fluvial Geomorphology, Root Distribution, and Tensile Strength of the Invasive Giant Reed, Arundo Donax and Its Role on Stream Bank Stability in the Santa Clara River, Southern California
Abstract
:1. Introduction
1.1. Objectives and Significance of the Research
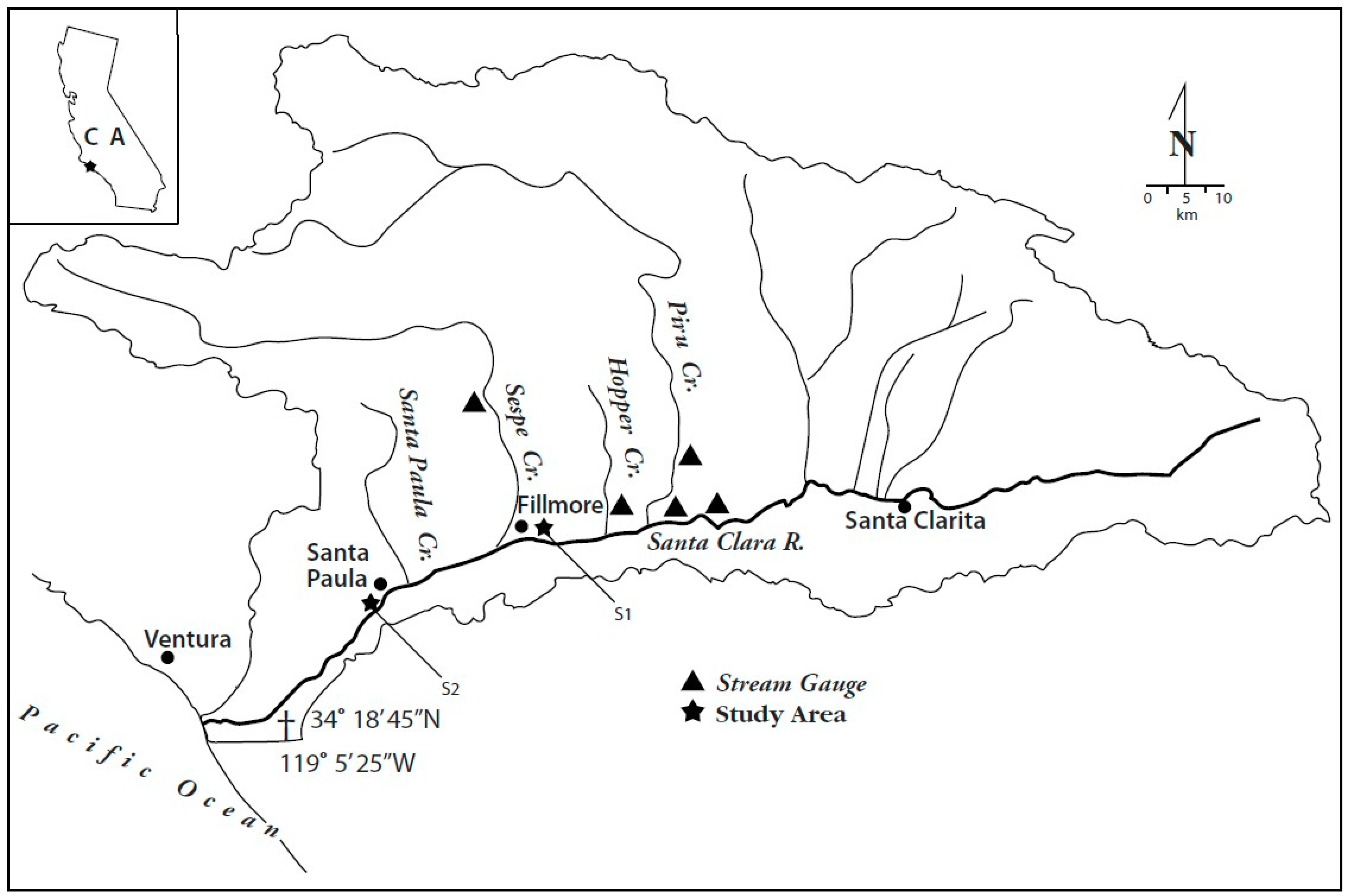
1.2. Study Area
1.3. Drainage Basin Characteristics
1.4. Arundo Donax Biology
1.5. Previous Work
2. Methods
2.1. Peak Discharge
2.2. Channel Change over Time
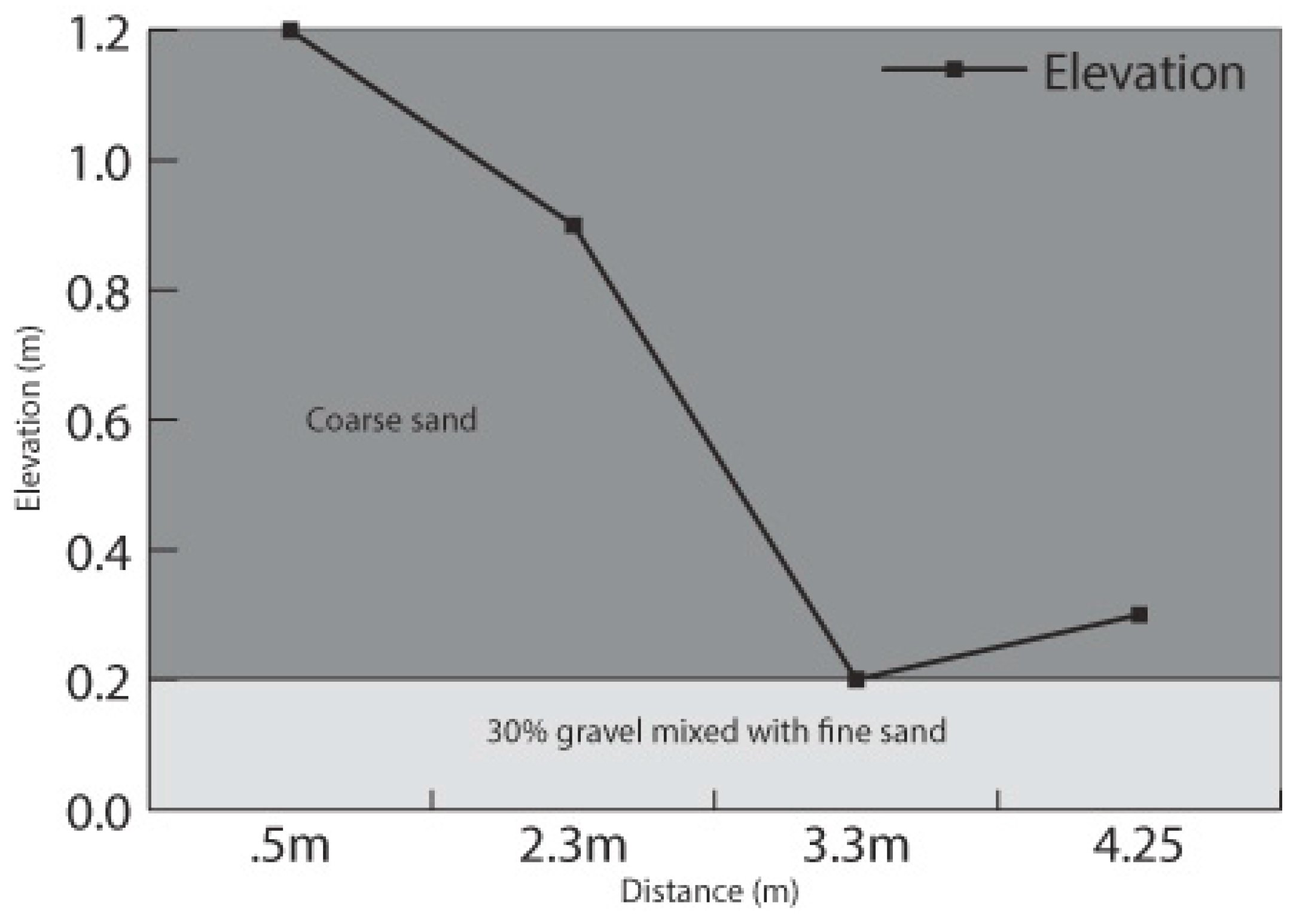
2.3. Root Distribution and Tensile Strength Measurements
2.4. Experimental Modeling of Bank Stability
3. Results
3.1. Peak Discharges
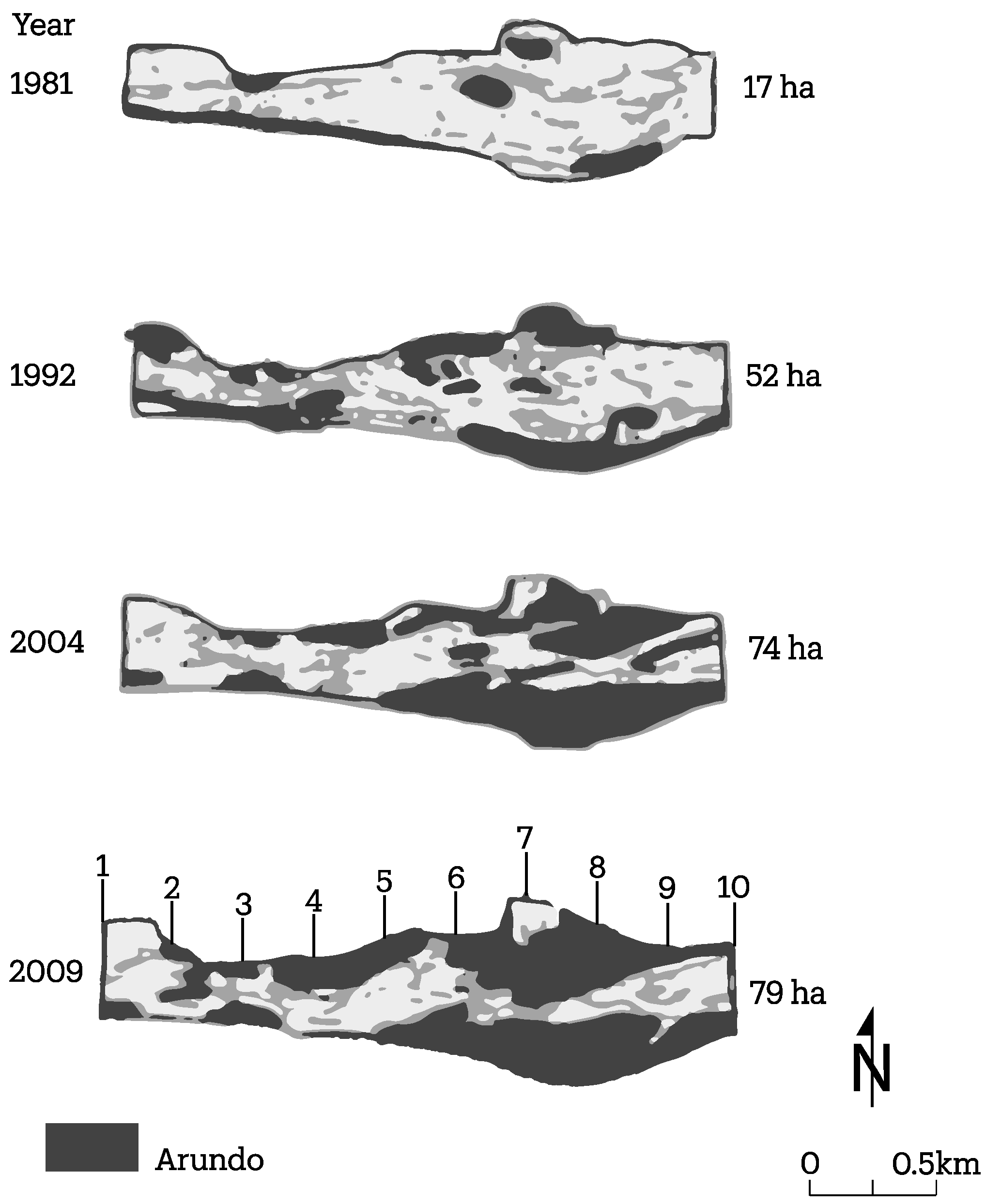
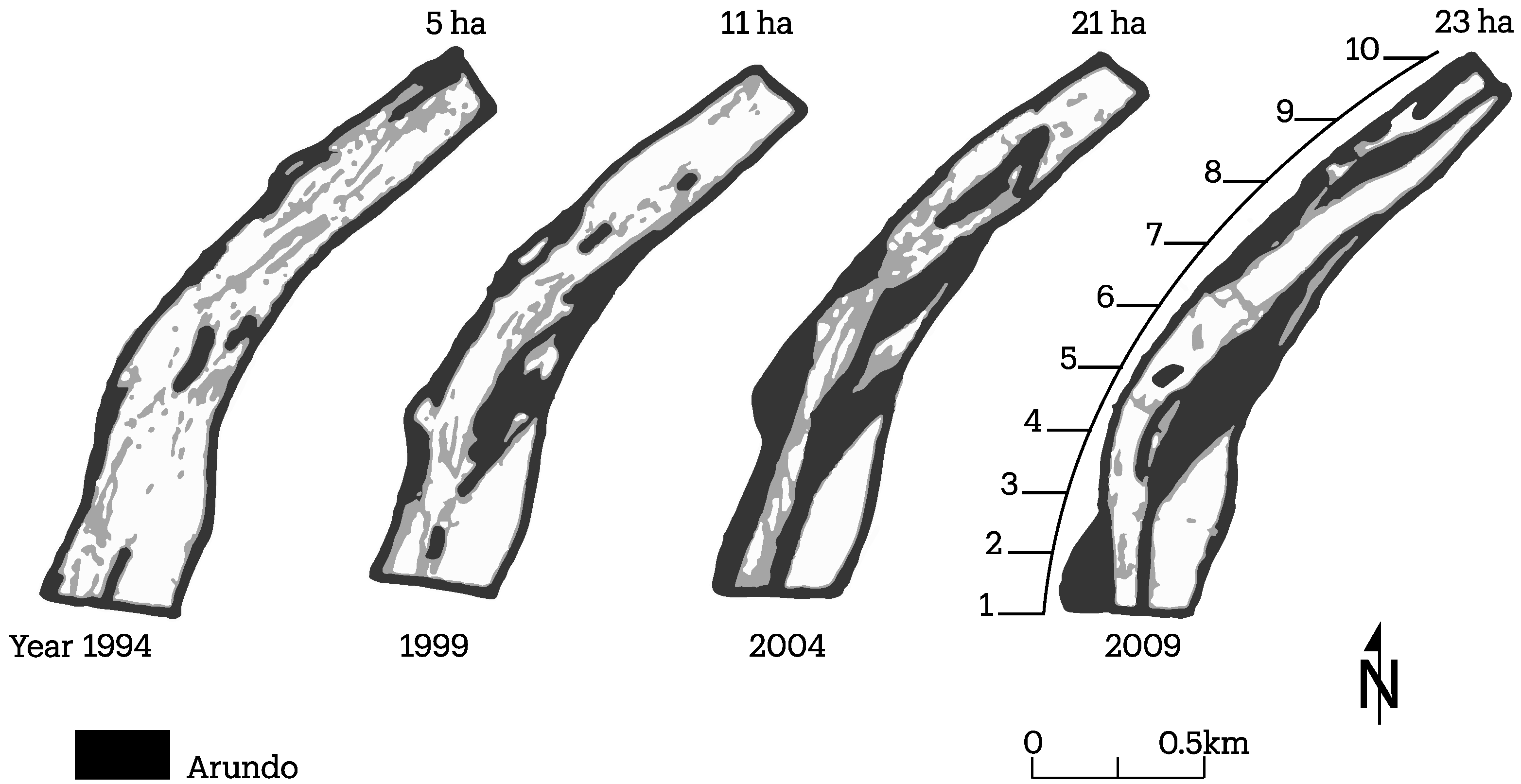
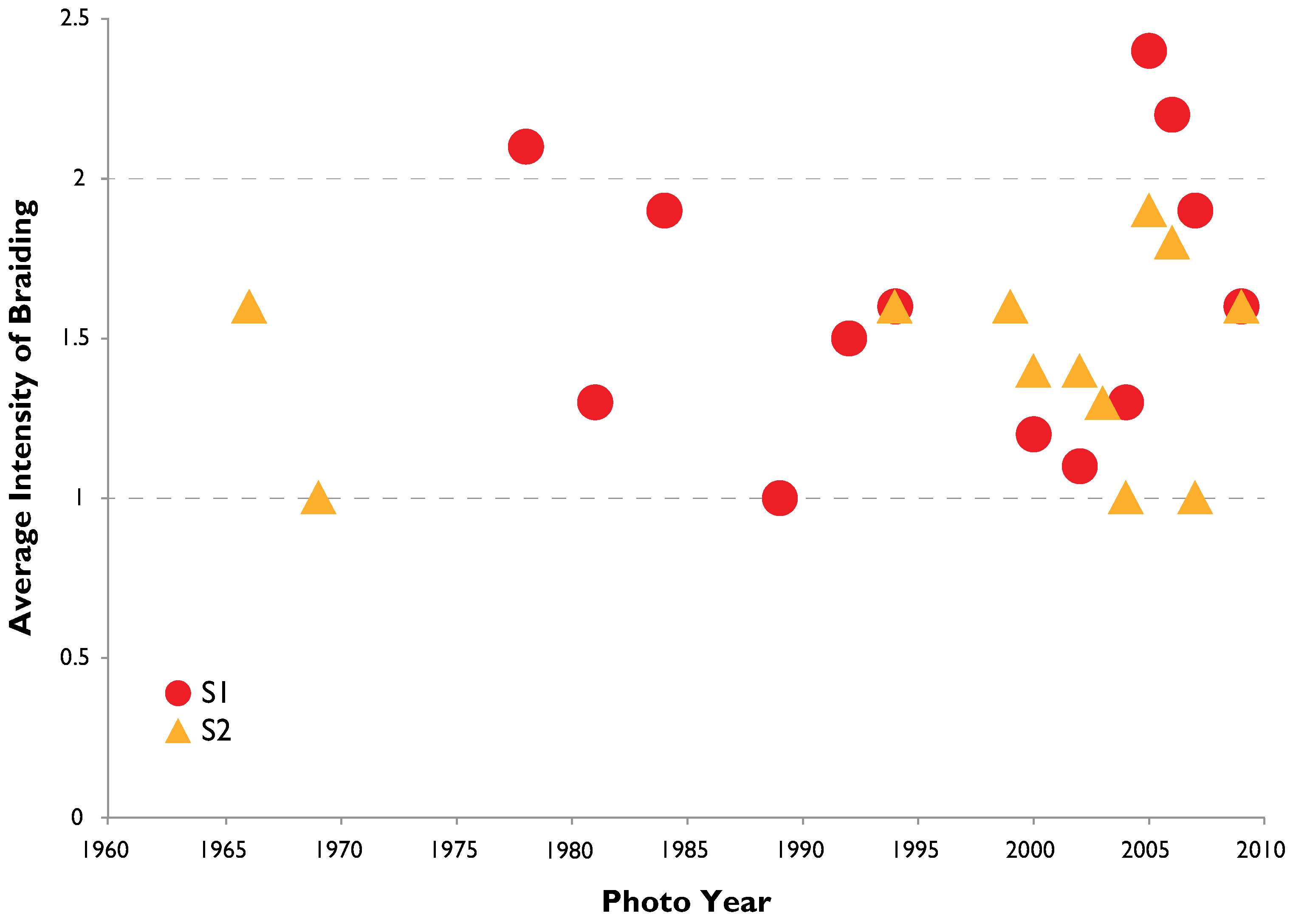
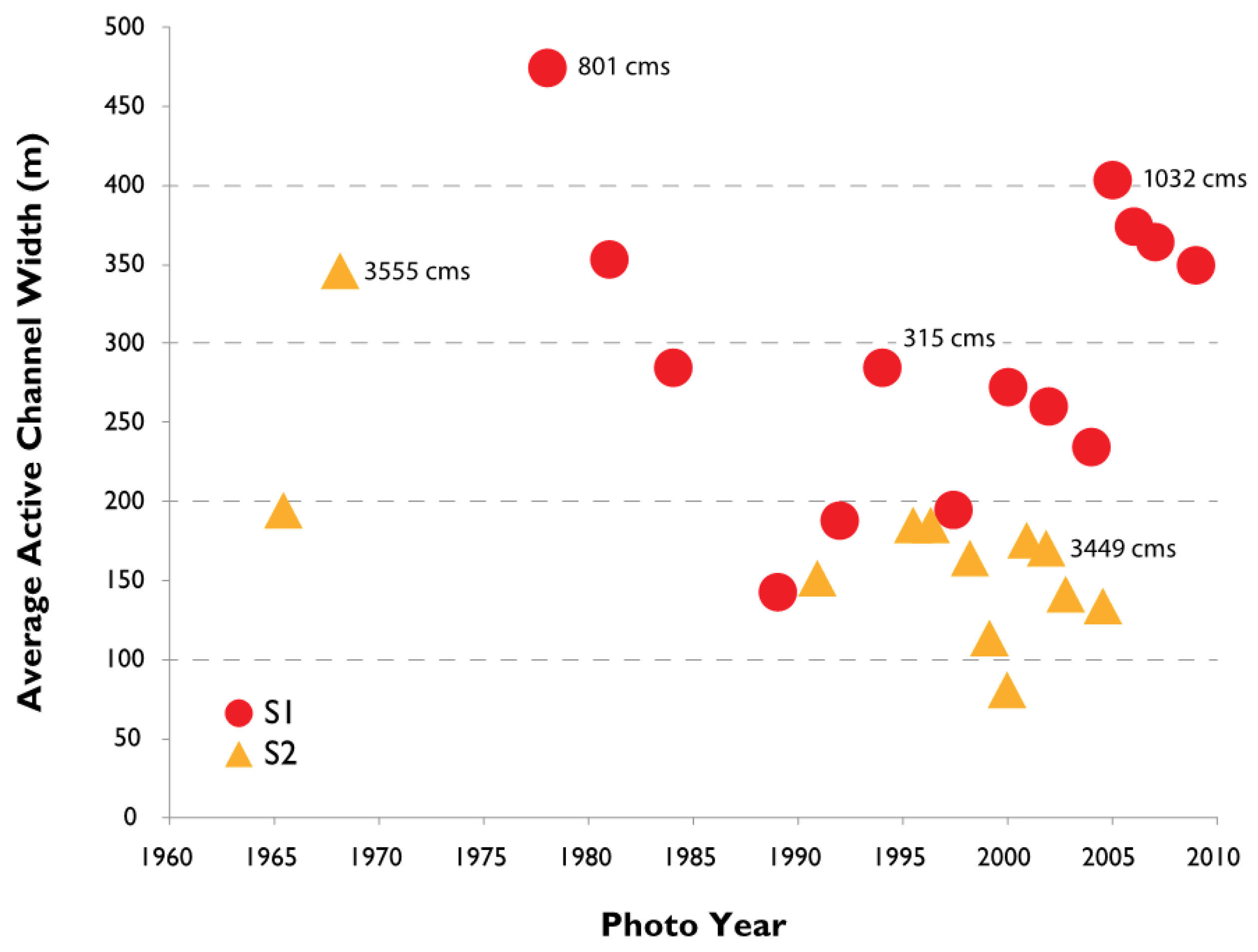
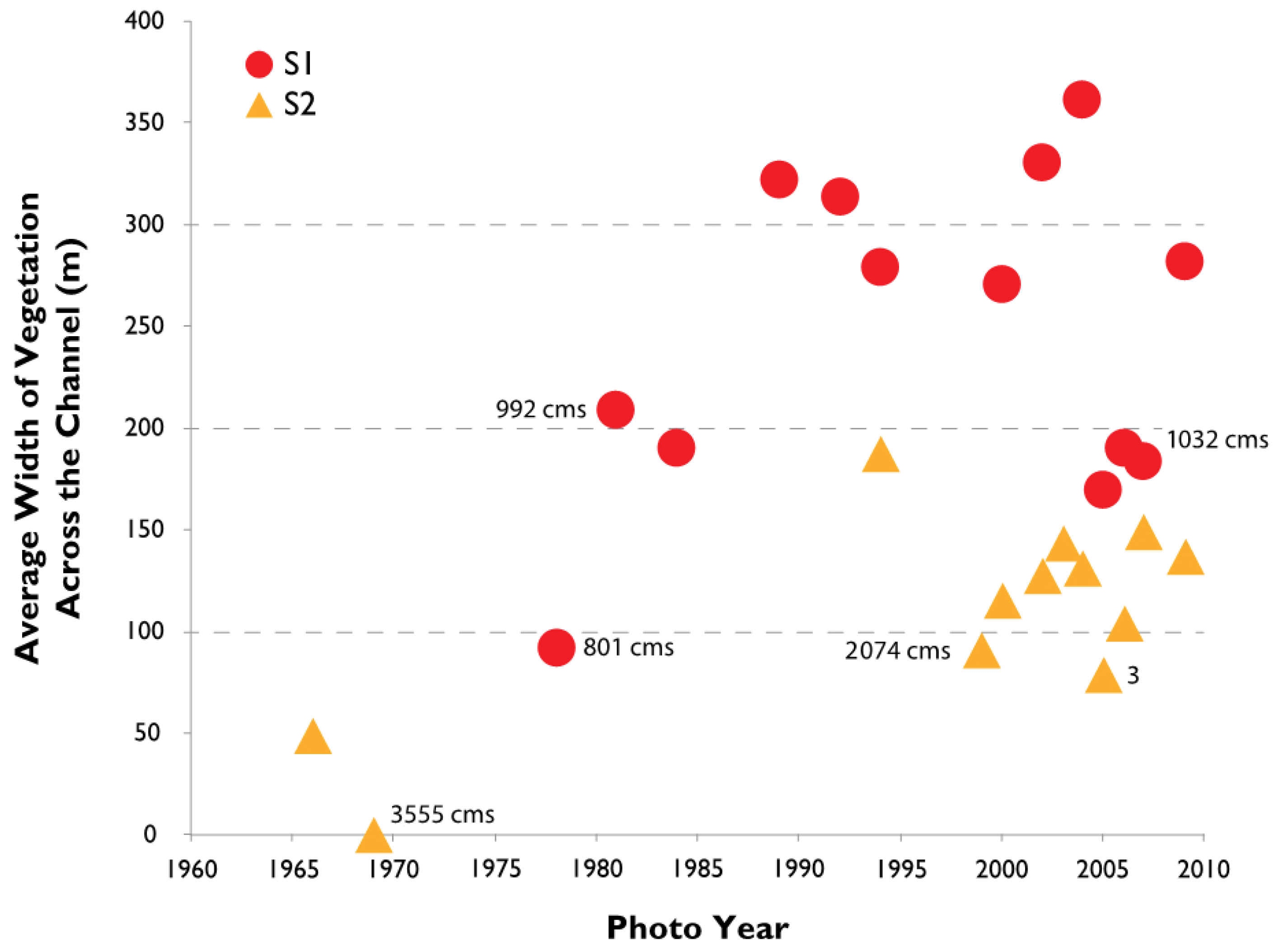
3.2. Channel Change over Time
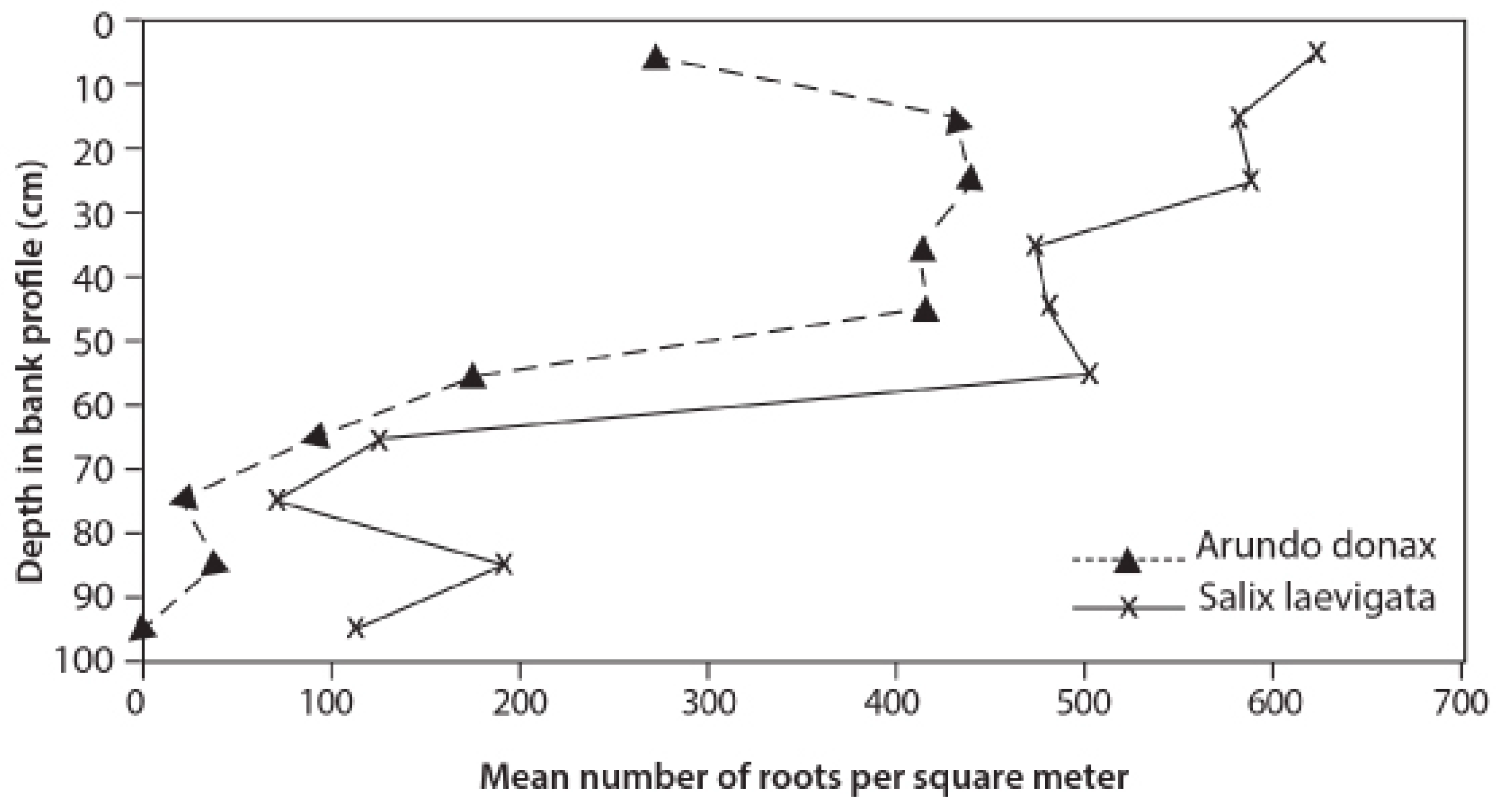
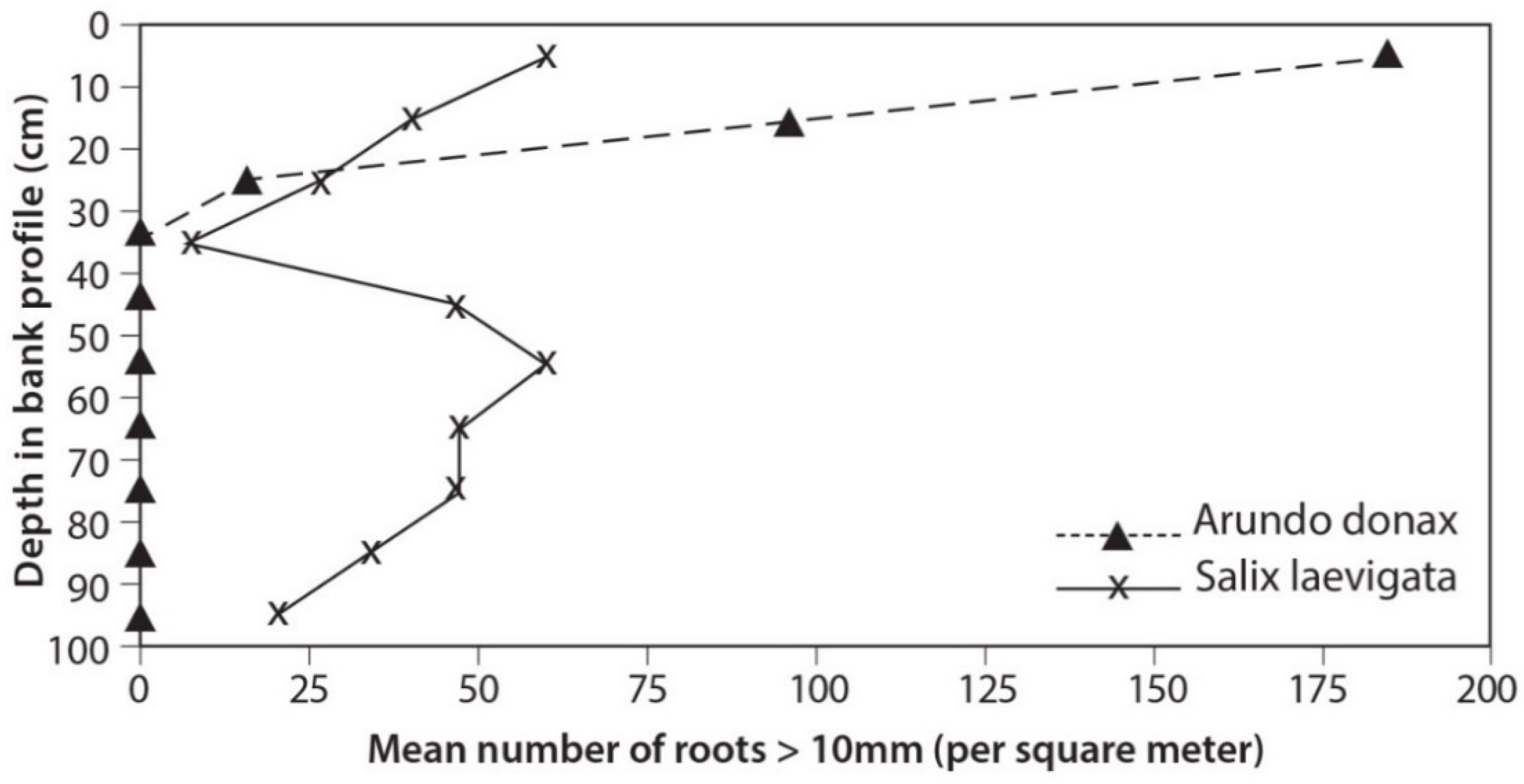
3.3. Root Distribution
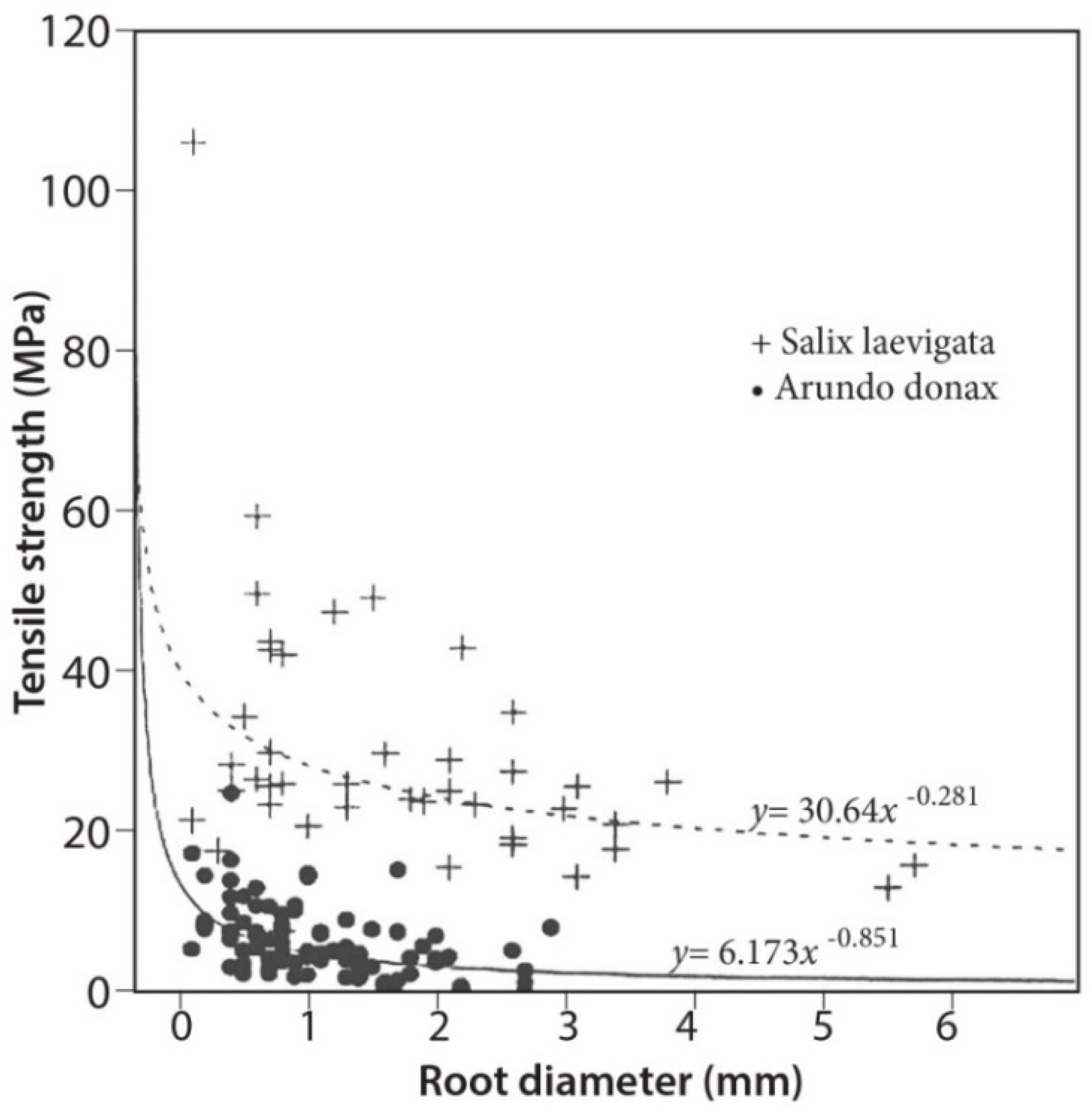
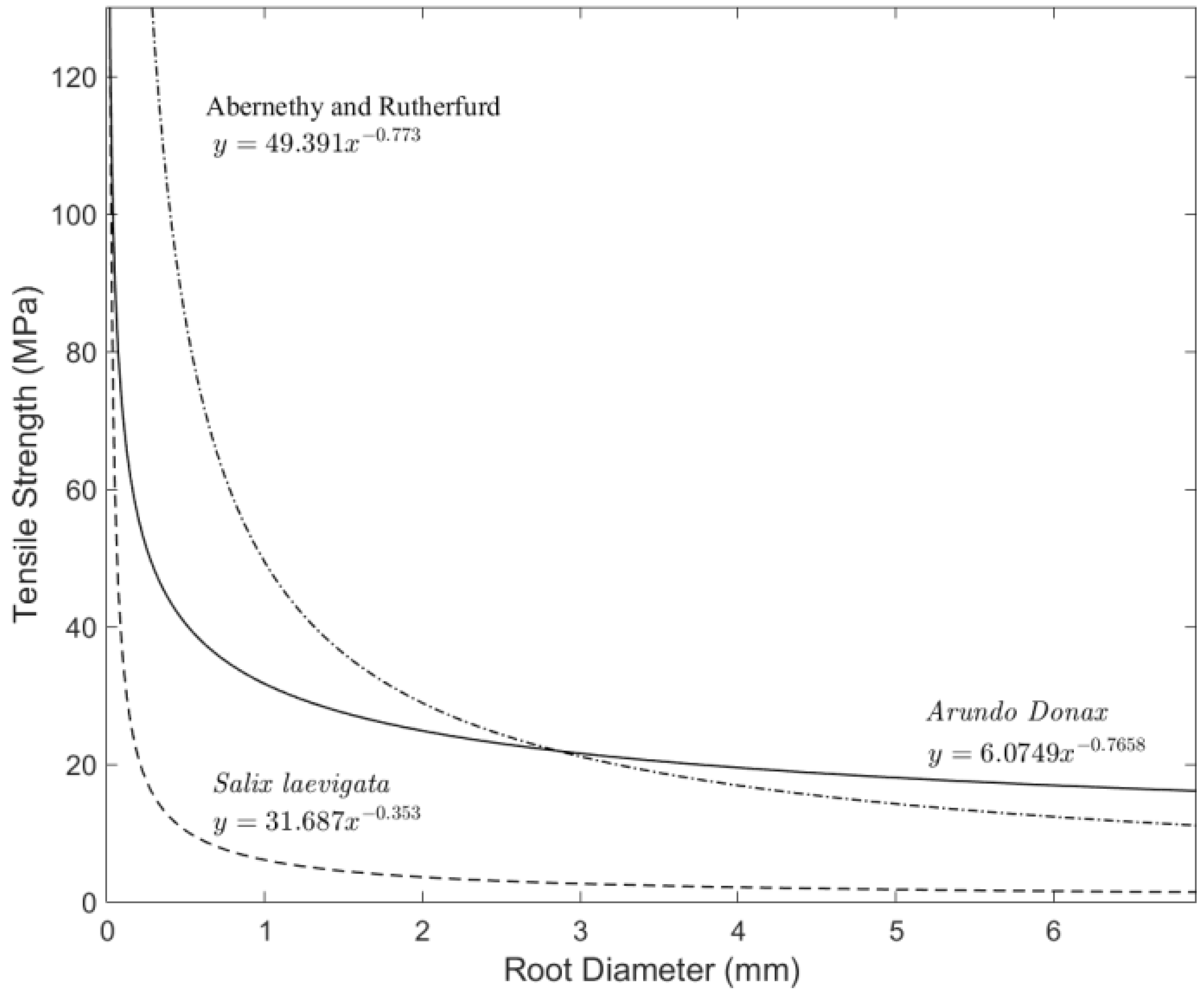
3.4. Tensile Strength
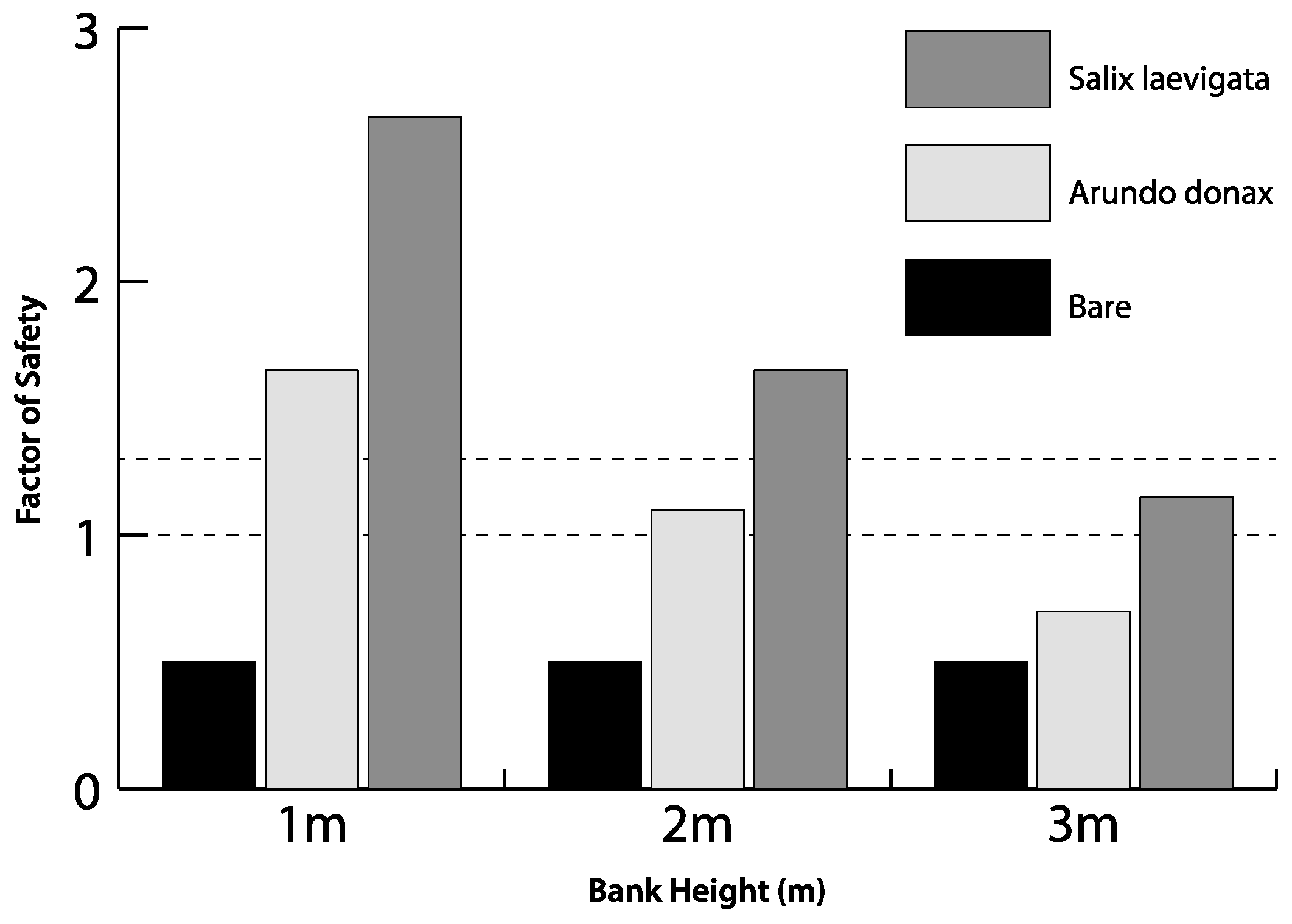
3.5. Experimental Modeling of Slope Stability
4. Discussion
4.1. Channel Change over Time
4.2. Root Density and Tensile Strength
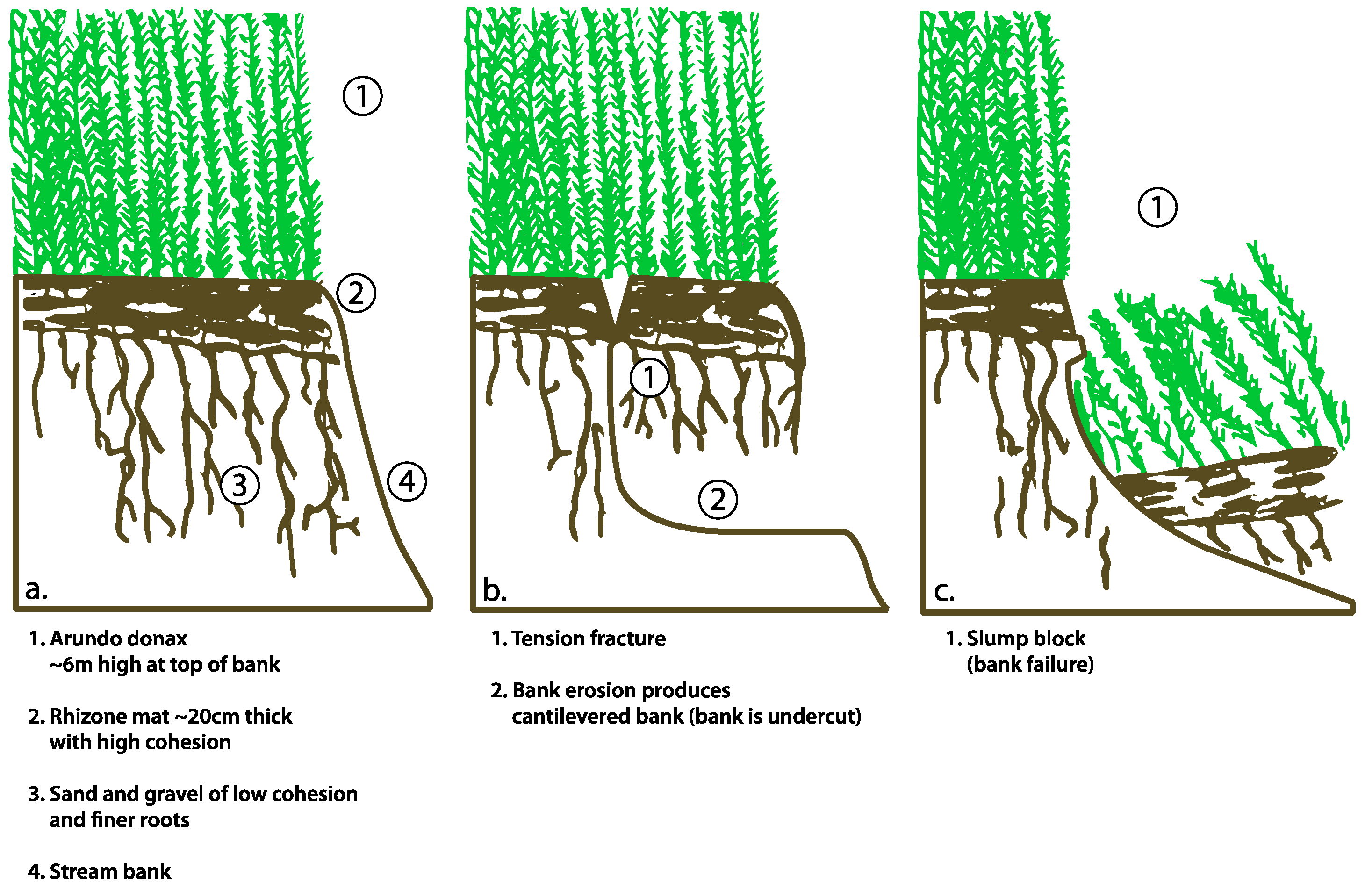
4.3. Bank Stability
5. Conclusions
- A. donax is displacing native vegetation at two field sites studied, which appear to be broadly representative of many reaches of the Santa Clara River. The below-ground architecture of the root system is significantly different between the two plant species, leading to significant differences in the mechanical strength added to the banks;
- Channel width and intensity of braiding varied over several decades with width and braiding linked in part to high flow events that removes A. donax.
- S. laevigata had more roots at greater depths and the roots are stronger for any given size than those of A. donax;
- Root tensile strength for S. laevigata (for roots of 1–6 mm in diameter) is about five times higher than for A. donax;
- The difference in the number and strength of roots produced different values in effective bank cohesion: S. laevigata adds over twice the amount of cohesion compared to A. donax (8.6 kPa versus 3.3 kPa);
- Modeling of bank stability, for banks of variable height, suggests that S. laevigata, compared to A. donax, increases the FS by ~60% for banks 1 m high, ~55% for banks 2 m high and ~40% for banks 3 m high. For 3 m high banks, the FS for banks with A. donax is <1. Therefore, there may be a decrease in the lateral stability of channels if the mixed riparian forest is converted to be dominated by A. donax.
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| S1 (Fillmore Fish Hatchery) | Discharge in Cubic Feet per Second (cfs) | Peak Discharge for Study Reach | |||||
|---|---|---|---|---|---|---|---|
| Photo Year | Photo Month | Peak Date | (1) Santa Clara River | (2) Hopper Creek | (3) Piru Creek | Tot Qmax (cfs) | Tot Qmax (cms) |
| 2009 | 4 | 1 January 2008 | 3120 * | 274 ** | 7 | 3411 | 97 |
| 2007 | 7 | Monthly | 20 * | 0 °° | 5 | 265 | 8 |
| 2006 | 6 | 2 January 2006 | 12,500 * | 240 °° | 7 | 12,747 | 361 |
| 2005 | 9 | 9 January 2005 | 32,000 * | 4290 °° | 124 | 36,414 | 1032 |
| 2004 | 9 | 25 February 2004 | 2640 * | 289 °° | 5 | 2934 | 83 |
| 2003 | 1 | 12 February 2003 | 2330 * | 128 °° | 6 | 2464 | 70 |
| 2002 | 7 | Monthly | 26 * | 0 °° | 9 | 35 | 1 |
| 2000 | 4 | 23 February 2000 | 2440 * | 2680 °° | 8 | 5128 | 145 |
| 1994 | 11 | 18 February 1993 | 10,700 * | 314 °° | 97 | 11,111 | 315 |
| 1992 | 11 | 12 February 1992 | 12,300 ° | 1270 °° | 328 | 13,898 | 394 |
| 1989 | 6 | 16 December 1988 | 11,000 ° | 4 °° | 5 | 11,009 | 312 |
| 1984 | 1 | 1 March 1983 | 30,600 ° | 4410 °° | 1 | 35,011 | 992 |
| 1981 | 6 | 16 February 1980 | 13,900 ° | 8120 *** | 33 | 22,053 | 625 |
| 1978 | 9 | 9 February 1978 | 22,800 ° | 5450 *** | 11 | 28,271 | 801 |
| S2 (TNC-BRIGGS RD) | Discharge in Cubic Feet per Second (ds) | Peak Discharge at Reach | ||||
|---|---|---|---|---|---|---|
| Photo Year | Photo Month | Peak Date | S1 Tot Qmax | Sespe Creek * | S2 Tot Qmax (ds) | S2 Tot Qmax (cms) |
| 2009 | 4 | 27 January 2008 | 2252 | 30,800 | 33,052 | 937 |
| 2007 | 7 | 28 January 2007 | 147 | 641 | 641 | 16 |
| 2006 | 6 | 4 April 2006 | 1682 | 44,500 | 46,252 | 1311 |
| 2005 | 9 | 9 January 2005 | 36,414 | 55,300 | 121,714 | 3449 |
| 2004 | 9 | 25 February 2004 | 2934 | 17,700 | 20,534 | 585 |
| 2003 | 1 | 12 February 2003 | 2454 | 7630 | 10,094 | 285 |
| 2002 | 7 | 6 March 2001 | 1553 | 25,900 | 27,563 | 781 |
| 2000 | 4 | 23 February 2000 | 2440 | 4900 | 7340 | 208 |
| 1999 | 10 | 3 February 1998 | 10,691 | 62,500 | 73,191 | 2074 |
| 1994 | 11 | 12 February 1994 | 150 | 44,000 | 44,150 | 1251 |
| 1969 | 2 | 25 January 1969 | 77,200 | 50,000 | 137,200 | 3555 |
| 1966 | 7 | 29 December 1965 | 32,023 | 21,500 | 53,623 | 1520 |
| 1959 | 10 | 16 February 1959 | 2051 | 8280 | 10331 | 293 |
| Braiding Intensity: S2 | Cross Section | |||||||||||
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | AVE | ||
| 1978 | 1 | 1 | 1 | 1 | 1 | 3 | 3 | 4 | 4 | 2.1 | ||
| 1981 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 1.3 | ||
| 1984 | 2 | 2 | 3 | 3 | 2 | 2 | 1 | 1 | 1 | 1.9 | ||
| 1989 | ND | ND | ND | 1 | 1 | 1 | 1 | 1 | 1 | 1.0 | ||
| 1992 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 1.5 | ||
| 1994 | 2 | 2 | 2 | 1 | 1 | 2 | 2 | 2 | 1 | 1.6 | ||
| 2000 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 1.2 | ||
| 2002 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.1 | ||
| 2004 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1.3 | ||
| 2005 | 3 | 3 | 2 | 2 | 3 | 2 | 4 | 3 | 1 | 2.4 | ||
| 2006 | 3 | 2 | 2 | 2 | 2 | 2 | 3 | 4 | 1 | 2.2 | ||
| 2007 | 1 | 1 | 1 | 3 | 4 | 2 | 3 | 2 | 1 | 1.9 | ||
| 2009 | 1 | 1 | 1 | 2 | 2 | 1 | 2 | 3 | 2 | 1.6 | ||
| Active Width: S1 | Cross Section | |||||||||||
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | AVE | |
| 1978 | 399 | 452 | 291 | 297 | 427 | 543 | 718 | 626 | 557 | 436 | 474 | |
| 1981 | 320 | 410 | 212 | 195 | 301 | 403 | 472 | 391 | 413 | 416 | 353 | |
| 1984 | 328 | 300 | 221 | 192 | 221 | 441 | 373 | 300 | 206 | 266 | 285 | |
| 1989 | ND | ND | ND | 68 | 110 | 184 | 206 | 212 | 150 | 68 | 143 | |
| 1992 | 231 | 172 | 49 | 53 | 138 | 212 | 163 | 295 | 305 | 261 | 188 | |
| 1994 | 395 | 223 | 195 | 233 | 265 | 254 | 250 | 371 | 305 | 352 | 284 | |
| 2000 | 248 | 411 | 132 | 310 | 345 | 240 | 184 | 150 | 311 | 392 | 272 | |
| 2002 | 266 | 382 | 116 | 271 | 311 | 195 | 219 | 139 | 311 | 390 | 260 | |
| 2004 | 269 | 226 | 105 | 240 | 319 | 201 | 189 | 99 | 300 | 396 | 234 | |
| 2005 | 577 | 297 | 184 | 365 | 407 | 393 | 421 | 481 | 455 | 447 | 403 | |
| 2006 | 571 | 382 | 229 | 266 | 407 | 317 | 246 | 433 | 444 | 441 | 374 | |
| 2007 | 472 | 365 | 206 | 243 | 407 | 348 | 266 | 500 | 438 | 441 | 364 | |
| 2009 | 461 | 311 | 184 | 274 | 404 | 359 | 271 | 351 | 450 | 433 | 350 | |
| Vegetation Width: S1 | Cross Section | |||||||||||
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | AVE | |
| 1978 | 0.00 | 0.00 | 59 | 136 | 78 | 114 | 272 | 0.00 | 82 | 182 | 92 | |
| 1981 | 0.00 | 0.00 | 119 | 104 | 14 | 217 | 691 | 420 | 271 | 260 | 209 | |
| 1984 | 0.00 | 0.00 | 82 | 89 | 130 | 193 | 460 | 319 | 430 | 200 | 190 | |
| 1989 | ND | ND | ND | 214 | 67 | 245 | 601 | 346 | 445 | 334 | 322 | |
| 1992 | 189 | 78 | 222 | 219 | 341 | 423 | 783 | 345 | 323 | 215 | 314 | |
| 1994 | 189 | 87 | 163 | 163 | 222 | 360 | 697 | 342 | 346 | 218 | 279 | |
| 2000 | 256 | 39 | 163 | 94 | 134 | 334 | 727 | 496 | 287 | 184 | 271 | |
| 2002 | 226 | 161 | 215 | 245 | 167 | 378 | 801 | 609 | 293 | 215 | 331 | |
| 2004 | 253 | 134 | 291 | 273 | 170 | 417 | 879 | 654 | 401 | 152 | 362 | |
| 2005 | 0.00 | 85 | 145 | 93 | 74 | 211 | 593 | 308 | 142 | 52 | 170 | |
| 2006 | 0.00 | 60 | 86 | 145 | 78 | 282 | 671 | 360 | 172 | 48 | 190 | |
| 2007 | 0.00 | 78 | 164 | 137 | 82 | 226 | 701 | 274 | 156 | 26 | 184 | |
| 2009 | 30 | 52 | 148 | 145 | 263 | 252 | 679 | 623 | 366 | 257 | 282 | |
| Braiding Intensity: S2 | Cross Section | ||||||||||
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | AVE |
| 1966 | * | * | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 2 | 1.6 |
| 1969 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.0 |
| 1994 | 1 | 2 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | 2 | 1.6 |
| 1999 | 1 | 1 | 3 | 1 | 1 | 1 | 2 | 3 | 2 | 1 | 1.6 |
| 2000 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 1.4 |
| 2002 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 1.4 |
| 2003 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 2 | 1.3 |
| 2004 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.0 |
| 2005 | 1 | 1 | 2 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 1.9 |
| 2006 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 1 | 1.8 |
| 2007 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.0 |
| 2009 | 2 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 1.6 |
| Active Width: S2 | Cross Section | ||||||||||
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | AVE |
| 1966 | * | * | 328 | 228 | 204 | 204 | 206 | 127 | 133 | 129 | 195 |
| 1969 | 426 | 467 | 467 | 411 | 346 | 318 | 280 | 266 | 258 | 216 | 346 |
| 1994 | 79 | 567 | 160 | 187 | 226 | 170 | 172 | 172 | 131 | 170 | 152 |
| 1999 | 107 | 103 | 172 | 253 | 276 | 207 | 159 | 219 | 210 | 150 | 185 |
| 2000 | 107 | 114 | 169 | 261 | 293 | 206 | 162 | 199 | 203 | 149 | 186 |
| 2002 | 106 | 103 | 158. | 238 | 284 | 188 | 145 | 196 | 154 | 71 | 164 |
| 2003 | 106 | 100 | 93 | 128 | 118 | 86 | 141 | 198 | 115 | 41 | 113 |
| 2004 | 85 | 97 | 79 | 127 | 82 | 71 | 67 | 72 | 93 | 38 | 81 |
| 2005 | 198 | 124 | 176 | 192 | 186 | 170 | 175 | 221 | 236 | 74 | 175 |
| 2006 | 193 | 124 | 182 | 189 | 179 | 188 | 151 | 214 | 205 | 79 | 170 |
| 2007 | 198 | 116 | 177 | 179 | 171 | 152 | 155 | 104 | 79 | 75 | 142 |
| 2009 | 149. | 121 | 162 | 184 | 172 | 163 | 126 | 113 | 95 | 55 | 134 |
| Vegetation Width: S2 | Cross Section | ||||||||||
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | AVE |
| 1966 | 69 | 0 | 0 | 0 | 103 | 130 | 49 | 15 | 66 | 60 | 49 |
| 1969 | * | * | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1994 | 169 | 146 | 180 | 268 | 153 | 209 | 223 | 261 | 199 | 63 | 187 |
| 1999 | 104 | 73 | 124 | 190 | 97 | 76 | 85 | 90 | 18 | 49 | 91 |
| 2000 | 144 | 71 | 128 | 209 | 184 | 145 | 93 | 91 | 37 | 50 | 115 |
| 2002 | 147 | 66 | 167 | 219 | 153 | 172 | 104 | 123 | 37 | 80 | 127 |
| 2003 | 113 | 78 | 153 | 229 | 208 | 190 | 176 | 122 | 38 | 121 | 143 |
| 2004 | 113 | 76 | 148 | 206 | 181 | 127 | 140 | 125 | 96 | 103 | 131 |
| 2005 | 71 | 38 | 97 | 161 | 143 | 109 | 61 | 29 | 25 | 56 | 79 |
| 2006 | 78 | 51 | 140 | 172 | 146 | 125 | 89 | 60 | 68 | 106 | 104 |
| 2007 | 98 | 121 | 183 | 262 | 225 | 159 | 131 | 115 | 120 | 79 | 149 |
| 2009 | 135 | 54 | 151 | 224 | 147 | 190 | 176 | 74 | 118 | 102 | 137 |
| Depth (cm) | Root Diameter (mm) |
|---|---|
| 0–10 | 0.40 (2), 0.50, 0.60, 0.70 (2), 0.80, 0.90, 1.00 (2), 1.20 (2), 1.30, 1.40, 1.50 (2), 1.80, 1.90 (5), 2.00, 2.22 (2), 2.30 (2), 2.50 (2), 2.60, 2.70, 2.90 (2), 3.10, 4.10, 6.70, 10.00, 10.90, 12.20 (2), 12.50, 13.60, 14.00, 14.20, 14.60, 15.2, 15.3 (2), 16.5, 16.6, 16.90, 17.80 (2), 17.90, 18.60, 19.20, 19.30, 19.40 (3), 19.50, 19.70, 20.00, 20.10, 20.30, 20.70, 22.00, 22.50 (2), 23.00, 23.30, 24.30, 24.50, 24.70, 27.70 (2), 27.90, 28.30, 29.30, 29.60, 30.00, 30.50, 30.60, 30.10, 32.20, 32.60, 34.40, 35.30, 36.30, 37.00, 37.10, 37.90, 38.40, 39.40, 39.90, 41.80 (2), 42.30, 43.40, 47.00, 48.30, 48.40, 48.50, 57.90, 61.40, 62.70, 74.20, 125.70. (108 measurements) |
| 10–20 | 0.10 (2), 0.20 (4), 0.30 (5), 0.40 (3), 0.50 (3), 0.60 (6), 0.70 (4), 0.80 (5), 0.90 (2), 1.00 (7), 1.10 (4), 1.20 (3), 1.30 (4), 1.40 (14), 1.50 (9), 1.60 (9), 1.70 (5), 1.80 (4), 1.90 (3), 2.00, 2.20, 2.30, 2.40 (3), 2.60, 2.80 (2), 3.30, 26.70, 30.60, 35.50, 39.00. (110 measurements) |
| 20–30 | 0.10, 0.30 (6), 0.40 (5), 0.50 (3), 0.60 (3), 0.70 (6), 0.80 (4), 0.90 (9), 1.00 (4), 1.10 (4), 1.20 (13), 1.30 (15), 1.40 (7), 1.50 (5), 1.60 (5), 1.70 (4), 1.80, 1.90 (3), 2.10 (2), 2.50, 3.70. (102 measurements) |
| 30–40 | 0.10 (2), 0.20 (8), 0.30 (5), 0.40 (7), 0.50 (4), 0.60 (3), 0.70 (5), 0.80 (4), 0.9 (4), 1.00 (15), 1.10 (15), 1.20 (10), 1.30 (5), 1.40, 1.50 (3), 1.60 (2), 1.70 (3), 1.90, 2.00 (2), 2.30, 2.70, 3.10, 3.50, 7.00. (103 measurements) |
| 40–50 | 0.10 (2), 0.20 (4), 0.30 (11), 0.40 (10), 0.50 (10), 0.60 (6), 0.70 (9), 0.80 (9), 0.90 (4), 1.00 (3). (68 measurements) |
| 50–60 | 0.10, 0.30 (2), 0.40, 0.60 (7), 0.70 (4), 0.80 (8), 1.00, 1.10 (3), 1.20 (2), 1.30 (3), 1.40 (3), 1.50 (3), 1.80, 1.90, 2.00, 2.20, 3.00. (43 measurements) |
| 60–70 | 0.10, 0.20, 0.30, 0.40 (2), 0.50 (5), 0.60 (2), 0.70, 0.80, 1.20 (2), 1.30, 1.40, 1.50, 1.60, 2.10, 2.30 (2). (23 measurements) |
| 70–80 | 0.30 (2), 0.70, 1.00 (2), 1.10. (6 measurements) |
| 80–90 | 0.10, 0.20, 0.30, 0.40, 0.50, 0.60 (2), 0.80, 1.20, 1.50. (10 measurements) |
| Depth (cm) | Root Diameter (mm) |
|---|---|
| 0–10 | 0.01 (4), 0.04, 0.05, 0.07, 0.10 (26), 0.11, 0.15, 0.20 (2), 0.21, 0.22, 0.26, 0.28 (2), 0.30 (8), 0.33, 0.34 (2), 0.35, 0.38, 0.40 (4), 0.42, 0.45 (4), 0.47, 0.48, 0.49, 0.50, 0.53, 0.60, 0.64, 0.70, 0.78, 0.80, 1.00, 1.10, 1.30, 1.40, 1.50, 1.55, 1.64, 1.87, 2.18, 3.55, 13.80, 14.00, 14.90, 15.00, 17.00, 17.49, 22.75, 47.86, 97.00. (93 measurements) |
| 10–20 | 0.01 (3), 0.20 (2), 0.30, 0.40, 0.50. 0.60, 0.10 (15), 0.11, 0.13, 0.14, 0.15, 0.20 (4), 0.23 (2), 0.28 (2), 0.29, 0.30 (8), 0.35, 0.39 (2), 0.40 (5), 0.43, 0.49, 0.50 (2), 0.60, 0.67 (2), 0.70 (2), 0.73, 0.78, 0.79, 0.85, 0.90, 1.11, 1.46, 1.47 (2), 1.79, 1.85, 2.04, 2.25, 2.21, 2.89, 3.05, 4.50, 6.14, 9.50, 12.19, 24.73, 28.27, 79.53, 100.00, 119.63. (87 measurements) |
| 20–30 | 0.01 (4), 0.05, 0.10 (13), 0.17, 0.18 (3), 0.19, 0.20 (5), 0.21 (2), 0.26, 0.30 (3), 0.34, 0.37, 0.40 (6), 0.42, 0.43 (4), 0.47 (2), 0.48, 0.50 (2), 0.51, 0.60 (2), 0.62, 0.67, 0.68 (2), 0.71, 0,79 (2), 0.82, 0.83, 0.85, 0.86, 0.92, 0.97, 1.41 (2), 1.60, 1.66, 1.74, 1.98, 2.11, 2.20, 2.31, 2.35, 2.62, 2.65, 2.88, 3.01, 3.18, 4.79, 15.90, 23.54, 62.29, 63.42. (88 measurements) |
| 30–40 | 0.01 (6), 0.03 (4), 0.10 (10), 0.13, 0.16 (2), 0.18, 0.19, 0.20, 0.23 (2), 0.25 (2), 0.26, 0.27, 0.30 (7), 0.35 (2), 0.40 (3), 0.53 (2), 0.56, 0.65, 0.69, 0.70, 0.71, 0.84, 0.90, 0.91, 0.93, 0.97, 0.99, 1.00, 1.04, 1.19, 1.54, 1.67, 1.86, 1.91, 1.95, 2.00, 2.26, 2.31, 2.85, 2.87, 23.3. (71 measurements) |
| 40–50 | 0.01, 0.03 (2), 0.07, 0.08, 0.09, 0.10 (3), 0.12, 0.07 (3), 0.23, 0,24 (3), 0.25, 0.30, (3), 0.32 (2), 0.34, 0.36, 0.40 (4), 0.43, 0.50, 0.52, 0.54, 0.55, 0.60, 0.63, 0.64, 0.66, 0.67, 0.71, 0.73, 0.86, 0.89, 0.97 (2), 1.00 (3), 1.10, 1.20, 1.25, 1.26, 1.34, 1.40, 1.61, 1.63, 1.71, 2.00, 2.05, 2.26, 2.28, 2.52, 2.59, 7.00 (2), 12.00, 13.68, 15.03, 22.70, 36.60, 60.00, 73.00. (72 measurements) |
| 50–60 | 0.01, 0.03, 0.06, 0. 07, 0.09 (3), 0.10, 0.14, 0.16, 0.20, 0.21 (2), 0.25 (2), 0.26, 0.29, 0.30, 0.34 (3), 0.35, 0.36 (2), 0.37, 0.40 (2), 0.42, 0.43, 0.45, 0.49, 0.50 (2), 0.53, 0.62, 0.68, 0.70, 0.80 (2), 0.86, 0.90 (4), 0.93, 0.96, 1.00 (2), 1.13, 1.23 (2), 1.35, 1.45, 1.64, 1.75, 2.07, 2.16, 2.76, 4.00, 4.71, 6.00 (3) 7.00, 7.79, 8.23, 10.21, 20.09, 20.33, 22.33, 26.00, 27.00, 30.99, 63.00, 78.00. (75 measurements) |
| 60–70 | 0.01 (2), 0.03, 0.15, 0.20, 0.41, 0.50 (2), 0.60, 0.63, 1.00, 1.56, 10.00, 18.09, 29.00, 32.00, 38.00, 39.00, 100.00. (19 measurements) |
| 70–80 | 0.01, 0.19, 0.22, 0.74, 21.00, 24.00 (2), 31.00, 40.00, 73.00. (10 measurements) |
| 80–90 | 0.01 (4), 0.10 (4), 0.23, 0.24, 0.30 (3), 0.50 (4), 1.00 (2), 1.60, 2.00, 2.20, 2.50, 3.00, 10.00, 14.50, 16.00, 43.00, 76.00. (29 measurements) |
| 90–100 | 0.10 (2), 0.50, 1.00 (5), 2.00 (2), 3.00, 3.10, 7.50, 9.00, 20.00, 22.00, 77.00. (17 measurements) |
| Diameter (mm) | kgf | kgf/cm2 | MPa |
|---|---|---|---|
| 0.5 | 1.36 | 173.29 | 16.99 |
| 0.5 | 0.41 | 51.95 | 5.09 |
| 0.6 | 1.64 | 144.74 | 14.19 |
| 0.6 | 0.99 | 87.80 | 8.61 |
| 0.6 | 0.93 | 82.58 | 8.10 |
| 0.6 | 0.93 | 82.58 | 8.10 |
| 0.6 | 0.88 | 77.37 | 7.59 |
| 0.8 | 5.01 | 249.18 | 24.44 |
| 0.8 | 3.31 | 164.68 | 16.15 |
| 0.8 | 2.79 | 138.76 | 13.61 |
| 0.8 | 2.37 | 117.77 | 11.55 |
| 0.8 | 1.96 | 97.68 | 9.58 |
| 0.8 | 1.51 | 74.90 | 7.35 |
| 0.8 | 1.30 | 64.51 | 6.33 |
| 0.8 | 0.58 | 28.65 | 2.81 |
| 0.9 | 3.02 | 118.72 | 11.64 |
| 0.9 | 2.18 | 85.75 | 8.41 |
| 0.9 | 1.28 | 50.30 | 4.93 |
| 0.9 | 1.27 | 49.91 | 4.89 |
| 0.9 | 0.85 | 33.52 | 3.29 |
| 0.9 | 0.53 | 20.67 | 2.03 |
| 1.0 | 4.06 | 129.23 | 12.67 |
| 1.0 | 3.36 | 106.86 | 10.48 |
| 1.0 | 2.32 | 73.78 | 7.24 |
| 1.0 | 2.20 | 69.87 | 6.85 |
| 1.0 | 1.74 | 55.29 | 5.42 |
| 1.0 | 1.67 | 53.00 | 5.20 |
| 1.1 | 4.02 | 105.73 | 10.37 |
| 1.1 | 2.40 | 63.00 | 6.18 |
| 1.1 | 1.57 | 41.41 | 4.06 |
| 1.1 | 1.45 | 38.07 | 3.73 |
| 1.1 | 1.03 | 27.10 | 2.66 |
| 1.1 | 0.79 | 20.89 | 2.05 |
| 1.2 | 4.34 | 95.96 | 9.41 |
| 1.2 | 3.74 | 82.67 | 8.11 |
| 1.2 | 3.36 | 74.21 | 7.28 |
| 1.2 | 2.72 | 60.17 | 5.90 |
| 1.2 | 2.09 | 46.13 | 4.52 |
| 1.2 | 1.61 | 35.50 | 3.48 |
| 1.3 | 5.69 | 107.17 | 10.51 |
| 1.3 | 5.37 | 101.07 | 9.91 |
| 1.3 | 1.85 | 34.84 | 3.42 |
| 1.3 | 1.85 | 34.84 | 3.42 |
| 1.3 | 0.89 | 16.74 | 1.64 |
| 1.4 | 9.07 | 147.33 | 14.45 |
| 1.4 | 8.80 | 142.98 | 14.02 |
| 1.4 | 3.01 | 48.83 | 4.79 |
| 1.4 | 2.59 | 42.06 | 4.12 |
| 1.4 | 1.19 | 19.33 | 1.90 |
| 1.5 | 5.18 | 73.28 | 7.19 |
| 1.5 | 5.05 | 71.41 | 7.00 |
| 1.5 | 3.35 | 47.39 | 4.65 |
| 1.5 | 2.99 | 42.36 | 4.15 |
| 1.5 | 2.66 | 37.60 | 3.69 |
| 1.6 | 4.05 | 50.31 | 4.93 |
| 1.6 | 3.91 | 48.55 | 4.76 |
| 1.7 | 8.06 | 88.77 | 8.71 |
| 1.7 | 4.61 | 50.81 | 4.98 |
| 1.7 | 4.22 | 46.46 | 4.56 |
| 1.7 | 3.42 | 37.67 | 3.69 |
| 1.7 | 1.42 | 15.64 | 1.53 |
| 1.8 | 4.74 | 46.57 | 4.57 |
| 1.8 | 4.33 | 42.56 | 4.17 |
| 1.8 | 3.58 | 35.20 | 3.45 |
| 1.8 | 3.15 | 30.93 | 3.03 |
| 1.8 | 1.93 | 18.94 | 1.86 |
| 1.8 | 1.79 | 17.56 | 1.72 |
| 1.8 | 1.47 | 14.48 | 1.42 |
| 1.9 | 8.71 | 76.79 | 7.53 |
| 1.9 | 3.24 | 28.57 | 2.80 |
| 20. | 1.20 | 9.53 | 0.93 |
| 2.0 | 0.68 | 5.38 | 0.53 |
| 2.1 | 21.09 | 152.24 | 14.93 |
| 2.1 | 10.17 | 73.44 | 7.20 |
| 2.1 | 1.62 | 11.72 | 1.15 |
| 2.2 | 6.14 | 40.39 | 3.96 |
| 2.2 | 3.06 | 20.10 | 1.97 |
| 2.3 | 9.22 | 55.48 | 5.44 |
| 2.4 | 12.37 | 68.35 | 6.70 |
| 2.4 | 7.21 | 39.86 | 3.91 |
| 2.4 | 6.27 | 34.64 | 3.40 |
| 2.5 | 8.22 | 41.88 | 4.11 |
| 2.6 | 0.98 | 4.61 | 0.45 |
| 3.0 | 14.17 | 50.10 | 4.91 |
| 3.1 | 7.34 | 24.31 | 2.38 |
| 3.1 | 2.58 | 8.55 | 0.84 |
| 3.3 | 27.19 | 79.48 | 7.79 |
| 10.0 | 68.10 | 21.68 | 2.13 |
| 12.0 | 158.90 | 0.35 | 0.03 |
| Diameter (mm) | kgf | kgf/cm2 | MPa |
|---|---|---|---|
| 0.5 | 2.10 | 1069.52 | 104.88 |
| 0.5 | 0.42 | 214.92 | 21.08 |
| 0.7 | 0.68 | 176.69 | 17.33 |
| 0.8 | 1.43 | 285.09 | 27.96 |
| 0.8 | 1.27 | 252.66 | 24.78 |
| 0.9 | 2.20 | 345.82 | 33.91 |
| 1.0 | 4.69 | 597.15 | 58.56 |
| 1.0 | 3.93 | 500.77 | 49.11 |
| 1.0 | 2.10 | 266.87 | 26.17 |
| 1.1 | 4.18 | 440.06 | 43.15 |
| 1.1 | 4.09 | 430.06 | 42.17 |
| 1.1 | 2.86 | 300.74 | 29.49 |
| 1.1 | 2.45 | 258.23 | 25.32 |
| 1.1 | 2.23 | 234.34 | 22.98 |
| 1.2 | 4.80 | 424.32 | 41.61 |
| 1.2 | 2.95 | 261.10 | 25.61 |
| 1.2 | 0.84 | 74.18 | 7.27 |
| 1.4 | 3.20 | 207.88 | 20.39 |
| 1.6 | 9.61 | 477.81 | 46.86 |
| 1.7 | 5.90 | 259.80 | 25.48 |
| 1.7 | 5.25 | 231.21 | 22.67 |
| 1.9 | 14.06 | 495.79 | 48.62 |
| 2.0 | 9.41 | 299.59 | 29.38 |
| 2.2 | 9.20 | 242.10 | 23.74 |
| 2.3 | 9.92 | 238.67 | 23.41 |
| 2.5 | 12.36 | 251.80 | 24.69 |
| 2.5 | 7.63 | 155.38 | 15.24 |
| 2.6 | 22.99 | 432.98 | 42.46 |
| 2.7 | 13.44 | 234.81 | 23.03 |
| 3.0 | 24.88 | 351.91 | 34.51 |
| 3.0 | 19.56 | 276.70 | 27.14 |
| 3.0 | 13.64 | 192.90 | 18.92 |
| 3.0 | 13.06 | 184.80 | 18.12 |
| 3.4 | 20.92 | 230.46 | 22.60 |
| 3.5 | 24.88 | 258.55 | 25.35 |
| 3.5 | 13.85 | 143.99 | 14.12 |
| 3.8 | 23.92 | 210.90 | 20.68 |
| 3.8 | 20.34 | 179.38 | 17.59 |
| 4.2 | 36.56 | 263.89 | 25.88 |
| 5.9 | 35.54 | 130.01 | 12.75 |
| 6.1 | 46.42 | 158.82 | 15.58 |
| 10.0 | 68.10 | 86.71 | 8.50 |
References
- Dudley, T.L. Arundo donax. In Invasions Plants of California’s Wildlands; Bossard, C.C., Randal, J.M., Hoshovsky, M.C., Eds.; University of California Press: Berkeley, CA, USA, 2000; pp. 53–58. [Google Scholar]
- Bell, I.E.; Prentice-Dekker, B.B.; McKelvey, Z.; Steele, M. Economic Analysis of Invasive Giant Reed (Arundo donax) Control for the Lower Santa Clara River; Group Masters Project; Bren School of Environmental Science & Management, UC Santa Barbara: Santa Barbara, CA, USA, 2016. [Google Scholar]
- Bell, G. Ecology and management of Arundo donax, and approaches to riparian habitat restoration in southern California. In Plant Invasions: Studies from North America and Europe; Brock, J.H., Wade, M., Pysek, P., Green, D., Eds.; California Natural Resources Agency: Sacramento, CA, USA, 1997; pp. 103–113. [Google Scholar]
- Coffman, G. Factors Influencing the Invasion of Giant Reed (Arundo donax) in Riparian Ecosystems of Mediterranean-Type Climate Regions. Ph.D. Thesis, University of California Los Angeles, Los Angeles, CA, USA, 2007. [Google Scholar]
- Lambert, A.M.; Dudley, T.L.; Saltonstall, K. Ecology and impacts of the large-statured invasive grasses Arundo donax and Phragmites australis in North America. Invasive Plant Sci. Manag. 2010, 3, 489–494. [Google Scholar] [CrossRef]
- Stillwater Sciences. Geomorphic Assessment of the Santa Clara River Watershed: Synthesis of the Lower and Upper Watershed Studies, Ventura and Los Angeles Counties, California. Available online: http://www.ladpw.org/wmd/scr/docs/SCR_Geomorph%20Synthesis_SWS_2011_FINAL.pdf (accessed on 10 April 2018).
- Stillwater Sciences. Analysis of Riparian Vegetation Dynamics for the Lower Santa Clara River and Major Tributaries, Ventura County, California. Available online: http://s3-us-west-2.amazonaws.com/ucldc-nuxeo-ref-media/59ffdf02-975f-4f0f-898c-09422cb8538b (accessed on 10 April 2018).
- Ten Brinke, J. Effects of the Invasive Reed Arundo Donax on Rivers in Southern California. Ph.D. Thesis, University of California Santa Barbara, Santa Barbara, CA, USA, 2010; 87p. [Google Scholar]
- Rockwell, T. Neotectonics of the san cayetano fault, transverse ranges, California. Geol. Soc. Am. Bull. 1988, 100, 500–513. [Google Scholar] [CrossRef]
- Yeats, R.S. Evluation of fault hazard: Surface rupture vs. earthquake potential. Geol. Soc. Am. Abstr Programm. 1977, 9, 529. [Google Scholar]
- Azor, A.; Keller, E.A.; Yeats, R.S. Geomorphic indicators of active fold growth: South Mountain-Oak Ridge anticline, Ventura basin, southern California. Geol. Soc. Am. Bull. 2002, 117, 745–753. [Google Scholar] [CrossRef]
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braiding, Meandering, and Straight; U.S. Geological Survey Professional Paper 262-B; US Government Printing Office: Washington, DC, USA, 1957; pp. 39–85.
- Eaton, B.C.; Millar, G.M.; Davidson, S. Channel patterns: Braided, anabranching, and single-thread. Geomorphology 2010, 120, 353–364. [Google Scholar] [CrossRef]
- Ventura County Watershed Protection District. 2010. Available online: www.vcw.org (accessed on 10 April 2018).
- Harrison, L.R.; Keller, E.A.; Mertes, L.A.K. Minimum Flow Requirements for Southern Steelhead Passage on the Lower Santa Clara River, CA; Prepared for The Nature Conservancy; University of California: Santa Barbara, CA, USA, 2006. [Google Scholar]
- Johnson, M.; Dudley, T.; Burns, C. Cal-IPC News: Seed production in Arundo donax? Available online: https://www.cal-ipc.org/wp-content/uploads/2017/03/Fall2006-6.pdf#page=12 (accessed on 10 April 2018).
- Khudamrongsawat, J.; Tayyar, R.; Holt, J.S. Genetic diversity of giant reed (Arundo donax) in the Santa Ana River, CA. Weed Sci. 2004, 52, 395–405. [Google Scholar] [CrossRef]
- Hickin, E.J. Vegetation and river channel dynamics. Can. Geogr. 1984, 28, 111–126. [Google Scholar] [CrossRef]
- Thorne, C.R. Effect of vegetation on riverbank erosion and stability. In Vegetation and Erosion; Thornes, J.B., Ed.; John Wiley & Sons: Chichester, UK, 1990; pp. 125–144. [Google Scholar]
- Hupp, C.R.; Osterkamp, W.R. Riparian vegetation and fluvial geomorphic processes. Geomorphology 1996, 14, 277–295. [Google Scholar] [CrossRef]
- Huang, H.Q.; Nanson, G.C. The influence of bank strength on channel geometry: An integrated analysis of some observations. Earth Surf. Process. Landf. 1998, 23, 865–876. [Google Scholar] [CrossRef]
- Millar, R.G. Influence of bank vegetation on alluvial channel patterns. Water Resour. Res. 2000, 36, 1109–1118. [Google Scholar] [CrossRef] [Green Version]
- Abernathy, B.; Rutherford, I.D. The effect of tree roots on the mass-stability of riverbanks. Earth Surf. Process. Landf. 2000, 25, 921–937. [Google Scholar] [CrossRef]
- Abernathy, B.; Rutherford, I.D. The distribution and strength of tree roots in relation to riverbank reinforcement. Hydrol. Process. 2001, 15, 63–79. [Google Scholar] [CrossRef]
- Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability. Earth Surf. Process. Landf. 2002, 27, 527–546. [Google Scholar] [CrossRef]
- Tal, M.; Gran, K.; Murray, A.B.; Paola, C.; Murray Hicks, D. Riparian vegetation as a primary control in multi-thread rivers. In Riparian Vegetation and Fluvial Geomorphology; Bennett, S.J., Simon, A., Eds.; American Geophysical Union: Washington, DC, USA, 2004. [Google Scholar]
- Gurnell, A.M.; Petts, G.E. Trees as riparian engineers: The Tagliamento River, Italy. Earth Surf. Process. Landf. 2006, 31, 1558–1574. [Google Scholar] [CrossRef]
- Stallins, J.A. Geomorphology and ecology: Unifying themes for complex systems in biogeomorphology. Geomorphology 2006, 77, 207–216. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Van De Wiel, M.J.; Darby, S.E. A new model to analyse the impact of woody riparian vegetation on the geotechnical stability of riverbanks. Earth Surf. Process. Landf. 2007, 32, 2185–2198. [Google Scholar] [CrossRef]
- Merritt, D.M. Reciprocal relations between riparian vegetation, fluvial landforms, and channel processes. In Treatise on Geomorphology; Shroder, J.F., Ed.; Academic Press: San Diego, CA, USA, 2013; pp. 219–243. [Google Scholar] [CrossRef]
- Dean, D.J.; Schmidt, J.C. The role of feedback mechanisms in historic channel changes of the lower Rio Grande in the Big Bend region. Geomorphology 2015, 126, 333–349. [Google Scholar] [CrossRef]
- Manners, R.B.; Wilcox, A.C.; Kui, L.; Lightbody, A.F.; Stella, J.C.; Leonard, S.; Sklar, L.S. When do plants modify fluvial processes? Plant-hydraulic interactions under variable flow and sediment supply rates. J. Geophys. Res. Earth Surf. 2015, 120. [Google Scholar] [CrossRef]
- Fei, S.; Phillips, J.; Shouse, M. Biogeomorphic impacts of invasive species. Annu. Rev. Ecol. Evol. Syst. 2014, 45, 69–87. [Google Scholar] [CrossRef]
- Endo, T.; Tsuruta, T. On the Effect of Tree Roots upon Shearing Strength of Soil; Annual Report of the Hokkaido Branch, Forest Place Experimental Station; Hokkaido Research Organization: Sapporo, Japan, 1969; pp. 167–183. [Google Scholar]
- Wu, T.H.; McKinnell, W.P., III; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41, W07025. [Google Scholar] [CrossRef]
- Simon, A.; Curini, A.; Darby, S.E.; Langendoen, E.J. Bank and near-bank processes in an incised channel. Geomorphology 2000, 35, 193–217. [Google Scholar] [CrossRef]
- Simon, A.; Pollen-Bankhead, N.; Thomas, R.E. Development and application of a deterministic bank stability and toe erosion model for stream restoration. In Stream Restoration in Dynamic Fluvial Systems: Scientific Approaches, Analyses, and Tools; Simon, A., Bennett, S.J., Castro, J.M., Eds.; Geophysical Union: Washington, DC, USA, 2011; Volume 194, pp. 453–474. [Google Scholar]
- United States Department of Agriculture, Agriculture Research Service. Bank Stability and Toe Erosion Model. 2016. Available online: https://www.ars.usda.gov/southeast-area/oxford-ms/national-sedimentation-laboratory/watershed-physical-processes-research/research/bstem/overview/ (accessed on 10 April 2018).
- Pollen-Bankhead, N.; Simon, A. Enhanced application of root-reinforcement algorithms for bank-stability modeling. Earth Surf. Process. Landf. 2009, 34, 471–480. [Google Scholar] [CrossRef]
- Magillian, F.J.; Nislow, K.H.; Renshaw, C.E. Flow regulation by dams. In Treatise on Geomorphology; Volume 9 Fluvial Geomorphology; Shroder, J., Wohl, E., Eds.; Academic Press: San Diego, CA, USA, 2013; pp. 794–808. [Google Scholar]
- Corenblit, D.; Tabacchi, E.; Steiger, J.; Gurnell, A.M. Reciprocal interactions and adjustments between fluvial landforms and vegetation dynamics in river corridors: A review of complementary approaches. Earth Sci. Rev. 2007, 84, 56–86. [Google Scholar] [CrossRef]
- Zegeye, A.D.; Langendoen, E.J.; Tilahun, S.A.; Mekuria, W.; Poesen, J.; Steenhuls, T.S. Root reinforcement to soil provided by common Ethiopian highland plants for gully erosion control. Ecohydrology 2018, e1940. [Google Scholar] [CrossRef]




| Year | Resolution (Pixel Width in Meters) | Scale | Source |
|---|---|---|---|
| 2009 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 2007 | 1.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2006 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 2005 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 2004 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 2003 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 2002 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 2000 | 1.5 | 1:24,000 | Ventura County Watershed Protection District |
| 1999 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1994 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1969 | 0.5 | 1:24,000 | UC Santa Barbara Maps and Imagery Laboratory |
| 1966 | 1.0 | 1:24,000 | UC Santa Barbara Maps and Imagery Laboratory |
| Year | Resolution (Pixel Width in Meters) | Scale | Source |
|---|---|---|---|
| 2009 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2007 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2006 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2005 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2004 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2003 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2002 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 2000 | 3.0 | 1:24,000 | Ventura County Watershed Protection District |
| 1994 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1992 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1989 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1984 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1981 | 1.0 | 1:24,000 | Pacific Western Aerial Surveys |
| 1978 | 2.0 | 1:24,000 | US Department of Agriculture |
| Bank Material Size (mm) | Angle of Internal Friction (Degrees) | Cohesion (kPa) | Saturated Unit Weight (kN·m−3) | Matric Suction (Degrees) |
|---|---|---|---|---|
| 0.35 | 27 | 0 | 18 | 15 |
| Layer | Thickness (m) | Bank Material Size (mm) | Angle of Internal Friction (Degrees) | Cohesion (kPa) | Saturated Weight (kN·m−3) | Matric Suction (Degrees) |
|---|---|---|---|---|---|---|
| Bank Top | ||||||
| 1 | 0.3 | 0.35 | 27 | 0 | 18 | 15 |
| 2 | 0.7 | 0.35 | 27 | 0 | 18 | 15 |
| 3 | 0.1 | 11.3 | 36 | 0 | 20 | 15 |
| 4 | 0.3 | 0.35 | 27 | 0 | 18 | 15 |
| Size Classes (mm) | <1 | 1.01–2 | 2.01–3 | 3.01–5 | 5.01–10 | 10.01–20 | >20.01 |
|---|---|---|---|---|---|---|---|
| Arundo donax | 107 | 77 | 11 | 2 | 1 | 10 | 20 |
| Salix laevigata | 270 | 33 | 17 | 7 | 8 | 5 | 0 |
| Site | Year | Sparse Veg (km2) | Dense Veg (km2) | A. donax (km2) | Tot. Veg * (km2) | Percent A. donax ** (% of tot. veg) |
|---|---|---|---|---|---|---|
| S1 | 2009 | 0.28 | 1.16 | 0.79 | 1.44 | 55 |
| 2004 | 0.29 | 1.12 | 0.74 | 1.41 | 52 | |
| 1992 | 0.23 | 0.96 | 0.52 | 1.19 | 44 | |
| 1981 | 0.35 | 0.75 | 0.17 | 1.10 | 15 | |
| S2 | 2009 | 0.16 | 0.02 | 0.23 | 0.41 | 57 |
| 2004 | 0.25 | 0.08 | 0.21 | 0.54 | 39 | |
| 1999 | 0.15 | 0.19 | 0.11 | 0.34 | 32 | |
| 1994 | 0.03 | 0.34 | 0.05 | 0.37 | 12 |
| Site | Veg. Type | 2004 Pre-Flood (km2) | 2005 Post-Flood (km2) | Percent Removed (%) | 2009 Re-Growth (km) | Growth Rate (ha/year) |
|---|---|---|---|---|---|---|
| S1 | A. donax | 0.74 | 0.28 | 62 | 0.79 | 12.75 |
| Native Veg. | 0.67 | 0.39 | 42 | 0.65 | 6.6 | |
| S2 | A. donax | 0.21 | 0.13 | 38 | 0.23 | 2.5 |
| Native Veg. | 0.33 | 0.02 | 94 | 0.18 | 3.9 |
| Mean Number of Roots Per m2 | ||||||
|---|---|---|---|---|---|---|
| Root Size Class | Fine Roots (<1–3 mm) | Medium Roots (3–10 mm) | Large Roots (>10 mm) | |||
| Depth in Profile (cm) | Arundo donax | Salix laevigata | Arundo donax | Salix laevigata | Arundo donax | Salix laevigata |
| 0–10 | 72 | 553 | 16 | 7 | 184 | 60 |
| 10–20 | 332 | 513 | 4 | 27 | 96 | 40 |
| 20–30 | 420 | 540 | 4 | 20 | 16 | 27 |
| 30–40 | 408 | 467 | 4 | 0 | 0 | 7 |
| 40–50 | 404 | 420 | 12 | 13 | 0 | 47 |
| 50–60 | 172 | 387 | 4 | 53 | 0 | 60 |
| 60–70 | 92 | 80 | 0 | 0 | 0 | 47 |
| 70–80 | 24 | 27 | 0 | 0 | 0 | 47 |
| 80–90 | 40 | 153 | 0 | 7 | 0 | 33 |
| 90–100 | 0 | 67 | 0 | 27 | 0 | 20 |
| Mean Number of Roots Per m2 | |||
|---|---|---|---|
| Size Class | Fine: <1–3 mm | Medium: 3–10 mm | Large: >10 mm |
| A. donax | 196 | 4 | 30 |
| S. laevigata | 321 | 15 | 37 |
| Plant Type | Common Name | Mean Age (years) | RAR ** | Cohesion (kPa) | Source |
|---|---|---|---|---|---|
| Arundo donax | Arundo | 15 | 2.83 × 10−2 | 3.3 | This study |
| Arundo donax | Arundo | N/A | 6.0 × 10−2 | 1.2 | [34] |
| Salix laevigata | Red Willow | 15 | 6.40 × 10−2 | 8.6 | This study |
| Salix nigra | Black Willow | 5 | 8.70 × 10−5 | 2 | [25] |
| Panicum vigratum | Switch Grass | 5 | 1.40 × 10−4 | 18 | [25] |
| Melaleuca ericifolia | Swamp Paperback | N/A | 3.50 × 10−1 | N/A * | [24] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stover, J.E.; Keller, E.A.; Dudley, T.L.; Langendoen, E.J. Fluvial Geomorphology, Root Distribution, and Tensile Strength of the Invasive Giant Reed, Arundo Donax and Its Role on Stream Bank Stability in the Santa Clara River, Southern California. Geosciences 2018, 8, 304. https://doi.org/10.3390/geosciences8080304
Stover JE, Keller EA, Dudley TL, Langendoen EJ. Fluvial Geomorphology, Root Distribution, and Tensile Strength of the Invasive Giant Reed, Arundo Donax and Its Role on Stream Bank Stability in the Santa Clara River, Southern California. Geosciences. 2018; 8(8):304. https://doi.org/10.3390/geosciences8080304
Chicago/Turabian StyleStover, Jiana E., Edward A. Keller, Tom L. Dudley, and Eddy J. Langendoen. 2018. "Fluvial Geomorphology, Root Distribution, and Tensile Strength of the Invasive Giant Reed, Arundo Donax and Its Role on Stream Bank Stability in the Santa Clara River, Southern California" Geosciences 8, no. 8: 304. https://doi.org/10.3390/geosciences8080304





