Temporal and Spatial Variability of Sediment Transport in a Mountain River: A Preliminary Investigation of the Caldone River, Italy
Abstract
1. Introduction
2. Materials
2.1. Case Study
2.2. Subcatchments of the Caldone River
2.3. Water Discharge Measurement
2.4. Surveyed Events
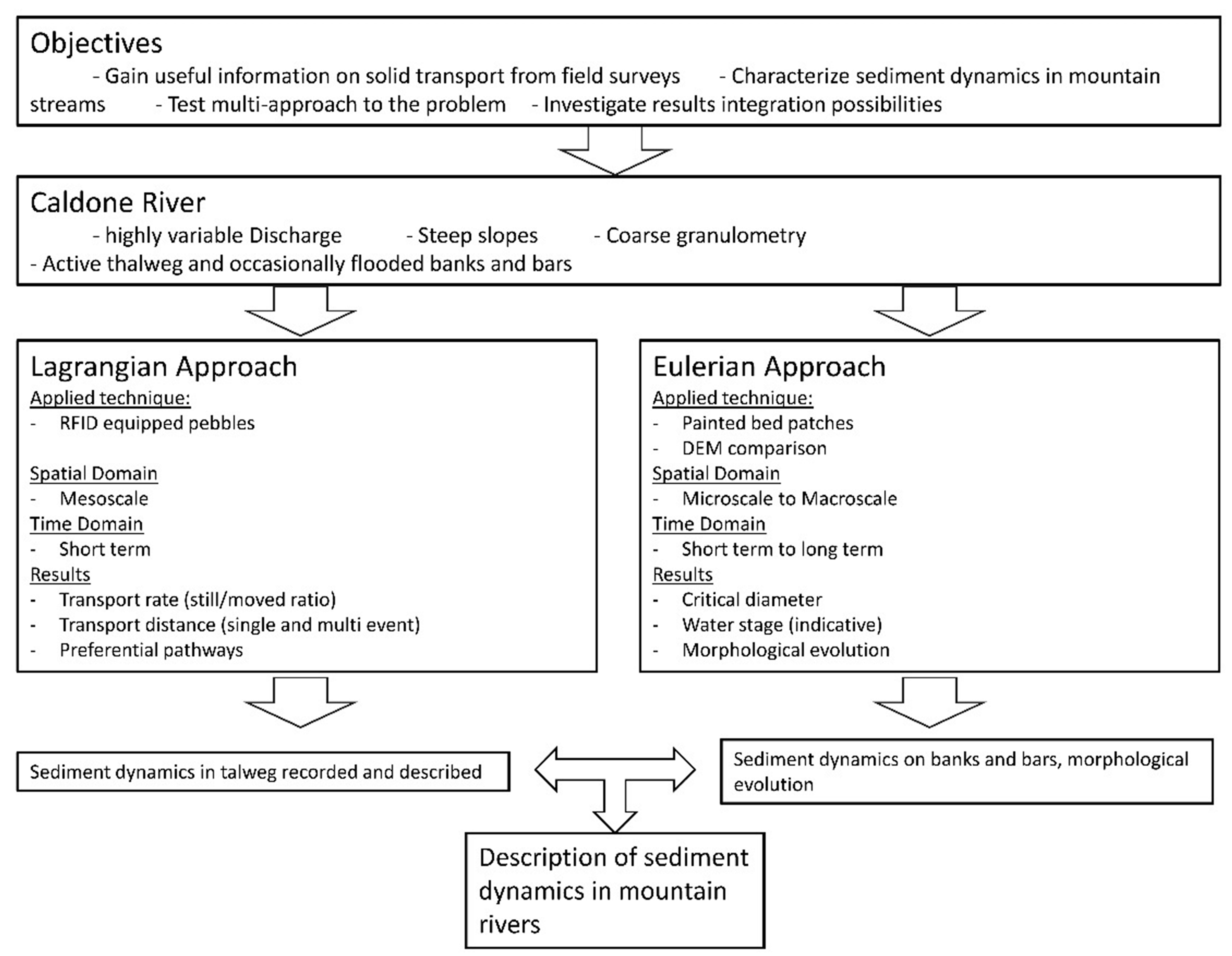
3. Methods and Results
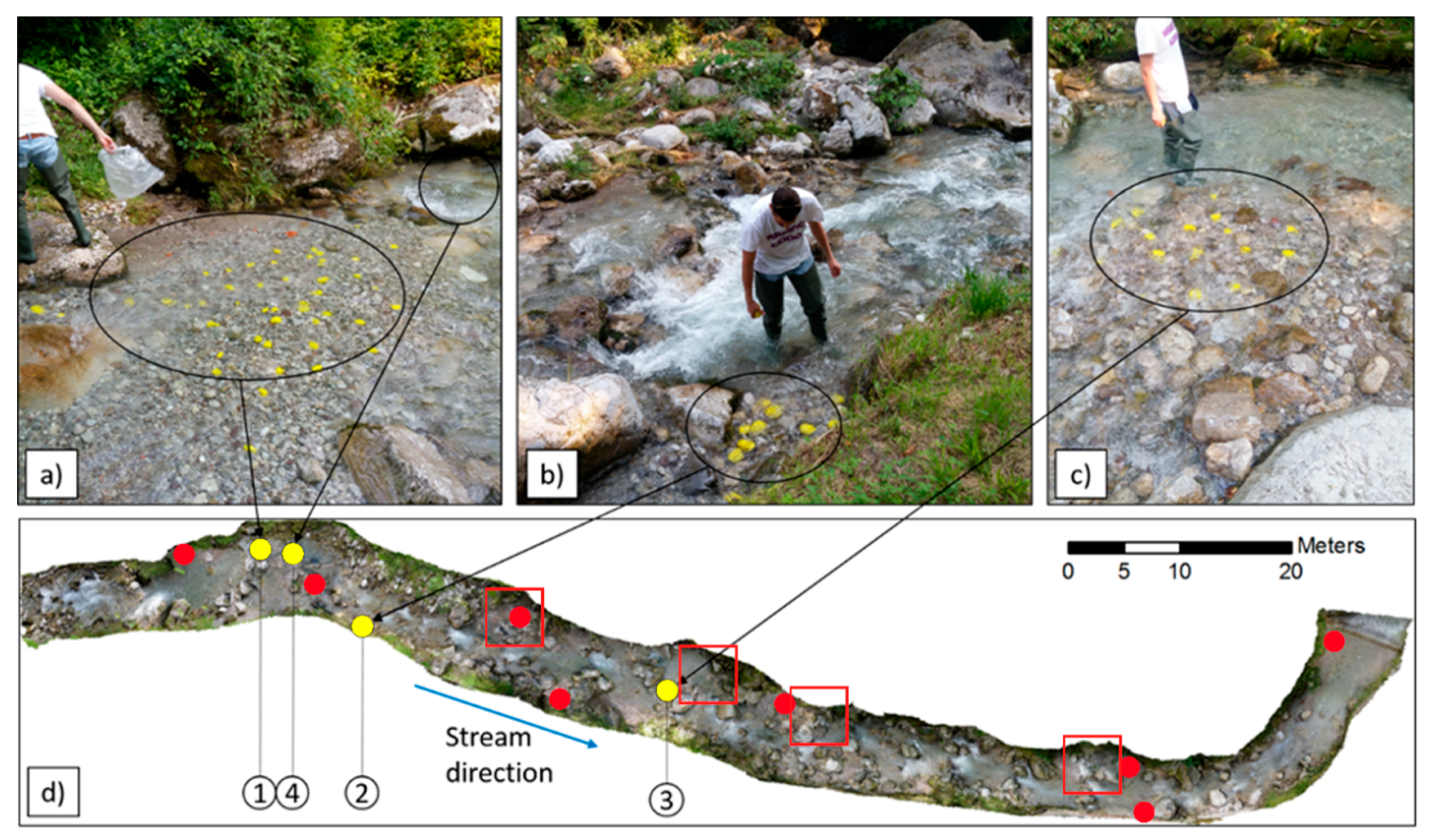
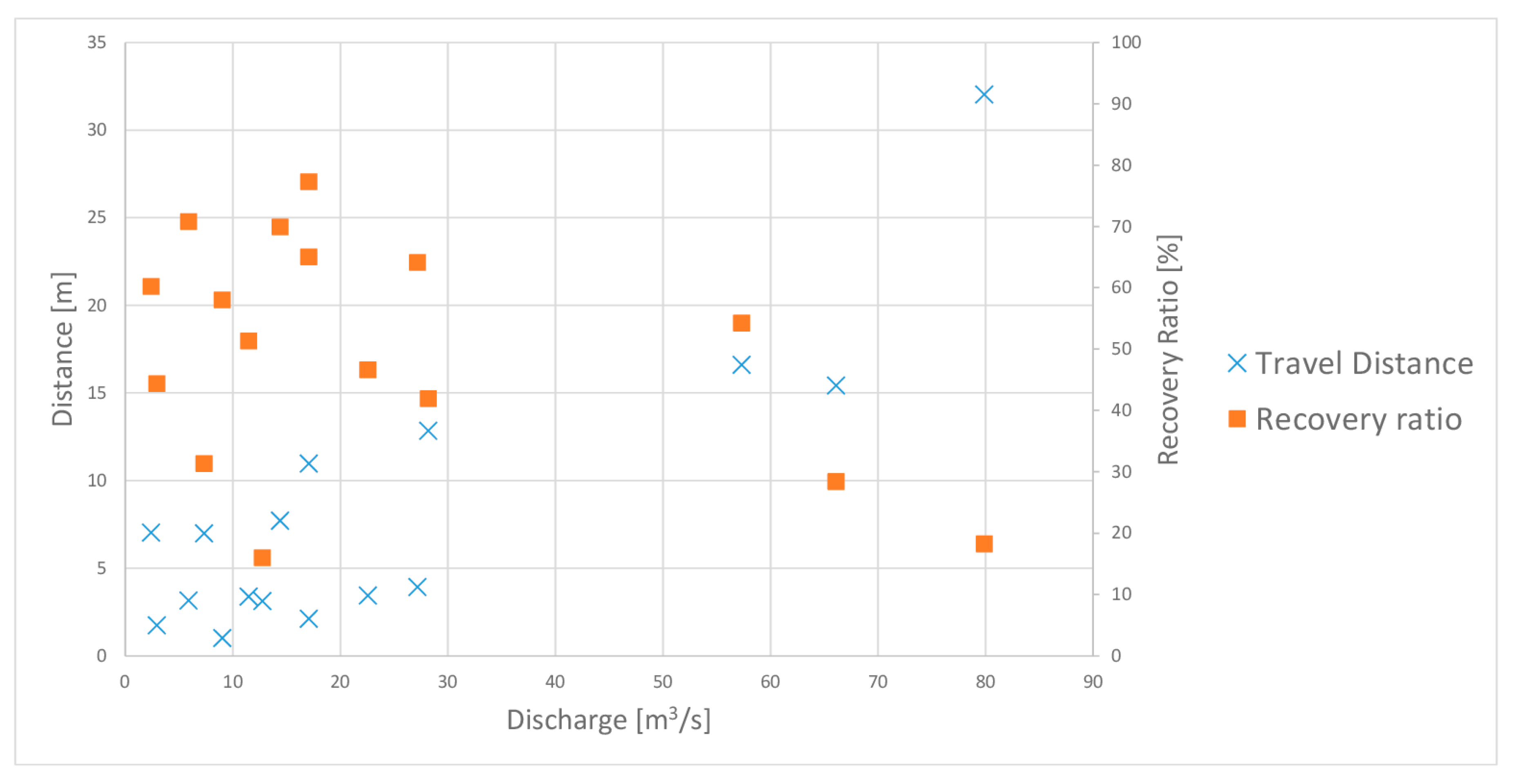
3.1. Lagrangian Method
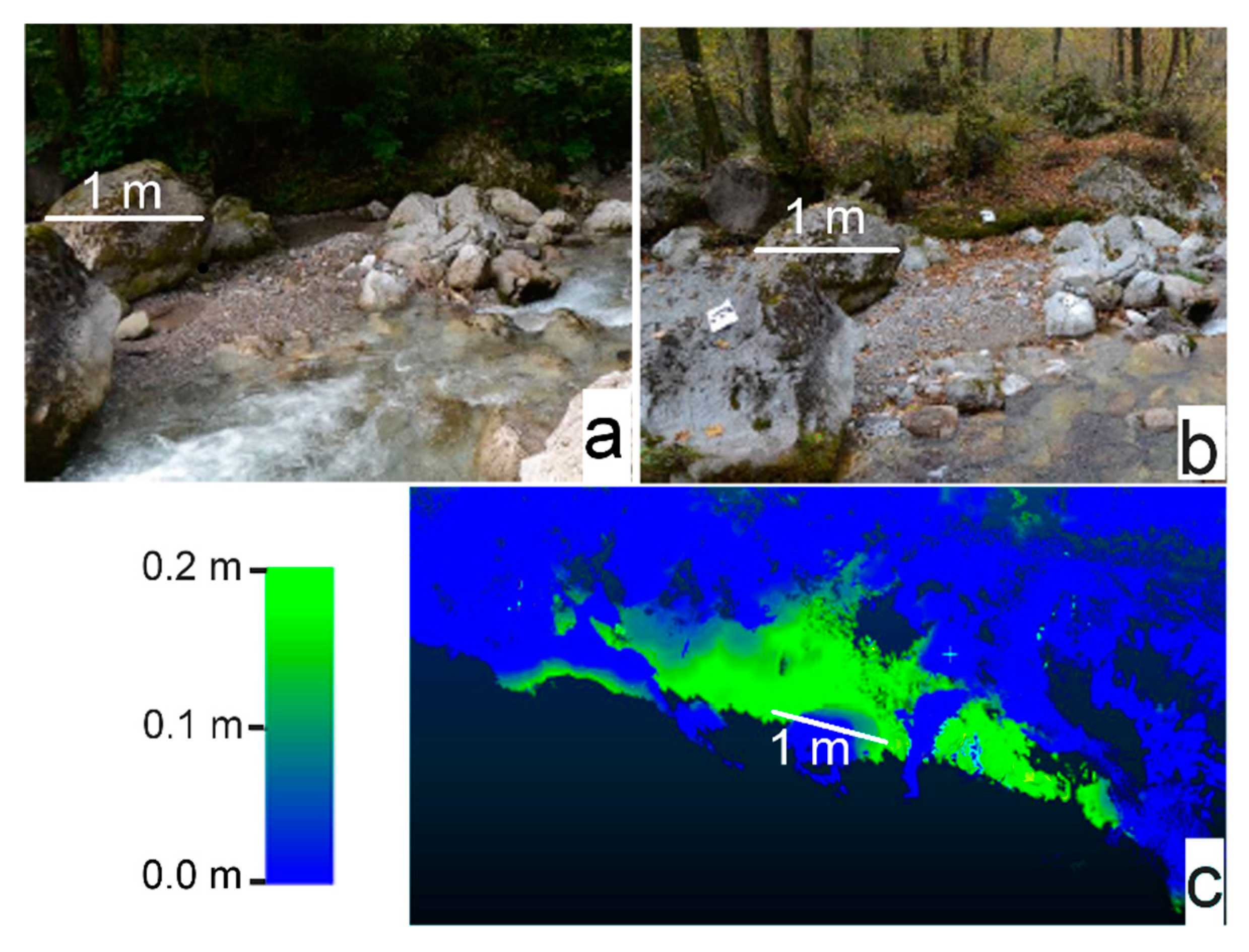
3.2. Eulerian Method
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Radice, A.; Giorgetti, E.; Brambilla, D.; Longoni, L.; Papini, M. On integrated sediment transport modelling for flash events in mountain environments. Acta Geophys. 2012, 60, 191–213. [Google Scholar] [CrossRef]
- Papini, M.; Ivanov, V.I.; Brambilla, D.; Arosio, D.; Longoni, L. Monitoring bedload sediment transport in a pre-alpine river: An experimental method. Rendiconti Online Societa Geologica Italiana 2017, 43, 57–63. [Google Scholar] [CrossRef]
- Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the assessment and management of flood risks. Off. J. Eur. Union 2007, 288, 27–34.
- Totschnig, R.; Sedlacek, W.; Fuchs, S. A quantitative vulnerability function for fluvial sediment transport. Natl. Hazards 2011, 58, 681–703. [Google Scholar] [CrossRef]
- Ballio, F.; Brambilla, D.; Giorgetti, E.; Longoni, L.; Papini, M.; Radice, A. Evaluation of sediment yield from valley slopes: A case study. WIT Trans. Eng. Sci. 2010, 67, 149–160. [Google Scholar]
- Longoni, L.; Ivanov, V.I.; Brambilla, D.; Radice, A.; Papini, M. Analysis of the temporal and spatial scales of soil erosion and transport in a mountain basin. Ital. J. Eng. Geol. Environ. 2016, 16, 17–30. [Google Scholar]
- Brambilla, D.; Longoni, L.; Papini, M.; Giorgetti, E.; Radice, A. On analysis of sediment sources toward proper characterization of hydro-geological hazard for mountain environments. Int. J. Saf. Secur. Eng. 2011, 1, 423–437. [Google Scholar] [CrossRef]
- Rainato, R.; Mao, L.; García-Rama, A.; Picco, L.; Cesca, M.; Vianello, A.; Preciso, E.; Scussel, G.; Lenzi, M. Three decades of monitoring in the rio cordon instrumented basin: Sediment budget and temporal trend of sediment yield. Geomorphology 2017, 291, 45–56. [Google Scholar] [CrossRef]
- Cavalli, M.; Goldin, B.; Comiti, F.; Brardinoni, F.; Marchi, L. Assessment of erosion and deposition in steep mountain basins by differencing sequential digital terrain models. Geomorphology 2017, 291, 4–16. [Google Scholar] [CrossRef]
- Lazzari, M.; Gioia, D.; Piccarreta, M.; Danese, M.; Lanorte, A. Sediment yield and erosion rate estimation in the mountain catchments of the camastra artificial reservoir (southern Italy): A comparison between different empirical methods. Catena 2015, 127, 323–339. [Google Scholar] [CrossRef]
- Schneider, J.; Hegglin, R.; Meier, S.; Turowski, J.; Nitsche, M.; Rickenmann, D. Studying sediment transport in mountain rivers by mobile and stationary rfid antennas. River Flow 2010, 2014, 1723–1730. [Google Scholar]
- Montgomery, D.R.; Buffington, J.M. Channel-reach morphology in mountain drainage basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]
- Hassan, M.A.; Church, M.; Lisle, T.E.; Brardinoni, F.; Benda, L.; Grant, G.E. Sediment transport and channel morphology of small, forested streams. Jawra J. Am. Water Resour. Assoc. 2005, 41, 853–876. [Google Scholar] [CrossRef]
- Hay, W.W. Detrital sediment fluxes from continents to oceans. Chem. Geol. 1998, 145, 287–323. [Google Scholar] [CrossRef]
- Holland, H.D. The Chemistry of the Atmosphere and Oceans (v. 1); John Wiley & Sons Inc: Hoboken, NJ, USA, 1978. [Google Scholar]
- Milliman, J.D.; Syvitski, J.P. Geomorphic/tectonic control of sediment discharge to the ocean: The importance of small mountainous rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Summerfield, M.; Hulton, N. Natural controls of fluvial denudation rates in major world drainage basins. J. Geophys. Res. Solid Earth 1994, 99, 13871–13883. [Google Scholar] [CrossRef]
- Lane, E.; Borland, W. Estimating bed load. Eos Trans. Am. Geophys. Union 1951, 32, 121–123. [Google Scholar] [CrossRef]
- Walling, D.E.; Webb, B.W. The Reliability of Suspended Sediment Load Data [River Creedy, England]; Food and Agriculture Organization of the United Nations: Rome, Italy, 1981. [Google Scholar]
- Whittaker, J. Sediment transport in step-pool streams. In Sediment Transport in Gravel-Bed Rivers; John Wiley and Sons: New York, NY, USA, 1987; pp. 545–579. [Google Scholar]
- Diez, J.-C.; Alvera, B.; Puigdefabregas, J.; Gallart, F. Assessing Sediment Sources in a Small Drainage Basin above the Timberline in the Pyrenees. 1988; Available online: http://hydrologie.org/redbooks/a174/iahs_174_0197.pdf (accessed on 28 December 2017).
- Billi, P.; D’Agostino, V.; Lenzi, M.A.; Marchi, L. Bed-load, slope and channel processes in a high-altitude alpine torrent. In Gravel-Bed Rivers in the Environment; Klingeman, P.C., Bechsta, R.L., Komar, P.D., Bradley, J.R., Eds.; Water Resource Publications, LLC: Highlands Ranch, CO, USA, 1998; pp. 15–38. [Google Scholar]
- Marquis, G.; Roy, A. Using multiple bed load measurements: Toward the identification of bed dilation and contraction in gravel—Bed rivers. J. Geophys. Res. Earth Surf. 2012, 117, F1. [Google Scholar] [CrossRef]
- Gray, J.R.; Gartner, J.W.; Barton, J.S.; Gaskin, J.; Pittman, S.A.; Rennie, C.D. Surrogate technologies for monitoring bed-load transport in rivers. Sedimentol. Aqueous Syst. 2010, 2, 45–79. [Google Scholar]
- Radice, A.; Sarkar, S.; Ballio, F. Image-based lagrangian particle tracking in bed-load experiments. J. Vis. Exp. JoVE 2017, 125, 55874. [Google Scholar] [CrossRef] [PubMed]
- Radice, A.; Ballio, F.; Nikora, V. Statistics and characteristic scales for bed load in a channel flow with sidewall effects. Acta Geophys. 2010, 58, 1072–1093. [Google Scholar] [CrossRef]
- Ramesh, B.; Kothyari, U.C.; Murugesan, K. Near-bed particle motion over transitionally-rough bed. J. Hydr. Res. 2011, 49, 757–765. [Google Scholar] [CrossRef]
- Niño, Y.; García, M. Using lagrangian particle saltation observations for bedload sediment transport modelling. Hydrol. Process. 1998, 12, 1197–1218. [Google Scholar] [CrossRef]
- Takayama, S. Bedload movement in torrential mountain streams. Tokyo Geogr. Pap. 1965, 9, 169–188. (In Japanese) [Google Scholar]
- Leopold, L.B. Channel and Hillslope Processes in a Semiarid Area, New Mexico; US Government Printing Office: Washington, DC, USA, 1966; Volume 352. [Google Scholar]
- Benelli, G.; Bertoni, D.; Sarti, G. An analysis on the use of lf rfid for the tracking of different typologies of pebbles on beaches. In Proceedings of the 2011 IEEE International Conference on RFID-Technologies and Applications (RFID-TA), Sitges, Spain, 15–16 September 2011; pp. 426–431. [Google Scholar]
- Camenen, B.; Le Coz, J.; Paquier, A.; Lagouy, M. In An estimation of gravel mobility over an alpine river gravel bar (arc en Maurienne, France) using pit-tag tracers. In Proceedings of the 5th International Conference on Fluvial Hydraulics (River Flow 2010), Braunschweig, Germany, 8–10 September 2010; p. 8. [Google Scholar]
- Chapuis, M.; Dufour, S.; Provansal, M.; Couvert, B.; De Linares, M. Coupling channel evolution monitoring and rfid tracking in a large, wandering, gravel-bed river: Insights into sediment routing on geomorphic continuity through a riffle–pool sequence. Geomorphology 2015, 231, 258–269. [Google Scholar] [CrossRef]
- Vázquez-Tarrío, D.; Menéndez-Duarte, R. Bedload transport rates for coarse-bed streams in an atlantic region (Narcea river, nw Iberian Peninsula). Geomorphology 2014, 217, 1–14. [Google Scholar] [CrossRef]
- Hassan, M.A.; Ergenzinger, P. Use of tracers in fluvial geomorphology. Tools Fluv. Geomorphol. 2003, 397–423. [Google Scholar] [CrossRef]
- Lamarre, H.; Roy, A.G. Reach scale variability of turbulent flow characteristics in a gravel-bed river. Geomorphology 2005, 68, 95–113. [Google Scholar] [CrossRef]
- Sear, D.; Wilcock, D.; Robinson, M.; Fisher, K. River channel modification in the UK. In The Hydrology of the United Kingdom: A Study of Change; Routledge: London, UK, 2000; pp. 55–81. [Google Scholar]
- Liébault, F.; Bellot, H.; Chapuis, M.; Klotz, S.; Deschâtres, M. Bedload tracing in a high-sediment-load mountain stream. Earth Surf. Process. Landf. 2012, 37, 385–399. [Google Scholar] [CrossRef]
- Liedermann, M.; Tritthart, M.; Habersack, H. Particle path characteristics at the large gravel-bed river danube: Results from a tracer study and numerical modelling. Earth Surf. Process. Landf. 2013, 38, 512–522. [Google Scholar] [CrossRef]
- Mao, L.; Carrillo, R.; Escauriaza, C.; Iroume, A. Flume and field-based calibration of surrogate sensors for monitoring bedload transport. Geomorphology 2016, 253, 10–21. [Google Scholar] [CrossRef]
- Habersack, H. Radio-tracking gravel particles in a large braided river in New Zealand: A field test of the stochastic theory of bed load transport proposed by Einstein. Hydrol. Process. 2001, 15, 377–391. [Google Scholar] [CrossRef]
- Rickenmann, D.; McArdell, B.W. Continuous measurement of sediment transport in the erlenbach stream using piezoelectric bedload impact sensors. Earth Surf. Process. Landf. 2007, 32, 1362–1378. [Google Scholar] [CrossRef]
- Dell’Agnese, A.; Brardinoni, F.; Toro, M.; Mao, L.; Engel, M.; Comiti, F. Bedload transport in a formerly glaciated mountain catchment constrained by particle tracking. Earth Surf. Dynam. 2015, 3, 527. [Google Scholar] [CrossRef]
- Scheingross, J.S.; Winchell, E.W.; Lamb, M.P.; Dietrich, W.E. Influence of bed patchiness, slope, grain hiding, and form drag on gravel mobilization in very steep streams. J. Geophys. Res. Earth Surf. 2013, 118, 982–1001. [Google Scholar] [CrossRef]
- Shields, A. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 1936. (In German). [Google Scholar]
- Lenzi, M.; D’Agostino, V. Step-Pool Evolution in an Alpine Torrent. New Trends in Water and Environmental Engineering for Safety and Life; AA. Balkema: Rotterdam, The Netherlands, 2000; Volume 31. [Google Scholar]
- Langhammer, J.; Hartvich, F.; Kliment, Z.; Jeníček, M.; Bernsteinová, J.; Vlček, L.; Su, Y.; Štych, P.; Miřijovský, J. The impact of disturbance on the dynamics of fluvial processes in mountain landscapes. Silva Gabreta 2015, 21, 105–116. [Google Scholar]
- Hassan, M.A.; Bradley, D.N. Geomorphic controls on tracer particle dispersion in gravel-bed rivers. In Gravel-Bed Rivers Process Disasters; Wiley/John Wiley & Sons Inc: Hoboken, NJ, USA, 2017. [Google Scholar]
- Garzanti, E.; Gamba, A.; Malara, F.; Vidimari, C. Evoluzione della mineralogia del detrito in sistemi fluviali segmentati da sbarramenti naturali o artificiali e attraverso la pianura: Il bacino idrografico dell’adda (Lombardia). Geol. Insubr. 1999, 3, 43–60. [Google Scholar]
- Detert, M.; Weitbrecht, V. Automatic object detection to analyze the geometry of gravel grains—A free stand-alone tool. In River Flow; Taylor & Francis Group: London, UK, 2012; pp. 595–600. [Google Scholar]
- Rinaldi, M.; Surian, N.; Comiti, F.; Bussettini, M. Manuale Tecnico-Operativo per la Valutazione ed il Monitoraggio dello Stato Morfologico dei Corsi D’acqua; ISPRA: Roma, Italy, 2010. (In Italian) [Google Scholar]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydr. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Radice, A.; Malavasi, S.; Ballio, F. Solid transport measurements through image processing. Exp. Fluids 2006, 41, 721–734. [Google Scholar] [CrossRef]
- Longoni, L.; Ivanov, V.; Brambilla, D.; Papini, M.; Brebbia, C.; Teanini, E.; Radice, A. Application of multiple surveying techniques at a to-be-gauged river section. In Proceedings of the HydroSenSoft, Madrid, Spain, 1–3 March 2017; pp. 246–253. [Google Scholar]
- Ivanov, V.I.; Brambilla, D.; Longoni, L.; Arosio, D.; Papini, M. Rfid-aided sediment transport monitoring—Laboratory and preliminary field test results. In Workshop on World Landslide Forum; Springer: Berlin, Germany, 2017; pp. 623–630. [Google Scholar]
- Brunner, G.W. HEC-RAS (river analysis system). In North American Water and Environment Congress & Destructive Water; ASCE: New York, NY, USA, 2002; pp. 3782–3787. [Google Scholar]
- Limerinos, J.T.; California Department of Water Resources. Determination of the Manning Coefficient from Measured Bed Roughness in Natural Channels; U.S. Department of the Interior, Geological Survey, Water Resources Division, Ground Water Branch: Washington, DC, USA, 1970. [Google Scholar]
- Ferguson, R. Flow resistance equations for gravel- and boulder-bed streams. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Haschenburger, J.K.; Church, M. Bed material transport estimated from the virtual velocity of sediment. Earth Surf. Process. Landf. 1998, 23, 791–808. [Google Scholar] [CrossRef]




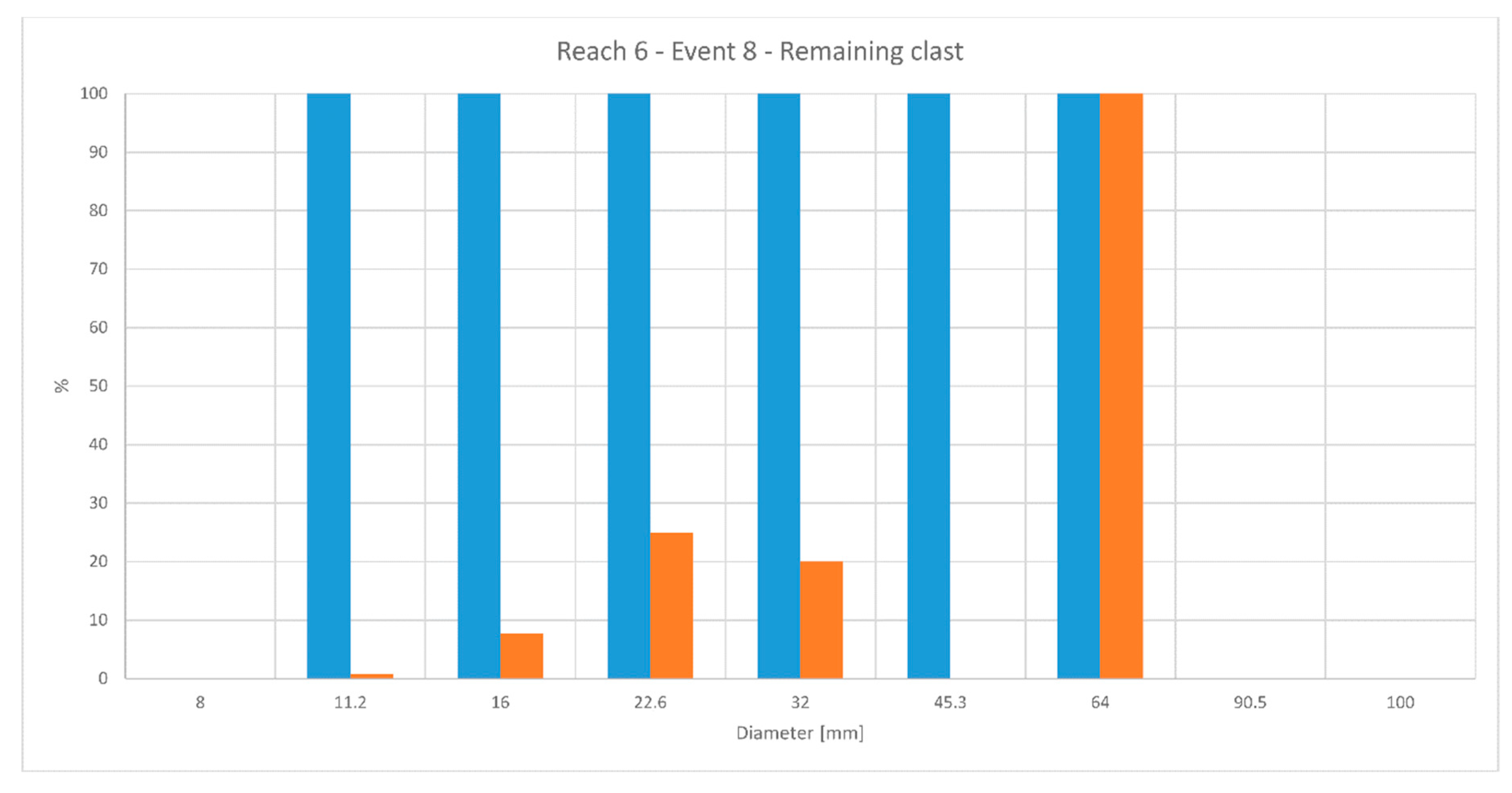
| Instrument | Elevation (m a.s.l.) | Measurement Frequency | Remote Controlled | Reach Number |
|---|---|---|---|---|
| Water level gauge | 210 | Hourly | Yes | 11 |
| Rain gauge | 210 | Hourly | Yes | 11 |
| Water level gauge | 350 | Event | No | 7 |
| Reach Number | Morphology Type | Reach Length (m) | Mean Width (m) | Mean Slope (%) | D90 (mm) | D50 (mm) | D10 (mm) |
|---|---|---|---|---|---|---|---|
| 6 | Boulder and cascade | 1000 | 8 | 5.5 | 51 | 12.3 | 1 |
| 7 | Step and pool | 375 | <10 | 3.7 | 68 | 17.5 | 3.7 |
| 11 | Plane bed | 800 | 6 | 1.5 | 110 | 19 | 0.95 |
| Event Number | Date | Cumulative Rain Depth (mm) | Rain Duration (h) | Peak Discharge (m3/s) | Mean Distance (m) | RFID Recovery Ratio (%) |
|---|---|---|---|---|---|---|
| 1 | 26 June 2016 | 26 | 4 | 17.06 | 10.9 | 77.3 |
| 2 | 2 July 2016 | 11 | 7 | 2.41 | 7.0 | 60.2 |
| 3 | 13 July 2016 | 27 | 13 | 22.56 | 3.4 | 46.6 |
| 4 | 22 July 2016 | 44 | 35 | 14.39 | 7.7 | 69.9 |
| 5 | 31 July 2016 | 29 | 18 | 5.88 | 3.1 | 70.8 |
| 6 | 5 August 2016 | 67 | 9 | 57.31 | 16.5 | 54.2 |
| 8 | 14 October 2016 | 43 | 42 | 11.48 | 3.3 | 51.3 |
| 9 | 20 November 2016 | 94 | 132 | 28.18 | 12.8 | 41.9 |
| 10 | 4 March 2017 | 14 | 31 | 2.95 | 1.7 | 44.3 |
| 12 | 3 May 2017 | 21 | 16 | 9.01 | 1.0 | 58.0 |
| 13 | 13 May 2017 | 35 | 8 | 17.06 | 2.1 | 65.0 |
| 14 | 6 June 2017 | 132 | 62 | 27.18 | 3.9 | 64.1 |
| 15 | 28 June 2017 | 110 | 18 | 66.09 | 15.4 | 28.4 |
| 16 | 8 September 2017 | 27 | 5 | 7.33 | 6.9 | 31.3 |
| 17 | 10 September 2017 | 94 | 56 | 79.89 | 32.0 | 18.2 |
| 18 | 5 November 2017 | 53 | 26 | 12.76 | 3.1 | 16.0 |
| Reach Number | Event Number | Morphology Type | Flow Rate (m3/s) | Dc Measured (mm) | Dc Calculated (mm) | Manning Resistance n (s/m1/3) |
|---|---|---|---|---|---|---|
| 6 | 6 | Bank | 5.88 | >90.5 | 93.5 | 0.04 |
| 6 | 7 | Bank | 1.12 | 45.3–64 | 50 | 0.04 |
| 6 | 7 | Bar | 1.12 | 64–90.5 | 80 | 0.03 |
| 6 | 8 | Bank | 0.67 | 45.3–64 | 42 | 0.04 |
| 6 | 8 | Bar | 0.67 | 45.3–64 | 65 | 0.03 |
| 7 | 8 | Bar | 0.67 | 32–45.3 | 32 | 0.04 |
| 7 | 8 | Bar | 0.67 | 64–90.5 | 68 | 0.03 |
| 6 | 10 | Bar | 1.4 | 45.3–64 | 60 | 0.04 |
| 6 | 10 | Bank | 1.4 | 45.3–64 | 40 | 0.03 |
| 6 | 14 | Bar | 5.88 | >90.5 | 92 | 0.05 |
| 6 | 14 | Bar | 5.88 | 45.3–64 | 135 | 0.07 |
| 6 | 17 | Bar | 1.55 | >90.5 | 87 | 0.04 |
| 6 | 17 | Bank | 1.55 | >64 | 91 | 0.05 |
| 6 | 17 | Bank | 1.55 | >100 | 99 | 0.04 |
| 6 | 17 | Bank | 1.55 | >100 | 106 | 0.04 |
| 6 | 18 | Bar | 3.19 | 22.6–32 | 68 | 0.04 |
| 6 | 18 | Bank | 3.19 | <10 | 67 | 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brambilla, D.; Papini, M.; Longoni, L. Temporal and Spatial Variability of Sediment Transport in a Mountain River: A Preliminary Investigation of the Caldone River, Italy. Geosciences 2018, 8, 163. https://doi.org/10.3390/geosciences8050163
Brambilla D, Papini M, Longoni L. Temporal and Spatial Variability of Sediment Transport in a Mountain River: A Preliminary Investigation of the Caldone River, Italy. Geosciences. 2018; 8(5):163. https://doi.org/10.3390/geosciences8050163
Chicago/Turabian StyleBrambilla, Davide, Monica Papini, and Laura Longoni. 2018. "Temporal and Spatial Variability of Sediment Transport in a Mountain River: A Preliminary Investigation of the Caldone River, Italy" Geosciences 8, no. 5: 163. https://doi.org/10.3390/geosciences8050163
APA StyleBrambilla, D., Papini, M., & Longoni, L. (2018). Temporal and Spatial Variability of Sediment Transport in a Mountain River: A Preliminary Investigation of the Caldone River, Italy. Geosciences, 8(5), 163. https://doi.org/10.3390/geosciences8050163







