Measuring Hyperscale Topographic Anisotropy as a Continuous Landscape Property
Abstract
:1. Introduction
2. Materials and Methods
2.1. Directional LTP Sampling
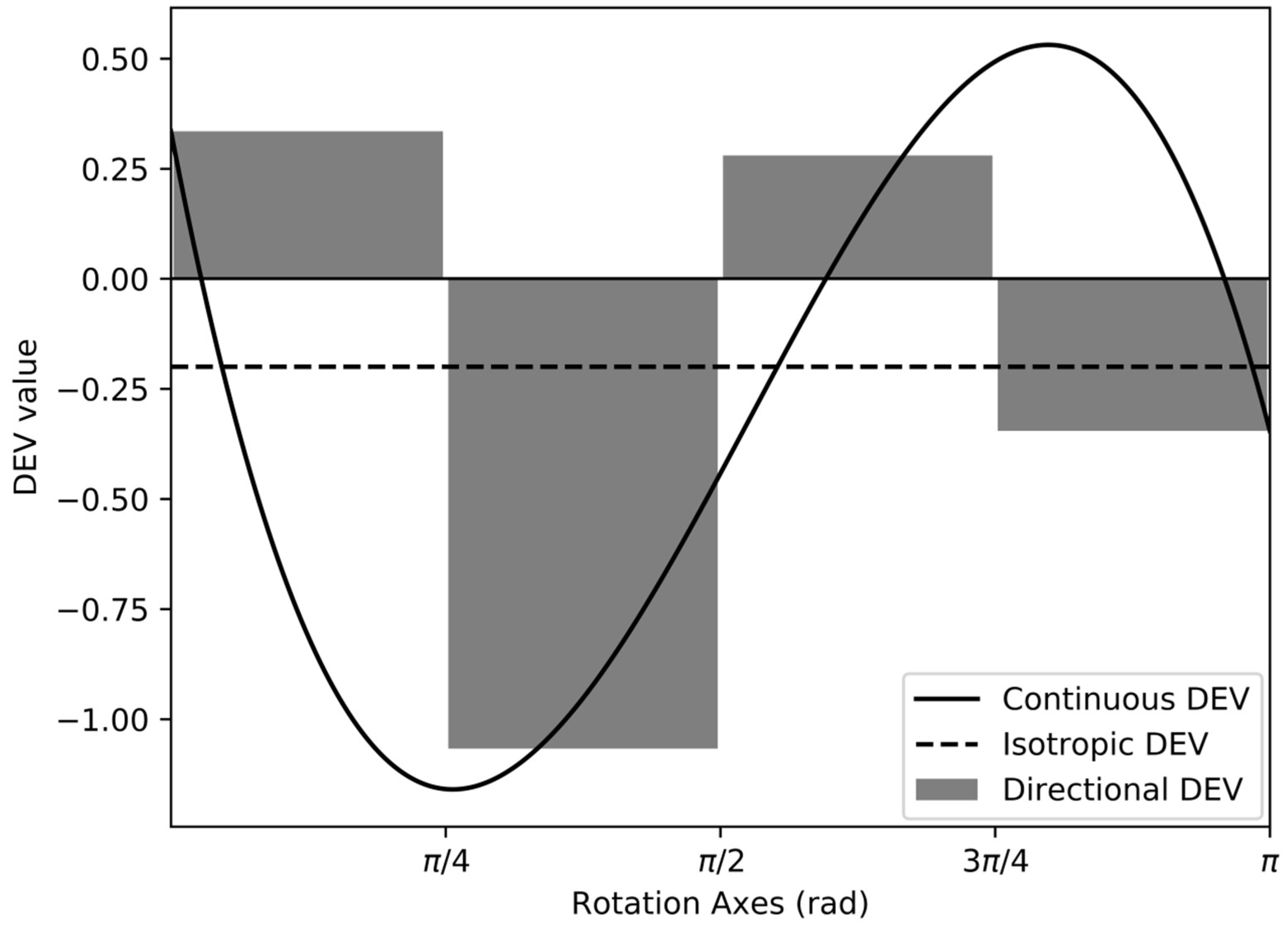
2.2. Anisotropy Model
2.3. Analysis
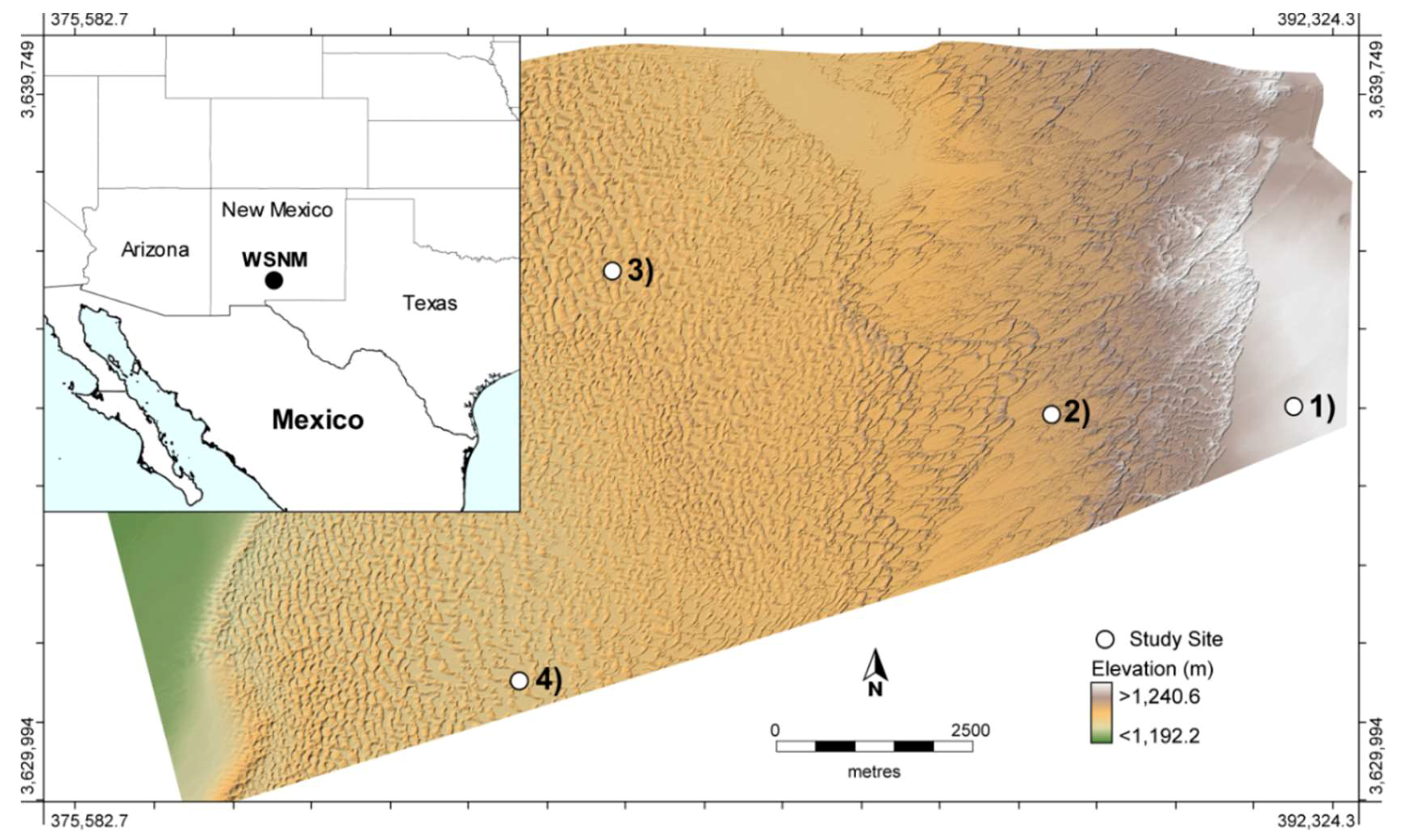
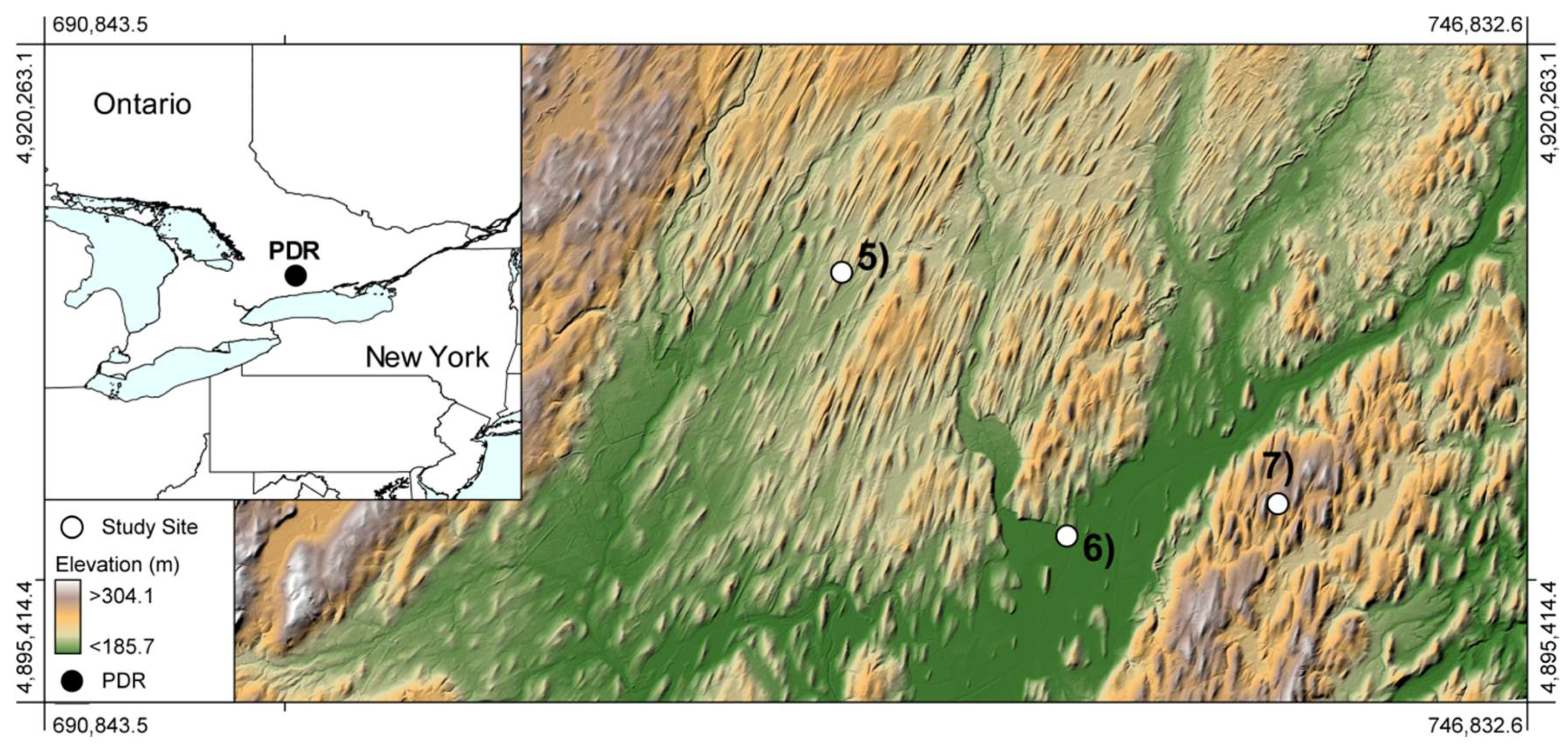
2.4. Data Sets and Study Sites
3. Results
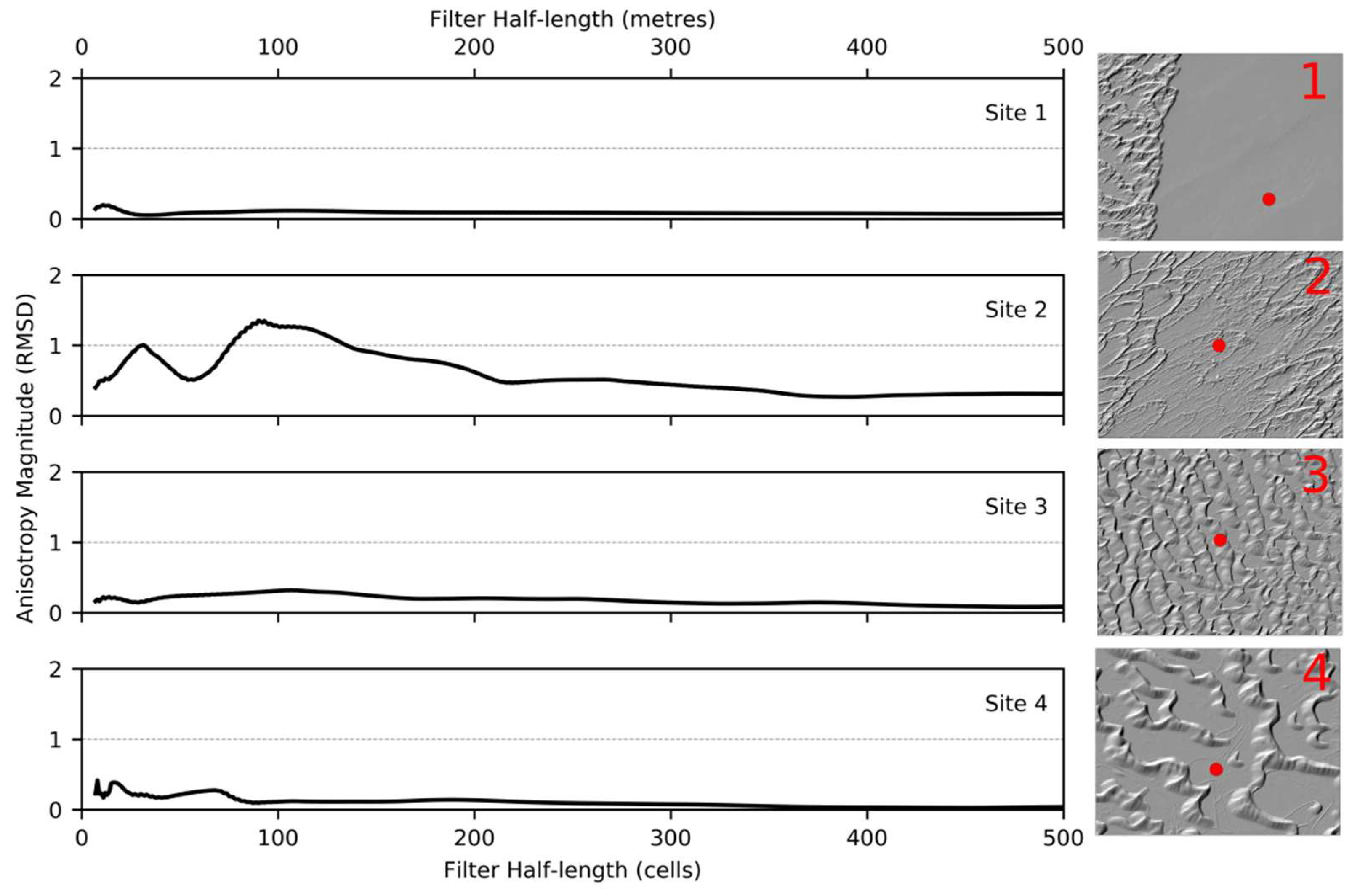
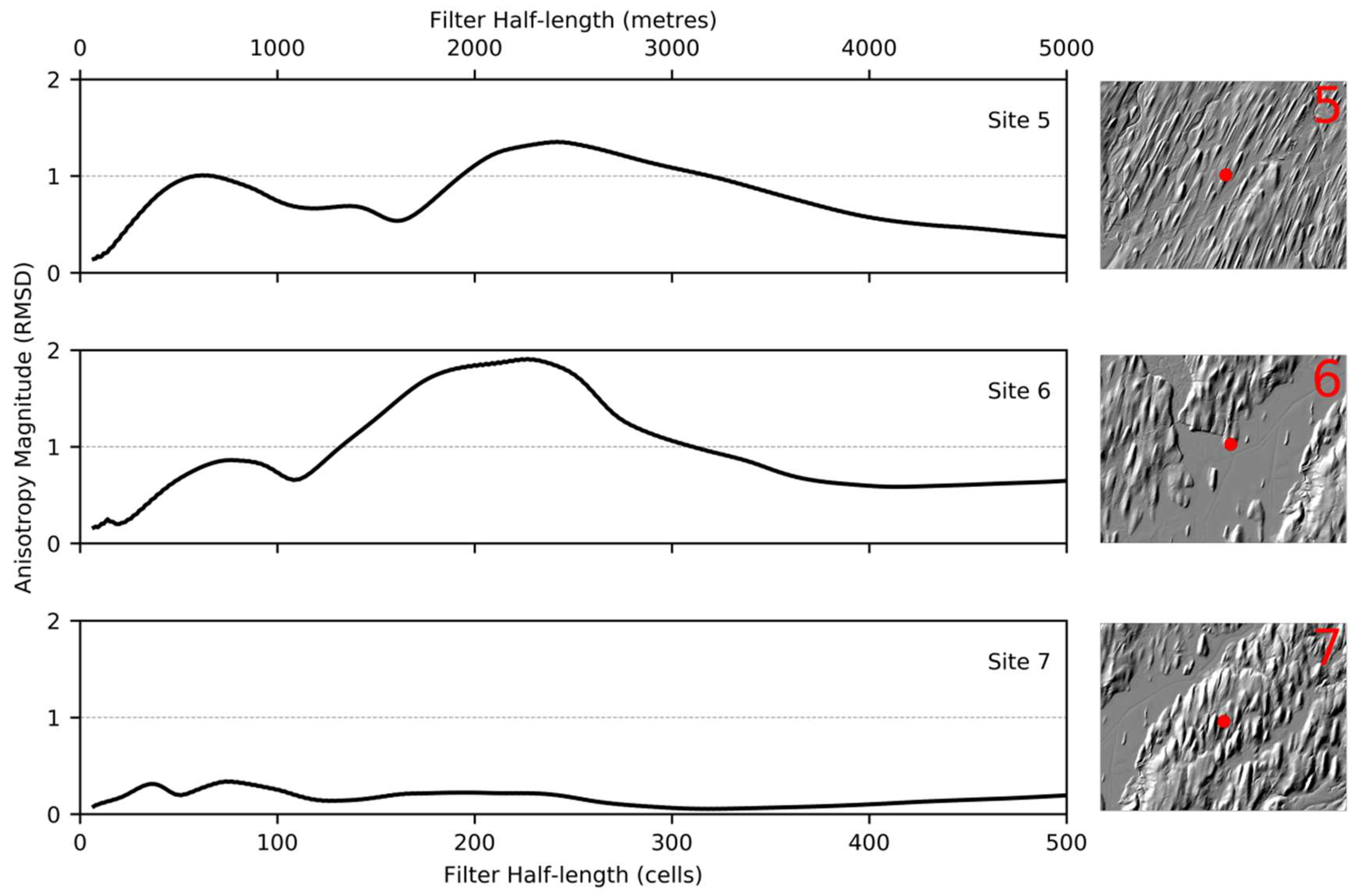
3.1. Topographic Anisotropy-Scale Signatures
3.2. Spatial Distribution of Topographic Anisotropy
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roy, S.G.; Koons, P.O.; Osti, B.; Upton, P.; Tucker, G.E. Multi-scale characterization of topographic anisotropy. Comput. Geosci. 2016, 90, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Ortega-Becerril, J.; Gomez-Heras, M.; Fort, R.; Wohl, E. How does anisotropy in bedrock river granitic outcrops influence pothole genesis and development? Earth Surf. Processes Landforms 2017, 42, 956–968. [Google Scholar] [CrossRef]
- Kaplan, D.A.; Paudel, R.; Cohen, M.J.; Jawitz, J.W. Orientation matters: Patch anisotropy controls discharge competence and hydroperiod in a patterned peatland. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, J.; Andrew, R. Multi-scale landform characterization. Area 2005, 37, 341–350. [Google Scholar] [CrossRef]
- Brardinoni, F.; Hassan, M.A. Glacial erosion, evolution of river long profiles, and the organization of process domains in mountain drainage basins of coastal British Columbia. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Maclachlan, J.C.; Eyles, C.H. Quantitative geomorphological analysis of drumlins in the Peterborough drumlin field, Ontario, Canada. Geografiska Annaler 2013, 95, 125–144. [Google Scholar] [CrossRef]
- Houser, C.; Bishop, M.; Wernette, P. Multi-scale topographic anisotropy patterns on a Barrier Island. Geomorphology 2017, 297, 153–158. [Google Scholar] [CrossRef]
- Markofsky, S.; Bevan, A. Directional analysis of surface artefact distributions: A case study from the Murghab Delta, Turkmenistan. J. Archaeol. Sci. 2012, 39, 428–439. [Google Scholar] [CrossRef]
- Mucha, J.; Wasilewska-Błaszczyk, M. Variability anisotropy of mineral deposits parameters and its impact on resources estimation—A geostatistical approach/Anizotropia Zmienności Parametrów I Jej Wpływ Na Szacowanie Zasobów W Ujęciu Geostatystycznym. Gospodarka Surowcami Mineralnymi Mineral Resour. Manag. 2012, 28, 113–135. [Google Scholar] [CrossRef]
- Zimmerman, D.L. Another look at anisotropy in geostatistics. Mathem. Geol. 1993, 25, 453–470. [Google Scholar] [CrossRef]
- Eriksson, M.; Siska, P.P. Understanding anisotropy computations. Mathem. Geol. 2000, 32, 683–700. [Google Scholar] [CrossRef]
- Trevisani, S.; Cavalli, M.; Marchi, L. Surface texture analysis of a high-resolution DTM: Interpreting an alpine basin. Geomorphology 2012, 161–162, 26–39. [Google Scholar] [CrossRef]
- Vamshi, G.T.; Martha, T.R.; Kumar, K.V. An object-based classification method for automatic detection of lunar impact craters from topographic data. Adv. Space Res 2016, 57, 1978–1988. [Google Scholar] [CrossRef]
- Deumlich, D.; Schmidt, R.; Sommer, M. A multiscale soil-landform relationship in the glacial-drift area based on digital terrain analysis and soil attributes. J. Plant Nutr. Soil Sci. 2010, 173, 843–851. [Google Scholar] [CrossRef]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Finke, P.; Van Meirvenne, M.; Verniers, J.; Crombé, P. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Phillips, R.L.; Ngugi, M.K.; Hendrickson, J.; Smith, A.; West, M. Mixed-grass prairie canopy structure and spectral reflectance vary with topographic position. Environ. Manag. 2012, 50, 914–928. [Google Scholar] [CrossRef] [PubMed]
- Riley, J.W.; Calhoun, D.L.; Barichivich, W.J.; Walls, S.C. Identifying Small Depressional Wetlands and Using a Topographic Position Index to Infer Hydroperiod Regimes for Pond-Breeding Amphibians. Wetlands 2017, 37, 325–338. [Google Scholar] [CrossRef]
- Mieza, M.S.; Cravero, W.R.; Kovac, F.D.; Bargiano, P.G. Delineation of site-specific management units for operational applications using the topographic position index in La Pampa, Argentina. Comput. Electron. Agric. 2016, 127, 158–167. [Google Scholar] [CrossRef] [Green Version]
- Vinod, P.G. Development of topographic position index based on Jenness algorithm for precision agriculture at Kerala, India. Spat. Inf. Res. 2017, 25, 381–388. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Cockburn, J.M.H.; Russell, H.A.J. An integral image approach to performing multi-scale topographic position analysis. Geomorphology 2015, 245, 51–61. [Google Scholar] [CrossRef]
- Zhilin, L. Multi-Scale Digital Terrain Modeling and Analysis. In Advances in Digital Terrain Analysis; Zhou, Q., Lees, B., Tang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 59–84. [Google Scholar]
- Behrens, T.; Zhu, A.X.; Schmidt, K.; Scholten, T. Multi-scale digital terrain analysis and feature selection for digital soil mapping. Geoderma 2010, 155, 175–185. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Mocko, D. Multiscale Evaluation of the Improvements in Surface Snow Simulation through Terrain Adjustments to Radiation. Hydrometeorology 2013, 14, 220–232. [Google Scholar] [CrossRef]
- Miller, B.A. Semantic Calibration of digital terrain analysis scale. Cartogrphy Geogrph. Inf. Sci. 2014, 41, 166–176. [Google Scholar] [CrossRef]
- Huang, T.S.; Yang, G.J.; Tang, G.Y. A Fast Two-Dimensional Median Filtering Algorithm. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 13–18. [Google Scholar] [CrossRef]
- Crow, F.C. Summed-Area Tables for Texture Mapping. Comput. Graph. 1984, 18, 207–212. [Google Scholar] [CrossRef]
- Newman, D.R.; Lindsay, J.B.; Cockburn, J.M.H. Evaluating metrics of local topographic position for multiscale geomorphometric analysis. Geomorphology 2018, 312, 40–50. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M.J. Robust Real-Time Face Detection. Int. J. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Sizintsev, M.; Derpanis, K.G.; Hogue, A. Histogram-based search: A comparative study. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, Alaska, 23–28 June 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Lindsay, J.B. Whitebox GAT: A case study in geomorphometric analysis. Comput. Geosci. 2016, 95, 75–84. [Google Scholar] [CrossRef]
- Arundel, S.T.; Archuleta, C.M.; Phillips, L.A.; Roche, B.L.; Constance, E.W. 1-Meter Digital Elevation Model Specification; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2015.
- Anderson, W.; Chamecki, M. Numerical study of turbulent flow over complex aeolian dune fields: The White Sands National Monument. Phys. Rev. E 2014, 89, 013005. [Google Scholar] [CrossRef] [PubMed]
- Kocurek, G.; Carr, M.; Ewing, R.; Havholm, K.G.; Nagar, Y.C.; Singhvi, A.K. White Sands Dune Field, New Mexico: Age, dune dynamics and recent accumulations. Sediment. Geol. 2007, 107, 313–331. [Google Scholar] [CrossRef]
- Ministry of Natural Resources (MNR). Provincial DEM Version 2.0.0 Product Specification, Geographic Information Branch, Science and Information Resources Division; Ministry of Natural Resources (MNR): Dar Es Salaam, Tanzania, 2008.
- Kerr, M.; Eyles, N. Origin of drumlins on the floor of Lake Ontario and in upper New York State. Sediment. Geol. 2007, 103, 7–20. [Google Scholar] [CrossRef]
- Xianfang, S.; Rosin, P.L.; Martin, R.R.; Langbein, F.C. Fast and effective feature-preserving mesh denoising. IEEE Trans. Vis. Comput. Graph. 2007, 13, 925–938. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Riccomini, C. Comparison of roving-window and search-window techniques for characterising landscape morphometry. Comput. Geosci. 2009, 35, 2164–2169. [Google Scholar] [CrossRef] [Green Version]
- Minár, J.; Evans, I.S. Elementary forms for land surface segmentation: The theoretical basis of terrain analysis and geomorphological mapping. Geomorphology 2008, 95, 236–259. [Google Scholar] [CrossRef]
- Gessler, P.; Pike, R.; MacMillan, R.A.; Hengl, T.; Reuter, H.I. The Future of Geomorphometry. In Geomorphometry—Concepts, Software, Applications; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 637–652. [Google Scholar]
- Damon, J. Properties of ridges and cores for two-dimensional images. J. Math. Imaging Vis. 1999, 10, 163–174. [Google Scholar] [CrossRef]
- Lindeberg, T. Edge detection and ridge detection with automatic scale selection. Int. J. Comput. Vis. 1998, 30, 117–154. [Google Scholar] [CrossRef]
- Cova, T.J.; Goodchild, M.F. Extending geographical representation to include fields of spatial objects. Int. J. Geogrph. Inf. Sci. 2002, 16, 509–532. [Google Scholar] [CrossRef]
- Evans, I.S. Geomorphometry and landform mapping: What is a landform? Geomorphology 2012, 137, 94–106. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newman, D.R.; Lindsay, J.B.; Cockburn, J.M.H. Measuring Hyperscale Topographic Anisotropy as a Continuous Landscape Property. Geosciences 2018, 8, 278. https://doi.org/10.3390/geosciences8080278
Newman DR, Lindsay JB, Cockburn JMH. Measuring Hyperscale Topographic Anisotropy as a Continuous Landscape Property. Geosciences. 2018; 8(8):278. https://doi.org/10.3390/geosciences8080278
Chicago/Turabian StyleNewman, Daniel R., John B. Lindsay, and Jaclyn M. H. Cockburn. 2018. "Measuring Hyperscale Topographic Anisotropy as a Continuous Landscape Property" Geosciences 8, no. 8: 278. https://doi.org/10.3390/geosciences8080278
APA StyleNewman, D. R., Lindsay, J. B., & Cockburn, J. M. H. (2018). Measuring Hyperscale Topographic Anisotropy as a Continuous Landscape Property. Geosciences, 8(8), 278. https://doi.org/10.3390/geosciences8080278




