Abstract
Seismic coda measurements retrieve parameters linked to the physical characteristics of rock volumes illuminated by high frequency scattered waves. Space weighting functions (SWF) and kernels are different tools that model the spatial sensitivity of coda envelopes to scattering and absorption anomalies in these rock matrices, allowing coda-wave attenuation () imaging. This note clarifies the difference between SWF and sensitivity kernels developed for coda wave imaging. It extends the SWF previously developed in 2D to the third dimension by using radiative transfer and the diffusion equation, based on the assumption that variations of depend solely on variations of the extinction length. When applied to active data (Deception Island, Antarctica), 3D SWF images strongly resemble 2D images, making this 3D extension redundant. On the other hand, diffusion does not efficiently model coda waveforms when using earthquake datasets spanning depths between 0 and 20 km, such as at Mount St. Helens volcano. In this setting, scattering attenuation and absorption suffer tradeoffs and cannot be separated by fitting a single seismogram energy envelope for SWF imaging. We propose that an approximate analytical 3D SWF, similar in shape to the common coda kernels used in literature, can still be used in a space weighted back-projection approach. While is not a physical parameter of the propagation medium, its spatially-dependent modeling allows improved reconstruction of crustal-scale tectonic and geological features. It is even more efficient as a velocity independent imaging tool for magma and fluid storage when applied to deep volcanism.
1. Introduction
Seismic attenuation imaging performed using coda waves provides novel information about tectonic structures and fluid content at crustal [1,2], regional [3], and local [4] scales. The attenuation coefficient is proportional to the sum of the inverse intrinsic () and scattering () quality factors. A separate estimate of scattering attenuation and absorption is crucial for understanding seismic wave propagation in highly-heterogeneous volcanic environments [5], or when targeting areas having different tectonic and scattering properties at crustal and lithospheric scales [6,7,8]. A scattering ellipsoid has been adopted for decades by scientists to map the sensitivity of coda waves to Earth’s heterogeneities, and map scattering attenuation and absorption in space [9]. More recently, 2D and 3D coda sensitivity kernels based on multiple scattering propagation have been proposed to separate and [8,10] and to invert for attenuation in the subsurface at different scales and depths [2,11,12]. These sensitivity kernels define the source parameters observed at a station as a space-weighted average of attenuation characteristics of the sampled medium, where the weights are defined via integral equations [10,12]. Their application has led to absorption mapping at lithospheric scales [2] and are considered important for the evaluation of the effective sensitivity in ambient noise imaging [12].
The space-weighting functions (SWF) discussed in this note are designed to be applied in the back-projection (or regionalization) method to retrieve the attenuation parameters in space [9,13]. In this case, and estimated for a single source–receiver couple characterize the entire space volume, weighted by SWF values between zero and one. The SWF are designed with a Monte Carlo simulation of the multiple scattering process, following the method of Yoshimoto [14]. Each SWF value, associated with a point in space for a single station observation, is proportional to the probability that at that point the attenuation value is equal to the single sstation observation. At a point in space, we thus have as many probabilities as observations. The average of all the observed values weighted by the SWFs provides the value of the attenuation at the point. These SWFs have been expressively designed to map scattering attenuation and absorption in volcanoes using a diffusion model and active sources [4,15,16]. In the resulting models, the high attenuation contrasts are often related to magma/fluid storage under volcanoes and ongoing volcano dynamics.
For a full discussion of the practice of attenuation mapping by weighted back-projection in volcanoes, the reader is refered to Del Pezzo et al. [17]. These authors obtain SWF for and . The two parameters can be rewritten using the associated parameters; either the seismic albedo , the inverse extinction length (, or the intrinsic ) and scattering ) attenuation coefficients (Throughout this paper the syntactic rules used by theWolfram Mathematica software for the use of parentheses is used: square brackets indicate the argument of a function; curly brackets indicate the elements of a matrix; round brackets indicate an algebraic grouping.):
With an SWF, the spatial and are obtained using the following equations:
where and are the intrinsic and scattering SWF, and represent the estimates calculated from the fit of experimental energy envelopes with the diffusion model, and k spans the available energy envelopes. The uncertainties of the estimates of and can be propagated in Equations (2) and (3) to estimate the variances of and , with the assumption of small covariance and null uncertainty in the determination of the weighting functions.
Del Pezzo et al. [17] additionally obtained that, in the case of a uniform half space and for diffusive propagation, the following function well approximates the numerically calculated SWF for both absorption and scattering attenuation:
In Equation (4), D is the source receiver distance, x and y are the spatial coordinates, and the source coordinates, and and the receiver coordinates. The function fits the numerically calculated SWF reasonably well in the case of a short lapse time (around 15 s), a highly diffusive media, and . These parameters represent the spatial aperture of the weighting function. The two numerically evaluated SWF have approximately the same shape once the level of heterogeneity increases (i.e., when the scattering processes approach the diffusion regime). This is contrary to what happens for lower heterogeneity [18,19] and as a result is valid only for volcanoes and the active data geometry.
The spatial patterns described by the SWF depict the contribution of each cell to the coda formation and is thus proportional to the sensitivity kernels, for scattering and intrinsic dissipation. Equation (4) is indeed equal to that proposed at crustal scales for absorption mapping, however only at late lapse times [2,10,11]. The sensitivity is maximum at the source and receiver stations, remains high across the area contouring the seismic ray, then decreases at a distance controlled by the extinction length. This similarity in shape goes even further, as the spatial pattern of the function is identical to the depth-dependent diffusive sensitivity kernels in 3D defined by Obermann et al. [12]. The difference is in that the kernels do not assume a depth-dependent velocity structure, an approximation that is unfulfilled for shallow volcanic sources, but rather a constant velocity in half-space approximation. The analytical solution of Equation (4) is thus an approximate analytical equation for mapping , similar in shape and meaning to those developed to map absorption. The equation was re-framed as a forward problem in a 5 km deep volcanic medium [20] to map coda attenuation at the Campi Flegrei caldera. The results of the inversion show the increased illumination provided by this technique and additionally demonstrated important correlations of the coda attenuation anomalies with deformation sources at the volcano.
The present note investigates how effective the SWF are in illuminating multi-scale volcanism in 3D. It is divided into three parts:
- Equation (4) is extended to the third dimension, maintaining the assumptions of shallow source and receiver in a diffusive Earth medium with no depth dependency—this is the case for the analysis of active seismic shots in volcanoes.
- We propose and discuss an SWF for mapping , calculated for a deep source in a non-diffusive medium and discuss its limits.
- We check the reliability and limits of the new approaches by applying 3D SWFs to published seismic databases. We use precalculated attenuation measurements for single source station paths from active data recorded at the Deception Island volcano (Antarctica) [21] and volcano tectonic earthquakes at the Mount St. Helens volcano (USA) [22].
In the Appendix, we report the main tests which were carried out in developing the applications. Test images are compared with previous tomography results obtained in the same areas using different seismic attributes, and show consistent features.
2. Results
2.1. 3D Extension of the 2D Weighting Functions
2.1.1. Diffusive Earth Media
We extended the numerical simulations described above to the third (depth) dimension, introducing the z-axis and keeping the half space approximation. For the assumption of no anomalous relevant depth dependency, we rely on the results of Reference [1]. The weighting function remains symmetrical around the axis connecting the source to the receiver, in analogy with simulations using radiative transfer theory [10] and spectral elements methods [12]. This symmetry allows one to evaluate the 3D SWF analytically for source (a shot) and receiver both placed at the surface. In the case of a uniform half space, the function:
approximates the numerically calculated SWF in 3D to the first order (Figure 1). This analytical approximation is valid for the same range of and values and the same lapse time (15 s) used in Del Pezzo et al. [17]. This approximated space weighting function is actually a “kernel” function. Different from the other diffusive kernels, it is valid solely for diffusive fields, short seismograms, and surface sources, like those recorded from shots fired in volcanoes for tomography purposes [21].
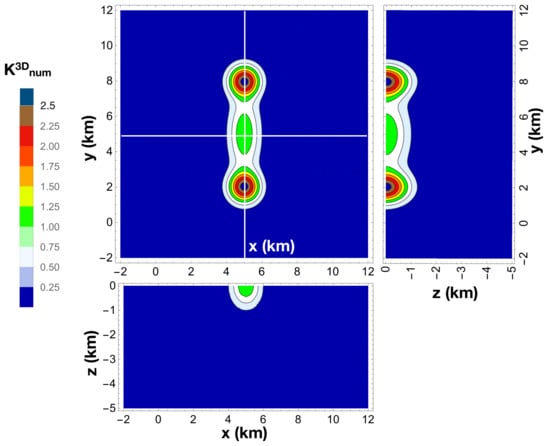
Figure 1.
Plot of the 3D kernel function obtained using Equation (5). The source and receiver are set at [xs = 5 km, ys = 2 km] and [xr = 5 km, yr = 8 km], respectively. The color scale marks the isosurfaces. The kernel function is normalized to its value at [x = 5 km, y = 5 km]. The vertical sections correspond to the white lines shown on the x-y plane.
2.1.2. Deep Sources (Natural Events) and Non-Diffusive Fields
In the case of deep earthquakes, the assumptions made in calculating the approximate SWF given by Equation (4) are invalid, and a multiple scattering regime better models coda wave propagation. We thus adopt the Paasschens [23] approximation of the energy transport equation solution in three dimensions to describe the seismogram energy envelope:
where:
and and H are the Dirac delta and the Heaviside step functions, respectively. Here, is the source energy and v is the seismic velocity. Fitting Equation (6) to the experimental energy envelopes, the single path separate estimates of and are possible in principle; however, in 2D, a severe tradeoff affects the two parameters as discussed in Del Pezzo et al. [17]. An alternative is the use of a simplified formula, which estimates and by fitting the data to a first order approximation of the energy transport model equation, as given by Zeng et al. [24]:
With such a fit, the severe tradeoffs disappear. Equation (7) is equivalent to the single scattering model developed by Sato [25] and is valid for low heterogeneity and short lapse times. In this case, intrinsic attenuation controls , since is small. The physical meanings of the retrieved and become controversial when the energy envelopes are recorded in media with high heterogeneity and modeled with Equation (7). In this case, the fit function is based on improper assumptions and is proportional to the widely measured , the coda quality factor [25] used to map different tectonic settings at the crustal scale [1].
The downside is that is not a physical parameter of the propagation medium; however, the (or ) spatiak distribution can still depict attenuation properties, and the corresponding SWF, , can be calculated. For this task, we use the hypothesis of Pacheco and Snieder [26], setting to an average value and . Hence:
where is the point with coordinates , T is the lapse time, is the integration variable (time). The integral can be numerically calculated. In Figure A1, we show the contour plot of as a function of and . For low scattering attenuation, is independent of and similar to (see Appendix, Figure A1, left panel). An increase of scattering (right panel) increases the tradeoff. In Figure 2, we reproduce the SWF calculated using Equation (8).
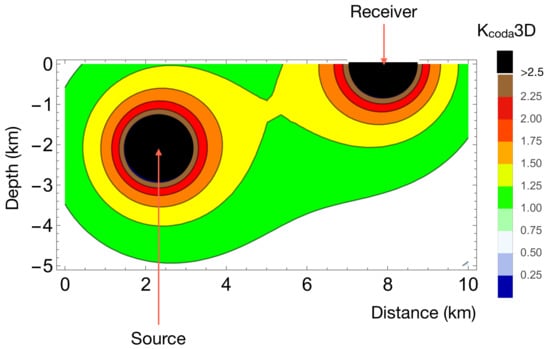
Figure 2.
Vertical section showing the 3D kernel function obtained using Equation (8). The color scale marks the isosurfaces. The kernel function is normalized to its value at [x = 5 km, z = km].
2.2. Application Examples
The final image as a function of the spatial coordinates in a 3D space is thus obtained with a back-projection analogous to that used in Equations (2) and (3):
where is the weighting function for the k-th source–receiver couple, is the k-th estimate, and k spans over the available source–receiver couples. To avoid confusion with respect to the definition of source station kernels we remind the reader that:
- The values of express the probability that the estimated at a station is equal to the one measured at [x, y, z].
- Equation (9) is to be used exclusively for back-projection.
- The kernel in Equation (5) can still be used in an inversion for the space-dependent parameters, if the underlying hypotheses are fulfilled.
2.2.1. Deception Island Volcano—Diffusive Approximation
The Deception Island volcano (Antarctica) is an extraordinary natural laboratory, characterized by a horseshoe shape which permits one to design seismic active field surveys characterized by elaborate source and receiver geometries. To test the 3D SWF discussed in this note, we used data from the seismic experiment TOMO-DEC (Tomography at Deception) [21] publicly available from the Australian Antarctic Data Center (AADC) repository. The same data set was used by Prudencio et al. [16], who obtained a 2D attenuation image of this island using a simplified, Gaussian SWF (data and final models also are available from the AADC repository). Del Pezzo et al. [17] improved this image using the 2D weighting function of Equation (4), applied to data filtered in several frequency bands centered from 4 to 20 Hz. The present test is carried out using data filtered in the 4 Hz band, where the highest attenuation contrasts were previously observed. Using the 3D SWF of Equation (5), we show the attenuation coefficient space distribution calculated at depths of 2 and 4 km, with a horizontal grid of 4 km (Figure 3). The two panels are similar, with high absorption affecting the eastern and southwestern parts of the island. Since the SWF are practically null at 6 km, no images can be calculated below this depth.
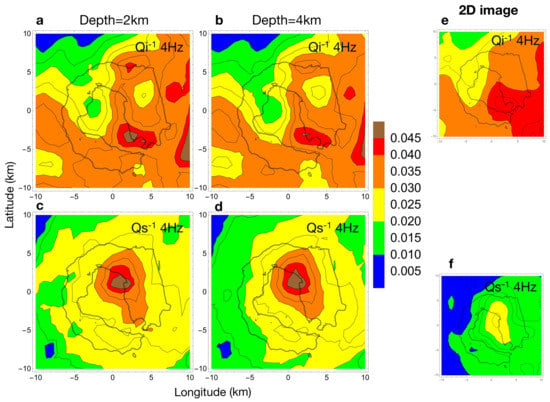
Figure 3.
The three-dimensional images obtained for Deception Island at 4 Hz are compared with the bi-dimensional images in Del Pezzo et al., 2016. Horizontal slices cut the inverse intrinsic, (a,b), and scattering, (c,d), quality factors at depths of 2 km and 4km, as noted. The 2D (e) and (f) models from Del Pezzo et al. [17] are redrawn for comparison using the same color scale. We use the same distribution of sources and receivers as in Prudencio et al. [15].
2.2.2. 3D SWF at Mount St. Helens Volcano—Non-Diffusive Media
Mount St. Helens volcano (US) is a central-cone stratovolcano, characterized by 0–7 km deep earthquakes (under the central cone) and lateral fault seismicity (down to 20 km). A 3D attenuation model of the area has been calculated using the SWF described in Equations (8) and (9) at Mount St. Helens, with a test passive dataset of 451 waveforms ([27], available from the PANGAEA Data Centre). We use the single-path estimates obtained by De Siena et al. [3] at 6 Hz. In the Appendix, a sensitivity test, carried out to check the reliability of the method, is described. Equation (9) has been applied to a spatial grid with points separated by a distance of 4 km. In this way, we obtain the space values at 500 3D grid points.
The 3D spatial distribution is plot for two horizontal slices, crossing the z-axis at depths of 0.5 km and 4 km (Figure 4, uppermost panels). The vertical slice (lower panel) intersects the surface along the white line drawn in the upper left panel. A sensitivity test using a hemispherical anomaly centered in the middle of the study area is described in the Appendix. The input test is only roughly reproduced: the small number of data available would correspond to an underdetermined inversion problem. This strongly reduces the sensitivity of the method to small anomalies; making any checkerboard test unsuccessful.
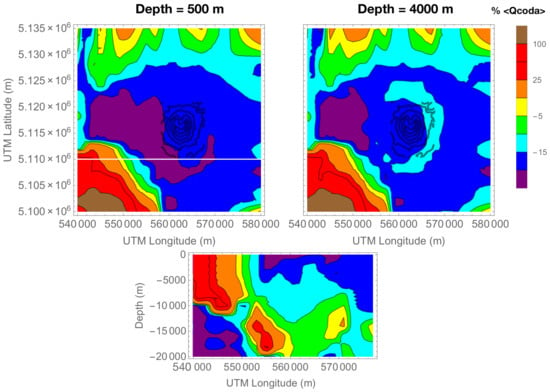
Figure 4.
spatial distribution at Mount St. Helens. Horizontal slices are calculated at depths of 0.5 km and 4.0 km. The vertical section intersects the horizontal plane along the white line in the upper left panel. Topography isolines (only in the zone of Mount St. Helens) are superimposed. The discrete spatial distribution has been interpolated before plotting the average inverse , . All panels are drawn using Mathematica 10.
3. Discussion
Figure 1 shows that, in areas of high heterogeneity (diffusion approximation) and for data shots fired at the surface, the sensitivity of the SWF method strongly reduces on increasing depth; since the SWF values strongly decrease with depth. Coda waves recorded from shots fired at the surface in a diffusive Earth media and recorded at short distances, as for the Deception Island case study, propagate mainly in the upper 3–4 km of the crust (Figure 3). The northern part of the island is associated with the crystalline basement and shows low attenuation, while high-attenuation bodies, spatially-correlated to high-velocity structures [28,29], characterize the southern part of the volcano. There is a consistent agreement between low/high coda attenuation and high/low velocity structure from the first scattering/absorption separations [16]. The correlation between the SWF-dependent 2D models [17] and the 3D models indicates that coda attenuation estimates are stable using this dataset. Comparing the present 3D attenuation images with the total-Q images obtained by Prudencio et al. [30], which used direct-P coda-normalized waves (MuRAT code-De Siena et al. [22]), we observe a good match between the 3D intrinsic-Q and the total-Q distributions. The location of the main total high attenuation body retrieved by Prudencio et al. [30] spatially fits the main absorption anomaly.
To investigate greater depths, deeper sources (passive data) are necessary. In this case, the diffusion equation is inappropriate, as the Earth’s heterogeneity strongly reduces with depth, and a theory based on multiple scattering is necessary. However, inverting a multiple scattering model for the energy envelopes associated with single source–receiver couples prevents the recovery of separate scattering and intrinsic tomography images due to the tradeoff between and . The only possibility is thus the use of an approximate kernel to invert for a unique parameter, , a quantity proportional to the widely measured parameter. In this case, we proposed to calculate the corresponding SWF by using the approach described by Pacheco and Snieder [26]. Despite the controversial physical meaning of , images of the spatial variations of are still retrievable, like those recently described by Mayor et al. [2], which depict the attenuation structure of the Alps.
Following this approach, we calculated the 3D image of Mount St. Helens volcano (Figure 4). We compared it to a map of the 2D spatial distribution obtained by De Siena et al. [3]. The authors used maps of late lapse time —assuming they measured absorption, and energy envelope peak delays, which are proportional to scattering-Q—to separate scattering attenuation from absorption. They back-project the single station value assuming that it is distributed on a strip connecting the source and ray, derived from pre-calculated 3D rays.
At both depths shown in Figure 4, the low inverse west of Mount St. Helens is a major feature, similar to that observed by De Siena et al. [3] (see their Figure 5, 6 Hz panel). Nevertheless, this area is a unique anomaly in our analysis, located west of the volcano at a depth of 4 km, and extends to the south at 500 m. A wide area inside this anomaly was not sampled in the previous study, as it assumed a back-projection of the single station along a strip. In the case of Mount St. Helens, many of the seismic sources are located at, or below, 8 km. The SWF theoretically produce an improved resolution at this depth range due to the wider illumination at near-source nodes. The example reported in the present paper is made with a limited amount of data. The images obtained for Mount St. Helens are thus defocused and need to be improved by using a latger data set. Despite this limitation, the use of SWF is promising in enlightening the space attenuation contrasts. We are confident that it may become a useful tool to complement tomography images achieved with different techniques, especially due to its independence of velocity tomography results.
Author Contributions
Edoardo Del Pezzo wrote the paper together with Francesca Bianco, Jesus Ibanez, and Luca De Siena. Edoardo del Pezzo, Simona Gabrielli, and Luca De Siena analyzed the data and calculated the 3D SWF derived models for all the examples reported. Angel de La Torre wrote the software reported in the Appendix implementing the SWF.
Acknowledgments
This research was partly supported by the Projects TEC2015-68752 (MINECO/FEDER), TEC2015-68752 (KNOWAVES).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SWF | Space-Weighted Functions |
Appendix A. Demonstration that Approaches in Media with Small
We have fit the Paasschens model calculated for several couples to the Aki and Chouet formula [31] and inverted for . The contours are shown in Figure A1. Vertical contours in the left panel show that, independent of , practically coincides with .
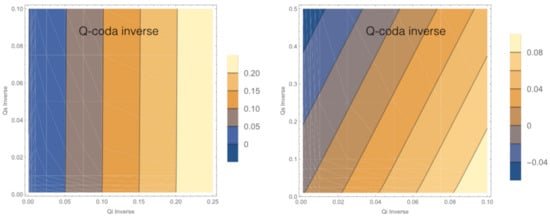
Figure A1.
(Left) is independent of in media with low values of . (Right) In case of high scattering attenuation (approaching to the diffusion regime) the plots show some tradeoff.
Appendix B. Sensitivity Tests for 3D SWF
At Deception Island, we use as input a checkerboard structure; laterally extended km parallelepipeds extending down to 10 km depth (Figure A2). Q-values alternate between 50 and 500. We do not report the results obtained for inputs with a cell structure alternating in depth, as the SWF for shallow source and receiver are about zero below six kilometers, producing false uniform structures at increasing depth.
At Mount St. Helens, the available data set is much smaller than at Deception Island. The corresponding sensitivity tests thus show that the SWF calculated using Equation (8) does not reproduce the input values adequately, mainly since poor sampling in space affects the averaging process described by Equation (2). Despite this limitation, the input values are reproduced in the central part of the area (i.e., the volcanic edifice). The input values are underestimated elsewhere, with blurring and ghosts emerging around the volcano.
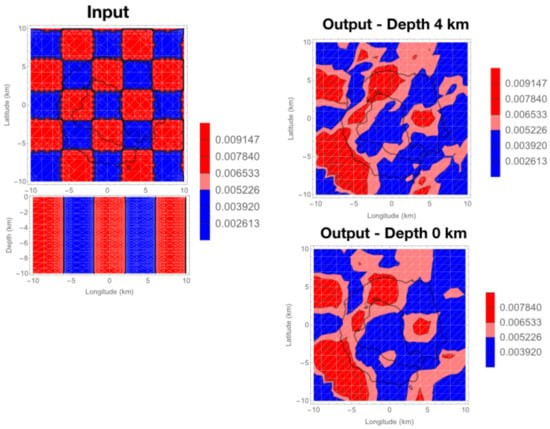
Figure A2.
Synthetic test for the space-weighted function (SWF). (Left) panels: input. (Right) panels: output.
At Mount St. Helens (Figure A3) we built as a second synthetic input a hemisphere with a contrast in Q of with respect to the background. The process of averaging yields a blurred image on the sides; the vertical profile shows a similar contrast with respect to input down to 10 km, with consistent ghosts to the side and deeper than the central anomaly. A larger amount of data would improve the image definition, as the SWF maps the structures around the central cone insufficiently.
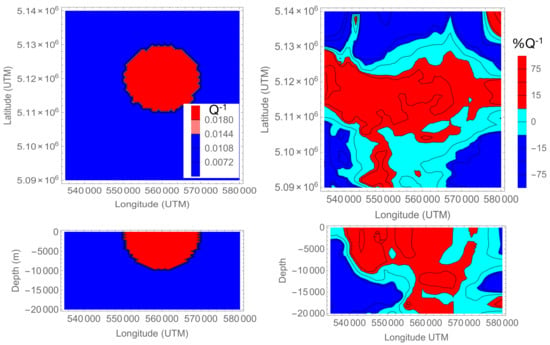
Figure A3.
Synthetic test at Mount St. Helens volcano. (Left) panels: test input, where the contrasts are expressed as a percentage with respect to the average, and correspond to (red) and (blue). (Right) panels: output, where the attenuation contrast is reproduced only in the center of the area.
Appendix C. Numerical Integration of Equation (8)
The function to be integrated (Equation (8)) is a product of two functions, each one including a delta and a continuously decaying term, which here we call “coda”. Hereafter we drop out the dependence of Equation (8) on and v leaving unaltered and t. Therefore, the integral can be decomposed into four integrals (i.e., delta·delta, delta·coda, coda·delta and coda·coda):
each of them null for where and are respectively the time the perturbation reaches position from the source and the time from to the receiver. These integrals are defined as:
where refers to the wavefront (or delta) contribution, refers to the coda contribution, refers to the source- impulsive response, and refers to the receiver- impulsive response.
Taking into account the sampling property of the Dirac delta function:
the integrals , and can easily be solved:
Additionally, It can be demonstrated that if functions and are known, then , , and are immediately known and easily evaluated functions.
The last integral is obtained by convolving both codas. It is a continuous function with null value for and with an exponential decay for large times. Its computation requires a numerical integration to solve the convolution. The entire procedure, with demonstrations, is reported in (De La Torre and del Pezzo, in preparation. A pre-print draft can be requested from the authors). The Matlab code to perform the calculation is reported in the Appendix, together with the entire algorithm estimating the SWF as a function of the 3D spatial coordinates, with , and v as parameters.
References
- Calvet, M.; Sylvander, M.; Margerin, L.; Villasenor, A. Spatial variations of seismic attenuation and heterogeneity in the Pyrenees: Coda Q and peak delay time analysis. Tectonophysics 2013, 608, 428–439. [Google Scholar] [CrossRef]
- Mayor, J.; Calvet, M.; Margerin, L.; Vanderhaeghe, O.; Traversa, P. Crustal structure of the Alps as seen by attenuation tomography. Earth Planet. Sci. Lett. 2016, 439, 71–80. [Google Scholar] [CrossRef]
- De Siena, L.; Calvet, M.; Watson, K.J.; Jonkers, A.R.T.; Thomas, C. Seismic scattering and absorption mapping of debris flows, feeding paths, and tectonic units at Mount St. Helens volcano. Earth Planet. Sci. Lett. 2016, 442, 21–31. [Google Scholar] [CrossRef]
- Prudencio, J.; Del Pezzo, E.; Ibanez, J.; Giampiccolo, E.; Patane, D. Two-dimensional seismic attenuation images of Stromboli Island using active data. Geophys. Res. Lett. 2015, 42, 1717–1724. [Google Scholar] [CrossRef]
- Del Pezzo, E.; Ibáñez, J.; Morales, J.; Akinci, A.; Maresca, R. Measurements of intrinsic and scattering seismic attenuation in the crust. Bull. Seismol. Soc. Am. 1995, 85, 1373–1380. [Google Scholar]
- Akinci, A.; Del Pezzo, E.; Ibañez, J. Separation of scattering and intrinsic attenuation in the Southern Spain and Western Anatolia (Turkey). Geophys. J. Int. 1995, 121, 337–353. [Google Scholar] [CrossRef]
- Wegler, U.; Luhr, B. Scattering behaviour at Merapi volcano(Java) revealed from an active seismic experiment. Geophys. J. Int. 2001, 145, 579–592. [Google Scholar] [CrossRef]
- Lacombe, C.; Campillo, M.; Paul, A.; Margerin, L. Separation of intrinsic absorption and scattering attenuation from Lg coda decay in central France using acoustic radiative transfer theory. Geophys. J. Int. 2003, 154, 417–425. [Google Scholar] [CrossRef]
- Xie, J.; Mitchell, B. A back-projection method for imaging lLarge-scale lateral variations of Lg Coda Q with application to Continental Africa. Geophys. J. Int. 1990, 100, 161–181. [Google Scholar] [CrossRef]
- Margerin, L.; Planes, T.; Mayor, J.; Calvet, M. Sensitivity kernels for coda-wave interferometry and scattering tomography: Theory and numerical evaluation in two-dimensional anisotropically scattering media. Geophys. J. Int. 2016, 204, 650–666. [Google Scholar] [CrossRef]
- Rossetto, V.; Margerin, L.; Planès, T.; Larose, É. Locating a weak change using diffuse waves (LOCADIFF): Theoretical approach and inversion procedure. arxiv, 2010; arXiv:1007.3103. [Google Scholar]
- Obermann, A.; Planès, T.; Larose, E.; Sens-Schönfelder, C.; Campillo, M. Depth sensitivity of seismic coda waves to velocity perturbations in an elastic heterogeneous medium. Geophys. J. Int. 2013, 194, 372–382. [Google Scholar] [CrossRef]
- Singh, S.; Herrmann, R.B. Regionalization of Crustal Coda Q in the continental United States. J. Geophys. Res. 1983, 88, 527–538. [Google Scholar] [CrossRef]
- Yoshimoto, K. Monte Carlo simulation of seismogram envelopes in scattering media. J. Geophys. Res. 2000, 105, 6153–6161. [Google Scholar] [CrossRef]
- Prudencio, J.; Del Pezzo, E.; Garcia Yeguas, A.; Ibanez, J.M. Spatial distribution of intrinsic and scattering seismic attenuation in active volcanic islands—I: Model and the case of Tenerife Island. Geophys. J. Int. 2013, 195, 1942–1956. [Google Scholar] [CrossRef]
- Prudencio, J.; Ibanez, J.M.; Garcia Yeguas, A.; Del Pezzo, E.; Posadas, A.M. Spatial distribution of intrinsic and scattering seismic attenuation in active volcanic islands—II: Deception Island images. Geophys. J. Int. 2013, 195, 1957–1969. [Google Scholar] [CrossRef]
- Del Pezzo, E.; Ibañez, J.; Prudencio, J.; Bianco, F.; De Siena, L. Absorption and scattering 2-D volcano images from numerically calculated space-weighting functions. Geophys. J. Int. 2016, 206, 742–756. [Google Scholar] [CrossRef][Green Version]
- Sato, H. Study of seismogram envelopes based on scattering by random inhomogeneities in the lithosphere: A review. Phys. Earth Planet. Inter. 1991, 67, 4–19. [Google Scholar] [CrossRef]
- Hoshiba, M. Simulation Of Multiple-scattered Coda Wave Excitation Based On The Energy-conservation Law. Phys. Earth Planet. Inter. 1991, 67, 123–136. [Google Scholar] [CrossRef]
- De Siena, L.; Amoruso, A.; Pezzo, E.D.; Wakeford, Z.; Castellano, M.; Crescentini, L. Space-weighted seismic attenuation mapping of the aseismic source of Campi Flegrei 1983–1984 unrest. Geophys. Res. Lett. 2017, 44, 1740–1748. [Google Scholar]
- Ibañez, J.M.; Díaz-Moreno, A.; Prudencio, J.; Zandomeneghi, D.; Wilcock, W.; Barclay, A.; Almendros, J.; Benítez, C.; García-Yeguas, A.; Alguacil, G. Database of multi-parametric geophysical data from the TOMO-DEC experiment on Deception Island, Antarctica. Sci. Data 2017, 4, 170128. [Google Scholar] [CrossRef] [PubMed]
- De Siena, L.; Thomas, C.; Aster, R. Multi-scale reasonable attenuation tomography analysis (MuRAT): An imaging algorithm designed for volcanic regions. J. Volcanol. Geotherm. Res. 2014, 277, 22–35. [Google Scholar] [CrossRef]
- Paasschens, J. Solution of the time-dependent Boltzmann equation. Phys. Rev. E 1997, 56, 1135–1141. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, F.; Aki, K. Scattering wave energy propagation in a random isotropic scattering medium. Part 1. Theory. J. Geophys. Res. Solid Earth 1991, 96, 607–619. [Google Scholar] [CrossRef]
- Sato, H. Single isotropic scattering model including wave convesions Simple theoretical model of the short period body wave propagation. J. Phys. Earth 1977, 25, 163–176. [Google Scholar] [CrossRef]
- Pacheco, C.; Snieder, R. Time-lapse travel time change of multiply scattered acoustic waves. J. Acoust. Soc. Am. 2005, 118, 1300–1310. [Google Scholar] [CrossRef]
- De Siena, L.; Thomas, C.; Waite, G.P.; Moran, S.C.; Klemme, S. Attenuation and scattering tomography of the deep plumbing system of Mount St. Helens. J. Geophys. Res. Solid Earth 2014, 119, 8223–8238. [Google Scholar] [CrossRef]
- Ben-Zvi, T.; Wilcock, W.S.D.; Barclay, A.H.; Zandomeneghi, D.; Ibanez, J.M.; Almendros, J. The P-wave velocity structure of Deception Island, Antarctica, from two-dimensional seismic tomography. J. Volcanol. Geotherm. Res. 2009, 180, 67–80. [Google Scholar] [CrossRef]
- Zandomeneghi, D.; Barclay, A.; Almendros, J.; Godoy, J.M.I.; Wilcock, W.S.D.; Ben-Zvi, T. The Crustal Structure of Deception Island Volcano from P-wave Seismic Tomography: Tectonic and Volcanic Implications. J. Geophys. Res. Solid Earth 2009, 114, 16. [Google Scholar] [CrossRef]
- Prudencio, J.; De Siena, L.; Ibanez, J.M.; Del Pezzo, E.; Garcia Yeguas, A.; Díaz-Moreno, A. The 3D attenuation structure of deception island (Antarctica). Surv. Geophys. 2015, 36, 371–390. [Google Scholar] [CrossRef]
- Aki, K.; Chouet, B. Origin of coda waves: Source, attenuation, and scattering effects. J. Geophys. Res. Solid Earth 1975, 80, 3322–3342. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).