Reliable Predictors of Arsenic Occurrence in the Southern Gulf Coast Aquifer of Texas
Abstract
1. Introduction
2. Materials and Methods
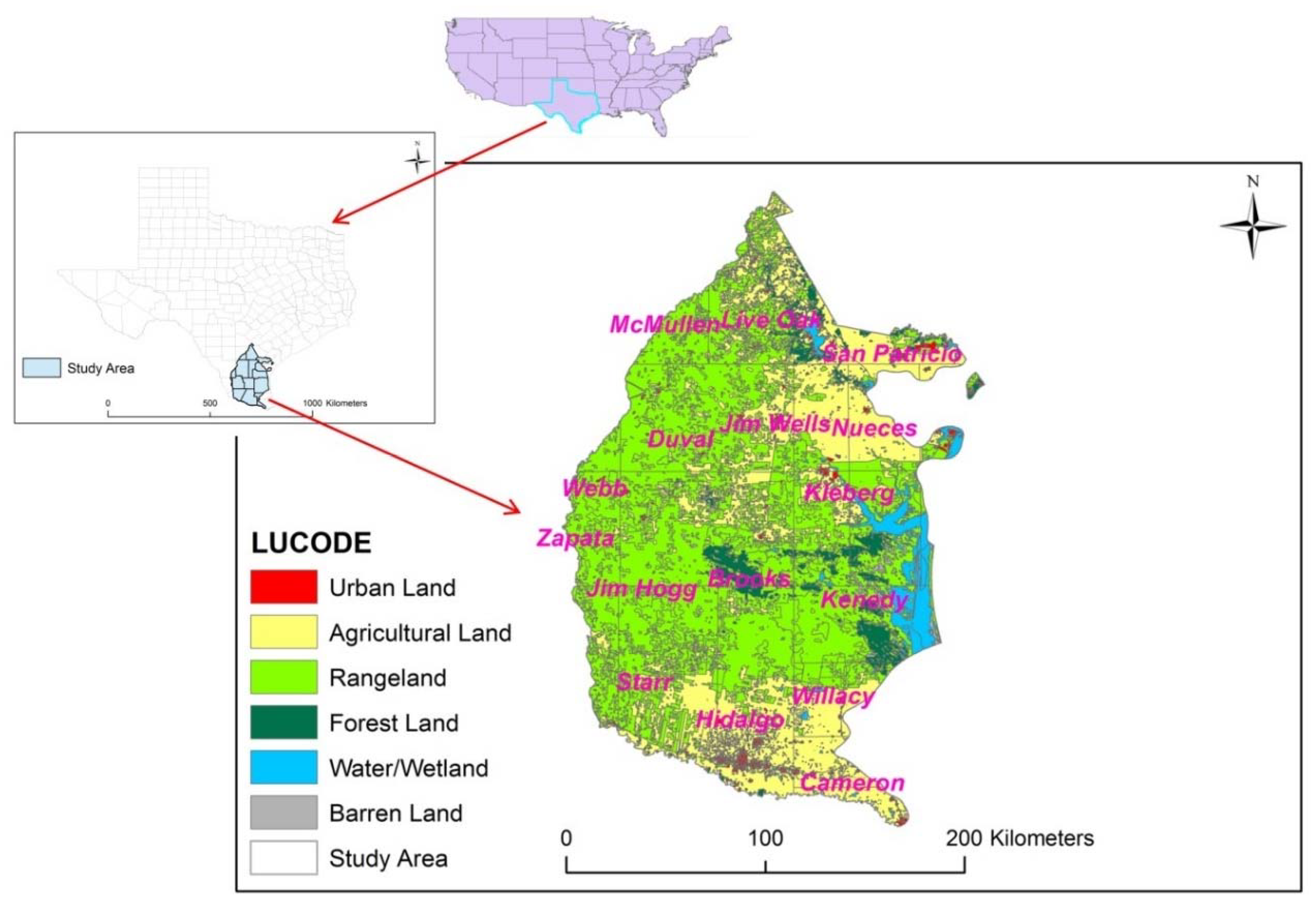
2.1. Study Area Characteristics
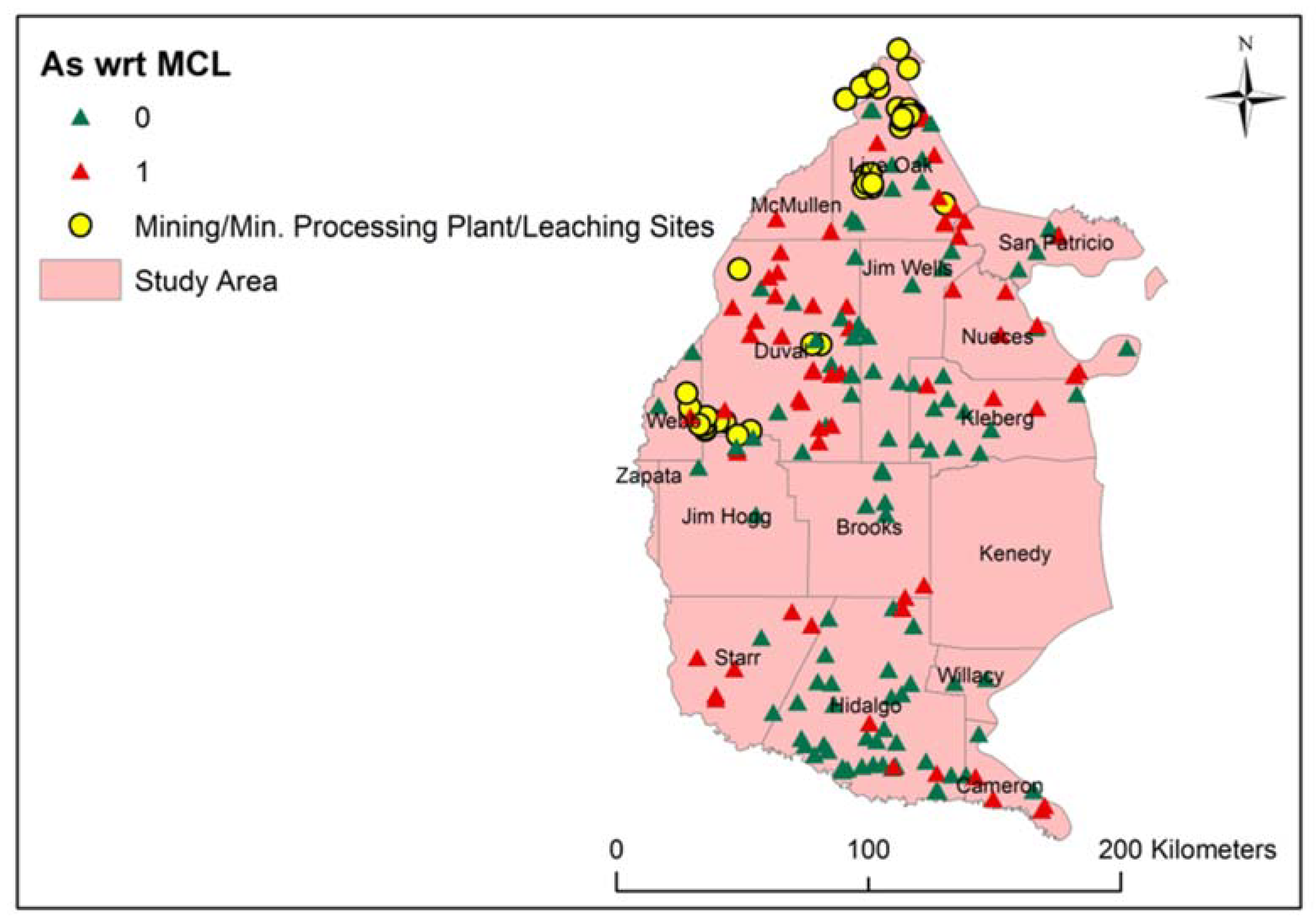
2.2. Data and Selection of Explanatory Variables
2.3. Logistic Regression (LR) Model Development and Evaluation
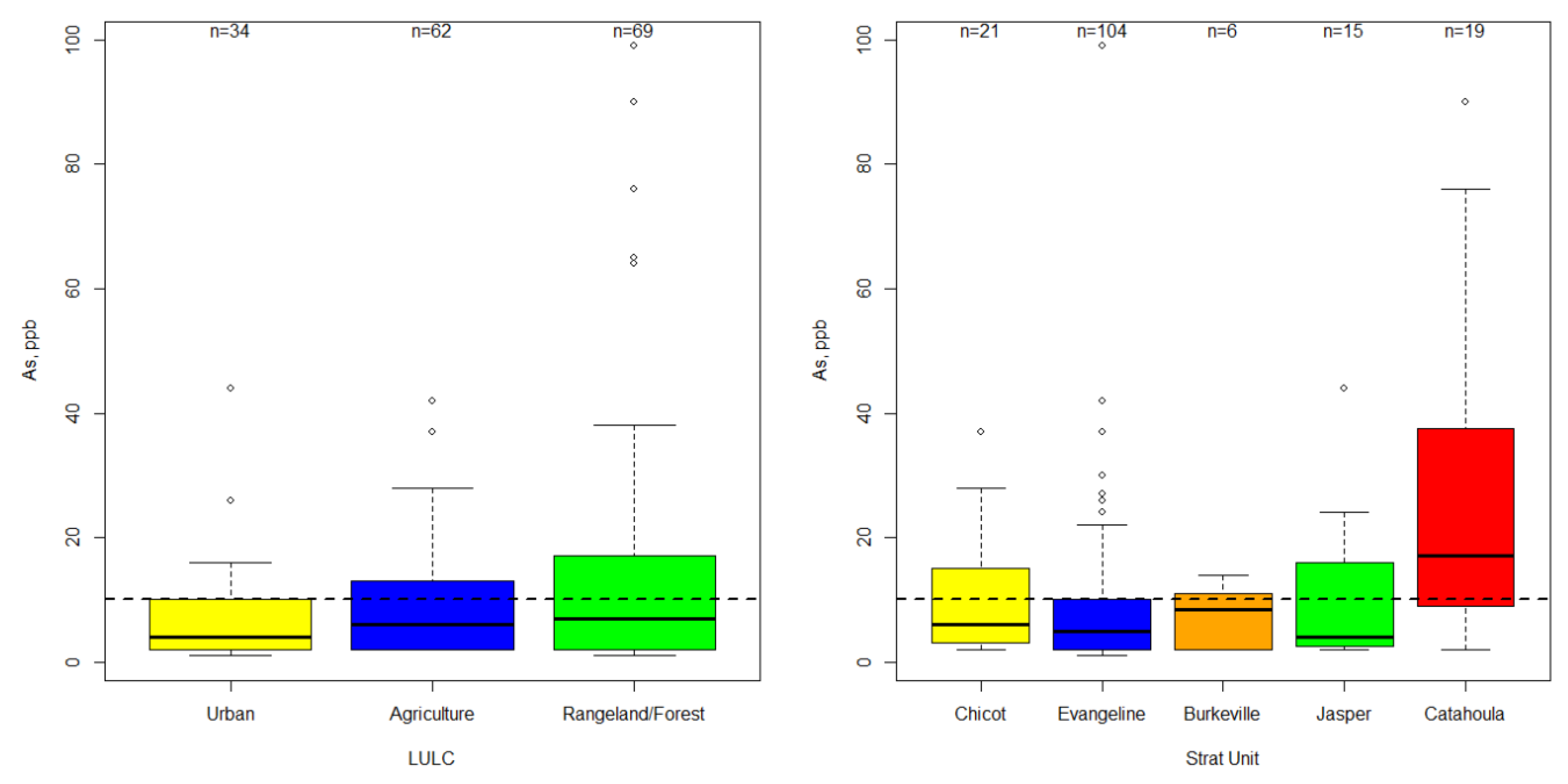
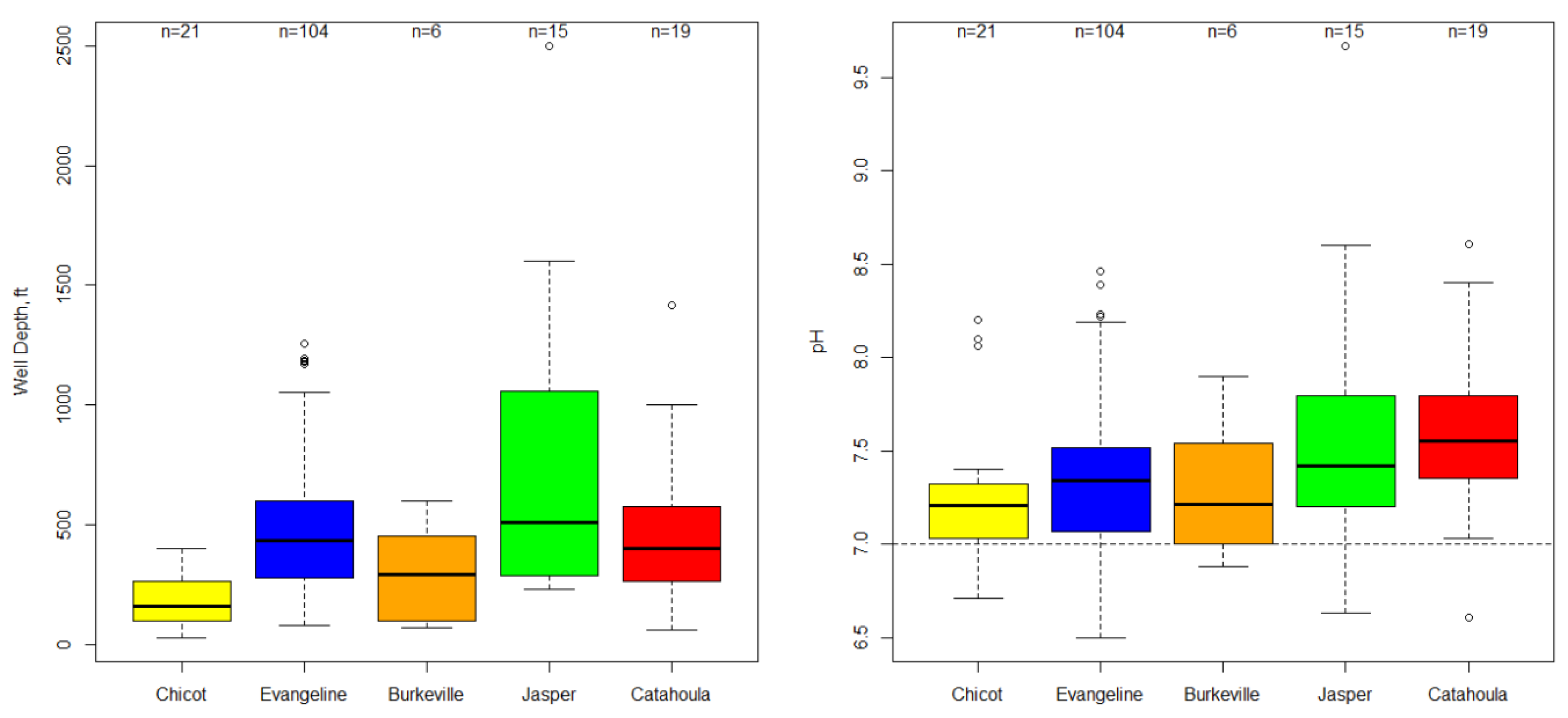
3. Results
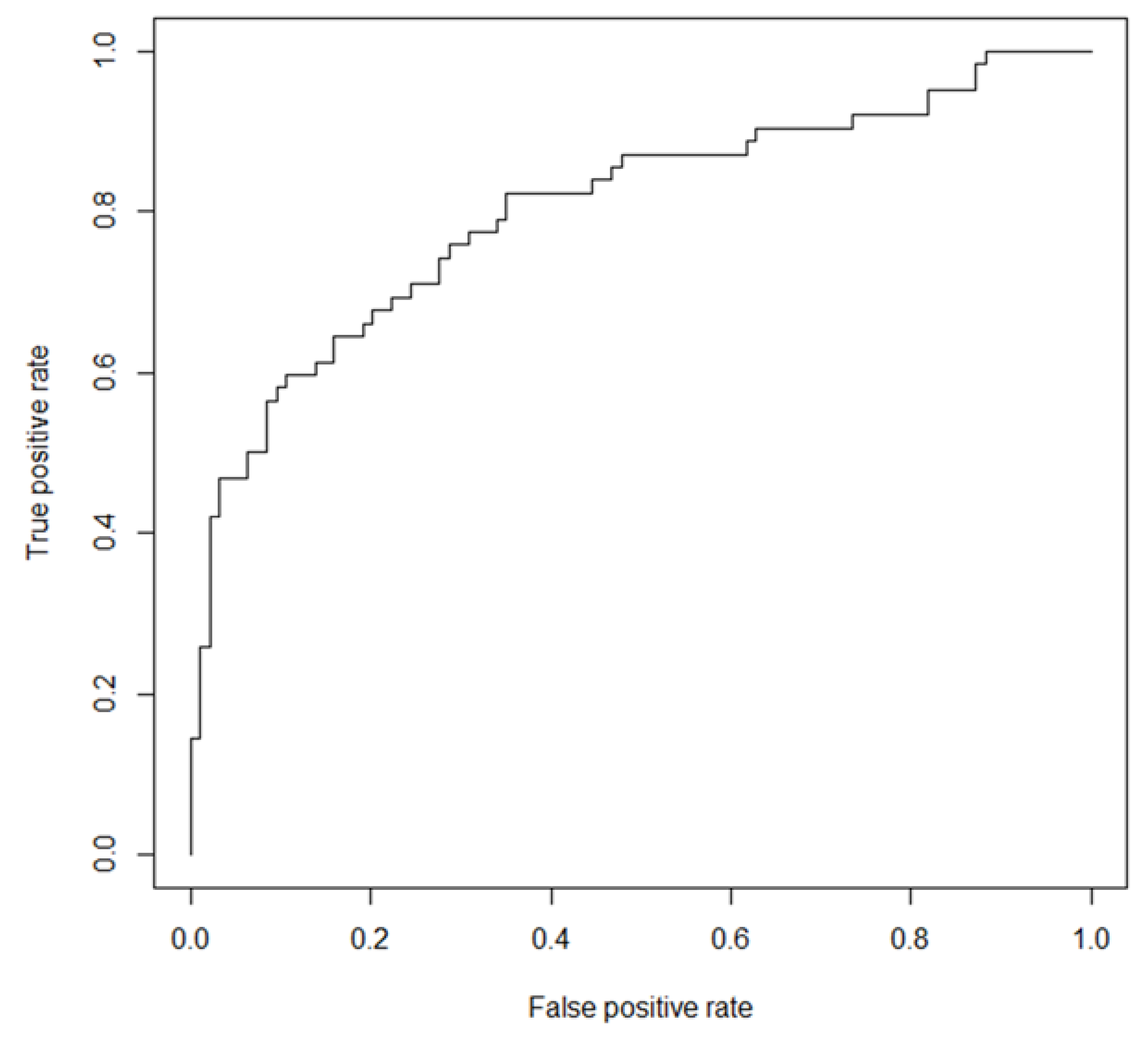
3.1. Performance of the Master LR Model
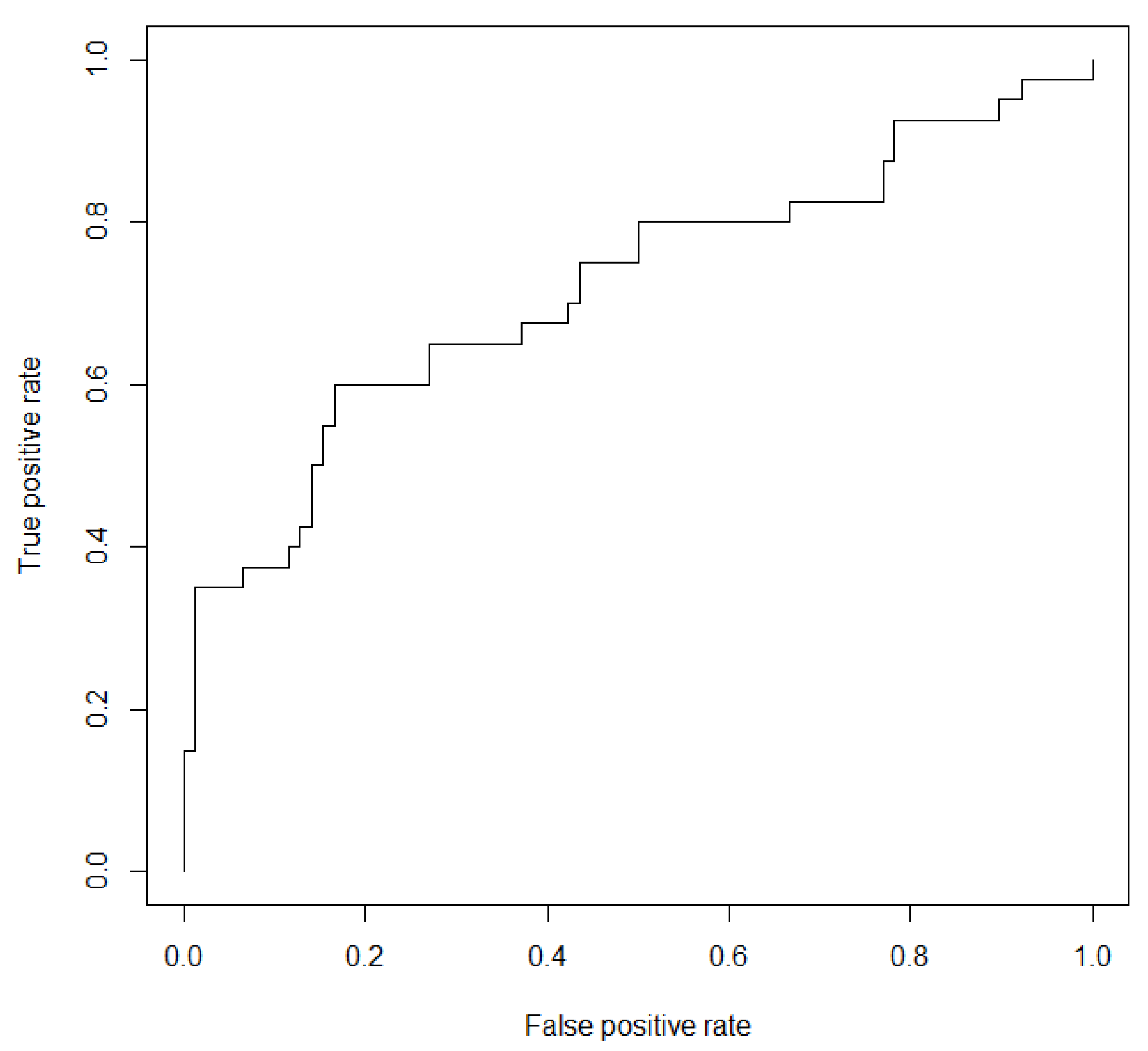
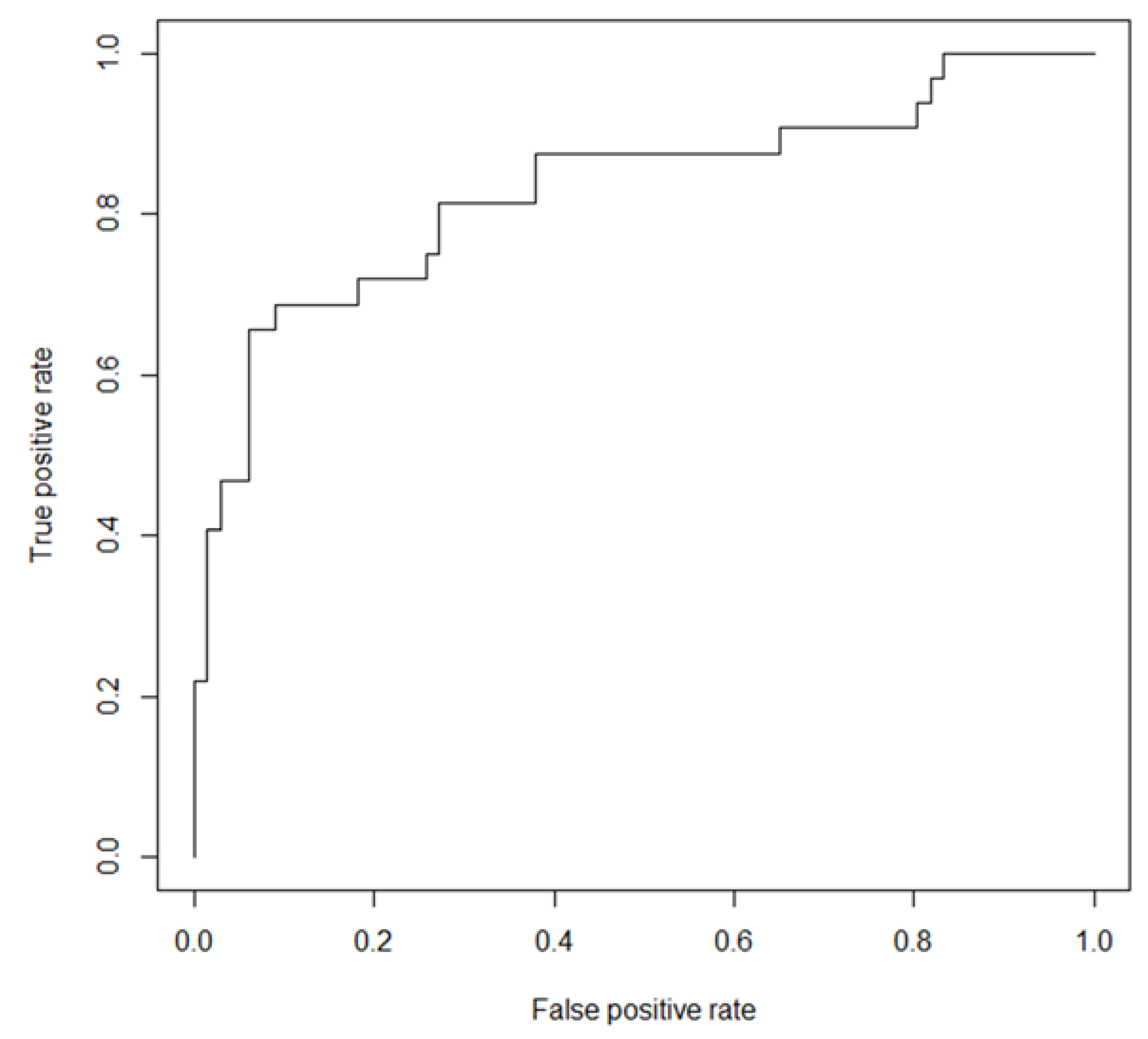
3.2. Performance of the Unconfined and Evangeline LR Models
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Abernathy, C.O.; Liu, Y.P.; Longfellow, D.; Aposhian, H.V.; Beck, B.; Fowler, B.; Waalkes, M. Arsenic: Health effects, mechanisms of actions, and research issues. Environ. Health Perspect. 1999, 107, 593. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, T.; Yamauchi, H.; Sun, G.F. Chronic health effects in people exposed to arsenic via the drinking water: Dose-response relationships in review. Toxicol. Appl. Pharmacol. 2004, 198, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Duker, A.A.; Carranza, E.; Hale, M. Arsenic geochemistry and health. Environ. Int. 2005, 31, 631–641. [Google Scholar] [CrossRef] [PubMed]
- Naujokas, M.F.; Anderson, B.; Ahsan, H.; Aposhian, H.V.; Graziano, J.H.; Thompson, C.; Suk, W.A. The broad scope of health effects from chronic arsenic exposure: Update on a worldwide public health problem. Environ. Health Perspect. 2013, 121, 295. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Arsenic Fact Sheet. Available online: http://www.who.int/mediacentre/factsheets/fs372/en/ (accessed on 22 January 2018).
- Shim, M.J.; Kim, H.J.; Yang, S.J.; Lee, I.S.; Choi, H.I.; Kim, T.U. Arsenic trioxide induces apoptosis in chronic myelogenous leukemia K562 cells: Possible involvement of p38 MAP kinase. BMB Rep. 2002, 35, 377–383. [Google Scholar] [CrossRef]
- Guo, H.; Yang, S.; Tang, X.; Li, Y.; Shen, Z. Groundwater geochemistry and its implications for arsenic mobilization in shallow aquifers of the Hetao Basin, Inner Mongolia. Sci. Total Environ. 2008, 393, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Lado, L.; Sun, G.; Berg, M.; Zhang, Q.; Xue, H.; Zheng, Q.; Johnson, C.A. Groundwater arsenic contamination throughout China. Science 2013, 341, 866–868. [Google Scholar] [CrossRef] [PubMed]
- Neumann, R.B.; Ashfaque, K.N.; Badruzzaman, A.B.M.; Ali, M.A.; Shoemaker, J.K.; Harvey, C.F. Anthropogenic influences on groundwater arsenic concentrations in Bangladesh. Nat. Geosci. 2010, 3, 46. [Google Scholar] [CrossRef]
- Flanagan, S.V.; Johnston, R.B.; Zheng, Y. Arsenic in tube well water in Bangladesh: Health and economic impacts and implications for arsenic mitigation. Bull. World Health Organ. 2012, 90, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Dong, Z.; Naidu, R. Concentrations of arsenic and other elements in groundwater of Bangladesh and West Bengal, India: Potential cancer risk. Chemosphere 2015, 139, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Aziz, Z.; Van Geen, A.; Stute, M.; Versteeg, R.; Horneman, A.; Zheng, Y.; Hoque, M.A. Impact of local recharge on arsenic concentrations in shallow aquifers inferred from the electromagnetic conductivity of soils in Araihazar, Bangladesh. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Mukherjee, A.; von Brömssen, M.; Scanlon, B.R.; Bhattacharya, P.; Fryar, A.E.; Hasan, M.A.; Sracek, O. Hydrogeochemical comparison and effects of overlapping redox zones on groundwater arsenic near the Western (Bhagirathi sub-basin, India) and Eastern (Meghna sub-basin, Bangladesh) margins of the Bengal Basin. J. Contam. Hydrol. 2008, 99, 31–48. [Google Scholar] [CrossRef] [PubMed]
- Armienta, M.A.; Segovia, N. Arsenic and fluoride in the groundwater of Mexico. Environ. Geochem. Health 2008, 30, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Bundschuh, J.; Litter, M.I.; Parvez, F.; Román-Ross, G.; Nicolli, H.B.; Jean, J.S.; Cuevas, A.G. One century of arsenic exposure in Latin America: A review of history and occurrence from 14 countries. Sci. Total Environ. 2012, 429, 2–35. [Google Scholar] [CrossRef] [PubMed]
- George, C.M.; Sima, L.; Arias, M.; Mihalic, J.; Cabrera, L.Z.; Danz, D.; Gilman, R.H. Arsenic exposure in drinking water: An unrecognized health threat in Peru. Bull. World Health Organ. 2014, 92, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Aiuppa, A.; D’Alessandro, W.; Federico, C.; Palumbo, B.; Valenza, M. The aquatic geochemistry of arsenic in volcanic groundwaters from southern Italy. Appl. Geochem. 2003, 18, 1283–1296. [Google Scholar] [CrossRef]
- Cinti, D.; Poncia, P.P.; Brusca, L.; Tassi, F.; Quattrocchi, F.; Vaselli, O. Spatial distribution of arsenic, uranium and vanadium in the volcanic-sedimentary aquifers of the Vicano-Cimino Volcanic District (central Italy). J. Geochem. Explor. 2015, 152, 123–133. [Google Scholar] [CrossRef]
- Katsoyiannis, I.A.; Mitrakas, M.; Zouboulis, A.I. Arsenic occurrence in Europe: Emphasis in Greece and description of the applied full-scale treatment plants. Desalin. Water Treat. 2015, 54, 2100–2107. [Google Scholar] [CrossRef]
- Welch, A.H.; Westjohn, D.B.; Helsel, D.R.; Wanty, R.B. Arsenic in ground water of the United States: Occurrence and geochemistry. Groundwater 2000, 38, 589–604. [Google Scholar] [CrossRef]
- Ren, Z.A.; Che, G.C.; Dong, X.L.; Yang, J.; Lu, W.; Yi, W.; Zhao, Z.X. Superconductivity and phase diagram in iron-based arsenic-oxides ReFeAsO1−δ (Re = rare-earth metal) without fluorine doping. EPL Europhys. Lett. 2008, 83, 17002. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Nicot, J.P.; Reedy, R.C.; Kurtzman, D.; Mukherjee, A.; Nordstrom, D.K. Elevated naturally occurring arsenic in a semiarid oxidizing system, Southern High Plains aquifer, Texas, USA. Appl. Geochem. 2009, 24, 2061–2071. [Google Scholar] [CrossRef]
- Camacho, L.M.; Gutiérrez, M.; Alarcón-Herrera, M.T.; de Lourdes Villalba, M.; Deng, S. Occurrence and treatment of arsenic in groundwater and soil in northern Mexico and southwestern USA. Chemosphere 2011, 83, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Andy, C.M.; Fahnestock, M.F.; Lombard, M.A.; Hayes, L.; Bryce, J.G.; Ayotte, J.D. Assessing models of arsenic occurrence in drinking water from bedrock aquifers in New Hampshire. J. Contemp. Water Res. Educ. 2017, 160, 25–41. [Google Scholar] [CrossRef]
- Mukherjee, A.; Bhattacharya, P.; Shi, F.; Fryar, A.E.; Mukherjee, A.B.; Xie, Z.M.; Bundschuh, J. Chemical evolution in the high arsenic groundwater of the Huhhot basin (Inner Mongolia, PR China) and its difference from the western Bengal basin (India). Appl. Geochem. 2009, 24, 1835–1851. [Google Scholar] [CrossRef]
- Anawar, H.M.; Freitas, M.C.; Canha, N.; Santa Regina, I. Arsenic, antimony, and other trace element contamination in a mine tailings affected area and uptake by tolerant plant species. Environ. Geochem. Health 2011, 33, 353–362. [Google Scholar] [CrossRef] [PubMed]
- Venkataraman, K.; Uddameri, V. Modeling simultaneous exceedance of drinking-water standards of arsenic and nitrate in the Southern Ogallala aquifer using multinomial logistic regression. J. Hydrol. 2012, 458, 16–27. [Google Scholar] [CrossRef]
- National Groundwater Association. Groundwater Use in the United States of America. Available online: http://www.ngwa.org/Fundamentals/Documents/usa-groundwater-use-fact-sheet.pdf (accessed on 21 January 2018).
- Texas Water Development Board. Texas Aquifers. Available online: http://www.twdb.texas.gov/groundwater/aquifer/index.asp (accessed on 31 January 2018).
- Lesikar, B.J.; Melton, R.; Hare, M.; Hopkins, J.; Dozier, M. Drinking Water Problems: Arsenic. Texas FARMER Collection 2005. Available online: http://hdl.handle.net/1969.1/87346 (accessed on 5 April 2018).
- U.S. Department of Agriculture. Texas Town Gets out the Arsenic with Help from USDA. Available online: https://www.usda.gov/media/blog/2013/08/1/texas-town-gets-out-arsenic-help-usda (accessed on 22 January 2018).
- U.S. Environmental Protection Agency. Arsenic Treatment Technology Demonstrations by Location. Available online: https://www.epa.gov/water-research/arsenic-treatment-technology-demonstrations-location (accessed on 21 January 2018).
- Scanlon, B.R.; Nicot, J.P.; Reedy, R.C.; Tachovsky, J.A.; Nance, S.H.; Smyth, R.C.; Christian, L. Evaluation of Arsenic Contamination in Texas; Report Prepared for Texas Commission on Environmental Quality, Bureau of Economic Geology; The University of Texas at Austin: Austin, TX, USA, 2005. [Google Scholar]
- Hudak, P. Arsenic, nitrate, chloride and bromide contamination in the gulf coast aquifer, south-central Texas, USA. Int. J. Environ. Stud. 2003, 60, 123–133. [Google Scholar] [CrossRef]
- Gates, J.B.; Nicot, J.P.; Scanlon, B.R.; Reedy, R.C. Arsenic enrichment in unconfined sections of the southern Gulf Coast aquifer system, Texas. Appl. Geochem. 2011, 26, 421–431. [Google Scholar] [CrossRef]
- Chowdhury, A.H.; Boghici, R.; Hopkins, J. Hydrochemistry, salinity distribution, and trace constituents: Implications for salinity sources, geochemical evolution, and flow systems characterization, Gulf Coast Aquifer, Texas. In Aquifers of the Gulf Coast of Texas; Texas Water Development Board Report; Texas Water Development Board: Austin, TX, USA, 2006; Volume 365, pp. 81–128. [Google Scholar]
- Glenn, S.M.; Lester, L.J. An analysis of the relationship between land use and arsenic, vanadium, nitrate and boron contamination in the Gulf Coast aquifer of Texas. J. Hydrol. 2010, 389, 214–226. [Google Scholar] [CrossRef]
- Tesoriero, A.J.; Voss, F.D. Predicting the probability of elevated nitrate concentrations in the Puget Sound Basin: Implications for aquifer susceptibility and vulnerability. Groundwater 1997, 35, 1029–1039. [Google Scholar] [CrossRef]
- Nolan, B.T. Relating nitrogen sources and aquifer susceptibility to nitrate in shallow ground waters of the United States. Groundwater 2001, 39, 290–299. [Google Scholar] [CrossRef]
- Twarakavi, N.K.; Kaluarachchi, J.J. Aquifer vulnerability assessment to heavy metals using ordinal logistic regression. Groundwater 2005, 43, 200–214. [Google Scholar] [CrossRef] [PubMed]
- Cotton Production Regions for Texas: Texas A&M AgriLife. Available online: https://cottonbugs.tamu.edu/cotton-production-regions-of-texas/ (accessed on 14 March 2018).
- Hunter, D.G.; Baker, W.S. Excavations in the Atkins Midden at the Troyville Site, Catahoula Parish, Louisiana. Louisiana Arch. 1979, 4, 21–52. [Google Scholar]
- Young, S.C.; Knox, P.R.; Budge, T.; Kelley, V.; Deeds, N.; Galloway, W.E.; Baker, E.T. Stratigraphy, lithology, and hydraulic properties of the Chicot and Evangeline aquifers in the LSWP Study Area, Central Texas Coast. In Aquifers of the Gulf Coast; Texas Water Development Board Report; Texas Water Development Board: Austin, TX, USA, 2006; Volume 365, pp. 129–138. [Google Scholar]
- Brandenberger, J.; Louchouarn, P.; Herbert, B.; Tissot, P. Geochemical and hydrodynamic controls on arsenic and trace metal cycling in a seasonally stratified US sub-tropical reservoir. Appl. Geochem. 2004, 19, 1601–1623. [Google Scholar] [CrossRef]
- Hudak, P. Distribution and sources of arsenic in the southern high plains Aquifer, Texas, USA. Environ. Sci. Health A 2000, 35, 899–913. [Google Scholar] [CrossRef]
- Mineral Resource Data System: United States Geological Survey. Available online: https://mrdata.usgs.gov/mrds/ (accessed on 11 March 2018).
- Groundwater Availability Model: Texas Water Development Board. Available online: http://www.twdb.texas.gov/groundwater/models/gam/index.asp (accessed on 13 March 2018).
- Baker, E., Jr. Stratigraphic and Hydrogeologic Framework of Part of the Coastal Plain of Texas; Report: 236; Texas Department of Water Resources: Austin, TX, USA, 1979.
- Soil Survey Geographic Database: U.S. Department of Agriculture. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/main/soils/survey/geo/ (accessed on 18 January 2018).
- Lakes Environmental. LULC Data. Available online: http://www.webgis.com/lulcdata.html (accessed on 21 January 2018).
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Winkel, L.; Berg, M.; Amini, M.; Hug, S.J.; Johnson, C.A. Predicting groundwater arsenic contamination in Southeast Asia from surface parameters. Nat. Geosci. 2008. [Google Scholar] [CrossRef]
- Worrall, F.; Kolpin, D.W. Aquifer vulnerability to pesticide pollution—Combining soil, land-use and aquifer properties with molecular descriptors. J. Hydrol. 2004, 293, 191–204. [Google Scholar] [CrossRef]
- Amini, M.; Abbaspour, K.C.; Berg, M.; Winkel, L.; Hug, S.J.; Hoehn, E.; Johnson, C.A. Statistical modeling of global geogenic arsenic contamination in groundwater. Environ. Sci. Technol. 2008, 42, 3669–3675. [Google Scholar] [CrossRef] [PubMed]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 5th ed.; Allyn & Bacon/Pearson Education: Boston, MA, USA, 2007. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Agresti, A. Logistic regression. In An Introduction to Categorical Data Analysis, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 99–136. [Google Scholar]
- Peduzzi, P.; Concato, J.; Kemper, E.; Holford, T.R.; Feinstein, A.R. A simulation study of the number of events per variable in logistic regression analysis. J. Clin. Epidemiol. 1996, 49, 1373–1379. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Ijcai; Stanford University: Stanford, CA, USA, 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Altman, D.G.; Royston, P. What do we mean by validating a prognostic model? Stat. Med. 2000, 19, 453–473. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Eijkemans, M.J.; Harrell, F.E.; Habbema, J.D.F. Prognostic modelling with logistic regression analysis: A comparison of selection and estimation methods in small data sets. Stat. Med. 2000, 19, 1059–1079. [Google Scholar] [CrossRef]
- Gude, J.A.; Mitchell, M.S.; Ausband, D.E.; Sime, C.A.; Bangs, E.E. Internal validation of predictive logistic regression models for decision-making in wildlife management. Wildl. Biol. 2009, 15, 352–369. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform. 2014, 6, 10. [Google Scholar] [CrossRef] [PubMed]
- Adjei, I.A.; Karim, R. An Application of Bootstrapping in Logistic Regression Model. OALib J. 2016, 3, 1. [Google Scholar] [CrossRef][Green Version]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied regression analysis. Stat. Med. 1989, 31, 10. [Google Scholar]
- Hilbe, J.M. Logistic regression. In International Encyclopedia of Statistical Science; Springer: Heidelberg/Berlin, Germany, 2011; pp. 755–758. [Google Scholar]
- R Core Team: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 24 December 2017).
- Bundschuh, J.; Farias, B.; Martin, R.; Storniolo, A.; Bhattacharya, P.; Cortes, J.; Bonorino, G.; Albouy, R. Groundwater arsenic in the Chaco-Pampean Plain, Argentina: Case study from Robles county, Santiago del Estero Province. Appl. Geochem. 2004, 231–243. [Google Scholar] [CrossRef]
- Podgorski, J.E.; Eqani, S.A.M.A.S.; Khanam, T.; Ullah, R.; Shen, H.; Berg, M. Extensive arsenic contamination in high-pH unconfined aquifers in the Indus Valley. Sci. Adv. 2017, 3, e1700935. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.H.; Sthiannopkao, S.; Pachepsky, Y.A.; Kim, K.W.; Kim, J.H. Prediction of contamination potential of groundwater arsenic in Cambodia, Laos, and Thailand using artificial neural network. Water Res. 2011, 45, 5535–5544. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.M.; Piantanakulchai, M. Groundwater arsenic contamination risk prediction using GIS and classification tree method. Eng. Geol. 2013, 156, 37–45. [Google Scholar] [CrossRef]
- Ghadimi, F. Prediction of soil contamination based on support vector machine and k-nearest neighbor methods: A case study in Arak, Iran. Iranica J. Energy Environ. 2014, 5, 345–353. [Google Scholar]
- Nolan, B.T.; Fienen, M.N.; Lorenz, D.L. A statistical learning framework for groundwater nitrate models of the Central Valley, California, USA. J. Hydrol. 2015, 531, 902–911. [Google Scholar] [CrossRef]
| Model Summary | Likelihood Ratio Test (LRT) Results Summary | |||||
|---|---|---|---|---|---|---|
| Parameter | Estimate | Std. Error | p-Value | Parameter | Deviance | Pr (>Chi) |
| Intercept | 2.1414 | 1.7188 | 0.2128 | NULL | 209.65 | - |
| F * | 0.6572 | 0.3096 | 0.0338 | F * | 200.73 | 0.0028 |
| Aq Strat Unit 2 | −1.0517 | 0.5853 | 0.0723 | Aq Stat Unit * | 189.47 | 0.0327 |
| Aq Strat Unit 3 | −1.6687 | 1.2302 | 0.1750 | |||
| Aq Strat Unit 4 | 0.4209 | 0.8028 | 0.5997 | |||
| Aq Strat Unit 5 | 0.7737 | 0.8462 | 0.3606 | |||
| pH | −0.5065 | 0.2348 | 0.0551 | pH * | 181.93 | 0.0042 |
| V * | 0.0461 | 0.0098 | <1 × 10−4 | V * | 156.66 | <1 × 10−6 |
| Parameter | Master LR | Unconfined LR | Evangeline LR |
|---|---|---|---|
| Accuracy | 0.7628 | 0.7458 | 0.7959 |
| True Positive Rate | 0.5645 | 0.4250 | 0.5455 |
| False Positive Rate | 0.1064 | 0.0897 | 0.0769 |
| True Negative Rate | 0.8936 | 0.9103 | 0.9231 |
| False Negative Rate | 0.4355 | 0.5750 | 0.4545 |
| Positive Predictive Value | 0.7778 | 0.7083 | 0.7826 |
| Negative Predictive Value | 0.7568 | 0.7553 | 0.8000 |
| Model Summary | LRT Results Summary | |||||
|---|---|---|---|---|---|---|
| Parameter | Estimate | Std. Error | p-Value | Parameter | Deviance | Pr (<Chi) |
| Intercept | 0.9843 | 1.6711 | 0.5585 | NULL | 151.12 | - |
| F * | 0.6921 | 0.3292 | 0.0355 | F * | 146.56 | 0.0325 |
| Well Depth | −0.0007 | 0.0345 | 0.4533 | Well Depth | 146.34 | 0.2344 |
| pH | −0.4450 | 0.2364 | 0.0597 | pH * | 140.89 | 0.0172 |
| V * | 0.0349 | 0.0104 | <1 × 10−3 | V * | 127.36 | <1 × 10−3 |
| Model Summary | LRT Results Summary | |||||
|---|---|---|---|---|---|---|
| Parameter | Estimate | Std. Error | p-Value | Parameter | Residual Deviance | Pr (<Chi) |
| Intercept | −0.2339 | 1.1887 | 0.8440 | NULL | 123.81 | - |
| pH | −0.3175 | 0.1752 | 0.0699 | pH | 122.33 | 0.2237 |
| F | 0.6476 | 0.3894 | 0.0966 | F * | 115.61 | 0.0168 |
| V * | 0.0473 | 0.0111 | <1 × 10−3 | V * | 99.34 | <1 × 10−4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkataraman, K.; Lozano, J.W. Reliable Predictors of Arsenic Occurrence in the Southern Gulf Coast Aquifer of Texas. Geosciences 2018, 8, 155. https://doi.org/10.3390/geosciences8050155
Venkataraman K, Lozano JW. Reliable Predictors of Arsenic Occurrence in the Southern Gulf Coast Aquifer of Texas. Geosciences. 2018; 8(5):155. https://doi.org/10.3390/geosciences8050155
Chicago/Turabian StyleVenkataraman, Kartik, and John W. Lozano. 2018. "Reliable Predictors of Arsenic Occurrence in the Southern Gulf Coast Aquifer of Texas" Geosciences 8, no. 5: 155. https://doi.org/10.3390/geosciences8050155
APA StyleVenkataraman, K., & Lozano, J. W. (2018). Reliable Predictors of Arsenic Occurrence in the Southern Gulf Coast Aquifer of Texas. Geosciences, 8(5), 155. https://doi.org/10.3390/geosciences8050155




