Probabilistic Estimates of Ground Motion in the Los Angeles Basin from Scenario Earthquakes on the San Andreas Fault
Abstract
1. Introduction
2. Earthquake Source Models and Associated Probabilities
2.1. Source Models
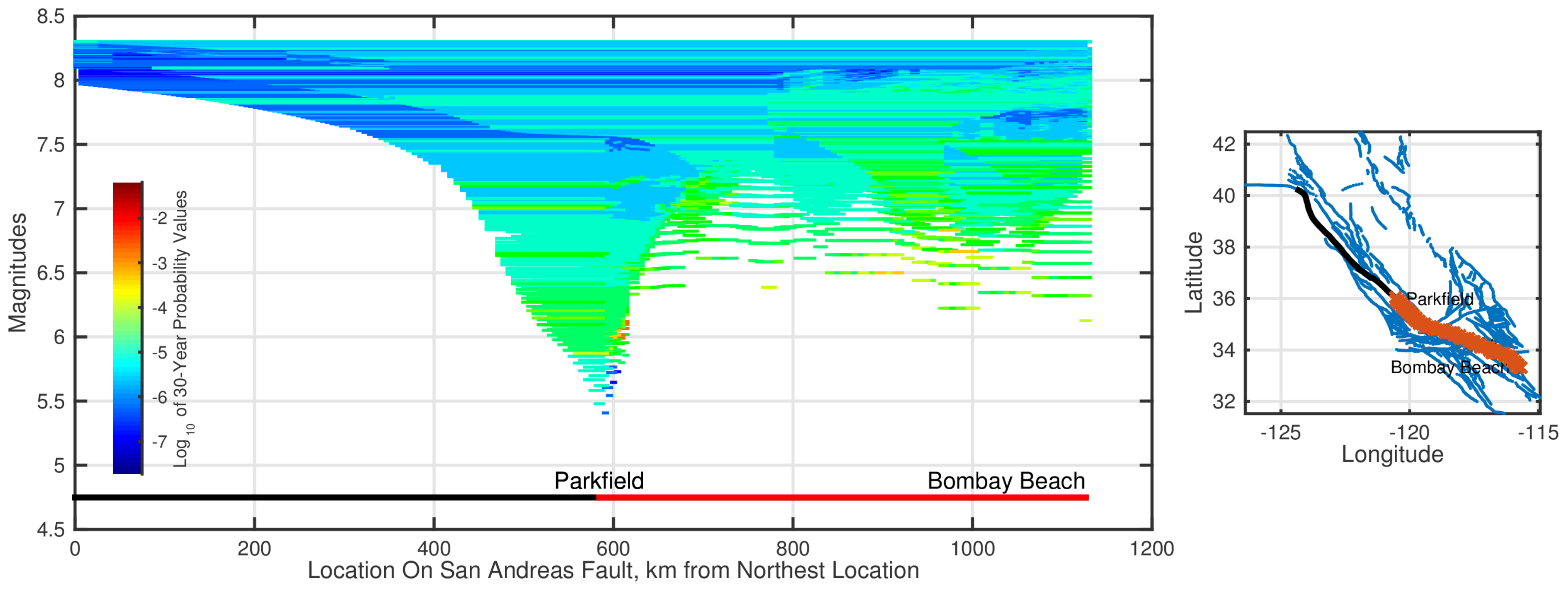
2.2. Scenario Earthquake Probabilities
- (i)
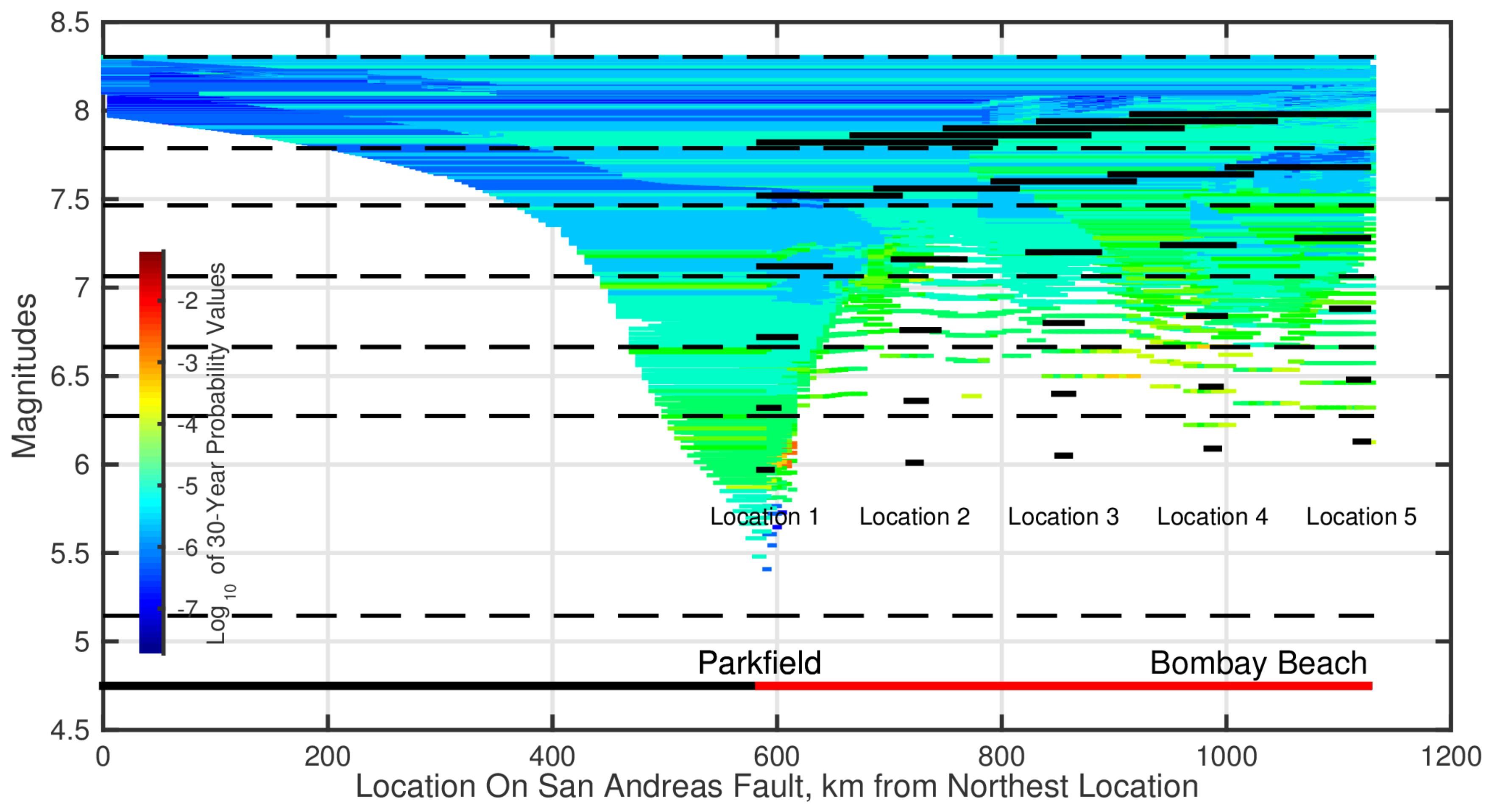
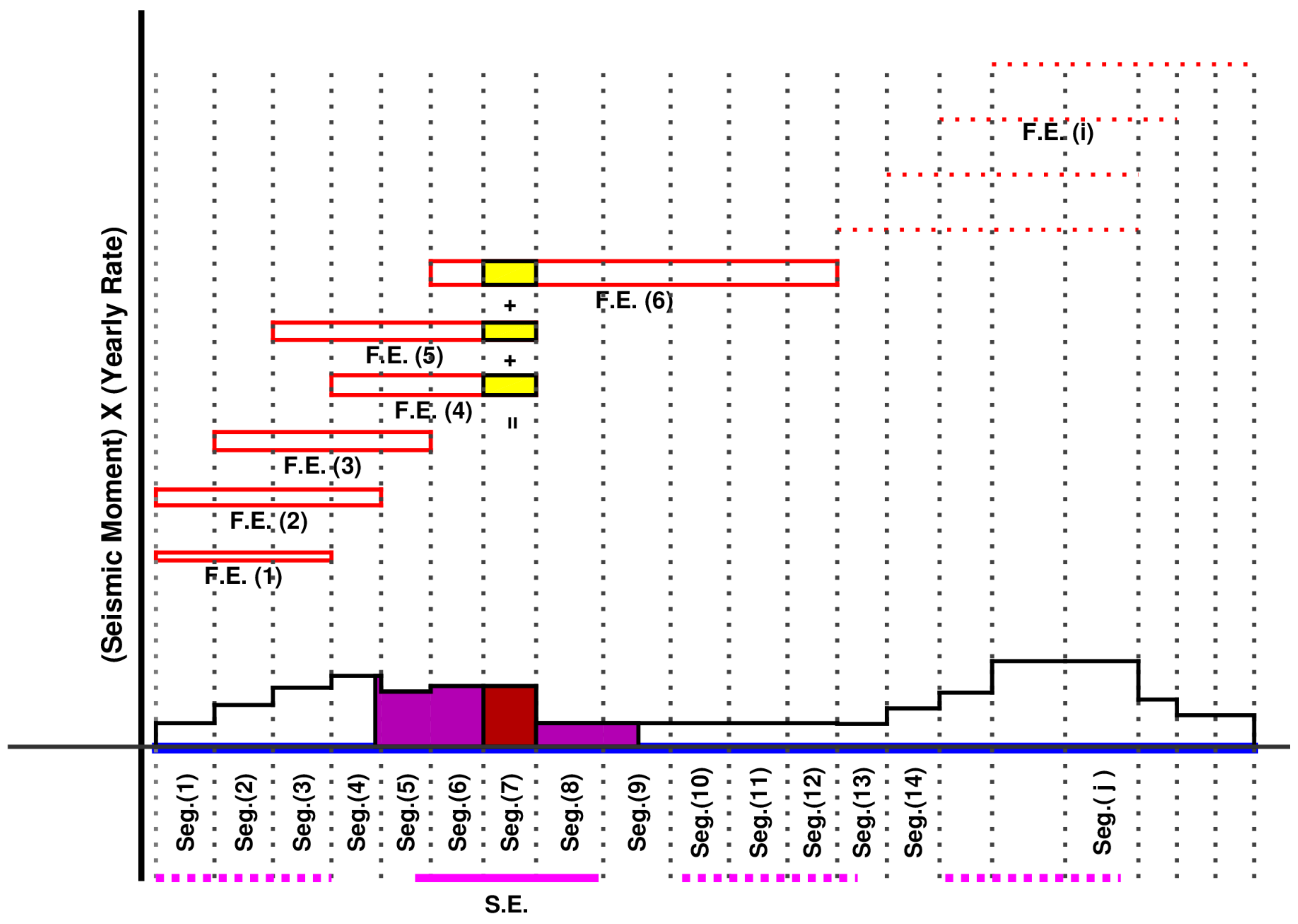
- We start with “magnitude binning” of forecast earthquakes. We define as many bins as the number of distinct magnitude scenario earthquakes. The lower and upper magnitude limits of a magnitude bin are the magnitudes derived from the averages of the seismic moments of the corresponding scenario earthquake and the scenario earthquakes tied to the previous and next bins, respectively. Corresponding to the six scenario earthquake magnitudes of 6.00, 6.56, 6.92, 7.28, 7.59, and 7.89, the following six magnitude bins are defined: [5.90–6.42], (6.42–6.80], (6.80–7.15] , (7.15–7.45], (7.47–7.78], and (7.78–8.34]. The seismic moments of the 6.00, 6.56, 6.92, 7.28, 7.59, and 7.89 scenario earthquakes correspond to the average of the seismic moments of the upper and lower magnitude limits of the first five bins, respectively. The upper limit of the last bin is assumed higher to include all forecast earthquakes with magnitude greater than 7.89. Each of the forecast earthquakes will be assigned to one of these magnitude bins. For instance, a forecast earthquake with magnitude, say, between 6.42 and 6.80 will be assigned to the magnitude bin tied to the scenario earthquake with magnitude 6.56. Its probability of occurrence will be redistributed among the ten 6.56 scenario earthquakes (five rupture locations and two rupture directions). The dashed black lines in Figure 3 demarcate the magnitude bins.
- (ii)
- The seismic moment of forecast earthquake i, , is multiplied by the UCERF yearly occurrence rate to arrive at what may be termed as the seismic moment release rate with a unit of “seismic moment/year”. Seismic moment release rates are determined for all forecast earthquakes in this manner.
- (iii)
- Within each magnitude bin, the seismic moment release rate of a forecast earthquake is distributed among the UCERF segments being ruptured by that forecast earthquake in proportion to their areas. This is based on the fact that seismic moment release rate, given by where is the average slip rate on the fault, is the shear modulus, and A is the area of rupture, scales linearly with segment area (see Equation (4.8) and Appendix G of [19]). Thus the seismic moment release rate contribution of the forecast earthquake to the UCERF segment equals , where is the area of forecast earthquake i and is the area of the UCERF segment j.
- (iv)
- Within each magnitude bin, the contributions to fault segment j of all N forecast earthquakes in that bin are summed: . This represents the yearly seismic moment buildup in segment j that is expected to be released periodically by earthquakes with magnitudes lying within the bin. It may be termed as the seismic moment release rate for segment j in earthquakes from that magnitude bin.
- (v)
- Within each magnitude bin, the cumulative seismic moment release rate of segment j, determined in the previous step, is assigned to the scenario earthquake tied to that bin and whose rupture location is closest to segment j. Then the seismic moment release rate of that scenario earthquake is given by , where M is the number of UCERF segments occurring within the rupture extent of that scenario earthquake. It is possible that the rupture extents of two or more scenario earthquakes may extend over the same fault segment(s). The moment release rates on such segments are evenly distributed among the overlapping scenario earthquakes.
- (vi)
- The seismic moment release rate, obtained from the last step, for scenario earthquake k is divided by its seismic moment to obtain its yearly occurrence rate .
- (vii)
- The probability of occurrence of scenario earthquake k over a period of years is then given by the Poisson distribution as: .
- (viii)
- Steps (iii)–(vii) are repeated for all magnitude bins and the scenario earthquakes associated with them.
3. Ground Motion Simulation
4. Probabilistic Estimates of Ground Shaking
5. Discussion and Limitations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heaton, T.H.; Hall, J.F.; Wald, D.J.; Halling, M.W. Response of High-Rise and Base-Isolated Buildings to a Hypothetical Mw 7.0 Blind Thrust Earthquake. Science 1995, 267, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.F.; Heaton, T.H.; Halling, M.W.; Wald, D.J. Near-Source Ground Motion and its Effects on Flexible Buildings. Earthq. Spectra 1995, 11, 569–605. [Google Scholar] [CrossRef]
- Hall, J.F. Seismic Response of Steel Frame Buildings to Near-Source Ground Motions. Earthq. Eng. Struct. Dyn. 1998, 27, 1445–1464. [Google Scholar] [CrossRef]
- Krishnan, S.; Ji, C.; Komatitsch, D.; Tromp, J. Case Studies of Damage to Tall Steel Moment-Frame Buildings in Southern California during Large San Andreas Earthquakes. Bull. Seismol. Soc. Am. 2006, 96, 1523–1537. [Google Scholar] [CrossRef][Green Version]
- Krishnan, S.; Ji, C.; Komatitsch, D.; Tromp, J. Performance of two 18-story steel moment-frame buildings in southern California during two large simulated San Andreas earthquakes. Earthq. Spectra 2006, 22, 1035–1061. [Google Scholar] [CrossRef]
- Muto, M.; Krishnan, S.; Beck, J.; Mitrani-Reiser, J. Seismic loss estimation based on end-to-end simulation. In Proceedings of the First International Symposium on Life-Cycle Civil Engineering, Varenna, Lake Como, Italy, 10–14 June 2008; pp. 215–232. [Google Scholar]
- Muto, M.; Krishnan, S. Hope for the Best, Prepare for the Worst: Response of Tall Steel Buildings to the ShakeOut Scenario Earthquake. Earthq. Spectra 2011, 27, 375–398. [Google Scholar] [CrossRef]
- Field, E.H.; Dawson, T.E.; Felzer, K.R.; Frankel, A.D.; Gupta, V.; Jordan, T.H.; Parsons, T.; Petersen, M.D.; Stein, R.S.; Weldon, R.J.; et al. Uniform California Earthquake Rupture Forecast, Version 2 (UCERF 2). Bull. Seismol. Soc. Am. 2009, 99, 2053–2107. [Google Scholar] [CrossRef]
- Field, E.; Biasi, G.; Bird, P.; Dawson, T.; Felzer, K.; Jackson, D.; Johnson, K.; Jordan, T.; Madden, C.; Michael, A.; et al. Uniform California Earthquake Rupture Forecast, Version 3 (UCERF3)—The Time-Independent Model: U.S. Geological Survey Open-File Report 2013-1165; California Geological Survey Special Report 228, and Southern California Earthquake Center Publication 1792; 2013; p. 97. Available online: http://pubs.usgs.gov/of/2013/1165/ (accessed on 15 January 2015).
- Biasi, G.; Anderson, J.G. Disaggregating UCERF3 for Site-Specific Applications. Earthq. Spectra 2016, 32, 2009–2026. [Google Scholar] [CrossRef]
- Porter, K.; Field, E.; Milner, K. Disaggregating UCERF3 for Site-Specific Applications. Earthq. Spectra 2017, 33, 857–874. [Google Scholar] [CrossRef]
- SRCMOD (Finite-Source Rupture Model Database). Finite-Source Rupture Model Database (Initiated by Martin Mai). Available online: http://equake-rc.info/SRCMOD/ (accessed on 15 September 2014).
- Ji, C.; Helmberger, D.; Wald, D. Preliminary slip history of the 2002 Denali earthquake. AGU Fall Meet. Abstr. 2002, 1, 1344. [Google Scholar]
- Bouchon, M.; Toksöz, M.N.; Karabulut, H.; Bouin, M.P.; Dietrich, M.; Aktar, M.; Edie, M. Space and time evolution of rupture and faulting during the 1999 Izmit (Turkey) earthquake. Bull. Seismol. Soc. Am. 2002, 92, 256–266. [Google Scholar] [CrossRef]
- Wald, D.J.; Heaton, T.H. Spatial and Temporal Distribution of Slip for the 1992 Landers, California, Earthquake. Bull. Seismol. Soc. Am. 1994, 84, 668–691. [Google Scholar]
- Wald, D.J. Slip History of the 1995 Kobe, Japan, Earthquake Determined from Strong Motion, Teleseismic, and Geodetic Data. J. Phys. Earth 1996, 44, 489–504. [Google Scholar] [CrossRef]
- Hartzell, S.H.; Heaton, T.H. Inversion of Strong Ground Motion and Teleseismic Waveform Data for the Fault Rupture History of the 1979 Imperial Valley, California, Earthquake. Bull. Seismol. Soc. Am. 1983, 73, 1553–1583. [Google Scholar]
- Custódio, S.; Liu, P.; Archuleta, R.J. The 2004 Mw 6.0 Parkfield, California, earthquake: Inversion of near-source ground motion using multiple data sets. Geophys. Res. Lett. 2005, 32, L23312. [Google Scholar] [CrossRef]
- WGCEP (Working Group on California Earthquake Probabilities). Earthquake Probabilities in the San Francisco Bay Region: 2002–2031; U.S. Geological Survey Open-File Report 03-214; Working Group On California Earthquake Probabilities: Los Angeles, CA, USA, 2003. [Google Scholar]
- Sieh, K. Prehistoric Large Earthquakes Produced by Slip on the San Andreas Fault at Pallett Creek, California. J. Geophys. Res. Solid Earth 1978, 83, 3907–3939. [Google Scholar] [CrossRef]
- Bakun, W.H.; Lindh, A.G. The Parkfield, California, Earthquake PredictionExperiment. Science 1985, 229, 619–624. [Google Scholar] [CrossRef] [PubMed]
- Magistrale, H.; McLaughlin, K.; Day, S. A geology-based 3D velocity model of the Los Angeles basin sediments. Bull. Seismol. Soc. Am. 1996, 86, 1161–1166. [Google Scholar]
- Magistrale, H.; Day, S.; Clayton, R.W.; Graves, R. The SCEC Southern California Reference Three-Dimensional Seismic Velocity Model Version 2. Bull. Seismol. Soc. Am. 2000, 90, S65–S76. [Google Scholar] [CrossRef]
- Kohler, M.D.; Magistrale, H.; Clayton, R.W. Mantle Heterogeneities and the SCEC Reference Three-Dimensional Seismic Velocity Model Version 3. Bull. Seismol. Soc. Am. 2003, 93, 757–774. [Google Scholar] [CrossRef]
- Süss, M.P.; Shaw, J.H. P wave seismic velocity structure derived from sonic logs and industry reflection data in the Los Angeles basin, California. J. Geophys. Res. 2003, 108, 1–18. [Google Scholar] [CrossRef]
- Prindle, K.; Tanimoto, T. Teleseismic surface wave study for S-wave velocity structure under an array: southern California. Geophys. J. Int. 2006, 166, 601–621. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Adjoint tomography of the southern California crust. Science 2009, 325, 988–992. [Google Scholar] [CrossRef] [PubMed]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Seismic tomography of the southern California crust based on spectral element and adjoint methods. Geophys. J. Int. 2010, 180, 433–462. [Google Scholar] [CrossRef]
- Ely, G.; Jordan, T.H.; Small, P.; Maechling, P.J. A derived Near-surface Seismic Velocity Model. In Proceedings of the American Geophysical Union Fall Meeting, San Francisco, CA, USA, 13–17 December 2010. [Google Scholar]
- Plesch, A.; Tape, C.; Graves, R.; Shaw, J.H.; Small, P.; Ely, G. Updates for the CVM-H including new representations of the offshore Santa Maria and San Bernardino basins and a new Moho surface. In Proceedings of the SCEC 2011 Annual Meeting, Southern California Earthquake Center, Palm Springs, CA, USA, 11–14 September 2011; p. Poster B-128. [Google Scholar]
- Olsen, K.; Archuleta, R.; Matarese, J. Three dimensional simulation of a magnitude 7.75 earthquake on the San Andreas fault. Science 1995, 270, 1628–1632. [Google Scholar] [CrossRef]
- Bao, H.; Bielak, J.; Ghattas, O.; Kallivokas, L.F.; O’Hallaron, D.R.; Shewchuk, J.R.; Xu, J. Large-scale simulation of elastic wave propagation in heterogeneous media on parallel computers. Comput. Methods Appl. Mech. Eng. 1998, 152, 85–102. [Google Scholar] [CrossRef]
- Graves, R.W. Three-dimensional finite-difference modeling of the San Andreas fault: Source parameterization and ground-motion levels. Bull. Seismol. Soc. Am. 1998, 88, 881–897. [Google Scholar]
- Akcelik, V.; Bielak, J.; Biros, G.; Epanomeritakis, I.; Fernandez, A.; Ghattas, O.; Kim, E.J.; Lopez, J.; O’Hallaron, D.; Tu, T.; et al. High resolution forward and inverse earthquake modeling on terascale computers. In Proceedings of the IEEE 2003 ACM/IEEE Conference Supercomputing, Phoenix, AZ, USA, 15–21 November 2003; p. 52. [Google Scholar]
- Komatitsch, D.; Liu, Q.; Tromp, J.; Süss, P.; Stidham, C.; Shaw, J.H. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method. Bull. Seismol. Soc. Am. 2004, 94, 187–206. [Google Scholar] [CrossRef]
- Liu, Q.; Polet, J.; Komatitsch, D.; Tromp, J. Spectral-element moment tensor inversions for earthquakes in Southern California. Bull. Seismol. Soc. Am. 2004, 94, 1748–1761. [Google Scholar] [CrossRef]
- Komatitsch, D.; Erlebacher, G.; Göddeke, D.; Michéa, D. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster. J. Comput. Phys. 2010, 229, 7692–7714. [Google Scholar] [CrossRef]
- Komatitsch, D. Fluid-solid coupling on a cluster of GPU graphics cards for seismic wave propagation. C. R. Mécanique 2011, 339, 125–135. [Google Scholar] [CrossRef]
- Mai, P.M.; Imperatori, W.; Olsen, K.B. Hybrid Broadband Ground-Motion Simulations: Combining Long-Period Deterministic Synthetics with High-Frequency Multiple S-to-S Backscattering. Bull. Seismol. Soc. Am. 2010, 100, 2124–2142. [Google Scholar] [CrossRef]
- Graves, R.; Pitarka, A. Broadband ground-motion simulation using a hybrid approach. Bull. Seismol. Soc. Am. 2010, 100, 2095–2113. [Google Scholar] [CrossRef]
- Mourhatch, R. Quantifying Earthquake Collapse Risk of Tall Steel Braced Frame Buildings Using Rupture-to-Rafters Simulations. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2015. [Google Scholar]
- Kellogg, L. Computational Infrastructure for Geodynamics. 2011. Available online: http://geodynamics.org. (accessed on 06 April 2018).
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Hauksson, E. Crustal structure and seismicity distribution adjacent to the Pacific and the north America plate boundary in southern California. J. Geophys. Res. 2000, 105, 13875–13903. [Google Scholar] [CrossRef]
- Lin, G.; Shearer, P.M.; Hauksson, E.; Thurber, C.H. A three-dimensional crustal seismic velocity model for southern California from a composite event method. J. Geophys. Res. Solid Earth (1978–2012) 2007, 112. [Google Scholar] [CrossRef]
- Casarotti, E.; Stupazzini, M.; Lee, S.J.; Komatitsch, D.; Piersanti, A.; Tromp, J. CUBIT and seismic wave propagation based upon the spectral-element method: An advanced unstructured mesher for complex 3D geological media. In Proceedings of the 16th International Meshing Roundtable, Seattle, WA, USA, 2 October 2017; Springer: Berlin, Germany, 2008; pp. 579–597. [Google Scholar]
- Sandia National Laboratory. CUBIT: Geometry and Mesh Generation Toolkit. 2011. Available online: http://cubit.sandia.gov. (accessed on 06 April 2018).
- Hartzell, S.H. Earthquake Aftershocks as Green’s Functions. Geophys. Res. Lett. 1978, 5, 1–4. [Google Scholar] [CrossRef]
- Irikura, K. Semi-empirical estimation of strong ground motions during large earthquakes. Bull. Disaster Prev. Res. Inst. 1983, 33, 63–104. [Google Scholar]
- Irikura, K. Prediction of Strong Acceleration Motions Using empirical Green’s Functions. In Proceedings of the Seventh Japan Earthquake Engineering Symposium, Tokyo, Japan, 2–9 August 1986; pp. 151–156. [Google Scholar]
- Joyner, W.; Boore, D. On simulating large earthquakes by Green’s-function addition of smaller earthquakes. Earthq. Source Mech. 1986. [Google Scholar] [CrossRef]
- Heaton, T.H.; Hartzell, S.H. Estimation of strong ground motions from hypothetical earthquakes on the Cascadia subduction zone, Pacific Northwest. Pure Appl. Geophys. 1989, 129, 131–201. [Google Scholar] [CrossRef]
- Hutchings, L.; Wu, F. Empirical Green’s Functions From Small Earthquakes A Waveform Study of Locally Recorded Aftershocks of The San Fernando Earthquake. J. Geophys. Res. 1990, 95, 1187–1214. [Google Scholar] [CrossRef]
- Somerville, P.; Sen, M.; Cohee, B. Simulation of strong ground motions recorded during the 1985 Michoacan, Mexico and Valparaiso, Chile earthquakes. Bull. Seismol. Soc. Am. 1991, 81, 1–27. [Google Scholar]
- Hutchings, L. Prediction of Strong Ground Motion for the 1989 Loma Prieta earthquake using Empirical Green’s Functions. Bull. Seismol. Soc. Am. 1991, 81, 88–122. [Google Scholar]
- Hutchings, L. Kinematic Earthquake Models and Synthesized Ground Motion using empirical Green’s functions. Bull. Seismol. Soc. Am. 1994, 84, 1028–1050. [Google Scholar]
- Tumarkin, A.G.; Archuleta, R.J. Empirical ground Motion Prediction. Annali Di Geofisica 1994, XXXVII, 1691–1720. [Google Scholar]
- Frankel, A. Simulating Strong motions of large earthquakes using recordings of small earthquakes: The Loma Prieta mainshock as a test case. Bull. Seismol. Soc. Am. 1995, 85, 1144–1160. [Google Scholar]
- Brune, J.N. Tectonic Stress and the Spectra of Seismic Shear Waves from Earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
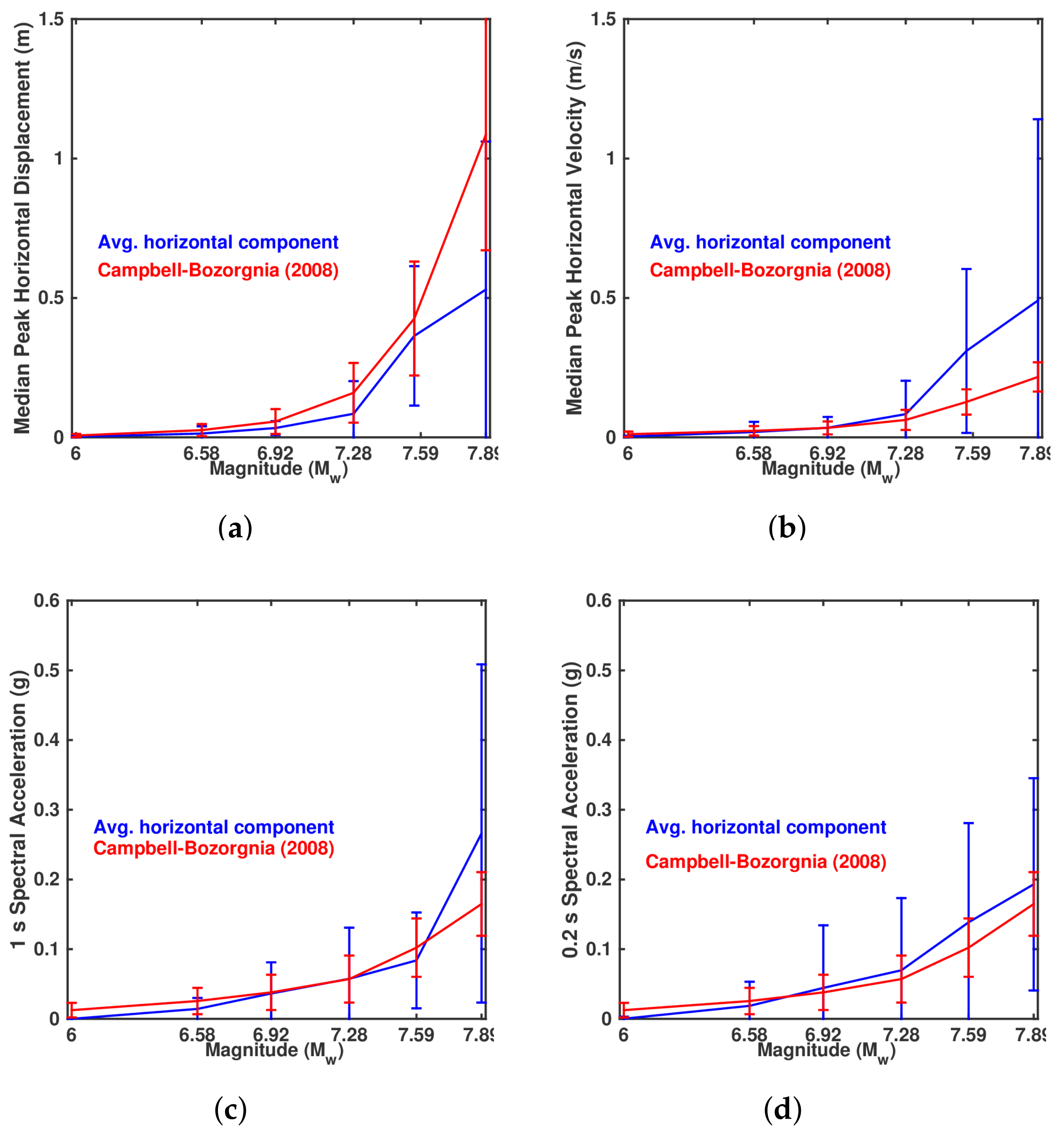
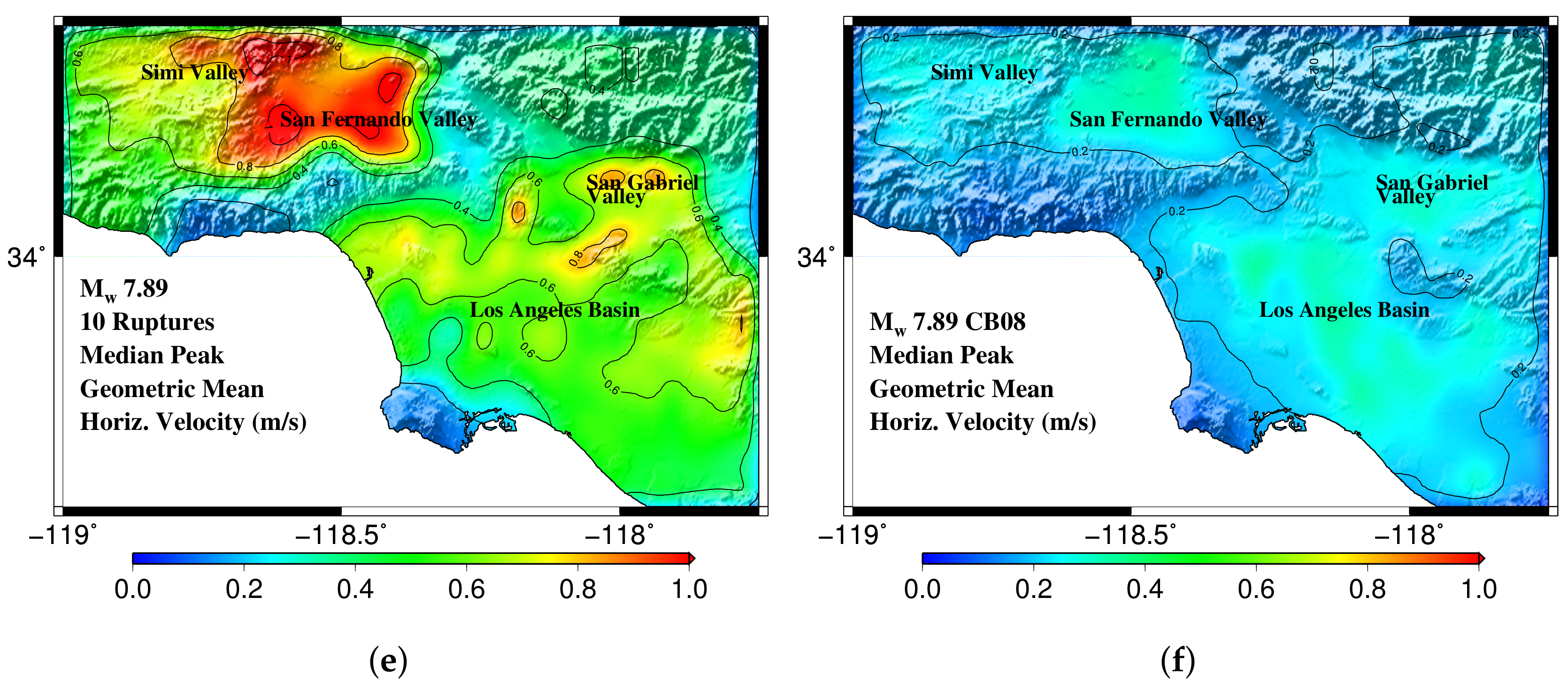
- Campbell, K.W.; Bozorgnia, Y. NGA Ground Motion Model for the Geometric Mean Horizontal Component of PGA, PGV, PGD and 5% Damped Linear Elastic Response Spectra for Periods Ranging from 0.01 to 10 s. Earthq. Spectra 2008, 24, 139–171. [Google Scholar] [CrossRef]
- Wald, D.J.; Allen, T.I. Topographic Slope as a Proxy for Seismic Site Conditions and Amplification. Bull. Seismol. Soc. Am. 2007, 97, 1379–1395. [Google Scholar] [CrossRef]
- Bozorgnia, Y.; Abrahamson, N.A.; Al Atik, L.; Ancheta, T.D.; Atkinson, G.M.; Baker, J.W.; Baltay, A.; Booreg, D.M.; Campbell, K.W.; Chioui, B.S.J.; et al. NGA-West2 Research Project. Earthq. Spectra 2014, 30, 973–987. [Google Scholar] [CrossRef]
- Hudnut, K.; Aagaard, B.; Graves, R.; Jones, L.; Jordan, T.; Star, L.; Stewart, J. ShakeOut Earthquake Source Description, Surface Faulting and Ground Motions. US Geol. Surv. Open File Rep. 2008, 1150, 2008. [Google Scholar]
- Graves, R.W.; Aagaard, B.T.; Hudnut, K.W. The ShakeOut Earthquake Source and Ground Motion Simulations. Earthq. Spectra 2011, 27, 273–291. [Google Scholar] [CrossRef]
- Bielak, J.; Graves, R.W.; Olsen, K.B.; Taborda, R.; Ramírez-Guzmán, L.; Day, S.M.; Ely, G.P.; Roten, D.; Jordan, T.H.; Maechling, P.J.; et al. The ShakeOut earthquake scenario: Verification of three simulation sets. Geophys. J. Int. 2010, 180, 375–404. [Google Scholar] [CrossRef]
- Olsen, K.; Day, S.; Dalguer, L.; Mayhew, J.; Cui, Y.; Zhu, J.; Cruz-Atienza, V.; Roten, D.; Maechling, P.; Jordan, T.; et al. ShakeOut-D: Ground Motion Estimates Using an Ensemble of Large Earthquakes on the Southern San Andreas Fault with Spontaneous Rupture Propagation. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Krishnan, S.; Muto, M. Sensitivity of the Earthquake Response of Tall Steel Moment Frame Buildings to Ground Motion Features. J. Earthq. Eng. 2013, 17, 673–698. [Google Scholar] [CrossRef]
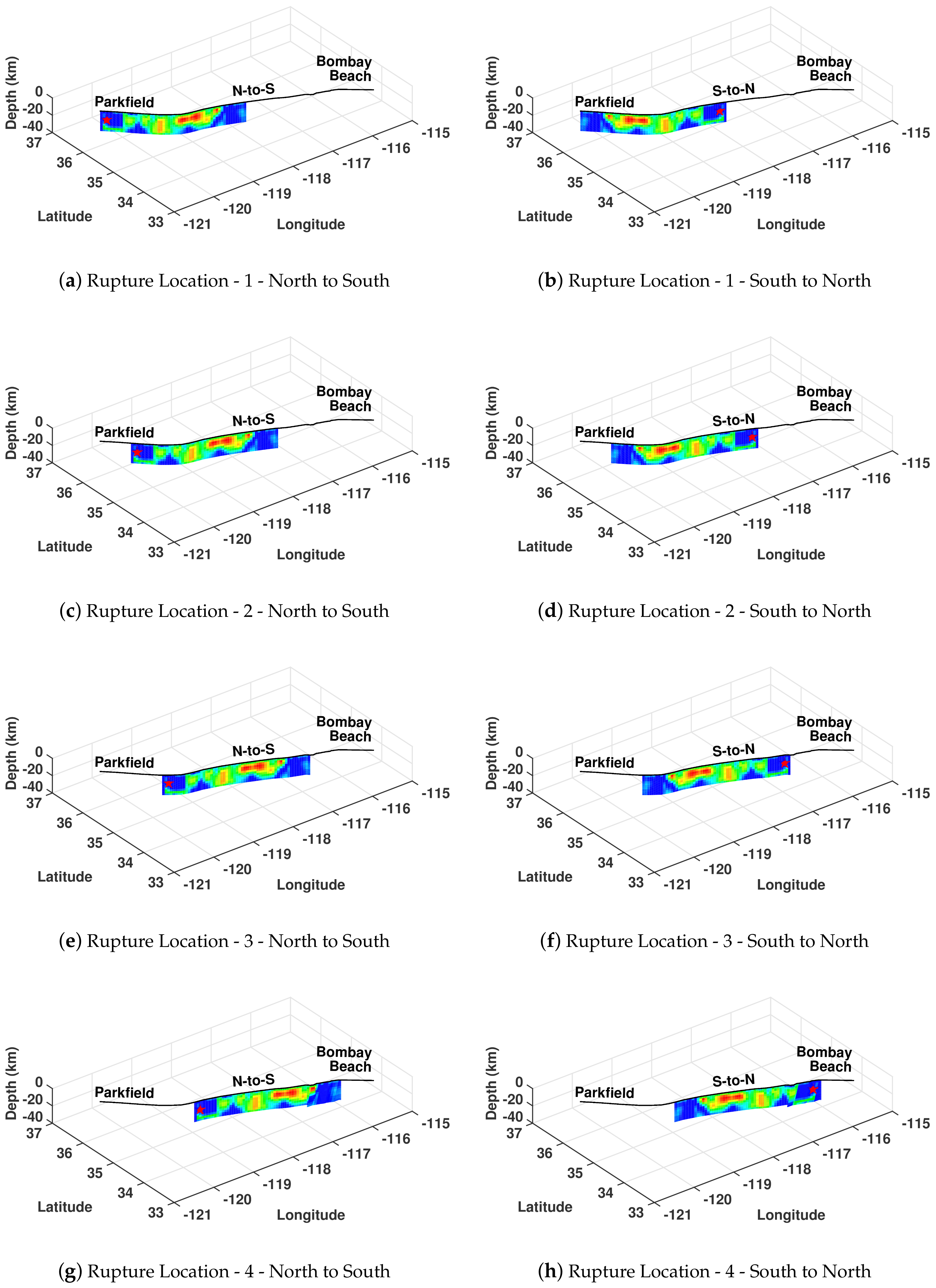
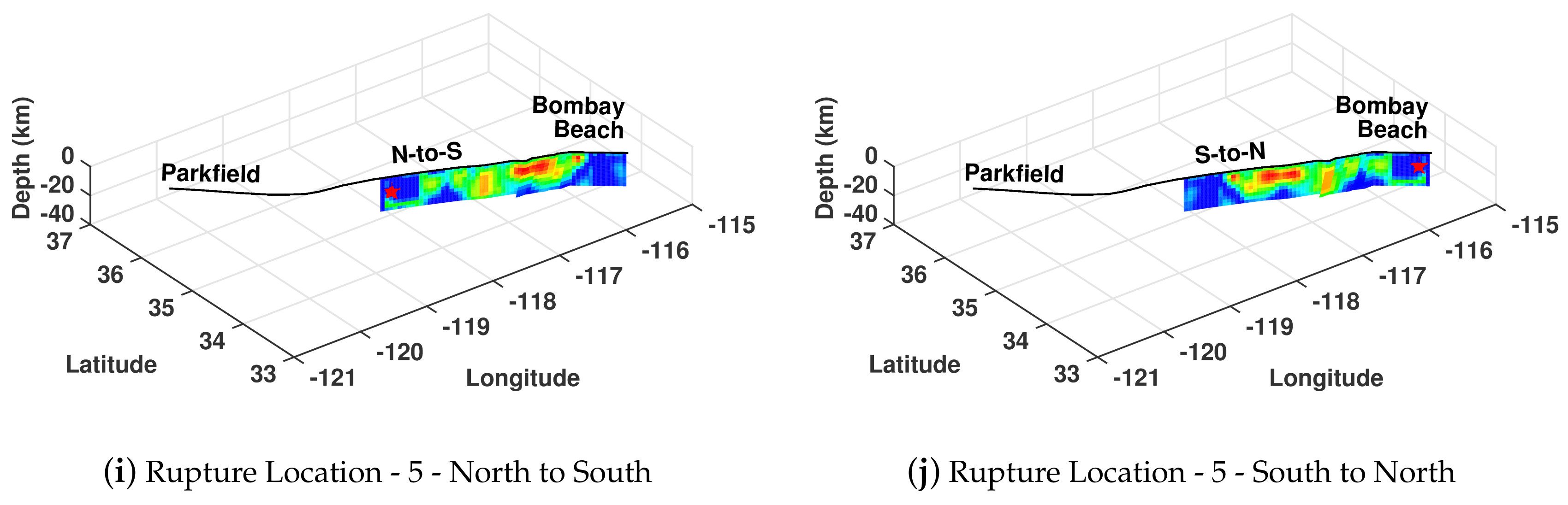
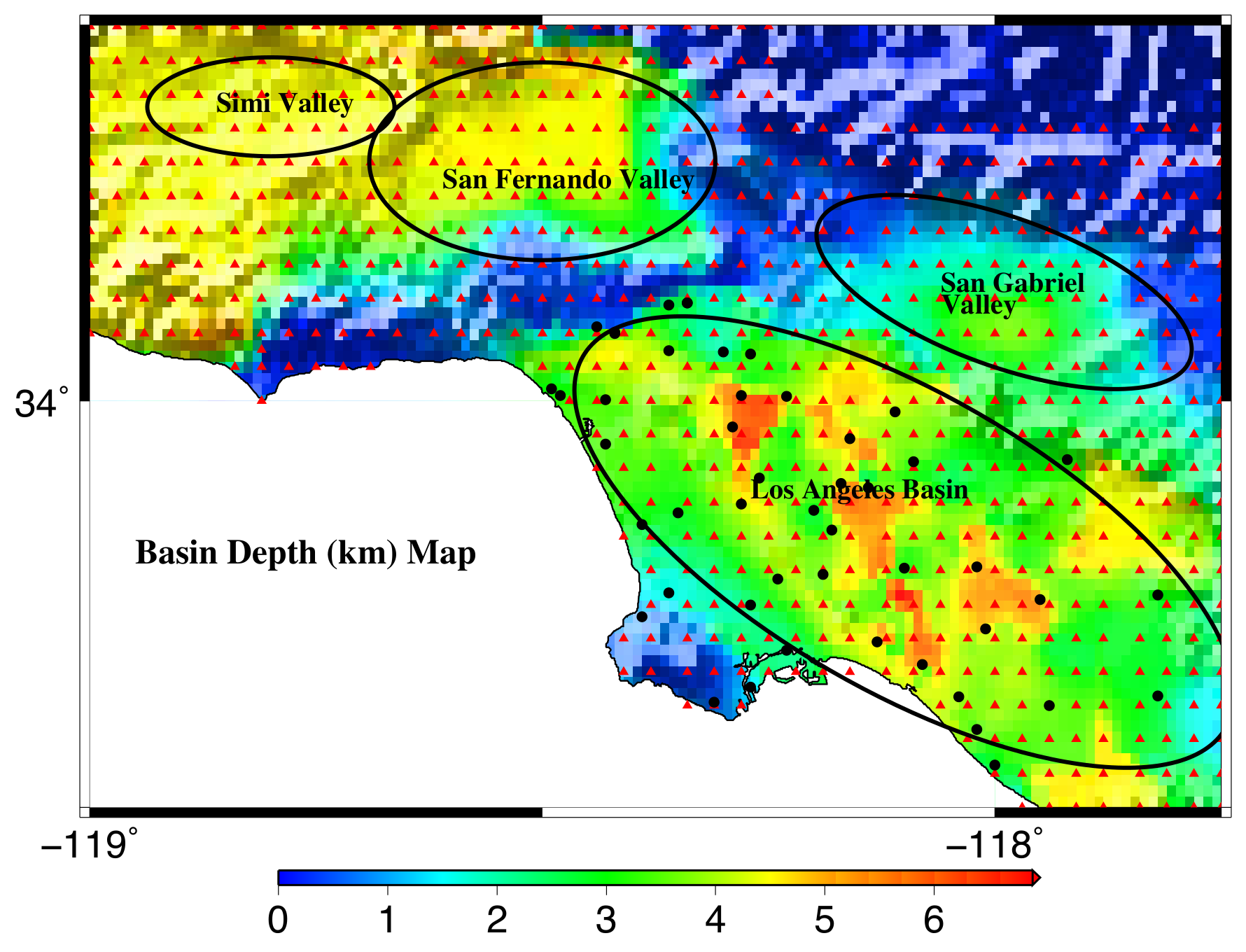
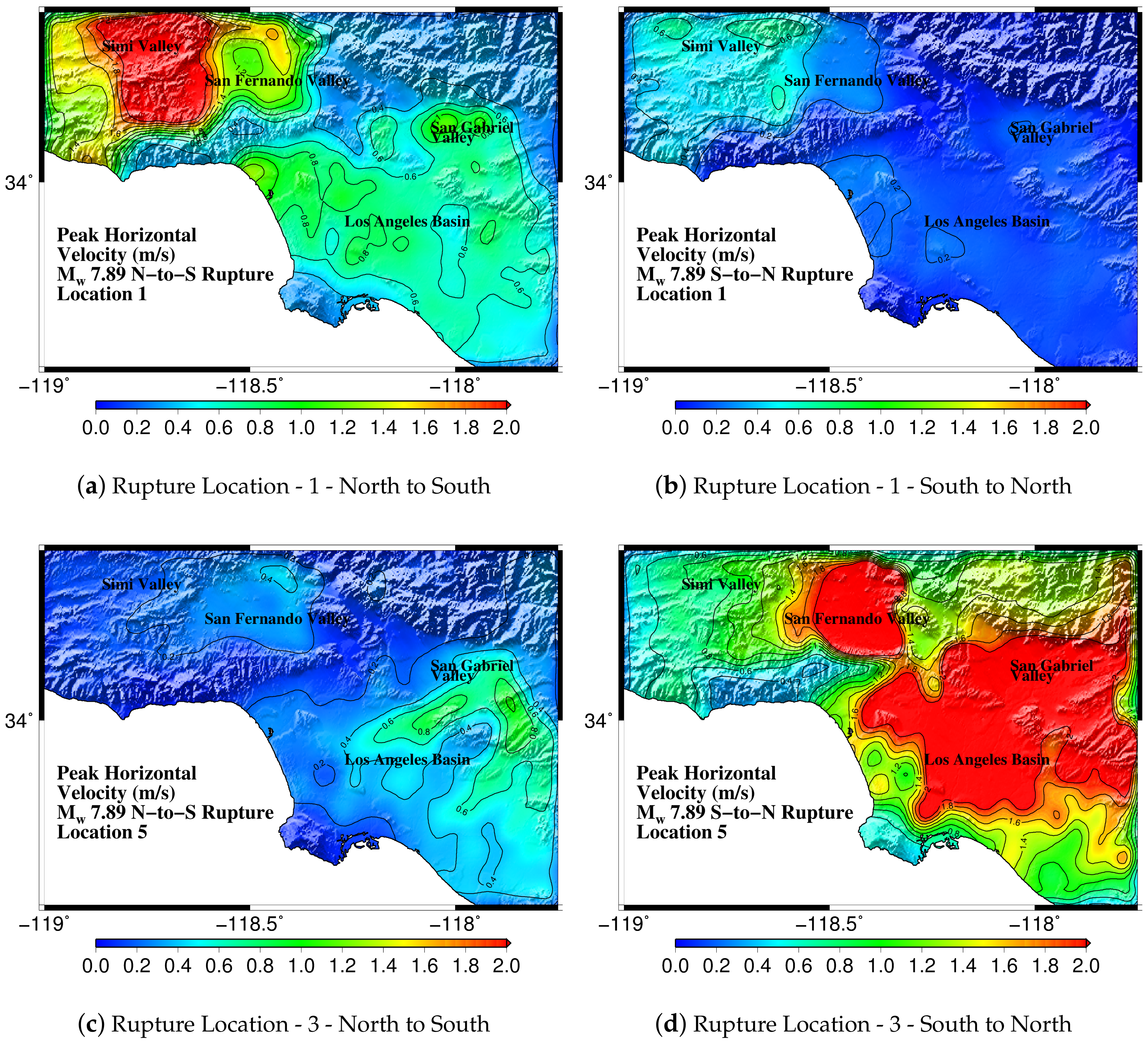
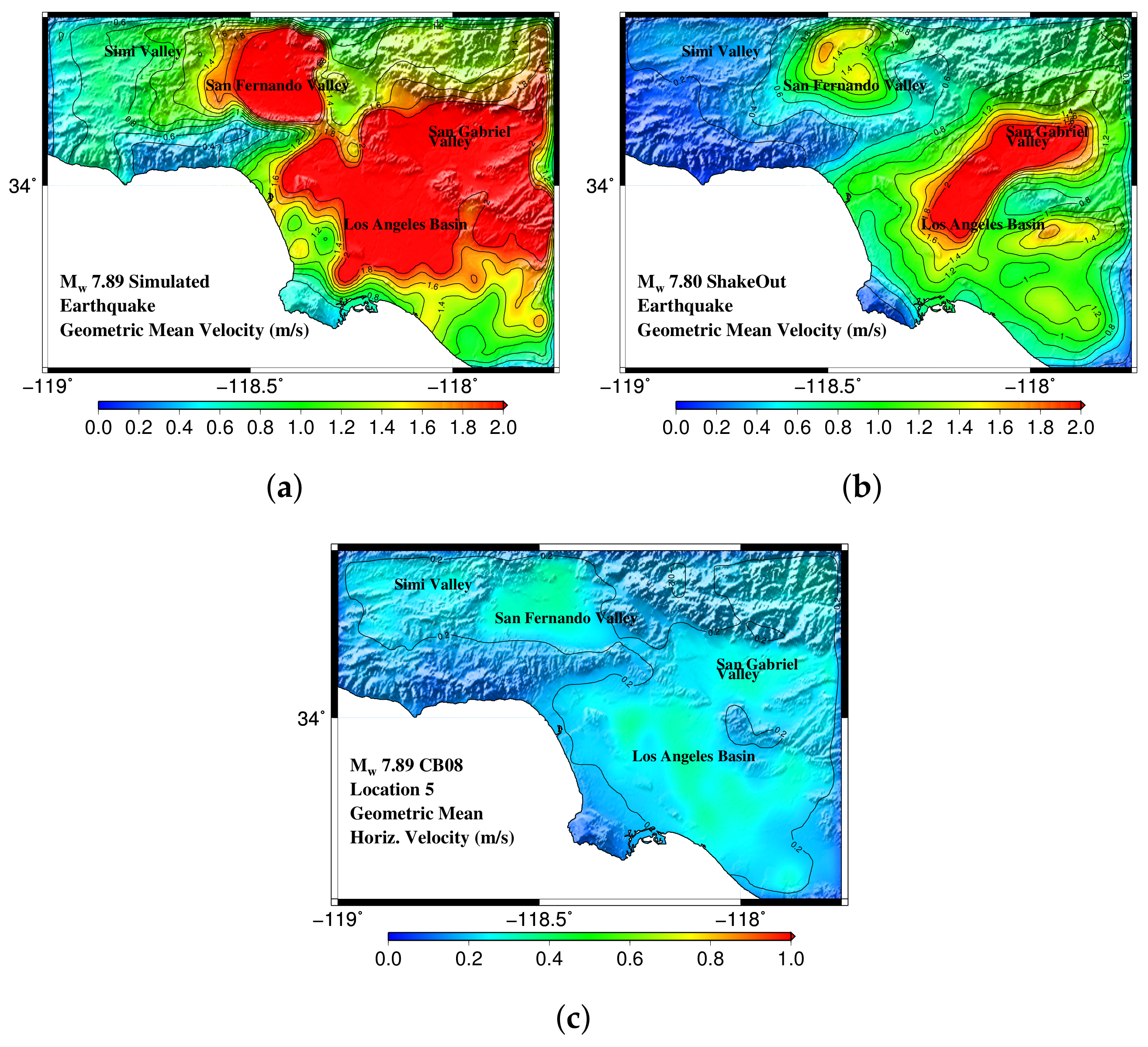
| Name | Date | Location | Length (km) | Depth (km) | Dip () | Rake () | Reference | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Denali | 2002 | AK, USA | 7.89 | 290.0 | 20.0 | 90.0 | 180.0 | [13] |
| 2 | Izmit | 1999 | Turkey | 7.59 | 155.0 | 18.0 | 90.0 | 180.0 | [14] |
| 3 | Landers | 1992 | CA, USA | 7.28 | 78.0 | 15.0 | 89.0 | 180.0 | [15] |
| 4 | Kobe | 1995 | Japan | 6.92 | 60.0 | 20.0 | 85.0 | 180.0 | [16] |
| 5 | Imperial Valley | 1979 | CA, USA | 6.58 | 42.0 | 10.4 | 90.0 | 180.0 | [17] |
| 6 | Parkfield | 2004 | CA, USA | 6.00 | 40.0 | 14.5 | 83.0 | 180.9 | [18] |
| [Bin] | Location 1 | Location 2 | Location 3 | Location 4 | Location 5 | Total Probability |
|---|---|---|---|---|---|---|
| (Parkfield) | (Bombay Beach) | (All Locations) | ||||
| 6.00 [5.90–6.42] | 0.6449 | 0.0459 | 0.1910 | 0.2485 | 0.0685 | 0.8081 |
| 6.58 (6.42–6.80] | 0.0051 | 0.0100 | 0.0854 | 0.1280 | 0.0183 | 0.2288 |
| 6.92 (6.80–7.15] | 0.0180 | 0.0171 | 0.0060 | 0.0764 | 0.0271 | 0.1380 |
| 7.28 (7.15–7.45] | 0.0211 | 0.0182 | 0.0059 | 0.0153 | 0.0365 | 0.0935 |
| 7.59 (7.47–7.78] | 0.0124 | 0.0121 | 0.0061 | 0.0082 | 0.0192 | 0.0568 |
| 7.89 (7.78–8.34] | 0.0339 | 0.0281 | 0.0236 | 0.0225 | 0.0215 | 0.1231 |
| Total Probability | ||||||
| [5.90–8.34] | 0.6760 | 0.1249 | 0.2904 | 0.4221 | 0.1773 | 0.8553 |
| Site Location | Latitude | Longitude | Simulated | CB-08 | Soil Type | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PGV (m/s) | PGD (m) | (g) | (g) | PGV (m/s) | PGD (m) | (g) | (g) | UBC | UBC | |||||||
| 94 | 97 | |||||||||||||||
| Irvine | 33.67 | 117.80 | 0.46 | 0.35 | 0.56 | 0.29 | 0.21 | 0.17 | 0.15 | 0.18 | 0.21 | 1.18 | 0.17 | 0.08 | ||
| Encino | 34.16 | 118.50 | 0.30 | 0.46 | 0.43 | 0.24 | 0.12 | 0.19 | 0.13 | 0.27 | 0.19 | 0.89 | 0.14 | 0.06 | ||
| Downtown LA | 34.05 | 118.25 | 0.79 | 0.75 | 0.79 | 0.60 | 0.26 | 0.15 | 0.38 | 0.43 | 0.28 | 1.70 | 0.23 | 0.10 | ||
| Canoga Park | 34.20 | 118.60 | 0.94 | 0.53 | 0.70 | 0.41 | 0.38 | 0.24 | 0.30 | 0.37 | 0.18 | 0.87 | 0.14 | 0.06 | ||
| Pasadena | 34.16 | 118.13 | 0.13 | 0.09 | 0.20 | 0.13 | 0.04 | 0.10 | 0.01 | 0.03 | 0.15 | 0.77 | 0.12 | 0.05 | ||
| Anaheim | 33.84 | 117.89 | 0.73 | 0.61 | 0.70 | 0.48 | 0.26 | 0.18 | 0.42 | 0.41 | 0.22 | 1.16 | 0.17 | 0.07 | ||
| Long Beach | 33.77 | 118.19 | 0.26 | 0.21 | 0.33 | 0.27 | 0.14 | 0.10 | 0.08 | 0.09 | 0.23 | 1.38 | 0.19 | 0.09 | ||
| Glendale | 34.17 | 118.25 | 0.26 | 0.33 | 0.40 | 0.30 | 0.15 | 0.09 | 0.08 | 0.15 | 0.20 | 0.93 | 0.15 | 0.06 | ||
| Hollywood | 34.10 | 119.33 | 0.31 | 0.41 | 0.49 | 0.27 | 0.16 | 0.12 | 0.19 | 0.29 | 0.18 | 0.85 | 0.14 | 0.06 | ||
| El Segundo | 33.92 | 118.41 | 0.63 | 0.39 | 0.60 | 0.29 | 0.18 | 0.13 | 0.22 | 0.19 | 0.20 | 1.09 | 0.16 | 0.07 | ||
| Santa Monica | 34.02 | 118.48 | 0.66 | 0.32 | 0.68 | 0.30 | 0.17 | 0.10 | 0.16 | 0.12 | 0.19 | 0.94 | 0.14 | 0.06 | ||
| Century City | 34.08 | 118.42 | 0.66 | 0.41 | 0.68 | 0.45 | 0.16 | 0.10 | 0.21 | 0.16 | 0.20 | 0.99 | 0.15 | 0.06 | ||
| Universal City | 34.14 | 118.35 | 0.27 | 0.13 | 0.38 | 0.19 | 0.06 | 0.05 | 0.06 | 0.06 | 0.14 | 0.54 | 0.10 | 0.04 | ||
| Park La Brea | 34.06 | 118.35 | 0.30 | 0.46 | 0.43 | 0.24 | 0.12 | 0.19 | 0.13 | 0.27 | 0.19 | 0.89 | 0.14 | 0.06 | ||
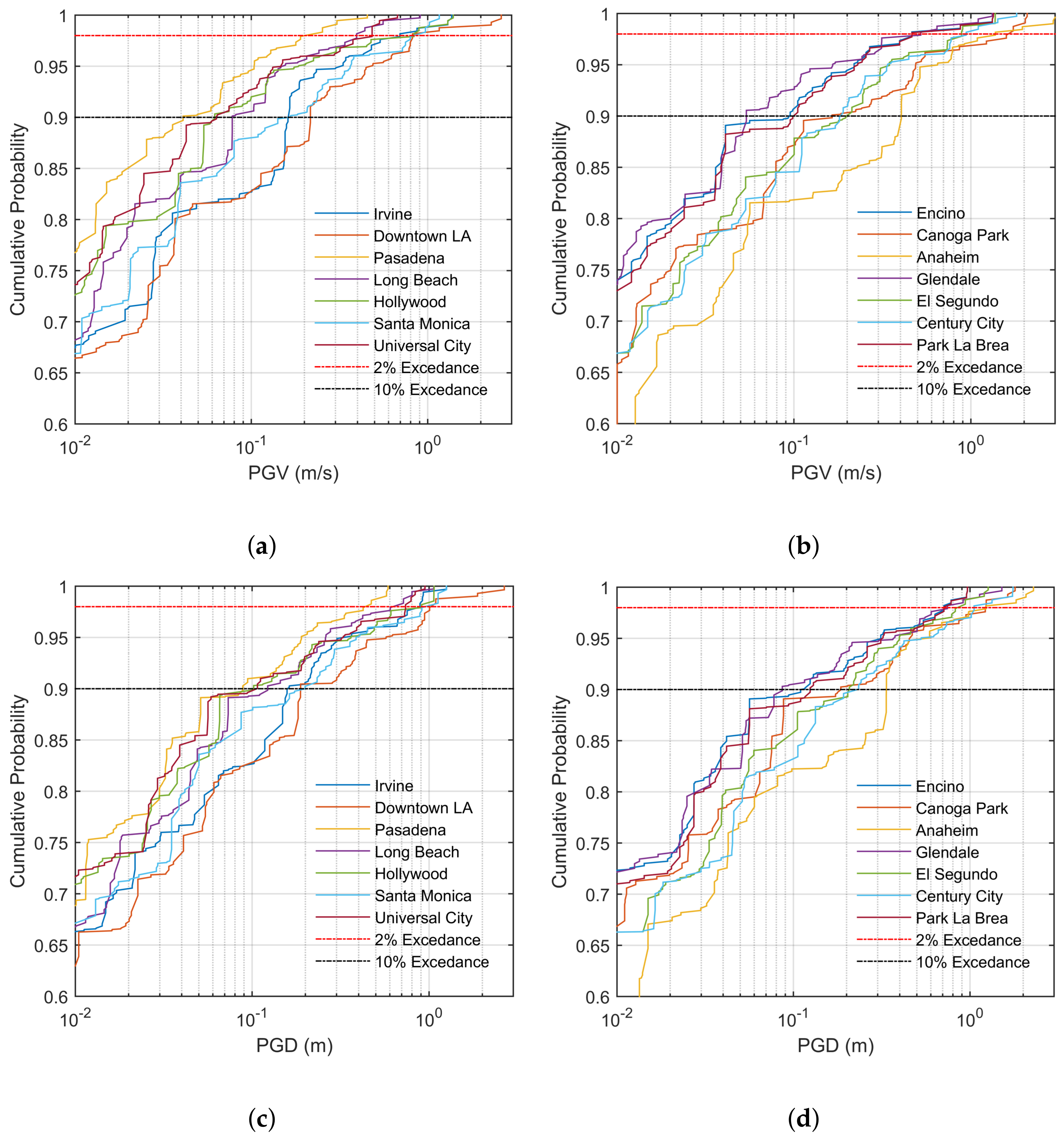
| Location | PGV (m/s) | PGD (m) | ||
|---|---|---|---|---|
| 10% | 2% | 10% | 2% | |
| Irvine | 0.16 | 0.70 | 0.16 | 0.89 |
| Encino | 0.09 | 0.46 | 0.11 | 0.71 |
| Downtown LA | 0.22 | 0.82 | 0.19 | 1.02 |
| Canoga Park | 0.16 | 1.63 | 0.19 | 1.22 |
| Pasadena | 0.04 | 0.20 | 0.09 | 0.44 |
| Anaheim | 0.40 | 1.38 | 0.34 | 1.23 |
| Long Beach | 0.08 | 0.40 | 0.12 | 0.63 |
| Glendale | 0.05 | 0.52 | 0.09 | 0.74 |
| Hollywood | 0.06 | 0.84 | 0.10 | 0.91 |
| El Segundo | 0.20 | 0.89 | 0.21 | 0.85 |
| Santa Monica | 0.16 | 0.83 | 0.20 | 0.95 |
| Century City | 0.18 | 0.94 | 0.23 | 1.05 |
| Universal City | 0.06 | 0.48 | 0.11 | 0.74 |
| Park La Brea | 0.09 | 0.46 | 0.11 | 0.71 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mourhatch, R.; Krishnan, S. Probabilistic Estimates of Ground Motion in the Los Angeles Basin from Scenario Earthquakes on the San Andreas Fault. Geosciences 2018, 8, 126. https://doi.org/10.3390/geosciences8040126
Mourhatch R, Krishnan S. Probabilistic Estimates of Ground Motion in the Los Angeles Basin from Scenario Earthquakes on the San Andreas Fault. Geosciences. 2018; 8(4):126. https://doi.org/10.3390/geosciences8040126
Chicago/Turabian StyleMourhatch, Ramses, and Swaminathan Krishnan. 2018. "Probabilistic Estimates of Ground Motion in the Los Angeles Basin from Scenario Earthquakes on the San Andreas Fault" Geosciences 8, no. 4: 126. https://doi.org/10.3390/geosciences8040126
APA StyleMourhatch, R., & Krishnan, S. (2018). Probabilistic Estimates of Ground Motion in the Los Angeles Basin from Scenario Earthquakes on the San Andreas Fault. Geosciences, 8(4), 126. https://doi.org/10.3390/geosciences8040126





