Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler
Abstract
1. Introduction
2. Materials and Methods
2.1. Marine Geomorphometry Algorithms
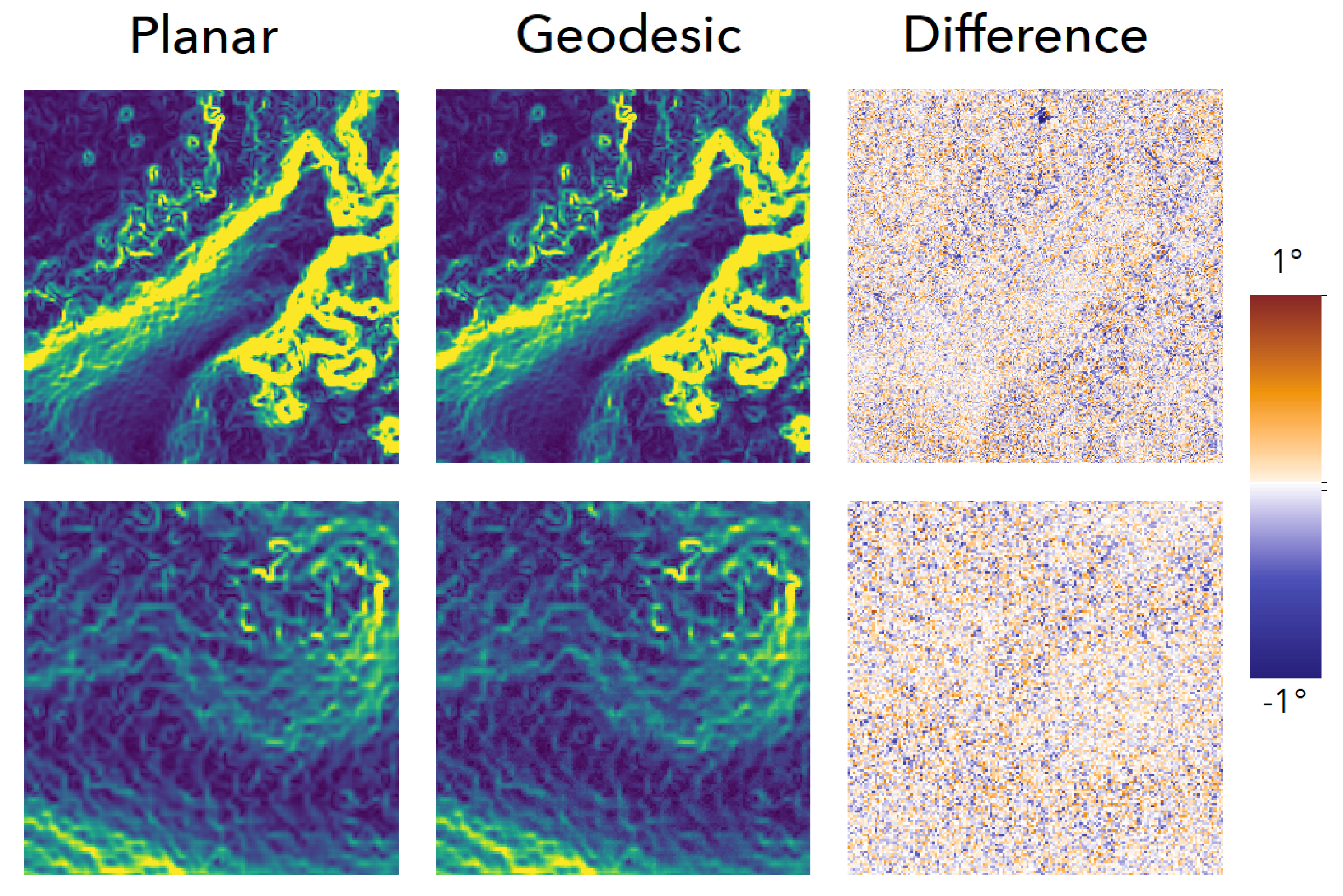
2.1.1. Surface Gradients
2.1.2. Curvature/Relative Position
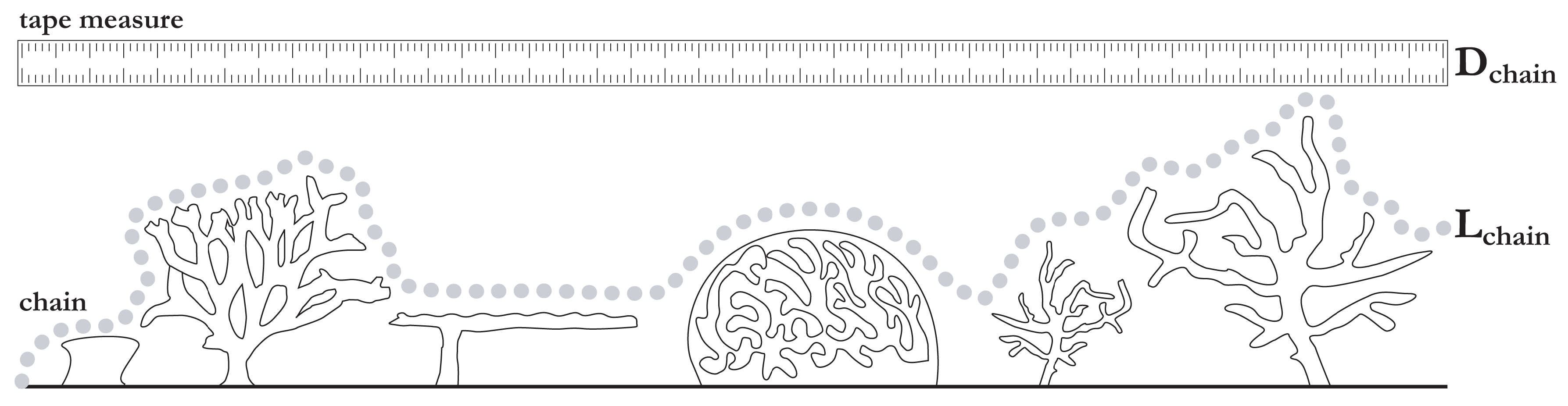
2.1.3. Rugosity/Surface Roughness
2.1.4. Distribution Moments
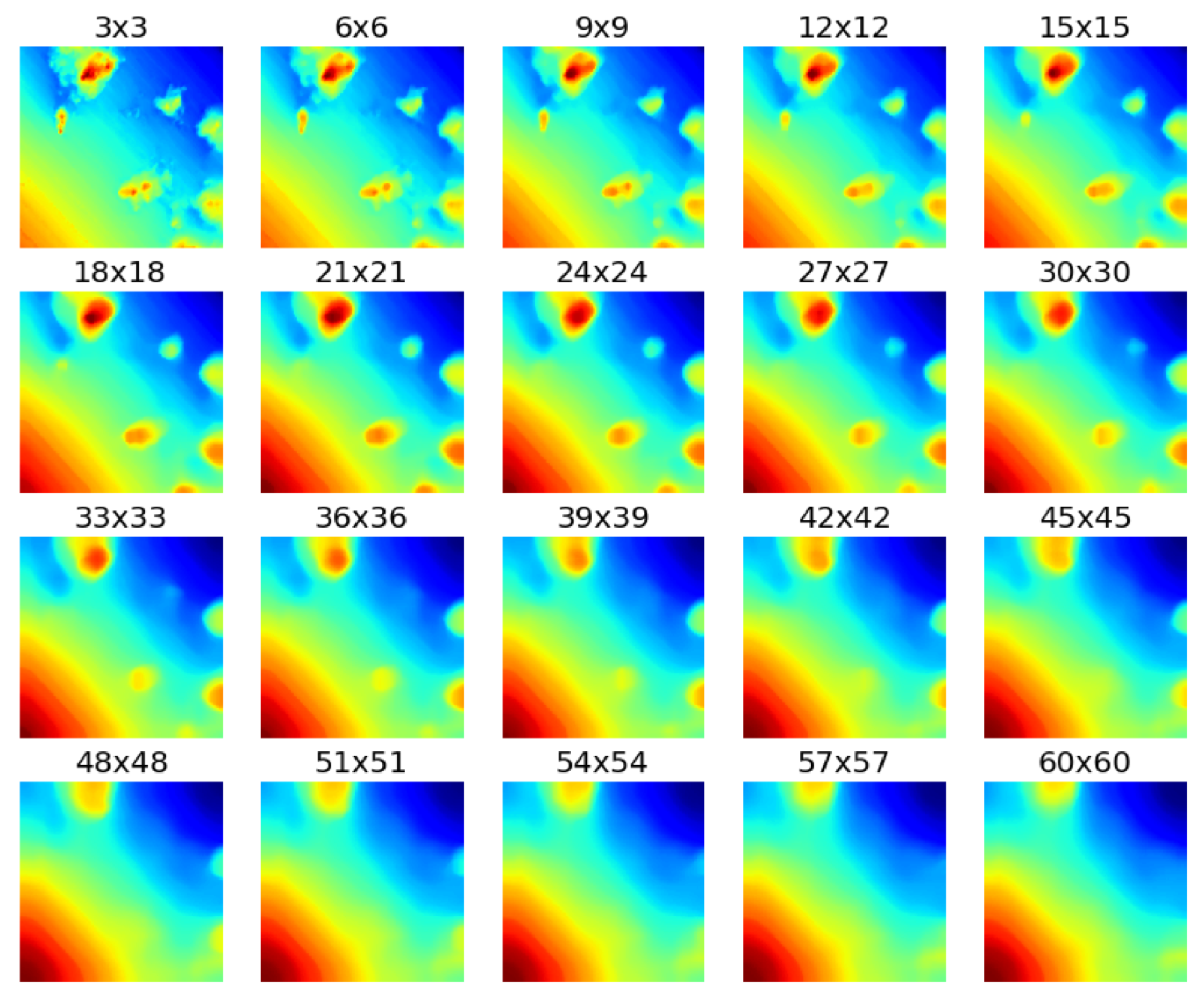
2.1.5. Multiscale Analysis
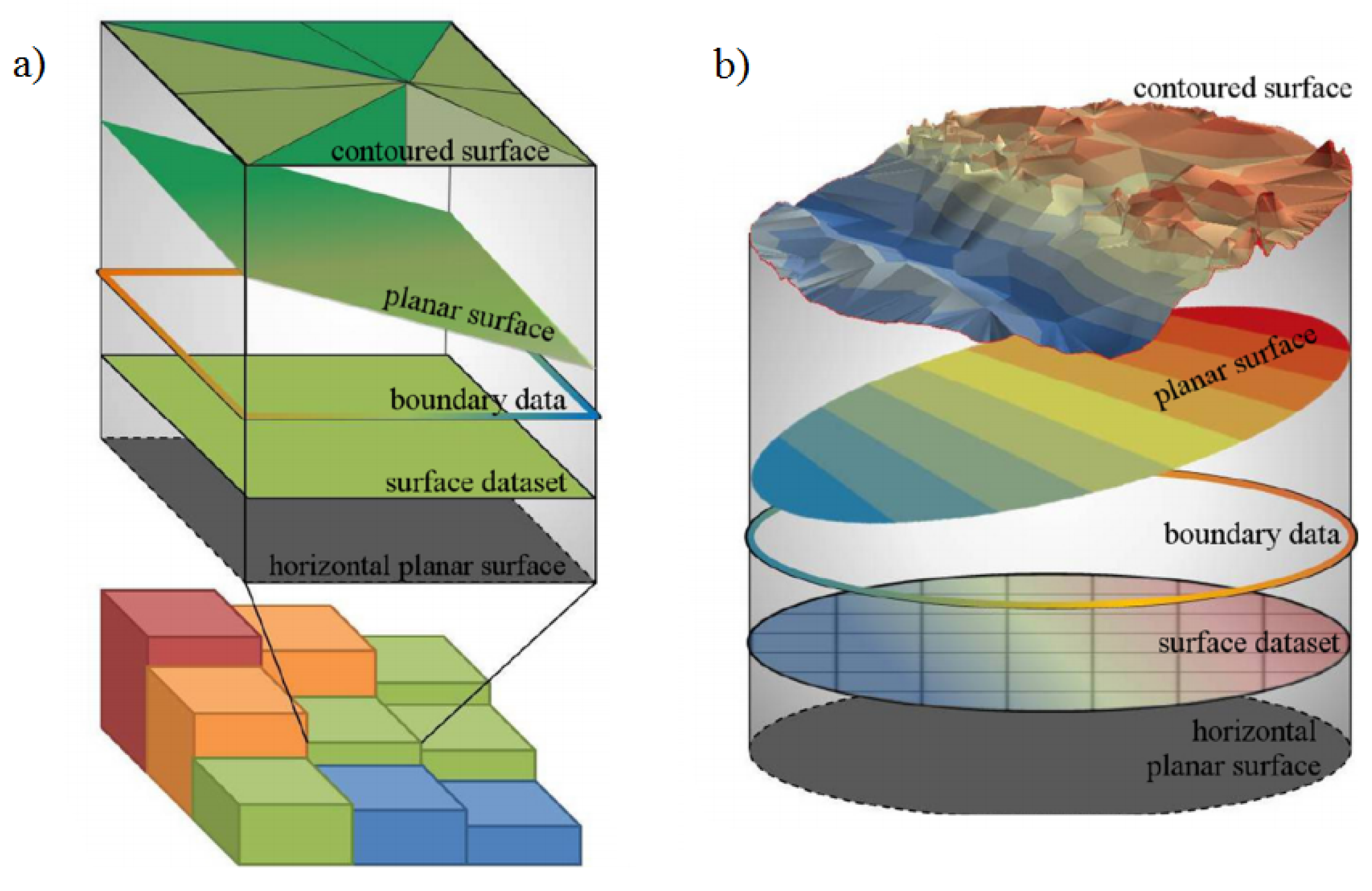
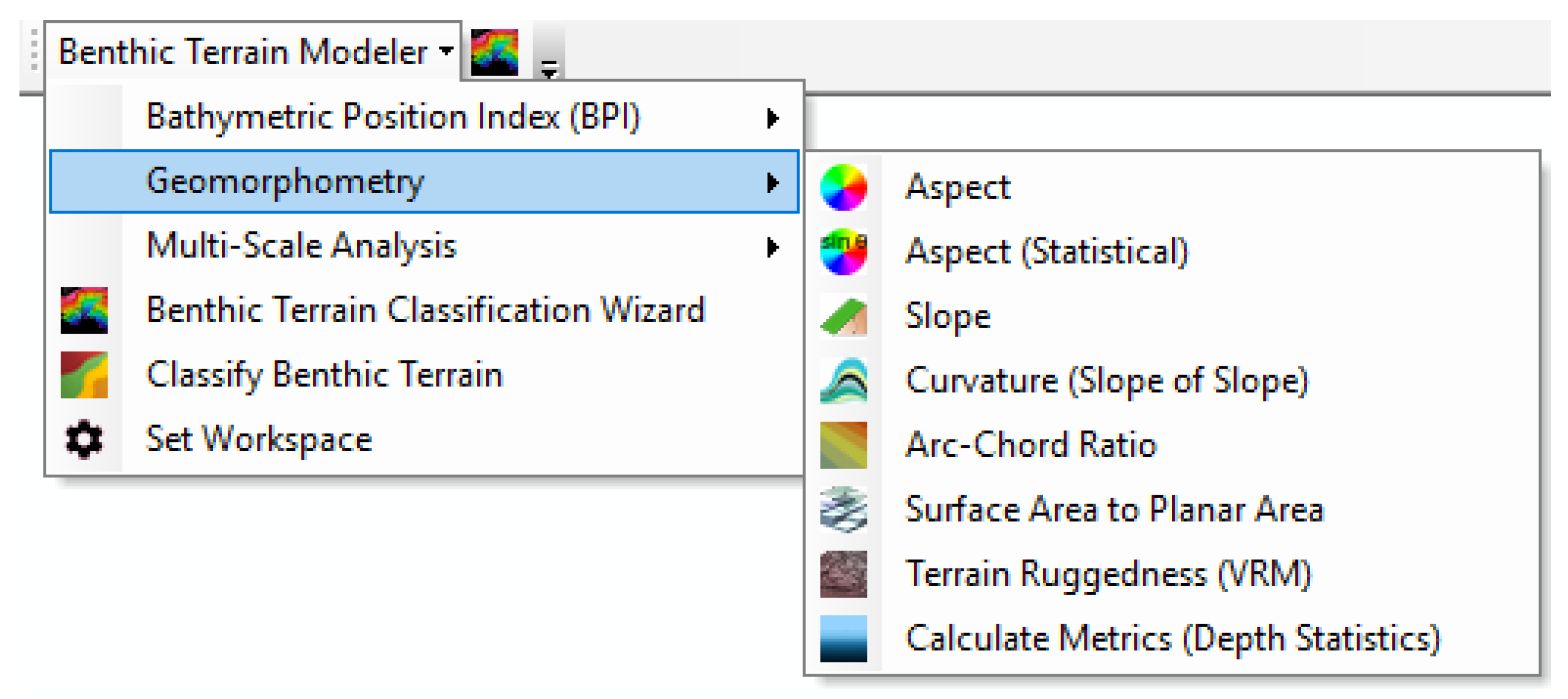
2.2. Software Architecture
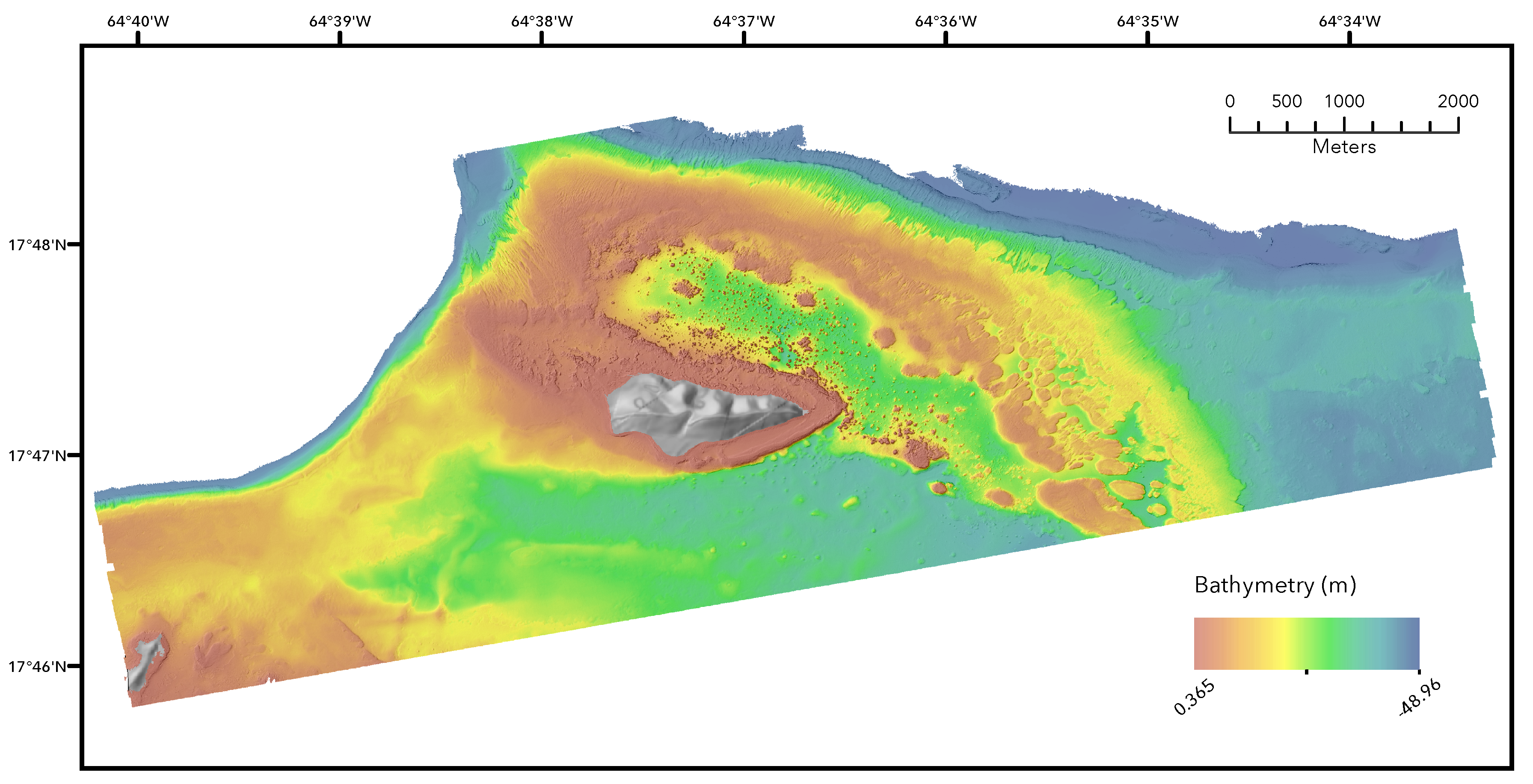
2.3. Example Study Site
3. Results
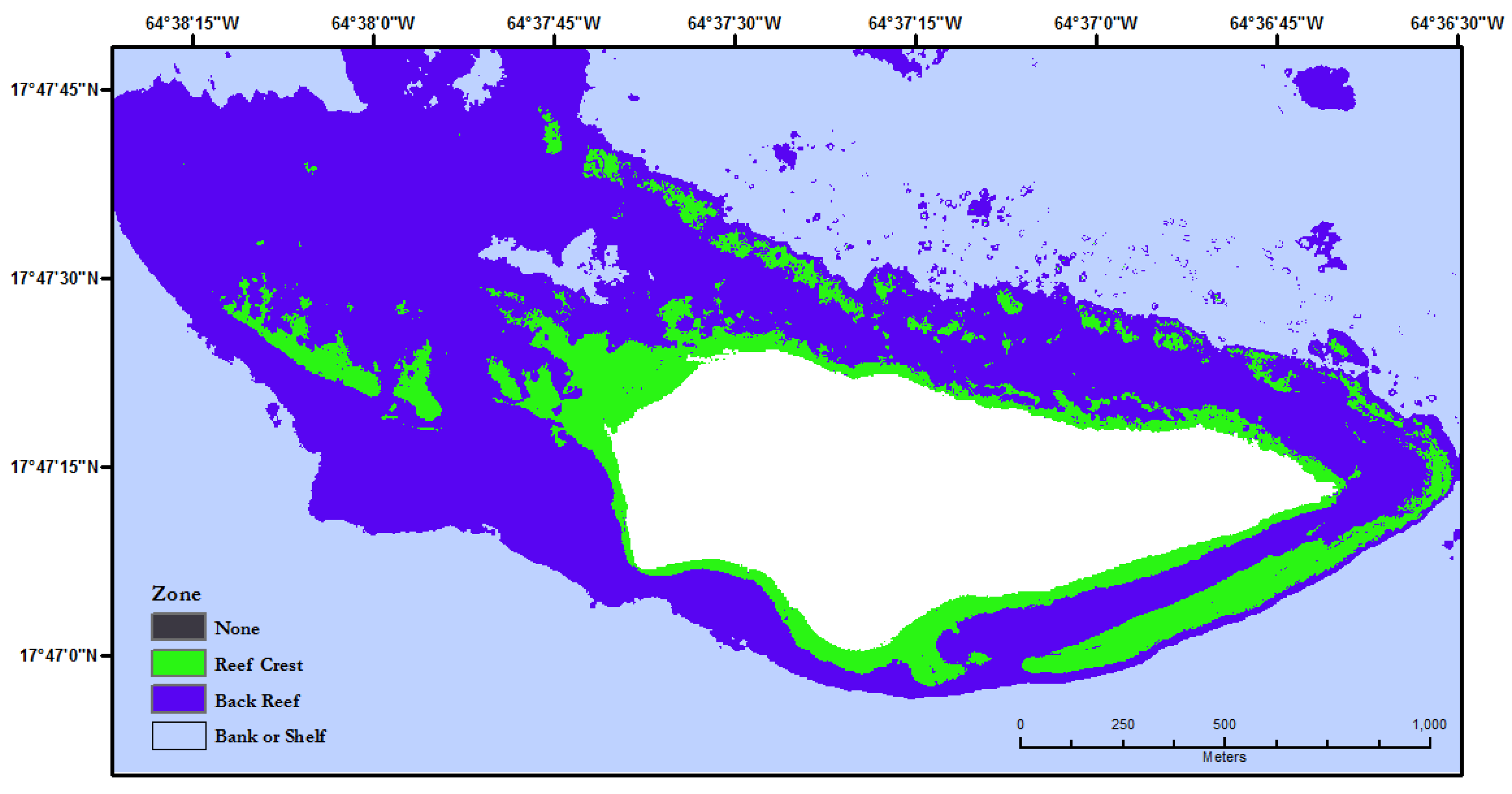
3.1. Classified Benthnic Zone Mapping
- Scale and resolution of the input data
- Scale of focal operations used to calculate BPI and slope
- Previous studies of the area of interest
- Typical values observed for the benthic zone of interest
- The range of values in each classification artifact
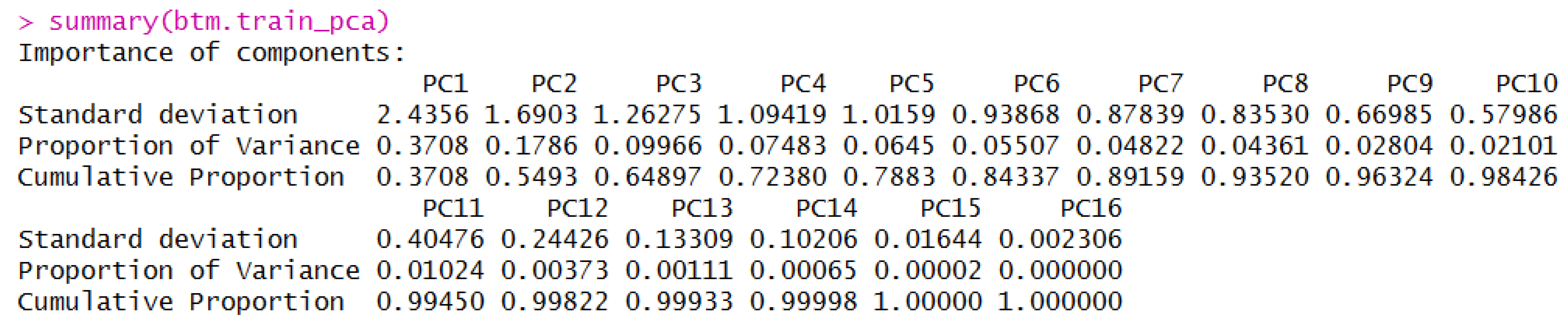
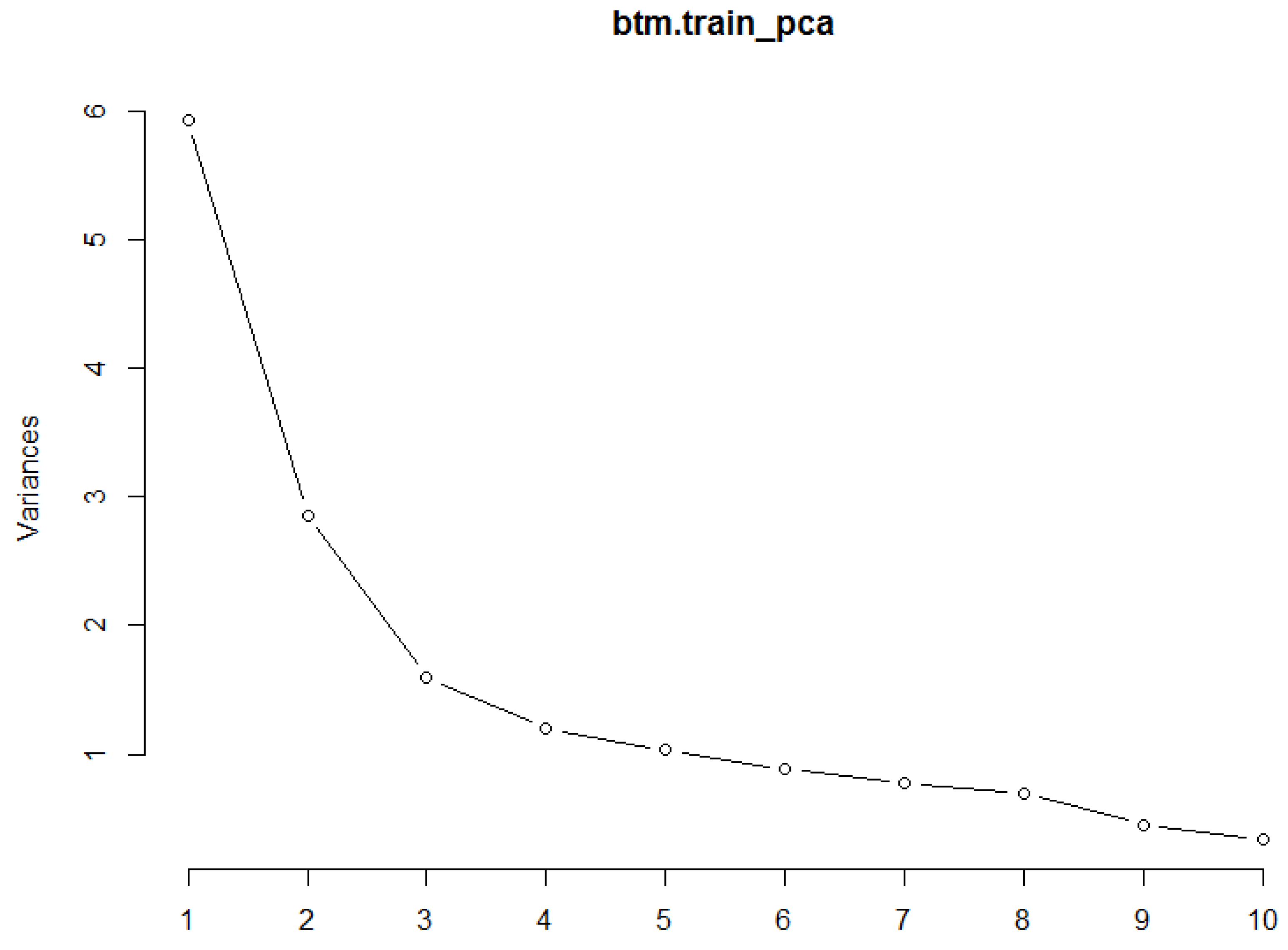
3.2. Integrating R Statistical Analysis
# Load library containing R-ArcGIS bridge functionality library(arcgisbinding) # Check connection between R and ArcGIS has been established arc.check_product() input_gdb <- “C:/ArcGIS/Projects/BTM/BTM.gdb” feature_class <- “Field_AAData_ClassifiedLocations” # Establish pointer to desired data’s stored location arc_locations <- arc.open(file.path(input_gdb, feature_class)) # Convert from an ArcGIS data type to an R data frame object df_locations <- arc.select(arc_locations) # Convert from an R data frame object to a spatial data frame object # from the R package sp spdf_locations <- arc.data2sp(df_locations) |
# Remove NAs df_locations <- na.omit(df_locations) # Creation of training/testing datasets smp_size <- floor(0.80 * nrow(df_locations)) # Randomly select observation numbers to ensure sample is randomly selected train_ind <- sample(seq_len(nrow(df_locations)), size = smp_size) # Subset the original data based on the randomly selected observation # numbers to make the training data set df_locations_train <- df_locations[train_ind, ] # Subset the original data on the remaining observations to make the # testing data set df_locations_test <- df_locations[-train_ind, ] # Make predictor variable into a factor df_locations_train$D_STRUCT <- as.factor(df_locations_train$D_STRUCT) # Separate response from the covariates btm.train_covariates <- df_locations_train[, 2:17] btm.train_response <- df_locations_train[, 1] # Apply Principal Component Analysis btm.train_pca <- prcomp(btm.train_covariates, center = TRUE, scale. = TRUE) |
3.3. Terrain Attribute Relationships
3.3.1. Slope
3.3.2. Covariate Selection
3.3.3. Remarks
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AOI | Area of interest |
| BIRNM | Buck Island Reef National Monument |
| BPI | Bathymetric Position Index |
| BTM | Benthic Terrain Modeler |
| DTM | Digital terrain model |
| GIS | Geographic information system |
| IQR | Interquartile range |
| LiDAR | Light Detection and Ranging |
| MBES | Multibeam Ecosounder |
| NOAA | National Oceanic and Atmospheric Administration |
| POBF | Plane of best fit |
| SAPA | Surface area to planar area |
| TIN | Triangulated irregular network |
| VRM | Vector ruggedness measure |
Appendix A.
Appendix A.1. Derived Parameters
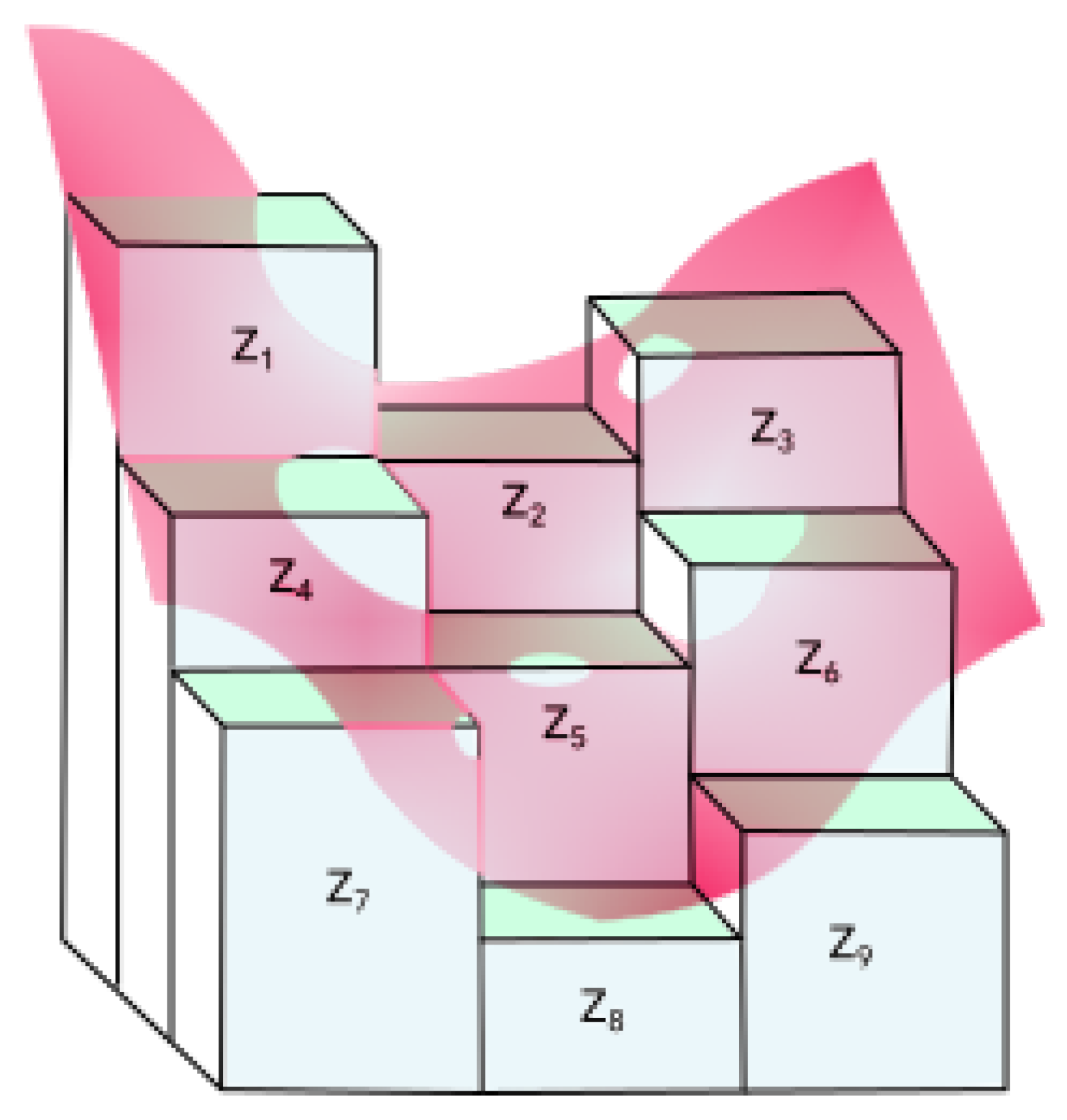
- k denotes the position of the current raster cell;
- Z is the value of the cell;
- i and j are the two rasters being compared;
- is the mean of the raster;
- N is the total number of cells.
| Layer | Environmental Covariate |
|---|---|
| 1 | Aspect easterness |
| 2 | Aspect northerness |
| 3 | Broad scale BPI standardized (60–80) |
| 4 | Fine scale BPI standardized (10–15) |
| 5 | Interquartile range (IQR) |
| 6 | Bathymetry (LiDAR) |
| 7 | Kurtosis (Pearson) |
| 8 | Mean |
| 9 | Relative difference to mean |
| 10 | Standard deviation |
| 11 | Reflectance (LiDAR) |
| 12 | Slope (planar) |
| 13 | Slope of the slope (max in slope) |
| 14 | Rugosity (ACR) |
| 15 | Rugosity (SAPA) |
| 16 | Rugosity (VRM) |
| Layer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.001505 | −0.000064 | −0.000070 | −0.000074 | −0.001187 | −0.000116 | −0.001187 | −0.000151 | −0.000113 | 0.000753 | −0.000293 | −0.001150 | −0.000004 | −0.000014 | −0.000005 | |
| 2 | −0.02035 | −0.000174 | −0.000018 | 0.000274 | −0.005216 | −0.000269 | −0.005231 | 0.000012 | 0.000360 | 0.002170 | 0.000938 | 0.003334 | 0.000013 | 0.000045 | 0.000013 | |
| 3 | −0.00781 | −0.02005 | 0.000123 | 0.000072 | 0.000495 | −0.000025 | 0.000460 | 0.000110 | 0.000102 | −0.000443 | 0.000236 | 0.000704 | 0.000010 | 0.000036 | 0.000022 | |
| 4 | −0.01952 | −0.00471 | 0.29382 | 0.000070 | −0.000161 | −0.000008 | −0.000159 | 0.000063 | 0.000099 | −0.000181 | 0.000223 | 0.000489 | 0.000016 | 0.000040 | 0.000031 | |
| 5 | −0.02094 | 0.0727 | 0.17456 | 0.38188 | −0.000080 | −0.000094 | −0.000078 | 0.000012 | 0.000235 | −0.000157 | 0.000551 | 0.001311 | 0.000020 | 0.000083 | 0.000033 | |
| 6 | −0.0371 | −0.15321 | 0.13208 | −0.09758 | −0.04917 | −0.000071 | 0.014664 | −0.000356 | −0.000091 | −0.005869 | −0.000263 | −0.001478 | −0.000001 | 0.000015 | 0.000014 | |
| 7 | −0.01123 | −0.02448 | −0.02069 | −0.0156 | −0.17901 | −0.01488 | −0.000068 | −0.000030 | −0.000077 | −0.000073 | −0.000219 | 0.000277 | 0.000003 | −0.000013 | 0.000002 | |
| 8 | −0.03705 | −0.15354 | 0.12279 | −0.09619 | −0.0476 | 0.99459 | −0.0142 | −0.000357 | −0.000091 | −0.005891 | −0.000261 | −0.001482 | −0.000001 | 0.000015 | 0.000014 | |
| 9 | −0.01078 | 0.00082 | 0.06726 | 0.0872 | 0.01686 | −0.05514 | −0.01445 | −0.05526 | 0.000016 | −0.000172 | 0.000040 | −0.000146 | 0.000002 | 0.000005 | 0.000004 | |
| 10 | −0.02384 | 0.07124 | 0.18349 | 0.40352 | 0.96982 | −0.0415 | −0.10875 | −0.04173 | 0.01651 | −0.000540 | −0.002241 | −0.000031 | −0.000086 | −0.000055 | 0.000048 | |
| 11 | 0.03378 | 0.0915 | −0.16976 | −0.15727 | −0.13822 | −0.57182 | −0.02204 | −0.57346 | −0.0384 | −0.15457 | −0.000540 | −0.002241 | −0.000031 | −0.000086 | −0.000055 | |
| 12 | −0.02606 | 0.0785 | 0.17926 | 0.38571 | 0.96182 | −0.05086 | −0.1308 | −0.0505 | 0.01777 | 0.99042 | −0.14996 | 0.004609 | 0.000066 | 0.000245 | 0.000106 | |
| 13 | −0.02568 | 0.06997 | 0.13414 | 0.21164 | 0.57397 | −0.07169 | 0.04158 | −0.0718 | −0.0162 | 0.61259 | −0.15597 | 0.63653 | 0.000182 | 0.000415 | 0.000301 | |
| 14 | −0.0055 | 0.01546 | 0.10146 | 0.38474 | 0.48963 | −0.00152 | 0.02906 | −0.00171 | 0.00986 | 0.54408 | −0.11896 | 0.50955 | 0.35024 | 0.000012 | 0.000013 | |
| 15 | −0.00734 | 0.02177 | 0.16034 | 0.40183 | 0.83457 | 0.01642 | −0.04372 | 0.01634 | 0.01338 | 0.85408 | −0.13833 | 0.78137 | 0.33215 | 0.54067 | 0.000020 | |
| 16 | −0.00395 | 0.0102 | 0.15266 | 0.48178 | 0.51791 | 0.02527 | 0.0124 | 0.02513 | 0.01487 | 0.5628 | −0.13889 | 0.52841 | 0.37625 | 0.89434 | 0.5639 |
References
- Halpern, B.S.; Walbridge, S.; Selkoe, K.A.; Kappel, C.V.; Micheli, F.; D’Agrosa, C.; Bruno, J.F.; Casey, K.S.; Ebert, C.; Fox, H.E.; et al. A global map of human impact on marine ecosystems. Science 2008, 319, 948–952. [Google Scholar] [CrossRef] [PubMed]
- Wright, D.J.; Heyman, W.D. Introduction to the Special Issue: Marine and Coastal GIS for Geomorphology, Habitat Mapping, and Marine Reserves. Mar. Geodesy 2008, 31, 1–8. [Google Scholar] [CrossRef]
- Becker, J.J.; Sandwell, D.T.; Smith, W.H.; Braud, J.; Binder, B.; Depner, J.; Fabre, D.; Factor, J.; Ingalls, S.; Kim, S.H.; et al. Global Bathymetry and Elevation Data at 30 Arc Seconds Resolution: SRTM30_PLUS. Mar. Geodesy 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Sayre, R.; Wright, D.; Aniello, P.; Breyer, S.; Cribbs, D.; Frye, C.; Vaughan, R.; Van Esch, B.; Stephens, D.; Harris, P.; et al. Mapping EMUs (Ecological Marine Units)–the creation of a global GIS of distinct marine environments to support marine spatial planning, management and conservation. In Proceedings of the Fifteenth International Symposium of Marine Geological and Biological Habitat Mapping (GEOHAB 2015), Bahia, Brazil, 1–8 May 2015; p. 21. [Google Scholar]
- Pittman, S.J. Seascape Ecology; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Brock, J.C.; Wright, C.W.; Clayton, T.D.; Nayegandhi, A. LIDAR optical rugosity of coral reefs in Biscayne National Park, Florida. Coral Reefs 2004, 23, 48–59. [Google Scholar] [CrossRef]
- García-Alegre, A.; Sánchez, F.; Gómez-Ballesteros, M.; Hinz, H.; Serrano, A.; Parra, S. Modelling and mapping the local distribution of representative species on the Le Danois Bank, El Cachucho Marine Protected Area (Cantabrian Sea). In Deep-Sea Research Part II: Topical Studies in Oceanography; Elsevier: Amsterdam, The Netherlands, 2014; Volume 106, pp. 151–164. [Google Scholar]
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar. Coast. Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Bishop, M.P.; James, L.A.; Shroder, J.F.; Walsh, S.J. Geospatial technologies and digital geomorphological mapping: Concepts, issues and research. Geomorphology 2012, 137, 5–26. [Google Scholar] [CrossRef]
- Passalacqua, P.; Belmont, P.; Staley, D.M.; Simley, J.D.; Arrowsmith, J.R.; Bode, C.A.; Crosby, C.; DeLong, S.B.; Glenn, N.F.; Kelly, S.A.; et al. Analyzing high resolution topography for advancing the understanding of mass and energy transfer through landscapes: A review. Earth-Sci. Rev. 2015, 148, 174–193. [Google Scholar] [CrossRef]
- Lecours, V.; Dolan, M.F.; Micallef, A.; Lucieer, V.L. A review of marine geomorphometry, the quantitative study of the seafloor. Hydrol. Earth Syst. Sci. 2016, 20, 3207–3244. [Google Scholar] [CrossRef]
- Lundblad, E.R.; Wright, D.J.; Miller, J.; Larkin, E.M.; Rinehart, R.; Naar, D.F.; Donahue, B.T.; Anderson, S.M.; Battista, T. A Benthic Terrain Classification Scheme for American Samoa. Mar. Geodesy 2006, 29, 89–111. [Google Scholar] [CrossRef]
- Wright, D.; Pendleton, M.; Boulware, J.; Walbridge, S.; Gerlt, B.; Eslinger, D.; Sampson, D.; Huntley, E. ArcGIS Benthic Terrain Modeler (BTM), v. 3.0, Environmental Systems Research Institute, NOAA Coastal Services Center, Massachusetts Office of Coastal Zone Management. Available online: https://esriurl.com/5754 (accessed on 27 February 2018).
- Young, M.; Ierodiaconou, D.; Womersley, T. Forests of the sea: Predictive habitat modelling to assess the abundance of canopy forming kelp forests on temperate reefs. Remote Sens. Environ. 2015, 170, 178–187. [Google Scholar] [CrossRef]
- Dunn, D.; Halpin, P. Rugosity-based regional modeling of hard-bottom habitat. Mar. Ecol. Prog. Ser. 2009, 377, 1–11. [Google Scholar] [CrossRef]
- Verfaillie, E.; Degraer, S.; Schelfaut, K.; Willems, W.; Van Lancker, V. A protocol for classifying ecologically relevant marine zones, a statistical approach. Estuar. Coast. Shelf Sci. 2009, 83, 175–185. [Google Scholar] [CrossRef]
- Diesing, M.; Coggan, R.; Vanstaen, K. Widespread rocky reef occurrence in the central English Channel and the implications for predictive habitat mapping. Estuar. Coast. Shelf Sci. 2009, 83, 647–658. [Google Scholar] [CrossRef]
- Horn, B.K. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef]
- Olaya, V. Basic land-surface parameters. Geomorphometry Concepts Softw. Appl. 2009, 33, 141–169. [Google Scholar]
- Florinsky, I.V. An illustrated introduction to general geomorphometry. Prog. Phys. Geogr. 2017, 41, 723–752. [Google Scholar] [CrossRef]
- Zwillinger, D.; Kokoska, S. CRC Standard Probability and Statistics Tables and Formulae; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Sappington, J.M.; Longshore, K.M.; Thompson, D.B. Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert. J. Wildl. Manag. 2007, 71, 1419–1426. [Google Scholar] [CrossRef]
- Jenness, J.S. Calculating landscape surface area from digital elevation models. Wildl. Soc. Bull. 2004, 32, 829–839. [Google Scholar] [CrossRef]
- Du Preez, C. A new arc–chord ratio (ACR) rugosity index for quantifying three-dimensional landscape structural complexity. Landsc. Ecol. 2015, 30, 181–192. [Google Scholar] [CrossRef]
- Weisstein, E.W. MathWorld: Moore Neighborhood. Available online: http://mathworld.wolfram.com/MooreNeighborhood.html (accessed on 27 February 2018).
- Evans, I.S. An integrated system of terrain analysis and slope mapping. Z. fur Geomorphol. 1980, 36, 274–295. [Google Scholar]
- Wood, J. The Geomorphological Characterisation of Digital Elevation Models. PhD Thesis, University of Leicester, Leicester, UK, 1996. [Google Scholar]
- Rigol-Sanchez, J.P.; Stuart, N.; Pulido-Bosch, A. ArcGeomorphometry: A toolbox for geomorphometric characterisation of DEMs in the ArcGIS environment. Comput. Geosci. 2015, 85, 155–163. [Google Scholar] [CrossRef]
- Dolan, M.F.; Lucieer, V.L. Variation and Uncertainty in Bathymetric Slope Calculations Using Geographic Information Systems. Mar. Geodesy 2014, 37, 187–219. [Google Scholar] [CrossRef]
- Ligas, M.; Banasik, P. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations. Geodesy Cartogr. 2011, 60, 145–159. [Google Scholar] [CrossRef]
- Lecours, V.; Devillers, R.; Simms, A.E.; Lucieer, V.L.; Brown, C.J. Towards a framework for terrain attribute selection in environmental studies. Environ. Model. Softw. 2017, 89, 19–30. [Google Scholar] [CrossRef]
- Davies, A.J.; Wisshak, M.; Orr, J.C.; Murray Roberts, J. Predicting suitable habitat for the cold-water coral Lophelia pertusa (Scleractinia). In Deep-Sea Research Part I: Oceanographic Research Papers; Elsevier: Amsterdam, The Netherlands, 2008; Volume 55, pp. 1048–1062. [Google Scholar]
- Smith, N.; Van der Walt, S. A Better Default Colormap for Matplotlib. Available online: https://bids.github.io/colormap/ (accessed on 27 February 2018).
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geodesy 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Lucieer, V.; Pederson, H. Linking morphometric characterisation of rocky reef with fine scale lobster movement. ISPRS J. Photogramm. Remote Sens. 2008, 63, 496–509. [Google Scholar] [CrossRef]
- Pittman, S.J.; Hile, S.D.; Jeffrey, C.F.G.; Caldow, C.; Kendall, M.S.; Monaco, M.E.; Hillis-Starr, Z. Fish assemblages and benthic habitats of Buck Island Reef National Monument (St. Croix, U.S. Virgin Islands) and the surrounding seascape: A characterization of spatial and temporal patterns. NOAA Tech. Memo. NOS NCCOS 2008, 71, 1–80. [Google Scholar]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Weiss, A.D. Topographic Position and Landforms Analysis. In Proceedings of the Esri User Conference, San Diego, CA, USA, 26–30 June 2000; p. 1. [Google Scholar]
- Iampietro, P.; Kvitek, R. Quantitative seafloor habitat classification using GIS terrain analysis: Effects of data density, resolution, and scale. In Proceedings of the 22nd Annual ESRI User Conference, San Diego, CA, USA, 9–13 July 2002; pp. 8–12. [Google Scholar]
- Lecours, V. On the Use of Maps and Models in Conservation and Resource Management (Warning: Results May Vary). Front. Mar. Sci. 2017, 4, 1–18. [Google Scholar] [CrossRef]
- Riley, S.; Degloria, S.; Elliot, S. A Terrain Ruggedness Index that Quantifies Topographic Heterogeneity. Int. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Friedman, A.; Pizarro, O.; Williams, S.B.; Johnson-Roberson, M. Multi-Scale Measures of Rugosity, Slope and Aspect from Benthic Stereo Image Reconstructions. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Hobson, R. Surface roughness in topography: Quantitative approach. In Spatial Analysis in Geomorphology; Methuen: London, UK, 1972; pp. 221–245. [Google Scholar]
- Du Preez, C.; Curtis, J.M.; Clarke, M.E. The structure and distribution of benthic communities on a shallow seamount (Cobb Seamount, Northeast Pacific Ocean). PLoS ONE 2016, 11, e0165513. [Google Scholar] [CrossRef] [PubMed]
- Wedding, L.M.; Friedlander, A.M.; McGranaghan, M.; Yost, R.S.; Monaco, M.E. Using bathymetric lidar to define nearshore benthic habitat complexity: Implications for management of reef fish assemblages in Hawaii. Remote Sens. Environ. 2008, 112, 4159–4165. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale analysis of topographic surface roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools For Python. Available online: http://www.scipy.org/ (accessed on 10 January 2018).
- DeCarlo, L.T. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292. [Google Scholar] [CrossRef]
- Bartels, M.; Wei, H.; Mason, D.C. DTM generation from LIDAR data using skewness balancing. In Proceedings of the 18th IEEE International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; Volume 1, pp. 566–569. [Google Scholar]
- Mark, D.M. Geomorphometric parameters: A review and evaluation. Geogr. Ann. Ser. A Phys. Geogr. 1975, 165–177. [Google Scholar] [CrossRef]
- Hey, T.; Tansley, S.; Tolle, K. The Fourth Paradigm: Data-Intensive Scientific Discovery; Microsoft Research: Washington, DC, USA, 2009. [Google Scholar]
- Guo, P. Python Is Now the Most Popular Introductory Teaching Language at Top U.S. Universities. Available online: https://cacm.acm.org/blogs/blog-cacm/176450 (accessed on 27 February 2018).
- Walbridge, S.; Slocum, N. GitHub: Benthic Terrain Modeler. Available online: https://github.com/EsriOceans/btm (accessed on 27 February 2018).
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Neteler, M.; Bowman, M.; Landa, M.; Metz, M. GRASS GIS: A multi-purpose Open Source GIS. Environ. Model. Softw. 2012, 31, 124–130. [Google Scholar] [CrossRef]
- Lecours, V.; Brown, C.J.; Devillers, R.; Lucieer, V.L.; Edinger, E.N. Comparing selections of environmental variables for ecological studies: A focus on terrain attributes. PLoS ONE 2016, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.; Oakleaf, J.; Cushman, S. An ArcGIS Toolbox for Surface Gradient and Geomorphometric Modeling, Version 2.0-0. Available online: http://evansmurphy.wix.com/evansspatial (accessed on 3 January 2018).
- Trevisani, S.; Rocca, M. MAD: Robust image texture analysis for applications in high resolution geomorphometry. Comput. Geosci. 2015, 81, 78–92. [Google Scholar] [CrossRef]
- Roberts, J.J.; Best, B.D.; Dunn, D.C.; Treml, E.A.; Halpin, P.N. Marine Geospatial Ecology Tools: An integrated framework for ecological geoprocessing with ArcGIS, Python, R, MATLAB, and C++. Environ. Model. Softw. 2010, 25, 1197–1207. [Google Scholar] [CrossRef]
- Kendall, M.; Miller, T.; Pittman, S. Patterns of scale-dependency and the influence of map resolution on the seascape ecology of reef fish. Mar. Ecol. Prog. Ser. 2011, 427, 259–274. [Google Scholar] [CrossRef]
- Costa, B.M.; Tormey, S.; Battista, T.A. Benthic Habitats of Buck Island Reef National Monument; NOAA National Centers for Coastal Ocean Science: Silver Spring, MD, USA, 2012. [Google Scholar]
- Zavalas, R.; Ierodiaconou Daniel, D.; Ryan, D.; Rattray, A.; Monk, J. Habitat classification of temperate marine macroalgal communities using bathymetric LiDAR. Remote Sens. 2014, 6, 2154–2175. [Google Scholar] [CrossRef]
- Battista, T.; Costa, B. Buck Island Reef National Monument. Available online: https://products.coastalscience.noaa.gov/collections/benthic/e93stcroix/ (accessed on 10 January 2018).
- Walbridge, S. Buck Island, Covariate Geodatabase. Available online: https://figshare.com/articles/Buck_Island_-_Covariate_Stack/5946463 (accessed on 27 February 2018).
- Pittman, S.; Costa, B.; Battista, T. Using lidar bathymetry and boosted regression trees to predict the diversity and abundance of fish and corals. J. Coast. Res. 2009, 27–38. [Google Scholar] [CrossRef]
- Pavlushko, D.; Pobuda, M.; Walbridge, S.; Kopp, S.; Aydin, O.; Krivoruchko, K.; Janikas, M. R-ArcGIS Bridge, Environmental Systems Research Institute. Available online: https://r-arcgis.github.io (accessed on 27 February 2018).
- McNeil, M.A.; Webster, J.M.; Beaman, R.J.; Graham, T.L. New constraints on the spatial distribution and morphology of the Halimeda bioherms of the Great Barrier Reef, Australia. Coral Reefs 2016, 35, 1343–1355. [Google Scholar] [CrossRef]
- Miyamoto, M.; Kiyota, M.; Murase, H.; Nakamura, T.; Hayashibara, T. Effects of Bathymetric Grid-Cell Sizes on Habitat Suitability Analysis of Cold-water Gorgonian Corals on Seamounts. Mar. Geodesy 2017, 40, 205–223. [Google Scholar] [CrossRef]
- Li, D.; Tang, C.; Xia, C.; Zhang, H. Acoustic mapping and classification of benthic habitat using unsupervised learning in artificial reef water. Estuar. Coast. Shelf Sci. 2017, 185, 11–21. [Google Scholar] [CrossRef]
- D’Antonio, N.L.; Gilliam, D.S.; Walker, B.K. Investigating the spatial distribution and effects of nearshore topography on Acropora cervicornis abundance in Southeast Florida. PeerJ 2016, 4, e2473. [Google Scholar] [CrossRef] [PubMed]
- Mark, D.M.; Aronson, P.B. Scale-dependent fractal dimensions of topographic surfaces: An empirical investigation, with applications in geomorphology and computer mapping. J. Int. Assoc. Math. Geol. 1984, 16, 671–683. [Google Scholar] [CrossRef]
- Perron, J.T.; Kirchner, J.W.; Dietrich, W.E. Formation of evenly spaced ridges and valleys. Nature 2009, 460, 502–505. [Google Scholar] [CrossRef]
- Deng, Y.X.; Wilson, J.P. The Role of Attribute Selection in GIS Representations of the Biophysical Environment. Ann. Assoc. Am. Geogr. 2006, 96, 47–63. [Google Scholar] [CrossRef]
- Brasington, J.; Vericat, D.; Rychkov, I. Modeling river bed morphology, roughness, and surface sedimentology using high resolution terrestrial laser scanning. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Evans, J. Straightforward Statistics for the Behavioral Sciences; Brooks/Cole Publishing Company: Pacific Grove, CA, USA, 1996. [Google Scholar]


| Name | Algorithm | Notes | References |
|---|---|---|---|
| Slope | Computed over a neighborhood | [18] | |
| Statistical Aspect | Generates Easterness and Northerness | [19,20] | |
| Mean Depth | n is the size of a square neighborhood of cells | ||
| Standard Deviation | is the mean elevation of cells within the analysis neighborhood | ||
| Variance | is the standard deviation of a neighborhood of cells | ||
| Interquartile Range | is the cumulative distribution function of all cells in the analysis neighborhood | [21] | |
| Kurtosis | is the fourth central moment and is the standard deviation of all cells in the analysis neighborhood | [21] | |
| BPI | is the mean elevation value of all cells within an annulus-shaped neighborhood | [12] | |
| VRM | see Section 2.1.3 | [22] | |
| SAPA | see Section 2.1.3 | [23] | |
| SAPA (Slope-corrected) | see Section 2.1.3 | Decoupled from slope as per ACR | [24] |
| ACR | see Section 2.1.3 | [24] |
| Interface | Role |
|---|---|
| Graphical menu | Direct interaction (see Figure 6) |
| Python toolbox | Direct and scripted interaction |
| Command-line | Reproducible, scalable, programmatic |
| Jupyter Notebooks | Teaching and exploration |
| Class | Zone | Broad BPI (Lower) | Broad BPI (Upper) | Fine BPI (Lower) | Fine BPI (Upper) | Slope (Lower) | Slope (Upper) | Depth (Lower) | Depth (Upper) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Reef Crest | −87 | 541 | −907 | 2229 | 11 | −2 | ||
| 2 | Back Reef | −87 | 541 | −459 | 885 | 52 | −6 | ||
| 3 | Bank or Shelf | −402 | 699 | −1355 | 4469 | 74 | −18 | ||
| 4 | Reef Flat | −9 | 541 | −459 | 1333 | 67 | −8 | ||
| 5 | Channel | −323 | 384 | −907 | 1333 | 53 | −12 | −1 | |
| 6 | Fore Reef | −323 | 541 | −1355 | 2229 | 61 | −14 | ||
| 7 | Lagoon | −166 | 463 | −459 | 1333 | 49 | −7 | ||
| 8 | Salt Pond | −9 | −9 | −11 | −11 | 53 | −7 | ||
| 9 | Shoreline Intertidal | −9 | 384 | −11 | 436 | 19 | −2 |
| Parameter | Value |
|---|---|
| Bathymetry Raster: | LiDAR bathymetry (clipped) |
| Broad-scale BPI Inner Radius: | 25 |
| Broad-scale BPI Outer Radius: | 250 |
| Fine-scale BPI Inner Radius: | 5 |
| Fine-scale BPI Outer Radius: | 25 |
| Classification Dictionary: | See Table 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walbridge, S.; Slocum, N.; Pobuda, M.; Wright, D.J. Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler. Geosciences 2018, 8, 94. https://doi.org/10.3390/geosciences8030094
Walbridge S, Slocum N, Pobuda M, Wright DJ. Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler. Geosciences. 2018; 8(3):94. https://doi.org/10.3390/geosciences8030094
Chicago/Turabian StyleWalbridge, Shaun, Noah Slocum, Marjean Pobuda, and Dawn J. Wright. 2018. "Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler" Geosciences 8, no. 3: 94. https://doi.org/10.3390/geosciences8030094
APA StyleWalbridge, S., Slocum, N., Pobuda, M., & Wright, D. J. (2018). Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler. Geosciences, 8(3), 94. https://doi.org/10.3390/geosciences8030094




