Ground-Based Remote Sensing and Imaging of Volcanic Gases and Quantitative Determination of Multi-Species Emission Fluxes
Abstract
1. Introduction
- (A)
- Volcanic gas emissions influence the atmosphere and therefore also the climate and other Earth system parameters in a number of ways and on different temporal and spatial scales (e.g., [1,2,3]). Investigations of plume chemistry and plume dispersal will help constrain these influences (see e.g., [4,5]).
- (B)
- The composition and emission rate of volcanic gases are linked to processes occurring in the Earth’s interior, therefore measuring volcanic gases provides insights into these otherwise largely inaccessible processes. For instance, already Noguchi and Kamiya [6] showed that eruptions of Mt. Asama (Japan) could be forecast with some degree of accuracy by measuring the variable partitioning of sulphur species, chlorine species, and carbon dioxide in the emissions from the active crater. Malinconico [7] showed first that also the amount of gas, in particular the amount of emitted SO2 varies when the volcanic activity changes. Several authors (e.g., [8,9]) used the measured SO2 emission also to calculate the amount of magma involved in the simultaneously observed volcanic activity.
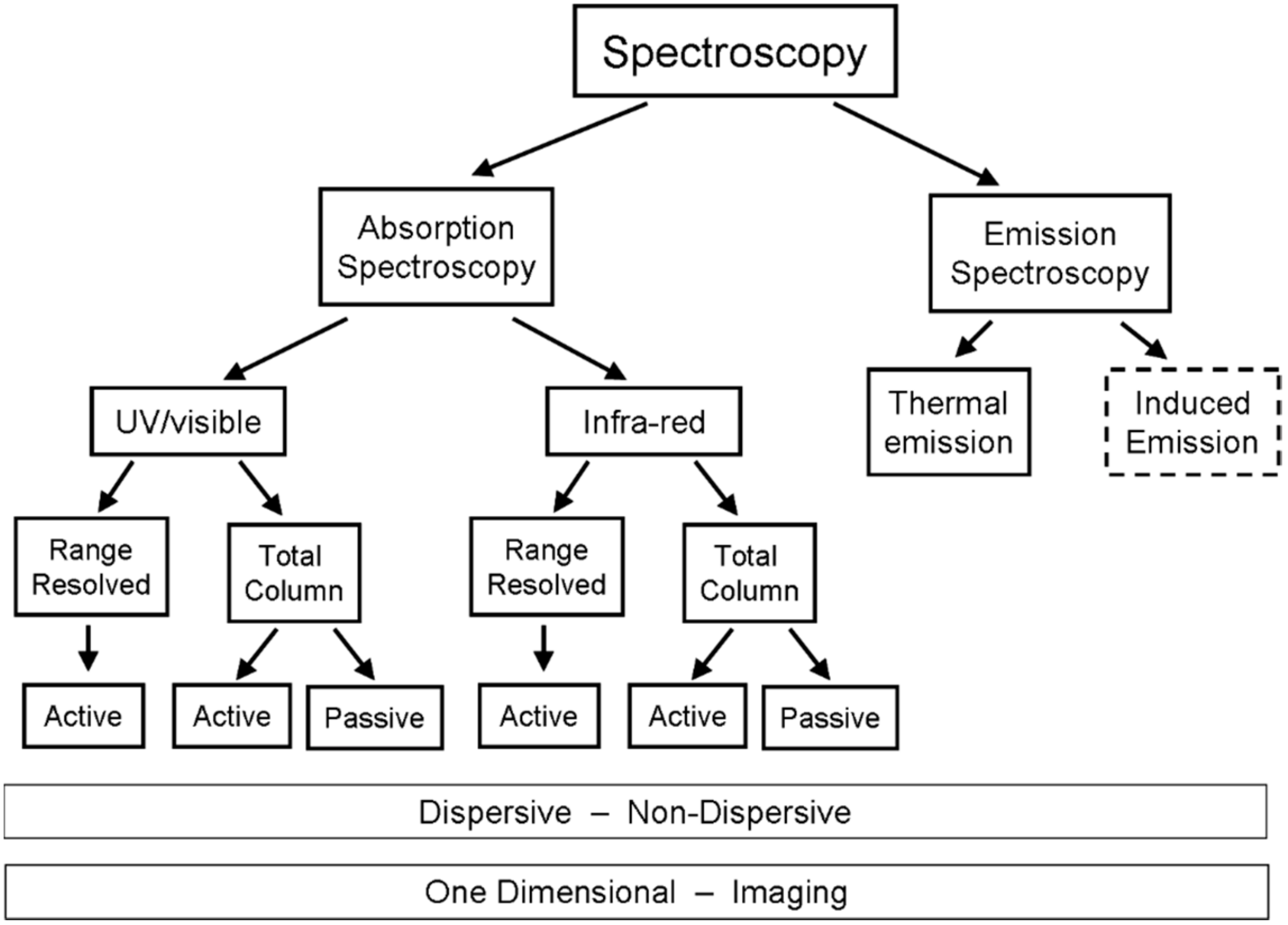
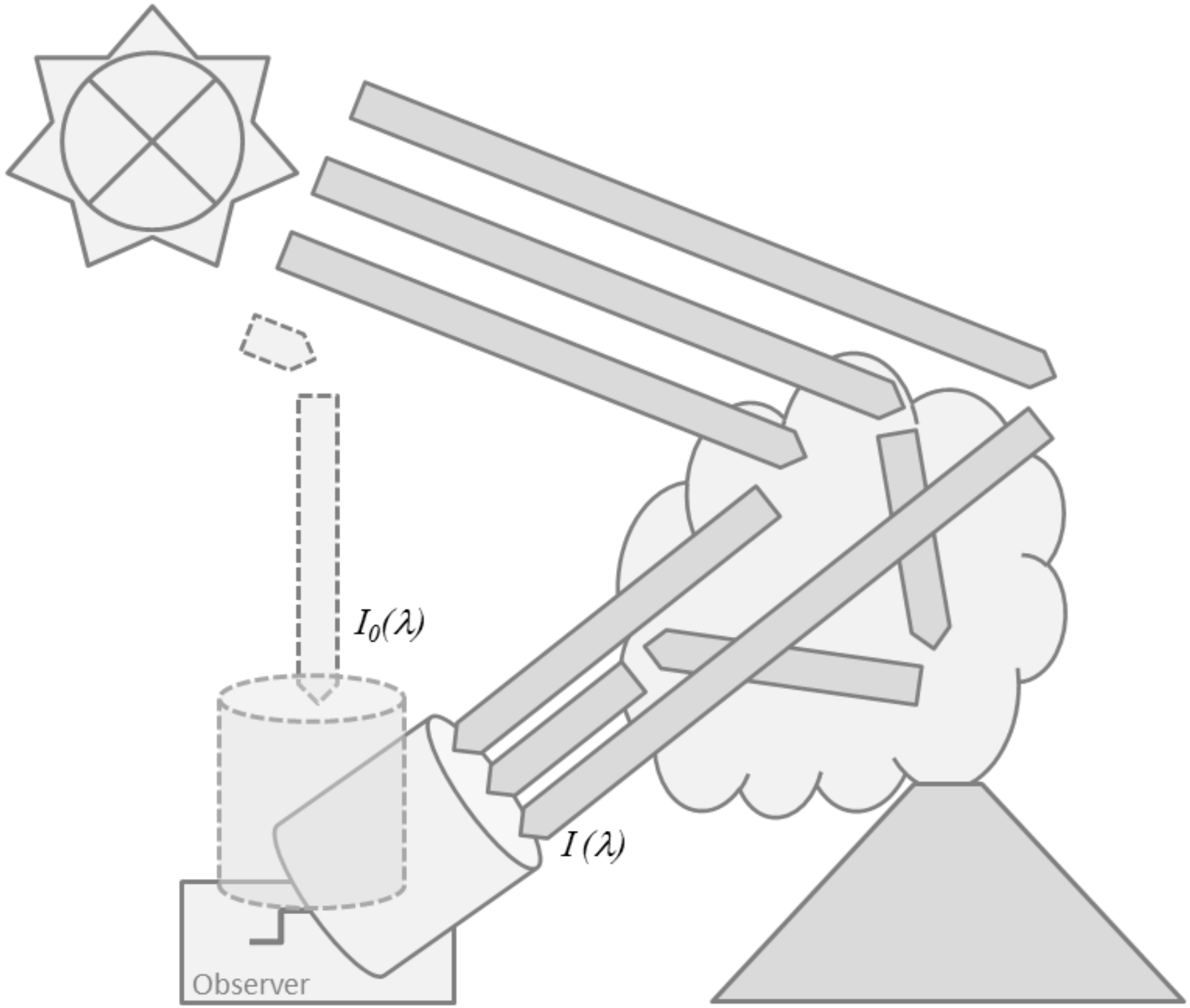
2. Remote Sensing of Volcanic Gases
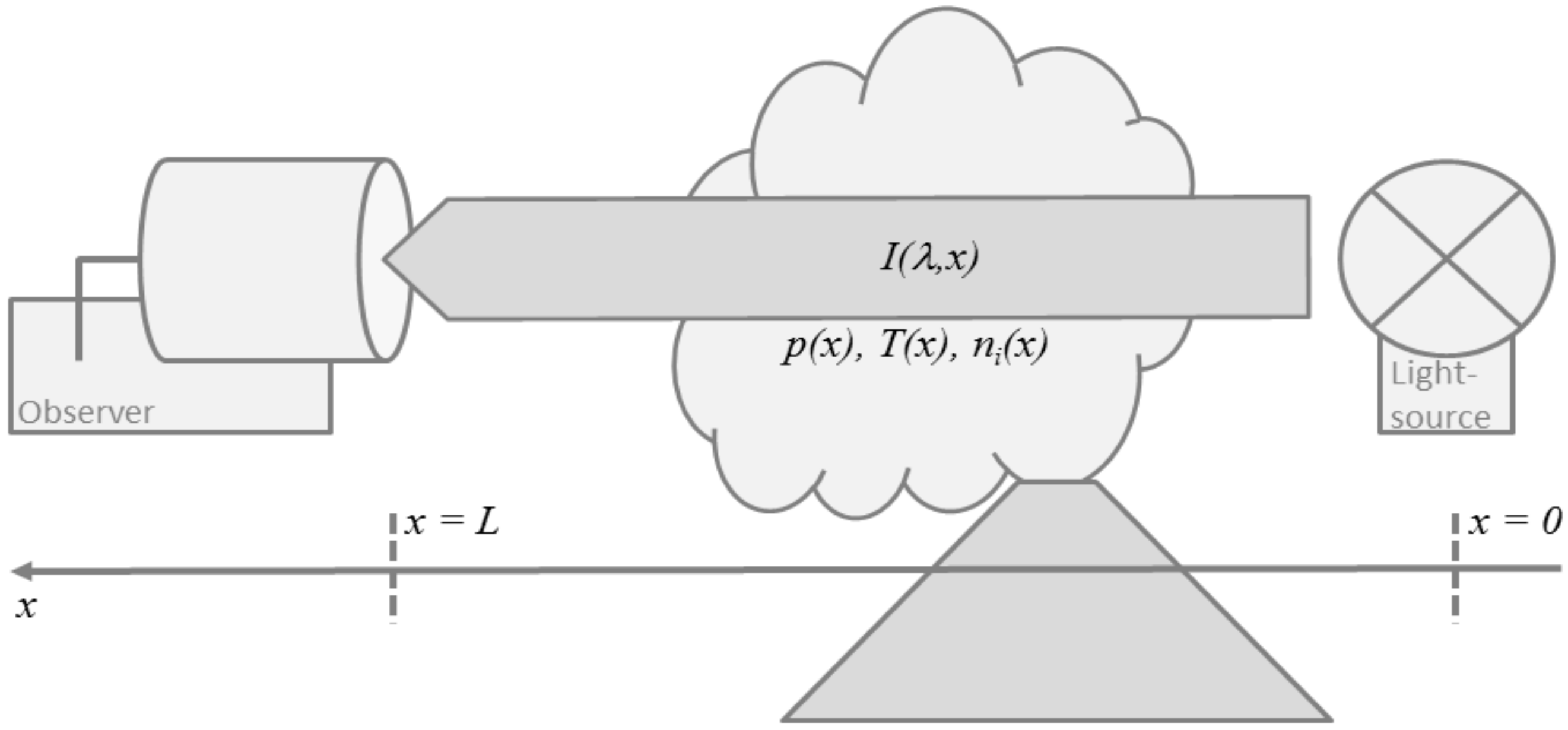
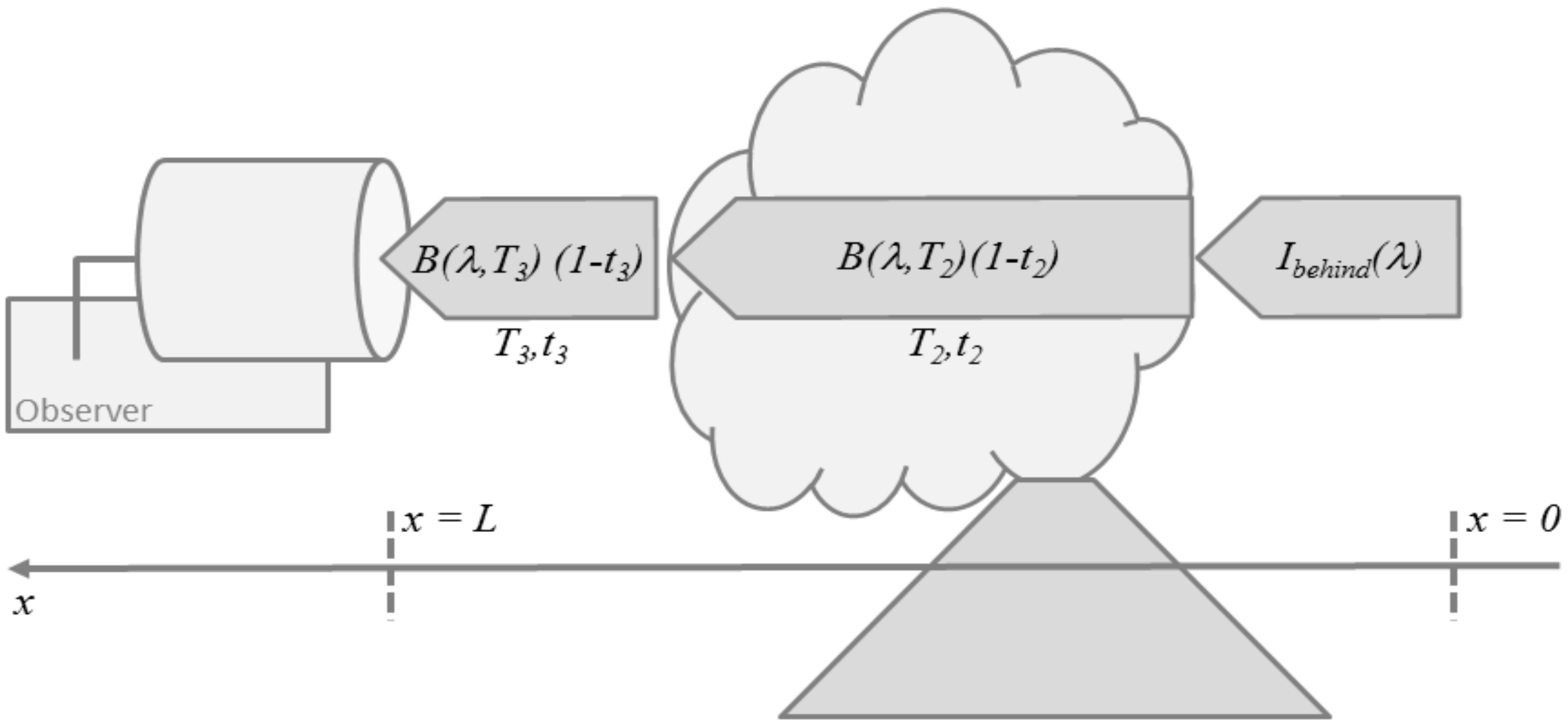
2.1. Absorption Spectroscopy
2.2. Thermal Emission Spectroscopy
2.3. Applications to Remote Sensing of Volcanic Plumes
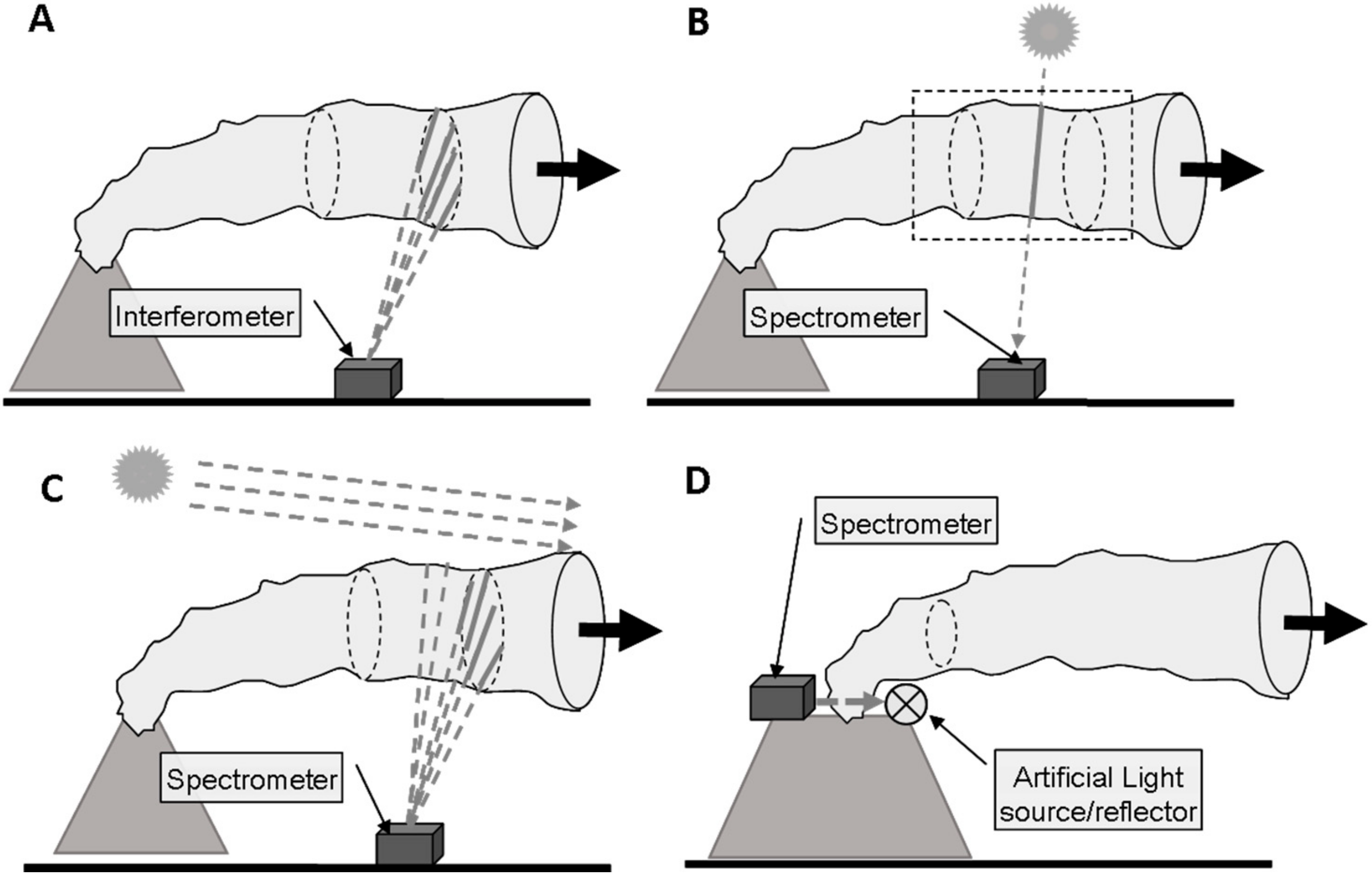
- Active or passive spectroscopy (i.e., will there be an artificial light source or a natural one)
- Arrangement of light path (source-detector, topographic reflector, artificial reflector, backscattered (artificial) light, scattered (sun) light)
- Path integrated column measurement or range resolved detection
- Dispersive or non-dispersive detection
- -
- For dispersive detection: Type of wavelength analysis (grating spectrometer,
- -
- Fourier transform interferometer, Fabry Pérot interferometer, tunable light source, ...)
- -
- For non-dispersive detection: Filter, narrow band emitting light source (e.g., laser, LED)
- One dimensional (single column) or two-dimensional (imaging) measurement (see Section 4)
- Active UV/vis absorption spectroscopy (e.g., DOAS) in Section 2.3.1
- Passive (i.e., scattered sunlight) UV/vis absorption spectroscopy in Section 2.3.1
- IR absorption spectroscopy in Section 2.3.2
- Thermal emission spectroscopy in Section 2.3.3
- LIght Detection And Ranging (LIDAR) in Section 2.3.4
2.3.1. Absorption Spectroscopy in the UV/Visible
2.3.2. Absorption Spectroscopy in the Infra-Red
- (a)
- With broad-band, thermal light sources, e.g., globars in combination with dispersive detection systems, typically Fourier-Transform interferometers of the Michelson type ([33,34,35]). At volcanoes hot lava can be used as source of radiation (e.g., [36], see below), which—according to our definition—would be classified as passive absorption spectroscopy.
- (b)
- Tunable Diode laser spectroscopy (TDLS), which (e.g., [37,38,39]) is a variety of dispersive spectroscopy where a narrow-band emitting light source (i.e., a semiconductor laser) is rapidly wavelength modulated in order to sweep across an absorption line of the gas to be measured. The original, rather unreliable lead salt diodes are now replaced by much more stable (though still expensive) quantum cascade laser diodes [40,41]. Since the light source is wavelength modulated there is no need for dispersive detection.
- (c)
- Passive IR spectroscopy using the sun (or the moon) as a direct light source is commonly referred to as the solar (or lunar) occultation technique which has been used for remote sensing of volcanic gases such as SO2, HF, HCl, and SiF4, e.g., [43,44,45]. The technique simplifies substantially if the target gas only exists (at relevant amounts) in the volcanic plume and not in the background atmosphere which is, however, not the case for the major volcanic plume constituents CO2 and H2O. Due to the rapid downwind dispersion of the volcanic plume, the volcanic enhancements (on top of the large background) become small and thus, increasingly difficult to measure the farther downwind the plume is sampled. Only recently, Butz et al. [46], demonstrated safe-distance remote sensing of volcanic CO2 in Mt. Etna’s plume during passive degassing conditions. They operated a sun-viewing, portable Fourier Transform Spectrometer (FTIR) on a truck in stop-and-go patterns underneath Mt. Etna’s plume such that the lines-of-sight to the sun sampled the plume in 5–10 km distance from the crater. Co-measuring O2 columns helped calibrating spurious variations in the targeted CO2 columns which were merely due changes in observer position. Sequentially measuring intra-plume and extra-plume spectra and using co-measured HF, HCl and SO2 as intra-plume tracers helped removing the atmospheric CO2 background. These current generation instruments were able to discriminate the volcanic CO2 signal out of a 300-1000 times larger atmospheric background path.
- (d)
- Hot volcanic material such as lava or volcanic rocks have been used heavily in open-path spectroscopic techniques, e.g., [33,35,36,43,47,48,49,50,51] Naughton et al. 1969, Mori et al. 1993, Notsu et al. 1993, Mori et al. 1995, Francis et al. 1998, Mori and Notsu, 1997, Burton et al. 2000, Gerlach et al. 2002, Allard et al. 2005] targeting volcanic SO2, HF, HCl, SiF4, CO, CO2, COS. Generally, the technique requires that the hot material or the lamp locates behind the plume and that it can be sighted by the observer. For many volcanoes, this requirement implies deploying instrumentation in the proximity of the crater or at the crater rim which spoils the general remote sensing advantage of avoiding hazards and hostile environments to operators and instrumentation. Recently, laser-based techniques for CO2 have been developed using topographic reflection targets, e.g., [52,53], promising greater deployment flexibility but still requiring plume sampling close to the source where CO2 enhancements are large compared to the atmospheric background.
2.3.3. Thermal Emission Spectroscopic Techniques
2.3.4. Range Resolved (LIDAR) Techniques
3. Imaging of Plumes
- Complex situations (multiple plumes, change of wind direction, etc.) can be recognised and analyzed (e.g., [68])
- Redundant measurements can be made by e.g., making trace gas flux determinations at several planes along the plume propagation direction allowing e.g., internal consistency checks (see e.g., [22])
- Redundant flux measurements can be used to determine the exact plume propagation direction (see [22])
- Last not least: the human visual system has powerful analysis capacities which can be used once images are available (‘seeing is believing’)
- Capability to specifically detect the desired gas (or parameter)
- To provide sufficient sensitivity (e.g., for SO2 measurements a detection limit for SO2-column densities of the order of 1017 molecules/cm2 or ca. 40 ppmm is required for volcanic emissions observations)
- To provide sufficient spatial resolution to allow discrimination of the relevant features within the plume(s)
- Sufficient time resolution (typically of the order of seconds) of the measurement is further required to be able to resolve the motion of the plume and variations in the volcanic source strength
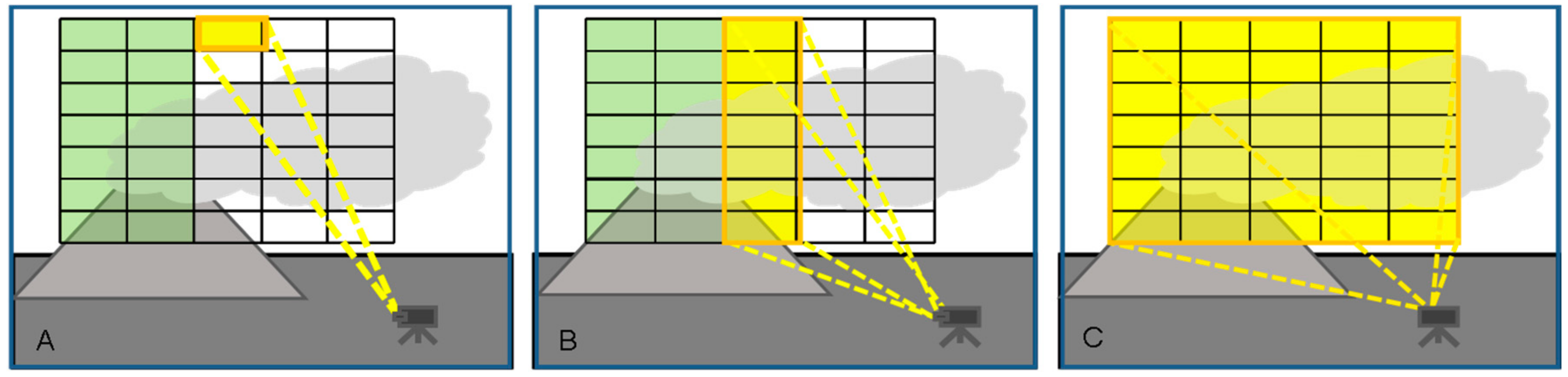
3.1. Categories of Plume Imaging
- (1)
- Pixel at a time scanning (“whiskbroom” imaging, see Figure 7A): In this approach all pixels of an image scene are scanned sequentially according to a particular scheme (e.g., line by line as in early TV cameras), for each pixel a spectrum is determined. In this approach all (of e.g., 105 pixels) have to be scanned individually, such that it is potentially a rather slow approach. Michelson interferometers have been combined with whisk-broom scanners to obtain 2-D images (e.g., [34,55,72]).
- (2)
- Column (or row) at a time scanning (“push-broom” imaging, see Figure 7B): Here all pixels of an image column are scanned simultaneously while the image columns are scanned sequentially. Because each column of the image is recorded at once, only of the order of several hundred columns have to be measured sequentially. Since only one scan-dimension is required the scanning mechanisms can become simpler though it is not necessarily faster. In fact, as will be explained below the amount of radiation collected by the entrance optics has to be split between all pixels of a column, thus, when the time to acquire an image is determined by the available number of photons the technique will not generally be faster than whiskbroom imaging. Push broom scanners have been realized with DOAS instruments as e.g., described by Lohberger et al. [73], Bobrowski et al. [74], Louban et al. [75] and Lee et al. [76], see Section 3.3, below. Michelson interferometers have also been combined with push-broom scanners (i.e., moving platform) to obtain 2-D images (e.g., [77]). A recent development based on a special type of interferometer (Sagnac interferometer) is the Thermal Hyperspectral Imager, which produces a spatial interferogram across the field of view, which is scanned across the image. After Fourier transformation a high resolution spectrum for each image pixel is obtained [57] (Gabrieli et al. 2016), which can be analysed for spectral signatures of volcanic gases. Gabrieli et al. [57,78] used such a device to produce images of the SO2 distribution derived from spectra around 8.6 μm at a spectral resolution of about 0.25 μm. Explorative measurements were made at Kilauea Halema’uma’u crater (Hawaii) with a scan duration of 1 s.
- (3)
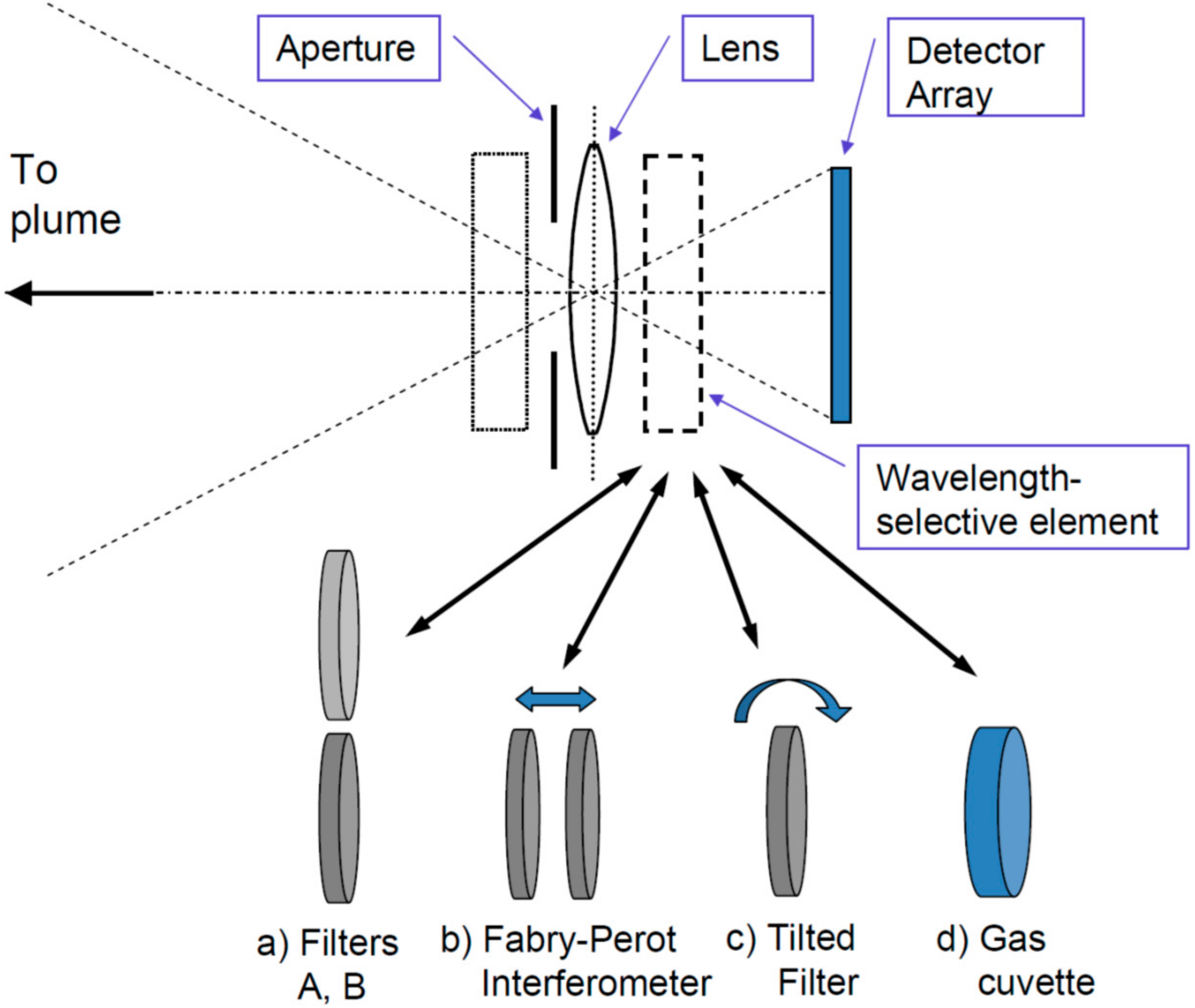
- Frame at a time scanning (“full frame” imaging, see Figure 7C): Here the entire frame is recorded at once (or in a sequence of steps in time). While in principle there could be large arrays of spectrometers determining the spectrum of each pixel (and in the future arrays of integrated micro-spectrometers could become viable), in practice the spectral information is usually determined by collecting sequential images with different wavelength selective elements (e.g., suitable filters, see Figure 8) in front of the camera sensors.
3.2. Non-Dispersive Plume Imaging
3.2.1. Quantifying Column Densities Using Classic (UV) SO2 Cameras
3.2.2. Non-dispersive IR Imaging of Plumes
- (1)
- IR-cameras with two or more filters similar to the SO2 camera principle (e.g., Prata and Bernardo 2009) have been developed for SO2 retrieval and ash detection ([56,85]). A four filter IR camera was actually used by Lopez et al. [86] to simultaneously determine plume the SO2 SCD, temperature, and ash content of the plume of Stromboli (Italy), Karymsky (Russia), and Láscar (Chile) volcanoes.
- (2)
3.3. Dispersive Imaging
3.4. Combining both Approaches
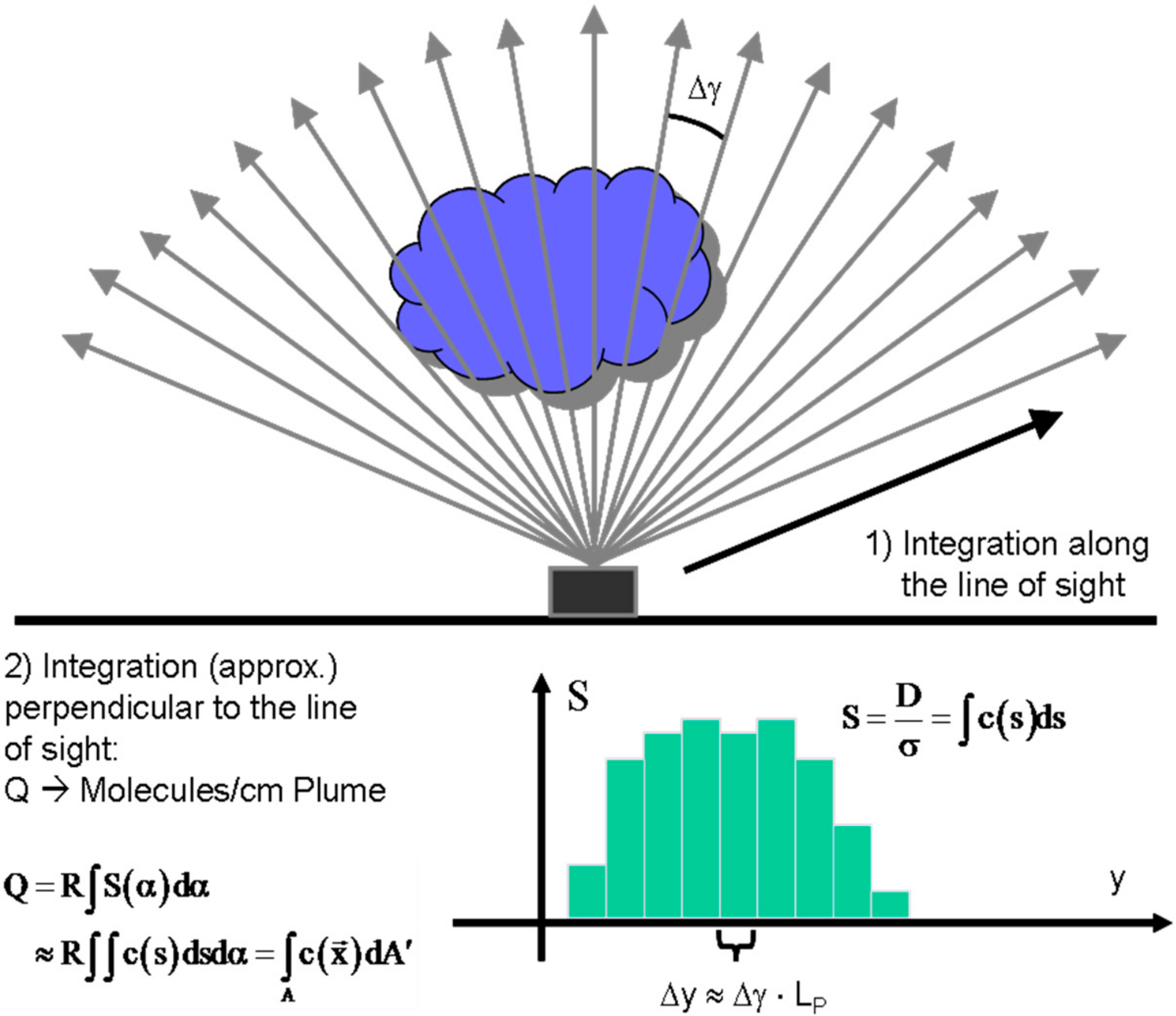
4. Volcanic Gas Flux Determination
4.1. The Principle of Volcanic Gas Flux Determination
- (1)
- From local measurements
- (2)
- From large scale wind fields, which are available from regional or global data bases (e.g., ECMWF or MERRA).
- (3)
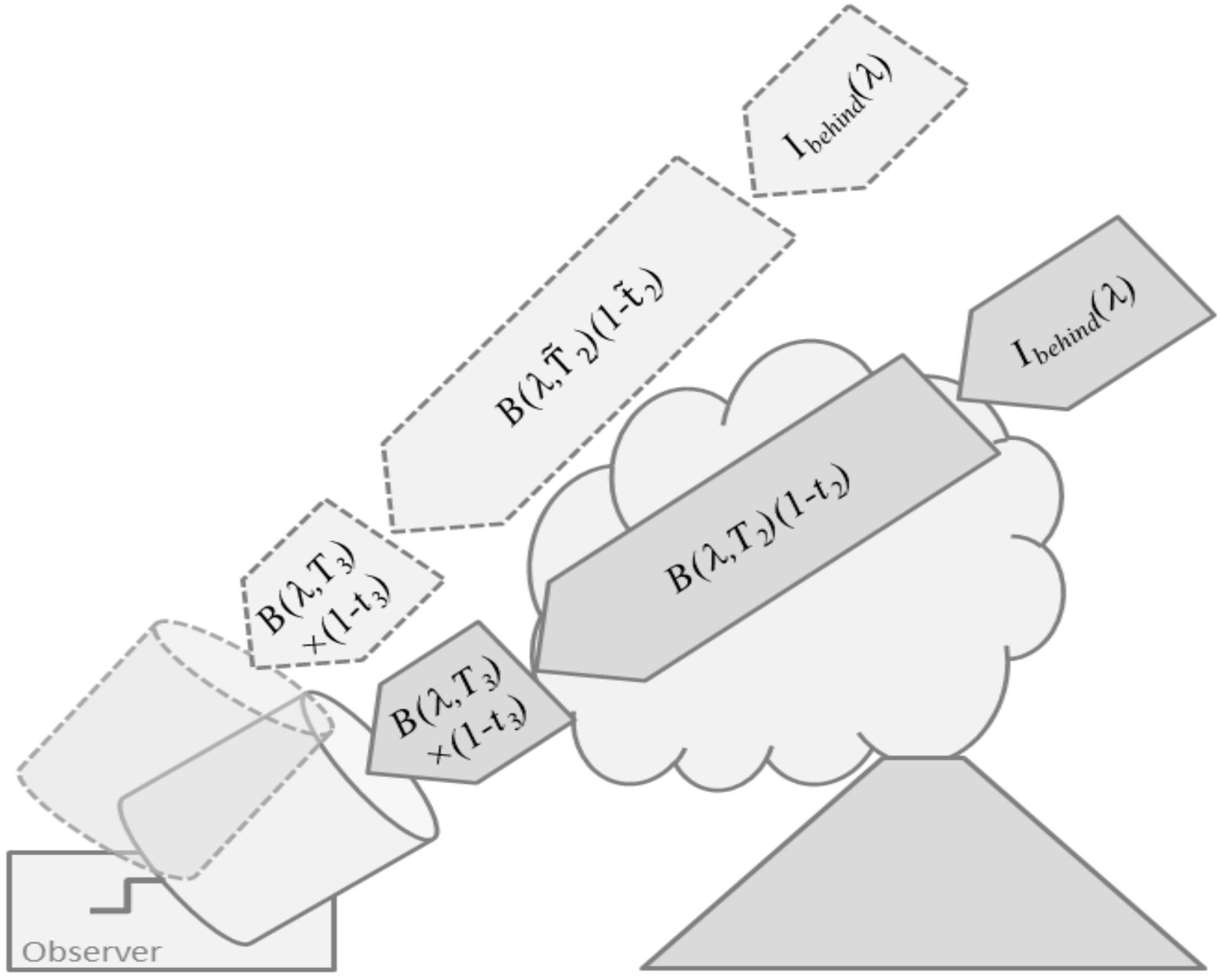
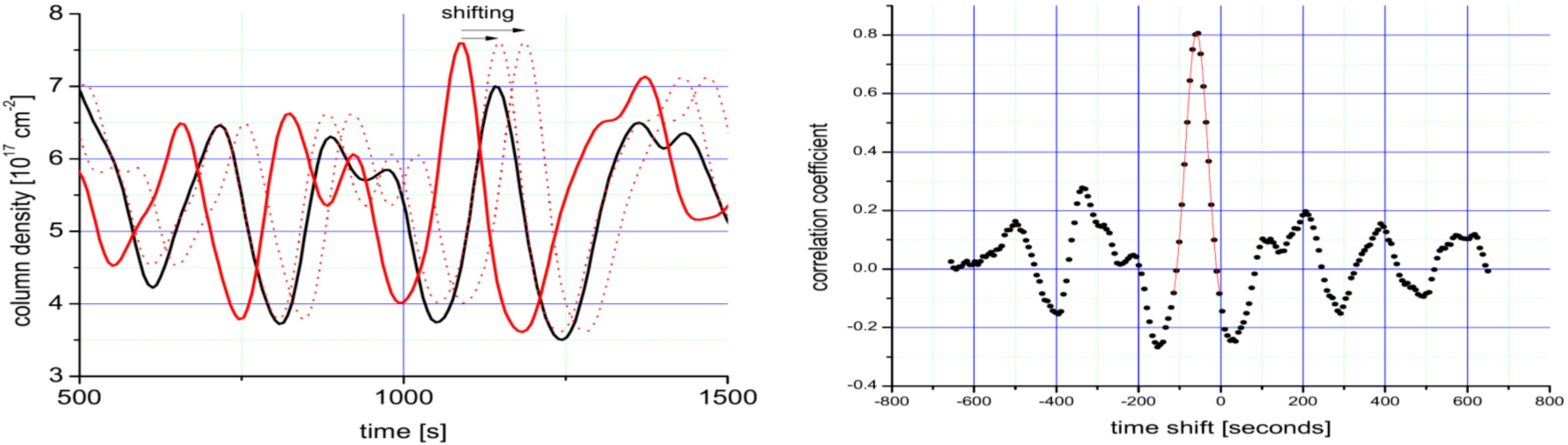
4.2. A More Detailed View—Determination of the Wind Direction
- (1)
- Light dilution may affect the accuracy of the column density retrieval
- (2)
- Multiple scattering inside the plume can also affect the column density retrieval
- (3)
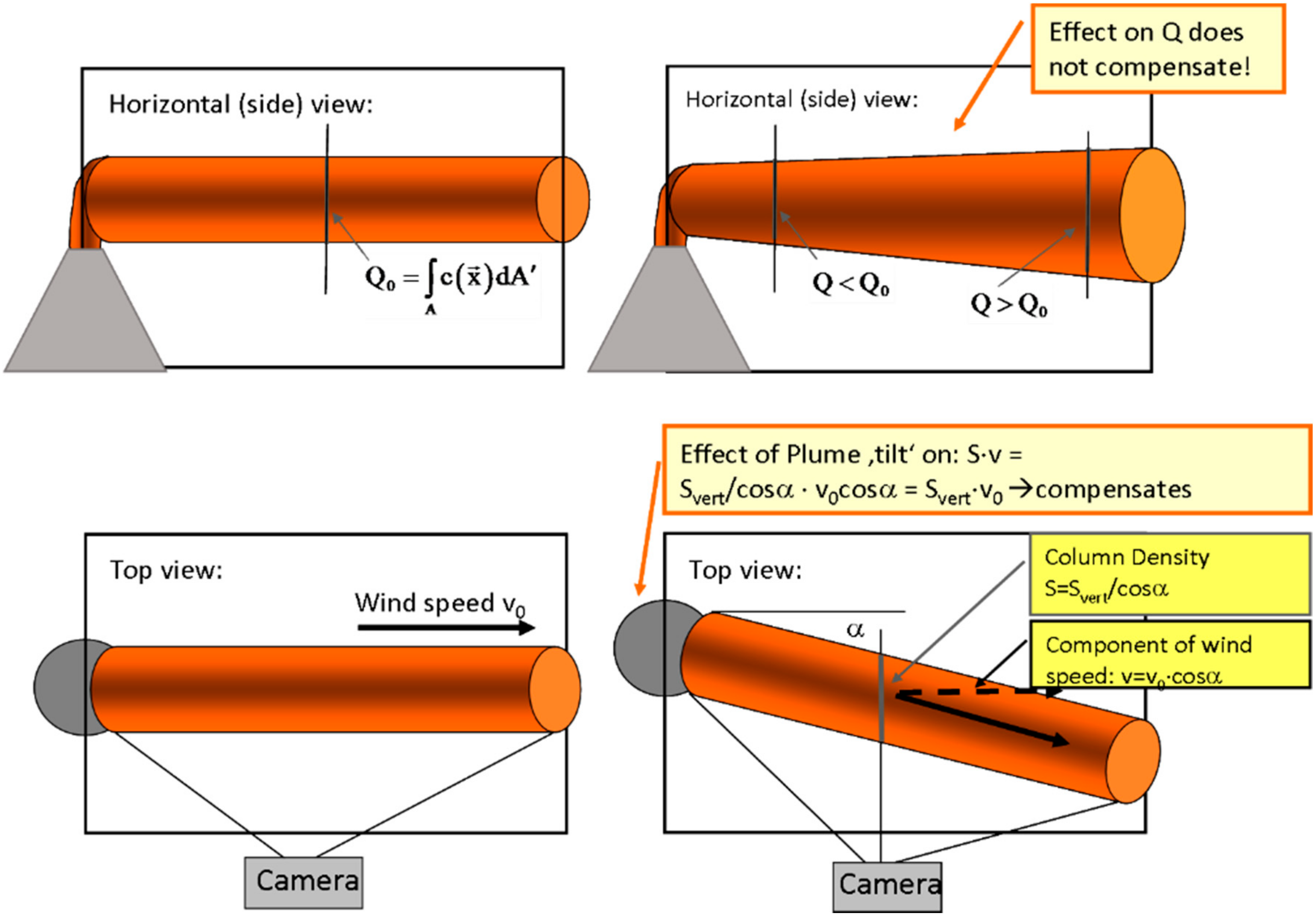
- The effect of the plume propagation direction being non-perpendicular to the viewing direction must be corrected
- (1)
- The length of the light path through the plume increases as 1/cos(α).
- (2)
- The determined apparent wind speed is reduced by the factor cos(α) since the determined d2–d1 appears shorter by this factor (see bottom right panel of Figure 12) while the determined time lag ∆tP stays the same.
- (1)
- Still the light path through the plume is larger towards the edges of the image, while the determined velocity vP stays the same. Thus the flux appears to increase somewhat towards the edges of the image compared to the centre.
- (2)
- A further effect of at “tilt” is due to geometry in that the closer part of the plume appears larger than the part which is further away from the camera (see top right panel of Figure 12) thus the integral (Equation (18)) will extend over a larger extent and thus be larger.
5. Sample Applications
5.1. UV Spectroscopy
5.2. IR Spectroscopy
6. Summary and Outlook
- (1)
- The relatively crude spectroscopic approach, basically just ratioing the intensities in two wavelength intervals leads to interferences by aerosol, (stratospheric) ozone, and possibly other species. Moreover, radiation transport issues may also influence the accuracy of the technique (see e.g., [71,82,129]).
- (2)
- UV cameras rely on sunlight and can thus only operate during daylight hours.
Acknowledgments
Conflicts of Interest
References
- Robock, A. Volcanic Eruptions and Climate. Rev. Geophys. 2000, 38, 191–219. [Google Scholar] [CrossRef]
- Von Glasow, R.; Bobrowski, N.; Kern, C. The effects of volcanic eruptions on atmospheric chemistry. Chem. Geol. 2009, 263, 131–142. [Google Scholar] [CrossRef]
- Kutterolf, S.; Hansteen, T.H.; Appel, K.; Freundt, A.; Krüger, K.; Pérez, W.; Wehrmann, H. Combined bromine and chlorine release from large explosive volcanic eruptions: A threat to stratospheric ozone? Geology 2013, 41, 707–710. [Google Scholar] [CrossRef]
- Platt, U.; Bobrowski, N. Quantification of volcanic reactive halogen emissions. In Volcanism and Global Change; Schmidt, A., Fristad, K., Elkins-Tanton, L., Eds.; Cambridge University Press: Cambridge, UK, 2015; ISBN 9781107058378. [Google Scholar]
- Platt, U.; Lübcke, P.; Kuhn, J.; Bobrowski, N.; Prata, F.; Burton, M.R.; Kern, C. Quantitative Imaging of Volcanic Plumes—Results, Future Needs, and Future Trends. J. Volcanol. Geotherm. Res. 2015, 300, 7–21. [Google Scholar] [CrossRef]
- Noguchi, K.; Kamiya, H. Prediction of volcanic eruption by measuring the chemical composition and amounts of gases. Bull. Volcanol. 1963, 26, 367–378. [Google Scholar] [CrossRef]
- Malinconico, L.L., Jr. On the Variation of SO2 emission from volcanoes. J. Volcanol. Geotherm. Res. 1987, 33, 231–237. [Google Scholar] [CrossRef]
- Sutton, A.J.; Elias, T.; Gerlach, T.M.; Stokes, J.B. Implications for eruptive proecesses as indicated by sulfur dioxide emissions from Kilauea Volcano, Hawai’i, 1979–1997. J. Volcanol. Geotherm. Res. 2001, 108, 283–302. [Google Scholar] [CrossRef]
- Burton, M.R.; Allard, P.; Mure, F.; Oppenheimer, C. FTIR remote sensing of fractional magma degassing at Mt. Etna, Sicily. Geol. Soc. 2003, 213, 281–293. [Google Scholar] [CrossRef]
- Galle, B.; Johansson, M.; Rivera, C.; Zhang, Y.; Kihlman, M.; Kern, C.; Lehmann, T.; Platt, U.; Arellano, S.; Hidalgo, S. Network for Observation of Volcanic and Atmospheric Change (NOVAC)—A global network for volcanic gas monitoring: Network layout and instrument description. J. Geophys. Res. 2010, 115, D05304. [Google Scholar] [CrossRef]
- Lübcke, P.; Bobrowski, N.; Arellano, S.; Galle, B.; Garzon, G.; Vogel, L.; Platt, U. BrO/SO2 ratios from the NOVAC Network. Solid Earth 2014, 5, 409–424. [Google Scholar] [CrossRef]
- Dinger, F.; Bobrowski, N.; Warnach, S.; Bredemeyer, S.; Hidalgo, S.; Arellano, S.; Galle, B.; Platt, U.; Wagner, T. Periodicity in the BrO/SO2 molar ratios in volcanic gas plumes and its correlation with the Earth tides, Part 1: Observation during the Cotopaxi eruption 2015. Solid Earth Discuss. 2017. [Google Scholar] [CrossRef]
- Weibring, P.; Andersson, M.; Edner, H.; Svanberg, S. Remote Monitoring of Industrial Emissions by Combination of Lidar and Plume Velocity Measurements. Appl. Phys. B 1998, 66, 383–388. [Google Scholar] [CrossRef]
- Weibring, P.; Swartling, J.; Edner, H.; Svanberg, S.; Caltabiano, T.; Condarelli, D.; Cecchi, G.; Pantani, L. Optical Monitoring of Volcanic Sulphur Dioxide Emissions—Comparison between four Different Remote Sensing Techniques. Opt. Lasers Eng. 2002, 37, 267–284. [Google Scholar] [CrossRef]
- Galle, B.; Oppenheimer, C.; Geyer, A.; McGonigle, A.J.; Edmonds, M.; Horrocks, L. A miniaturised ultraviolet spectrometer for remote sensing of SO2 fluxes: A new tool for volcano surveillance. J. Volcanol. Geotherm. Res. 2003, 119, 241–254. [Google Scholar] [CrossRef]
- McGonigle, A.J.S.; Pering, T.D.; Wilkes, T.C.; Tamburello, G.; D’Aleo, R.; Bitetto, M.; Aiuppa, A.; Willmott, J.R. Ultraviolet Imaging of Volcanic Plumes: A New Paradigm in Volcanology. Geosciences 2017, 7, 68. [Google Scholar] [CrossRef]
- McGonigle, A.J.S.; Hilton, D.R.; Fischer, T.P.; Oppenheimer, C. Plume velocity determination for volcanic SO2 flux measurements. Geophys. Res. Lett. 2005, 32, L11302. [Google Scholar] [CrossRef]
- McGonigle, A.J.S.; Inguaggiato, S.; Aiuppa, A.; Hayes, A.R.; Oppenheimer, C. Accurate measurement of volcanic SO2 flux: Determination of plume transport speed and integrated SO2 concentration with a single device. Geochem. Geophys. Geosyst. 2005, 6, Q02003. [Google Scholar] [CrossRef]
- Mori, T.; Burton, M. Quantification of the gas mass emitted during single explosions on Stromboli with the SO2 imaging camera. J. Volcanol. Geotherm. Res. 2009, 188, 395–400. [Google Scholar] [CrossRef]
- Kern, C.; Sutton, J.; Elias, T.; Lee, L.; Kamibayashi, K.; Antolik, L.; Werner, C. An automated SO2 camera system for continuous, real-time monitoring of gas emissions from Klauea Volcano’s summit Overlook Crater. J. Volcanol. Geotherm. Res. 2015, 300, 81–94. [Google Scholar] [CrossRef]
- Peters, N.; Hoffmann, A.; Barnie, T.; Herzog, M.; Oppenheimer, C. Use of motion estimation algorithms for improved flux measurements using SO2 cameras. J. Volcanol. Geotherm. Res. 2015, 300, 58–69. [Google Scholar] [CrossRef]
- Klein, A.; Lübcke, P.; Bobrowski, N.; Kuhn, J.; Platt, U. Plume Propagation Direction Determination with SO2 Cameras. Atmos. Meas. Tech. 2017, 10, 979–987. [Google Scholar] [CrossRef]
- General, S.; Pöhler, D.; Sihler, H.; Bobrowski, N.; Frieß, U.; Zielcke, J.; Horbanski, M.; Shepson, P.; Stirm, B.; Simpson, W.; et al. The Heidelberg Airborne Imaging DOAS Instrument (HAIDI) A Novel Imaging DOAS Device for 2-D and 3-D Imaging of Trace Gases. J. Atmos. Meas. Tech. 2014, 7, 3459–3485. [Google Scholar] [CrossRef]
- Krueger, A.J. Sighting of El Chichon sulfur dioxide clouds with the Nimbus 7 Total Ozone Mapping Spectrometer. Science 1983, 220, 1377–1378. [Google Scholar] [CrossRef] [PubMed]
- Hörmann, C.; Sihler, H.; Bobrowski, N.; Beirle, S.; Penning de Vries, M.; Platt, U.; Wagner, T. Systematic investigation of bromine monoxide in volcanic plumes from space by using the GOME-2 instrument. Atmos. Chem. Phys. 2013, 13, 4749–4781. [Google Scholar] [CrossRef]
- Carn, S.A.; Clarisse, L.; Prata, A.J. Multi-decadal satellite measurements of global volcanic degassing. J. Volcanol. Geotherm. Res. 2016, 311, 99–134. [Google Scholar] [CrossRef]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy, Principles and Applications; Springer: Heidelberg, Germany, 2008; p. 597. ISBN 978-3-540-21193-8. [Google Scholar]
- Moffat, A.J.; Millán, M.M. The application of optical correlation techniques to the remote sensing of SO2 plumes using sky light. Atmos. Environ. 1971, 5, 677–690. [Google Scholar] [CrossRef]
- Lübcke, P.; Lampel, J.; Arellano, S.; Bobrowski, N.; Dinger, F.; Galle, B.; Garzón, G.; Hidalgo, S.; Ortiz, Z.C.; Vogel, L. Retrieval of absolute SO2 column amounts from scattered-light spectra—Implications for the evaluation of data from automated DOAS Networks. Atmos. Meas. Tech. 2016, 9, 5677–5698. [Google Scholar] [CrossRef]
- Kern, C.; Sihler, H.; Vogel, L.; Rivera, C.; Herrera, M.; Platt, U. Halogen oxide measurements at Masaya volcano, Nicaragua using Active Long Path Differential Optical Absorption Spectroscopy. Bull. Volcanol. 2009, 71, 659–670. [Google Scholar] [CrossRef]
- Vita, F.; Kern, C.; Inguaggiato, S. Development of a portable active long-path differential optical absorption spectroscopy system for volcanic gas measurements. J. Sens. Sens. Syst. 2014, 3, 355–367. [Google Scholar] [CrossRef]
- Horton, K.A.; Williams-Jones, G.; Garbeil, H.; Elias, T.; Sutton, A.J.; Mouginis-Mark, P.; Porter, J.N.; Clegg, S. Real-time measurement of volcanic SO2 emissions: Validation of a new UV correlation spectrometer (FLYSPEC). Bull. Volcanol. 2005, 68, 323–327. [Google Scholar] [CrossRef]
- Mori, T.; Notsu, K. Remote CO, COS, CO2, SO2, HCl detection and temperature estimation of volcanic gas. Geophys. Res. Lett. 1997, 24, 2047–2050. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Francis, P.; Burton, M.; Maciejewski, A.; Boardman, L. Remote measurement of volcanic gases by Fourier transform infrared spectroscopy. Appl. Phys. B 1998, 67, 505–515. [Google Scholar] [CrossRef]
- Burton, M.R.; Oppenheimer, C.; Horrock, L.A.; Francis, P.W. Remote sensing of CO2 and H2O emission rates from Masaya volcano, Nicaragua. Geology 2000, 28, 915–918. [Google Scholar] [CrossRef]
- Allard, P.; Burton, M.; Muré, F. Spectroscopic evidence for a lava fountain driven by previously accumulated magmatic gas. Nature 2005, 433, 407–410. [Google Scholar] [CrossRef] [PubMed]
- Carapezza, M.L.; Barberi, F.; Ranaldi, M.; Ricci, T.; Tarchini, L.; Barrancos, J.; Fischer, L.C.; Perez, N.; Weber, K.; Gattuso, A.; et al. Diffuse CO2 soil degassing and CO2 and H2S concentrations in air and related hazards at Vulcano Island (Aeolian arc, Italy). J. Volcanol. Geotherm. Res. 2011, 207, 130–144. [Google Scholar] [CrossRef]
- Pedone, M.; Aiuppa, A.; Giudice, G.; Grassa, F.; Cardellini, C.; Chiodini, G.; Valenza, M. Volcanic CO2 flux measurement at Campi Flegrei by tunable diode laser absorption spectroscopy. Bull. Volcanol. 2015, 76, 812. [Google Scholar] [CrossRef]
- Chiarugi, A.; Viciani, S.; D’Amato, F.; Burton, M. Diode laser-based gas analyser for the simultaneous measurement of CO2 and HF in volcanic plumes. Atmos. Meas. Tech. 2018, 11, 329–339. [Google Scholar] [CrossRef]
- Weidmann, D.; Wysocki, G.; Oppenheimer, C.; Tittel, F.K. Development of a compact quantum cascade laser spectrometer for field measurements of CO2 isotopes. Appl. Phys. B Lasers Opt. 2005, 80, 255–260. [Google Scholar] [CrossRef]
- Richter, D.; Erdelyi, M.; Curl, R.F.; Tittel, F.K.; Oppenheimer, C.; Duffell, H.J.; Burton, M. Field measurements of volcanic gases using tunable diode laser based mid-infrared and Fourier transform infrared spectrometers. Opt. Lasers Eng. 2002, 37, 171–186. [Google Scholar] [CrossRef]
- Waxman, E.M.; Cossel, K.C.; Truong, G.-W.; Giorgetta, F.R.; Swann, W.C.; Coburn, S.; Wright, R.J.; Rieker, G.B.; Coddington, I.; Newbury, N.R. Intercomparison of open-path trace gas measurements with two dual-frequency-comb spectrometers. Atmos. Meas. Tech. 2017, 10, 3295–3311. [Google Scholar] [CrossRef] [PubMed]
- Francis, P.; Burton, M.R.; Oppenheimer, C. Remote measurements of volcanic gas compositions by solar occultation spectroscopy. Nature 1998, 396, 567–570. [Google Scholar] [CrossRef]
- Burton, M.R.; Oppenheimer, C.; Horrocks, L.A.; Francis, P.W. Diurnal changes in volcanic plume chemistry observed by lunar and solar occultation spectroscopy. Geophys. Res. Lett. 2001, 28, 843–846. [Google Scholar] [CrossRef]
- Duffell, H.; Oppenheimer, C.; Burton, M. Volcanic gas emission rates measured by solar occultation spectroscopy. Geophys. Res. Lett. 2001, 28, 3131–3134. [Google Scholar] [CrossRef]
- Butz, A.; Dinger, A.S.; Bobrowski, N.; Kostinek, J.; Fieber, L.; Fischerkeller, C.; Giuffrida, G.B.; Hase, F.; Klappenbach, F.; Kuhn, J.; et al. Remote sensing of volcanic CO2, HF, HCl, SO2, and BrO in the downwind plume of Mt. Etna. Atmos. Meas. Tech. 2017, 10, 1–14. [Google Scholar] [CrossRef]
- Naughton, J.J.; Derby, J.V.; Glover, R.B. Infrared measurements on volcanic gas and fume: Kilauea eruption, 1968. J. Geophys. Res. 1969, 74, 3273–3277. [Google Scholar] [CrossRef]
- Mori, T.; Notsu, K.; Tohjima, Y.; Wakita, H. Remote detection of HCl and SO2 in volcanic gas from Unzen volcano, Japan. Geophys. Res. Lett. 1993, 20, 1355–1358. [Google Scholar] [CrossRef]
- Notsu, K.; Mori, T.; Igarishi, G.; Tohjima, Y.; Wakita, H. Infrared spectral radiometer: A new tool for remote measurement of SO2 of volcanic gas. Geochem. J. 1993, 27, 361–366. [Google Scholar] [CrossRef]
- Mori, T.K.; Notsu, Y.; Tohjima, H.; Wakita, P.M.; Nuccio, M.; Italiano, F. Remote detection of fumarolic gas chemistry at Vulcano, Italy, using an FT-IR spectral radiometer. Earth Planet. Sci. Lett. 1995, 134, 219–224. [Google Scholar] [CrossRef]
- Gerlach, T.M.; McGee, K.A.; Elias, T.; Sutton, A.J.; Doukas, M.P. Carbon dioxide emission rate of Kilauea Volcano: Implications for primary magma and the summit reservoir. J. Geophys. Res. 2002, 107, 2189. [Google Scholar] [CrossRef]
- Aiuppa, A.; Fiorani, L.; Santoro, S.; Parracino, S.; Nuvoli, M.; Chiodini, G.; Minopoli, C.; Tamburello, G. New groundbased lidar enables volcanic CO2 flux measurements. Sci. Rep. 2015, 5, 13614. [Google Scholar] [CrossRef] [PubMed]
- Queisser, M.; Burton, M.; Allan, G.; Chiarugi, A. Portable laser spectrometer for airborne and ground-based remote sensing of geological CO2 emissions. Opt. Lett. 2017, 42, 2782–2785. [Google Scholar] [CrossRef] [PubMed]
- Goff, F.; Love, S.P.; Warren, R.G.; Counce, D.; Obenholzner, J.; Siebe, C.; Schmidt, S.C. Passive infrared remote sensing evidence for large, intermittent CO2 emissions at Popocatépetl volcano, Mexico. Chem. Geol. 2001, 177, 133–156. [Google Scholar] [CrossRef]
- Stremme, W.; Krueger, A.; Harig, R.; Grutter, M. Volcanic SO2 and SiF4 visualization using 2-D thermal emission spectroscopy-Part 1: Slant-columns and their ratios. Atmos. Meas. Tech. 2012, 5, 275–288. [Google Scholar] [CrossRef]
- Prata, A.; Bernardo, C. Retrieval of sulphur dioxide froma ground-based thermal infrared imaging camera. Atmos. Meas. Tech. 2014, 7, 2807–2828. [Google Scholar] [CrossRef]
- Gabrieli, A.; Wright, R.; Lucey, P.G.; Porter, J.N.; Garbeil, H.; Pilger, E.; Wood, M. Characterization and initial field test of an 8–14 μm thermal infrared hyperspectral imager for measuring SO2 in volcanic plumes. Bull. Volcanol. 2016, 78, 73. [Google Scholar] [CrossRef]
- Love, S.P.; Goff, F.; Counce, D.; Siebe, C.; Delgado, H. Passive infrared spectroscopy of the eruption plume at Popocatepetl volcano, Mexico. Nature 1998, 396, 563–567. [Google Scholar] [CrossRef]
- Krueger, A.; Stremme, W.; Harig, R.; Grutter, M. Volcanic SO2 and SiF4 visualization using 2-D thermal emission spectroscopy—Part 2: Wind propagation and emission rates. Atmos. Meas. Tech. 2013, 6, 47–61. [Google Scholar] [CrossRef]
- Friedl-Vallon, F.; Gulde, T.; Hase, F.; Kleinert, A.; Kulessa, T.; Maucher, G.; Neubert, T.; Olschewski, F.; Piesch, C.; Preusse, P.; et al. Instrument concept of the imaging Fourier transform spectrometer GLORIA. Atmos. Meas. Tech. 2014, 7, 3565–3577. [Google Scholar] [CrossRef]
- Hinkley, E.D. (Ed.) Laser Monitoring of the Atmosphere; Topics in Applied Physics; Springer: Berlin/Heidelberg, Germany, 1976; Volume 14. [Google Scholar]
- Svanberg, S. Atomic and Molecular Spectroscopy, 2nd ed.; Springer Series on Atoms and Plasmas; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Edner, H.; Ragnarson, P.; Svanberg, S.; Wallinder, E.; Ferrara, R.; Cioni, R.; Raco, B.; Taddeucci, G. Total Fluxes of Sulphur Dioxide from the Italian Volcanoes Etna, Stromboli and Vulcano Measured by Differential Absorption Lidar and Passive Differential Optical Absorption Spectroscopy. J. Geophys. Res. 1994, 99, 18827–18838. [Google Scholar] [CrossRef]
- Weibring, P.; Edner, H.; Svanberg, S.; Cecchi, G.; Pantani, L.; Ferrara, R.; Caltabiano, T. Monitoring of Volcanic Sulphur Dioxide Emissions using Differential Absorption Lidar (DIAL), Differential Optical Absorption Spectroscopy (DOAS) and Correlation Spectroscopy (COSPEC). Appl. Phys. B 1998, 67, 419–426. [Google Scholar] [CrossRef]
- Weckwerth, T.M.; Weber, K.J.; Turner, D.D.; Spuler, S.M. Validation of a Water Vapor Micropulse Differential Absorption Lidar (DIAL). J. Atmos. Ocean Technol. 2016, 33, 2353–2372. [Google Scholar] [CrossRef]
- Barnes, J.E.; Bronner, S.; Beck, R.; Parikh, N.C. Boundary layer scattering measurements with a charge-coupled device camera lidar. Appl. Opt. 2003, 42, 2647–2652. [Google Scholar] [CrossRef] [PubMed]
- Flock, S. LED-Lidar—Theoretische und Experimentelle Machbarkeitsstudie zur Realisierung Eines Bistatischen, LED-Basierten Lidarsystems. Master’s Thesis, University of Heidelberg, Heidelberg, Germany, 2012. (In German). [Google Scholar]
- Nadeau, P.A.; Palma, J.L.; Waite, G.P. Linking Volcanic Tremor, Degassing, and Eruption Dynamics via SO2 Imaging. Geophys. Res. Lett. 2011, 38, 1. [Google Scholar] [CrossRef]
- Kern, C.; Lübcke, P.; Bobrowski, N.; Campion, R.; Mori, T.; Smekens, J.-F.; Stebel, K.; Tamburello, G.; Burton, M.; Platt, U.; et al. Intercomparison of SO2 camera systems for imaging volcanic gas plumes. J. Volcanol. Geotherm. Res. 2015, 300, 22–36. [Google Scholar] [CrossRef]
- Gliß, J.; Stebel, K.; Kylling, A.; Sudbø, A. Optical flow gas velocity analysis in plumes using UV cameras—Implications for SO2-emission-rate retrievals investigated at Mt. Etna, Italy, and Guallatiri, Chile. Atmos. Meas. Tech. Discuss. 2017. [Google Scholar] [CrossRef]
- Lübcke, P.; Bobrowski, N.; Illing, S.; Kern, C.; Vogel, L.; Platt, U. On the absolute calibration of SO2 Cameras. Atmos. Meas. Tech. 2013, 6, 677–696. [Google Scholar] [CrossRef]
- Rusch, P.; Harig, R. 3-D Reconstruction of Gas Clouds by Scanning Imaging IR Spectroscopy and Tomography. IEEE Sens. J. 2010, 10, 599–603. [Google Scholar] [CrossRef]
- Lohberger, F.; Hönninger, G.; Platt, U. Ground Based Imaging Differential Optical Absorption Spectroscopy of Atmospheric Gases. Appl. Opt. 2004, 43, 4711–4717. [Google Scholar] [CrossRef] [PubMed]
- Bobrowski, N.; Hönninger, G.; Lohberger, F.; Platt, U. IDOAS: A new monitoring technique to study the 2D distribution of volcanic gas emissions. J. Volcanol. Geotherm. Res. 2006, 150, 329–338. [Google Scholar] [CrossRef]
- Louban, I.; Bobrowski, N.; Rouwet, D.; Inguaggiato, S.; Platt, U. Imaging DOAS for Volcanological Applications. Bull. Volcanol. 2009, 71, 753–765. [Google Scholar] [CrossRef]
- Lee, H.-L.; Kim, J.-H.; Ryu, J.; Kwon, S.; Noh, Y.; Gu, M. 2-dimensional Mapping of Sulfur Dioxide and Bromine Oxide at the Sakurajima Volcano with a Ground Based Scanning Imaging Spectrograph System. J. Opt. Soc. Korea 2010, 14, 204–208. [Google Scholar] [CrossRef]
- Wright, R.; Lucey, P.; Crites, S.; Horton, K.; Wood, M.; Garbeil, H. BBM/EM design of the thermal hyperspectral imager: An instrument for remote sensing of Earth’s surface, atmosphere and ocean, from a microsatellite platform. Acta Astronaut. 2013, 87, 182–192. [Google Scholar] [CrossRef]
- Gabrieli, A.; Porter, J.N.; Wright, R.; Lucey, P.G. Validating the accuracy of SO2 gas retrievals in the thermal infrared (8–14 μm). Bull. Volcanol. 2017, 79, 80. [Google Scholar] [CrossRef]
- Kuhn, J.; Bobrowski, N.; Lübcke, P.; Vogel, L.; Platt, U. A Fabry-Pérot Interferometer Based Camera for the two-dimensional Mapping of SO2-Distributions. J. Atmos. Meas. Tech. 2014, 7, 3705–3715. [Google Scholar] [CrossRef]
- Kuhn, J.; Platt, U.; Bobrowski, N.; Lübcke, P.; Wagner, T. Fabry-Perot interferometer based imaging of atmospheric trace gases. In Proceedings of the 10th EARSeL SIG Imaging Spectroscopy Workshop, Zurich, Switzerland, 19–21 April 2017. [Google Scholar]
- Eisenhauer, F.; Raab, W. Visible/infrared imaging spectroscopy and energy-resolving detectors. Annu. Rev. Astron. Astrophys. 2015, 53, 155–197. [Google Scholar] [CrossRef]
- Bluth, G.J.S.; Shannon, J.M.; Watson, I.M.; Prata, A.J.; Realmuto, V.J. Development of an ultra-violet digital camera for volcanic SO2 imaging. J. Volcanol. Geotherm. Res. 2007, 161, 47–56. [Google Scholar] [CrossRef]
- Kern, C.; Deutschmann, T.; Werner, C.; Sutton, A.J.; Elias, T.; Kelly, P.J. Improving the accuracy of SO2 column densities and emission rates obtained from upward-looking UV-spectroscopic measurements of volcanic plumes by taking realistic radiative transfer into account. J. Geophys. Res. 2012, 117, D20302. [Google Scholar] [CrossRef]
- Smekens, J.-F.; Burton, M.R.; Clarke, A.B. Validation of the SO2 Camera for High Temporal and Spatial Resolution Monitoring of SO2 Emissions. J. Volcanol. Geotherm. Res. 2015, 300, 37–47. [Google Scholar] [CrossRef]
- Prata, A.; Bernardo, C. Retrieval of volcanic ash particle size, mass and optical depth from a ground-based thermal infrared camera. J. Volcanol. Geotherm. Res. 2009, 186, 91–107. [Google Scholar] [CrossRef]
- Lopez, T.; Thomas, H.E.; Prata, A.J.; Amigo, A.; Fee, D.; Moriano, D. Volcanic plume characteristics determined using an infrared imaging camera. J. Volcanol. Geotherm. Res. 2015, 300, 148–166. [Google Scholar] [CrossRef]
- Sandsten, J.; Edner, H.; Svanberg, S. Gas imaging by infrared gas-correlation spectrometry. Opt. Lett. 1996, 21, 1945–1947. [Google Scholar] [CrossRef] [PubMed]
- Sandsten, J.; Edner, H.; Svanberg, S. Gas visualization of industrial hydrocarbon emissions. Opt. Express 2004, 12, 1443–1451. [Google Scholar] [CrossRef] [PubMed]
- Prata, A. Infrared radiative transfer calculations for volcanic ash clouds. Geophys. Res. Lett. 1989, 16, 1293–1296. [Google Scholar] [CrossRef]
- Levelt, P.F.; Hilsenrath, E.; Leppelmeier, G.W.; van Den Oord, G.H.J.; Bhartia, P.K.; Tamminen, J.; De Haan, J.F.; Veefkind, P. Science Objectives of the Ozone Monitoring Instrument. Geosci. Remote Sens. 2006, 44, 1199–1208. [Google Scholar] [CrossRef]
- General, S.; Bobrowski, N.; Pöhler, D.; Weber, K.; Fischer, C.; Platt, U. Airborne I-DOAS measurements at Mt. Etna BrO and OClO evolution in the plume. J. Volcanol. Geotherm. Res. 2015, 300, 175–186. [Google Scholar] [CrossRef]
- Kern, C.; Deutschmann, T.; Vogel, L.; Wöhrbach, M.; Wagner, T.; Platt, U. Radiative transfer corrections for accurate spectroscopic measurements of volcanic gas emissions. Bull. Volcanol. 2010, 72, 233–247. [Google Scholar] [CrossRef]
- Ward, T.V.; Zwick, H.H. Gas cell correlation spectrometer: GASPEC. Appl. Opt. 1975, 14, 2896–2904. [Google Scholar] [CrossRef] [PubMed]
- Bobrowski, N. Volcanic Gas Studies by Multi Axis Differential Optical Absorption Spectroscopy. Diploma Thesis, University of Heidelberg, Heidelberg, Germany, 2002. [Google Scholar]
- Johansson, M.; Galle, B.; Zhang, Y.; Rivera, C.; Chen, D.; Wyser, K. The dual-beam mini-DOAS technique—Measurements of volcanic gas emission, plume height and plume speed with a single instrument. Bull. Volcanol. 2009, 71, 747–751. [Google Scholar] [CrossRef]
- Mori, T.; Burton, M. The SO2 camera: A simple, fast and cheap method for ground-based imaging of SO2 in volcanic plumes. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Valade, S.A.; Harris, A.J.L.; Cerminara, M. Plume Ascent Tracker: Interactive Matlab Software for Analysis of Ascending Plume. Comput. Geosci. C 2014, 66, 132–144. [Google Scholar] [CrossRef]
- Fickel, M. Measurement of Trace Gas Fluxes from Point Sources with Multi-Axis Differential Optical Absorption Spectroscopy. Diploma Thesis, University of Heidelberg, Heidelberg, Germany, 2008. [Google Scholar]
- Millán, M.M. Remote sensing of Air Pollutants. A Study of some Atmospheric Scattering Effects. Atmos. Environ. 1980, 14, 1241–1253. [Google Scholar] [CrossRef]
- Kern, C. Spectroscopic Measurements of Volcanic Gas Emissions in the Ultra-Violet Wavelength Region. Ph.D. Thesis, Institute of Environmental Physics, The Faculty of Physics and Astronomy, University of Heidelberg, Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Boichu, M.; Oppenheimer, C.; Tsanev, V.; Kyle, P.R. High temporal resolution SO2 flux measurements at Erebus volcano, Antarctica. J. Volcanol. Geotherm. Res. 2010, 190, 325–336. [Google Scholar] [CrossRef]
- McGonigle, A.J.S.; Aiuppa, A.; Ripepe, M.; Kantzas, E.P.; Tamburello, G. Spectroscopic capture of 1 Hz volcanic SO2 fluxes and integration with volcano geophysical data. Geophys. Res. Lett. 2009, 36, L21309. [Google Scholar] [CrossRef]
- Moussallam, Y.; Philipson, B.; Curtis, A.; Barnie, T.; Moussallam, M.; Peters, N.; Schipper, C.I.; Aiuppa, A.; Giudice, G.; Amigo, A.; et al. Sustaining persistent lava lakes: Observations from high-resolution gas measurements at Villarrica volcano, Chile. Earth Planet. Sci. Lett. 2016, 454, 237–247. [Google Scholar] [CrossRef]
- Allard, P.; Burton, M.; Sawyer, G.; Bani, P. Degassing dynamics of basaltic lava lake at a top-ranking volatile emitter: Ambrym volcano, Vanuatu arc. Earth Planet. Sci. Lett. 2016, 448, 69–80. [Google Scholar] [CrossRef]
- Nadeau, P.A.; Werner, C.A.; Waite, G.P.; Carn, S.A.; Brewer, I.D.; Elias, T.; Sutton, A.J.; Kern, C.; Patrick, M.R. Using SO2 camera imagery and seismicity to examine degassing and gas accumulation at Kīlauea Volcano, May 2010. J. Volcanol. Geotherm. Res. 2015, 300, 70–80. [Google Scholar] [CrossRef]
- Tamburello, G.; Aiuppa, A.; Kantzas, E.P.; McGonigle, A.J.S.; Ripepe, M. Passive vs. active degassing modes at an open-vent volcano (Stromboli, Italy). Earth Planet. Sci. Lett. 2012, 359, 106–116. [Google Scholar] [CrossRef]
- Tamburello, G.; Aiuppa, A.; McGonigle, A.J.S.; Allard, P.; Cannata, A.; Giudice, G.; Kantzas, E.P.; Pering, T.D. Periodic volcanic degassing behavior: The Mount Etna example. Geophys. Res. Lett. 2013, 40, 4818–4822. [Google Scholar] [CrossRef]
- Waite, G.P.; Nadeau, P.A.; Lyons, J.J. Variability in eruption style and associated very long period events at Fuego volcano, Guatemala. J. Geophys. Res. Solid Earth 2013, 118, 1526–1533. [Google Scholar] [CrossRef]
- Burton, M.R.; Prata, F.; Platt, U. Volcanological applications of SO2 cameras. J. Volcanol. Geotherm. Res. 2015, 300, 2–6. [Google Scholar] [CrossRef]
- Dalton, M.P.; Waite, G.P.; Watson, I.M.; Nadeau, P.A. Multiparameter quantification of gas release during weak Strombolian eruptions at Pacaya Volcano, Guatemala. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Lopez, T.; Wilson, D.F.; Prata, F.; Dehn, J. Characterization and interpretation of volcanic activity at Karymsky Volcano, Kamchatka, Russia, using observations of infrasound, volcanic emissions, and thermal imagery. Geochem. Geophys. Geosyst. 2013, 14. [Google Scholar] [CrossRef]
- Pering, T.D.; Tamburello, G.; McGonigle, A.J.S.; Aiuppa, A.; Cannata, A.; Giudice, G.; Patanè, D. High time resolution fluctuations in volcanic carbon dioxide degassing from Mount Etna. J. Volcanol. Geotherm. Res. 2014, 270, 115–121. [Google Scholar] [CrossRef]
- Barnie, T.; Bombrun, M.; Burton, M.R.; Harris, A.J.L.; and Sawyer, G. Quantification of gas and solid emissions during Strombolian explosions using simultaneous sulphur dioxide and infrared camera observations. J. Volcanol. Geothermal Res. 2015, 167–174. [Google Scholar] [CrossRef]
- D’Aleo, R.; Bitetto, M.; Delle Donne, D.; Tamburello, G.; Battaglia, A.; Coltelli, M.; Aiuppa, A. Spatially resolved SO2 flux emissions from Mt Etna. Geophys. Res. Lett. 2016, 43, 7511–7519. [Google Scholar] [CrossRef] [PubMed]
- Delle Donne, D.; Ripepe, M.; Lacanna, G.; Tamburello, G.; Bitetto, M.; Aiuppa, A. Gas mass derived by infrasound and UV cameras: Implications for mass flow rate. J. Volcanol. Geotherm. Res. 2016, 325, 169–178. [Google Scholar] [CrossRef]
- Delle Donne, D.; Tamburello, G.; Aiuppa, A.; Bitetto, M.; Lacanna, G.; D’Aleo, R.; Ripepe, M. Exploring the explosive-effusive transition using permanent ultra-violet cameras. J. Geophys. Res. Solid Earth 2017, 122, 4377–4394. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Kyle, P.R. Probing the magma plumbing of Erebus volcano, Antarctica, by open-path FTIR spectroscopy of gas emissions. J. Volcanol. Geotherm. Res. 2008, 177, 743–754. [Google Scholar] [CrossRef]
- La Spina, A.; Burton, M.; Salerno, G.G. Unravelling the processes controlling gas emissions from the central and northeast craters of Mt. Etna. J. Volcanol. Geotherm. Res. 2010, 198, 368–376. [Google Scholar] [CrossRef]
- La Spina, A.; Burton, M.; Allard, P.; Alparone, S.; Muré, F. Open-path FTIR spectroscopy of magma degassing processes during eight lava fountains on Mount Etna. Earth Planet. Sci. Lett. 2015, 413, 123–134. [Google Scholar] [CrossRef]
- Burton, M.; Allard, P.; Muré, F.; La Spina, A. Magmatic gas composition reveals the source depth of slug-driven Strombolian explosive activity. Science 2007, 317, 227–230. [Google Scholar] [CrossRef] [PubMed]
- La Spina, A.; Burton, M.R.; Harig, R.; Mure, F.; Rusch, P.; Jordan, M.; Caltabiano, T. New insights into volcanic processes at Stromboli from Cerberus, a remote-controlled open-path FTIR scanner system. J. Volcanol. Geotherm. Res. 2013, 249, 66–76. [Google Scholar] [CrossRef]
- Schwandner, F.M.; Gunson, M.R.; Miller, C.E.; Carn, S.A.; Eldering, A.; Krings, T.; Verhulst, K.R.; Schimel, D.S.; Nguyen, H.M.; Crisp, D.; et al. Spaceborne detection of localized carbon dioxide sources. Science 2017, 358, eaam5782. [Google Scholar] [CrossRef] [PubMed]
- Oppenheimer, C.; Bani, P.; Calkins, J.; Burton, M.; Sawyer, G. Rapid FTIR sensing of volcanic gases released by Strombolian explosions at Yasur volcano, Vanuatu. Appl. Phys. B 2006, 85, 453–460. [Google Scholar] [CrossRef]
- Francis, P.; Chaffin, C.; Maciejewski, A.; Oppenheimer, C. Remote determination of SiF4 in volcanic plumes: A new tool for volcano monitoring. Geophys. Res. Lett. 1996, 23, 249–252. [Google Scholar] [CrossRef]
- Taquet, N.; Meza Hernández, I.; Stremme, W.; Bezanilla, A.; Grutter, M.; Campion, R.; Palm, M.; Boulesteix, T. Continuous measurements of SiF4 and SO2 by thermal emission spectroscopy: Insight from a 6-month survey at the Popocatépetl volcano. J. Volcanol. Geotherm. Res. 2017, 341, 255–268. [Google Scholar] [CrossRef]
- Edmonds, M.; Herd, R.A.; Galle, B.; Oppenheimer, C. Automated, high time-resolution measurements of SO2 flux at Soufrière Hills Volcano, Montserrat. Bull. Volcanol. 2003, 65, 578–586. [Google Scholar] [CrossRef]
- Wilkes, T.C.; McGonigle, A.J.R.; Willmott, T.D.; Pering, T.D.; Cook, J.M. Low-cost 3D printed 1 nm resolution smartphone sensor-based spectrometer: Instrument design and application in ultraviolet spectroscopy. Opt. Lett. 2017, 42, 4323–4326. [Google Scholar] [CrossRef] [PubMed]
- Wilkes, T.C.; Pering, T.D.; McGonigle, A.J.S.; Tamburello, G.; Willmott, J.R. A low cost smartphone sensor-based UV camera for volcanic SO2 emission measurements. Remote Sens. 2017, 9, 27. [Google Scholar] [CrossRef]
- Kern, C.; Werner, C.; Elias, T.; Sutton, A.J.; Lübcke, P. Applying UV cameras for SO2 detection to distant or optically thick plumes. J. Volcanol. Geotherm. Res. 2013, 262, 80–89. [Google Scholar] [CrossRef]
- Wagner, T.; Dix, B.; Friedeburg, C.; Frieß, U.; Sanghavi, S.; Sinreich, R.; Platt, U. MAX-DOAS O4 measurements: A new technique to derive information on atmospheric aerosols—Principles and Information content. J. Geophys. Res. 2004, 109, D22205. [Google Scholar] [CrossRef]
- Frieß, U.; Monks, P.S.; Remedios, J.J.; Rozanov, A.; Sinreich, R.; Wagner, T.; Platt, U. MAX-DOAS O4 measurements: A new technique to derive information on atmospheric aerosols. (II) Modelling studies. J. Geophys. Res. 2006, 111, D14203. [Google Scholar] [CrossRef]
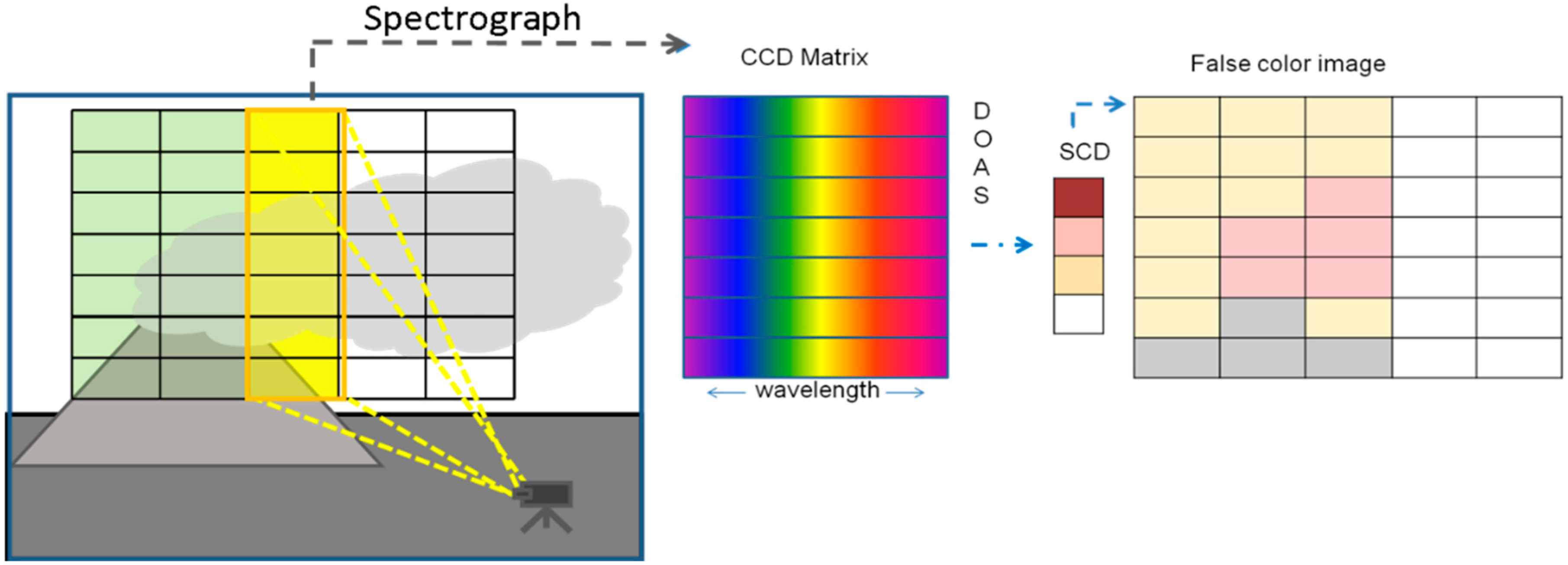
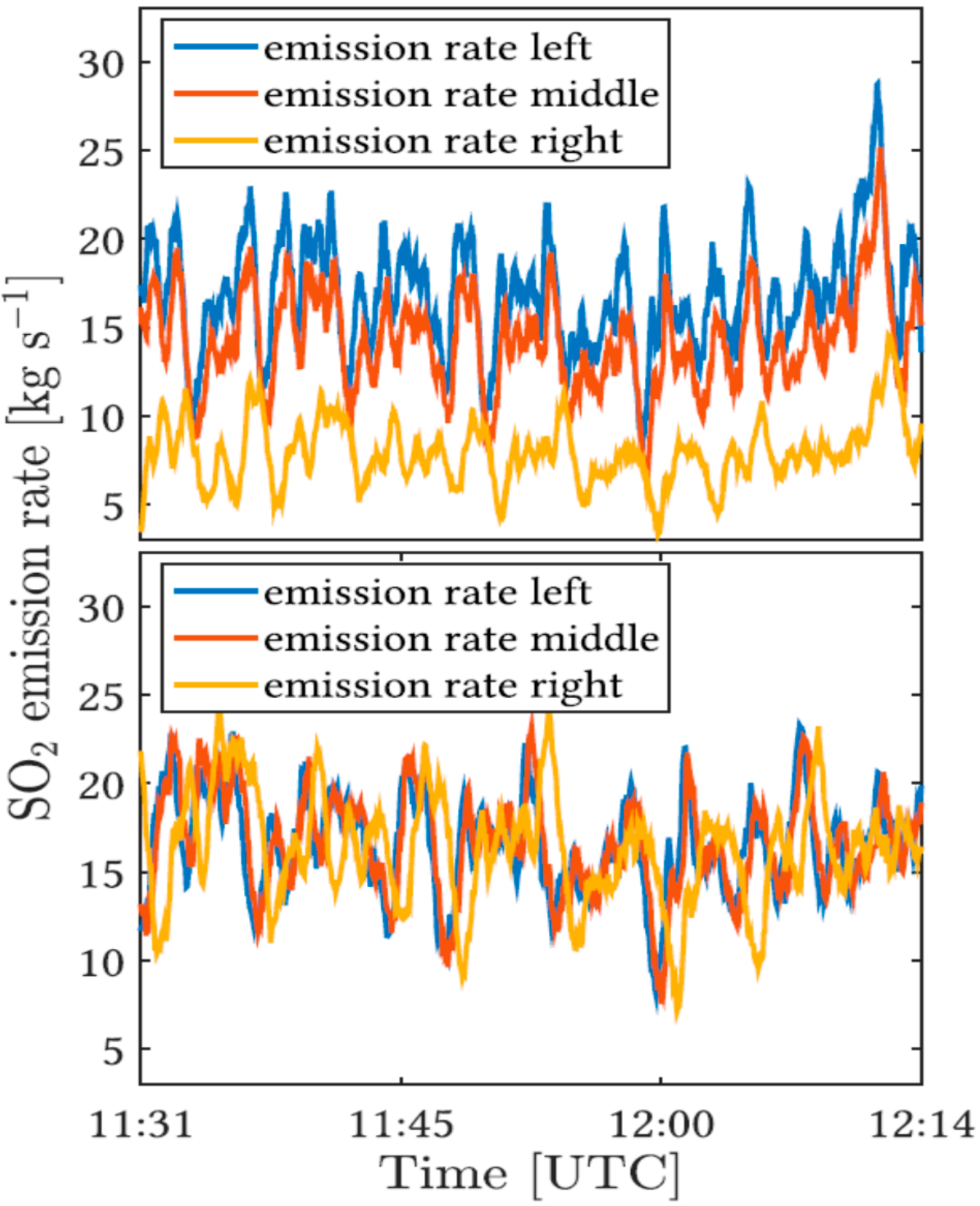
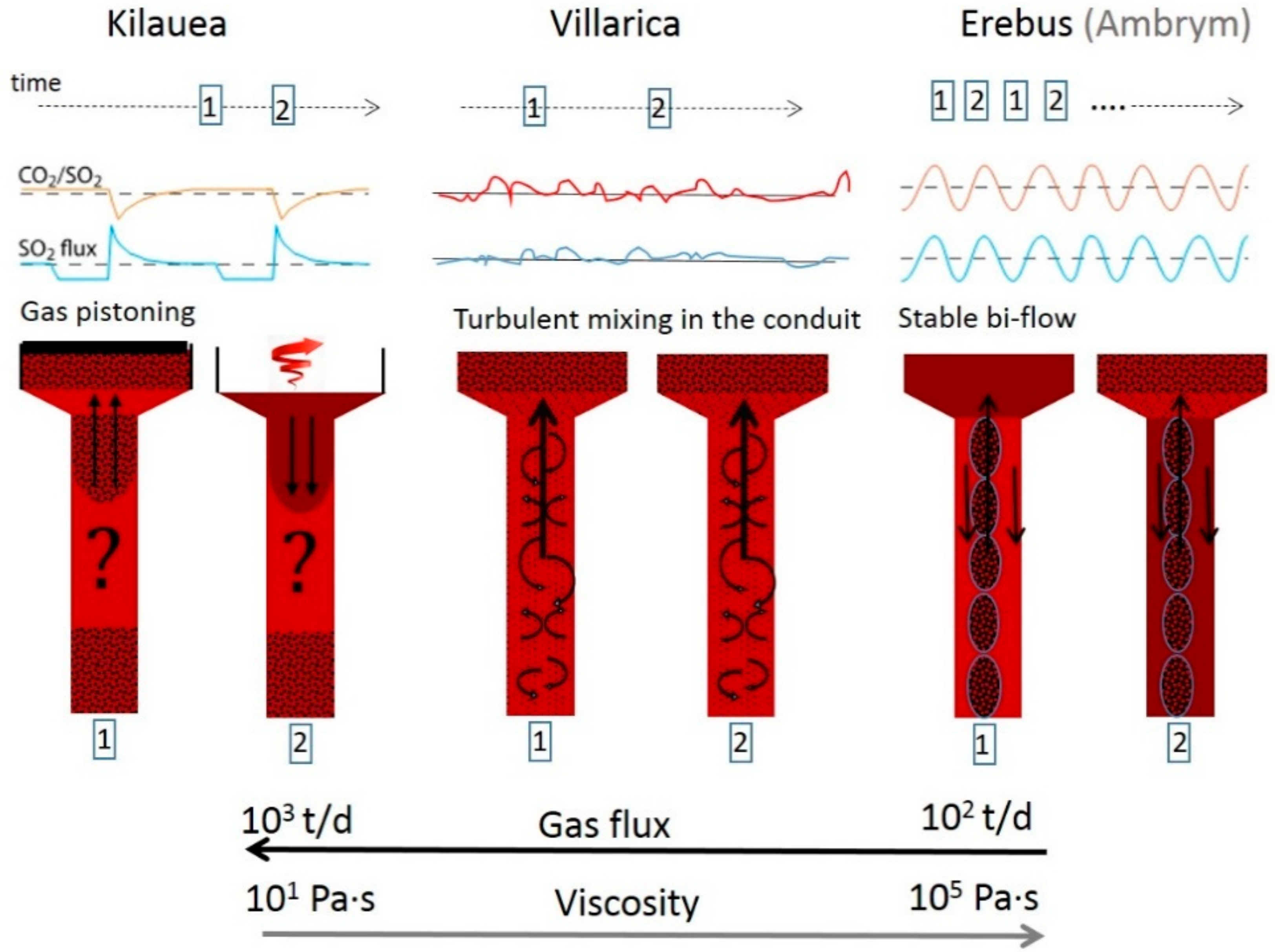
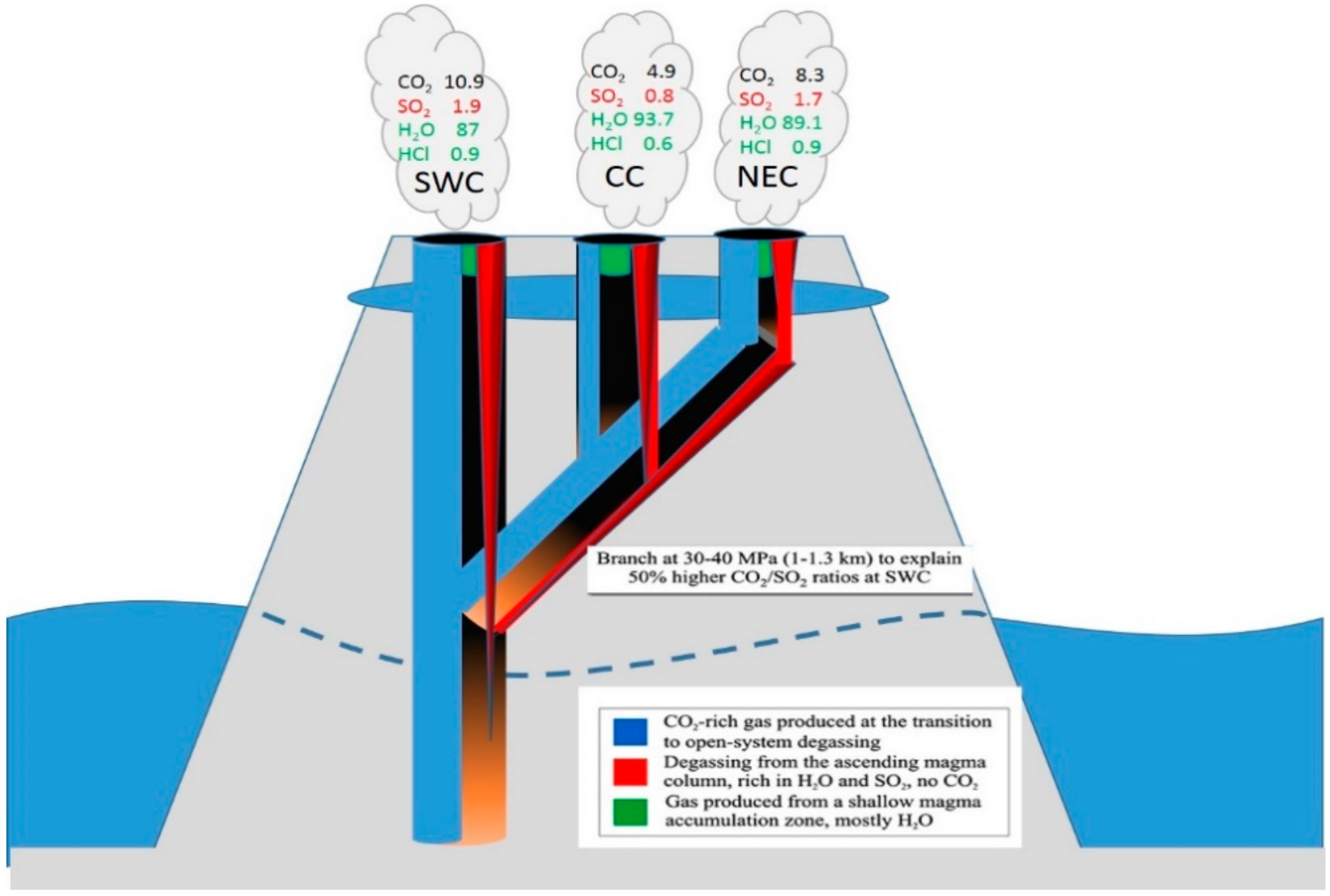
| Imaging Principle | Detector Type | Examples/Comments |
|---|---|---|
| Whisk-broom | Spectrometer or Michelson Interferometer | Experimental instruments [55] |
| Filter | not used | |
| Fabry-Pérot Interferometer | Theoretical studies, [79,80] | |
| Gas Correlation | Presently not used | |
| Push-broom | Spectrometer | I-DOAS, [74], Imaging Sagnac-Interferometer [57] FTIR |
| Filter | Presently not used A | |
| Fabry-Pérot Interferometer | Presently not used A | |
| Gas Correlation | Presently not used A | |
| Full-Frame | Wavelength sensitive pixels | Future Technology (e.g., [81]) |
| Filter | UV SO2-camera e.g., [19,82] and references in the text | |
| Fabry-Pérot Interferometer | Theoretical studies in the UV [79], in use in the IR [60] | |
| Gas correlation | Presently not used A |
| Volcano | Seismic VLP | Seismic Tremor | Acoustic | Thermal | Reference |
|---|---|---|---|---|---|
| Pacaya, Guatemala | − | − | − | − | [110] |
| Asama, Japan | + | − | − | − | [107] |
| Fuego, Guatemala | − | + (time shifted) | − | − | [68] |
| Stromboli, Italy | + | − | − | − | [106] |
| Etna, Italy | − | + | − | − | [107] |
| Karymsky, Kamchatka | − | − | 0 | 0 | [111] |
| Fuego, Guatemala | + | − | − | − | [108] |
| Etna, Italy | − | + | − | − | [112] |
| Stromboli, Italy | − | − | − | − | [113] |
| Stromboli, Italy | + | − | − | − | [109] |
| Hawaii, USA | − | + | − | − | [105] |
| Etna, Italy | − | 0 | 0 | − | [114] |
| Stromboli, Italy | − | − | + | 0 | [115] |
| Stromboli, Italy | + | − | 0 | 0 | [116] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platt, U.; Bobrowski, N.; Butz, A. Ground-Based Remote Sensing and Imaging of Volcanic Gases and Quantitative Determination of Multi-Species Emission Fluxes. Geosciences 2018, 8, 44. https://doi.org/10.3390/geosciences8020044
Platt U, Bobrowski N, Butz A. Ground-Based Remote Sensing and Imaging of Volcanic Gases and Quantitative Determination of Multi-Species Emission Fluxes. Geosciences. 2018; 8(2):44. https://doi.org/10.3390/geosciences8020044
Chicago/Turabian StylePlatt, Ulrich, Nicole Bobrowski, and Andre Butz. 2018. "Ground-Based Remote Sensing and Imaging of Volcanic Gases and Quantitative Determination of Multi-Species Emission Fluxes" Geosciences 8, no. 2: 44. https://doi.org/10.3390/geosciences8020044
APA StylePlatt, U., Bobrowski, N., & Butz, A. (2018). Ground-Based Remote Sensing and Imaging of Volcanic Gases and Quantitative Determination of Multi-Species Emission Fluxes. Geosciences, 8(2), 44. https://doi.org/10.3390/geosciences8020044




