Interception of Rainfall in Successional Tropical Dry Forests in Brazil and Costa Rica
Abstract
1. Introduction
2. Materials and Methods
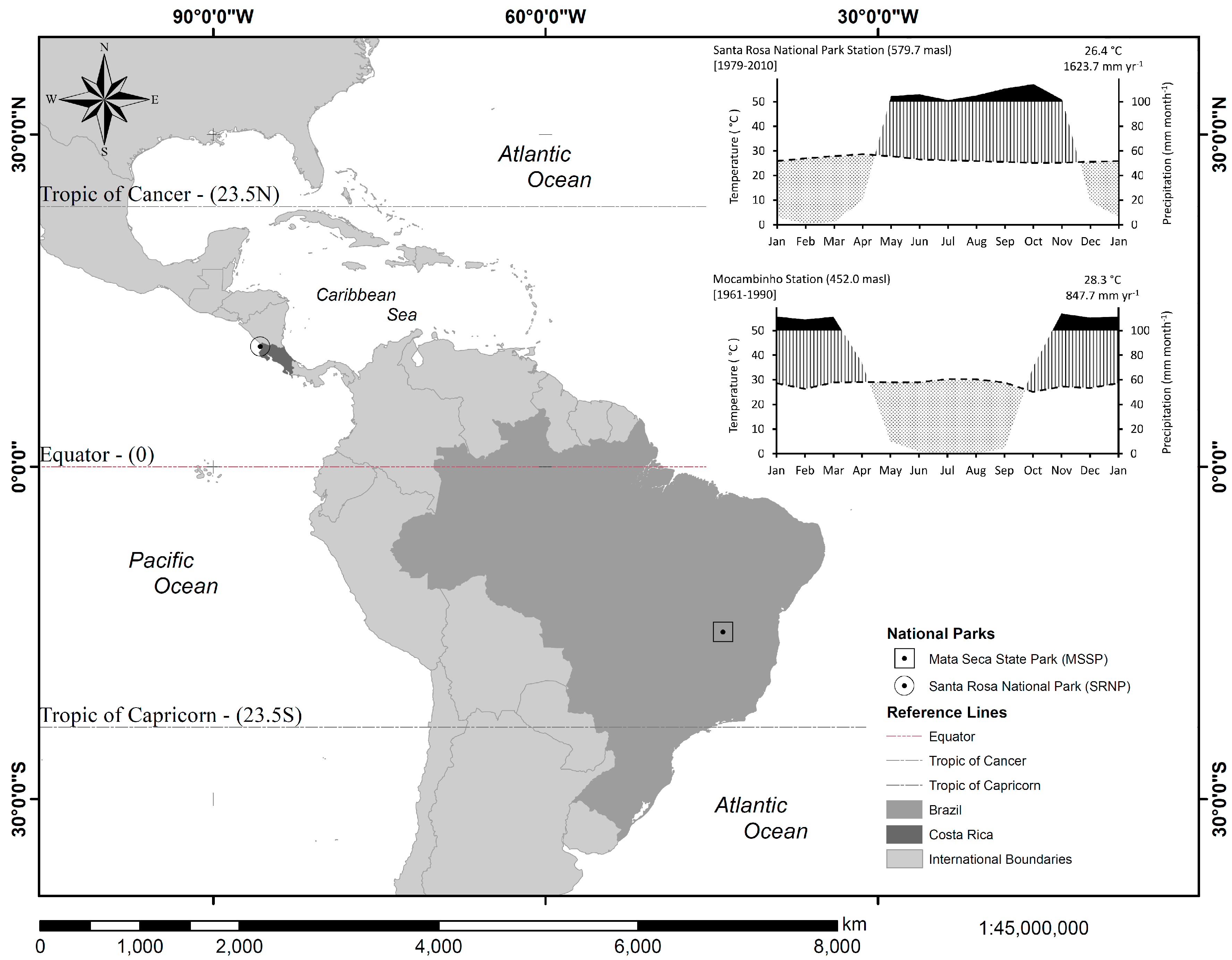
2.1. Study Sites
2.2. Experimental Design
2.3. Data Analysis
3. Results and Discussion
3.1. Meteorological Conditions
3.2. Structural Characteristics of Forests
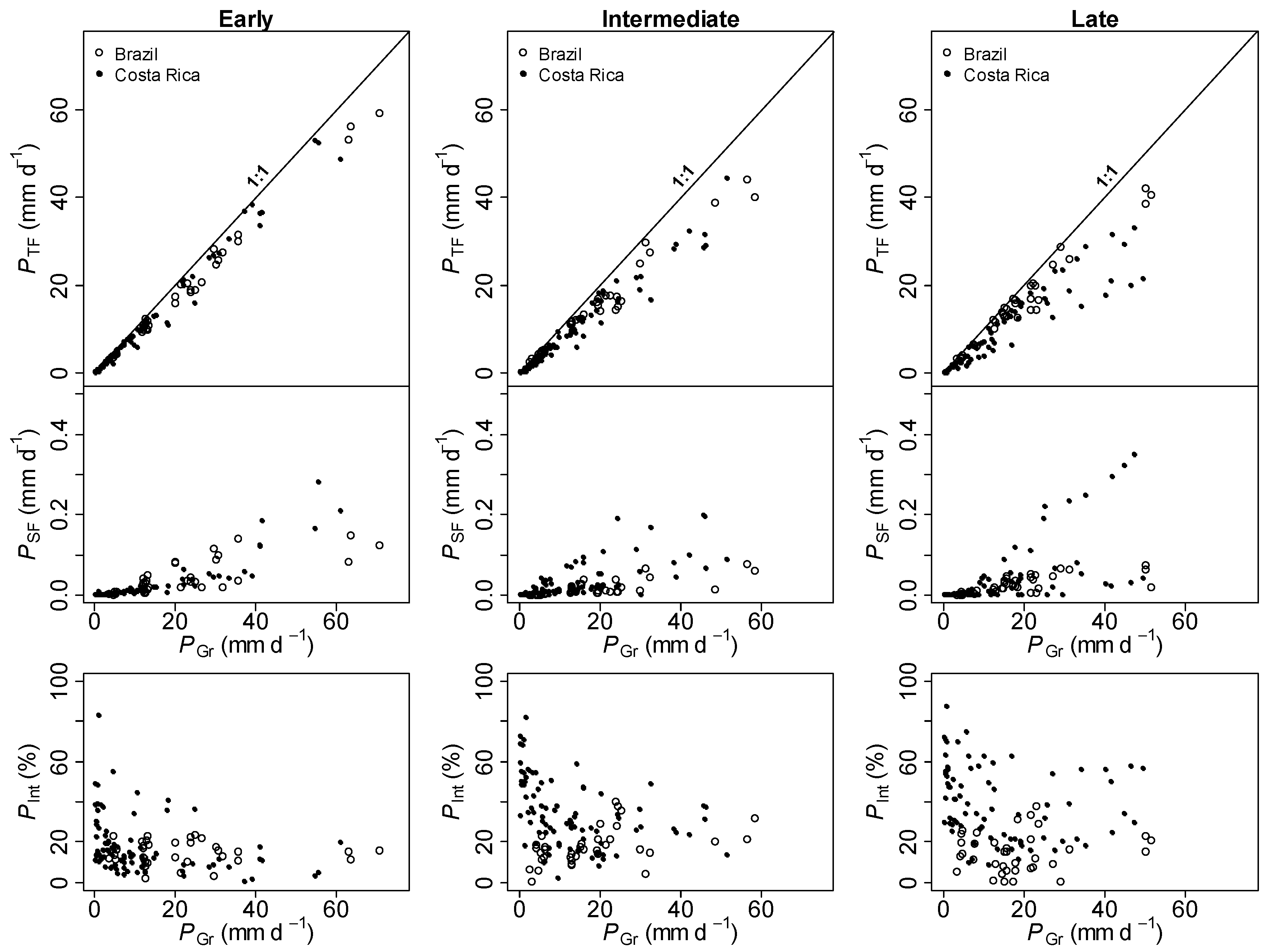
3.3. Water Fluxes and Forest Structure
3.4. Regression Models for Forest Interception Fluxes
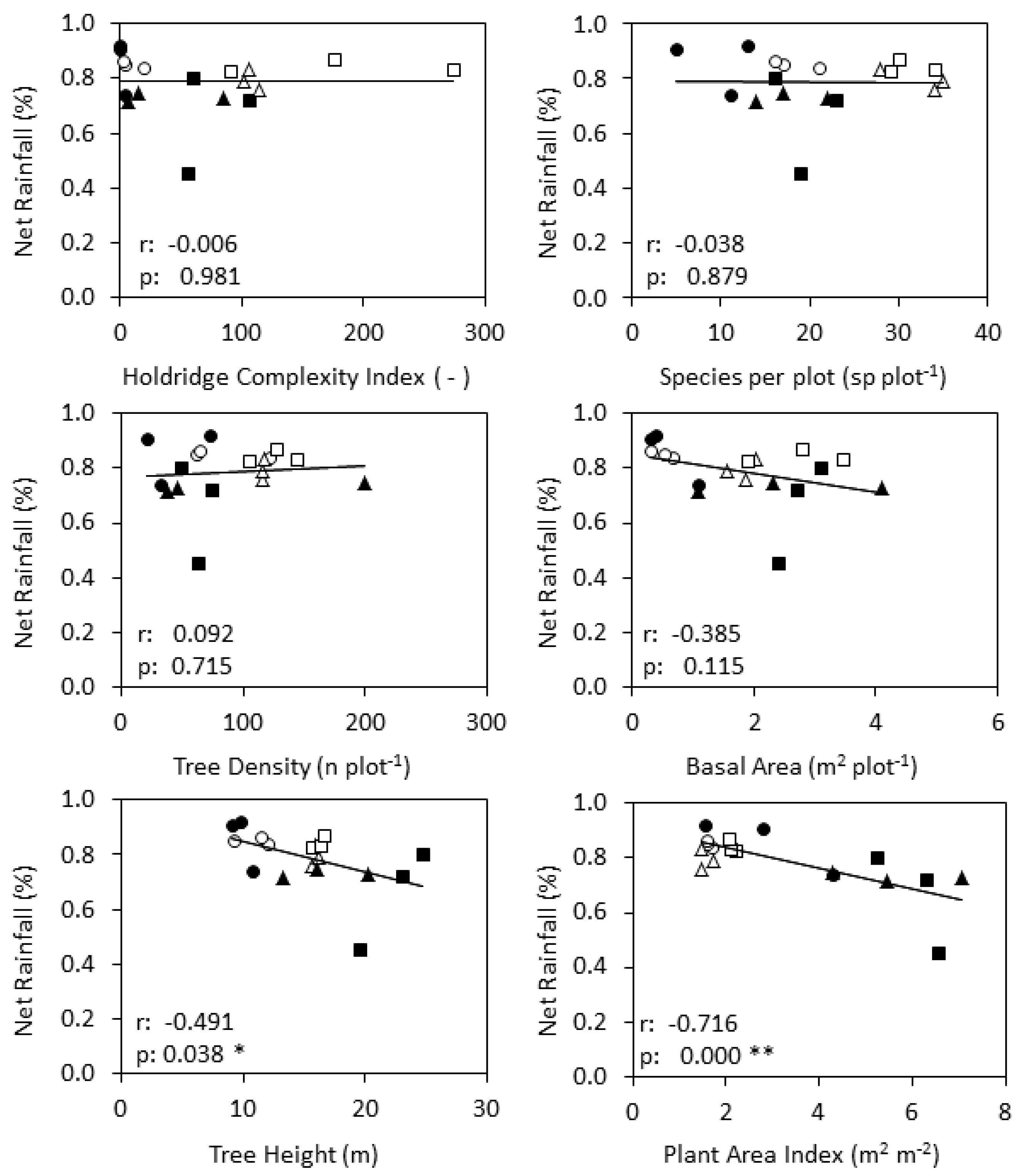
3.5. Relationship between Net Rainfall and Forest Structural Parameters
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holdridge, L.R.; Tosi, J.A. Life Zone Ecology; Tropical Science Center: San Jose, Costa Rica, 1967. [Google Scholar]
- Calvo-Alvarado, J.; Sánchez-Azofeifa, A.; Portillo-Quintero, C. Neotropical Seasonally Dry Forests. In Encyclopedia of Biodiversity, 2nd ed.; Levin, S., Ed.; Academic Press: New York, NY, USA, 2013; pp. 488–500. [Google Scholar] [CrossRef]
- Portillo-Quintero, C.; Sánchez-Azofeifa, G. Extent and conservation of tropical dry forests in the Americas. Biol. Conserv. 2010, 143, 144–155. [Google Scholar] [CrossRef]
- Portillo-Quintero, C.; Sánchez-Azofeifa, A.; Calvo-Alvarado, J.; Quesada, M.; Espírito-Santo, M.M. The role of tropical dry forests for biodiversity, carbon and water conservation in the neotropics: Lessons learned and opportunities for its sustainable management. Reg. Environ. Chang. 2015, 15, 1039–1049. [Google Scholar] [CrossRef]
- Guswa, A.J. Canopy vs. Roots: Production and Destruction of Variability in Soil Moisture and Hydrologic Fluxes. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Pypker, T.; Levia, D.; Staelens, J.; Van Stan, J. Canopy structure in relation to hydrological and biogeochemical fluxes. In Forest Hydrology and Biogeochemistry. Ecological Studies (Analysis and Synthesis); Levia, D.F., Carlyle-Moses, D., Tanaka, T., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 371–388. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Cavelier, J.; Vargas, G. Procesos hidrológicos. In Ecología y Conservación de Bosques Neotropicales; Guariguata, M.R., Kattan, G.H., Eds.; Libro Universitario Regional (LUR): Cartago, Costa Rica, 2002; pp. 145–165. [Google Scholar]
- Gerrits, A. The Role of Interception in the Hydrological Cycle. Doctoral Thesis, Delft University of Technology, TU-Delf, The Netherlands, 2010. [Google Scholar]
- Crockford, R.; Richardson, D. Partitioning of rainfall into throughfall, stemflow and interception: Effect of forest type, ground cover and climate. Hydrol. Process. 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Oliveira-Freitas, J.P.; Teixeira-Dias, C.; Silva, E.; Tonello, K.C. Net precipitation in a semideciduous forest fragment in Vicosa city, MG. Rev. Árvore 2016, 40, 793–801. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, C.; Calvo-Alvarado, J.C. An Evaluation of Chapter 14: Rainfall Interception in Secondary Tropical Dry Forests. In Tropical Dry Forests in the Americas: Ecology, Conservation and Management; Sanchez-Azofeifa, A., Powers, J.S., Fernandes, G.W., Quesada, M., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 249–265. [Google Scholar]
- Zimmermann, B.; Zimmermann, A.; Scheckenbach, H.; Schmid, T.; Hall, J.; van Breugel, M. Changes in rainfall interception along a secondary forest succession gradient in lowland Panama. Hydrol. Earth Syst. Sci. 2013, 17, 4659–4670. [Google Scholar] [CrossRef]
- Calvo-Rodríguez, S.; Calvo-Alvarado, J.; Do Espírito-Santo, M.M.; Nunes, Y.R. Changes in forest structure and composition in a successional dry forest of Brazil. Rev. For. Mesoam. Kurú 2017, 14, 12–23. [Google Scholar] [CrossRef]
- Álvarez, M.; Cançado Anaya, F.; Ávila-Cabadilla, L.D.; Berbara, R.; Calvo-Alvarado, J.C.; Castillo Álvarez, A.; Quesada, M.; Rivard, B.; Sanza, V.; Stoner, K.; et al. Manual of Methods. Human, Ecological and Biophysical Dimensions of Tropical Dry Forests; Nassar, J.M., Rodríguez, J.P., Sánchez-Azofeifa, A., Garvin, T., Quesada, M., Eds.; Instituto Venezolano de Investigaciones Científicas (IVIC): Caracas, Venezuela, 2008.
- Kalacska, M.; Sanchez-Azofeifa, A.; Calvo-Alvarado, J.C.; Quesada, M.; Rivard, B.; Janzen, D. Species composition, similarity and diversity in three successional stages of a seasonally dry tropical forest. For. Ecol. Manag. 2004, 200, 227–247. [Google Scholar] [CrossRef]
- Madeira, B.G.; Espírito-Santo, M.M.; D’Ângelo Neto, S.; Nunes, Y.R.; Sánchez-Azofeifa, G.A. Changes in tree and liana communities along a successional gradient in a tropical dry forest in south-eastern Brazil. Plant Ecol. 2009, 201, 291–304. [Google Scholar] [CrossRef]
- Lloyd, C.R.; Marques ó, A. Spatial variability of throughfall and stemflow measurements in Amazonian rainforest. Agric. For. Meteorol. 1988, 42, 63–73. [Google Scholar] [CrossRef]
- Gerrits, A.; Savenije, H.; Veling, E.; Pfister, L. Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Frazer, G.; Canham, C.; Lertzman, K. Gap Light Analyzer (GLA), Version 2.0: Imaging Software to Extract Canopy Structure and Gap Light Transmission Indices from True-Colour Fisheye Photographs, Users Manual and Program Documentation; Simon Fraser University: Burnaby, BC, Canada; Institute of Ecosystem Studies: Millbrook, NY, USA, 1999. [Google Scholar]
- Paternoster, R.; Brame, R.; Mazerolle, P.; Piquero, A. Using the Correct Statistical Test for Equality of Regression Coefficients. Criminology 1998, 36, 859–866. [Google Scholar] [CrossRef]
- Lorenzon, A.S.; Dias, H.T.; Leite, H. Precipitação efetiva e interceptação da chuva em um fragmento florestal com diferentes estágios de regeneração. Rev. Árvore 2013, 37, 619–627. [Google Scholar] [CrossRef]
- Carlyle-Moses, D.E.; Gash, J.H. Rainfall Interception Loss by Forest Canopies. In Forest Hydrology and Biogeochemistry; Ecological Studies (Analysis and Synthesis); Levia, D., Carlyle-Moses, D., Tanaka, T., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 216, pp. 407–423. [Google Scholar]
- Spencer, S.; van Meerveld, H. Double funnelling in a mature coastal British Columbia forest: Spatial patterns of stemflow after infiltration. Hydrol. Process. 2016, 30, 4185–4201. [Google Scholar] [CrossRef]
| Stage | Brazil | Costa Rica |
|---|---|---|
| Early | Myracrodruon urundeuva | Cochlospermum vitifolium |
| Senegalia polyphylla | Genipa americana | |
| Gliricidia sepium | ||
| Luehea candida | ||
| Machaerium biovulatum | ||
| Quercus oleoides | ||
| Rehdera trinervis | ||
| Intermediate | Cnidoscolus pubescens | Astronium graveolens |
| Cochlospermum vitifolium | Ateleia hebert-smithii | |
| Handroanthus reticulatus | Bursera simarouba | |
| Cochlospermum vitifolium | ||
| Cordia panamensis | ||
| Lonchocarpus minimiflorus | ||
| Spondias mombin | ||
| Trophis racemosa | ||
| Late | Casearia selloana | Chrysophyllum brenesii |
| Combretum duarteanum | Exostema mexicanum | |
| Handroanthus chrysotrichus | Guettarda macrosperma | |
| Pseudopiptadenia contorta | Lysiloma divaricatum | |
| Sapranthus palanga | ||
| Semialarium mexicanum |
| Fluxes | Brazil | Costa Rica | ||||
|---|---|---|---|---|---|---|
| Early | Intermediate | Late | Early | Intermediate | Late | |
| Rainfall | 248.2 | 218.8 | 219.5 | 330.1 | 400.9 | 376.2 |
| Throughfall | 211.4 (85.2%) | 173.4 (79.2%) | 185.1 (84.3%) | 288.2 (87.3%) | 291.4 (72.7%) | 237.6 (63.2%) |
| Stemflow | 0.5 (0.2%) | 0.2 (0.1%) | 0.3 (0.1%) | 0.6 (0.2%) | 1.1 (0.3%) | 1.0 (0.3%) |
| Net Rainfall | 211.9 (85.4%) | 173.6 (79.3%) | 185.4 (84.4%) | 288.8 (87.5%) | 292.5 (73.0%) | 238.6 (63.4%) |
| Interception | 36.3 (14.6%) | 45.2 (20.7%) | 34.2 (15.6%) | 41.3 (12.5%) | 108.4 (27.0%) | 137.6 (36.6%) |
| Fluxes | Forest Stage | Country | n | Regression Parameters | Regression Coefficients | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | F | P | SE | α | β | ||||||
| Throughfall | Early | Costa Rica | 89 | 0.992 | 5512.9 | 0.000 | 1.564 | −0.285 | 0.899 | *** | |
| Brazil | 34 | 0.997 | 4733.1 | 0.000 | 1.186 | −0.131 | 0.858 | *** | |||
| Intermediate | Costa Rica | 89 | 0.980 | 2133.4 | 0.000 | 2.264 | −0.670 | ** | 0.776 | *** | |
| Brazil | 36 | 0.983 | 1002.5 | 0.000 | 1.944 | 0.903 | 0.743 | *** | |||
| Late | Costa Rica | 78 | 0.940 | 574.2 | 0.000 | 3.229 | 0.938 | * | 0.567 | *** | |
| Brazil | 36 | 0.982 | 898.7 | 0.000 | 1.947 | 0.750 | 0.802 | *** | |||
| Stemflow | Early | Costa Rica | 89 | 0.888 | 322.7 | 0.000 | 0.022 | −0.012 | *** | 0.003 | *** |
| Brazil | 34 | 0.762 | 46.8 | 0.000 | 0.027 | 0.001 | 0.002 | *** | |||
| Intermediate | Costa Rica | 89 | 0.759 | 39.6 | 0.000 | 0.052 | 0.005 | 0.002 | *** | ||
| Brazil | 36 | 0.764 | 42.1 | 0.000 | 0.013 | −0.002 | 0.001 | *** | |||
| Late | Costa Rica | 78 | 0.565 | 35.6 | 0.000 | 0.064 | −0.002 | 0.003 | *** | ||
| Brazil | 36 | 0.708 | 31.7 | 0.000 | 0.016 | 0.004 | 0.001 | *** | |||
| Net Rainfall | Early | Costa Rica | 89 | 0.992 | 5537.1 | 0.000 | 1.565 | −0.298 | 0.902 | *** | |
| Brazil | 34 | 0.997 | 4701.8 | 0.000 | 1.193 | −0.129 | 0.860 | *** | |||
| Intermediate | Costa Rica | 89 | 0.980 | 2160.1 | 0.000 | 2.257 | −0.665 | * | 0.779 | *** | |
| Brazil | 36 | 0.983 | 1002.1 | 0.000 | 1.948 | 0.901 | 0.744 | *** | |||
| Late | Costa Rica | 78 | 0.939 | 566.7 | 0.000 | 3.267 | 0.936 | * | 0.570 | *** | |
| Brazil | 36 | 0.981 | 892.8 | 0.000 | 1.957 | 0.754 | 0.803 | *** | |||
| Interception | Early | Costa Rica | 89 | 0.656 | 65.8 | 0.000 | 1.565 | 0.298 | 0.098 | *** | |
| Brazil | 34 | 0.893 | 125.4 | 0.000 | 1.193 | 0.129 | 0.140 | *** | |||
| Intermediate | Costa Rica | 89 | 0.817 | 174.3 | 0.000 | 2.257 | 0.665 | * | 0.221 | *** | |
| Brazil | 36 | 0.882 | 118.7 | 0.000 | 1.948 | −0.901 | 0.256 | *** | |||
| Late | Costa Rica | 78 | 0.900 | 71.0 | 0.000 | 3.267 | −0.936 | * | 0.430 | *** | |
| Brazil | 36 | 0.782 | 53.6 | 0.000 | 1.957 | −0.754 | 0.197 | *** | |||
| Generalized equations | |||||||||||
| Net Rainfall | Early | 123 | 0.988 | 9706.2 | 0.000 | 1.513 | −0.220 | 0.881 | *** | ||
| Intermediate | 125 | 0.962 | 3129.7 | 0.000 | 2.212 | −0.323 | 0.774 | *** | |||
| Stage | Country | Plot | Height (m) | Tree Density (trees plot−1) | Species (sp plot−1) | Basal Area (m2 plot−1) | Holdridge Complexity Index | Plant Area Index (m2 m−2) |
|---|---|---|---|---|---|---|---|---|
| Early | Brazil | CC3 | 11.9 | 121 | 21 | 0.7 | 20.0 | 1.7 |
| CC4 | 9.2 | 61 | 17 | 0.5 | 4.9 | 1.6 | ||
| CC5 | 11.4 | 64 | 16 | 0.3 | 3.6 | 1.6 | ||
| Average | 10.8 | 82 | 18 | 0.5 | 9.5 | 1.6 | ||
| Costa Rica | CR1E1 | 9.0 | 21 | 5 | 0.3 | 0.3 | 2.8 | |
| CR1E2 | 9.8 | 72 | 13 | 0.4 | 3.7 | 1.5 | ||
| CR1E3 | 10.8 | 32 | 11 | 1.1 | 4.4 | 4.3 | ||
| Average | 9.9 | 41.7 | 9.7 | 0.6 | 2.7 | 2.9 | ||
| Early Average | 10.4 | 61.8 | 13.8 | 0.5 | 6.1 | 2.2 | ||
| Intermediate | Brazil | IC1 | 15.6 | 116 | 34 | 1.9 | 114.8 | 1.5 |
| IC2 | 16.2 | 116 | 35 | 1.6 | 102.1 | 1.7 | ||
| IC7 | 15.9 | 117 | 28 | 2.0 | 106.1 | 1.5 | ||
| Average | 15.9 | 116.3 | 32.3 | 1.8 | 107.7 | 1.5 | ||
| Costa Rica | CR1I1 | 20.3 | 46 | 22 | 4.1 | 84.2 | 7.1 | |
| CR1I4 | 16.0 | 199 | 17 | 2.3 | 125.6 | 4.3 | ||
| CR1I5 | 13.3 | 38 | 14 | 1.1 | 7.8 | 5.5 | ||
| Average | 16.5 | 94.3 | 17.7 | 2.5 | 72.5 | 5.6 | ||
| Intermediate Averge | 16.2 | 105.3 | 25 | 2.2 | 90.1 | 3.6 | ||
| Late | Brazil | MC5 | 15.6 | 105 | 29 | 1.9 | 90.7 | 2.2 |
| MC6 | 16.3 | 143 | 34 | 3.5 | 273.9 | 2.1 | ||
| MC7 | 16.6 | 127 | 30 | 2.8 | 176.0 | 2.0 | ||
| Average | 16.2 | 125 | 31 | 2.7 | 180.2 | 2.1 | ||
| Costa Rica | CR1L1 | 23.0 | 74 | 23 | 2.7 | 105.7 | 6.3 | |
| CR1L2 | 19.5 | 63 | 19 | 2.4 | 56.0 | 6.6 | ||
| CR1L3 | 24.7 | 49 | 16 | 3.1 | 60.0 | 5.2 | ||
| Average | 22.4 | 62 | 19.3 | 2.7 | 73.9 | 6.0 | ||
| Late Average | 19.3 | 93.5 | 25.2 | 2.7 | 127.1 | 4.1 |
| Regional [Costa Rica + Brazil] | |||||||
|---|---|---|---|---|---|---|---|
| Regional Costa Rica + Brazil | Tree Height | Tree Density | Species | Basal Area | HCI | PAI | Rainfall Interception |
| Tree Height | 1.000 | ||||||
| Tree Density | 0.128 | 1.000 | |||||
| Species | 0.383 | 0.619 ** | 1.000 | ||||
| Basal Area | 0.847 ** | 0.271 | 0.494 * | 1.000 | |||
| HCI | 0.456 | 0.462 | 0.812 ** | 0.694 ** | 1.000 | ||
| PAI | 0.608 ** | −0.373 | −0.307 | 0.518 * | −0.113 | 1.000 | |
| Rainfall Interception | 0.491 * | 0.092 | 0.038 | 0.385 | 0.006 | 0.717 ** | 1.000 |
| Only Costa Rica | |||||||
| Tree Height | 1.000 | ||||||
| Tree Density | 0.137 | 1.000 | |||||
| Species | 0.808 ** | 0.321 | 1.000 | ||||
| Basal Area | 0.886 ** | 0.199 | 0.835 ** | 1.000 | |||
| HCI | 0.888 ** | −0.021 | 0.851 ** | 0.841 ** | 1.000 | ||
| PAI | 0.767 * | −0.055 | 0.766 * | 0.820 ** | 0.783 * | 1.000 | |
| Rainfall Interception | 0.463 | 0.085 | 0.559 | 0.456 | 0.423 | 0.755 * | 1.000 |
| Only Brazil | |||||||
| Tree Height | 1.000 | ||||||
| Tree Density | 0.809 ** | 1.000 | |||||
| Species | 0.918 ** | 0.800 ** | 1.000 | ||||
| Basal Area | 0.843 ** | 0.806 ** | 0.801 ** | 1.000 | |||
| HCI | 0.790 * | 0.797 * | 0.787 * | 0.977 ** | 1.000 | ||
| PAI | 0.430 | 0.428 | 0.345 | 0.587 | 0.563 | 1.000 | |
| Rainfall Interception | 0.409 | 0.341 | 0.662 | 0.174 | 0.186 | 0.273 | 1.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calvo-Alvarado, J.C.; Jiménez-Rodríguez, C.D.; Calvo-Obando, A.J.; Marcos do Espírito-Santo, M.; Gonçalves-Silva, T. Interception of Rainfall in Successional Tropical Dry Forests in Brazil and Costa Rica. Geosciences 2018, 8, 486. https://doi.org/10.3390/geosciences8120486
Calvo-Alvarado JC, Jiménez-Rodríguez CD, Calvo-Obando AJ, Marcos do Espírito-Santo M, Gonçalves-Silva T. Interception of Rainfall in Successional Tropical Dry Forests in Brazil and Costa Rica. Geosciences. 2018; 8(12):486. https://doi.org/10.3390/geosciences8120486
Chicago/Turabian StyleCalvo-Alvarado, Julio César, César Dionisio Jiménez-Rodríguez, Ana Julieta Calvo-Obando, Mário Marcos do Espírito-Santo, and Thiago Gonçalves-Silva. 2018. "Interception of Rainfall in Successional Tropical Dry Forests in Brazil and Costa Rica" Geosciences 8, no. 12: 486. https://doi.org/10.3390/geosciences8120486
APA StyleCalvo-Alvarado, J. C., Jiménez-Rodríguez, C. D., Calvo-Obando, A. J., Marcos do Espírito-Santo, M., & Gonçalves-Silva, T. (2018). Interception of Rainfall in Successional Tropical Dry Forests in Brazil and Costa Rica. Geosciences, 8(12), 486. https://doi.org/10.3390/geosciences8120486






