Geometric Versus Anemometric Surface Roughness for a Shallow Accumulating Snowpack
Abstract
1. Introduction
2. Materials and Methods
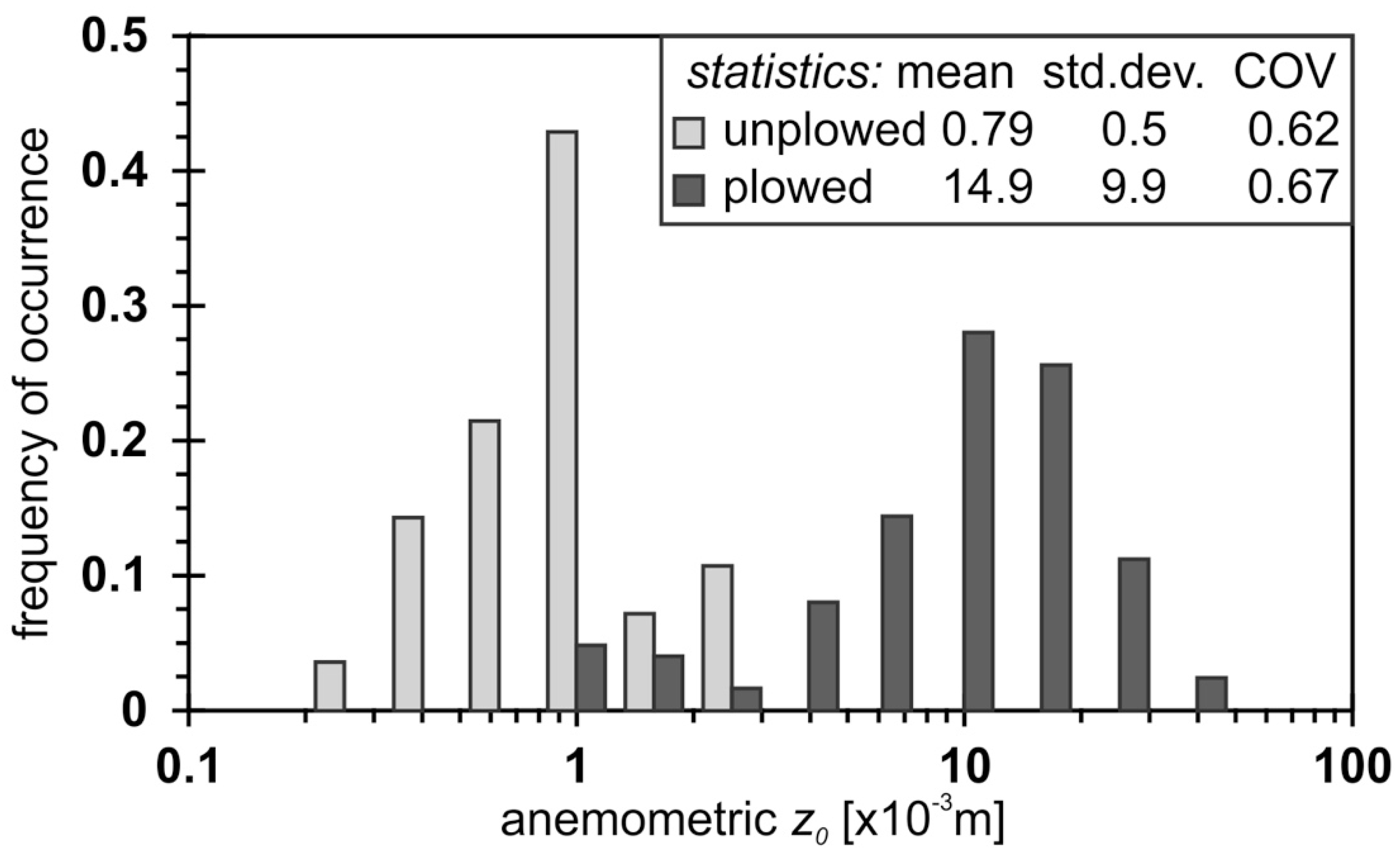
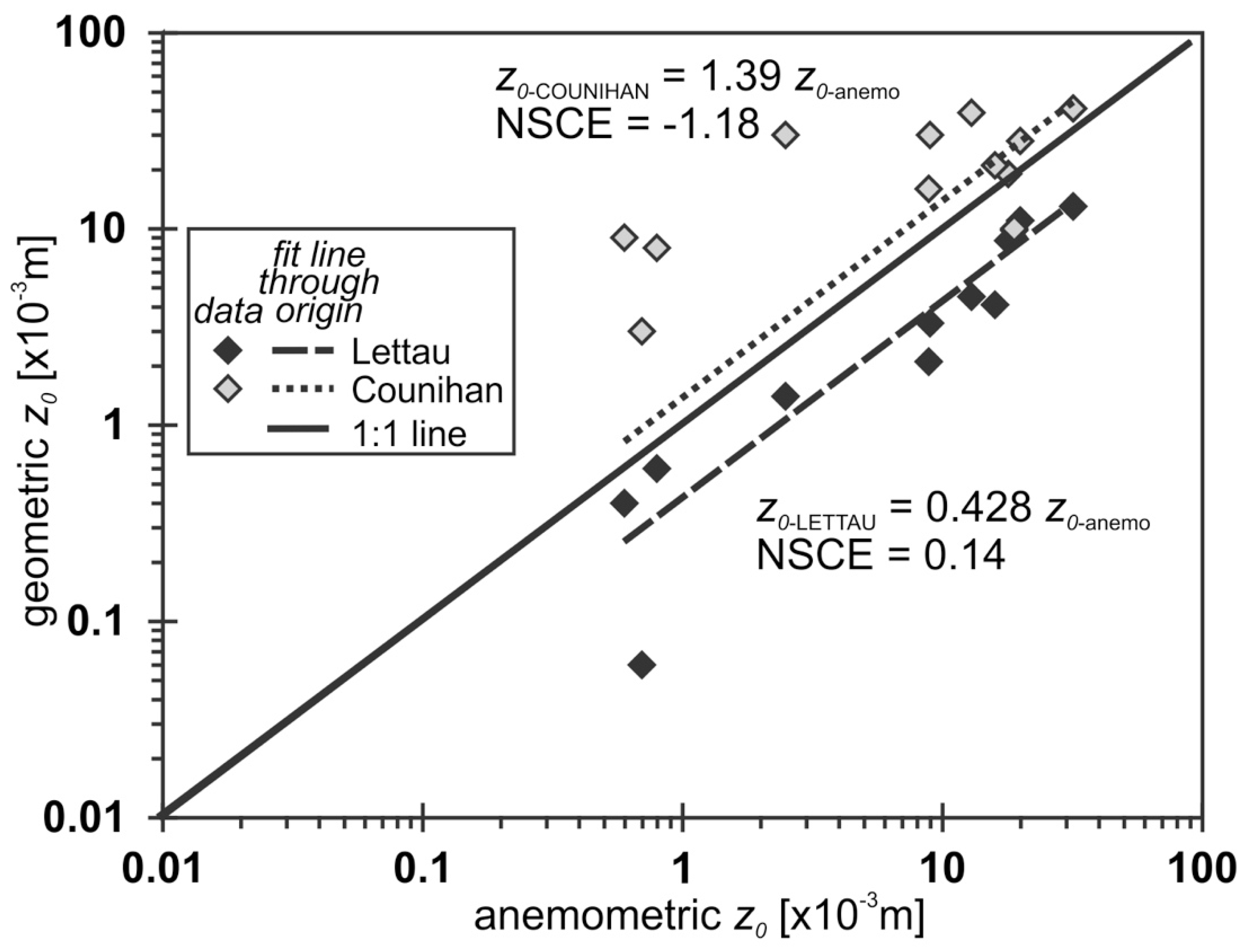
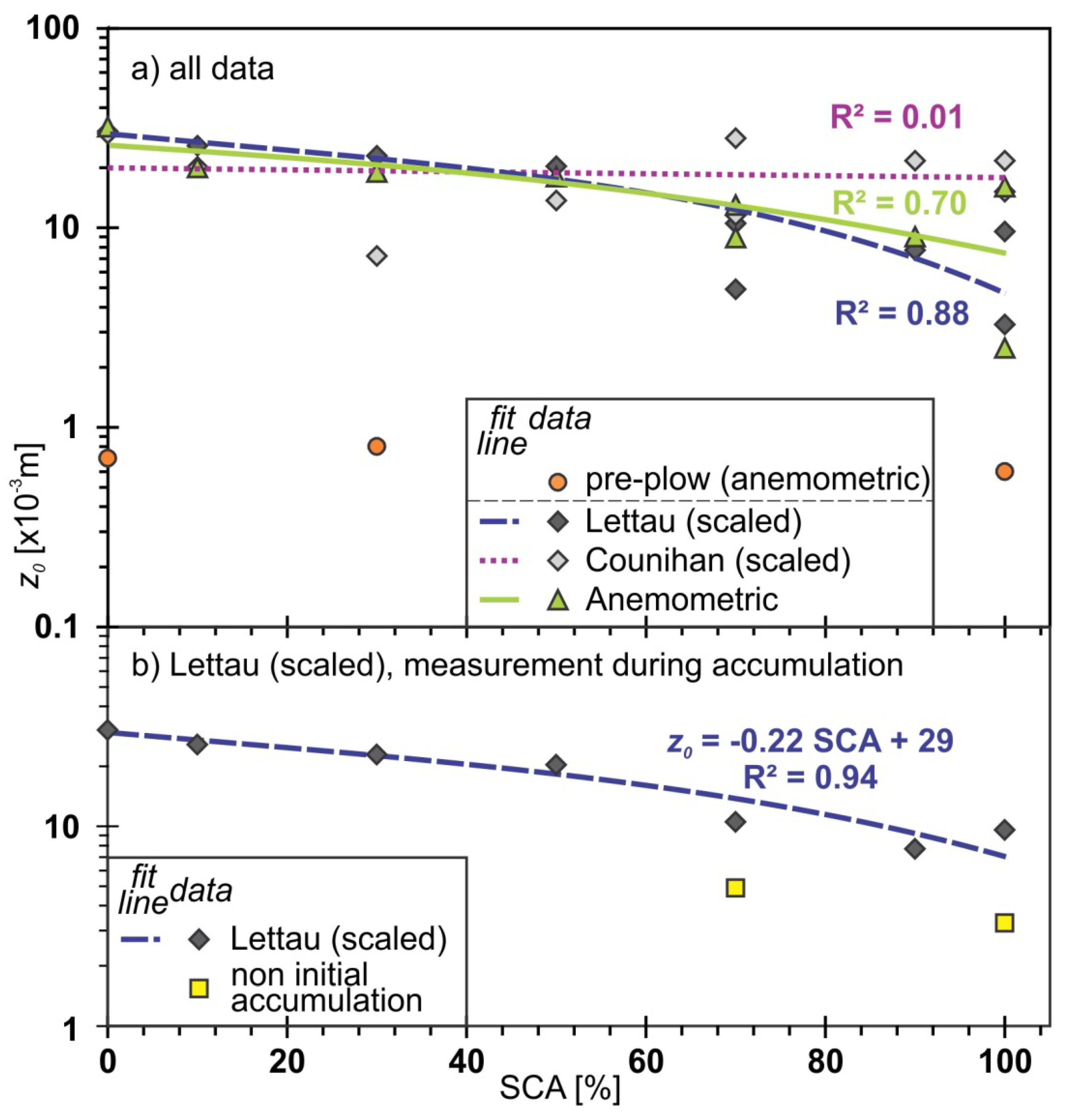
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mialon, A.; Royer, A.; Fily, M. Wetland seasonal dynamics and inter-annual variability over northern high latitudes, derived from microwave satellite data. J. Geophys. Res. 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Munro, D.S. Surface roughness and bulk heat transfer on a glacier: Comparison with eddy correlation. J. Glaciol. 1989, 35, 343–348. [Google Scholar] [CrossRef]
- Lehning, M.; Fierz, C. Assessment of snow transport in avalanche terrain. Cold Reg. Sci. Technol. 2008, 51, 240–252. [Google Scholar] [CrossRef]
- Amory, C.; Naaim-Bouvet, F.; Gallee, H.; Vignon, E. Breif communication: Two well-marked cases of aerodynamic adjustment of sastrugi. Cryosphere 2016, 10, 743–750. [Google Scholar] [CrossRef]
- Manes, C.; Guala, M.; Löwe, H.; Bartlett, S.; Egli, L.; Lehning, M. Statistical properties of fresh snow roughness. Water Resour. Res. 2008, 44, 1–9. [Google Scholar] [CrossRef]
- Gromke, C.; Manes, C.; Walter, B.; Lehning, M.; Guala, M. Aerodynamic roughness length of fresh snow. Bound.-Lay. Meteorol. 2011, 141, 21–34. [Google Scholar] [CrossRef]
- Brock, B.; Willis, I.; Sharp, M. Measurement and parameterization of aerodynamic roughness length variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2006, 52, 281–297. [Google Scholar] [CrossRef]
- Andreas, E.L. Parameterizing scalar transfer over snow and ice: A review. J. Hydrometeorol. 2002, 3, 417–432. [Google Scholar] [CrossRef]
- Fassnacht, S.R. Temporal changes in small scale snowpack surface roughness length for sublimation estimates in hydrological modeling. J. Geogr. Res. 2010, 36, 43–57. [Google Scholar] [CrossRef]
- Rott, H. The analysis of backscattering properties from SAR data of mountain regions. IEEE J. Ocean. Eng. 1984, 9, 347–355. [Google Scholar] [CrossRef]
- Williams, L.D.; Gallagher, J.G.; Sugden, D.E.; Birnie, R.V. Surface snow properties effect on millimeter-wave backscatter. IEEE Geosci. Remote Sens. Soc. 1988, 26, 300–306. [Google Scholar] [CrossRef]
- Lacroix, P.; Legrésy, B.; Langley, K.; Hamran, S.E.; Kohler, J.; Roques, S.; Dechambre, M. In situ measurements of snow surface roughness using a laser profiler. J. Glaciol. 2008, 54, 753–762. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Williams, M.W.; Corrao, M.V. Changes in the surface roughness of snow from millimetre to metre scales. Ecol. Complex. 2009, 6, 221–229. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Stednick, J.D.; Deems, J.S.; Corrao, M.V. Metrics for assessing snow surface roughness from digital imagery. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Toro Velasco, M.; Meiman, P.J.; Whitt, Z.C. The effect of aeolian deposition on the surface roughness of melting snow, Byers Peninsula, Antarctica. Hydrol. Process. 2010, 24, 2007–2013. [Google Scholar] [CrossRef]
- Manninen, T.; Anttila, K.; Karjalainen, T.; Lahtinen, P. Instruments and methods automatic snow surface roughness estimation using digital photos. J. Glaciol. 2012, 58, 993–1007. [Google Scholar] [CrossRef]
- Deems, J.S.; Fassnacht, S.R.; Elder, K.J. Fractal distribution of snow depth from lidar data. J. Hydrometeorol. 2006, 7, 285–297. [Google Scholar] [CrossRef]
- Cline, D.; Yueh, S.; Chapman, B.; Stankov, B.; Gasiewski, A.; Masters, D.; Elder, K.; Kelly, R.; Painter, T.H.; Miller, S.; et al. NASA cold processes experiment (CLPX 2002/03): Airborne remote sensing. J. Hydrometeorol. 2009, 10, 338–346. [Google Scholar] [CrossRef]
- Harpold, A.A.; Guo, Q.; Molotch, N.; Brooks, P.D.; Bales, R.; Fernandez-Diaz, J.C.; Musselman, K.N.; Swetnam, T.L.; Kirchner, P.; Meadows, M.W.; et al. LiDAR-derived snowpack data sets from mixed conifer forests across the Western United States. Water Resour. Res. 2014, 50, 2749–2755. [Google Scholar] [CrossRef]
- Hood, J.L.; Hayashi, M. Assessing the application of a laser range finder for determining snow depth in inaccessible alpine terrain. Hydrol. Earth Syst. Sci. 2010, 14, 901. [Google Scholar] [CrossRef]
- Prokop, A. Assessing the applicability of terrestrial laser scanning for spatial snow depth measurements. Cold Reg. Sci. Technol. 2008, 54, 155–163. [Google Scholar] [CrossRef]
- Revuelto, J.; Lopez-Mureno, J.I.; Azorin-Molina, C.; Zabalza, J.; Arguedas, G.; Vicente-Serrano, S.M. Mapping the annual evolution of snow depth in a small catchment in the Pyrenees using the long-range terrestrial laser scanning. J. Maps 2014, 10, 379–393. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Boike, J.; Sanchez-Lorenzo, A.; Pomeroy, J.W. Impact of climate warming on snow processes in Ny-Ålesund, a polar maritime site at Svalbard. Glob. Planet. Chang. 2016, 146, 10–21. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Revuelto, J.; Alonso-Gonzalez, E.; Sanmiguel-Vallelado, A.; Fassnacht, S.R. Using very long-range terrestrial laser scanner to analyze the temporal consistency of the snowpack distribution in a high mountain environment. J. Mt. Sci. 2017, 14, 823–842. [Google Scholar] [CrossRef]
- Nolan, M.; Larsen, C.F.; Strum, M. Mapping snow-depth from manned-aircraft on landscape scales at centimeter resolution using structure-from-motion photogrammetry. Cryosphere Discuss. 2015, 9, 333–381. [Google Scholar] [CrossRef]
- Deems, J.S.; Painter, T.; Finnegan, D. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Oprea, I.; Borleske, G.; Kamin, D.J. Comparing snow surface roughness metrics with a geometric-based roughness length. Proc. Hydrol. Days 2014, 34, 44–52. [Google Scholar]
- Fassnacht, S.R.; Records, R.M. Large snowmelt versus rainfall events in the mountains. J. Geophys. Res. 2015, 120, 2375–2381. [Google Scholar] [CrossRef]
- Lettau, H. Note on aerodynamic roughness-parameter estimation on the basis of roughness-element description. J. Appl. Meteorol. 1969, 8, 828–832. [Google Scholar] [CrossRef]
- Andreas, E.L. A relationship between the aerodynamic and physical roughness of winter sea ice. Q. J. R. Meteorol. Soc. 2011, 137, 1581–1588. [Google Scholar] [CrossRef]
- Miles, E.S.; Steiner, J.F.; Brun, F. Highly variable aerodynamic roughness length (z0) for a hummocky debris-covered glacier. J. Geophys. Res. Atmos. 2017, 122, 8447–8466. [Google Scholar] [CrossRef]
- Jacobson, M.Z. Fundamentals of Atmospheric Modeling, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005; ISBN 978-0-521-54865-6. [Google Scholar]
- Raupach, M.R.; Antonia, R.A.; Rajagopalan, S. Rough-wall turbulent boundary layers. Appl. Mech. Rev. 1991, 44, 1–25. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Foken, T. Micrometeorology; Springer-Verlag: Berlin, Germany; New York, NY, USA, 2008; ISBN 978-3-540-74666-9. [Google Scholar]
- Smith, M. Roughness in the earth sciences. Earth-Sci. Rev. 2014, 136, 202–225. [Google Scholar] [CrossRef]
- Schuepp, P.H.; Leclerc, M.Y.; Macpherson, J.I.; Desjardins, R.L. Footprint prediction of scalar fluxes from analytical solutions of the diffusion equation. Appl. Mech. Rev. 1990, 50, 355–373. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Clow, D.; Stannard, D.; Fassnacht, S.R. Comparison of methods for quantifying surface sublimation over seasonally snow-covered terrain. Hydrol. Process. 2016, 30, 3373–3389. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Cambridge University Press: Cambridge, UK, 1987; ISBN 0-415-04319-0. [Google Scholar]
- Raupach, M.R. Drag and drag partition on rough surfaces. Bound.-Lay. Meteorol. 1992, 60, 375–395. [Google Scholar] [CrossRef]
- Counihan, J. Wind tunnel determination of the roughness length as a function of the fetch and the roughness density of three-dimensional roughness elements. Atmos. Environ. 1971, 5, 637–642. [Google Scholar] [CrossRef]
- Macdonald, R.W.; Griffiths, R.F.; Hall, D.J. An improved method for the estimation of surface roughness of obstacle arrays. Atmos. Environ. 1998, 32, 1857–1864. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Luce, C.H.; Tarboton, D.G.; Cooley, K.R. Sub-grid parameterization of snow distribution for an energy and mass balance snow cover model. Hydrol. Process. 1999, 13, 1921–1933. [Google Scholar] [CrossRef]
- Luce, C.H.; Tarboton, D.G. The application of depletion curves for parameterization of subgrid variability of snow. Hydrol. Process. 2004, 18, 1409–1422. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.L. An observation-based formulation of snow cover fraction and its evaluation over large North American river basins. J. Geophys. Res. 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Moeser, D.; Stahli, M.; Jonas, T. Improved snow interception modeling using canopy parameters derived from airborne lidar data. Water Resour. Res. 2015, 51, 5041–5059. [Google Scholar] [CrossRef]
- Liston, G.E. Representing sub-grid snow cover heterogeneities in regional and global models. J. Clim. 2004, 17, 1381–1397. [Google Scholar] [CrossRef]
- Tedesche, M.E.; Fassnacht, S.R.; Meiman, P.J. Scales of Snow Depth Variability in High Elevation Rangeland Sagebrush. Front. Earth Sci. 2017, 11, 469–481. [Google Scholar] [CrossRef]
- Magand, C.; Ducharne, A.; Le Moine, N. Introducing hysteresis in snow depletion curves to improve the water budget of a land surface model in an alpine catchment. J. Hydrometeorol. 2014, 15, 631–649. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Sexstone, G.A.; Kashipazha, A.H.; López-Moreno, J.I.; Jasinski, M.F.; Kampf, S.K.; Von Thaden, B.C. Deriving snow-cover depletion curves for different spatial scales from remote sensing and snow telemetry data. Hydrol. Process. 2016, 30, 1708–1717. [Google Scholar] [CrossRef]
- Quincey, D.; Smith, M.; Rounce, D.; Ross, A.; King, O.; Watson, C. Evaluating morphological estimates of the aerodynamic roughness of debris covered glacier ice. Earth Surf. Process. Landf. 2017, 42, 2541–2553. [Google Scholar] [CrossRef]
- DeBeer, C.M.; Pomeroy, J.W. Influence of snowpack and melt energy heterogeneity on snow cover depletion and snowmelt runoff simulation in a cold mountain environment. J. Hydrol. 2017, 553, 199–213. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Yang, Z.-L.; Snelgrove, K.R.; Soulis, E.D.; Kouwen, N. Effects of averaging and separating soil moisture and temperature in the presence of snow cover in a SVAT and hydrological model. J. Hydrometeorol. 2006, 7, 298–304. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanow, J.E.; Fassnacht, S.R.; Kamin, D.J.; Sexstone, G.A.; Bauerle, W.L.; Oprea, I. Geometric Versus Anemometric Surface Roughness for a Shallow Accumulating Snowpack. Geosciences 2018, 8, 463. https://doi.org/10.3390/geosciences8120463
Sanow JE, Fassnacht SR, Kamin DJ, Sexstone GA, Bauerle WL, Oprea I. Geometric Versus Anemometric Surface Roughness for a Shallow Accumulating Snowpack. Geosciences. 2018; 8(12):463. https://doi.org/10.3390/geosciences8120463
Chicago/Turabian StyleSanow, Jessica E., Steven R. Fassnacht, David J. Kamin, Graham A. Sexstone, William L. Bauerle, and Iuliana Oprea. 2018. "Geometric Versus Anemometric Surface Roughness for a Shallow Accumulating Snowpack" Geosciences 8, no. 12: 463. https://doi.org/10.3390/geosciences8120463
APA StyleSanow, J. E., Fassnacht, S. R., Kamin, D. J., Sexstone, G. A., Bauerle, W. L., & Oprea, I. (2018). Geometric Versus Anemometric Surface Roughness for a Shallow Accumulating Snowpack. Geosciences, 8(12), 463. https://doi.org/10.3390/geosciences8120463






