A New Geospatial Model Integrating a Fuzzy Rule-Based System in a GIS Platform to Partition a Complex Urban System in Homogeneous Urban Contexts
Abstract
1. Introduction
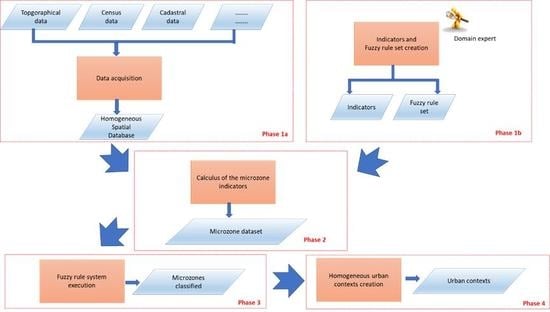
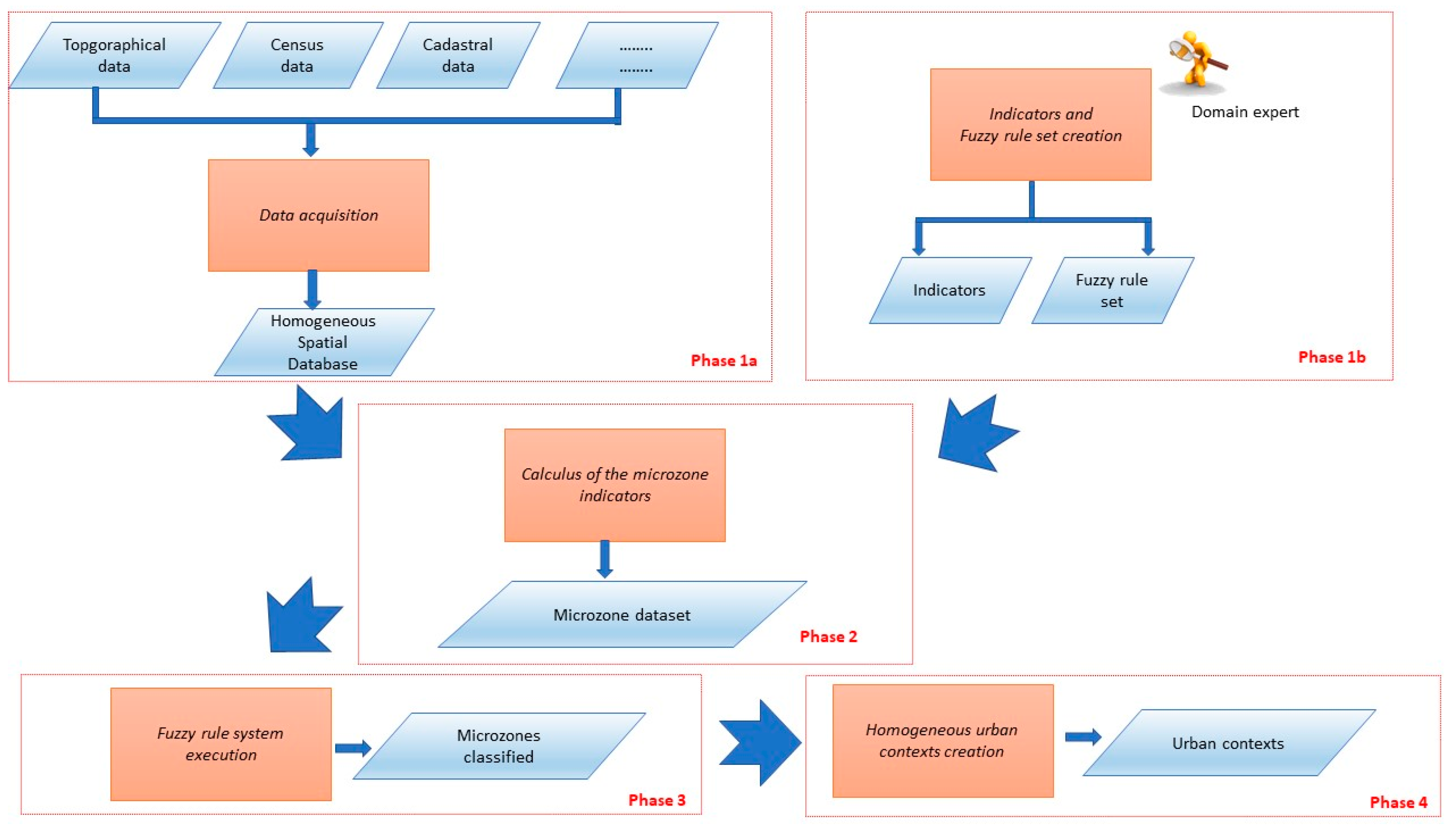
2. The Proposed Model
2.1. Phase 1a—Data Acquisition
- -
- Extracting themes from a dataset in various formats;
- -
- Merging datasets corresponding to a theme and distributed per tiles, clipped onto the area of study;
- -
- Applying spatial operators related to any feature of the theme information, inserted as annotation texts (for example, the road name assigned to any polyline of a road network).
2.2. Phase 1b—Indicators and Fuzzy Rule Set Creation
- IF
- (I4 == Null) AND (I6 == Discrete OR I6 == High) AND (I7 == High) THEN Z == Residential old town
- IF
- (I1 == Discrete OR I1 == High) AND (I3 == Discrete OR I3 == High) AND (I8 == Null) AND (I12 == High) THEN Z == Comfortable residential zone
- IF
- (I2 == Null) AND (I7 == Scanty OR I7 == Mean) AND (I12 == High) AND (I14 == Discrete OR I14 == High) THEN Z == Comfortable residential zone
- IF
- (I2 == Discrete OR I2 == High) AND (I6 == Null) AND (I7 == Scanty) THEN Z == Industrial zone
- R1:
- IF (I4 == Null) AND (I6 == Discrete OR I6 == High) AND (I7 == High) THEN Z == Residential old town
- R2:
- IF (I4 == Null) AND (I6 == High) AND (I7 == High) THEN Z == Residential old town
- R3:
- IF (I1 == Discrete) AND (I3 == Discrete) AND (I8 == Null) AND (I12 == High) THEN Z == Comfortable residential zone
- R4:
- IF (I1 == High) AND (I3 == Discrete) AND (I8 == Null) AND (I12 == High) THEN Z == Comfortable residential zone
- R5:
- IF (I1 == Discrete) AND (I3 == High) AND (I8 == Null) AND (I12 == High) THEN Z == Comfortable residential zone
- R6:
- IF (I1 == High) AND (I3 == High) AND (I8 == Null) AND (I12 == High) THEN Z == Comfortable residential zone
- R7:
- IF (I2 == Null) AND (I7 == Scanty) AND (I12 == High) AND (I14 == Discrete) THEN Z == Comfortable residential zone
- R8:
- IF (I2 == Null) AND (I7 == Mean) AND (I12 == High) AND (I14 == Discrete) THEN Z == Comfortable residential zone
- R9:
- IF (I2 == Null) AND (I7 == Scanty) AND (I12 == High) AND (I14 == High) THEN Z == Comfortable residential zone
- R10:
- IF (I2 == Null) AND (I7 == Mean) AND (I12 == High) AND (I14 == High) THEN Z == Comfortable residential zone
- R11:
- IF (I2 == Discrete) AND (I6 == Null) AND (I7 == Scanty) THEN Z == Industrial zone
- R12:
- IF (I2 == High) AND (I6 == Null) AND (I7 == Scanty) THEN Z == Industrial zone
2.3. Phase 2—Calculus of the Microzone Indicators
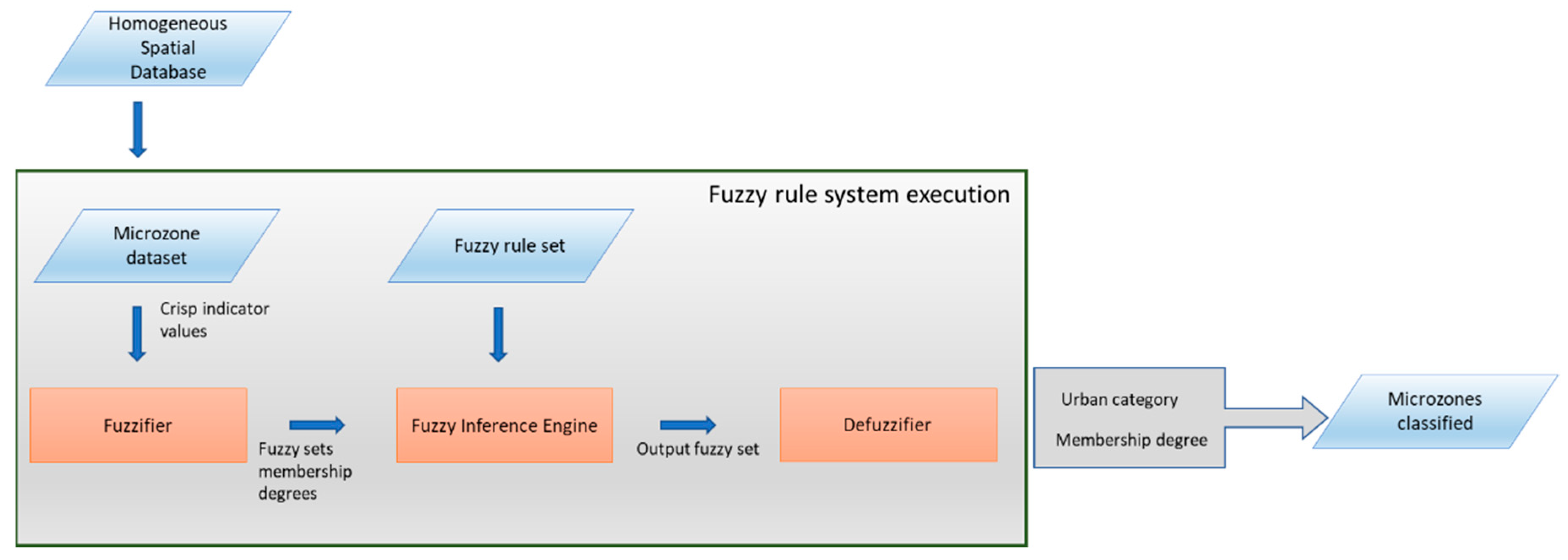
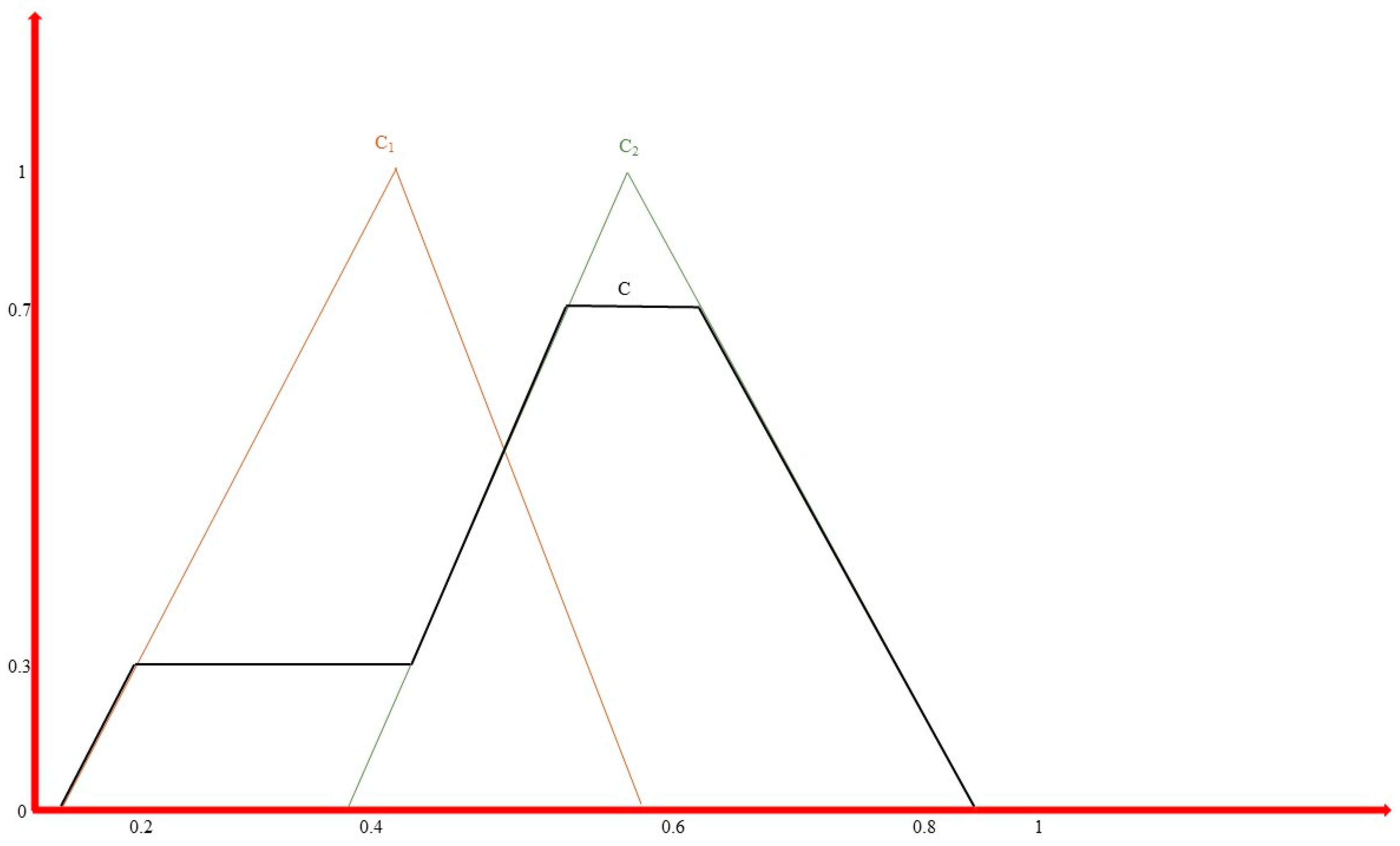
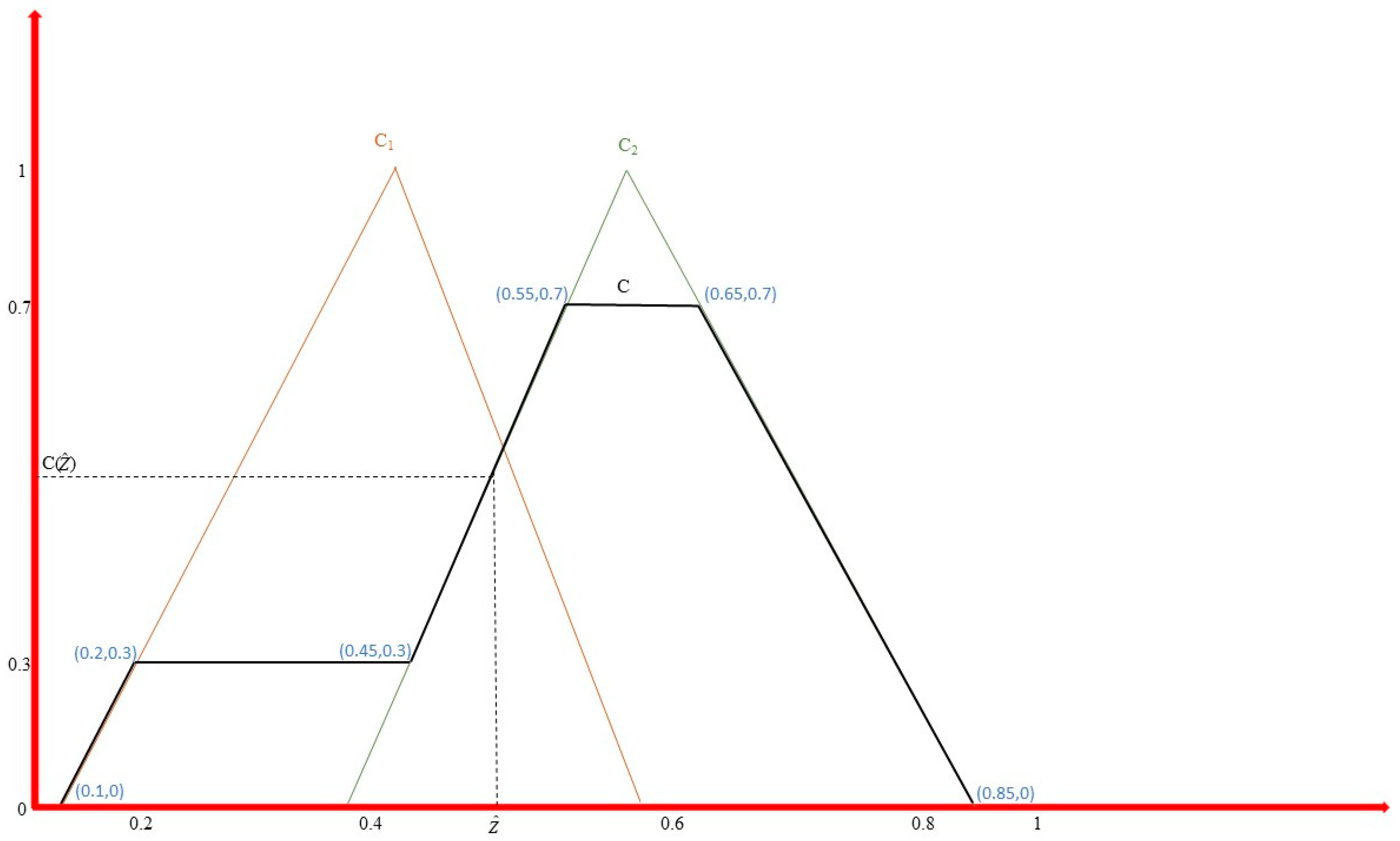
2.4. Phase 3—Fuzzy Rule System Execution
2.5. Phase 4—Homogeneous Urban Context Creation
3. Application to an Area of Study
3.1. The Area of Study
3.2. Spatial Data Sources
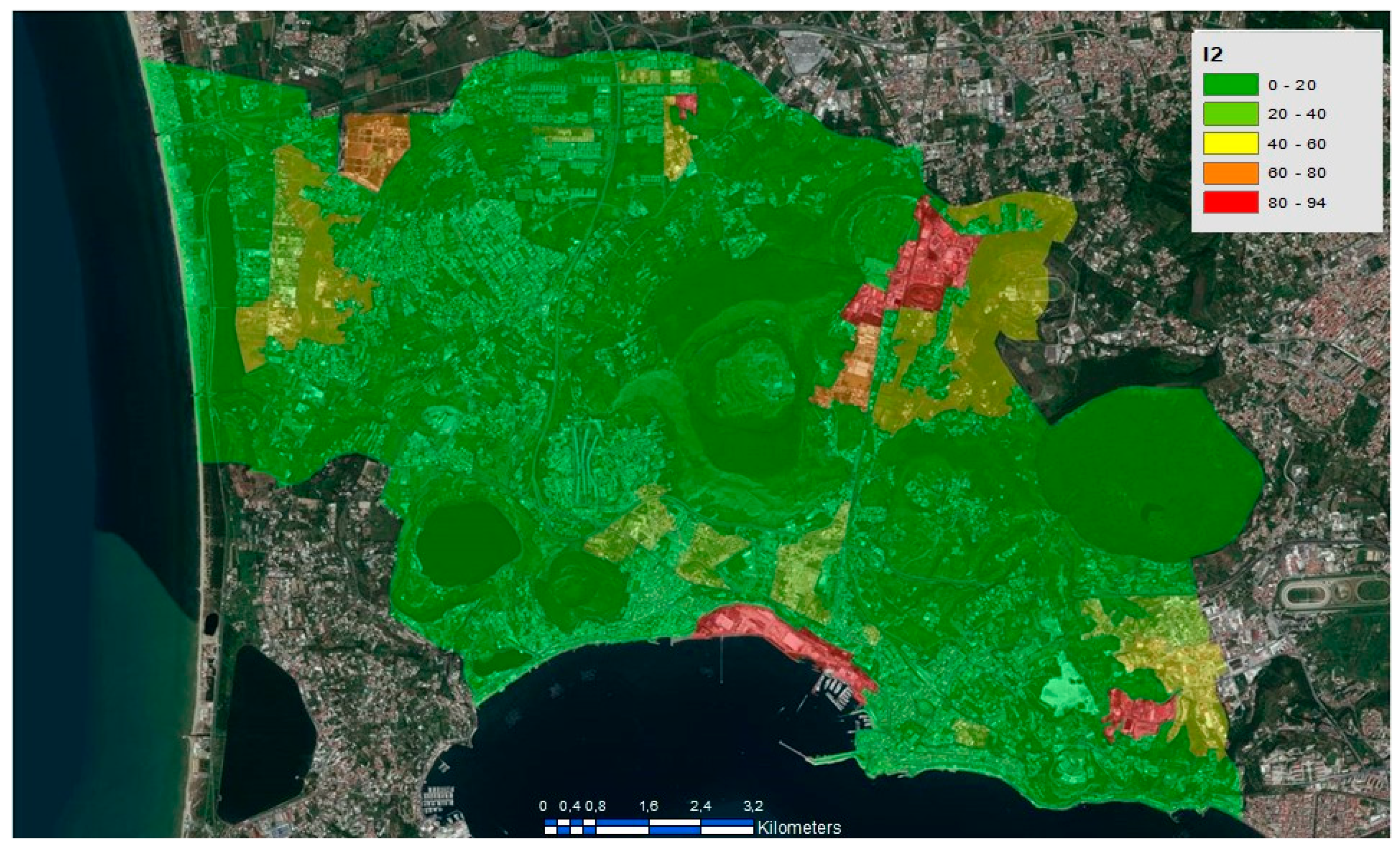
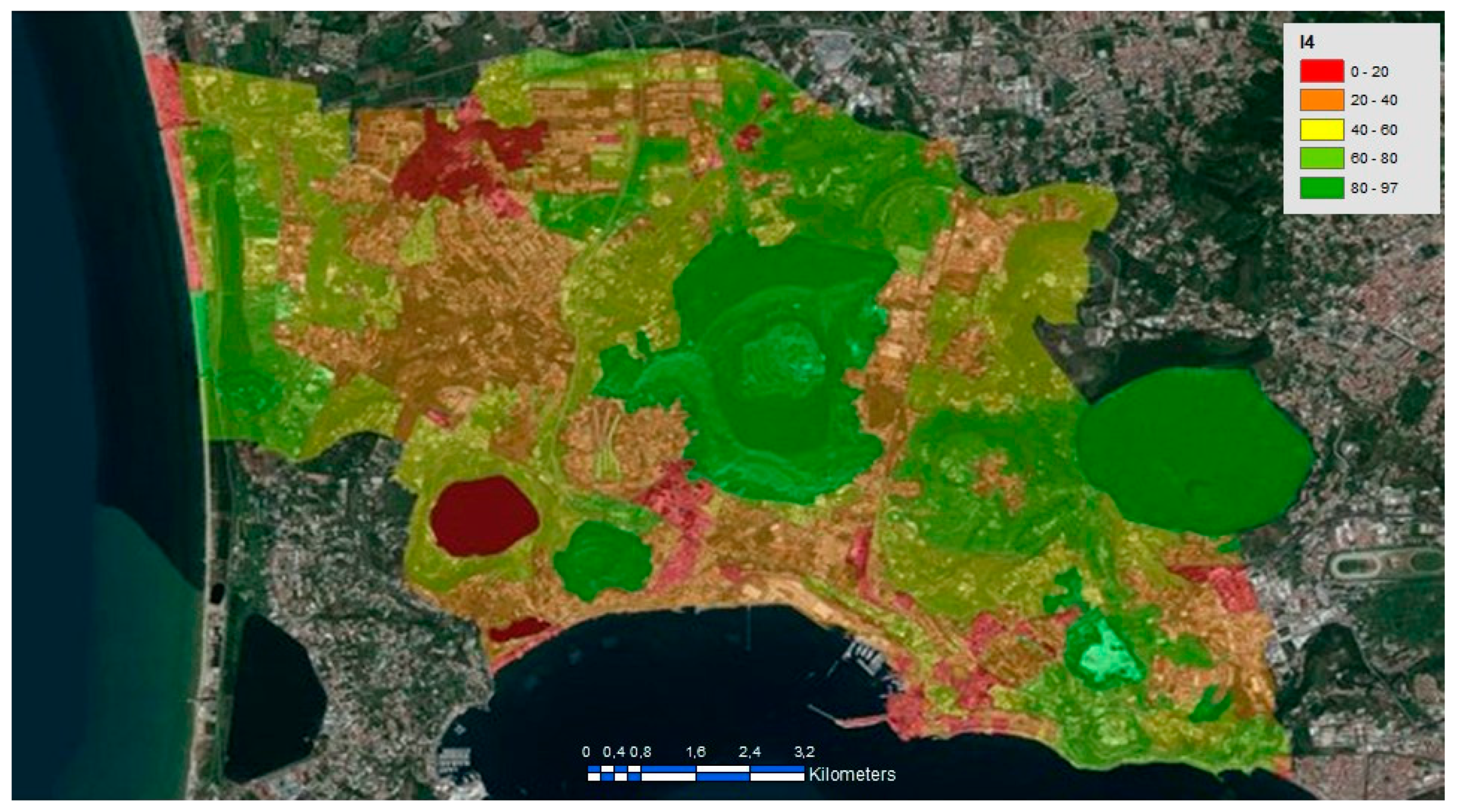
4. Test Results
- -
- TP (True Positive) is the number of microzones correctly assigned to the class;
- -
- TN (True Negative) is the number of microzones correctly not assigned to the class;
- -
- FP (False Positive) is the number of microzones wrongly assigned to the class;
- -
- FN (False Negative) is the number of microzones wrongly not assigned to the class.
5. Final Considerations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sheeren, D.; Quirin, A.; Puissant, A.; Gançarski, P.; Weber, C. Discovering rules with genetic algorithms to classify urban remotely sensed data. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3902–3905. [Google Scholar] [CrossRef]
- Forestier, G.; Wemmert, C.; Puissant, A. Coastal image interpretation using background knowledge and semantics. Comput. Geosci. 2013, 54, 89–96. [Google Scholar] [CrossRef]
- Leichtle, T.; Geiß, C.; Wurm, M.; Lakes, T.; Taubenböck, H. Unsupervised change detection in VHR remote sensing imagery—An object-based clustering approach in a dynamic urban environment. Int. J. Appl. Earth Observ. Geoinf. 2013, 2017, 15–27. [Google Scholar] [CrossRef]
- Chen, Y.; Su, W.; Li, J.; Sung, Z. Hierarchical object-oriented classification using very high-resolution imagery and LIDAR data over urban areas. Adv. Space Res. 2009, 43, 1101–1110. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, Q.; Jia, X.; Benediktsson, J.A. A Novel MKL Model of Integrating LiDAR Data and MSI for Urban Area Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5312–5326. [Google Scholar] [CrossRef]
- Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
- Rikalović, A.; Antunes Soares, G.; Ignjatić, J. Spatial analysis of logistics center location: A comprehensive approach. Decis. Mak. Appl. Manag. Eng. 2018, 1, 38–50. [Google Scholar] [CrossRef]
- Preradović, L.; Đajić, V.; Jakovljević, G. Gender and age structure as risk factors of carotid artery stenosis and specific themes areas of cartography. Decis. Mak. Appl. Manag. Eng. 2018, 1, 111–120. [Google Scholar] [CrossRef]
- Pamučar, D.; Gigović, L.; Ćirović, G.; Regodić, M. Transport spatial model for the definition of green routes for city logistics centers. Environ. Impact Assess. Rev. 2016, 56, 72–87. [Google Scholar] [CrossRef]
- Pamučar, D.; Gigović, L.; Bajić, Z.; Janošević, M. Location Selection for Wind Farms Using GIS Multi-Criteria Hybrid Model: An Approach Based on Fuzzy and Rough Numbers. Sustainability 2017, 9, 1315. [Google Scholar] [CrossRef]
- Di Martino, F.; Loia, V.; Sessa, S. A fuzzy-based tool for modelization and analysis of the vulnerability of aquifers: A case study. Int. J. Approx. Reason. 2005, 38, 99–111. [Google Scholar] [CrossRef]
- Mennis, J.; Liu, J.W. Mining Association Rules in Spatio-Temporal Data: An Analysis of Urban Socioeconomic and Land Cover Change. Remote Sens. Environ. 2005, 9, 5–17. [Google Scholar] [CrossRef]
- Bernábe, M.B.L.; Duque, J.C.; Ramirez, J.R.; Osorio, M.A.L. Classification over Geographical Zones: A Combinatorial O ptimization Approach to the Regional Partitioning Problem. In Proceedings of the 18th International Conference on Electronics, Communications and Computers, Puebla, Mexico, 3–5 March 2008; pp. 70–74. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S. Spatial analysis and fuzzy relation equations. Adv. Fuzzy Syst. 2011, 2011, 429498. [Google Scholar] [CrossRef]
- Arns Steiner, M.T.; Datta, D.; Steiner Neto, P.J.; Scarpin, C.T.; Figueira, J.R. Multi-objective optimization in partitioning the healthcare system of Parana State in Brazil. Omega 2015, 52, 53–64. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy logic to approximate reasoning using linguistic synthesis. IEEE Trans. Comput. 1977, 26, 1182–1191. [Google Scholar] [CrossRef]
- Lukovac, V.; Pamučar, D.; Popović, M.; Đorović, B. Portfolio model for analyzing human resources: An approach based on neuro-fuzzy modeling and the simulated annealing algorithm. Expert Syst. Appl. 2017, 90, 318–331. [Google Scholar] [CrossRef]
- Pamučar, D.; Vasin, L.; Atanasković, P.; Milicic, M. Planning the City Logistics Terminal Location by Applying the Green p-Median Model and Type-2 Neurofuzzy Network. Comput. Intell. Neurosci. 2016, 2. [Google Scholar] [CrossRef]
- Pamučar, D.; Atanasković, P.; Milicic, M. Modeling of fuzzy logic system for investment management in the railway infrastructure. Teh. Vjesn. 2015, 22, 1185–1192. [Google Scholar] [CrossRef]
- Tarigan, P.; Simurat, S. Implementation of A Mamdani Fuzzy Logic Controller for Building Automation Using Electronic Control Based on AT89S51. In Proceedings of the 2015 International Conference on Technology, Informatics, Management, Engineering & Environment (TIME-E), Samosir, Indonesia, 7–9 September 2015; pp. 87–92. [Google Scholar] [CrossRef]
- Mesran, M.; Syahrizal, M.; Suginam, S.; Kurniasih, N.; Gs, A.D. Expert System for Disease Risk Based on Lifestyle with Fuzzy Mamdani. Int. J. Eng. Technol. 2018, 7, 88–91. [Google Scholar] [CrossRef]
- Li, X.; Dan, G. Behavior-based Mamdani fuzzy controller for mobile robot wall-following. In Proceedings of the 2015 International Conference on Control, Automation and Robotics, Singapore, 20–22 May 2015; pp. 78–81. [Google Scholar] [CrossRef]
- Zareiforoush, H.; Minaei, S.; Alizadeh, M.R.; Banakar, A. A hybrid intelligent approach based on computer vision and fuzzy logic for quality measurement of milled rice. Measurement 2015, 66, 26–34. [Google Scholar] [CrossRef]
- Hasan, R.; Monir, S.M.G. Fruit maturity estimation based on fuzzy classification. In Proceedings of the 2017 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuching, Malaysia, 12–14 September 2017; pp. 27–32. [Google Scholar] [CrossRef]
- Mahalakshmi, P.; Ganesan, K. Mamdani fuzzy rule-based model to classify sites for aquaculture development. Indian J. Fish. 2015, 62, 110–115. [Google Scholar]
- Esposito, G.; Matano, F.; Sacchi, M. Detection and Geometrical Characterization of a Buried Landfill Site by Integrating Land Use Historical Analysis, Digital Photogrammetry and Airborne Lidar Data. Geosciences 2018, 8, 348. [Google Scholar] [CrossRef]
- Judenherc, S.; Zollo, A. The Bay of Naples (Southern Italy): Constraints on the volcanic structures inferred from a dense seismic survey. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Petrosino, S.; Cusano, P.; Madonia, P. Tidal and hydrological periodicities of seismicity reveal new risk scenarios at Campi Flegrei caldera. Sci. Rep. 2018, 8, 13808. [Google Scholar] [CrossRef] [PubMed]
- Gerundo, C.; Adad, G.N. Promoting Cultural Resources Integration Using GIS. The Case Study of Pozzuoli. In New Metropolitan Perspectives. ISHT 2018. Smart Innovation, Systems and Technologies; Calabrò, F., Della Spina, L., Bevilacqua, C., Eds.; Springer: Cham, Switzerland, 2018; Volume 100, pp. 182–188. [Google Scholar]
- Belussi, A.; Negri, M.; Pelagatti, G. GeoUML: A Geographic Conceptual Model Defined Through Specialization of Iso Tc211 Standards. In Proceedings of the 10th EC GI & GIS Workshop, ESDI State of the Art, Warsaw, Poland, 23–25 June 2004; 10p. [Google Scholar]
- Pelagatti, G.; Belussi, A.; Negri, M. GeoUML Methodology e Tools an Overview. Spatial DB Group Politecnico di Milano—Comitato di Progetto e Struttura Tecnica di Supporto CISISCPSG. 2011. Available online: http://geo.spatialdbgroup.polimi.it/en/documents/ (accessed on 25 November 2018).

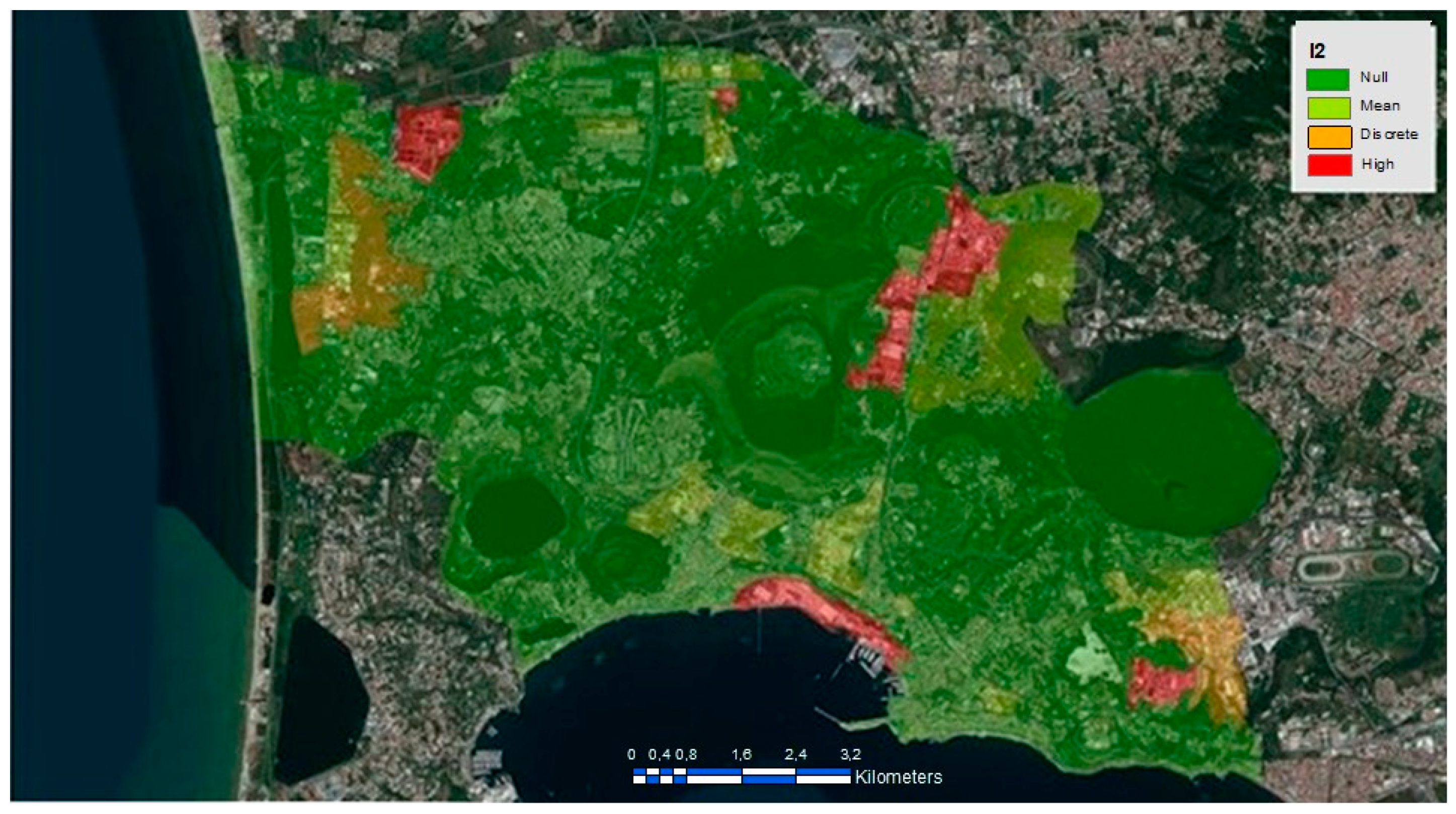

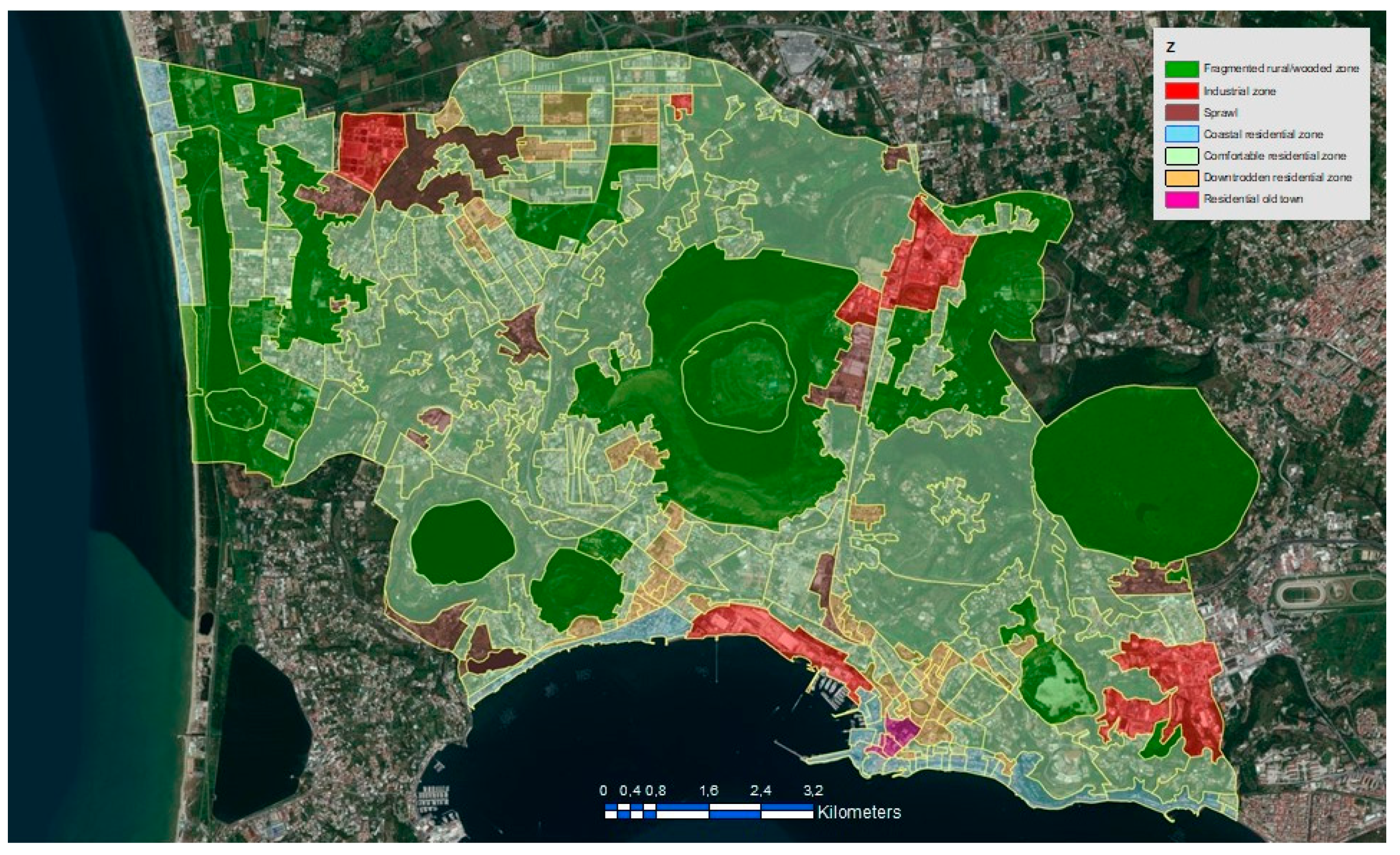
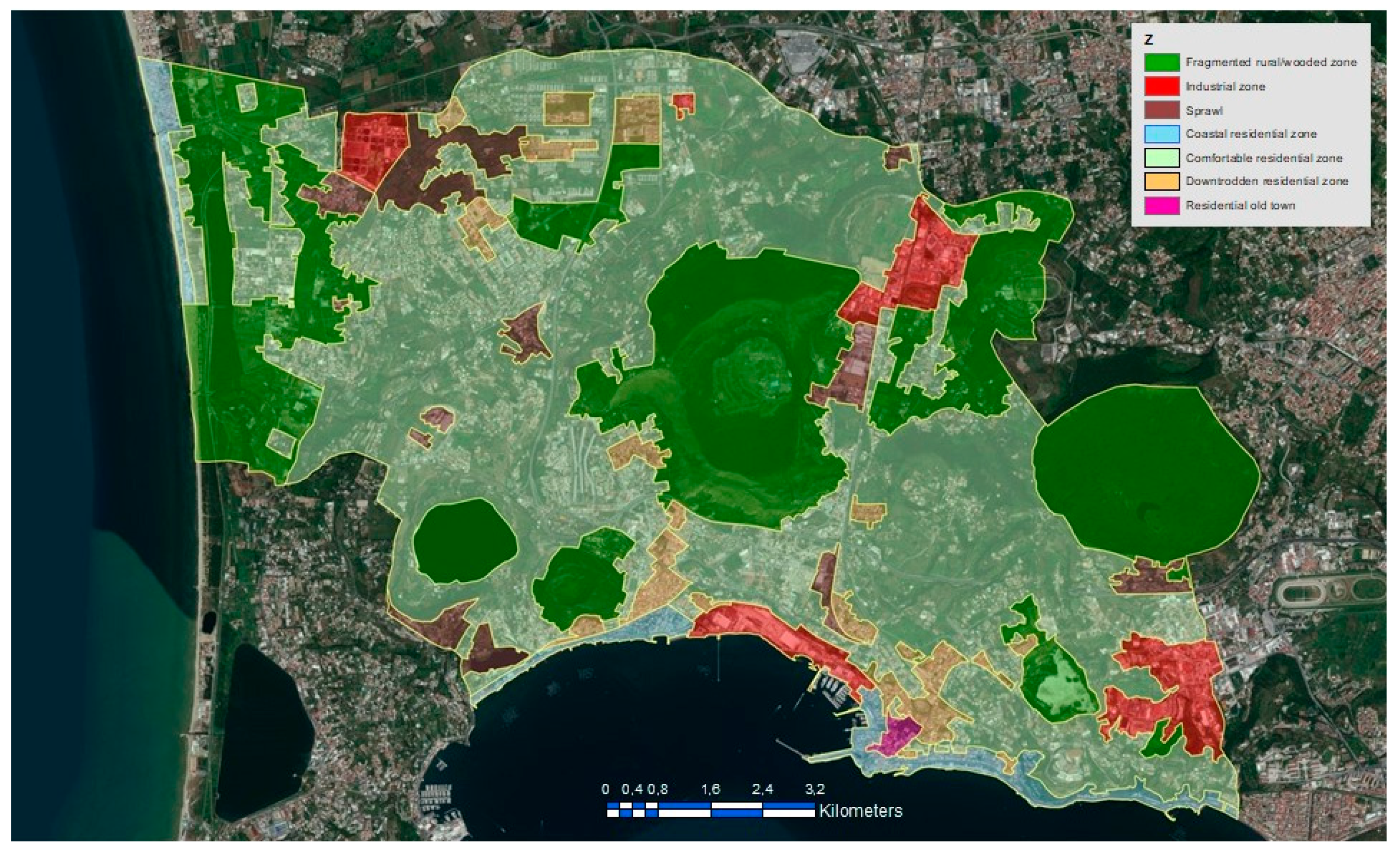
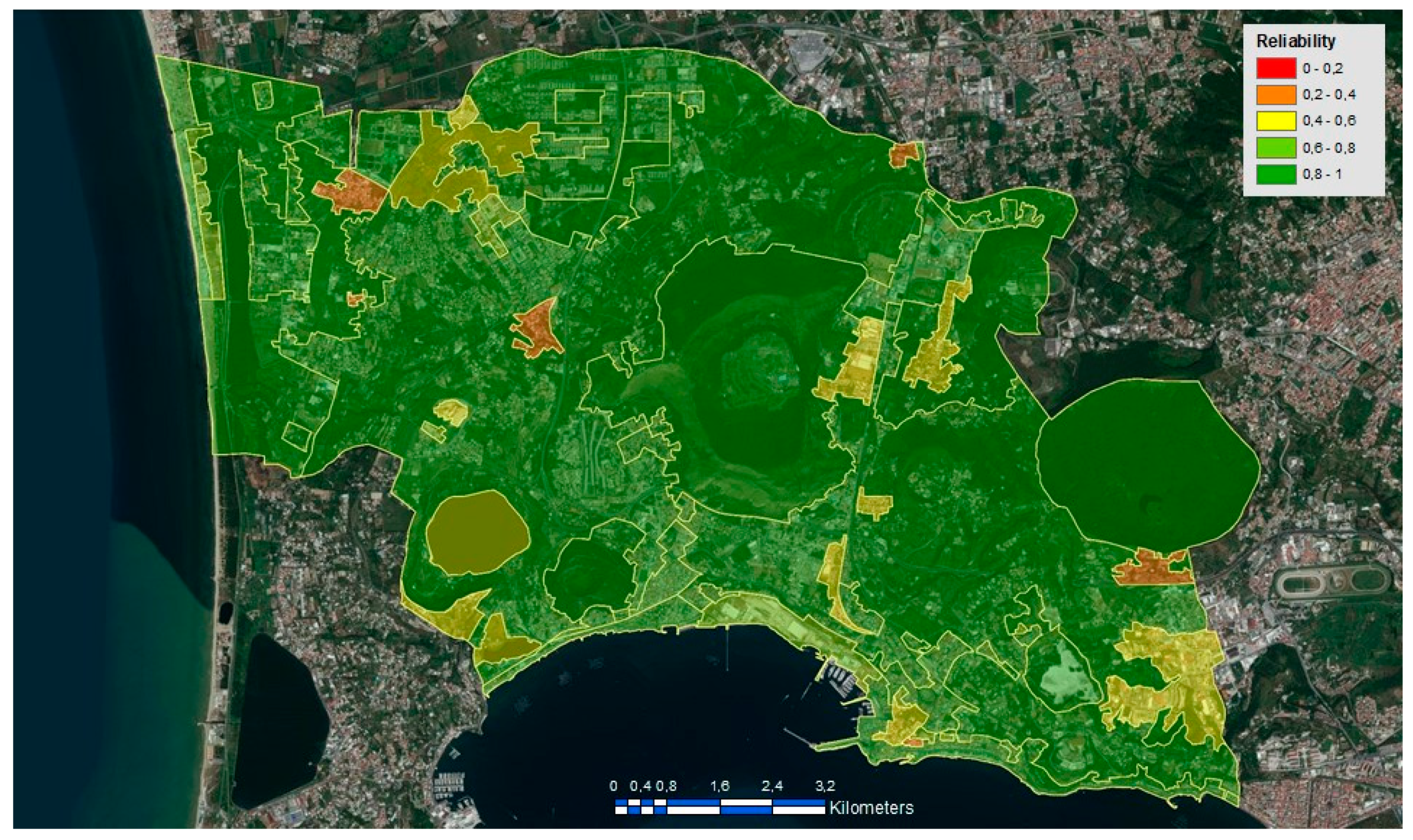
| Indicator | Type | Description | Unit of Measurement |
|---|---|---|---|
| Buildings | Mean square meters of residential buildings per resident | Square meters | |
| I2 | Buildings | Percent of industrial areas with respect to total built areas | Percent |
| I3 | Urban green | Mean square meters of green areas per resident | Square meters |
| I4 | Urban green | Percent of green areas with respect to area of the microzone | Percent |
| I5 | Roads | Percent of the overall length of district urban roads 1 with respect to the overall length of roads in the microzone | Percent |
| I6 | Roads | Percent of overall length of the district urban roads with a width of less than 7 m with respect to the overall length of all the district urban roads in the microzone | Percent |
| I7 | Population | Number of residents per square kilometer | (Square kilometers)−1 |
| I8 | Buildings | Percent of the number of residential buildings built before 1945 with respect to all residential buildings | Percent |
| I9 | buildings | Mean number of dwellings with at least one resident in the residential buildings | |
| I10 | Buildings | Percent of residential buildings with at least 16 dwellings with respect to all residential buildings | Percent |
| I11 | Schools | Accessibility and proximity of schools in the microzone | Percent |
| I12 | Public transportation | Usability of public transport networks | Percent |
| I13 | Coastal/marine zone | Coastal/marine area | Percent |
| I14 | Large public infrastructure | Presence of large public infrastructures | Percent |
| Indicator | Label | Inf | Mean | Sup | Type of Fuzzy Set |
|---|---|---|---|---|---|
| I1 | Scanty | 0 | 10 | 30 | ST |
| Mean | 20 | 30 | 50 | TR | |
| Discrete | 40 | 60 | 80 | TR | |
| High | 70 | 100 | ∞ | ST | |
| I2 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 40 | 50 | 70 | TR | |
| High | 60 | 70 | 100 | ST | |
| I3 | Scanty | 0 | 10 | 40 | ST |
| Mean | 30 | 50 | 70 | TR | |
| Discrete | 60 | 80 | 90 | TR | |
| High | 90 | 200 | ∞ | ST | |
| I4 | Null | 0 | 10 | 30 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 30 | 50 | 70 | TR | |
| High | 50 | 70 | 100 | ST | |
| I5 | Null | 0 | 20 | 30 | ST |
| Mean | 15 | 40 | 50 | TR | |
| Discrete | 40 | 50 | 70 | TR | |
| High | 60 | 70 | 100 | ST | |
| I6 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 40 | 50 | 70 | TR | |
| High | 60 | 70 | 100 | ST | |
| I7 | Scanty | 0 | 100 | 1000 | ST |
| Mean | 100 | 1000 | 5000 | TR | |
| Discrete | 1000 | 5000 | 10000 | TR | |
| High | 5000 | 10000 | ∞ | ST | |
| I8 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 40 | 50 | 70 | TR | |
| High | 60 | 80 | 100 | ST | |
| I9 | Scanty | 0 | 5 | 10 | ST |
| Mean | 5 | 20 | 30 | TR | |
| Discrete | 30 | 40 | 60 | TR | |
| High | 40 | 60 | ∞ | ST | |
| I10 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 40 | 60 | 80 | TR | |
| High | 60 | 80 | 100 | ST | |
| I11 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 50 | 70 | 90 | TR | |
| High | 70 | 90 | 100 | ST | |
| I12 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 30 | 50 | TR | |
| Discrete | 40 | 50 | 70 | TR | |
| High | 60 | 70 | 100 | ST | |
| I13 | Null | 0 | 10 | 30 | ST |
| Mean | 30 | 50 | 70 | TR | |
| High | 60 | 90 | 100 | ST | |
| I14 | Null | 0 | 10 | 20 | ST |
| Mean | 10 | 50 | 70 | TR | |
| Discrete | 50 | 80 | 90 | TR | |
| High | 60 | 90 | 100 | ST |
| Urban area class | Description |
|---|---|
| Residential old town | Residential agglomeration of ancient or recent formation characterized by historical, artistic, and environmental goods even if tampered with or degraded or not present at the same time |
| Comfortable residential zone | Dwelling place equipped with comfortable and modern/contemporary dwellings, infrastructures, sports facilities, and green spaces |
| Downtrodden residential zone | Dwelling place equipped with uncomfortable dwellings and lacking infrastructures, sports facilities, and green spaces |
| Industrial zone | Zone with prevalent or mixed industrial areas |
| Coastal residential zone | Area inclusive of a border with sea or great lakes with mainly maritime services |
| Fragmented rural/wooded zone | Mainly rural or wooded area with reduced settlement development |
| Sprawl | Informal modern/contemporary urban settlement |
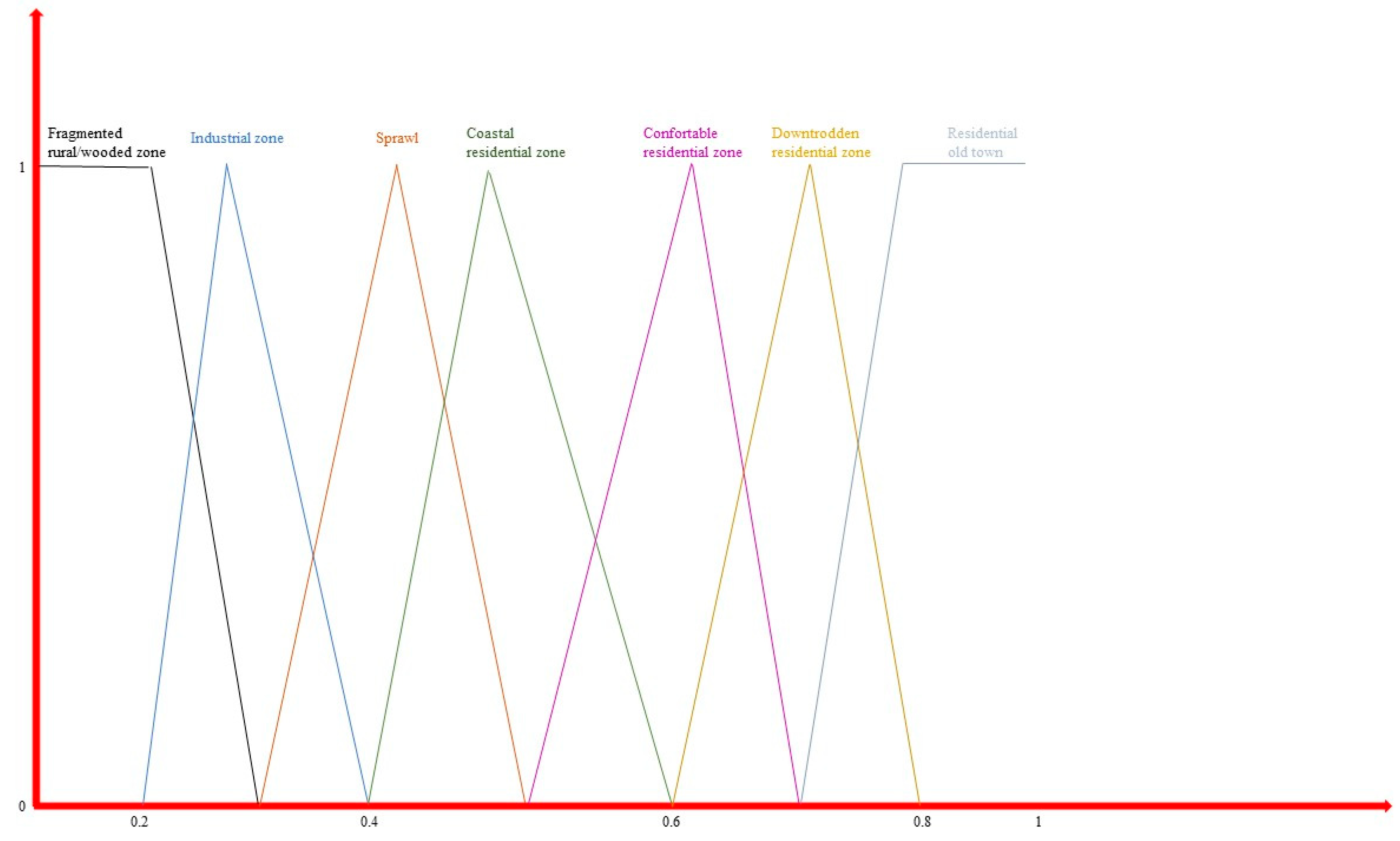
| Urban Area Class | Inf | Mean | Sup | Type of Fuzzy Set |
|---|---|---|---|---|
| Fragmented rural/wooded zone | 0 | 0.2 | 0.3 | ST |
| Industrial zone | 0.2 | 0.3 | 0.4 | TR |
| Sprawl | 0.3 | 0.4 | 0.5 | TR |
| Coastal residential zone | 0.4 | 0.5 | 0.6 | TR |
| Comfortable residential zone | 0.5 | 0.6 | 0.7 | TR |
| Downtrodden residential zone | 0.6 | 0.7 | 0.8 | TR |
| Residential old town | 0.7 | 0.8 | 1 | ST |
| Indicator | II Level Indicator | Type | Description | Unit of Measurement |
|---|---|---|---|---|
| I11 | I11a | Schools | Percent ratio between the service area (500 m radius around the primary school) and the extension of the microzone | Percent |
| I11b | Schools | Percent ratio between the service area (500 m radius around the lower secondary school) and the extension of the microzone | Percent | |
| I11c | Schools | Percent ratio between the service area (500 m radius around the secondary school) and the extension of the microzone | Percent | |
| I12 | I12a | Public transportation | Percent ratio between the bus stop service area (100 m radius around the bus stop) and the extension of the microzone | Percent |
| I12b | Public transportation | Percent ratio between the railway/subway station service area (300 m radius around the railway/subway station) and the extension of the microzone | Percent | |
| I13 | I13a | Coastal/marine zone | Coastal area (1 if the microzone is a coastal area; 0 otherwise) | {0,1} |
| I13b | Coastal/marine zone | Maritime terminal (1 if it is present in the microzone; 0 otherwise) | {0,1} | |
| I14 | I14a | Large public infrastructures | Presence of large public sport facilities (1 if large sports facilities are present in the microzone; 0 otherwise) | {0,1} |
| I14b | Large public infrastructures | Presence of public hospitals (1 if hospitals are present in the microzone; 0 otherwise) | {0,1} |
| Geo-Topographic Datasets | |
|---|---|
| Institution | Campania Region |
| Data Source | Municipality of Pozzuoli—2012 Geo-Topographic Database in a scale of 1:5000, coordinate system UTM WGS84 zone 33 N, plane coordinates. |
| Datasets | Industrial and residential buildings Schools Urban streets Urban green areas Woodlands and barred areas Transport facilities Hospitals Sports facilities |
| Institution | ISTAT—Italian National Institute of Statistics |
| Data Source | 2011 Census database–Socio-Demographic Database per census tract in a scale of 1:10,000, coordinate system UTM WGS84 zone 32 N, plane coordinates. Website: https://www.istat.it/it/archivio/104317. |
| Datasets | Census tracts Population dataset Building and dwelling dataset |
| Institution | Municipality of Pozzuoli |
| Data Source | Municipality spatial database, coordinate system UTM WGS84 zone 33 N, scale 1:4000, coordinate system UTM WGS84 zone 33 N, plane coordinates. |
| Datasets | Municipality Ortho Images Road network, railway network |
| Institution | OpenStreetMap (OSM) community |
| Data Source | OpenStreetMap spatial database, coordinate system UTM WGS84 zone 32 N, coordinate system UTM WGS84 zone 33 N, plane coordinates. Website: http://download.geofabrik.de/osm-data |
| Datasets | Road network Schools Transport facilities Bus and railway stops |
| Urban Area Class | Accuracy | Precision | Recall |
|---|---|---|---|
| Fragmented rural/wooded zone | 99.29% | 100.00% | 88.89% |
| Industrial zone | 100.00% | 100.00% | 100.00% |
| Sprawl | 100.00% | 84.62% | 100.00% |
| Coastal residential zone | 100.00% | 100.00% | 100.00% |
| Comfortable residential zone | 100.00% | 100.00% | 100.00% |
| Downtrodden residential zone | 100.00% | 100.00% | 100.00% |
| Residential old town | 100.00% | 100.00% | 100.00% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardone, B.; Di Martino, F. A New Geospatial Model Integrating a Fuzzy Rule-Based System in a GIS Platform to Partition a Complex Urban System in Homogeneous Urban Contexts. Geosciences 2018, 8, 440. https://doi.org/10.3390/geosciences8120440
Cardone B, Di Martino F. A New Geospatial Model Integrating a Fuzzy Rule-Based System in a GIS Platform to Partition a Complex Urban System in Homogeneous Urban Contexts. Geosciences. 2018; 8(12):440. https://doi.org/10.3390/geosciences8120440
Chicago/Turabian StyleCardone, Barbara, and Ferdinando Di Martino. 2018. "A New Geospatial Model Integrating a Fuzzy Rule-Based System in a GIS Platform to Partition a Complex Urban System in Homogeneous Urban Contexts" Geosciences 8, no. 12: 440. https://doi.org/10.3390/geosciences8120440
APA StyleCardone, B., & Di Martino, F. (2018). A New Geospatial Model Integrating a Fuzzy Rule-Based System in a GIS Platform to Partition a Complex Urban System in Homogeneous Urban Contexts. Geosciences, 8(12), 440. https://doi.org/10.3390/geosciences8120440