Application of Radial Basis Functions for Height Datum Unification
Abstract
:1. Introduction
2. Theory
3. Numerical Study
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tscherning, C.; Anderson, O.; Knudsen, P. Improvement of Gravity Prediction from Satellite Altimetry in Coastal Areas Using Data on Land; A Volume Dedicated to Milan Burša on the Occasion of his 80th Birthday. 2009. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.523.3031&rep=rep1&type=pdf (accessed on 30 September 2018).
- Davis, C. Growth of the Greenland Ice Sheet: A performance assessment of altimteter retracking algorithms. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1108–1116. [Google Scholar] [CrossRef]
- Tscherning, C.; Forsberg, R.; Knudsen, P. The GRAVSOFT Package for Geoid Determination. In Proceedings of the The first continental workshop on the Geoid in Europe, Prague, Czech Republic, 11–14 May 1992; Holota, P., Vermmer, M., Eds.; pp. 327–334. [Google Scholar]
- Sjöberg, L. General model for modifying Stokes’ formula and its least-square solution. J. Geod. 2003, 77, 459–464. [Google Scholar] [CrossRef]
- Forsberg, R.; Sideris, M. Co-geoid computations by the multiband spherical FFT approach. Manuscr. Geod. 1993, 18, 82–90. [Google Scholar]
- Schmidt, M.; Fengler, M.; Mayer-Guerr, T.; Eicker, A.; Kusche, J.; Sanchez, L.; Han, S. Regional gravity field modeling in terms of spherical base functions. J. Geod. 2007, 81, 17–38. [Google Scholar] [CrossRef]
- Klees, R.; Tenzer, R.; Prutkin, I.; Wittwer, T. A data-friven approach to local gravity field modelling using spheical radial basis functions. J. Geod. 2008, 82, 457–471. [Google Scholar] [CrossRef]
- Eicker, A. Gravity Field Refinement by Radial Basis Functions from In-Situ Satellite Data. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2008. [Google Scholar]
- Wittwer, T. Regional Gravity Field Modelling with Radial Basis Functions. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 2009. [Google Scholar]
- Naeimi, M. Inversion of Satellite Gravity Data Using Spherical Radial Base Functions. Ph.D. Thesis, Munchen, Germany, 2013. [Google Scholar]
- Safari, A.; Sharifi, M.; Amin, H.; Foroughi, I.; Tenzer, R. Determining the gravitational gradient tensor using satellite-altimetry observations over the Persian Gulf. Mar. Geod. 2014, 37, 404–418. [Google Scholar] [CrossRef]
- Foroughi, I.; Tenzer, R. Assessment of the direct inversion scheme for the quasigeoid modeling based on applying the Levenberg-Marquardt algorithm. Appl. Geomat. 2014, 6, 171–180. [Google Scholar] [CrossRef]
- Shahbazi, A.; Safari, A.; Foroughi, I.; Tenzer, R. A numerically efficient technique for regional gravity field modelling using radial basis functions. C. R. Geosci. 2016, 348, 99–105. [Google Scholar] [CrossRef]
- Mahbuby, H.; Safari, A.; Foroughi, I. Local gravity field modelling using spherical radial basis functions and a genetic algorithm. C. R. Geosci. 2017, 349, 106–113. [Google Scholar] [CrossRef]
- Naeimi, M.; Bouman, J. Contribution of the GOCE gradiometer components to regional gravity solutions. Geophys. J. Int. 2017, 209, 559–569. [Google Scholar] [CrossRef]
- Li, X. Using radial basis functions in airborne gravimetry for local geoid improvement. J. Geod. 2018, 92, 471–485. [Google Scholar] [CrossRef]
- Rummel, R.; Teunissen, P. Height datum definition, height datum connection and the role of the geodetic boundary value problem. Bulletin Géodésique 1988, 62, 477–498. [Google Scholar] [CrossRef]
- Featherstone, W. Do we need a gravimetric geoid or a model of the base of the Australian Height Datum to transform GPS heights. Aust. Surv. 1998, 43, 273–280. [Google Scholar] [CrossRef]
- Rapp, R. Separation between reference surfaces of selected vertical datums. Bull. Geod. 1994, 69, 26–31. [Google Scholar] [CrossRef]
- Bursa, M.; Kouba, J.; Muller, A.; Radej, K.; True, S.; Vartrt, V.; Vojtíšková, M. Determination of geopotential differences between local vertical datums and realization of a world height system. Studia Geophysica et Geodetica 2001, 45, 127–132. [Google Scholar] [CrossRef]
- Ardalan, A.; Grafarend, E.; Kakkuri, J. National height datum, the Gauss-Listing geoid level value w0 and its time variation ẇ0. J. Geod. 2002, 76, 1–28. [Google Scholar] [CrossRef]
- Hipkin, R. Vertical datum defined by Wo = Uo: Theory and practice of a modern height system. In Proceedings of the Third Meeting of the International Gravity and Geoid Commission, Thessaloniki, Greece, 26–30 August 2002; pp. 26–30. [Google Scholar]
- Ardalan, A.; Safari, A. Global height datum unification: A new approach in gravity potential space. J. Geod. 2005, 79, 512–523. [Google Scholar] [CrossRef]
- Sánchez, L. Approach for the establishment of a global vertical reference leve. In VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy, IAG Symposia; Xu, P., Liu, J., Dermanis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 119–125. [Google Scholar]
- Zhang, L.; Li, F.; Chen, W.; Zhang, C. Eight datum unification between Shenzhen and Hong Kong using the solution of the linearized fixed-gravimetric boundary value problem. J. Geod. 2009, 83, 411–417. [Google Scholar] [CrossRef]
- Gatti, A.; Reguzzoni, M.; Venuti, G. The height datum problem and the role of satellite gravity models. J. Geod. 2013, 87, 15–22. [Google Scholar] [CrossRef]
- Safari, A.; Sharifi, M.; Foroughi, I.; Amin, H. An Approach to Height Datum Unification Based on Local Gravity Field Modeling Using Radial Base Function Case Study: Height Datum Unification of Leveling Network of Class 1 in Iran. J. Earth Space Phys. 2014, 40, 69–81. [Google Scholar]
- Saadat, A.; Safari, A.; Needell, D. IRG2016: RBF-based regional geoid model of Iran. Stud. Geophys. Geod. 2018, 62, 380–407. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman and Company: San Francisco, CA, USA, 1967. [Google Scholar]
- Moritz, H. Advanced Physical Geodesy; Wichmann: Karlsrube, MI, USA, 1980. [Google Scholar]
- Tenzer, R.; Klees, R. The choice of the spherical radial basis functions in local gravity field modeling. Studia Geophysica et Geodetica 2008, 52, 287. [Google Scholar] [CrossRef]
- Holschneider, M.; Chambodut, A.; Mandea, M. From Global to regional analysis of the manetic field on the sphere using wavelet frames. Phys. Earth Planet. Inter. 2003, 135, 107–124. [Google Scholar] [CrossRef]
- Chambodut, A.; Panet, I.; Mandea, M.; Diament, M.; Holschneider, M.; Jamet, O. Wavelet frams: An alternative to spherical harmonic representatio of potential fields. Geophys. J. Int. 2005, 163, 875–899. [Google Scholar] [CrossRef]
- Tikhonov, A. Solution of incorrectly formulated problems and the regularization method. Sov. Math. 1963, 4, 1035–1038. [Google Scholar]
- Pavlis, N.; Holmes, S.; Kenyon, S.; Factor, J. The development and evaluation of the Earth Gravitional Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, 1–38. [Google Scholar] [CrossRef]
- Foroughi, I.; Afrasteh, Y.; Ramouz, S.; Safari, A. Local Evaluation of Earth Gravitional Models, case study: Iran. Geod. Cartogr. 2017, 43, 1–13. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.L.; Abrikosov, O.; Lemoine, J.-M.; Schaller, T.; Götze, H.-J.; Ebbing, J.; Marty, J.C.; Flechtner, F.; Balmino, B.; et al. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. In Proceedings of the 5th GOCE User Workshop, Paris, France, 25–28 November 2014. [Google Scholar]
- Bucha, B.; Janak, J. A MATLAB-based graphical user interface program for computing functionals of the geopotential up to ultra-high degrees and orders: Efficient computation at irregular surfaces. Comput. Geosci. 2014, 66, 219–227. [Google Scholar] [CrossRef]
- Sandwell, D.; Smith, W. Global marine gravity from retracked Geosat and ERS-1 altimetry: Ridge segmentation versus spreading rate. J. Geophys. Res. Lett. Solid Earh 2009, 114, B01411. [Google Scholar]
- Sandwell, D.; Muller, R.; Smith, W.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 6567. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P. Regularization tools version 4.0 for Matlab 7.3. Numer. Algorithms 2007, 46, 189–194. [Google Scholar] [CrossRef]
- Tenzer, R.; Vaníček, P.; Santos, M.; Featherstone, W.; Kuhn, M. The rigorous determination of the orthometric heihgts. J. Geod. 2005, 79, 82–92. [Google Scholar] [CrossRef]
- Tenzer, R.; Hirt, C.; Claessnes, S.; Novak, P. Spatial and spectral representations of the geoid-to-quasigeoid correction. Surv. Geophys. 2015, 36, 627. [Google Scholar] [CrossRef]
- Foroughi, I.; Vaníček, P.; Sheng, M.; Kingdon, R.; Santos, M. In defence of the classical height system. Geophys. J. Int. 2017, 211, 1176–1183. [Google Scholar] [CrossRef]
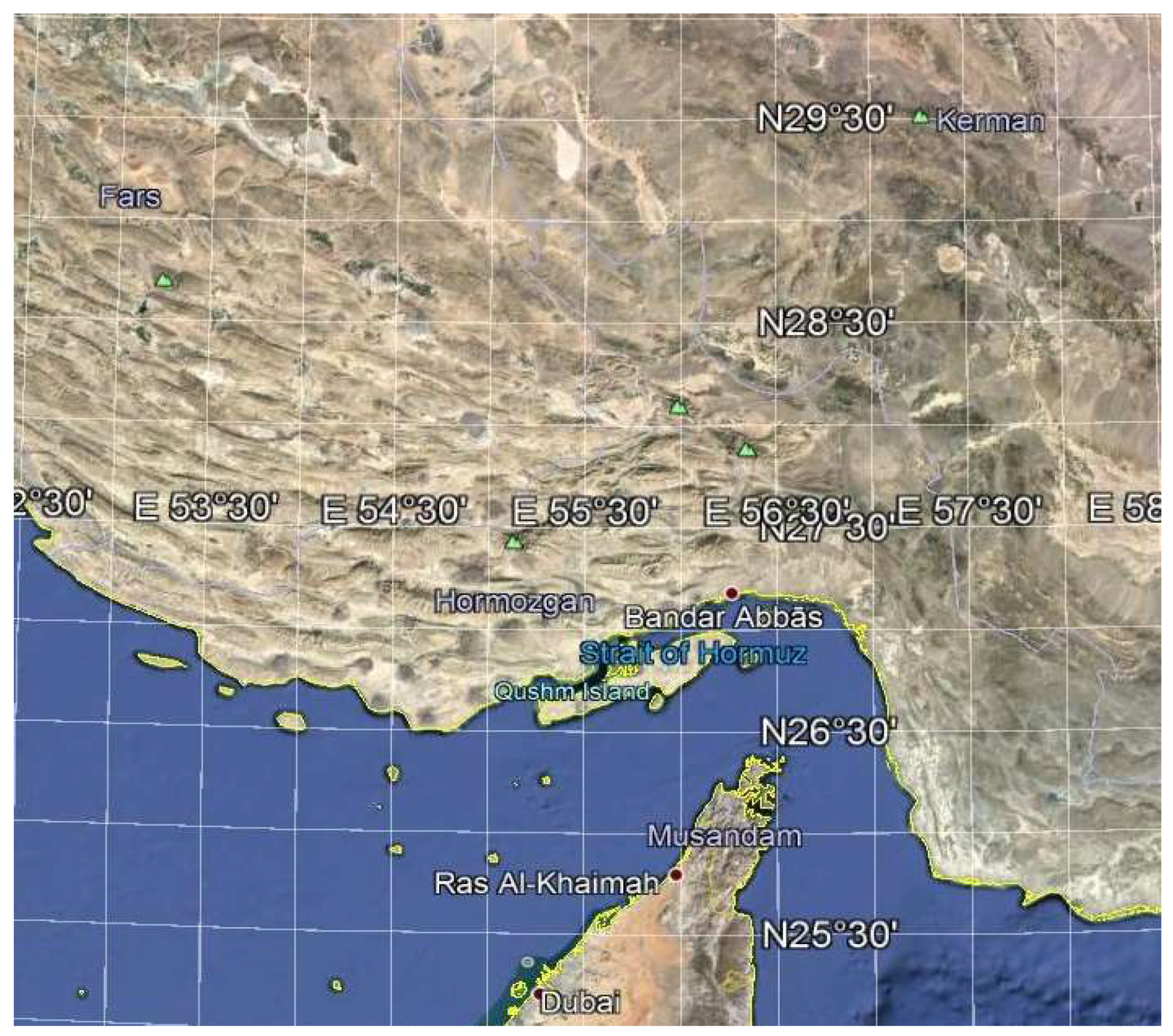
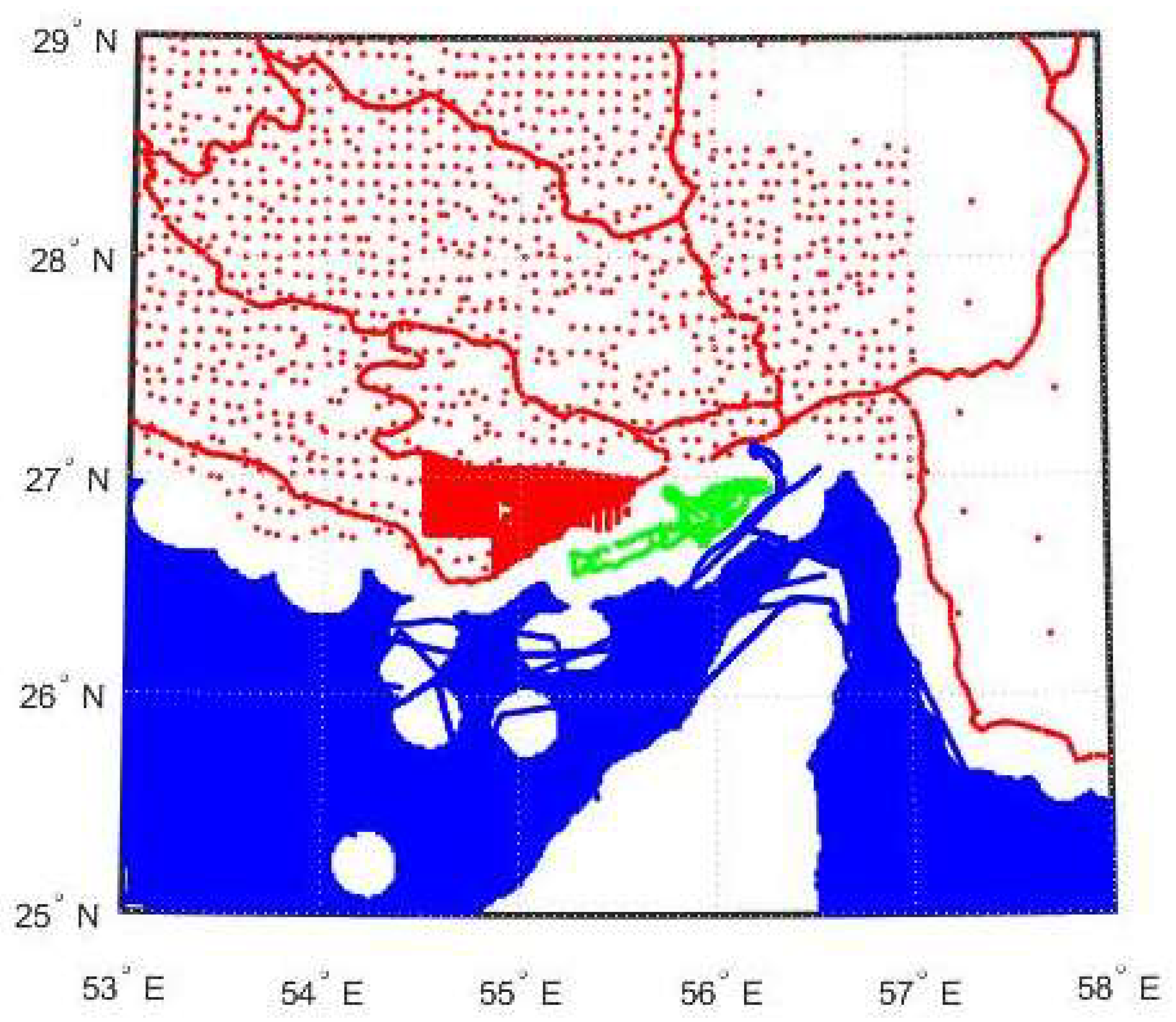
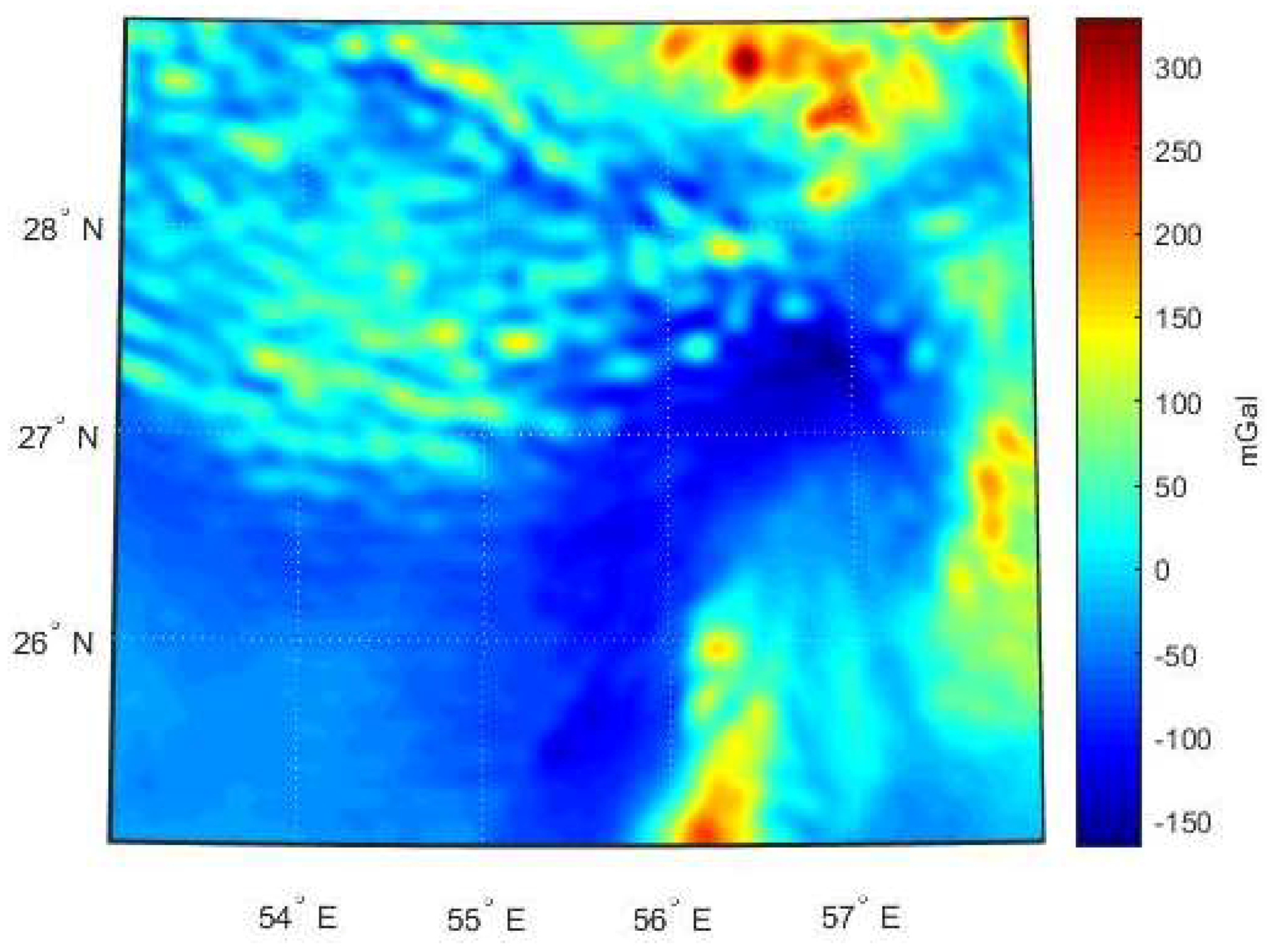

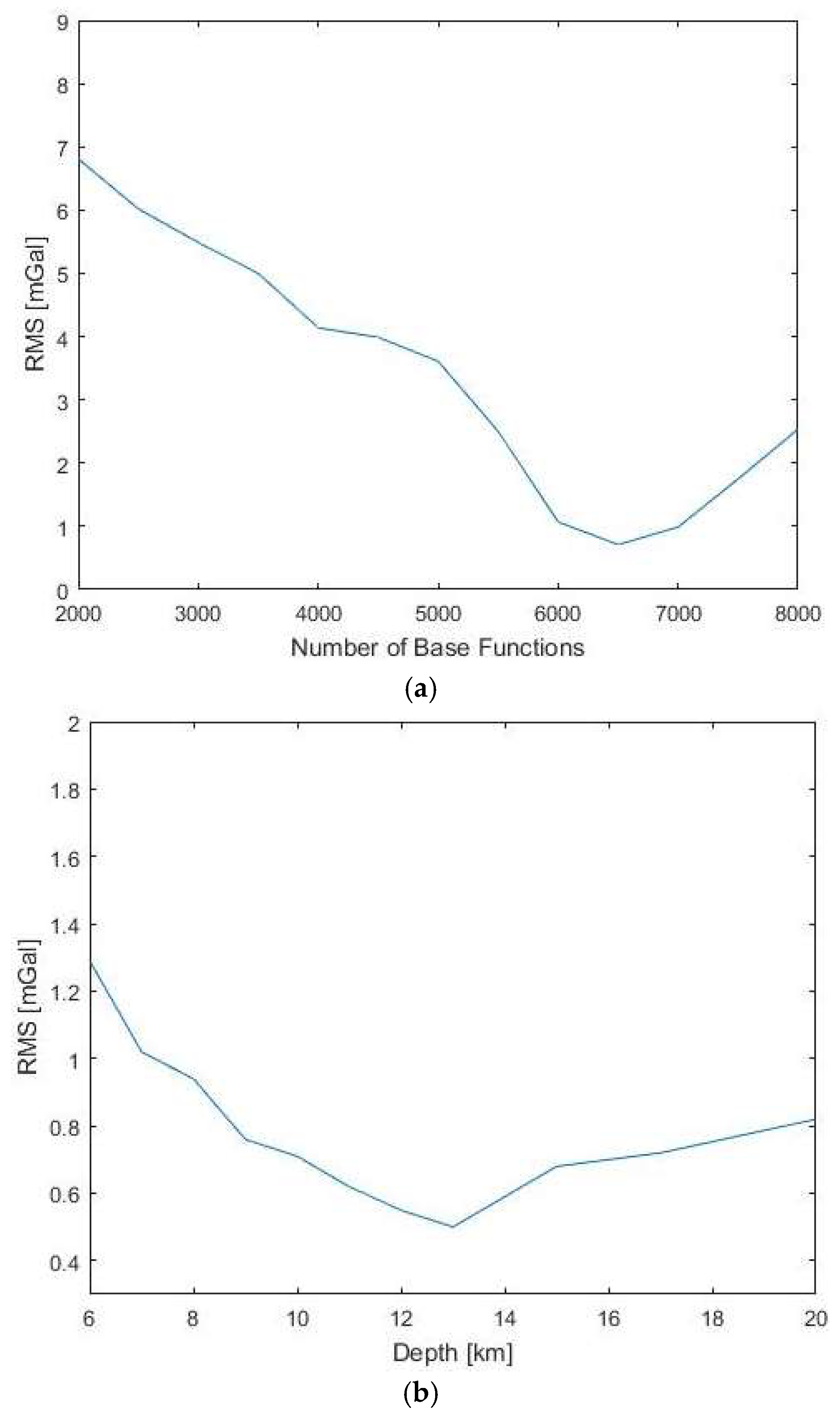
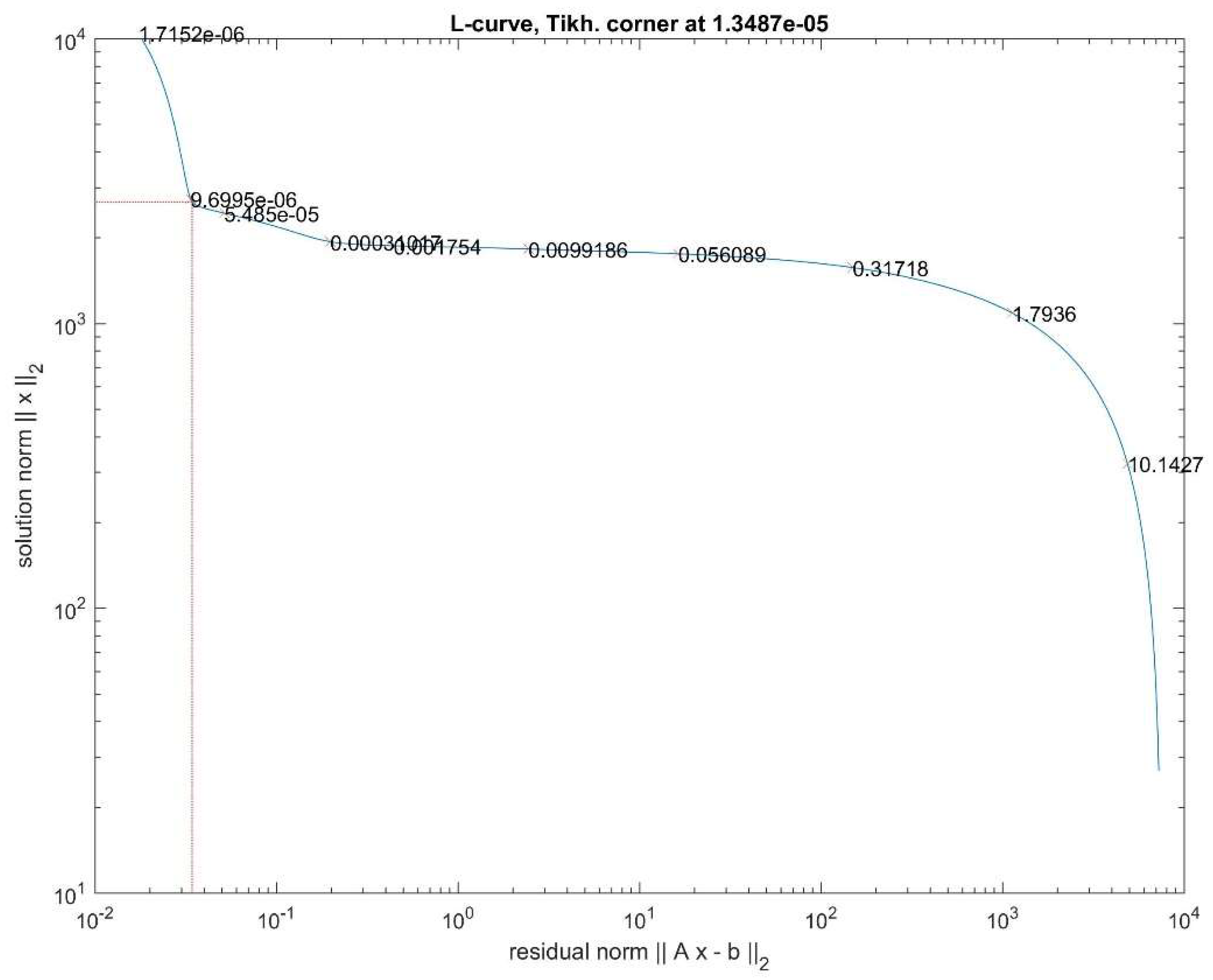
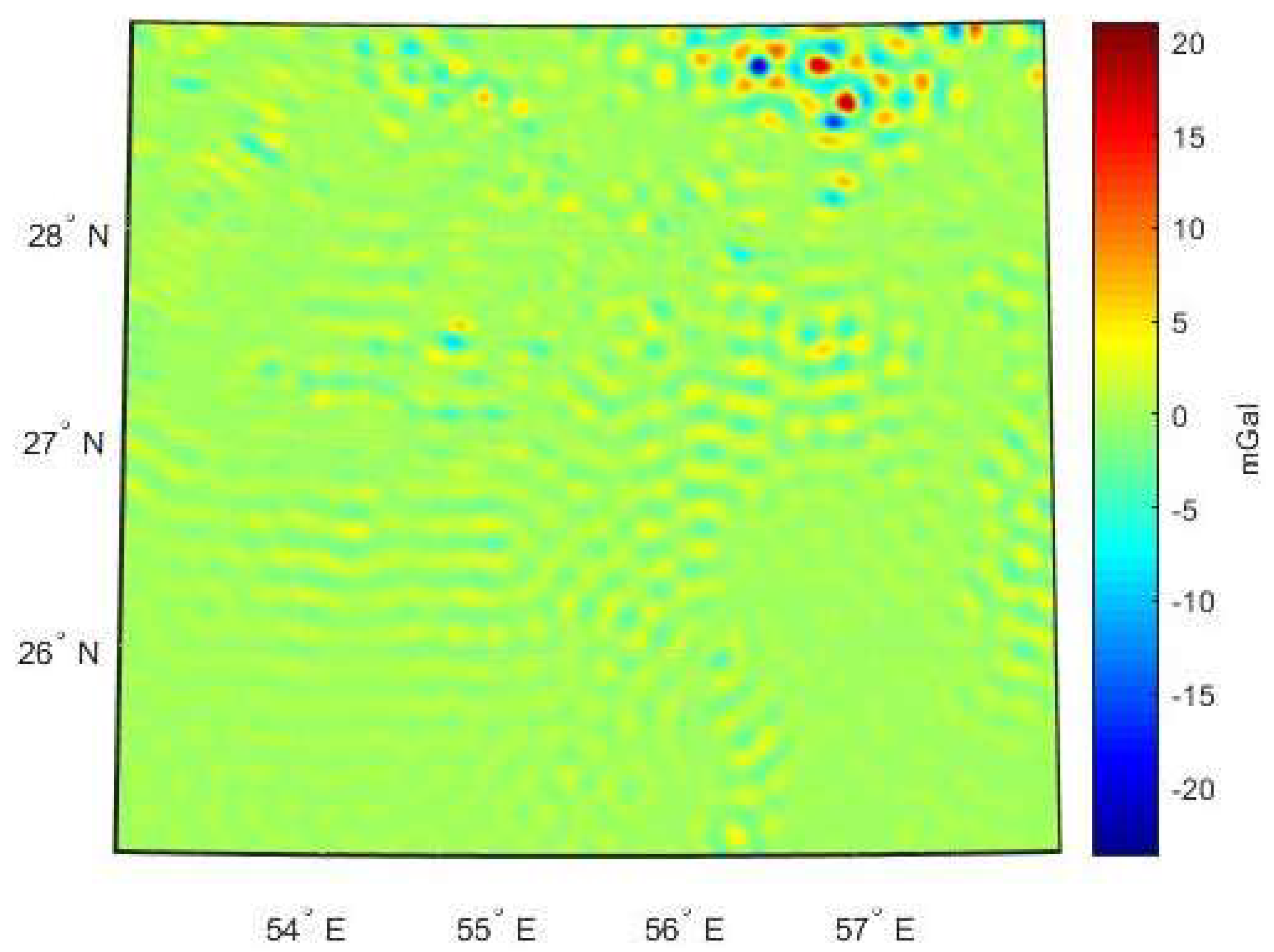
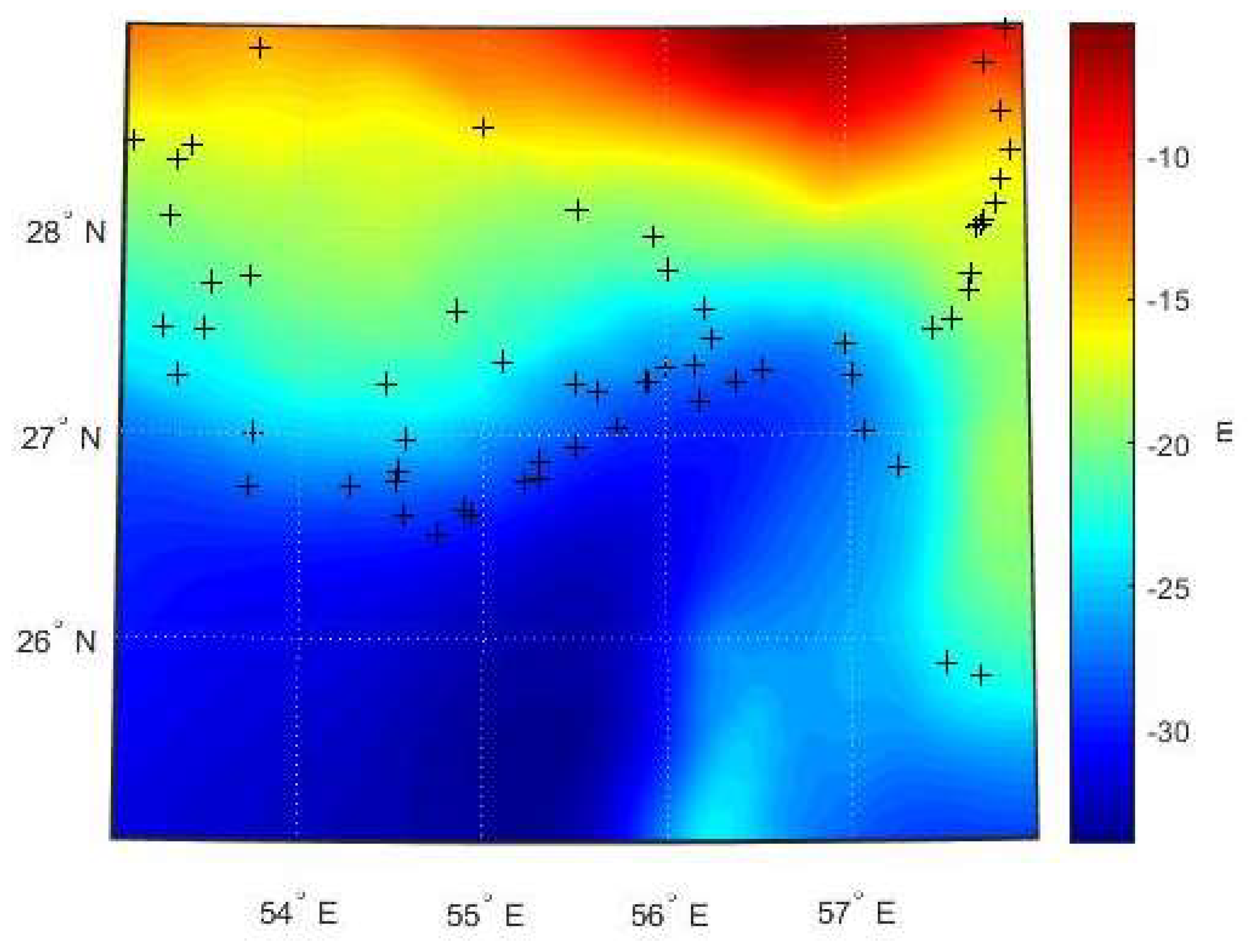
| Free Air Gravity Data | Source | Number of Points |
|---|---|---|
| Terrestrial | BGI-NCC | 5427 |
| Marine (Re-tracking) | Re-Tracked satellite altimetry | 20,951 |
| Global model | EGM2008 up to d/o 2160 | 6752 |
| Min (mGal) | Max (mGal) | Mean (mGal) | STD (mGal) | |
|---|---|---|---|---|
| Free-air gravity anomalies | −211.24 | 348.57 | −13.14 | 65.50 |
| Reference field | −145.12 | 174.77 | −12.17 | 57.40 |
| Min [mGal] | Max [mGal] | Mean [mGal] | STD [mGal] | |
|---|---|---|---|---|
| −23.90 | 21.13 | 0.00 | 1.41 |
| Min (m) | Max (m) | Mean (m) | STD (m) | |
|---|---|---|---|---|
| −0.11 | −0.18 | −0.120 | 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foroughi, I.; Safari, A.; Novák, P.; Santos, M.C. Application of Radial Basis Functions for Height Datum Unification. Geosciences 2018, 8, 369. https://doi.org/10.3390/geosciences8100369
Foroughi I, Safari A, Novák P, Santos MC. Application of Radial Basis Functions for Height Datum Unification. Geosciences. 2018; 8(10):369. https://doi.org/10.3390/geosciences8100369
Chicago/Turabian StyleForoughi, Ismael, Abdolreza Safari, Pavel Novák, and Marcelo C. Santos. 2018. "Application of Radial Basis Functions for Height Datum Unification" Geosciences 8, no. 10: 369. https://doi.org/10.3390/geosciences8100369
APA StyleForoughi, I., Safari, A., Novák, P., & Santos, M. C. (2018). Application of Radial Basis Functions for Height Datum Unification. Geosciences, 8(10), 369. https://doi.org/10.3390/geosciences8100369






