Suitability of Boulder Marl and Marsh Clay as Sealing Substrates for Landfill Capping Systems—A Practical Comparison
Abstract
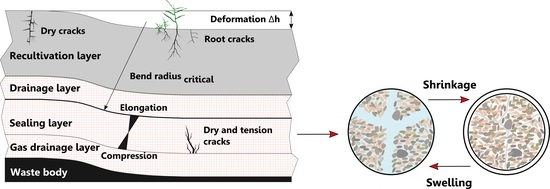
:1. Introduction
2. Materials and Methods
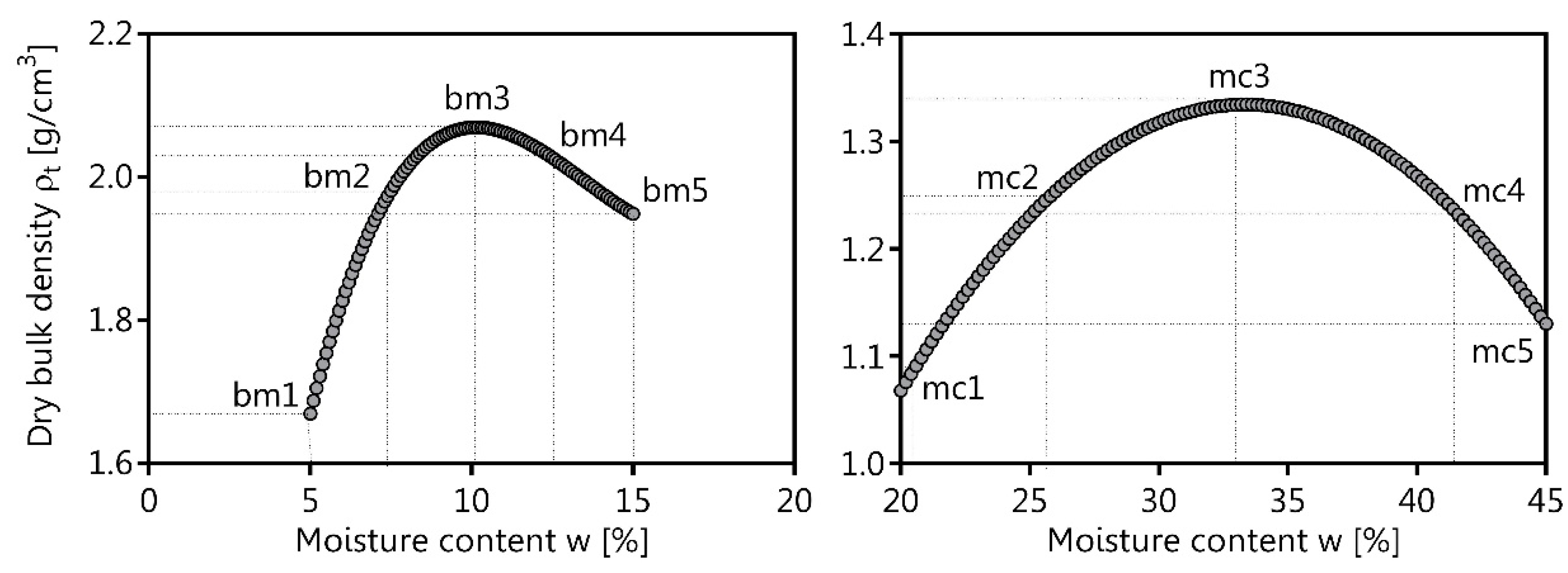
2.1. Standard Proctor Compaction Tests
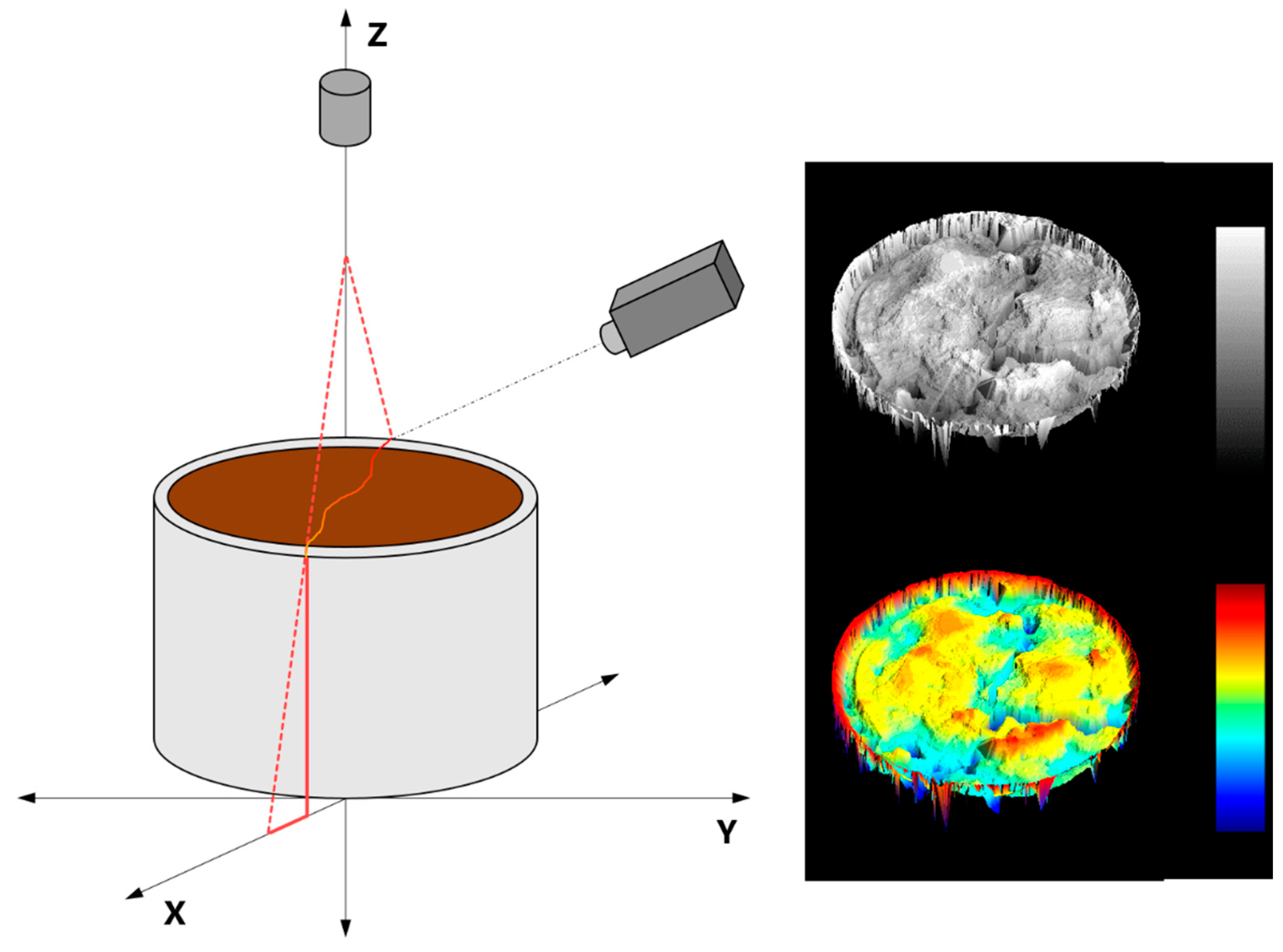
2.2. Laboratory Analysis
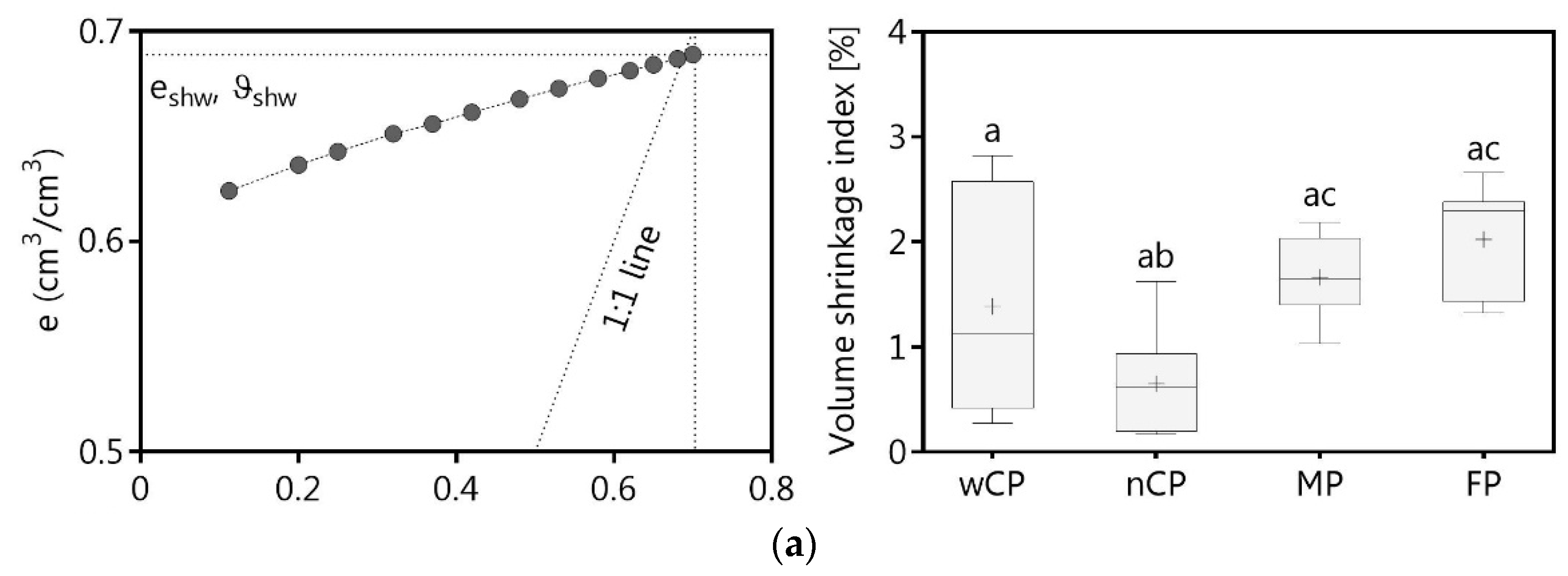
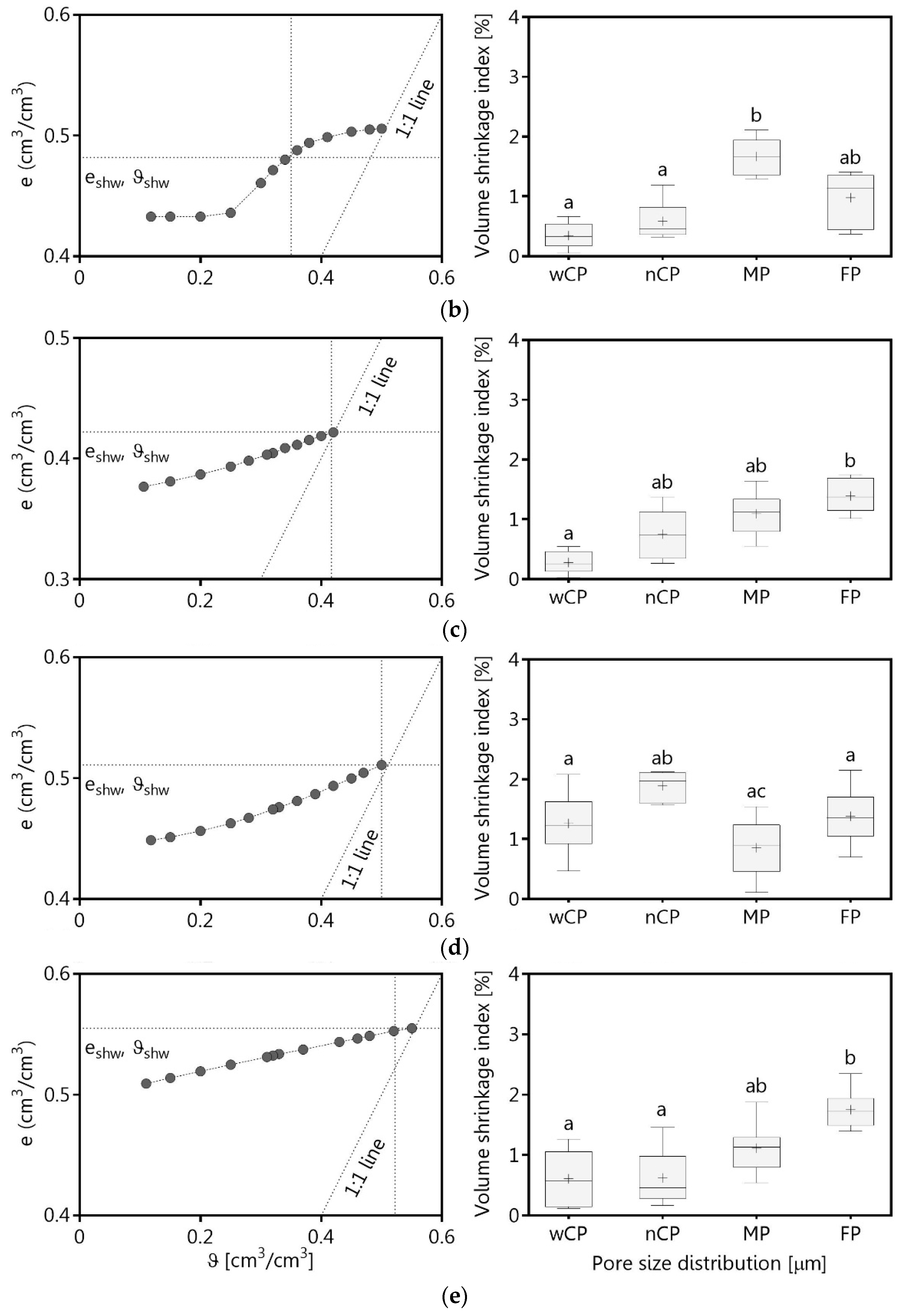
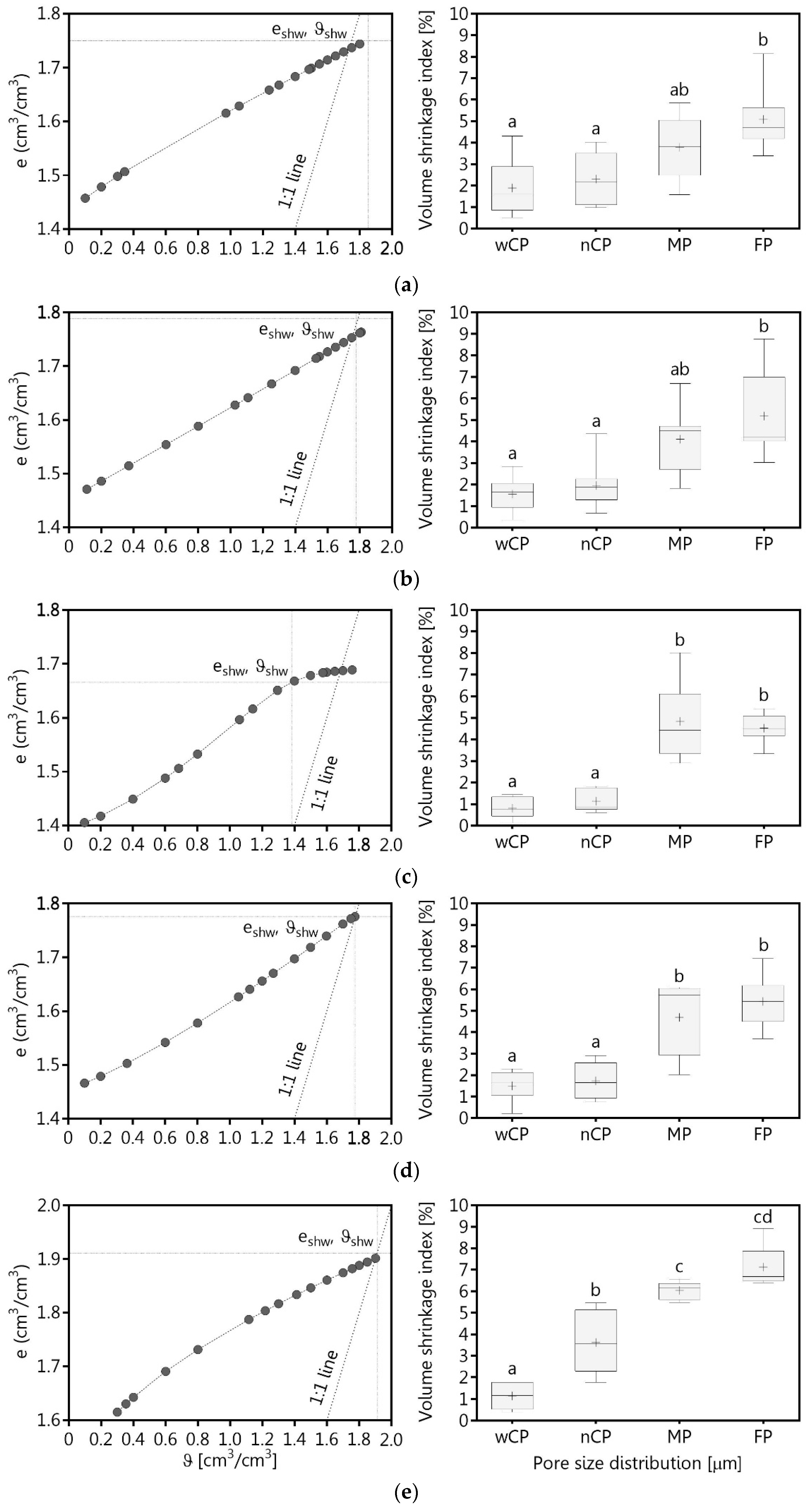
2.3. Shrinkage Behavior and Volume Shrinkage Index
2.4. Statistical Analysis
3. Results
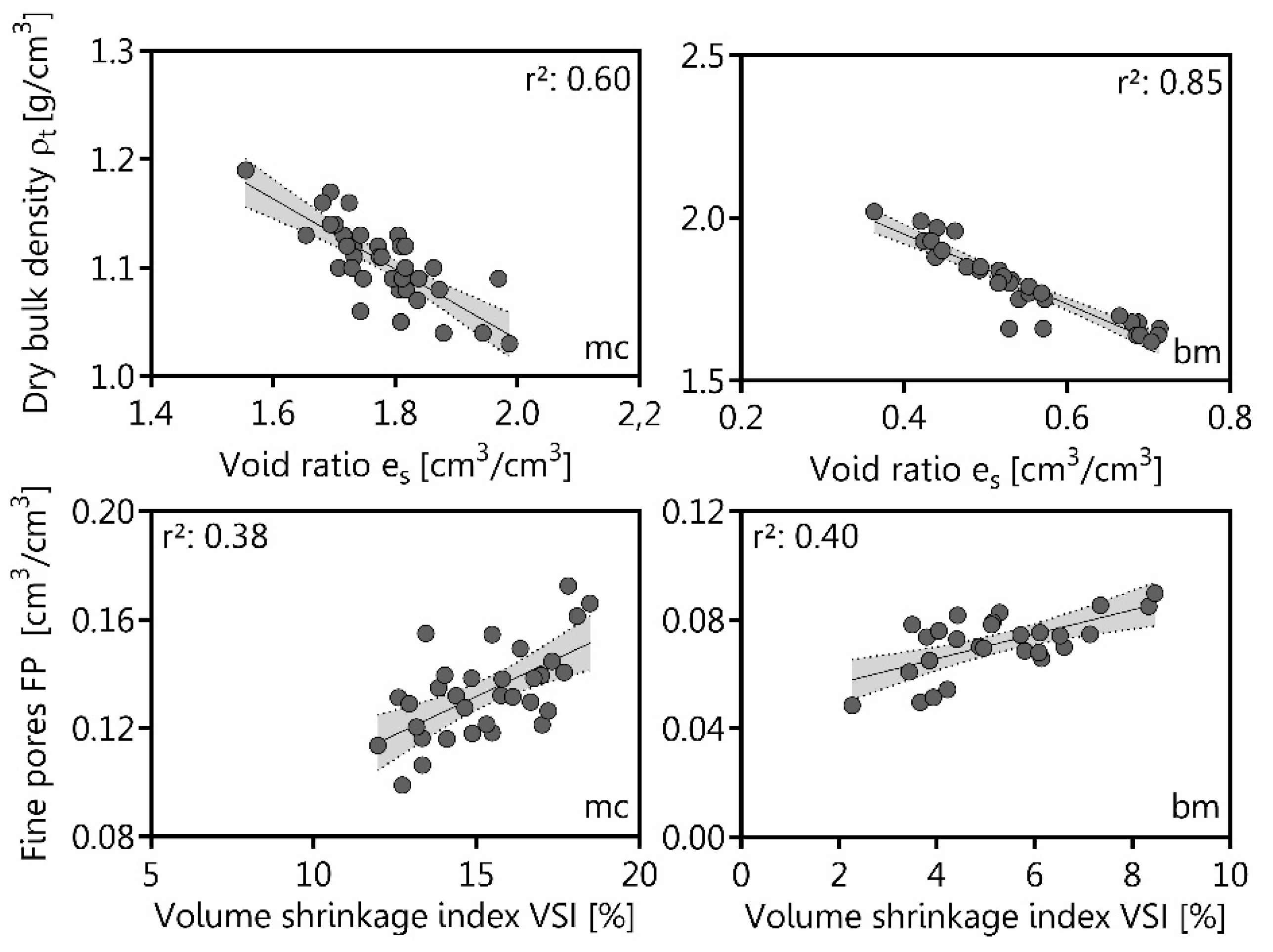
3.1. Basic Soil Characteristics
3.2. Shrinkage Behavior and Volume Shrinkage Index
4. Discussion
4.1. Statutory Requirements of the German Landfill Directive
4.2. Shrinkage Behavior of Marsh Clay and Boulder Marl
4.3. Suitability of Marsh Clay and Boulder Marl as Mineral Liner
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoornweg, D.; Bhada-Tata, P. What a Waste: A Global Review of Solid Waste Management; Urban Development Series, Knowledge Papers (15); The World Bank: Washington, DC, USA, 2012. [Google Scholar]
- The German Federal Government. Degree on Landfills (Ordinance to Simplify the Landfill Law)—Germany, in the Form of the Resolution of the Federal Cabinet; The German Federal Government: Berlin, Germany, 2009.
- Hauser, V.L. Evapotranspiration Covers for Landfills and Waste Sites; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2008. [Google Scholar]
- Arnold, S.; Schneider, A.; Doley, D.; Baumgartl, T. The limited impact of vegetation on the water balance of mine waste cover systems in semiarid Australia. Ecohydrology 2014, 8, 355–367. [Google Scholar] [CrossRef]
- Widomski, M.K.; Stępniewski, W.; Horn, R.; Bieganowski, A.; Gazda, L.; Franus, M.; Pawlowska, M. Shrink-swell potential, hydraulic conductivity and geotechnical properties of clay materials for landfill liner construction. Int. Agrophys. 2015, 29, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Laner, D.; Crest, M.; Schraff, H.; Morris, J.W.F.; Barlaz, M.A. A review of approaches for the long-term management of municipal solid waste landfills. Waste Manag. 2012, 32, 498–512. [Google Scholar] [CrossRef] [PubMed]
- Horn, R.; Stępniewski, W. Modification of mineral liner to improve its long-term stability. Int. Agrophys. 2004, 18, 317–323. [Google Scholar]
- Witt, K.J.; Zeh, R.M. Crack due Desiccation in Cover Lining Systems Phenomena and Design Strategy. In Proceedings of the Hydro-Physico-Mechanics of Landfills, Grenoble, France, 21–22 March 2005; Grenoble University: Grenoble, France, 2005. [Google Scholar]
- Costa, S.; Kodikara, J.; Shannon, B. Salient factors controlling desiccation cracking of clay in laboratory experiments. Géotechnique 2013, 63, 18–29. [Google Scholar] [CrossRef]
- Proctor, R.R. Design and Construction of Rolled Earth Dams. Master’s Thesis, University of Louisville, Louisville, France, 1933. [Google Scholar]
- Hartge, K.H.; Horn, R. Essential Soil Physics—An Introduction to Soil Processes, Structure, and Mechanics; Horton, R., Horn, R., Bachmann, J., Peth, S., Eds.; Schweizerbart Science Publishers: Stuttgart, Germany, 2016. [Google Scholar]
- Hartge, K.H. Ein Haubenpermeameter zum schnellen Durchmessen zahlreicher Stechzylinderproben. Z. Kulturtech. Flurbereinigung 1966, 7, 155–163. [Google Scholar]
- Peng, X.; Horn, R.; Peth, S.; Smucker, A. Quantification of soil shrinkage in 2D by digital image processing of soil surface. Soil Till Res. 2006, 91, 173–180. [Google Scholar] [CrossRef]
- Seyfarth, M.; Holldorf, J.; Pagenkemper, S.K. Investigation of shrinkage induced changes in soil volume with laser scanning technique and automated soil volume determination—A new approach/method to analyze pore rigidity limits. Soil Till Res. 2012, 125, 105–108. [Google Scholar] [CrossRef]
- Umwelt-Geräte-Technik GmbH. Soil-LT 100—Device for Combined Volume, Weight and Water Tension Measurement. Operating Instructions; Umwelt-Geräte-Technik GmbH: Müncheberg, Germany, 2015. [Google Scholar]
- Peng, X.; Horn, R. Modelling soil shrinkage curve across a wide range of soil types. Soil Sci. Soc. Am. J. 2005, 69, 584–592. [Google Scholar] [CrossRef]
- Chertkov, V.Y.; Ravina, I.; Zadoenko, V. An approach for estimating the shrinkage geometry factor at a moisture content. Soil Sci. Soc. Am. J. 2004, 68, 1807–1817. [Google Scholar] [CrossRef]
- Braudeau, E.; Frangi, J.P.; Mothar, R.H. Characterizing non-rigid dual porosity structured soil medium using its characteristic SC. Soil Sci. Soc. Am. J. 2004, 68, 359–370. [Google Scholar] [CrossRef]
- Gebhardt, S.; Fleige, H.; Horn, R. Anisotropic shrinkage of mineral and organic soils and its impact on soil hydraulic properties. Soil Till Res. 2012, 125, 96–104. [Google Scholar] [CrossRef]
- Peng, X.; Horn, R. Identifying six types of soil shrinkage curves from a large set of experimental data. Soil Sci. Soc. Am. J. 2013, 77, 372–381. [Google Scholar] [CrossRef]
- Peng, X.; Horn, R. Anisotropic shrinkage and swelling of some organic and inorganic soils. Eur. J. Soil Sci. 2007, 58, 98–107. [Google Scholar] [CrossRef]
- Groenevelt, P.H.; Grant, C.D. Curvature of shrinkage lines in relation to the consistency and structure of Norwegian clay soil. Geoderma 2002, 106, 235–245. [Google Scholar] [CrossRef]
- Horn, R.; Baumgartl, T. Dynamic properties of soils. In Soil Physics Companion; Warrick, A.W., Ed.; CRC Press LLC: Boca Raton, FL, USA, 2002; pp. 17–48. [Google Scholar]
- Alaoui, A.; Lipiec, J.; Gerke, H.H. A review of the changes in the soil pore system due to soil deformation: A hydrodynamic perspective. Soil Till Res. 2011, 115–116, 1–15. [Google Scholar] [CrossRef]
- Skempton, A.W. The Colloidal “Activity” of Clays. In Proceedings of the Third International Conference on Soil Mechanics, Zürich, Swiss, 16–27 August 1953; pp. 57–61. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practise; John Wiley: New York, NY, USA, 1967. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- FAO. Guidelines for Soil Description; FAO-ISRIC Press: Rome, Italy, 2006. [Google Scholar]
- Huang, C.; Shao, M.; Tan, W. Soil shrinkage and hydrostructural characteristics of three swelling soils in Shaanxi, China. J. Soils Sediments 2011, 11, 474–481. [Google Scholar] [CrossRef] [Green Version]
- Schäffer, B.; Schulin, R.; Boivin, P. Changes in shrinkage of restored soil caused by compaction beneath heavy agricultural machinery. Eur. J. Soil Sci. 2008, 59, 771–783. [Google Scholar] [CrossRef]
- Beck-Broichsitter, S.; Fleige, H.; Horn, R. Waste capping systems processes and consequences for the longterm impermeability. In Soils within Cities; Levin, M., Kim, H.J., Morel, J.L., Burghardt, W., Charzynski, P., Shaw, R.K., Eds.; Catena Soil Sciences: Stuttgart, Germany, 2018; pp. 148–152. [Google Scholar]
- Anlauf, R.; Rehrmann, P. Effect of compaction on soil hydraulic parameters of vegetative landfill covers. Geomaterials 2012, 2, 29–36. [Google Scholar] [CrossRef]
- Stępniewski, W.; Widomski, M.K.; Horn, R. Hydraulic conductivity and landfill construction. In Developments in Hydraulic Conductivity Research, Rijeka, Croatia, 2011; Dikinya, O., Ed.; Intech: Rijeka, Croatia, 2011; pp. 249–270. [Google Scholar]
- Zhang, S.L.; Grip, H.; Lovdahl, L. Effect of soil compaction on hydraulic properties of two loess soils in China. Soil Till Res. 2006, 90, 117–125. [Google Scholar] [CrossRef]
- Albright, W.; Benson, C.; Gee, G.; Abichou, T.; Tyler, S.; Rock, S. Field Performance of a compacted clay candfill final cover at a humid site. J. Geotech. Geoenviron. Engr. 2006, 132, 1393–1403. [Google Scholar] [CrossRef]
- Priyankara, N.H.; Abeyrathne, W.K.A.P.; Alagiyawanna, A.M.W.; Kawamoto, K. Investigation of suitability of expansive soil to use as clay liners. In Proceedings of the 14th International Waste Management and Landfill Symposium, Sardinia, Italy, 30 September–4 October 2013; pp. 55–62. [Google Scholar]
- Habib, A.S. Effect of compaction characteristics on shrinkage of expansive clay. Res. J. Eng. Appl. Sci. 2013, 2, 439–445. [Google Scholar]
- Horn, R.; Peng, X.; Fleige, H.; Dörner, J. Pore rigidy in structured soils—only a theoretical boundary condition for hydraulic properties. J. Soil Sci. Plant Nutr. 2014, 60, 3–14. [Google Scholar]
- Oleszczuk, R.; Brandyk, T. The analysis of shrinkage-swelling behavior of peat-moorsh soil aggregates during drying-wetting cycles. Agron. Res. 2008, 6, 131–140. [Google Scholar]
- Beck-Broichsitter, S.; Fleige, H.; Goebel, M.-O.; Dörner, J.; Bachmann, J.; Horn, R. Shrinkage potential and pore shrinkage capacity of differently developed volcanic ash soils under pastures in southern Chile. J. Plant Nutr. Soil Sci. 2016, 179, 799–808. [Google Scholar] [CrossRef]
- Ajayi, A.; Horn, R. Comparing the potentials of clay and biochar in improving water retention and mechanical resilience of sandy soil. Int. Agrophys. 2016, 30, 391–399. [Google Scholar] [CrossRef] [Green Version]
- Markgraf, W.; Watts, C.W.; Whalley, W.R.; Hrkac, T.; Horn, R. Influence of organic matter on rheological properties of soil. Appl. Clay Sci. 2012, 64, 25–33. [Google Scholar] [CrossRef]
- Li, J.H.; Li, L.; Chen, R.; Li, D.Q. Cracking and vertical preferential flow through landfill clay liners. Eng. Geol. 2016, 206, 33–41. [Google Scholar] [CrossRef]
- Melchior, S.; Sokollek, V.; Berger, K.; Vielhaber, B.; Steinert, B. Results from 18 Years of in-situ performance testing of landfill cover systems in Germany. J. Environ. Eng.-Am. Soc. Civ. Eng. 2010, 136, 815–823. [Google Scholar] [CrossRef]
- Gebhardt, S.; Fleige, H.; Horn, R. Shrinkage processes of a drained riparian peatland with subsidence morphology. J. Soils Sediments 2010, 10, 484–493. [Google Scholar] [CrossRef]
| Material | OC [%] | pH [CaCl2] | Sand [%] | Silt [%] | Clay [%] | ρt [g/cm3] | Texture * |
|---|---|---|---|---|---|---|---|
| bm | 0.05 ± 0.02 | 7.6 ± 0.3 | 68 ± 1 | 21 ± 2 | 11 ± 2 | 2.65 ± 0.2 | SL |
| mc | 0.25 ± 0.03 | 5.6 ± 0.2 | 18 ± 1 | 56 ± 2 | 26 ± 3 | 2.67 ± 0.3 | CL |
| Material | IA | Quarz | Calcite | Kaolinite | Smectite | Vermiculite | Illite | Mont-Morillonite |
|---|---|---|---|---|---|---|---|---|
| [-] | [%] | [%] | [%] | [%] | [%] | [%] | [%] | |
| bm | 0.18 ± 0.1 | 85–88 | 3–4 | - | 3–11 | 3–4 | - | - |
| mc | 0.69 ± 0.4 | 21–25 | 0.5–1 | 34–36 | - | - | 22–24 | 14–16 |
| ProctorStage | TP [cm3/cm3] | AC [cm3/cm3] | AWC [cm3/cm3] | ρt [g/cm3] | W [%] | ρPr [g/cm3] | DPr [%] | Ks [m/s] |
|---|---|---|---|---|---|---|---|---|
| mc1 | 0.657 | 0.115 | 0.256 | 1.10 | 20 | 1.09 | 80 | 7.4 ± 2.3 × 10−7 |
| mc2 | 0.648 | 0.096 | 0.253 | 1.09 | 25 | 1.25 | 81 | 3.2 ± 1.6 × 10−7 |
| mc3 | 0.637 | 0.582 | 0.244 | 1.11 | 33 | 1.35 | 82 | 1.2 ± 0.8 × 10−7 |
| mc4 | 0.604 | 0.043 | 0.255 | 1.09 | 41 | 1.23 | 80 | 3.8 ± 1.4 × 10−7 |
| mc5 | 0.592 | 0.033 | 0.271 | 1.08 | 45 | 1.10 | 80 | 6.8 ± 3.2 × 10−7 |
| bm1 | 0.426 | 0.051 | 0.081 | 1.66 | 5.0 | 1.67 | 78 | 1.6 ± 1.3 × 10−6 |
| bm2 | 0.401 | 0.054 | 0.076 | 1.85 | 7.5 | 1.98 | 88 | 1.8 ± 1.2 × 10−6 |
| bm3 | 0.302 | 0.026 | 0.059 | 1.94 | 10.1 | 2.07 | 92 | 1.2 ± 0.5 × 10−6 |
| bm4 | 0.329 | 0.049 | 0.069 | 1.85 | 12.5 | 2.03 | 87 | 7.8 ± 2.1 × 10−7 |
| bm5 | 0.352 | 0.056 | 0.067 | 1.78 | 15.0 | 1.95 | 84 | 3.8 ± 1.6 × 10−7 |
| Proctor Stage | χ | p | q | r2 | eshw, ϑshw | es-eshw, ϑs-ϑshw | eshw-eshd, ϑshw-ϑshd | |
|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [cm3/cm3] | [cm3/cm3] | [cm3/cm3] | ||
| mc1 | 0.539 | 61.85 | 0.014 | 0.99 | ϑ | 1.85 | 0.001 ± 0.001 | 1.75 ± 0.01 |
| e | 1.75 | 0.015 ± 0.001 | 1.15 ± 0.02 | |||||
| mc2 | 0.525 | 72.54 | 0.014 | 0.98 | ϑ | 1.79 | 0.001 ± 0.001 | 1.68 ± 0.03 |
| e | 1.77 | 0.02 ± 0.001 | 1.34 ± 0.01 | |||||
| mc3 | 0.716 | 11.62 | 0.120 | 0.99 | ϑ | 1.39 | 0.02 ± 0.003 | 1.29 ± 0.02 |
| e | 1.66 | 0.001 ± 0.001 | 1.30 ± 0.02 | |||||
| mc4 | 0.563 | 87.47 | 0.014 | 0.99 | ϑ | 1.77 | 0 ± 0.001 | 1.68 ± 0.01 |
| e | 1.77 | 0 ± 0.001 | 1.33 ± 0.02 | |||||
| mc5 | 0.504 | 275.1 | 0.002 | 0.99 | ϑ | 1.91 | 0 ± 0.001 | 1.71 ± 0.02 |
| e | 1.91 | 0 ± 0.001 | 1.42 ± 0.03 | |||||
| bm1 | 1.356 | 236.5 | 0.003 | 0.98 | ϑ | 0.70 | 0.001 ± 0.001 | 0.60 ± 0.06 |
| e | 0.692 | 0.001 ± 0.001 | 0.09 ± 0.003 | |||||
| bm2 | 10.2 | 6.269 | 1129 | 0.98 | ϑ | 0.35 | 0.15 ± 0.02 | 0.24 ± 0.04 |
| e | 0.48 | 0.02 ± 0.001 | 0.07 ± 0.01 | |||||
| bm3 | 2.40 | 0.014 | 4.116 | 0.97 | ϑ | 0.417 | 0.001 ± 0.001 | 0.32 ± 0.7 |
| e | 0.42 | 0.001 ± 0.001 | 0.06 ± 0.002 | |||||
| bm4 | 2.001 | 132.5 | 0.014 | 0.96 | ϑ | 0.50 | 0 ± 0.001 | 0.40 ± 0.05 |
| e | 0.510 | 0 ± 0.001 | 0.06 ± 0.002 | |||||
| bm5 | 1.81 | 64.19 | 0.014 | 0.99 | ϑ | 0.522 | 0.023 ± 0.001 | 0.44 ± 0.06 |
| e | 0.555 | 0 ± 0.0001 | 0.06 ± 0.003 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beck-Broichsitter, S.; Gerke, H.H.; Horn, R. Suitability of Boulder Marl and Marsh Clay as Sealing Substrates for Landfill Capping Systems—A Practical Comparison. Geosciences 2018, 8, 356. https://doi.org/10.3390/geosciences8100356
Beck-Broichsitter S, Gerke HH, Horn R. Suitability of Boulder Marl and Marsh Clay as Sealing Substrates for Landfill Capping Systems—A Practical Comparison. Geosciences. 2018; 8(10):356. https://doi.org/10.3390/geosciences8100356
Chicago/Turabian StyleBeck-Broichsitter, Steffen, Horst H. Gerke, and Rainer Horn. 2018. "Suitability of Boulder Marl and Marsh Clay as Sealing Substrates for Landfill Capping Systems—A Practical Comparison" Geosciences 8, no. 10: 356. https://doi.org/10.3390/geosciences8100356
APA StyleBeck-Broichsitter, S., Gerke, H. H., & Horn, R. (2018). Suitability of Boulder Marl and Marsh Clay as Sealing Substrates for Landfill Capping Systems—A Practical Comparison. Geosciences, 8(10), 356. https://doi.org/10.3390/geosciences8100356