The Study of Geological Structures in Suli and Tulehu Geothermal Regions (Ambon, Indonesia) Based on Gravity Gradient Tensor Data Simulation and Analytic Signal
Abstract
:1. Introduction
2. Geologic Settings
3. Methods
3.1. Gravity Method
3.2. Calculation of Gravity Gradient Tensor Based on Synthetic Model
3.3. The 3D Analytic Signal of Gravity Data
3.3.1. Forward Modeling of Gravity Gradient Tensor Based on Rectangular Prism
3.3.2. Horizontal Gradient and Analytic Signal Based on a Rectangular Prism
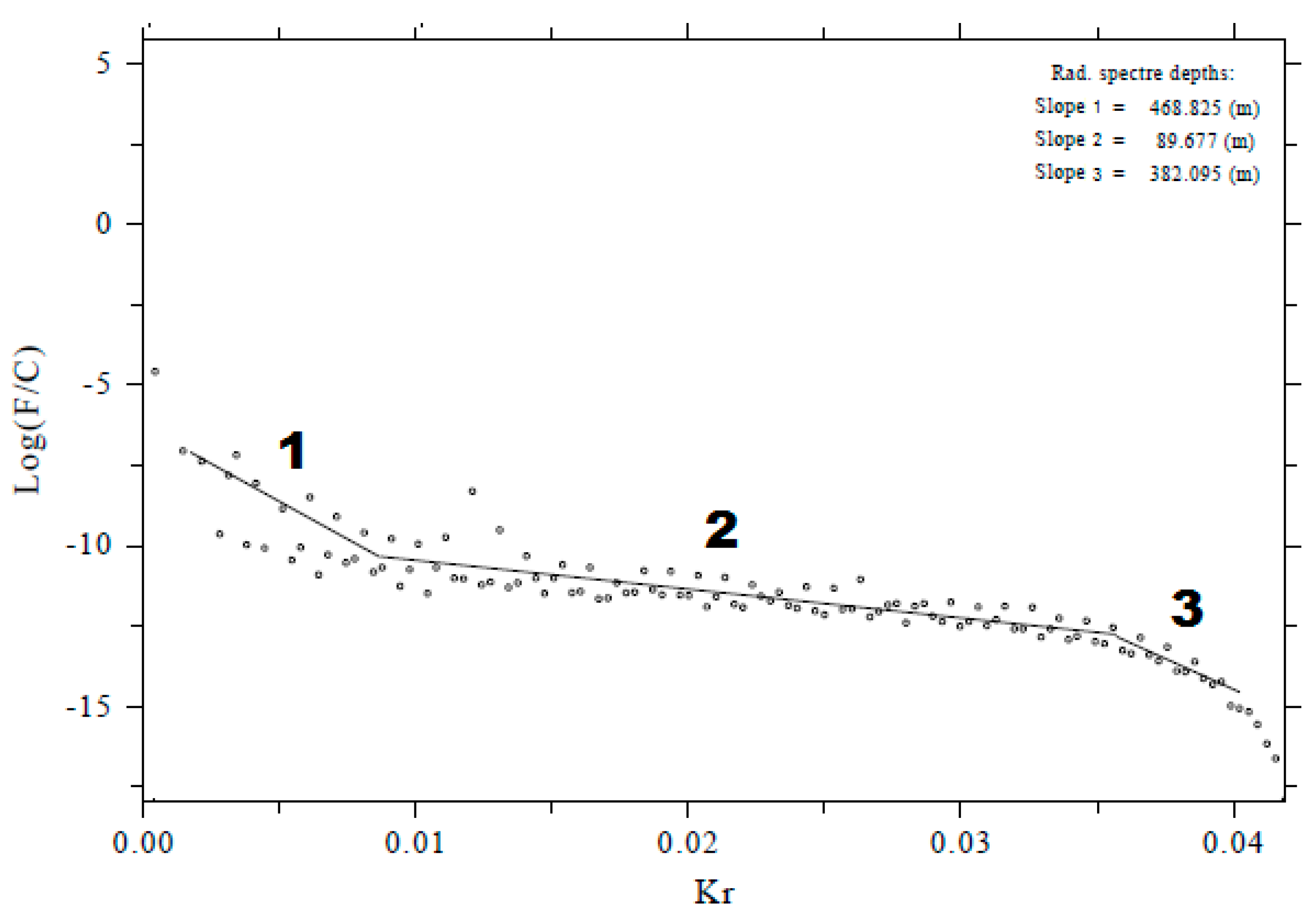
3.4. Depth Estimation and Anomaly Separation
4. Results
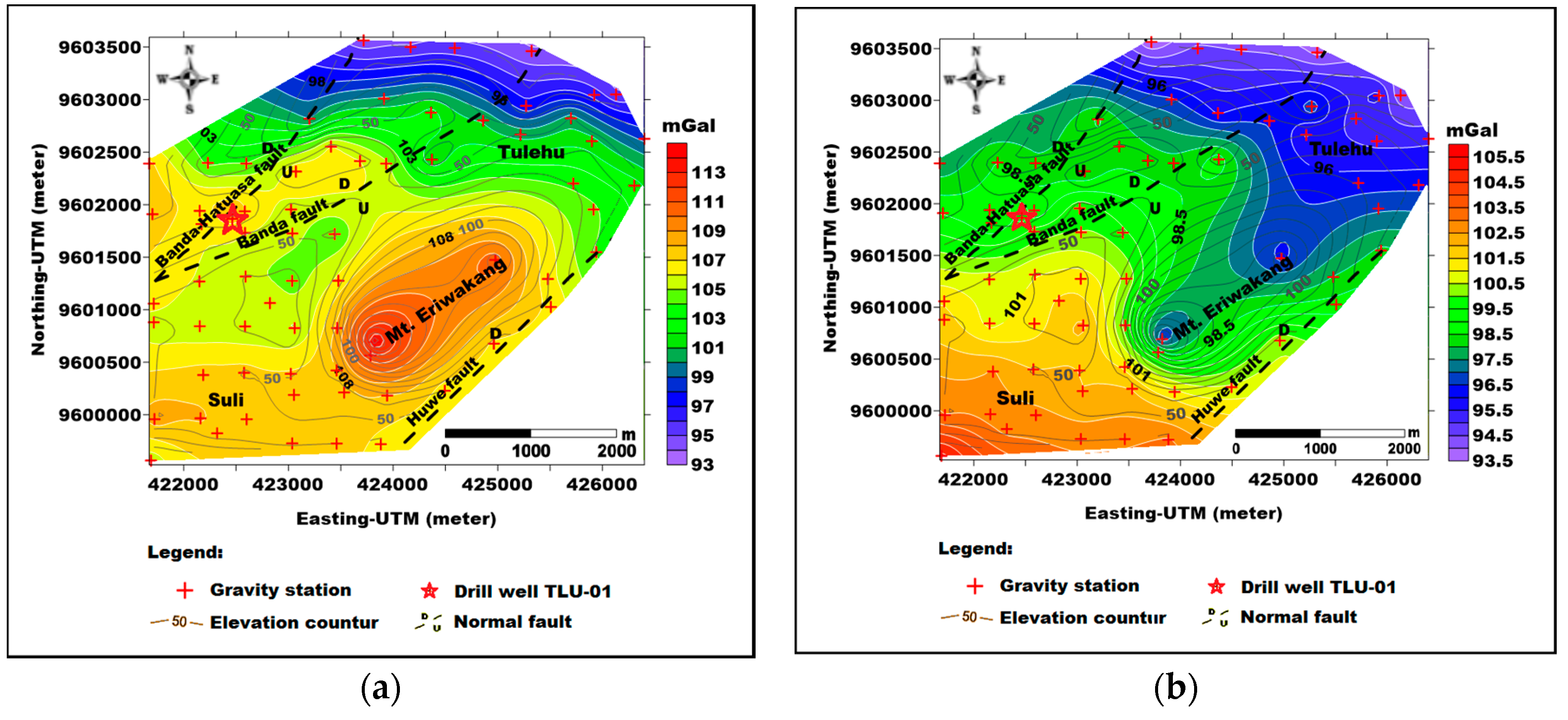
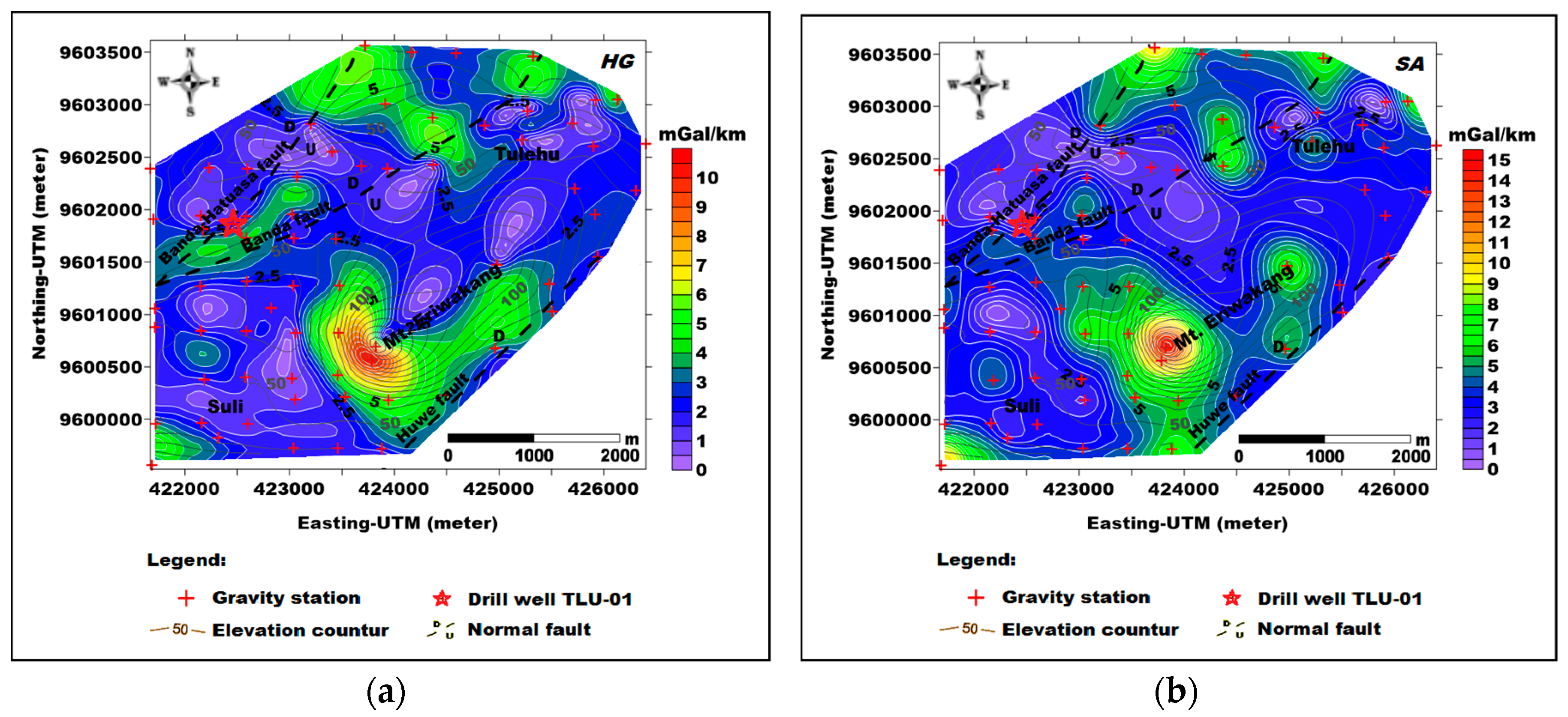
4.1. Gravity Variations
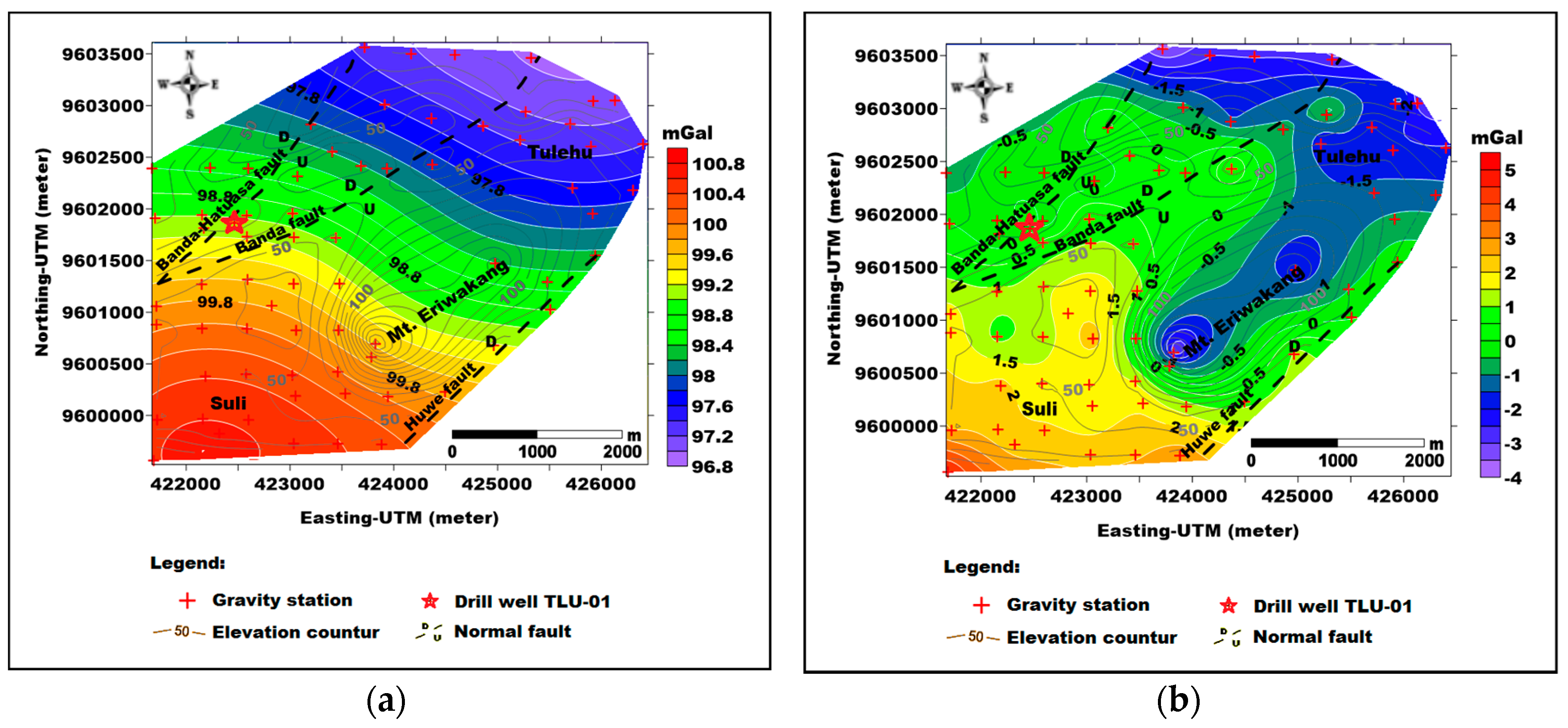
4.2. Deep Estimation and Anomaly Separation of Complete Bouguer Anomaly in Suli and Tulehu
4.3. Gravity Gradient Tensor Analysis of Suli and Tulehu Geothermal Areas
5. Discussion
5.1. Relationship between Gravity Anomaly and Geological Features
5.2. Significance of Using Gravity Gradient in Understanding the Suli and Tulehu Geothermal Areas
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sari, A.W.I.; Vandani, C.P.K.; Mulyaningsih, E.; Warmada, W.I.; Utami, P.; Yunis, Y. Studi alterasi hidrotermal bawah permukaan lapangan panas bumi “BETA”, Ambon dengan metode X-ray Diffraction. In Proceedings of the Seminar Nasional Kebumian KE-7, Yogyakarta, Indonesia, 30–31 October 2014. [Google Scholar]
- Munandar, A.; Risdianto, D.; Nursahan, I. Pengembangan Energi Panas Bumi Daerah-Daerah Pulau Terisolir. Badan Geologi Indonesia. 2017. Available online: http://www.bgl.esdm.go.id/index.php?option=com_content&task=view&id=654&Itemid=1&date=2021-11-01 (accessed on 15 November 2017).
- Vandani, K.P.C.; Sari, A.W.I.; Mulyaningsih, E.; Utami, P.; Yunis, Y. Studi alterasi hidrotermal bawah permukaan di lapangan panas bumi “BETA”, Ambon dengan metode Petrografi. In Proceedings of the Seminar Nasional Kebumian KE-7, Yogyakarta, Indonesia, 30–31 October 2014. [Google Scholar]
- Curewitz, D.; Karson, A.J. Structural settings of hydrothermal outflow: Fracture permeability maintained by fault propagation and interaction. J. Volcanol. Geotherm. Res. 1997, 79, 149–168. [Google Scholar] [CrossRef]
- Nasution, A.; Aviff, M.; Nugroho, S.; Yunis, Y.; Honda, M. The Preliminary Conceptual Model of Tolehu Geothermal Resource, Based on Geology, Water Geochemistry, MT, and Drilling; Proceedings World Geothermal Congress: Melbourne, Australia, 2015. [Google Scholar]
- Gottsman, J.; Camacho, G.A.; Marti, J.; Wooller, L.; Fernandez, J.; Garcia, A.; Rymer, H. Shallow structure beneath the Central Volcanic Complex of Tenerife from new gravity data: Implications for its evolution and recent reactivation. Phys. Earth Planet. Inter. 2008, 168, 212–230. [Google Scholar]
- Represas, P.; Santos, M.A.F.; Ribeiro, J.; Ribeiro, A.J.; Almeida, P.E.; Goncalves, R.; Moreira, M.; Victor-Mendes, A.L. Interpretation of gravity data to delineate structural features connected to low-temperature geothermal resources at Northeastern Portugal. J. Appl. Geophys. 2013, 92, 30–38. [Google Scholar]
- Moghaddam, M.M.; Mirzaei, S.; Nouraliee, J.; Porkhial, S. Integrated magnetic and gravity surveys for geothermal exploration in Central Iran. Arab. J. Geosci. 2016, 9, 1–12. [Google Scholar]
- Dubey, P.C.; Tiwari, M.V. Computation of the gravity field and its gradient: Some applications. Comput. Geosci. 2016, 88, 83–96. [Google Scholar] [CrossRef]
- Kohrn, B.S.; Bonet, C.; Difrancesco, D.; Gibson, H. Geothermal Exploration Using Gravity Gradiometry—A Salton Sea Example. Geotherm. Resour. Counc. Trans. 2011, 35, 1699–1702. [Google Scholar]
- Grandis, H.; Dahrin, D. Full Tensor Gradient of Simulated Gravity Data for Prospect Scale Delineation. J. Math. Fundam. Sci. 2014, 46, 107–124. [Google Scholar]
- Mickus, L.K.; Hinojosa, J.H. The complete gravity gradient tensor derived from the vertical component of gravity: A Fourier transform technique. J. Appl. Geophys. 2001, 46, 159–174. [Google Scholar] [CrossRef]
- Holis, Z.; Ponkarn, S.A.; Gunawan, A.; Damayanti, S.; Gunawan, K.B. Structural Evolution of Banda Arc, Eastern Indonesia: As a Future Indonesian Main Oil and Gas Development. In Proceedings of the Poster Presentation at AAPG International Convention and Exhibition, Singapore, 16–19 September 2012. [Google Scholar]
- Pairault, A.A.; Hall, R.; Elders, F.C. Structural styles and tetonic evolution of the Seram Trough, Indonesia. Mar. Pet. Geol. 2003, 20, 1141–1160. [Google Scholar] [CrossRef]
- Charlton, R.T. The Pliocene-Recent Anticlockwise Rotation of the Bird’s Head, the Opening of the Aru Trough—Cendrawasih Bay Spenochasm, and the Closure of the Banda Double Arc. In Proceedings of the IPA Thirty-Fourth Annual Convention an Exhibition, Jakarta, Indonesia, 18–20 May 2010. [Google Scholar]
- Honthaas, C.; Maury, C.R.; Priadi, B.; Bellon, H.; Cotton, J. The Plio-Quaternary Ambon arc, Eastern Indonesia. Tectonophysics 1999, 301, 261–281. [Google Scholar] [CrossRef]
- Van Bemmelen, R.W. The Geology of Indonesia; Government Printing Office: The Hague, The Netherlands, 1949; Volume 1, p. 732.
- Marini, L.; Susangkyono, E.A. Fluid geochemistry of Ambon Island (Indonesia). Geothermics 1999, 28, 189–204. [Google Scholar] [CrossRef]
- Jacoby, W.; Smilde, L.P. The gravity tensor (Eotvos Tensor) Gravity Interpretation. In Fundamentals and Application of Application of Gravity Inversion and Geological Interpretation, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 1, pp. 45–46. ISBN 978-3-540-85328-2. [Google Scholar]
- Beiki, M. Analytic signal of gravity gradient tensor and their application to estimate source location. Geophysics 2010, 75, 159–174. [Google Scholar] [CrossRef]
- Saibi, H.; Nishijima, J.; Ehara, S.; Aboud, E. Intergrated gradient interpretation techniques for 2D and 3D gravity data interpretation. Earth Planets Space 2006, 58, 815–821. [Google Scholar] [CrossRef]
- Arisoy, O.M.; Dikmen, U. Potensoft; MATLAB-based software for potenstial data processing, modeling and mapping. Comput. Geosci. 2011, 37, 935–942. [Google Scholar] [CrossRef]
- Pirttijarvi, M. FOURPOT: Potential Field Data Processing and Analysis of Using 2D Fourier Transform. Manual Software. 2014. Available online: https://wiki.oulu.fi/display/~mpi/ (accessed on 15 November 2017).
- Ansari, H.A.; Alamdar, K. A new edge detection method based on the analytic signal of tilt angle (ASTA) for magnetic and gravity anomalies. Iran. J. Sci. Technol. 2011, 35, 81–88. [Google Scholar]
- Roest, R.W.; Verhoel, J.; Pikington, M. Magnetic interpretation using the 3D analytic signal. Geophysics 1992, 57, 116–125. [Google Scholar] [CrossRef]
- Nishijima, J.; Naritomi, K. Interpretation of gravity data to delineate underground structure in the Beppu geothermal field, central Kyushu, Japan. J. Hydrol. Reg. Stud. 2017, 11, 84–95. [Google Scholar] [CrossRef]
- Blakely, J.R. Transformation. In Potential Theory in Gravity and Magnetic Applications, 1st ed.; Cambridge University Press: Cambride, UK, 1996; Volume 1, pp. 316–319. [Google Scholar]
- Nouraliee, J.; Porkhial, S.; Moghaddam, M.M.; Mirzaei, S.; Ebrahimi, D.; Rahmani, R.M. Investigation of density contrasts and geologic structures of hot springs in the Markazi Province of Iran using the gravity method. Russ. Geol. Geophys. 2015, 56, 1791–1800. [Google Scholar] [CrossRef]
- Khalil, A.M.; Santos, M.F.; Farzamian, M.; El-Kenawy, A. 2D Fourier transform analysis of the gravitational field of Northern Sinai Peninsula. J. Appl. Geophys. 2015, 115, 1–10. [Google Scholar] [CrossRef]
- Spicak, A.; Matejkova, R.; Vanek, J. Seismic response to recent tectonic processes in the Banda Arc region. J. Asian Earth Sci. 2013, 64, 1–133. [Google Scholar] [CrossRef]
- Abdeslem, G.J. The gravitational attraction of a right rectangular prism with density varying with depth following a cubic polynomial. Geophysics 2005, 70, J39–J42. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geodesy 2000, 74, 552–560. [Google Scholar] [CrossRef]


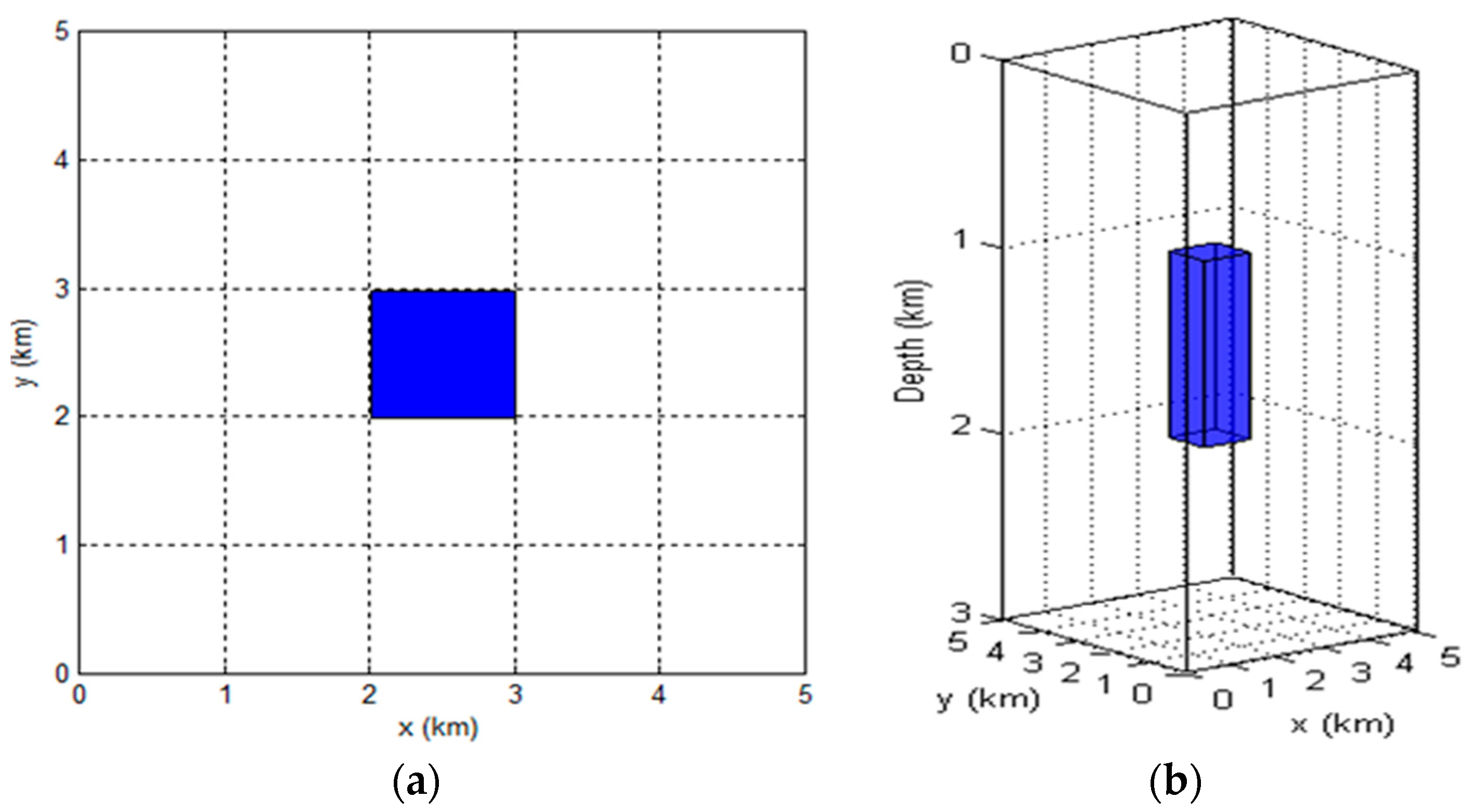
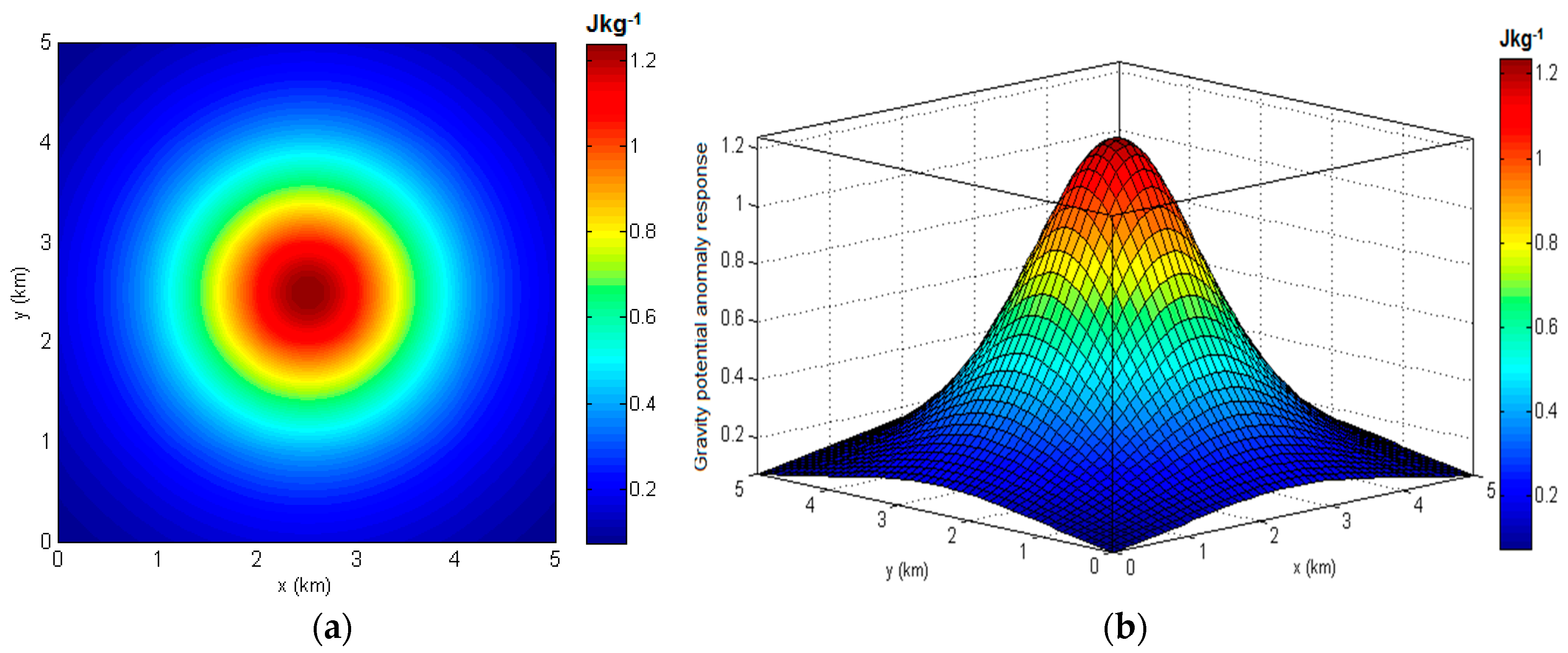

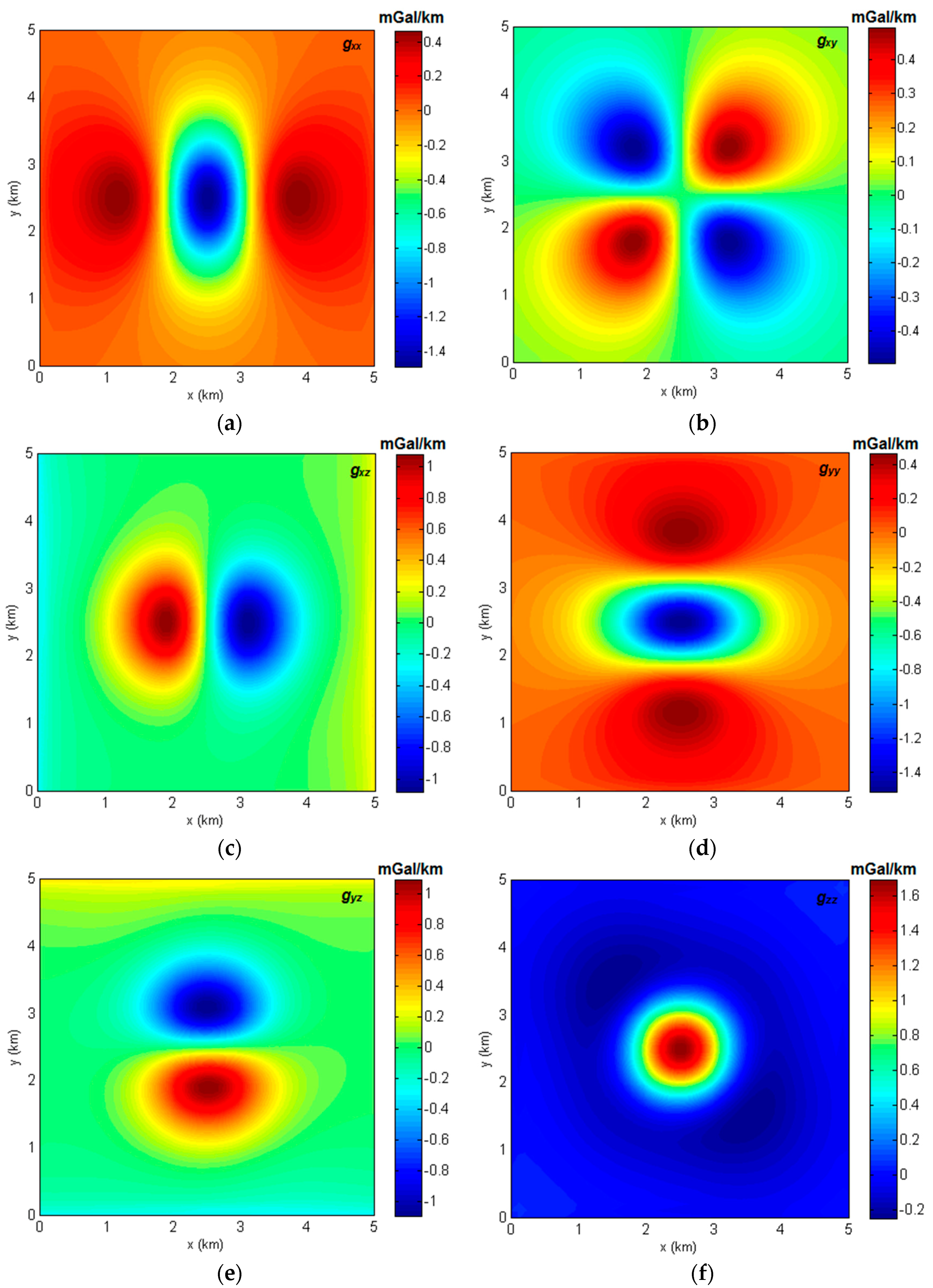
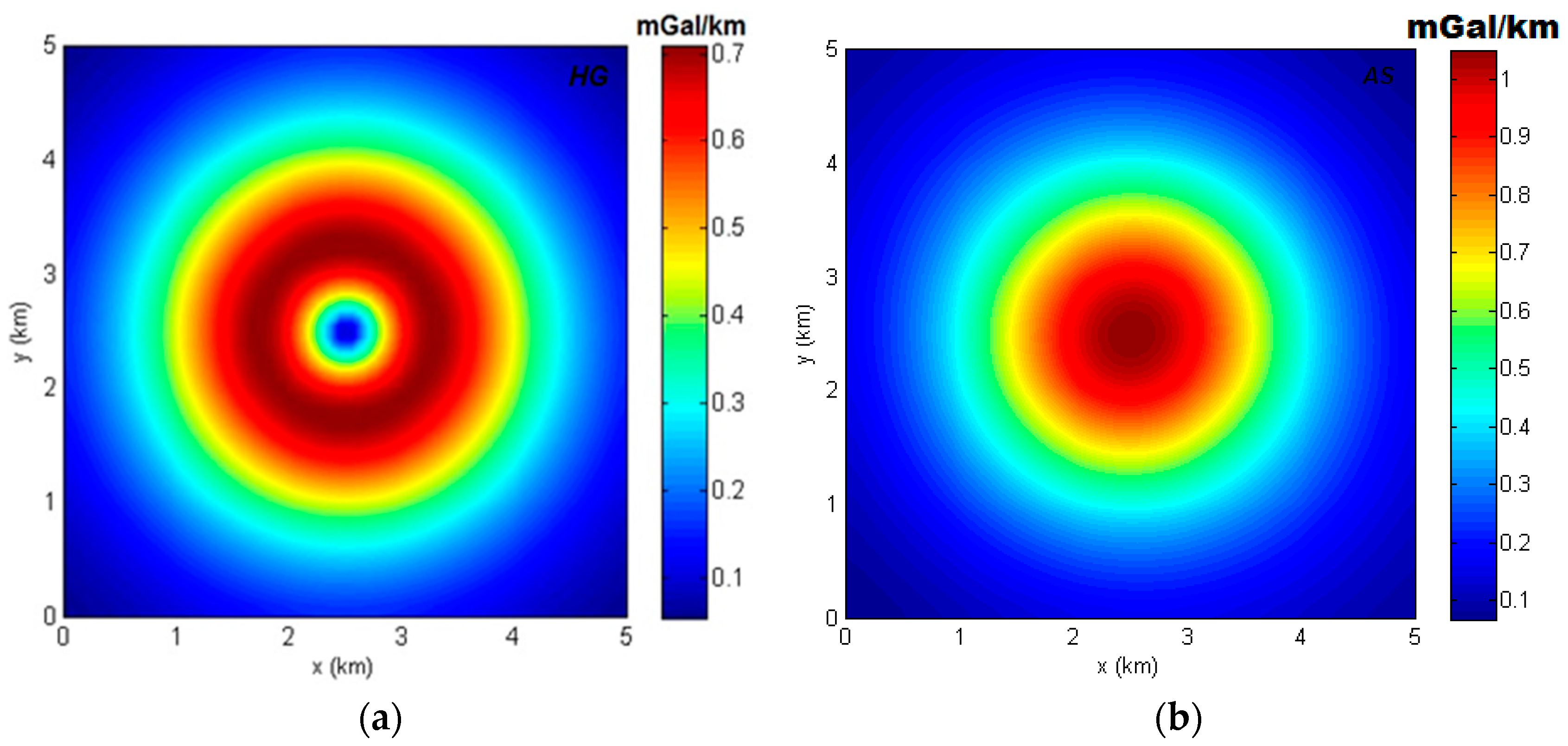
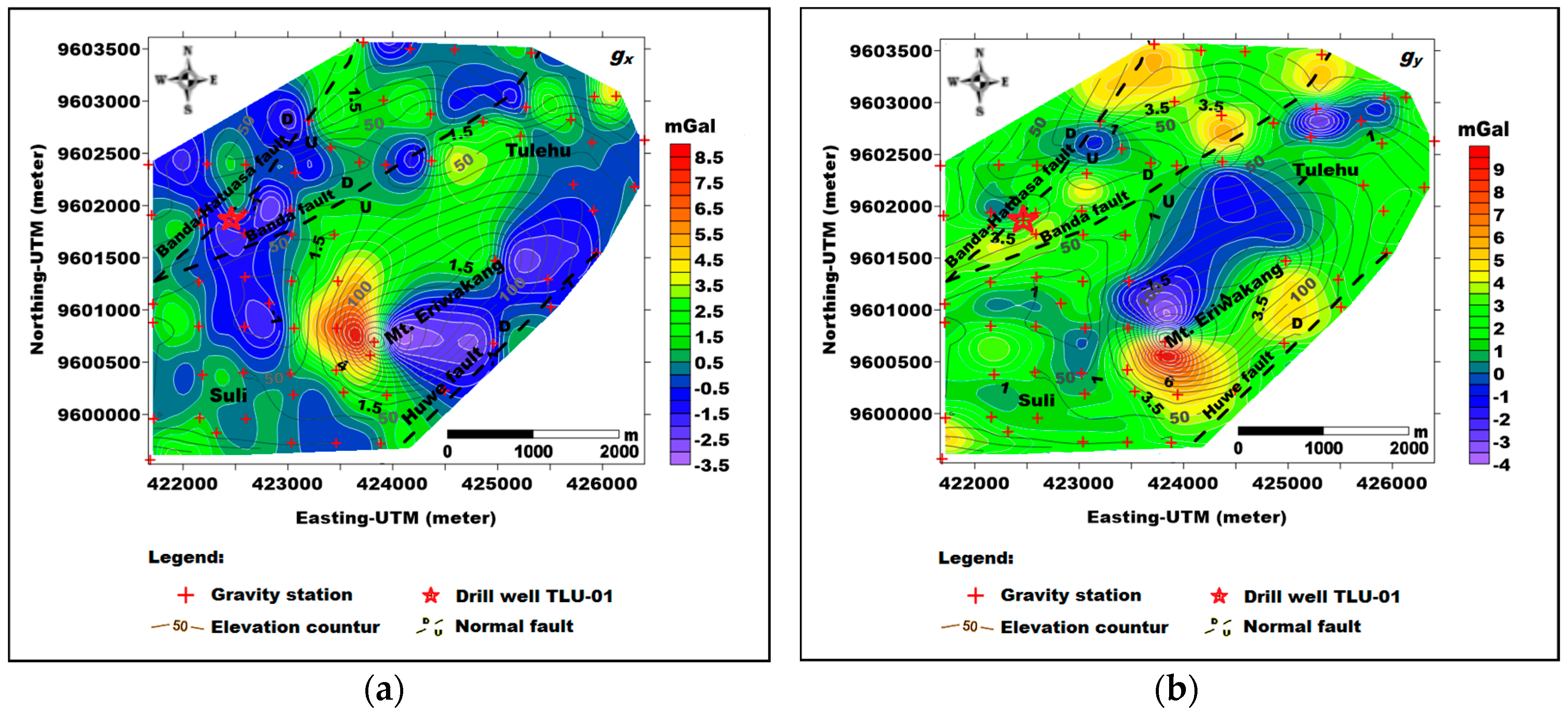
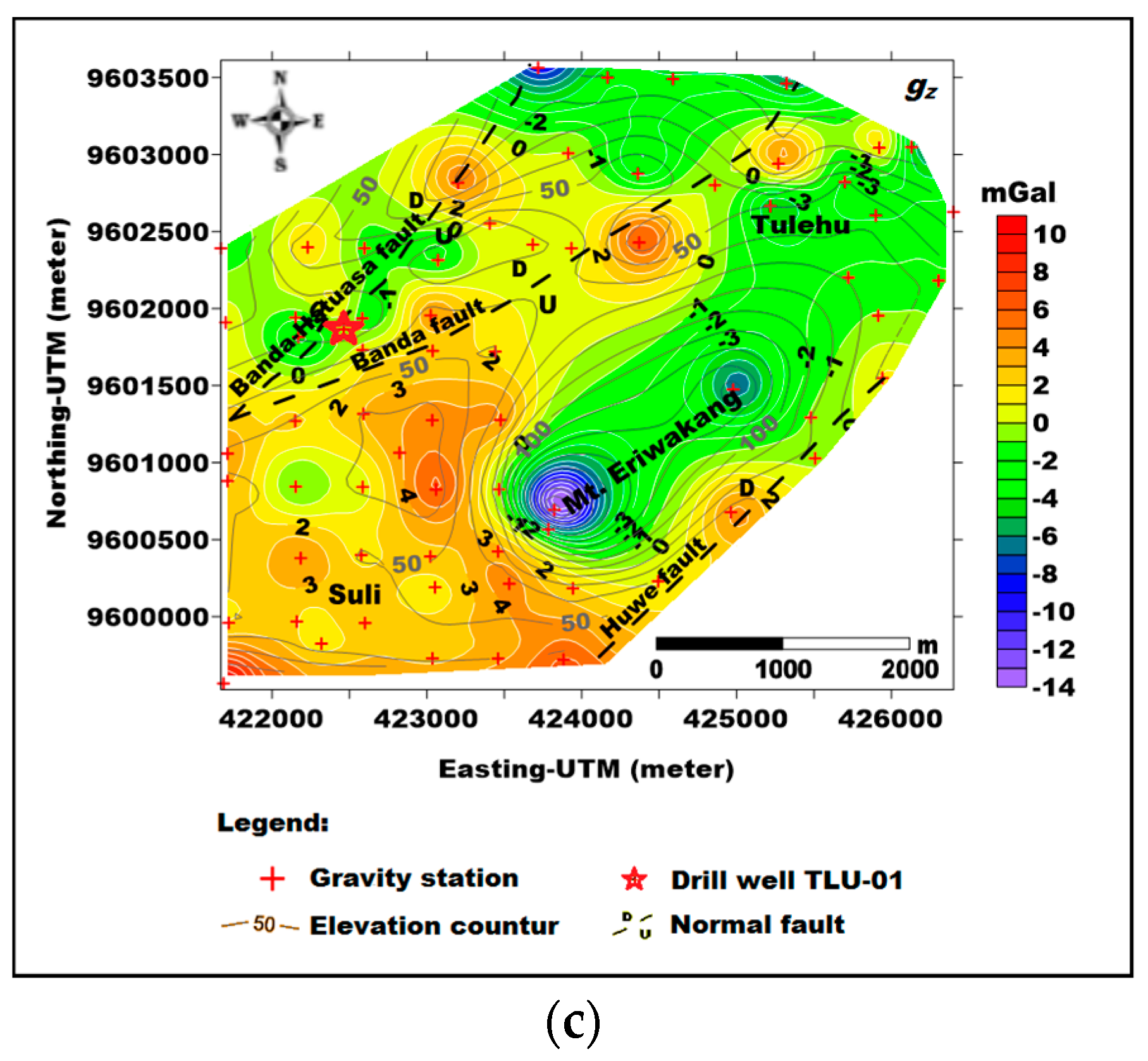
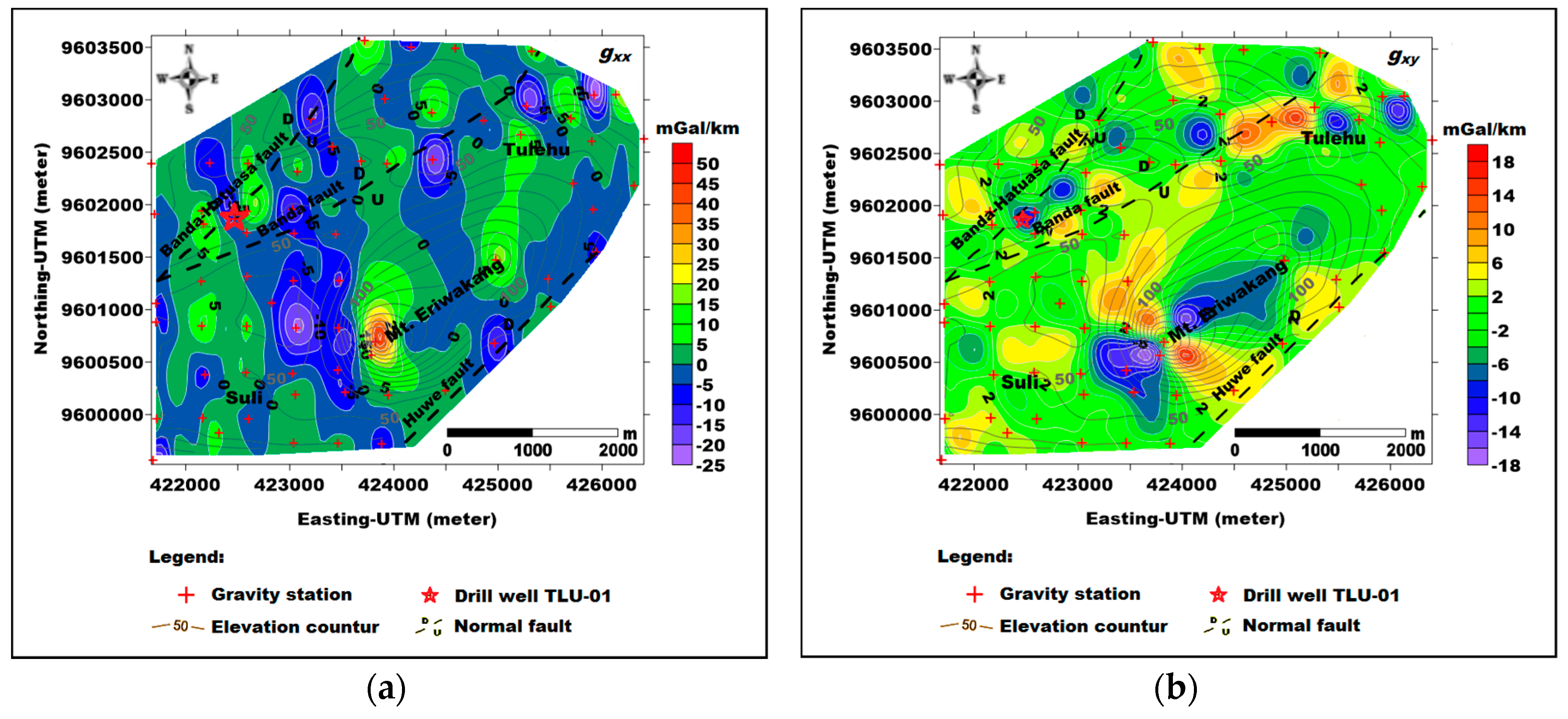
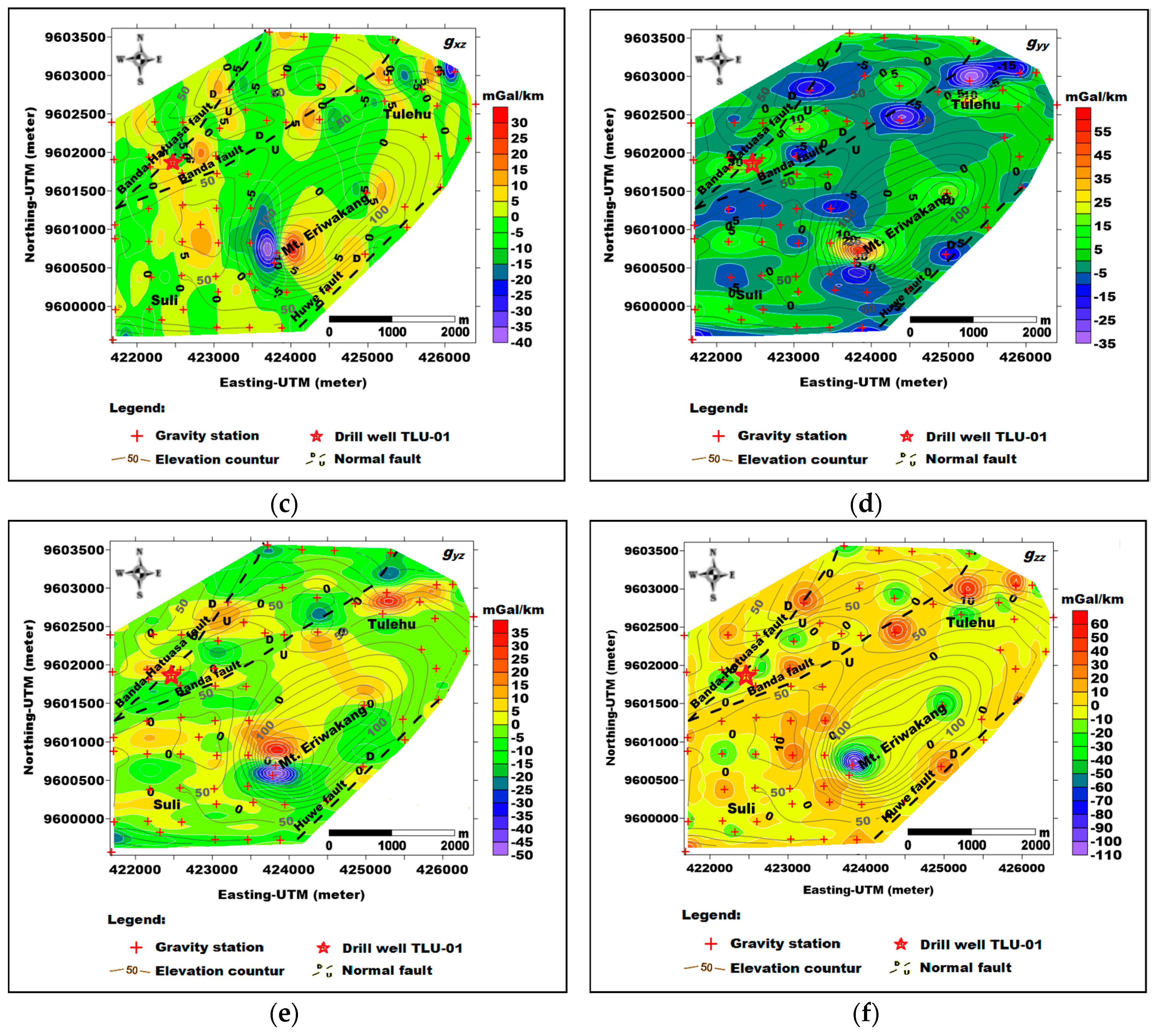
| Gradient Components | Minimum (mGal/km) | Maximum (mGal/km) |
|---|---|---|
| gxx | −1.489 | 0.465 |
| gxy | −0.495 | 0.495 |
| gxz | −1.081 | 1.081 |
| gyy | −1.489 | 0.465 |
| gyz | −1.081 | 1.081 |
| gzz | −0.250 | 1.689 |
| Gradient Cmponents | Minimum (mGal/km) | Maximum (mGal/km) |
|---|---|---|
| gxx | −23.073 | 46.522 |
| gxy | −17.961 | 17.099 |
| gxz | −39.934 | 29.058 |
| gyy | −33.693 | 56.786 |
| gyz | −49.769A | 35.051 |
| gzz | −103.072 | 51.843 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewerissa, R.; Sismanto, S.; Setiawan, A.; Pramumijoyo, S. The Study of Geological Structures in Suli and Tulehu Geothermal Regions (Ambon, Indonesia) Based on Gravity Gradient Tensor Data Simulation and Analytic Signal. Geosciences 2018, 8, 4. https://doi.org/10.3390/geosciences8010004
Lewerissa R, Sismanto S, Setiawan A, Pramumijoyo S. The Study of Geological Structures in Suli and Tulehu Geothermal Regions (Ambon, Indonesia) Based on Gravity Gradient Tensor Data Simulation and Analytic Signal. Geosciences. 2018; 8(1):4. https://doi.org/10.3390/geosciences8010004
Chicago/Turabian StyleLewerissa, Richard, Sismanto Sismanto, Ari Setiawan, and Subagyo Pramumijoyo. 2018. "The Study of Geological Structures in Suli and Tulehu Geothermal Regions (Ambon, Indonesia) Based on Gravity Gradient Tensor Data Simulation and Analytic Signal" Geosciences 8, no. 1: 4. https://doi.org/10.3390/geosciences8010004
APA StyleLewerissa, R., Sismanto, S., Setiawan, A., & Pramumijoyo, S. (2018). The Study of Geological Structures in Suli and Tulehu Geothermal Regions (Ambon, Indonesia) Based on Gravity Gradient Tensor Data Simulation and Analytic Signal. Geosciences, 8(1), 4. https://doi.org/10.3390/geosciences8010004





