Supercontinent Cycle and Thermochemical Structure in the Mantle: Inference from Two-Dimensional Numerical Simulations of Mantle Convection
Abstract
:1. Introduction
2. Model Description
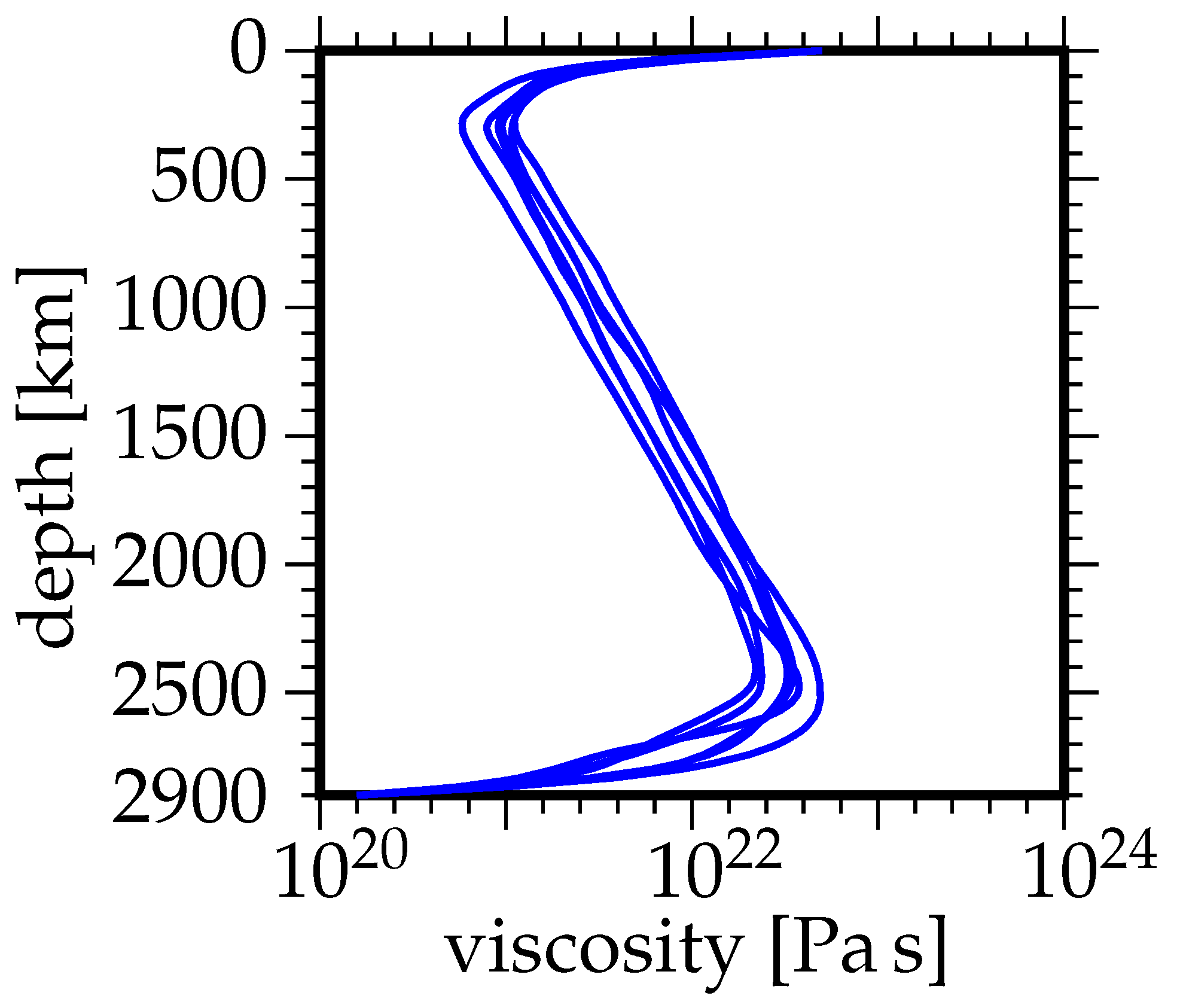
2.1. Physical Properties of Modeled Fluids
2.2. Fundamental Equations and Dimensionless Parameters
2.3. Model of Continental Drift
2.4. Initial Conditions
2.5. Numerical Techniques
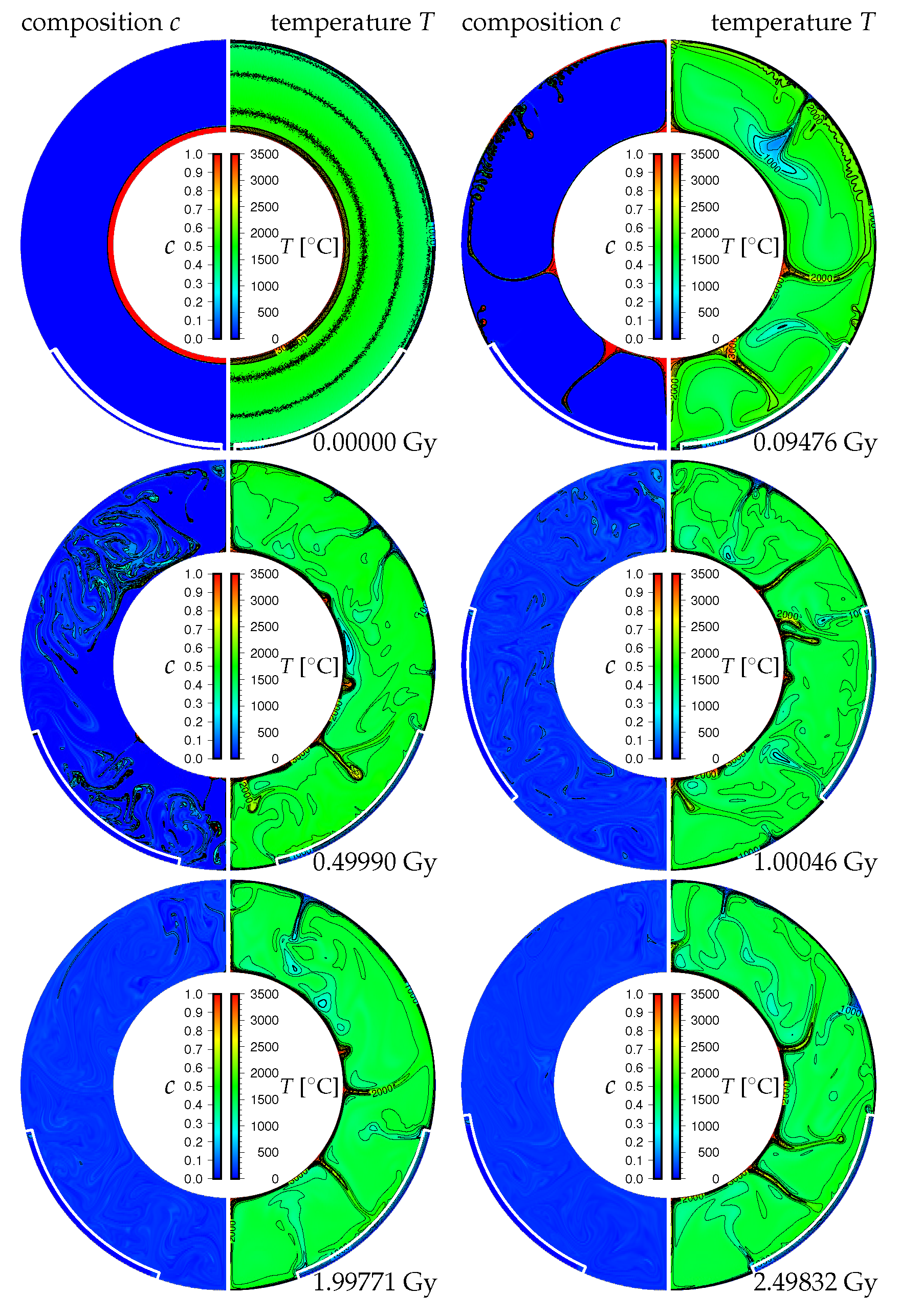
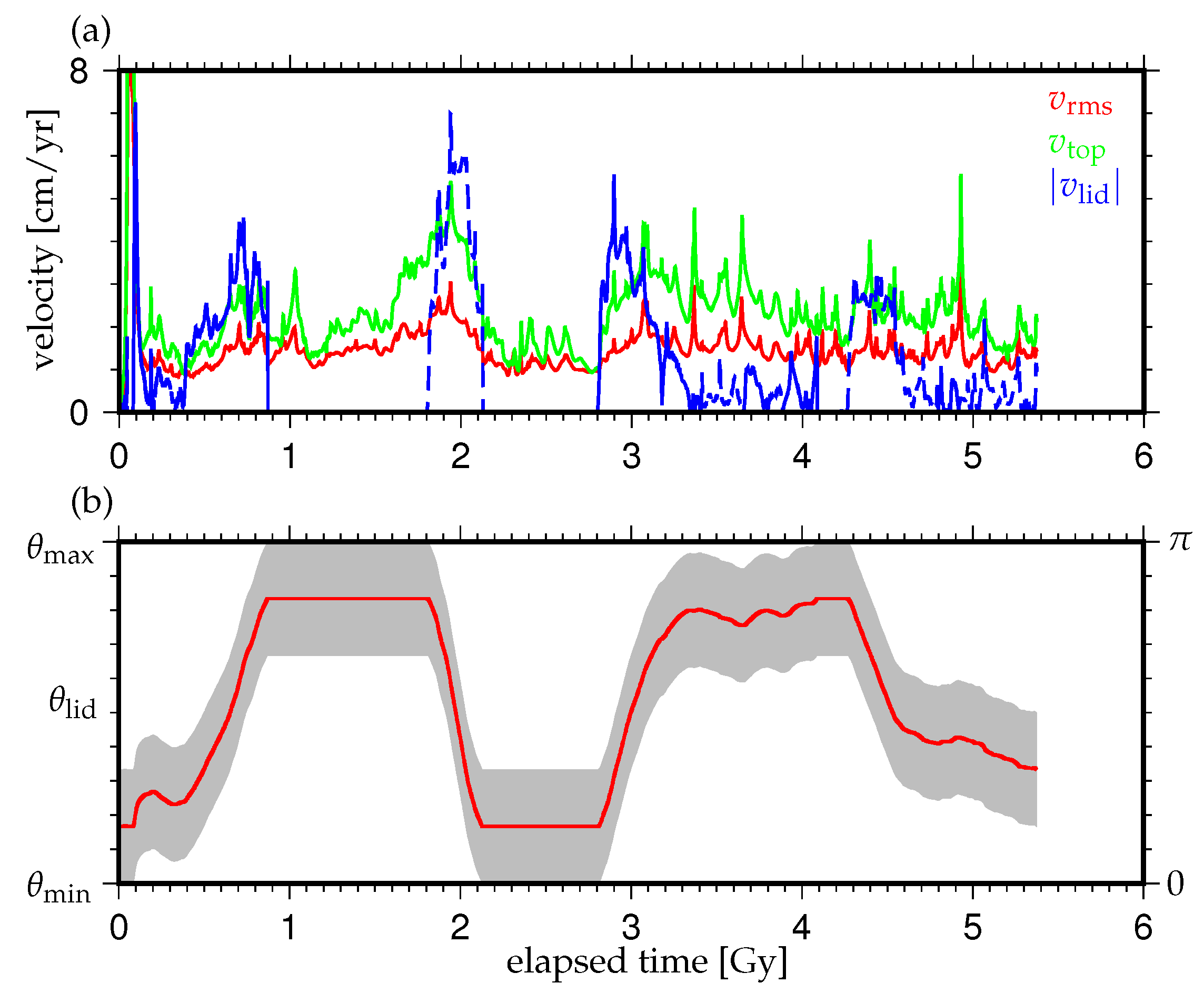
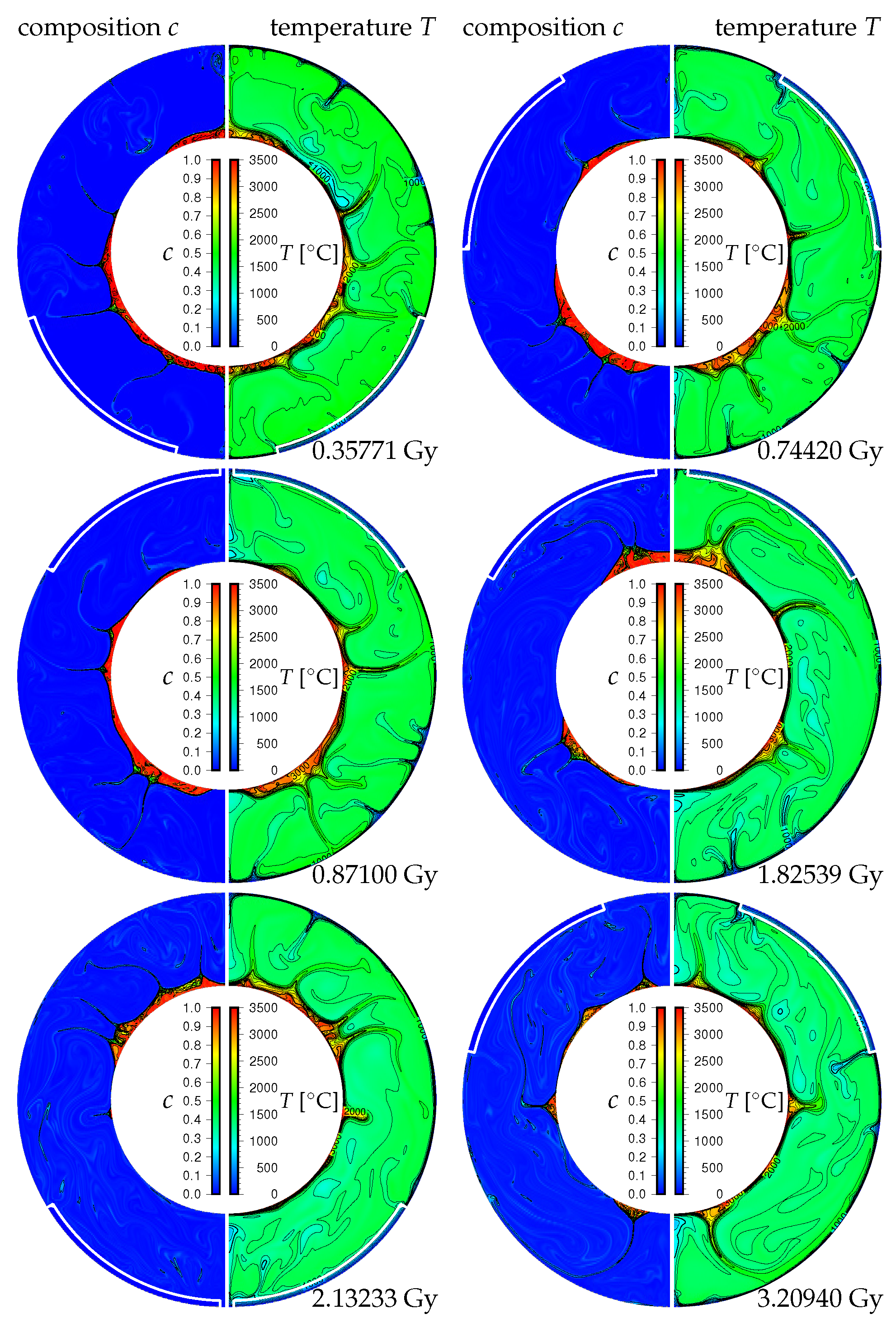
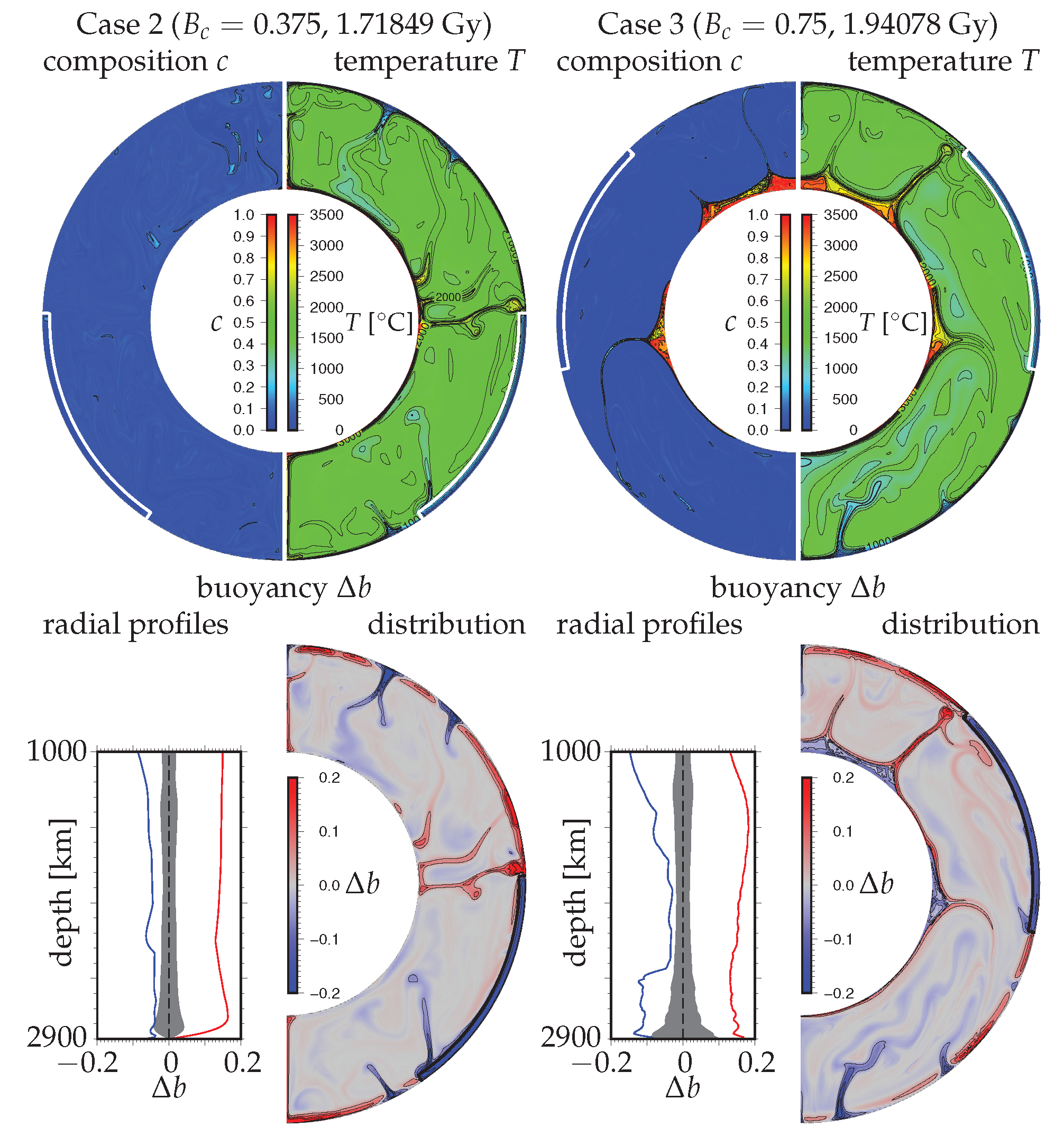
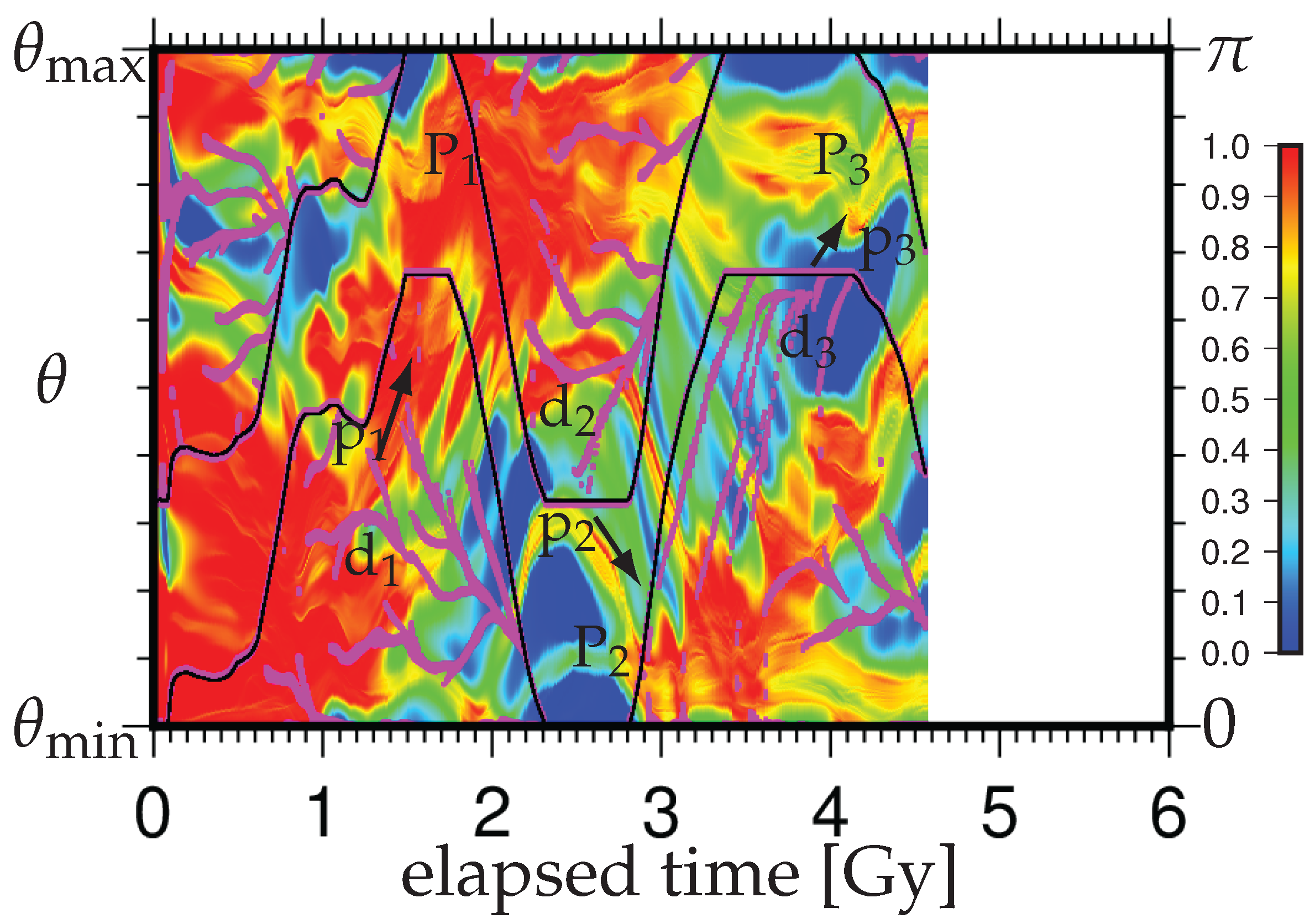
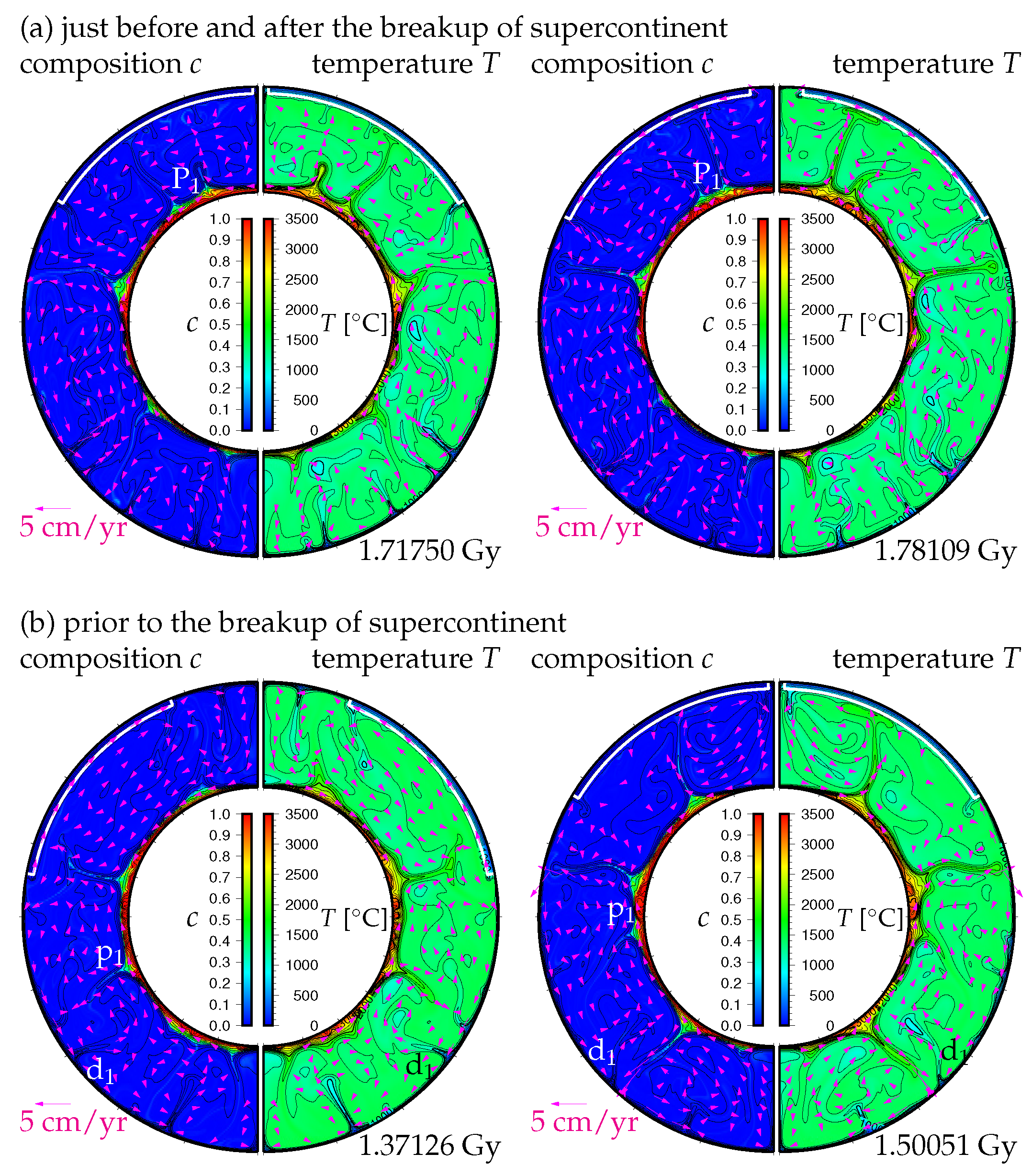
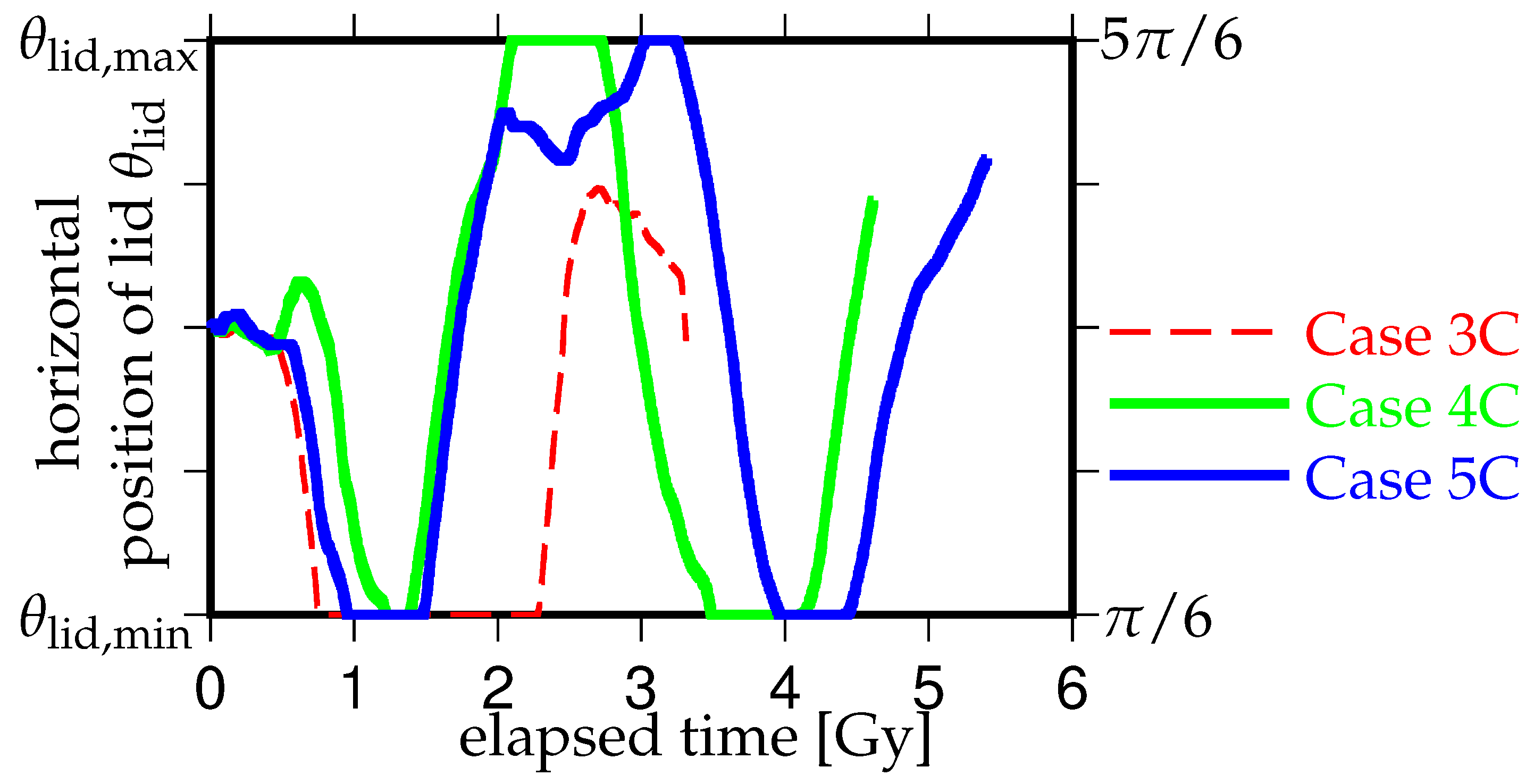
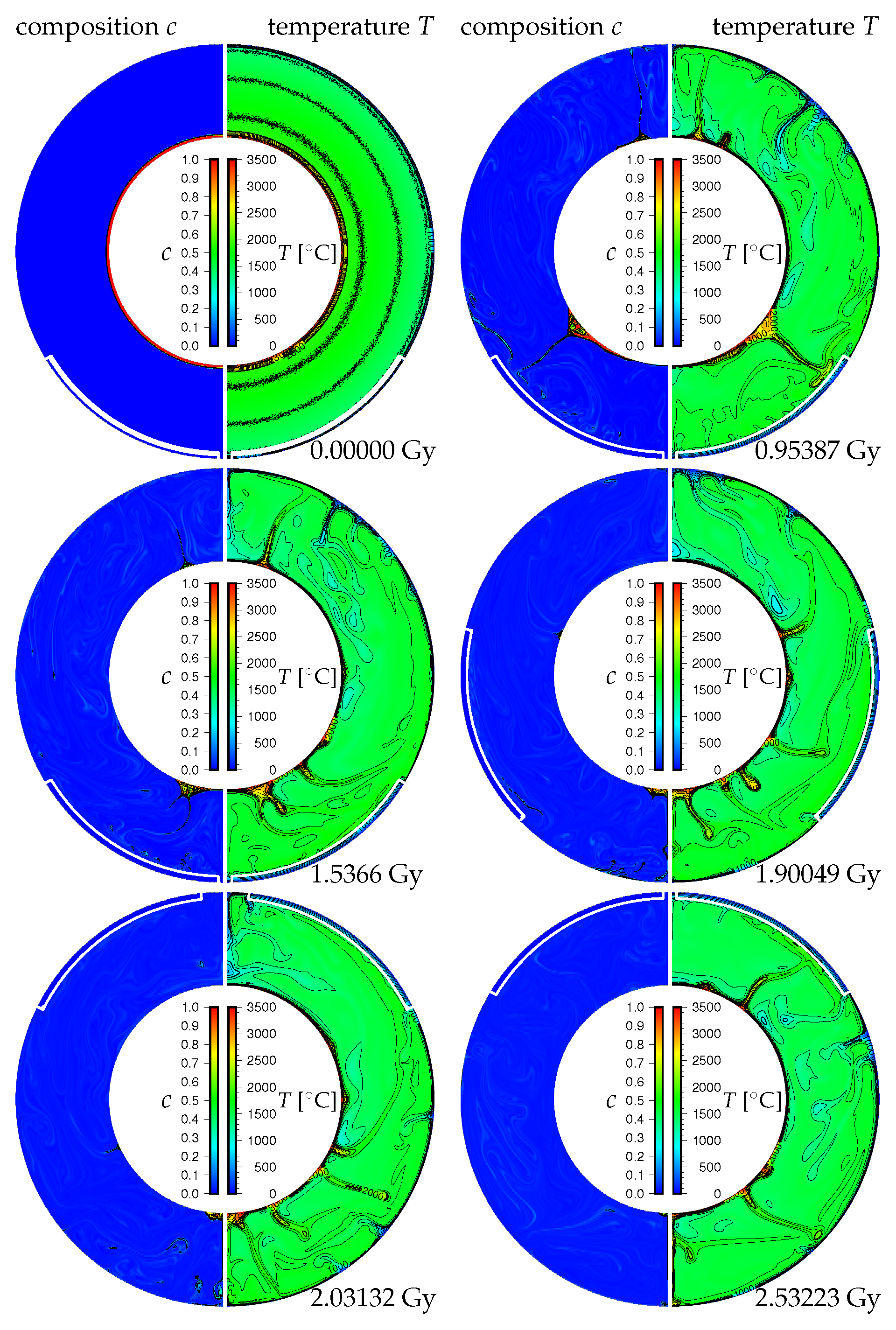
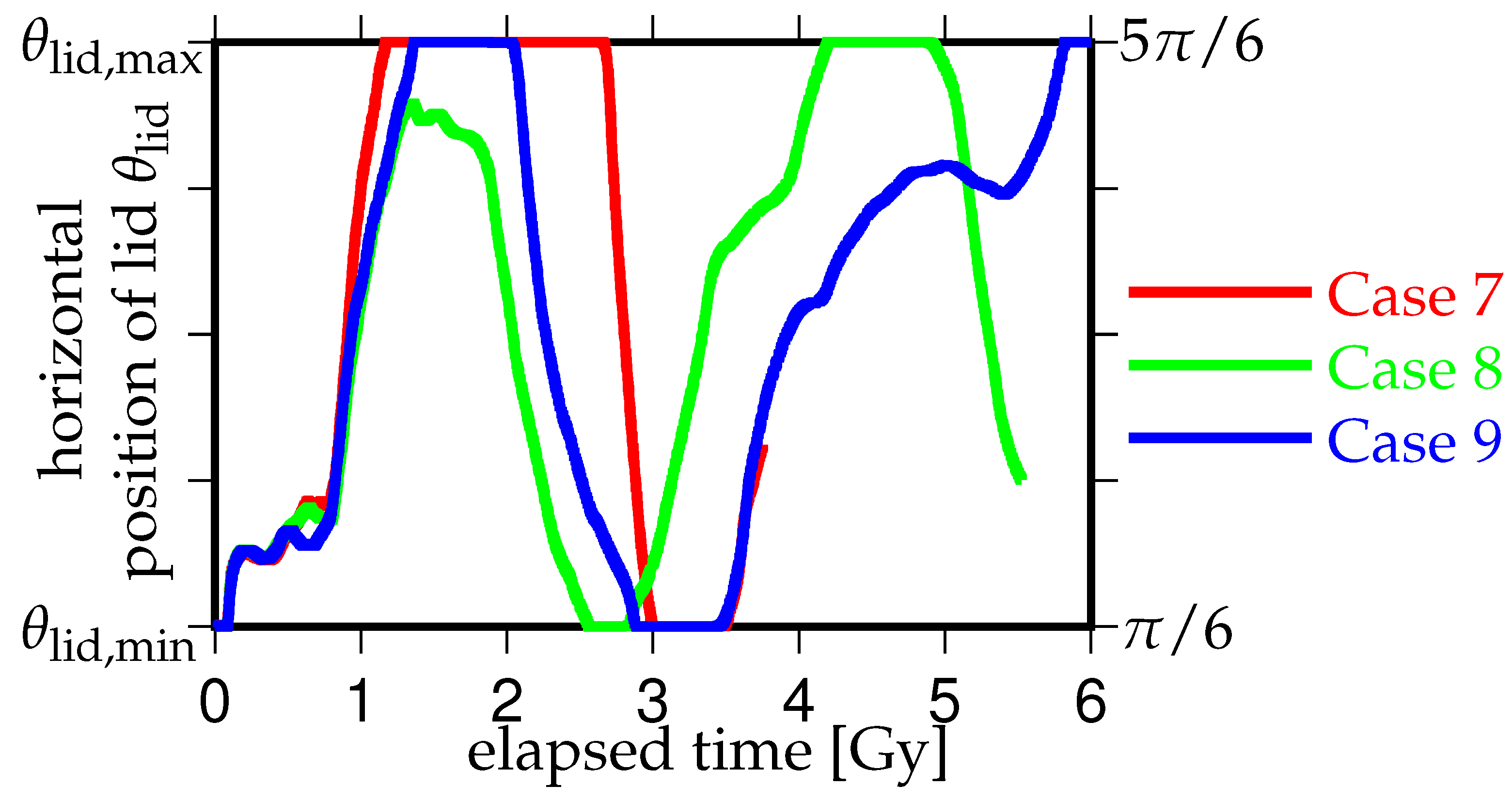
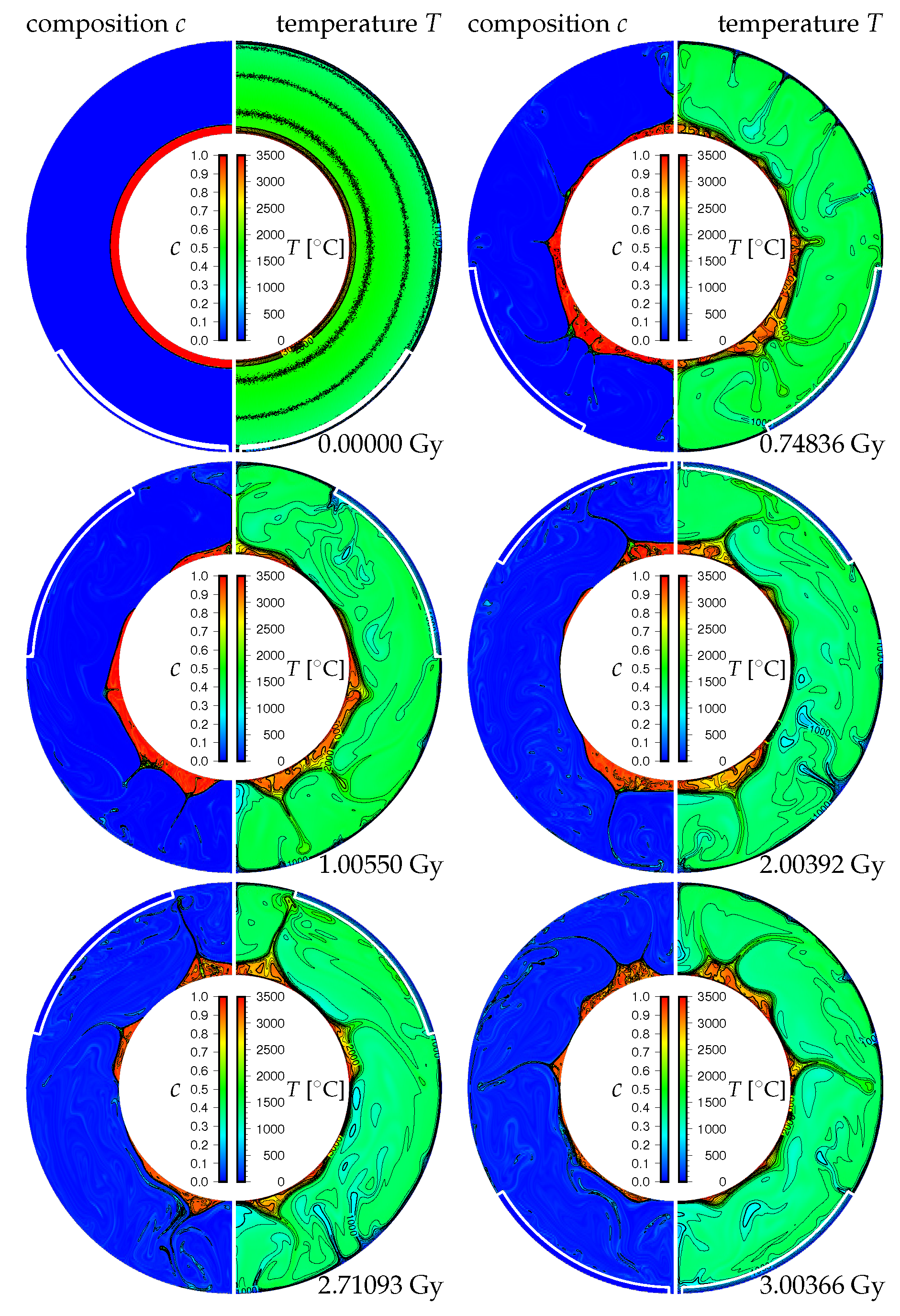
3. Results
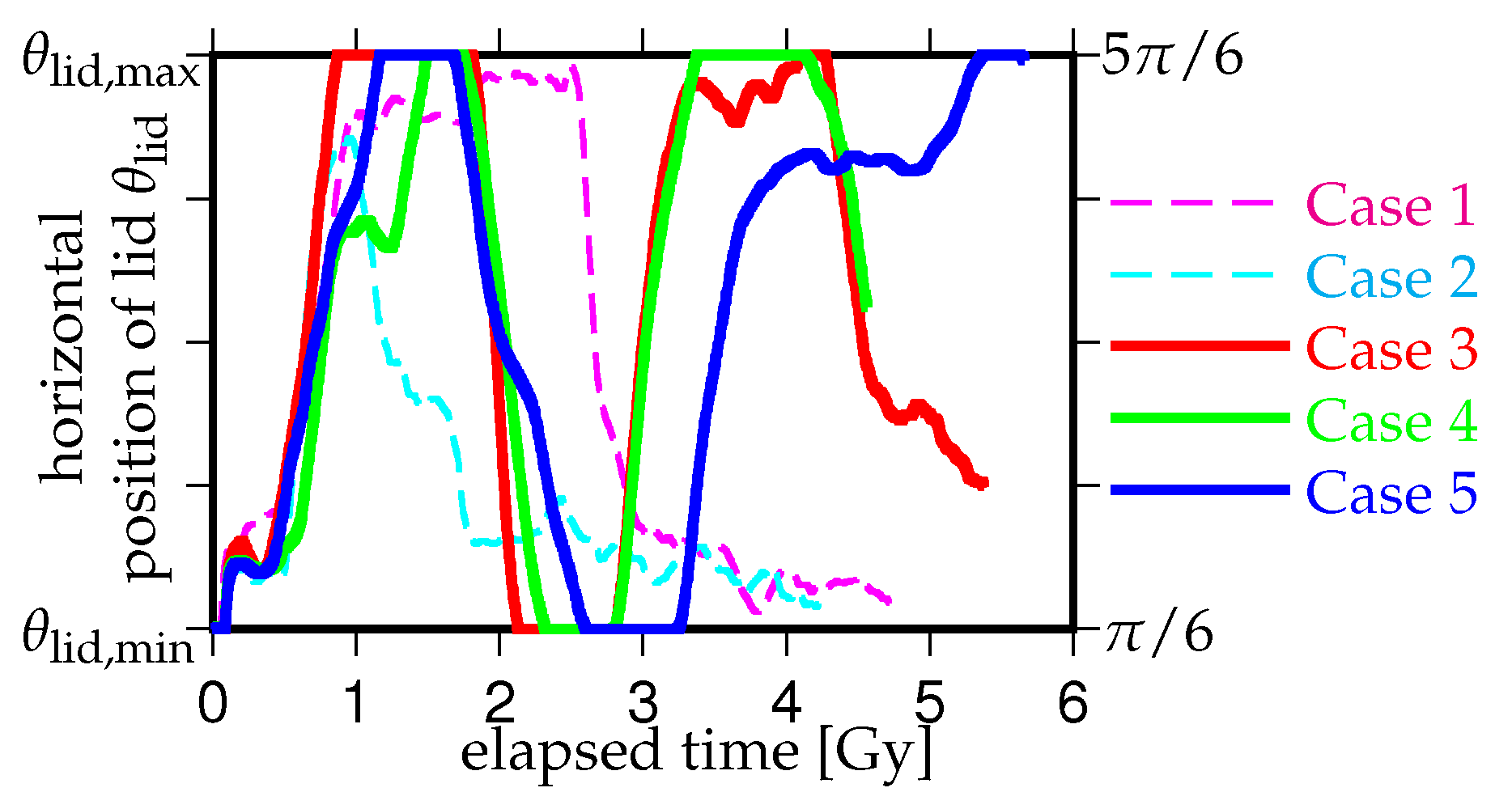
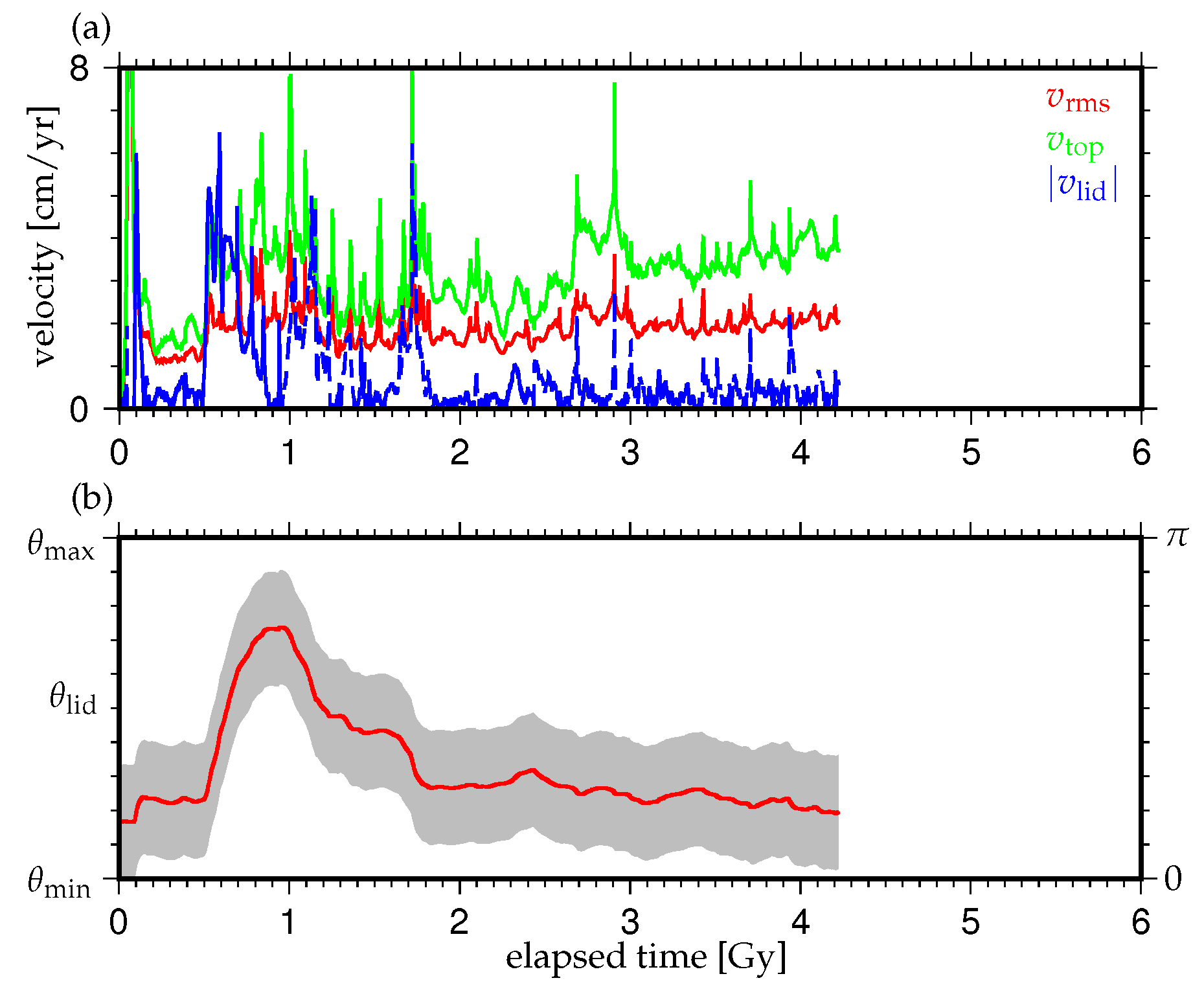
3.1. Effects of the Density Difference of Chemical Heterogeneity in the Lowermost Mantle on the Supercontinent Cycle
3.2. Effects of the Initial Positions of the Continental Lid
3.3. Effects of the Amount of Chemical Heterogeneity in the Lowermost Mantle on the Supercontinent Cycle
4. Discussion and Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Z.X.; Zhong, S. Supercontinent-Superplume coupling, true polar wander and plume mobility: Plate dominance in whole-mantle tectonics. Phys. Earth Planet. Inter. 2009, 176, 143–156. [Google Scholar] [CrossRef]
- Wilson, J.T. Did the Atlantic Close and then Re-Open? Nature 1966, 211, 676–681. [Google Scholar] [CrossRef]
- Hoffman, P.F. Did the Breakout of Laurentia Turn Gondwanaland Inside-Out? Science 1991, 252, 1409–1412. [Google Scholar] [CrossRef] [PubMed]
- Veevers, J.J. Gondwanaland from 650–500 Ma assembly through 320 Ma merger in Pangea to 185–100 Ma breakup: Supercontinental tectonics via stratigraphy and radiometric dating. Earth-Sci. Rev. 2004, 68, 1–132. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Schubert, G. Geodynamics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2014; p. 636. [Google Scholar]
- Li, Z.X.; Bogdanova, S.V.; Collins, A.S.; Davidson, A.; Waele, B.D.; Ernst, R.E.; Fitzsimons, I.C.W.; Fuck, R.A.; Gladkochub, D.P.; Jacobs, J.; et al. Assembly, configuration, and break-up history of Rodinia: A synthesis. Precambrian Res. 2008, 160, 179–210. [Google Scholar] [CrossRef]
- Storey, B.C. The role of mantle plumes in continental breakup: Case histories from Gondwanaland. Nature 1995, 377, 301–308. [Google Scholar] [CrossRef]
- Coltice, N.; Bertrand, H.; Rey, P.; Jourdan, F.; Phillips, B.R.; Ricard, Y. Global warming of the mantle beneath continents back to the Archaean. Gondwana Res. 2009, 15, 254–266. [Google Scholar] [CrossRef]
- Jellinek, A.M.; Manga, M. Links between long-lived hot spots, mantle plumes, D”, and plate tectonics. Rev. Geophys. 2004, 42, RG3002. [Google Scholar] [CrossRef]
- Garnero, E.J.; Lay, T.; McNamara, A. Implications of lower mantle structural heterogeneity for existence and nature of whole mantle plumes. In Plates, Plumes and Planetary Processes; GSA Special Papers; Foulger, G.R., Jurdy, D.M., Eds.; Geological Society of America: Boulder, CO, USA, 2007; Volume 430, pp. 79–101. [Google Scholar]
- Kawai, K.; Tsuchiya, T. Temperature profile in the lowermost mantle from seismological and mineral physics joint modeling. Proc. Natl. Acad. Sci. USA 2009, 106, 22119–22123. [Google Scholar] [CrossRef] [PubMed]
- Bull, A.L.; McNamara, A.K.; Becker, T.W.; Ritsema, J. Global scale models of the mantle flow field predicted by synthetic tomography models. Phys. Earth Planet. Inter. 2010, 182, 129–138. [Google Scholar] [CrossRef]
- Coffin, M.F.; Eldholm, O. Large igneous provinces: Crustal structure, dimensions, and external consequences. Rev. Geophys. 1994, 32, 1–36. [Google Scholar] [CrossRef]
- Burke, K.; Torsvik, T.H. Derivation of Large Igneous Provinces of the past 200 million years from long-term heterogeneities in the deep mantle. Earth Planet. Res. Lett. 2004, 227, 531–538. [Google Scholar] [CrossRef]
- Torsvik, T.H.; Smethurst, M.A.; Burke, K.; Steinberger, B. Large igneous provinces generated from the margins of the large low-velocity provinces in the deep mantle. Geophys. J. Int. 2006, 167, 1447–1460. [Google Scholar] [CrossRef]
- Burke, K.; Steinberger, B.; Torsvik, T.H.; Smethurst, M.A. Plume Generation Zones at the margins of Large Low Shear Velocity Provinces on the core-mantle boundary. Earth Planet. Sci. Lett. 2008, 265, 49–60. [Google Scholar] [CrossRef]
- McNamara, A.K.; Zhong, S. The influence of thermochemical convection on the fixity of mantle plumes. Earth Planet. Sci. Lett. 2004, 222, 485–500. [Google Scholar] [CrossRef]
- Zhong, S.; Gurnis, M. Dynamic feedback between continentlike raft and thermal convection. J. Geophys. Res. 1993, 98, 12219–12232. [Google Scholar] [CrossRef]
- Nakakuki, T.; Yuen, D.A.; Honda, S. The interaction of plumes with the transition zone under continents and oceans. Earth Planet. Sci. Lett. 1997, 146, 379–392. [Google Scholar] [CrossRef]
- Ichikawa, H.; Kameyama, M.; Kawai, K. Mantle convection with continental drift and heat source around the mantle transition zone. Gondwana Res. 2013, 24, 1080–1090. [Google Scholar] [CrossRef]
- McNamara, A.K.; Zhong, S. Degree-one mantle convection: Dependence on internal heating and temperature-dependent rheology. Geophys. Res. Lett. 2005, 32, L01301. [Google Scholar] [CrossRef]
- Yoshida, M. Mantle convection with longest-wavelength thermal heterogeneity in a 3-D spherical model: Degree one or two? Geophys. Res. Lett. 2008, 35, L23302. [Google Scholar] [CrossRef]
- Phillips, B.R.; Bunge, H.P. Supercontinent cycles disrupted by strong mantle plumes. Geology 2007, 35, 847–850. [Google Scholar] [CrossRef]
- Tackley, P.J. Self-consistent generation of tectonic plates in time-dependent, three-dimensional mantle convection simulations 1. pseudoplastic yielding. Geochem. Geophys. Geosyst. 2000, 1, 1021. [Google Scholar]
- Ogawa, M. Plate-like regime of a numerically modeled thermal convection in a fluid with temperature-, pressure-, and stress-history-dependent viscosity. J. Geophys. Res. 2003, 108, 2067. [Google Scholar] [CrossRef]
- Yoshida, M.; Santosh, M. Supercontinents, mantle dynamics and plate tectonics: A perspective based on conceptual vs. numerical models. Earth-Sci. Rev. 2011, 105, 1–24. [Google Scholar] [CrossRef]
- Rolf, T.; Coltice, N.; Tackley, P.J. Statistical cyclicity of the supercontinent cycle. Geophys. Res. Lett. 2014, 41, 2351–2358. [Google Scholar] [CrossRef]
- Rolf, T.; Capitanio, F.A.; Tackley, P.J. Constraints on mantle viscosity structure from continental drift histories in spherical mantle convection models. Tectonophysics 2017, in press. [Google Scholar] [CrossRef]
- Richter, F.M. Finite Amplitude Convection Through a Phase Boundary. Geophys. J. R. Astron. Soc. 1973, 35, 265–276. [Google Scholar] [CrossRef]
- Christensen, U.R.; Yuen, D.A. Layered convection induced by phase transitions. J. Geophys. Res. 1985, 90, 10291–10300. [Google Scholar] [CrossRef]
- Bunge, H.P.; Richards, M.A.; Baumgardner, J.R. Effect of depth-dependent viscosity on the planform of mantle convection. Nature 1996, 379, 436–438. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, N.; Li, Z.X.; Roberts, J.H. Supercontinent cycles, true polar wander, and very long-wavelength mantle convection. Earth Planet. Sci. Lett. 2007, 261, 551–564. [Google Scholar] [CrossRef]
- Hofmeister, A.M. Mantle values of thermal conductivity and the geotherm from photon lifetimes. Science 1999, 283, 1699–1706. [Google Scholar] [CrossRef] [PubMed]
- Kameyama, M.; Yuen, D.A. 3-D convection studies on the thermal state in the lower mantle with post-perovskite phase transition. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1982, 25, 297–356. [Google Scholar] [CrossRef]
- McNamara, A.K.; Garnero, E.J.; Rost, S. Tracking deep mantle reservoirs with ultra-low velocity zones. Earth Planet. Sci. Lett. 2010, 299, 1–9. [Google Scholar] [CrossRef]
- Ricolleau, A.; Perrillat, J.P.; Fiquet, G.; Daniel, I.; Matas, J.; Addad, A.; Menguy, N.; Cardon, H.; Mezouar, M.; Guignot, N. Phase relations and equation of state of a natural MORB: Implications for the density profile of subducted oceanic crust in the Earth’s lower mantle. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Ogawa, M. Two-stage evolution of the Earth’s mantle inferred from numerical simulation of coupled magmatism-mantle convection system with tectonic plates. J. Geophys. Res. Solid Earth 2014, 119, 2462–2486. [Google Scholar] [CrossRef]
- Reymer, A.; Schubert, G. Phanerozoic addition rates to the continental crust and crustal growth. Tectonics 1984, 3, 63–77. [Google Scholar] [CrossRef]
- Kameyama, M.; Fujimoto, H.; Ogawa, M. A thermo-chemical regime in the upper mantle in the early Earth inferred from a numerical model of magma migration in the convecting upper mantle. Phys. Earth Planet. Inter. 1996, 94, 187–216. [Google Scholar] [CrossRef]
- Ogawa, M. Superplumes, plates, and mantle magmatism in two-dimensional numerical models. J. Geophys. Res. 2007, 112, B06404. [Google Scholar] [CrossRef]
- Nakagawa, T.; Tackley, P.J.; Deschamps, F.; Connolly, J.A.D. The influence of MORB and harzburgite composition on thermo-chemical mantle convection in a 3-D spherical shell with self-consistently calculated mineral physics. Earth Planet. Sci. Lett. 2010, 296, 403–412. [Google Scholar] [CrossRef]
- Heron, P.J.; Lowman, J.P.; Stein, C. Influences on the positioning of mantle plumes following supercontinent formation. J. Geophys. Res. Solid Earth 2015, 120, 3628–3648. [Google Scholar] [CrossRef]
- Trim, S.J.; Lowman, J.P. Interaction between the supercontinent cycle and the evolution of intrinsically dense provinces in the deep mantle. J. Geophys. Res. Solid Earth 2016, 121, 8941–8969. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere: Washington, DC, USA, 1980; p. 197. [Google Scholar]
- Book, D.L.; Boris, J.P.; Zalesak, S.T. Flux-corrected transport. In Finite-Difference Techniques for Vectorized Fluid Dynamics Calculations; Book, D.L., Ed.; Springer: New York, NY, USA, 1981; pp. 29–55. [Google Scholar]
- Zalesak, S.T. Fully multidimensional flux-corrected-transport algorithms for fluids. J. Comput. Phys. 1979, 31, 335–362. [Google Scholar] [CrossRef]
- Trim, S.J.; Heron, P.J.; Stein, C.; Lowman, J.P. The feedback between surface mobility and mantle compositional heterogeneity: Implications for the Earth and other terrestrial planets. Earth Planet. Sci. Lett. 2014, 405, 1–14. [Google Scholar] [CrossRef]
- Zhang, N.; Zhong, S.; Leng, W.; Li, Z.X. A model for the evolution of the Earth’s mantle structure since the Early Paleozoic. J. Geophys. Res. 2010, 115, B06401. [Google Scholar] [CrossRef]
- Yoshida, M.; Santosh, M. Mantle convection modeling of the supercontinent cycle: Introversion, extroversion, or a combination? Geosci. Front. 2014, 5, 77–81. [Google Scholar] [CrossRef]
- Conrad, C.P.; Steinberger, B.; Torsvik, T.H. Stability of active mantle upwelling revealed by net characteristics of plate tectonics. Nature 2013, 498, 479–482. [Google Scholar] [CrossRef] [PubMed]
- Ballmer, M.D.; Houser, C.; Hernlund, J.W.; Wentzcovitch, R.M.; Hirose, K. Persistence of strong silica-enriched domains in the Earth’s lower mantle. Nat. Geosci. 2017, 10, 236–240. [Google Scholar] [CrossRef]
- Ammann, M.W.; Brodholt, J.P.; Wookey, J.; Dobson, D.P. First-principles constraints on diffusion in lower-mantle minerals and a weak D” layer. Nature 2010, 465, 462–465. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Deschamps, F.; Tackley, P.J. Small post-perovskite patches at the base of lower mantle primordial reservoirs: Insights from 2D numerical modeling and implications for ULVZs. Geophys. Res. Lett. 2016, 43, 3215–3225. [Google Scholar] [CrossRef]

| Symbols | Meanings | Values |
|---|---|---|
| density of Component A (“normal” mantle) | kg/m | |
| temperature difference across the mantle | 3500 K | |
| thickness of the mantle | m | |
| thermal expansivity | K | |
| specific heat | J/kg K | |
| viscosity | Pa s | |
| thermal diffusivity | m/s | |
| g | gravitational acceleration | m/s |
| Clapeyron slope of phase change at around 660 km depth | MPa/K |
| Cases | ||
|---|---|---|
| 1 | 0 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kameyama, M.; Harada, A. Supercontinent Cycle and Thermochemical Structure in the Mantle: Inference from Two-Dimensional Numerical Simulations of Mantle Convection. Geosciences 2017, 7, 126. https://doi.org/10.3390/geosciences7040126
Kameyama M, Harada A. Supercontinent Cycle and Thermochemical Structure in the Mantle: Inference from Two-Dimensional Numerical Simulations of Mantle Convection. Geosciences. 2017; 7(4):126. https://doi.org/10.3390/geosciences7040126
Chicago/Turabian StyleKameyama, Masanori, and Akari Harada. 2017. "Supercontinent Cycle and Thermochemical Structure in the Mantle: Inference from Two-Dimensional Numerical Simulations of Mantle Convection" Geosciences 7, no. 4: 126. https://doi.org/10.3390/geosciences7040126
APA StyleKameyama, M., & Harada, A. (2017). Supercontinent Cycle and Thermochemical Structure in the Mantle: Inference from Two-Dimensional Numerical Simulations of Mantle Convection. Geosciences, 7(4), 126. https://doi.org/10.3390/geosciences7040126





