Assessment of the Combined Sensitivity of Nadir TIR Satellite Observations to Volcanic SO2 and Sulphate Aerosols after a Moderate Stratospheric Eruption
Abstract
1. Introduction
2. Data and Methods
2.1. Satellite Data
2.1.1. IASI
2.1.2. MODIS
2.1.3. SEVIRI
2.2. Stratospheric Volcanic Sulphur Cycle
2.3. Radiative Transfer Simulations
3. Results and Discussion
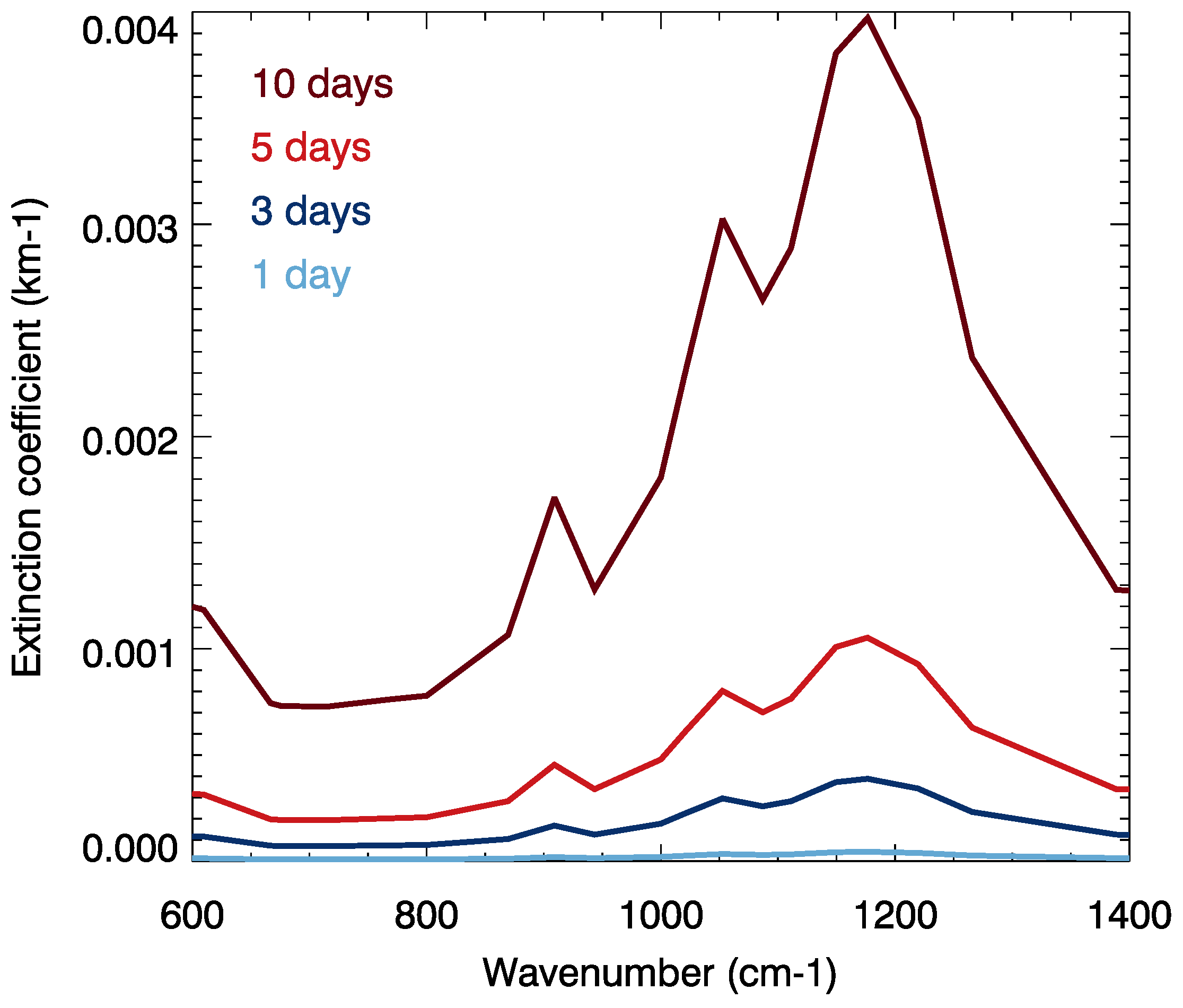
3.1. The SSA Spectral Extinction Coefficient Variability during Short-Term Plume Evolution
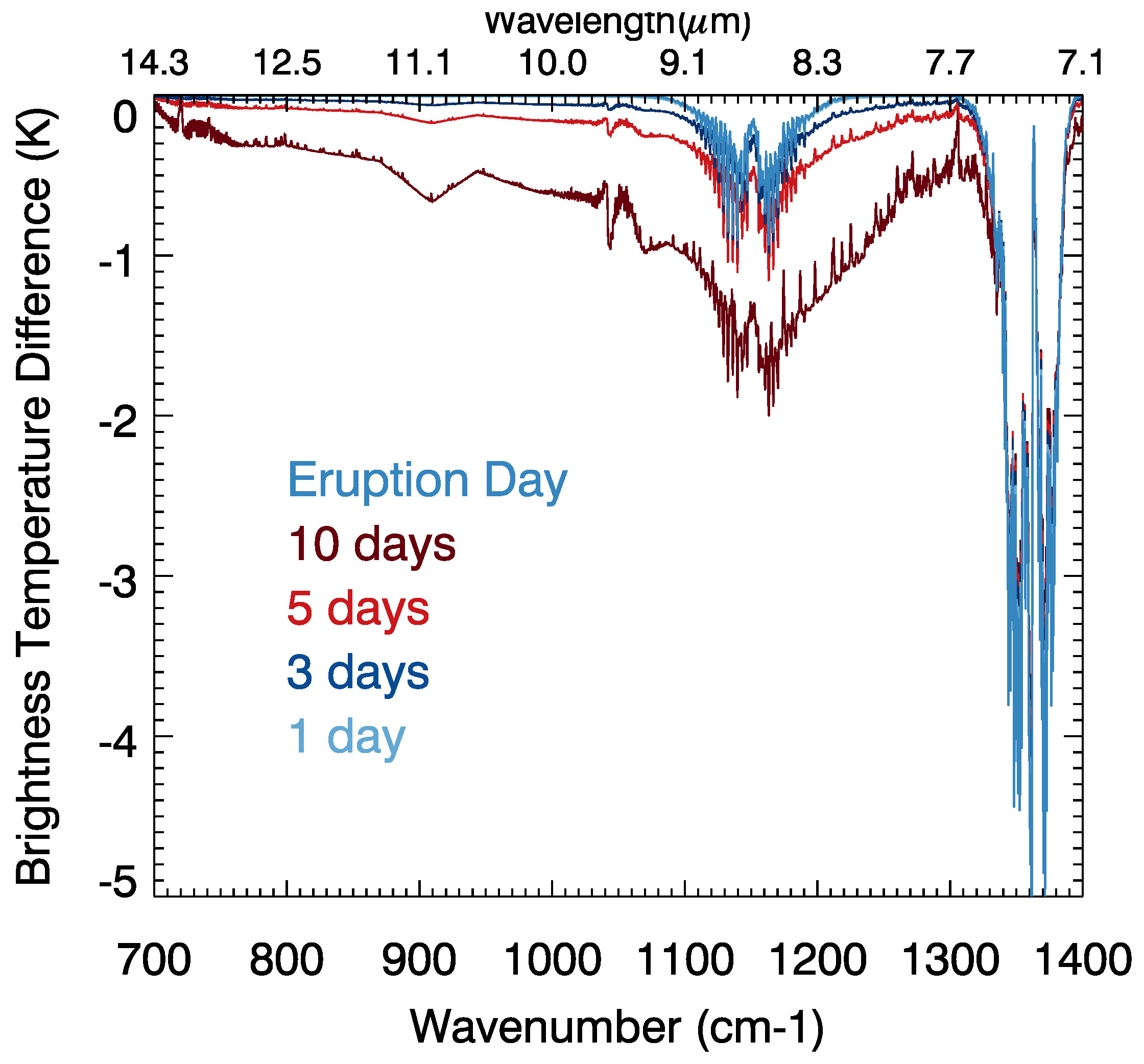
3.2. Brightness Temperature Pseudo-Observations Variability
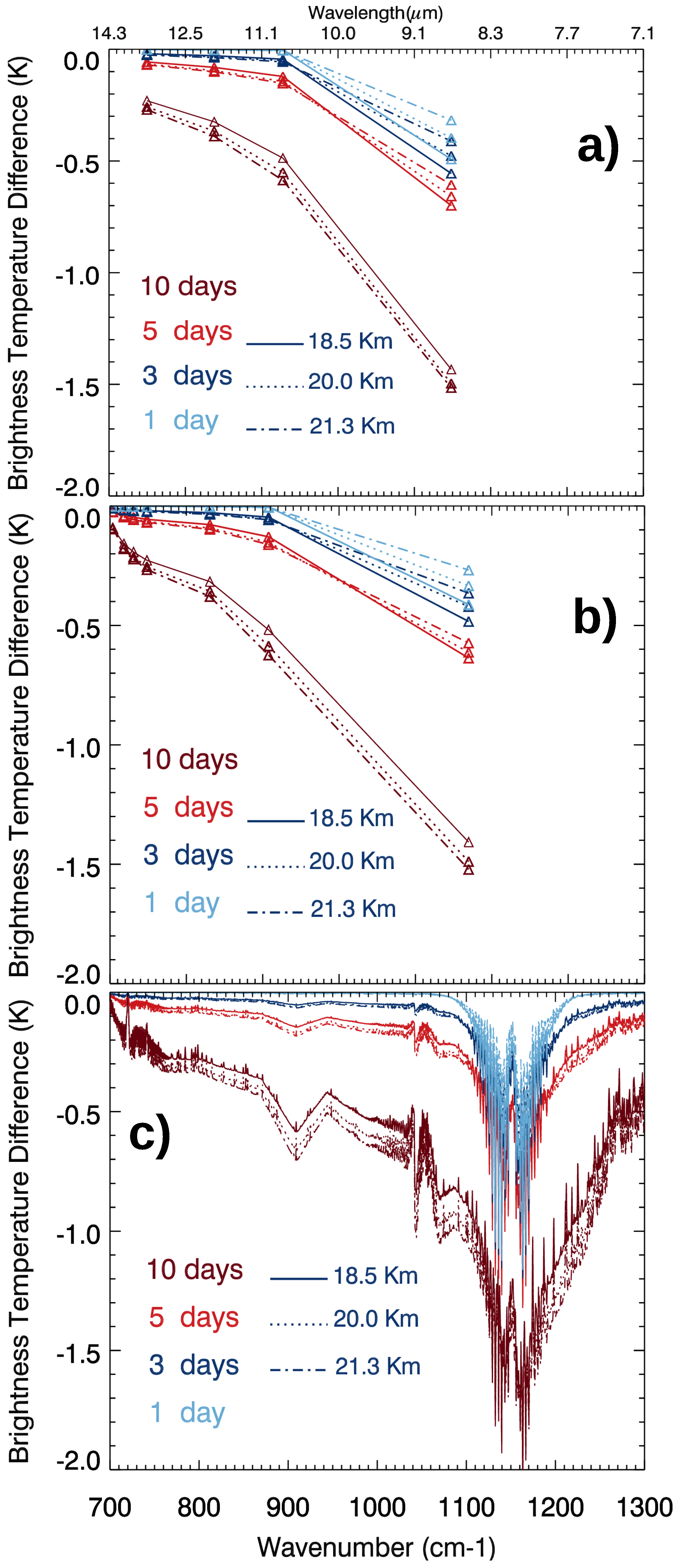
3.3. The Impact of the Plume Altitude
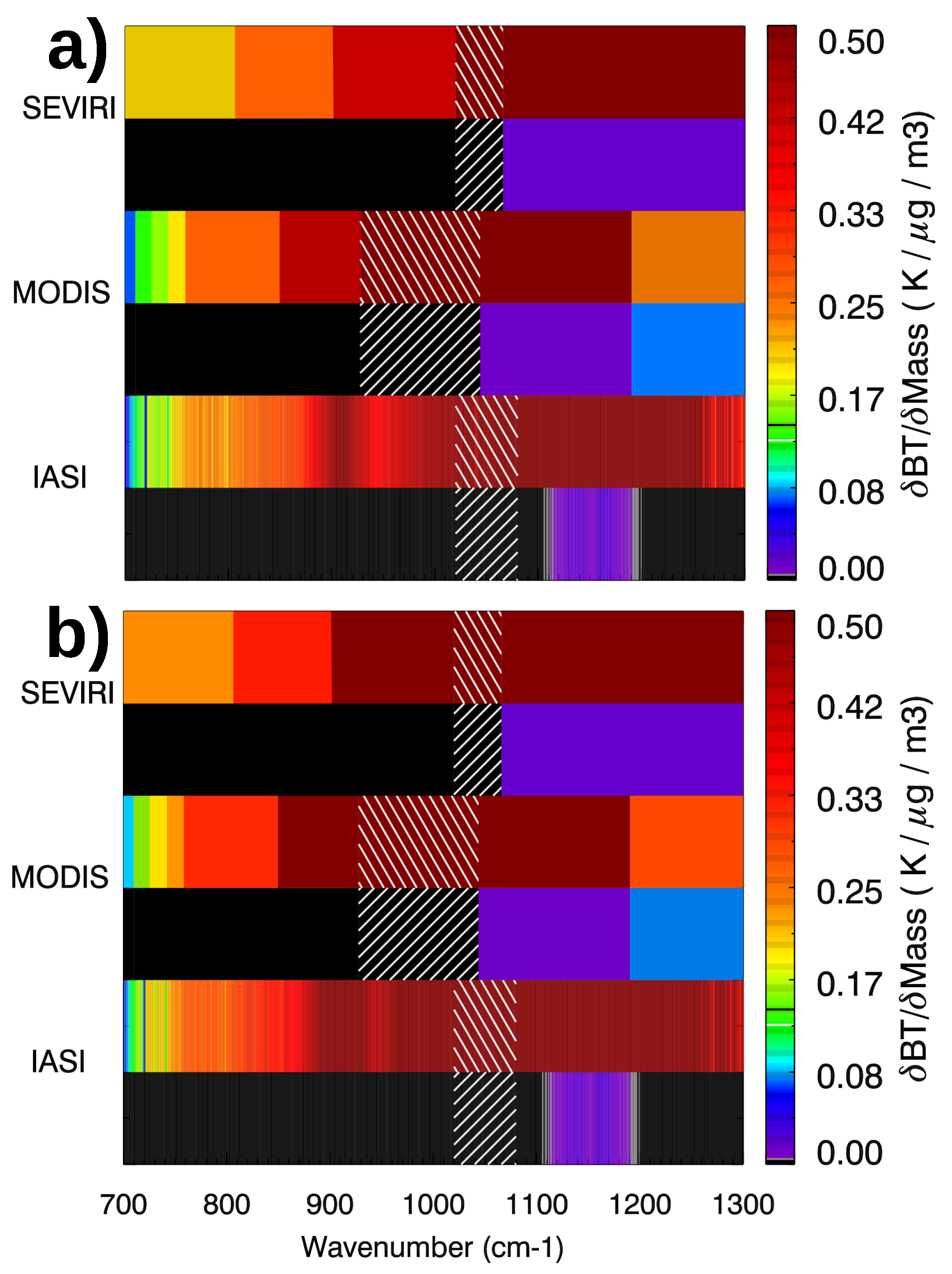
3.4. Information Content of SEVIRI, MODIS and IASI Pseudo-Observations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BT | Brightness Temperature |
| CNES | Centre National D’études Spatiales |
| DISORT | DIScrete ORdinaTe algorithm |
| DOF | Degrees of Freedom |
| DU | Dobson Unit |
| EOS | Earth Observing System |
| EUMETSAT | EUropean organisation for the exploitation of METeorological SATellite |
| H2SO4 | Sulphuric acid |
| IASI | Infrared Atmospheric Sounding Interferometer |
| IR | InfraRed |
| IDL | Interactive Data Language |
| GEISA | GEstion des Informations Spectroscopiques Atmosphériques |
| MetOP | METeorological OPerational |
| MODIS | MODerate resolution Imaging Spectroradiometer |
| MSG | Meteosat Second Generation |
| NASA | National Aeronautics and Space Administration |
| NEBT | Noise Equivalent Brightness Temperature |
| OH | Hydroxyl |
| O2 | Oxygen |
| RSR | Relative Spectral Response |
| RTM | Radiative Transfer Model |
| SEVIRI | Spinning Enhanced Visible and Infrared Imager |
| SO2 | Sulphur Dioxide |
| SSA | Secondary Sulphate Aerosol |
| TIR | Thermal InfraRed |
| UTLS | Upper Troposphere Lower Stratosphere |
| UV | UltraViolet |
| VIIRS | visible Infrared Imager Radiometer Suite |
| VNIR | Visible Near InfraRed |
| 4A | Automatized Atmospheric Absorption Atlas |
References
- Graf, H.F.; Langmann, B.; Feichter, J. The contribution of Earth degassing to the atmospheric sulfur budget. Chem. Geol. 1998, 147, 131–145. [Google Scholar] [CrossRef]
- Sellitto, P.; Zanetel, C.; di Sarra, A.; Salerno, G.; Tapparo, A.; Meloni, D.; Pace, G.; Caltabiano, T.; Briole, P.; Legras, B. The impact of Mount Etna sulfur emissions on the atmospheric composition and aerosol properties in the central Mediterranean: A statistical analysis over the period 2000–2013 based on observations and Lagrangian modelling. Atmos. Environ. 2017, 148, 77–88. [Google Scholar] [CrossRef]
- Robock, A. Volcanic eruptions and climate. Rev. Geophys. 2000, 38, 191–219. [Google Scholar] [CrossRef]
- Grainger, D.G.; Highwood, E.J. Changes in stratospheric composition, chemistry, radiation and climate caused by volcanic eruptions. Geol. Soc. 2013, 213, 329–347. [Google Scholar] [CrossRef]
- Halmer, M.; Schmincke, H.U.; Graf, H.F. The annual volcanic gas input into the atmosphere, in particular into the stratosphere: A global data set for the past 100 years. J. Volcanol. Geotherm. Res. 2002, 115, 511–528. [Google Scholar] [CrossRef]
- Ridley, D.A.; Solomon, S.; Barnes, J.E.; Burlakov, V.D.; Deshler, T.; Dolgii, S.I.; Herber, A.B.; Nagai, T.; Neely, R.R.; Nevzorov, A.V.; et al. Total volcanic stratospheric aerosol optical depths and implications for global climate change. Geophys. Res. Lett. 2014, 41, 7763–7769. [Google Scholar] [CrossRef]
- Stenchikov, G.L.; Kirchner, I.; Robock, A.; Graf, H.F.; Antuña, J.C.; Grainger, R.G.; Lambert, A.; Thomason, L. Radiative forcing from the 1991 Mount Pinatubo volcanic eruption. J. Geophys. Res. Atmos. 1998, 103, 13837–13857. [Google Scholar] [CrossRef]
- Solomon, S.; Portmann, R.W.; Garcia, R.R.; Thomason, L.W.; Poole, L.R.; McCormick, M.P. The role of aerosol variations in anthropogenic ozone depletion at northern midlatitudes. J. Geophys. Res. Atmos. 1996, 101, 6713–6727. [Google Scholar] [CrossRef]
- Malavelle, F.F.; Haywood, J.M.; Jones, A.; Gettelman, A.; Clarisse, L.; Bauduin, S.; Allan, R.P.; Karset, I.H.H.; Kristjánsson, J.E.; Oreopoulos, L.; et al. Strong constraints on aerosol-cloud interactions from volcanic eruptions. Nature 2017, 546, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Seinfeld, J.; Pandis, S. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; John Wiley: New York, NY, USA, 2012. [Google Scholar]
- Doeringer, D.; Eldering, A.; Boone, C.D.; González Abad, G.; Bernath, P.F. Observation of sulfate aerosols and SO2 from the Sarychev volcanic eruption using data from the Atmospheric Chemistry Experiment (ACE). J. Geophys. Res. Atmos. 2012, 117, D03203. [Google Scholar] [CrossRef]
- Castleman, A.W., Jr.; Davis, R.D.; Tang, I.N.; Ball, J.A. Heterogeneous processes and the chemistry of aerosol formation in the upper atmosphere. In Proceedings of the Fourth Conference on the Climatic Assessment Program DOT-TSC-OST-75-38, Department of Transportation, Cambridge, MD, USA, 4–7 February 1975. [Google Scholar]
- Oppenheimer, C.; Francis, P.; Stix, J. Depletion rates of sulfur dioxide in tropospheric volcanic plumes. Geophys. Res. Lett. 1998, 25, 2671–2674. [Google Scholar] [CrossRef]
- Pruppacher, J.; Klett, J. Microphyscics of Clouds and Precipitation, Atmospheric and Oceanic Sciences Library, 2nd ed.; Kluwer Academic Publishers: Norwell, MA, USA, 2004; p. 954. [Google Scholar]
- Steel, H.; Hamill, P. Effects of temperature and humidity on the grouwth and optical properties of sulfuric acid water droplets in the stratosphere. J. Aerosol Sci. 1981, 12, 517–528. [Google Scholar] [CrossRef]
- Bluth, G.J.S.; William, I.; Rose, I.E.S.; Krueger, A.J. Stratospheric Loading of Sulfur from Explosive Volcanic Eruptions. J. Geol. 1997, 1105, 671–683. [Google Scholar] [CrossRef]
- Stevenson, D.S.; Johnson, C.E.; Highwood, E.J.; Gauci, V.; Collins, W.J.; Derwent, R.G. Atmospheric impact of the 1783–1784 Laki eruption: Part I Chemistry modelling. Atmos. Chem. Phys. 2003, 3, 487–507. [Google Scholar] [CrossRef]
- Allen, A.G.; Oppenheimer, C.; Ferm, M.; Baxter, P.J.; Horrocks, L.A.; Galle, B.; McGonigle, A.J.S.; Duffell, H.J. Primary sulfate aerosol and associated emissions from Masaya Volcano, Nicaragua. J. Geophys. Res. Atmosp. 2002, 107, ACH 5-1–ACH 5-8. [Google Scholar] [CrossRef]
- Coffey, M.T. Observations of the impact of volcanic activity on stratospheric chemistry. J. Geophys. Res. Atmos. 1996, 101, 6767–6780. [Google Scholar] [CrossRef]
- Carn, S.; Clarisse, L.; Prata, A. Multi-decadal satellite measurements of global volcanic degassing. J. Volcanol. Geotherm. Res. 2016, 311, 99–134. [Google Scholar] [CrossRef]
- Clarisse, L.; Coheur, P.F.; Prata, F.; Hadji-Lazaro, J.; Hurtmans, D.; Clerbaux, C. A unified approach to infrared aerosol remote sensing and type specification. Atmos. Chem. Phys. 2013, 13, 2195–2221. [Google Scholar] [CrossRef]
- Sellitto, P.; Legras, B. Sensitivity of thermal infrared nadir instruments to the chemical and microphysical properties of UTLS secondary sulfate aerosols. Atmos. Meas. Tech. 2016, 9, 115–132. [Google Scholar] [CrossRef]
- Carboni, E.; Grainger, R.; Walker, J.; Dudhia, A.; Siddans, R. A new scheme for sulphur dioxide retrieval from IASI measurements: Application to the Eyjafjallajokull eruption of April and May 2010. Atmos. Chem. Phys. 2012, 12, 11417–11434. [Google Scholar] [CrossRef]
- Sellitto, P.; di Sarra, A.; Corradini, S.; Boichu, M.; Herbin, H.; Dubuisson, P.; Sèze, G.; Meloni, D.; Monteleone, F.; Merucci, L.; et al. Synergistic use of Lagrangian dispersion and radiative transfer modelling with satellite and surface remote sensing measurements for the investigation of volcanic plumes: The Mount Etna eruption of 25–27 October 2013. Atmos. Chem. Phys. 2016, 16, 6841–6861. [Google Scholar] [CrossRef]
- Karagulian, F.; Clarisse, L.; Clerbaux, C.; Prata, A.J.; Hurtmans, D.; Coheur, P.F. Detection of volcanic SO2, ash, and H2SO4 using the Infrared Atmospheric Sounding Interferometer (IASI). J. Geophys. Res. Atmos. 2010, 115, D00L02. [Google Scholar] [CrossRef]
- Sellitto, P.; Sèze, G.; Legras, B. Secondary sulphate aerosols and cirrus clouds detection with SEVIRI during Nabro volcano eruption. Int. J. Remote Sens. 2017, 38, 5657–5672. [Google Scholar]
- Clerbaux, C.; Coheur, P.F.; Clarisse, L.; Hadji-Lazaro, J.; Hurtmans, D.; Turquety, S.; Bowman, K.; Worden, H.; Carn, S.A. Measurements of SO2 profiles in volcanic plumes from the NASA Tropospheric Emission Spectrometer (TES). Geophys. Res. Lett. 2008, 35, L22807. [Google Scholar] [CrossRef]
- Carboni, E.; Grainger, R.G.; Mather, T.A.; Pyle, D.M.; Thomas, G.E.; Siddans, R.; Smith, A.J.A.; Dudhia, A.; Koukouli, M.E.; Balis, D. The vertical distribution of volcanic SO2 plumes measured by IASI. Atmos. Chem. Phys. 2016, 16, 4343–4367. [Google Scholar] [CrossRef]
- Corradini, S.; Merucci, L.; Prata, A.J. Retrieval of SO2 from thermal infrared satellite measurements: Correction procedures for the effects of volcanic ash. Atmos. Meas. Tech. 2009, 2, 177–191. [Google Scholar] [CrossRef]
- Dubuisson, P.; Herbin, H.; Minvielle, F.; Compiègne, M.; Thieuleux, F.; Parol, F.; Pelon, J. Remote sensing of volcanic ash plumes from thermal infrared: A case study analysis from SEVIRI, MODIS and IASI instruments. Atmos. Meas. Tech. 2014, 7, 359–371. [Google Scholar] [CrossRef]
- Prata, A.J.; Kerkmann, J. Simultaneous retrieval of volcanic ash and SO2 using MSG-SEVIRI measurements. Geophys. Res. Lett. 2007, 34, L05813. [Google Scholar] [CrossRef]
- Miles, G.M.; Grainger, R.G.; Highwood, E.J. The significance of volcanic eruption strength and frequency for climate. Q. J. R. Meteorol. Soc. 2004, 130, 2361–2376. [Google Scholar] [CrossRef]
- McCormick, B.T.; Herzog, M.; Yang, J.; Edmonds, M.; Mather, T.A.; Carn, S.A.; Hidalgo, S.; Langmann, B. A comparison of satellite- and ground-based measurements of SO2 emissions from Tungurahua volcano, Ecuador. J. Geophys. Res. Atmos. 2014, 119, 4264–4285. [Google Scholar] [CrossRef]
- Lambert, A.; Grainger, R.G.; Rodgers, C.D.; Taylor, F.W.; Mergenthaler, J.L.; Kumer, J.B.; Massie, S.T. Global evolution of the Mt. Pinatubo volcanic aerosols observed by the infrared limb-sounding instruments CLAES and ISAMS on the Upper Atmosphere Research Satellite. J. Geophys. Res. Atmos. 1997, 102, 1495–1512. [Google Scholar] [CrossRef]
- SPARC. SPARC Assessment of Stratospheric Aerosol Properties (ASAP); Technical Report No. 4, WCRP-124, WMO/TD-No. 1295; SPARC offices: Paris, French; Toronto, ON, Canada, 2006. [Google Scholar]
- Scott, N.; Chedin, A. A fast line-by-line method for atmospheric absorption computations: The Automatized Atmospheric Absorption Atlas. J. Appl. Meteorol. 1981, 20, 802–812. [Google Scholar] [CrossRef]
- Noveltis. L’innovation au Service de la Protection du Vivant. Available online: http://www.noveltis.com/ (accessed on 13 September 2017). (In French).
- Biermann, U.M.; Luo, B.P.; Peter, T. Absorption Spectra and Optical Constants of Binary and Ternary Solutions of H2SO4, HNO3, and H2O in the Mid Infrared at Atmospheric Temperatures. J. Phys. Chem. A 2000, 104, 783–793. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate- method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; Series on Atmospheric Oceanic and Planetary Physics; World Scientific: London, UK, 2000; Volume 2, pp. 43–64. [Google Scholar]
- Wan, Z. Estimate of noise and systematic error in early thermal infrared data of the Moderate Resolution Imaging Spectroradiometer (MODIS). Remote Sens. Environ. 2002, 80, 47–54. [Google Scholar] [CrossRef]
- EUMETSAT. Typical Radiometric Accuracy and Noise for MSG-1/2. Available online: http://www.eumetsat.int/website/wcm/idc/idcplg?IdcService=GET_FILE&dDocName=PDF_TYP_307RADIOMET_ACC_MSG-1-2&RevisionSelectionMethod=LatestReleased&Rendition=Web (accessed on 26 February 2007).
- Salerno, G.; Burton, M.; Oppenheimer, C.; Caltabiano, T.; Randazzo, D.; Bruno, N.; Longo, V. Three-years of SO2 flux measurements of Mt. Etna using an automated UV scanner array: Comparison with conventional traverses and uncertainties in flux retrieval. J. Volcanol. Geotherm. Res. 2009, 183, 76–83. [Google Scholar] [CrossRef]
- Pougatchev, N.; August, T.; Calbet, X.; Hultberg, T.; Oduleye, O.; Schlüssel, P.; Stiller, B.; Germain, K.S.; Bingham, G. IASI temperature and water vapor retrievals—Error assessment and validation. Atmos. Chem. Phys. 2009, 9, 6453–6458. [Google Scholar] [CrossRef]
| Instrument | Channel | Central Wavenumber (cm−1) | Central Wavelength (μm) | Minimum Wavelength (μm) | Maximum Wavelength (μm) |
|---|---|---|---|---|---|
| SEVIRI | IR8.7 | 1149.42 | 8.70 | 8.30 | 9.10 |
| IR9.7 * | 1035.19 | 9.66 | 9.38 | 9.94 | |
| IR10.8 | 925.93 | 10.80 | 9.80 | 11.80 | |
| IR12.0 | 833.33 | 12.00 | 11.00 | 13.00 | |
| IR13.4 | 746.27 | 13.40 | 12.40 | 14.40 | |
| MODIS | 28 | 1365.18 | 7.32 | 7.17 | 7.47 |
| 29 | 1169.60 | 8.55 | 8.40 | 8.70 | |
| 30 * | 1027.75 | 9.73 | 9.58 | 9.88 | |
| 31 | 909.62 | 11.03 | 10.78 | 11.28 | |
| 32 | 831.95 | 12.02 | 11.77 | 12.27 | |
| 33 | 749.91 | 13.34 | 13.18 | 13.48 | |
| 34 | 733.13 | 13.64 | 13.48 | 13.78 | |
| 35 | 717.36 | 13.94 | 13.78 | 14.08 | |
| 36 | 702.25 | 14.24 | 14.08 | 14.38 |
| Altitude (km) | Time (days) | (g/m3) | (g/m3) | N0 (particles cm−3) | (μm) | H2SO4 Mixing Ratio (%) |
|---|---|---|---|---|---|---|
| 18.5 | 0 | |||||
| 1 | 0.21 | 0.2 | 75 | |||
| 3 | 1.88 | |||||
| 5 | 5.11 | |||||
| 10 | 19.28 | |||||
| 20.0 | 0 | |||||
| 1 | 0.25 | 0.2 | 75 | |||
| 3 | 2.17 | |||||
| 5 | 5.89 | |||||
| 10 | 22.24 | |||||
| 21.3 | 0 | |||||
| 1 | 0.26 | 0.2 | 75 | |||
| 3 | 2.35 | |||||
| 5 | 6.39 | |||||
| 10 | 24.10 |
| Time (days) | 1 | 3 | 5 | 10 |
|---|---|---|---|---|
| SEVIRI | 0.92 | 0.92 | 0.88 | 0.94 |
| MODIS | 1.05 | 1.09 | 0.99 | 1.05 |
| IASI | 1.99 | 1.99 | 1.98 | 1.99 |
| Instrument | Parameters | Time (Days) | |||
|---|---|---|---|---|---|
| 1 | 3 | 5 | 10 | ||
| SEVIRI | SSA | 28.67 | 27.55 | 34.70 | 24.16 |
| SO2 | 49.98 | 49.98 | 49.99 | 49.99 | |
| MODIS | SSA | 7.94 | 7.95 | 8.76 | 7.61 |
| SO2 | 48.57 | 47.57 | 49.93 | 48.56 | |
| IASI | SSA | 0.28 | 0.27 | 0.56 | 0.23 |
| SO2 | 3.51 | 2.64 | 6.88 | 3.41 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guermazi, H.; Sellitto, P.; Serbaji, M.M.; Legras, B.; Rekhiss, F. Assessment of the Combined Sensitivity of Nadir TIR Satellite Observations to Volcanic SO2 and Sulphate Aerosols after a Moderate Stratospheric Eruption. Geosciences 2017, 7, 84. https://doi.org/10.3390/geosciences7030084
Guermazi H, Sellitto P, Serbaji MM, Legras B, Rekhiss F. Assessment of the Combined Sensitivity of Nadir TIR Satellite Observations to Volcanic SO2 and Sulphate Aerosols after a Moderate Stratospheric Eruption. Geosciences. 2017; 7(3):84. https://doi.org/10.3390/geosciences7030084
Chicago/Turabian StyleGuermazi, Henda, Pasquale Sellitto, Mohamed Moncef Serbaji, Bernard Legras, and Farhat Rekhiss. 2017. "Assessment of the Combined Sensitivity of Nadir TIR Satellite Observations to Volcanic SO2 and Sulphate Aerosols after a Moderate Stratospheric Eruption" Geosciences 7, no. 3: 84. https://doi.org/10.3390/geosciences7030084
APA StyleGuermazi, H., Sellitto, P., Serbaji, M. M., Legras, B., & Rekhiss, F. (2017). Assessment of the Combined Sensitivity of Nadir TIR Satellite Observations to Volcanic SO2 and Sulphate Aerosols after a Moderate Stratospheric Eruption. Geosciences, 7(3), 84. https://doi.org/10.3390/geosciences7030084





