A Method for Correcting Tidal Effect on Shoreline Position Extracted from an Image with Unknown Capture Time
Abstract
:1. Introduction
2. Methodologies
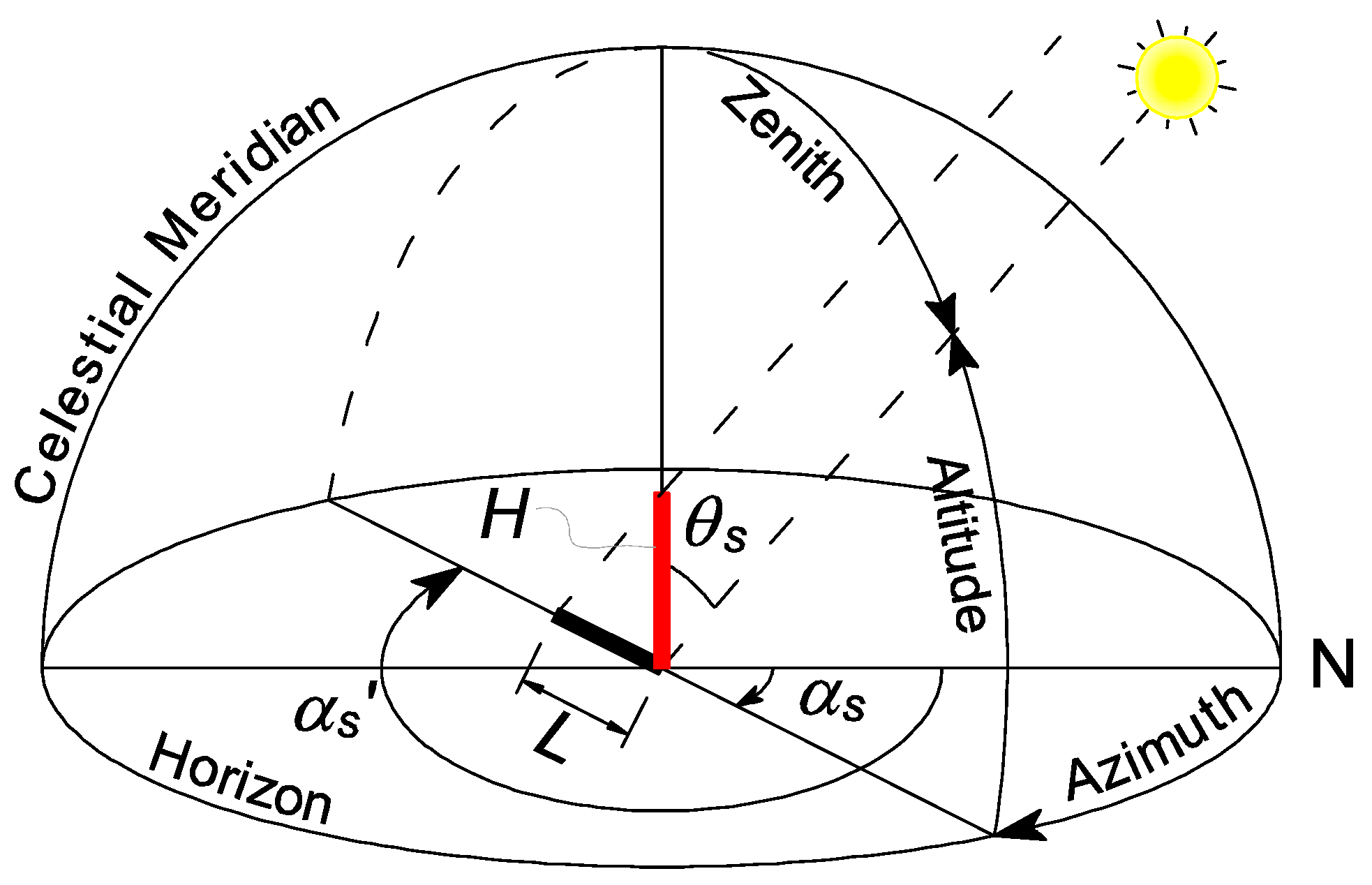
2.1. Method 1—Estimation of Image Capture Time From Solar Azimuth Angle,
2.2. Method 2—Estimation of Image Captured Time from the Length of Shadow on Horizontal Ground Surface (through Solar Zenith Angle, )
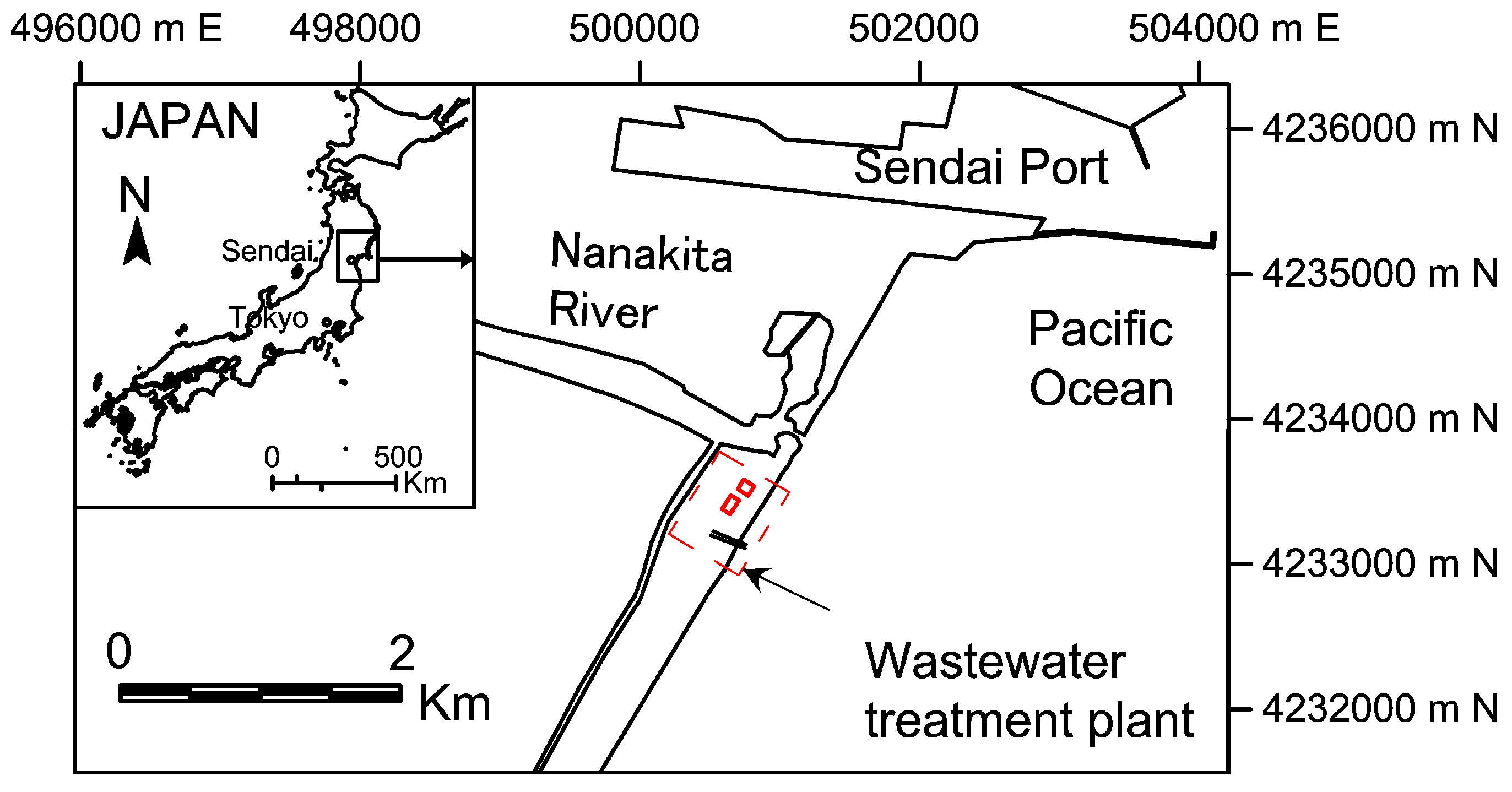
3. Study Area and Data Collection
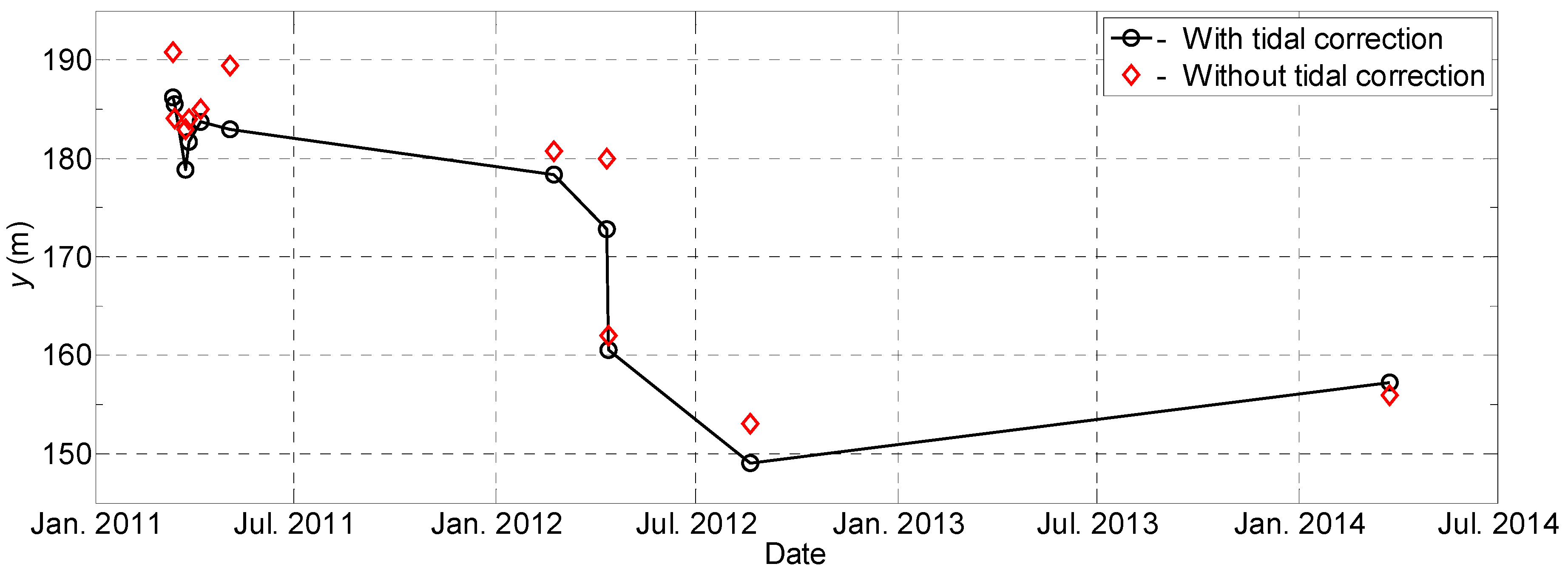
4. Results and Discussion
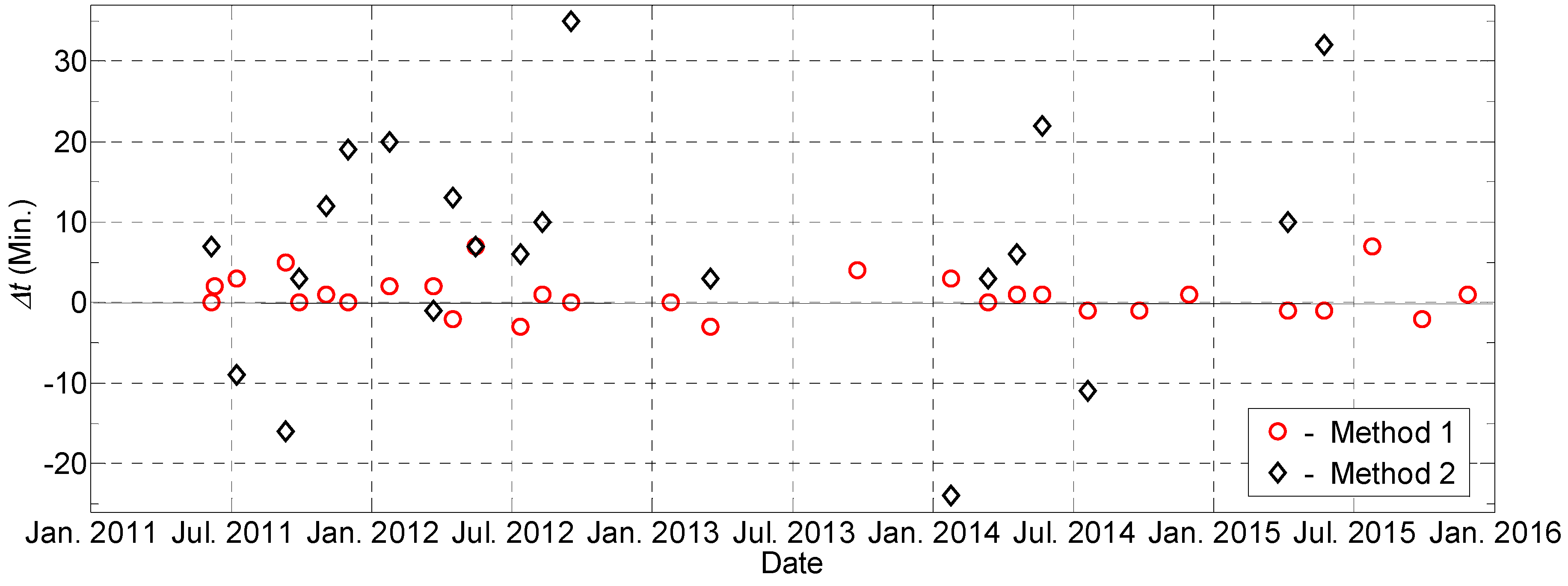
4.1. Estimation of Capture Time of Aerial Photograph and Satellite Image
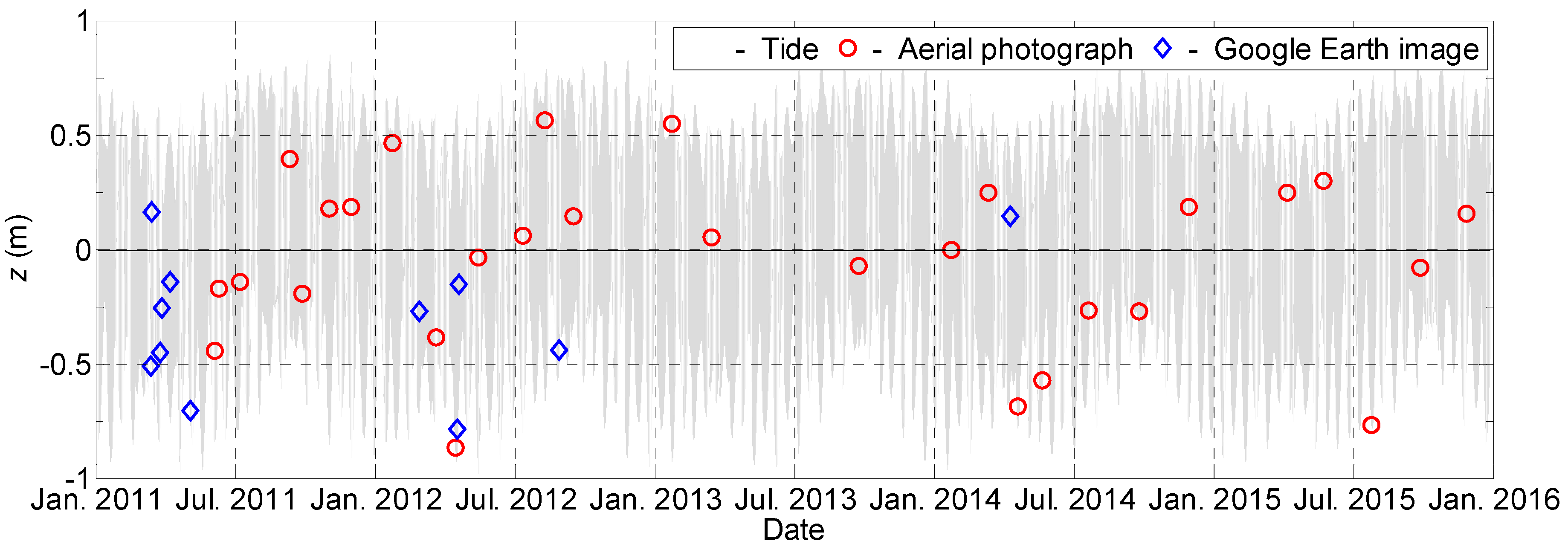
4.2. Tidal Correction for Satellite Image
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical shoreline change: Error analysis and mapping accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Leatherman, S.P. Shoreline change mapping and management along the U.S. east coast. J. Coast. Res. 2003, 38, 5–13. [Google Scholar]
- Chen, W.W.; Chang, H.K. Estimation of shoreline position and change from satellite images considering tidal variation. Estuar. Coast. Shelf Sci. 2009, 84, 54–60. [Google Scholar] [CrossRef]
- Hoang, V.C.; Tanaka, H.; Mitobe, Y. Analysis of shoreline behavior on Sendai coast before and after the 2011 tsunami. Coast. Eng. Proc. 2014. Available online: https://journals.tdl.org/icce/index.php/icce/article/view/7887 (accessed on 24 May 2017).
- Muslim, A.M.; Ismail, K.I.; Khalil, I.; Razman, N.; Zain, K. Detection of shoreline changes at Kuala Terengganu, Malaysia from multi-temporal satellite sensor imagery. In Proceedings of the 34th International Symposium on Remote Sensing of Environment, Sydney, Australia, 10–15 April 2011. [Google Scholar]
- Adityawan, M.B.; Tanaka, H. Shoreline changes at Sendai Port due to the Great North East Japan, Tsunami of 2011. In Proceedings of the 7th International Conference on Coastal Dynamics, Arcachon, France, 24–28 June 2013; pp. 63–72. [Google Scholar]
- Hoang, V.C.; Thanh, T.M.; Viet, N.T.; Tanaka, H. Shoreline change at the Da Rang River Mouth, Vietnam. In Proceedings of the 5th International Conference on Estuaries and Coasts, Muscat, Oman, 2–4 November 2015; pp. 312–318. [Google Scholar]
- Noshi, Y.; Uda, T.; Kobayashi, A.; Miyahara, S. Beach changes observed in Phan Rang City in southeast Vietnam. In Proceedings of the 8th International Conference on Asian and Pacific coasts, Chennai, India, 7–10 September 2015; pp. 163–170. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation, 1st ed.; Academic Press: New York, NY, USA, 1983; 390p, ISBN 9780123737526. [Google Scholar]
- Hartmann, L.D. Global Physical Climatology; Academic Press: New York, NY, USA, 1994; 411p, ISBN 9780080571638. [Google Scholar]
- Nagasawa, K. Computations of Sunrise and Sunset; Chijinshokan: Tokyo, Japan, 1999; 160p, ISBN 978-4805206348. (In Japanese) [Google Scholar]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Moore, L.J. Shoreline mapping techniques. J. Coast. Res. 2000, 16, 111–124. [Google Scholar]
- Kurosawa, T.; Tanaka, H. A study of detection of shoreline position with aerial photographs. J. JSCE Ser. B2 2001, 48, 586–590. (In Japanese) [Google Scholar] [CrossRef]
- Sunamura, T. Quantitative predictions of beach-face slopes. Geol. Soc. Am. Bull. 1984, 95, 242–245. [Google Scholar] [CrossRef]
- Virdis, S.G.P.; Oggiano, G.; Disperati, L. A geomatics approach to multitemporal shoreline analysis in Western Mediterranean: the case of Platamona-Maritza beach (northwest Sardinia, Italy). J. Coast. Res. 2012, 28, 624–640. [Google Scholar] [CrossRef]
- Fletcher, C.; Rooney, J.; Barbee, M.; Lim, S.C.; Richmond, B. Mapping shoreline change using digital orthophotogrammetry on Maui, Hawaii. J. Coast. Res. 2003, 38, 106–124. [Google Scholar]
- Cenci, L.; Disperati, L.; Sousa, L.P.; Phillips, M.; Alve, F.L. Geomatics for Integrated Coastal Zone Management: Multitemporal shoreline analysis and future regional perspective for the Portuguese Central Region. J. Coast. Res. 2013, 65, 1349–1354. [Google Scholar] [CrossRef]


| n | an | bn |
|---|---|---|
| 0 | 0.006918 | |
| 1 | −0.399912 | 0.070257 |
| 2 | −0.006758 | 0.000907 |
| 3 | −0.002697 | 0.001480 |
| No. | Date | Taking Time | Source | Scale | Spatial Resolution (m) |
|---|---|---|---|---|---|
| 1 | 6 March 2011 | 9:53 | Aerial photograph | 1:8000 | 0.5 |
| 2 | 12 March 2011 | NA | Google Earth Pro | NA | NA |
| 3 | 14 March 2011 | NA | Google Earth Pro | NA | NA |
| 4 | 24 March 2011 | NA | Google Earth Pro | NA | NA |
| 5 | 27 March 2011 | NA | Google Earth Pro | NA | NA |
| 6 | 6 April 2011 | NA | Google Earth Pro | NA | NA |
| 7 | 3 May 2011 | NA | Google Earth Pro | NA | NA |
| 8 | 8 June 2011 | 11:27 | Aerial photograph | 1:8000 | 0.5 |
| 9 | 6 July 2011 | 10:29 | Aerial photograph | 1:8000 | 0.5 |
| 10 | 7 September 2011 | 14:25 | Aerial photograph | 1:8000 | 0.5 |
| 11 | 24 September 2011 | 9:18 | Aerial photograph | 1:8000 | 0.5 |
| 12 | 29 October 2011 | 9:33 | Aerial photograph | 1:8000 | 0.5 |
| 13 | 26 November 2011 | 9:17 | Aerial photograph | 1:8000 | 0.5 |
| 14 | 18 January 2012 | 10:30 | Aerial photograph | 1:8000 | 0.5 |
| 15 | 22 February 2012 | NA | Google Earth Pro | NA | NA |
| 16 | 14 March 2012 | 11:36 | Aerial photograph | 1:8000 | 0.5 |
| 17 | 8 April 2012 | 9:59 | Aerial photograph | 1:8000 | 0.5 |
| 18 | 10 April 2012 | NA | Google Earth Pro | NA | NA |
| 19 | 12 April 2012 | NA | Google Earth Pro | NA | NA |
| 20 | 7 May 2012 | 14:28 | Aerial photograph | 1:8000 | 0.5 |
| 21 | 4 July 2012 | 14:10 | Aerial photograph | 1:8000 | 0.5 |
| 22 | 1 August 2012 | 15:46 | Aerial photograph | 1:8000 | 0.5 |
| 23 | 19 August 2012 | NA | Google Earth Pro | NA | NA |
| 24 | 7 September 2012 | 11:20 | Aerial photograph | 1:8000 | 0.5 |
| 25 | 12 January 2013 | 13:31 | Aerial photograph | 1:8000 | 0.5 |
| 26 | 4 March 2013 | 10:5 | Aerial photograph | 1:8000 | 0.5 |
| 27 | 9 September 2013 | 12:39 | Aerial photograph | 1:8000 | 0.5 |
| 28 | 7 January 2014 | 11:48 | Aerial photograph | 1:8000 | 0.5 |
| 29 | 24 February2014 | 11:6 | Aerial photograph | 1:8000 | 0.5 |
| 30 | 24 March 2014 | NA | Google Earth Pro | NA | NA |
| 31 | 2 April 2014 | 10:8 | Aerial photograph | 1:8000 | 0.5 |
| 32 | 4 May 2014 | 11:30 | Aerial photograph | 1:8000 | 0.5 |
| 33 | 2 July 2014 | 14:22 | Aerial photograph | 1:8000 | 0.5 |
| 34 | 6 September 2014 | 9:24 | Aerial photograph | 1:8000 | 0.5 |
| 35 | 8 November 2014 | 11:38 | Aerial photograph | 1:8000 | 0.5 |
| 36 | 15 March 2015 | 10:19 | Aerial photograph | 1:8000 | 0.5 |
| 37 | 1 May 2015 | 14:0 | Aerial photograph | 1:8000 | 0.5 |
| 38 | 2 July 2015 | 9:56 | Aerial photograph | 1:8000 | 0.5 |
| 39 | 3 September 2015 | 12:58 | Aerial photograph | 1:8000 | 0.5 |
| 40 | 1 November 2015 | 11:52 | Aerial photograph | 1:8000 | 0.5 |
| Image (Figure) | Capture Time | |||
|---|---|---|---|---|
| (UTC+9.00) Osaka, Sapporo, Tokyo | ||||
| Actual | Estimated (Unit: Minute) | Remark | ||
| Method 1 | Method 2 | |||
| Figure 4a | 9:53 | 9:53 | 10:00 (+7) | Aerial photograph |
| Figure 4b | NA | 13:50 | NA | Satellite image from Google Earth Pro |
| Figure 4c | NA | 14:32 | NA | Aerial photograph from GSI-Japan |
| Figure 4d | 14:25 | 14:30 (+5) | 14:15 (−10) | Aerial photograph |
| Figure 4e | 14:10 | 14:07 (−3) | 14:11 (+1) | Aerial photograph |
| Figure 4f | 11:20 | 11:20 | 11:55 (+35) | Aerial photograph |
| Figure 4g | 14:22 | 14:21 (−1) | 14:11 (−11) | Aerial photograph |
| Figure 4h | 14:00 | 13:59 (−1) | 14:23 (+23) | Aerial photograph |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, V.C.; Tanaka, H.; Mitobe, Y. A Method for Correcting Tidal Effect on Shoreline Position Extracted from an Image with Unknown Capture Time. Geosciences 2017, 7, 62. https://doi.org/10.3390/geosciences7030062
Hoang VC, Tanaka H, Mitobe Y. A Method for Correcting Tidal Effect on Shoreline Position Extracted from an Image with Unknown Capture Time. Geosciences. 2017; 7(3):62. https://doi.org/10.3390/geosciences7030062
Chicago/Turabian StyleHoang, Vo Cong, Hitoshi Tanaka, and Yuta Mitobe. 2017. "A Method for Correcting Tidal Effect on Shoreline Position Extracted from an Image with Unknown Capture Time" Geosciences 7, no. 3: 62. https://doi.org/10.3390/geosciences7030062
APA StyleHoang, V. C., Tanaka, H., & Mitobe, Y. (2017). A Method for Correcting Tidal Effect on Shoreline Position Extracted from an Image with Unknown Capture Time. Geosciences, 7(3), 62. https://doi.org/10.3390/geosciences7030062






