Strategies for the Simulation of Sea Ice Organic Chemistry: Arctic Tests and Development
Abstract
:1. Introduction
2. Model Description
2.1. Simplified Physical Model
2.2. Biogeochemistry
- auto (autotrophic organisms encompassing phytoplankton and/or ice algae)
- nut (the major inorganic nutrients including redox states plus iron)
- mac (fresh or aged biomacromolecules represented as lipids, oligomers and polymers).
- A1-5 (define the various ice biogeochemical quantities)
- A6-17 (limitations, autotrophic source-sink terms and biological rates of change)
- A18-22 (fixed ecodynamic fractionations and apportionments)
- A23-27 (nutrient uptake and recycling)
- A28-32 (organic processing of biomacromolecular detritus/exudate)
- A33-37 (vertical transport with flushing and continuity)
3. Observational Data
4. Model Validation and the Baseline
4.1. Accuracy and Sensitivity
4.2. Baseline Results: Inorganics and Biology
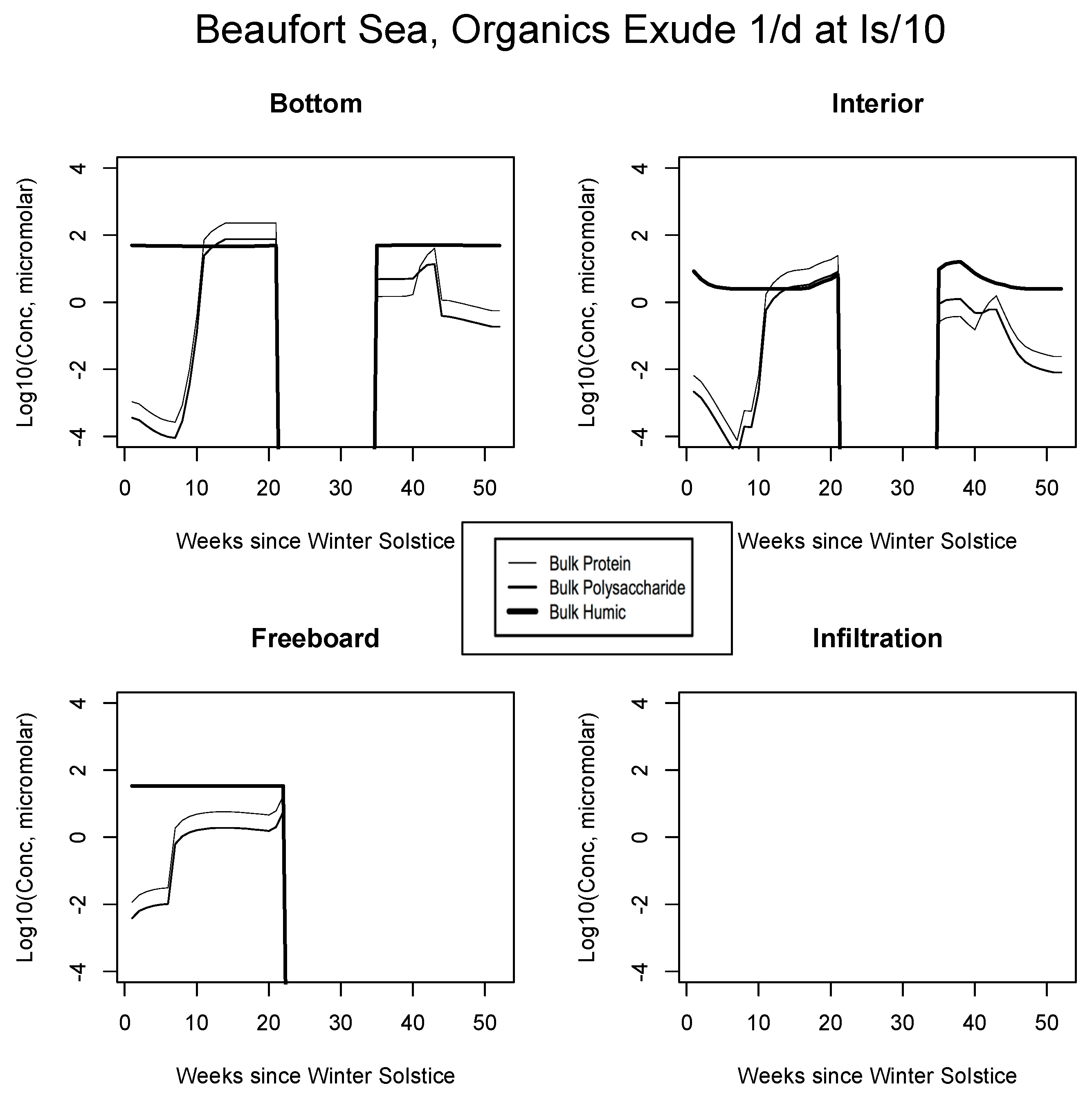
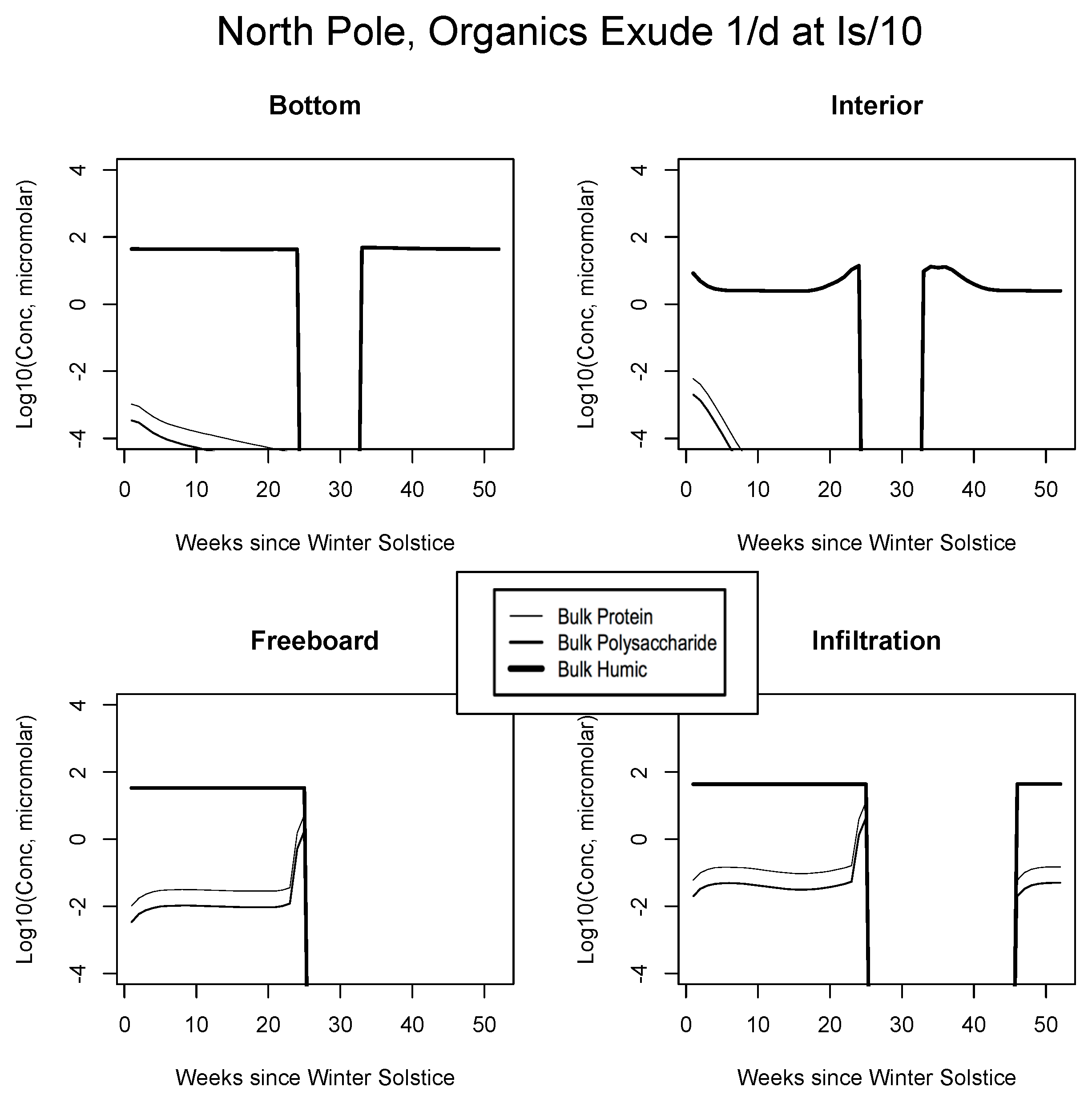
5. The Organics
5.1. Baseline Results
5.2. Exudation
6. Summary of Results
7. Discussion: Influence on Structure and Future Directions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Equations
Appendix B. Parameters
| Quantity | Diatoms | Flagellates | Phaeocystis | Units | Sources |
|---|---|---|---|---|---|
| RC/N | 7 | 7 | 7 | mole/mole | 57,58,113 |
| RC/Si | 5 | NA | NA | mole/mole | 25,54 |
| RC/Fe | 2 × 105 | 2 × 105 | 5 × 105 | mole/mole | 56,75,113 |
| RC/Chl | 40 | 40 | 100 | mass/mass | 57,62,113 |
| aChl | 0.03 | 0.01 | 0.05 | 1/m(mg/m3) | 25,44,57 |
| Is (low PAR) | 1.5 | 1.5 | 1.5 | W/m2 | 43,54,57,83 |
| Is (high PAR) | 4 | 4 | 4 | ||
| Is (pelagic) | 50 | 30 | 20 | 57,102 | |
| Iin | 100 | 100 | 100 | 33,39,44,127 | |
| KNO3− | 1 | 1 | 1 | μM | 54,57,58,113 |
| KNH4+ | 0.3 | 0.3 | 0.3 | ||
| KSi(OH4) | 3 | NA | NA | 25,128,129 | |
| KFe | 100 | 100 | 10 | pM | 56,113 |
| gpre | 0.85 | 0.85 | 0.85 | 1/d | 25,44,57,81 |
| gexp | 0.06 | 0.06 | 0.06 | 1/Co | 43,44 |
| fsal (50 ppt) | 1 | 1 | 1 | none | 43,44,54 |
| fsal (100 ppt) | 0 | 0 | 0 | ||
| fgraze (bottom) | 0 | 0.9 | 0.9 | See text | |
| fgraze (other) | NA | 0.1 | 0.1 | 14,25,39,54 | |
| fresp | 0.05 | 0.05 | 0.05 | 25,54,57 | |
| mpre | 0.02 | 0.02 | 0.02 | 1/d | 14,33,128,130 |
| mexp | 0.03 | 0.03 | 0.03 | 1/Co | |
| fspill | 0.5 | 0.5 | 0.5 | none | 14,98 |
| fassim | 0.5 | 0.5 | 0.5 | 1-fspill | |
| fexcr | 0.5 | 0.5 | 0.5 | 14 | |
| fremin | 1 | 1 | 1 | 14,33,98 | |
| knit | 0.015 | 0.015 | 0.015 | 1/d | 14,33 |
| fbiomass (protein) | 0.6 | 0.6 | 0.6 | none | 14,26,27 |
| fbiomass (poly) | 0.2 | 0.2 | 0.2 | ||
| fbiomass (lipid) | 0.2 | 0.2 | 0.2 | ||
| kexude | 0 | 0 | 0 | 1/d | 27,57,98 |
| kbac | 1 | 1 | 1 | 1/month | 84,85 |
References
- Lengaigne, M.; Madec, G.; Bopp, L.; Menkes, C.; Aumont, O.; Cadule, P. Bio-physical Feedbacks in the Arctic Ocean using an Earth system model. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Screen, J.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 2010, 464, 1334–1337. [Google Scholar] [CrossRef] [PubMed]
- Janech, M.; Krell, A.; Mock, T.; Kang, J.; Raymond, J. Ice-binding proteins from sea ice diatoms (Bacillariophyceae). J. Phycol. 2006, 42, 410–416. [Google Scholar] [CrossRef]
- Riedel, A.; Michel, C.; Gosselin, M.; LeBlanc, B. Winter-spring dynamics in sea-ice carbon cycling in the coastal Arctic Ocean. J. Mar. Syst. 2008, 74, 918–932. [Google Scholar] [CrossRef]
- McNeill, V.F.; Grannas, A.M.; Abbatt, J.P.D.; Ammann, M.; Ariya, P.; Bartels-Rausch, T.; Domine, F.; Donaldson, D.J.; Guzman, M.I.; Heger, D. Organics in environmental ices: Sources, chemistry and impacts. Atmos. Chem. Phys. 2012, 12, 9653–9678. [Google Scholar] [CrossRef]
- Underwood, G.; Aslam, S.; Michel, C.; Niemi, A.; Norman, L.; Meiners, K.; Laybourn-Parry, L.; Paterson, H.; Thomas, D. Broad-scale predictability of carbohydrates and exopolymers in Antarctic and Arctic sea ice. Proc. Natl. Acad. Sci. USA 2013, 110, 15734–15739. [Google Scholar] [CrossRef] [PubMed]
- Underwood, G.; Fietz, S.; Papadimitriou, S.; Thomas, D.; Dieckmann, G. Distribution and composition of dissolved extracellular polymeric substances in Antarctic sea ice. Mar. Ecol. Prog. Ser. 2010, 404, 1–19. [Google Scholar] [CrossRef]
- Krembs, C.; Eicken, H.; Deming, J. Exopolymer alteration of physical properties of sea ice and implication for ice habitability and biogeochemistry in a warmer Arctic. Proc. Natl. Acad. Sci. USA 2011, 108, 2653–2658. [Google Scholar] [CrossRef] [PubMed]
- Burrows, S.; Ogunro, O.; Frossard, A.; Russell, L.; Rasch, P.; Elliott, S. A physically based framework for modeling the organic fractionation of sea spray aerosol from bubble film Langmuir equilibria. Atmos. Chem. Phys. 2014, 14, 13601–13629. [Google Scholar] [CrossRef]
- Carpenter, L.; Nightingale, P. Chemistry and release of gases from the surface ocean. Chem. Rev. 2015, 115, 4015–4024. [Google Scholar] [CrossRef] [PubMed]
- Letscher, R.; Moore, J.; Teng, Y.; Primeaux, F. Variable C:N:P stoichiometry of dissolved organic matter cycling in the Community Earth System Model. Biogeosciences 2015, 12, 209–221. [Google Scholar] [CrossRef]
- Tedesco, L.; Vichi, M.; Thomas, D. Process studies on ecological coupling between sea ice algae and phytoplankton. Ecol. Model. 2012, 226, 120–138. [Google Scholar] [CrossRef]
- Deal, C.; Jin, M.; Elliott, S.; Hunke, E.; Maltrud, M.; Jeffery, N. Large scale modeling of primary production and ice algae within arctic sea ice in 1992. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Elliott, S.; Deal, C.; Humphries, G.; Hunke, E.; Jeffery, N.; Jin, M.; Levasseur, M.; Stefels, J. Pan-Arctic simulations of coupled nutrient-sulfur cycling due to sea ice biology. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Amon, R.; Pitznar, H.; Benner, R. Linkages among the bioreactivity, chemical composition and diagenetic state of marine dissolved organic matter. Limnol. Oceanogr. 2001, 46, 287–297. [Google Scholar] [CrossRef]
- Thomas, D.; Papadimitriou, S. Biogeochemistry of sea ice. In Sea Ice: An Introduction to its Physics, Chemistry, Biology and Geology; Thomas, D., Dieckmann, G., Eds.; Blackwell Science: London, UK, 2003. [Google Scholar]
- Aslam, S.; Cresswell-Maynard, T.; Thomas, D.; Underwood, G. Production and characterization of the intra- and extracellular carbohydrates and polymeric substances (EPS) of three sea-ice diatom species, and evidence for a cryoprotective role for EPS. J. Phycol. 2012, 48, 1494–1509. [Google Scholar] [CrossRef] [PubMed]
- Hunke, E.; Lipscomb, W.; Turner, A.; Jeffery, N.; Elliott, S. CICE: The Los Alamos Sea Ice Model Documentation and Software User’s Manual Version 5.0; LANL technical report LA-CC-06-012; Los Alamos National Laboratory: Los Alamos, NM, USA, 2015.
- Raymond, J.; Sullivan, C.; DeVries, A. Release of an ice-active substance by Antarctic sea ice diatoms. Polar Biol. 1994, 14, 71–75. [Google Scholar] [CrossRef]
- Krembs, C.; Eicken, H.; Junge, K.; Deming, J. High concentrations of exopolymeric substances in Arctic winter sea ice: Implications for the polar ocean carbon cycle and cryoprotection of diatoms. Deep Sea Res. I 2002, 49, 2163–2181. [Google Scholar] [CrossRef]
- Serreze, M.; Holland, M.; Stroeve, J. Perspectives on the Arctic’s shrinking sea-ice cover. Science 2007, 315, 1533–1536. [Google Scholar] [CrossRef] [PubMed]
- Krembs, C.; Deming, J. The role of exopolymers in microbial adaptations to sea ice. In Psychrophiles: From Biodiversity to Biotechnology; Margesin, R., Schinner, F., Marx, J.C., Gerday, C., Eds.; Springer: Berlin, Germany, 2008; pp. 247–264. [Google Scholar]
- Post, E.; Bhatt, U.; Bitz, C.; Brodie, J.; Fulton, T.; Hebblewhite, M.; Kerby, J.; Kutz, S.; Stirling, I.; Walker, D. Ecological consequences of sea-ice decline. Science 2013, 341, 519–524. [Google Scholar] [CrossRef] [PubMed]
- Chin, W.; Orellana, M.; Verdugo, P. Spontaneous assembly of marine dissolved organic matter into polymer gels. Nature 1998, 391, 568–572. [Google Scholar]
- Lavoie, D.; Denman, K.; Michel, C. Modeling ice algal growth and decline in a seasonally ice-covered region of the Arctic (Resolute Passage, Canadian Archipelago). J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Parsons, T.; Takahashi, M.; Hargrave, B. Biological Oceanographic Processes; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Benner, R. Chemical composition and reactivity. In Biogeochemistry of Dissolved Organic Matter; Hansell, D., Carlson, C., Eds.; Academic Press: New York, NY, USA, 2002; pp. 59–90. [Google Scholar]
- Elliott, S.; Burrows, S.; Liu, X.; Ogunro, O.; Russell, L.; Wingenter, O. Simulating macromolecular surfactant chemistry of the ocean-atmosphere boundary. Environ. Res. Lett. 2014, 9, 06412. [Google Scholar] [CrossRef]
- Calace, N.; Castrovinci, D.; Maresca, V.; Petronio, B.; Pietroletti, M.; Scardala, S. Aquatic humic substances in pack ice-seawater-sediment systems. Int. J. Environ. Anal. Chem. 2001, 79, 315–329. [Google Scholar] [CrossRef]
- Norman, L.; Thomas, D.; Stedmon, C.; Granskog, M.; Papadimitriou, S.; Krapp, R.; Meiners, K.; Lannuzel, D.; Van der Merwe, P.; Dieckmann, G. The characteristics of dissolved organic matter (DOM) and chromophoric dissolved organic matter (CDOM) in Antarctic sea ice. Deep Sea Res. II 2011, 58, 1075–1091. [Google Scholar] [CrossRef]
- Aslam, S.; Underwood, G.; Kaartokallio, H.; Norman, L.; Autio, R.; Fischer, M.; Kuosa, H.; Dieckmann, G.; Thomas, D. Dissolved extracellular polymeric substances (dEPS) dynamics and bacterial growth during sea ice formation in an ice tank study. Polar Biol. 2012, 35, 661–676. [Google Scholar] [CrossRef]
- Carmack, E.; Wassmann, P. Food webs and physical-biological coupling on pan-Arctic shelves: Unifying concepts and comprehensive perspectives. Prog. Oceangr. 2006, 71, 446–477. [Google Scholar] [CrossRef]
- Jin, M.; Deal, C.; Wang, J.; Shin, K.; Tang, N.; Whitledge, M.; Lee, S.; Gradinger, R. Controls of the landfast ice-ocean ecosystem offshore Barrow Alaska. Ann. Glaciol. 2006, 44, 63–72. [Google Scholar] [CrossRef]
- Vancoppenolle, M.; Goose, H.; Montety, A.; Fichelet, T.; Tremblay, B.; Tison, J. Modeling brine and nutrient dynamics in Antarctic sea ice: The case of dissolved silica. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Van der Merwe, P.; Lannuzel, D.; Mancuso Nichols, C.; Meiners, K.; Heil, P.; Norman, L.; Thomas, D.; Bowie, A. Biogeochemical observations during winter-spring transition in East Antarctic sea ice: Evidence of iron and exopolysaccharide controls. Mar. Chem. 2009, 115, 163–175. [Google Scholar] [CrossRef]
- Lannuzel, D.; Schoemann, V.; De Jong, J.; Pasquer, B.; Van der Merwe, P.; Masson, F.; Tison, J.; Bowie, A. Distribution of dissolved iron in Antarctic sea ice: Spatial, seasonal and inter-annual variability. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Aguilar-Islas, A.; Hurst, M.; Buck, K.; Sohst, B.; Smith, G.; Lohan, M.; Bruland, K. Micro- and macronutrients in the southeastern Bering Sea: Insight into iron replete versus depleted regimes. Prog. Oceanogr. 2007, 73, 99–126. [Google Scholar] [CrossRef]
- Aguilar-Islas, A.; Rember, R.; Mordy, C.; Wu, J. Sea ice-derived dissolved iron and its potential influence on the spring algal bloom in the Bering Sea. Geophys. Res. Lett. 2008, 35, 35. [Google Scholar] [CrossRef]
- Arrigo, K. Primary production in sea ice. In Sea Ice: An Introduction to its Physics, Chemistry, Biology and Geology; Thomas, D., Dieckmann, G., Eds.; Blackwell Science: London, UK, 2003. [Google Scholar]
- Ackley, S.; Sullivan, C. Physical controls on the development and characteristics of Antarctic sea ice biological communities—A review and synthesis. Deep Sea Res. I 1994, 10, 1583–1604. [Google Scholar] [CrossRef]
- Gradinger, R. Vertical structure of the biomass and composition of algal communities in Arctic pack ice. Mar. Biol. 1999, 133, 745–754. [Google Scholar] [CrossRef]
- Meiners, K.; Vancoppenolle, M.; Thanassekos, S.; Dieckmann, G.; Thomas, D.; Tison, J.; Arrigo, K.; Garrison, D.; McMinn, A.; Lannuzel, D.; et al. Chlorophyll a in Antarctic sea ice from historical ice core data. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Fritsen, C.; Ackley, S.; Kremer, J.; Sullivan, C. Flood-freeze cycles and microalgal dynamics in Antarctic pack ice. In Antarctic Sea Ice: Biological Processes, Interactions and Variability; American Geophysical Union: Washington, DC, USA, 1998; Volume 73, pp. 1–21. [Google Scholar]
- Arrigo, K.; Sullivan, C. The influence of salinity and temperature covariation on the photophysiological characteristics of antarctic sea ice microalgae. J. Phycol. 1992, 28, 746–756. [Google Scholar] [CrossRef]
- Jeffery, N.; Hunke, E.; Elliott, S. Modeling transport of passive tracers in sea ice. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Jeffery, N.; Hunke, E. Modeling the winter-spring transition of first-year ice in the western Weddell Sea. J. Geophys. Res. 2014, 119. [Google Scholar] [CrossRef]
- Collins, W.; Bitz, C.; Blackmon, M.; Bonan, G.; Bretherton, C.; Carton, J.; Chang, P.; Doney, S.; Hack, J.; Henderson, T.; et al. The Community Climate System Model version 3 (CCSM3). J. Clim. 2006, 19, 2122–2143. [Google Scholar] [CrossRef]
- Rae, J.; Hewitt, H.; Keen, A.; Ridley, J.; West, A.; Harris, C.; Hunke, E.; Walters, D. Development of global sea ice 5.0 and 6.0 CICE configurations for the Met Office Global Coupled Model. Geosci. Model Dev. 2015, 8, 2529–2554. [Google Scholar] [CrossRef]
- Large, W.; Yeager, S. The global climatology of an interannually varying air-sea flux data set. Clim. Dyn. 2009, 33, 341–364. [Google Scholar] [CrossRef]
- Hunke, E. Thickness sensitivities in the CICE sea ice model. Ocean Model. 2010, 3–4, 137–149. [Google Scholar] [CrossRef]
- Dittmar, T.; Kattner, G. Recalcitrant dissolved organic matter in the ocean: Major contribution of small amphiphiles. Mar. Chem. 2003, 82, 115–123. [Google Scholar] [CrossRef]
- Dittmar, T.; Kattner, G. The biogeochemistry of river and shelf ecosystems of the Arctic Ocean: A review. Mar. Chem. 2003, 83, 103–120. [Google Scholar] [CrossRef]
- Ackley, S.; Lewis, M.; Fritsen, C.; Xie, H. Internal melting in Antarctic sea ice: Development of “gap layers”. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Arrigo, K.; Kremer, J.; Sullivan, C. A simulated Antarctic fast ice ecosystem. J. Geophys. Res. 1993, 98, 6929–6946. [Google Scholar] [CrossRef]
- Reeburgh, W. Fluxes associated with brine motion in growing sea ice. Polar Biol. 1984, 3, 29–33. [Google Scholar] [CrossRef]
- Tagliabue, A.; Arrigo, K. Processes governing the supply of iron to phytoplankton in stratified seas. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Walsh, J.; Dieterle, D.; Lenes, J. A numerical analysis of carbon dynamics of the Southern Ocean phytoplankton community: The roles of light and grazing effecting both sequestration of atmospheric CO2 and food availability to larval krill. Deep Sea Res. I 2001, 48, 1–48. [Google Scholar] [CrossRef]
- Walsh, J.; Dieterle, D.; Maslowski, W.; Whitledge, T. Decadal shifts in biophysical forcing of arctic marine food webs: Numerical consequences. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Wang, S.; Moore, K. Variability of primary production and air-sea CO2 flux in the Southern Ocean. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Thomas, D.; Kattner, G.; Engbrodt, R.; Gianelli, V.; Kennedy, H.; Haas, C.; Dieckmann, G. Dissolved organic matter in Antarctic sea ice. Ann. Glaciol. 2001, 33, 297–303. [Google Scholar] [CrossRef]
- Gradinger, R.; Meiners, K.; Plumley, G.; Zhang, Q.; Bluhm, B. Abundance and composition of the sea-ice meiofauna in pack ice of the Beaufort Gyre in summer 2002/3. Polar Biol. 2005, 28, 171–181. [Google Scholar] [CrossRef]
- Ackley, S.; Buck, K.; Taguchi, S. Standing crop of algae in the sea ice of the Weddell Sea region. Deep Sea Res. 1979, 26, 269–281. [Google Scholar] [CrossRef]
- Haas, C.; Thomas, D.; Bareiss, J. Surface properties and processes of perennial Antarctic sea ice in summer. J. Glaciol. 2001, 47, 613–625. [Google Scholar] [CrossRef]
- Melnikov, I. The Arctic Sea Ice Ecosystem; Overseas Publishers Association: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Flato, G.; Brown, R. Variability and climate sensitivity of landfast Arctic sea ice. J. Geophys. Res. 1996, 101, 26767–26777. [Google Scholar] [CrossRef]
- Fritsen, C.; Coale, S.; Neenan, D.; Gibson, A.; Garrison, D. Biomass, production and microhabitat characteristics near the freeboard of ice floes in the Ross Sea, Antarctica, during the austral summer. Ann. Glaciol. 2001, 33, 280–286. [Google Scholar] [CrossRef]
- Zar, J. Biostatistical Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Press, W.; Teukolsky, S.; Vetterling, W.; Flannery, B. Numerical Recipes in Fortran 90: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Maeda, M. Transport of copper from the Bering Sea to the Northwestern North Pacific. J. Oceanogr. Soc. Jpn. 1986, 42, 333–346. [Google Scholar] [CrossRef]
- Hutchinson, G. The paradox of the plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- Uzuka, N. A time series observation of DMSP production in the fast ice zone near Barrow. Tohoku Geophys. J. 2003, 36, 439–442. [Google Scholar]
- Gradinger, R. Sea-ice algae: Major contributors to primary production and algal biomass in the Chukchi and Beaufort Seas during May/June 2002. Deep Sea Res. II 2009, 56, 1201–1212. [Google Scholar] [CrossRef]
- Eicken, H.; Krouse, H.; Kadko, D.; Perovich, D. Tracer studies of pathways and rates of meltwater transport through arctic summer sea ice. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Tison, J.; Brabant, F.; Dumont, I.; Stefels, J. High resolution dimethyl sulfide and dimethyl sulfoniopropionate time series profiles in decaying summer first-year sea ice at Ice Station Polarstern, western Weddell Sea, Antarctica. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Fung, I.; Meyn, S.; Tegen, I.; Doney, S.; John, J.; Bishop, J. Iron supply and demand in the upper ocean. Glob. Biogeochem. Cycles 2000, 14, 281–295. [Google Scholar] [CrossRef]
- Wang, S.; Bailey, D.; Lindsay, K.; Moore, K.; Holland, M. Impacts of sea ice on the marine iron cycle and phytoplankton productivity. Biogeosci. Discuss. 2014, 11, 2383–2418. [Google Scholar] [CrossRef]
- Malcolm, R. The uniqueness of humic substances in each of soil, stream and marine environments. Anal. Chim. Acta 1990, 232, 19–30. [Google Scholar] [CrossRef]
- Mundy, C.; Gosselin, M.; Ehn, J.; Gratton, Y.; Rossnagel, A.; Barber, D.; Martin, J.; Tremblay, J.; Palmer, M.; Arrigo, K.; et al. Contribution of under-ice primary production to an ice-edge upwelling phytoplankton bloom in the Canadian Beaufort Sea. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Arrigo, K.; Perovich, D.; Pickart, R.; Brown, Z.; Van Kijken, G.; Lowry, K.; Mills, M.; Palmer, M.; Balch, W.; Bahr, F.; et al. Massive phytoplankton blooms under Arctic sea ice. Science 2012, 336, 1408. [Google Scholar] [CrossRef]
- Wakeham, S.; Lee, C.; Hedges, J.; Hernes, P.; Peterson, M. Molecular indicators of diagenetic status in marine organic matter. Geochim. Cosmochim. Acta 1997, 61, 5363–5369. [Google Scholar] [CrossRef]
- Eppley, R. Temperature and phytoplankton growth in the sea. Fish. Bull. 1972, 70, 1068–1085. [Google Scholar]
- Sharma, S.; Barrie, L.; Plummer, D.; McConnell, J.; Brickell, P.; Levasseur, M.; Gosselin, M. Flux estimation of oceanic dimethyl sulfide around North America. J. Geophys. Res. 1999, 104, 21327–21342. [Google Scholar] [CrossRef]
- Arrigo, K.; Worthen, D.; Lizotte, M.; Dixon, P.; Dieckmann, G. Primary production in Antarctic sea ice. Science 1997, 276, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.; Gosselin, M.; Kudoh, S.; Robineau, B.; Taguchi, S. DOC and its relationship to algae in bottom ice communities. J. Mar. Syst. 1997, 11, 71–80. [Google Scholar] [CrossRef]
- Thomas, D.; Lara, R.; Eicken, H.; Kattner, G.; Skoog, A. Dissolved organic matter in Arctic multi-year sea ice during winter: Major components and relationship to ice characteristics. Polar Biol. 1995, 15, 477–483. [Google Scholar] [CrossRef]
- Walstra, P. Physical Chemistry of Foods; Marcel Dekker: New York, NY, USA, 2003. [Google Scholar]
- Golden, K.; Ackley, S.; Lytle, V. The percolation phase transition in sea ice. Science 1998, 282, 2238–2241. [Google Scholar] [CrossRef] [PubMed]
- Krembs, C.; Gradinger, R.; Spindler, M. Implications of brine channel geometry and surface area for the interaction of sympagic organisms in Arctic sea ice. J. Exp. Mar. Biol. Ecol. 2000, 243, 55–80. [Google Scholar] [CrossRef]
- Light, B.; Maykut, G.; Grenfell, T. Effects of temperature on the microstructure of first-year Arctic sea ice. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Davies, J.; Rideal, E. Interfacial Phenomena; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Birdi, K. Lipid and Biopolymer Monolayers at Interfaces; Plenum Press: New York, NY, USA, 1989. [Google Scholar]
- Verdugo, P.; Alldredge, A.; Azam, F.; Kirchman, D.; Passow, U.; Santschi, P. The oceanic gel phase: A bridge in the DOM-POM continuum. Mar. Chem. 2004, 92, 67–85. [Google Scholar] [CrossRef]
- Herborg, L.; Thomas, D.; Kennedy, H.; Haas, C.; Dieckmann, G. Dissolved carbohydrates in Antarctic sea ice. Antarct. Sci. 2001, 13, 119–125. [Google Scholar] [CrossRef]
- Arrigo, K.; Dieckmann, G.; Gosselin, M.; Robinson, D.; Fritsen, C.; Sullivan, C. High resolution study of the platelet ice ecosystem in McMurdo Sound, Antarctica: Biomass, nutrient and production profiles within a dense microalgal bloom. Mar. Ecol. Prog. Ser. 1995, 127, 255–268. [Google Scholar] [CrossRef]
- Fasham, M.; Sarmiento, J.; Slater, R.; Ducklow, H.; Williams, R. Ecosystem behavior at Bermuda station “S” and ocean weather station “India”: A general circulation model and observational analysis. Glob. Biogeochem. Cycles 1993, 7, 379–415. [Google Scholar] [CrossRef]
- Sarmiento, J.; Slater, R.; Fasham, M.; Ducklow, H.; Toggweiler, J.; Evans, G. A three dimensional ecosystem model of nitrogen cycling in the North Atlantic euphotic zone. Glob. Biogeochem. Cycles 1993, 7, 417–450. [Google Scholar] [CrossRef]
- Moore, J.; Doney, S.; Kleypas, J.; Glover, D.; Fung, I. Intermediate complexity marine ecosystem model for the global domain. Deep Sea Res. II 2002, 49, 403–462. [Google Scholar] [CrossRef]
- Moore, J.; Lindsay, K.; Doney, S. Upper ocean ecosystem dynamics and iron cycling in a global three dimensional model. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Hassler, C.; Schoemann, V. Bioavailability of organically bound Fe to model phytoplankton of the Southern Ocean. Biogeosciences 2009, 6, 2281–2296. [Google Scholar] [CrossRef]
- Hassler, C.; Schoemann, V.; Nichols, C.; Butler, E.; Boyd, P. Saccharides enhance iron bioavailability to Southern Ocean phytoplankton. Proc. Natl. Acad. Sci. USA 2011, 108, 1076–1081. [Google Scholar] [CrossRef] [PubMed]
- Thomas, D. Iron limitation in the Southern Ocean. Science 2003, 302, 565–566. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Moore, K. Incorporating Phaeocystis into a Southern Ocean ecosystem model. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Robineau, B.; Legendre, L.; Kishino, M.; Kudoh, S. Horizontal heterogeneity of microalgal biomass in the first year ice of Saroma-ko Lagoon (Hokkaido, Japan). J. Mar. Syst. 1997, 11, 81–91. [Google Scholar] [CrossRef]
- Welch, H.; Bergmann, M. Seasonal Development of ice algae and its prediction from environmental factors near Resolute, N.W.T. Canada. Can. J. Fish. Aquat. Sci. 1989, 46, 1793–1804. [Google Scholar] [CrossRef]
- Smith, R.; Anning, J.; Clement, P.; Cota, G. Abundance and production of ice algae in Resolute Passage, Canadian Arctic. Mar. Ecol. Prog. Ser. 1988, 48, 251–263. [Google Scholar] [CrossRef]
- Rysgaard, S.; Kuhl, M.; Glud, R.; Hansen, J. Biomass, production and horizontal patchiness of sea ice algae in a high-Arctic fjord (Young Sound, Greenland). Mar. Ecol. Prog. Ser. 2001, 223, 15–26. [Google Scholar] [CrossRef]
- Gosselin, M.; Levasseur, M.; Wheeler, P.; Horner, R.; Booth, B. New measurements of phytoplankton and ice algal production in the Arctic Ocean. Deep Sea Res. II 1997, 44, 1623–1644. [Google Scholar] [CrossRef]
- Guglielmo, L.; Carrada, G.; Catalano, G.; Dell’Ano, A.; Fabiano, M.; Lazzara, L.; Mangoni, O.; Pusceddu, A.; Saggiomo, V. Structural and functional properties of sympagic communities in the annual sea ice at Terra Nova Bay (Ross Sea, Antarctic). Polar Biol. 2000, 23, 137–146. [Google Scholar] [CrossRef]
- Gregg, W.; Ginoux, P.; Schopf, P.; Casey, N. Phytoplankton and iron: Validation of a global three dimensional ocean biogeochemical model. Deep Sea Res. II 2003, 50, 3143–3169. [Google Scholar] [CrossRef]
- Wells, M. Marine colloids and trace metals. In Biogeochemistry of Dissolved Organic Matter; Hansell, D., Carlson, C., Eds.; Academic Press: New York, NY, USA, 2002; pp. 267–297. [Google Scholar]
- Lizotte, M. Contributions of ice algae to Antarctic marine primary production. Am. Zool. 2001, 41, 57–73. [Google Scholar] [CrossRef]
- Lizotte, M. The microbiology of sea ice. In Sea Ice: An Introduction to its Physics, Chemistry, Biology and Geology; Thomas, D., Dieckmann, G., Eds.; Blackwell Science: London, UK, 2003. [Google Scholar]
- Schoemann, V.; Becquevort, S.; Stefels, J.; Rousseau, V.; Lancelot, C. Phaeocystis blooms in the global ocean and their control mechanisms: A review. J. Sea Res. 2005, 53, 43–66. [Google Scholar] [CrossRef]
- Tagliabue, A.; Bopp, L.; Aumont, O.; Arrigo, K. Influence of light and temperature on the marine iron cycle: From theoretical to global modeling. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
- Christian, J.; Anderson, T. Modeling DOM Biogeochemistry. In Biogeochemistry of Dissolved Organic Matter; Hansell, D., Carlson, C., Eds.; Academic Press: New York, NY, USA, 2002; pp. 717–755. [Google Scholar]
- Lavoie, D.; Macdonald, R.; Denman, K. Primary productivity and export fluxes on the Canadian shelf of the Beaufort Sea: A modeling study. J. Mar. Syst. 2009, 75, 17–32. [Google Scholar] [CrossRef]
- Passow, U.; Alldredge, A.; Logan, B. The role of particulate carbohydrates in the flocculation of diatom blooms. Deep Sea Res. I 1994, 2, 335–397. [Google Scholar] [CrossRef]
- Van Rijssel, M.; Janse, I.; Noordkamp, D.; Gieskes, W. An inventory of factors that affect saccharide production by Phaeocystis globosa. J. Sea Res. 2000, 43, 297–306. [Google Scholar] [CrossRef]
- Pomeroy, L.; Wiebe, W. Temperature and substrates as interactive limiting factors for marine heterotrophic bacteria. Aquat. Microb. Ecol. 2001, 23, 187–204. [Google Scholar] [CrossRef]
- Grossmann, S.; Gleitz, M. Microbial responses to experimental sea-ice formation: Implications for the establishment of Antarctic sea-ice communities. J. Exp. Mar. Biol. Ecol. 1993, 173, 273–289. [Google Scholar] [CrossRef]
- Grossmann, S.; Dieckmann, G. Bacterial standing stock, activity and carbon production during formation and growth of sea ice in the Weddell Sea, Antarctica. Appl. Environ. Microbiol. 1994, 60, 2746–2753. [Google Scholar] [PubMed]
- Nowlin, W.; Klinck, J. The physics of the Antarctic Circumpolar Current. Rev. Geophys. 1986, 24, 469–491. [Google Scholar] [CrossRef]
- Rampal, P.; Weiss, J.; Marsan, D.; Bourgoin, M. Arctic sea ice velocity field: General circulation and turbulent-like fluctuations. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Cox, G.; Weeks, W. Brine Drainage and Initial Salt Entrapment in Sodium Chloride Ice; Res. Rep. 345; U.S. Army, Cold Regions Engineering Laboratory: Hanover, Germany, 1975. [Google Scholar]
- Perovich, D.; Gow, A. A quantitative description of sea ice inclusions. J. Geophys. Res. 1996, 101, 18327–18343. [Google Scholar] [CrossRef]
- Stumm, W.; Morgan, J. Aquatic Chemistry: An Introduction Emphasizing Chemical Equilibria in Natural Waters; Wiley-Interscience: New York, NY, USA, 1981. [Google Scholar]
- Kirst, G.; Wiencke, C. Ecophysiology of polar algae. J. Phycol. 1995, 31, 181–199. [Google Scholar] [CrossRef]
- Eslinger, D.; Cooney, R.; McRoy, C.; Ward, A.; Kline, T.; Simpson, E.; Allen, J. Plankton dynamics: Observed and modeled responses to physical conditions in Prince William Sound, Alaska. Fish. Oceanogr. 2001, 10, 81–96. [Google Scholar] [CrossRef]
- Sarthou, G.; Timmermans, K.; Blain, S.; Treguer, P. Growth physiology and fate of diatoms in the ocean: A review. J. Sea Res. 2005, 53, 25–42. [Google Scholar] [CrossRef]
- Eslinger, D.; Iverson, R. The effects of convective and wind-driven mixing on spring phytoplankton dynamics in the Southeastern Bering Sea middle shelf domain. Cont. Shelf Res. 2001, 21, 627–650. [Google Scholar] [CrossRef]


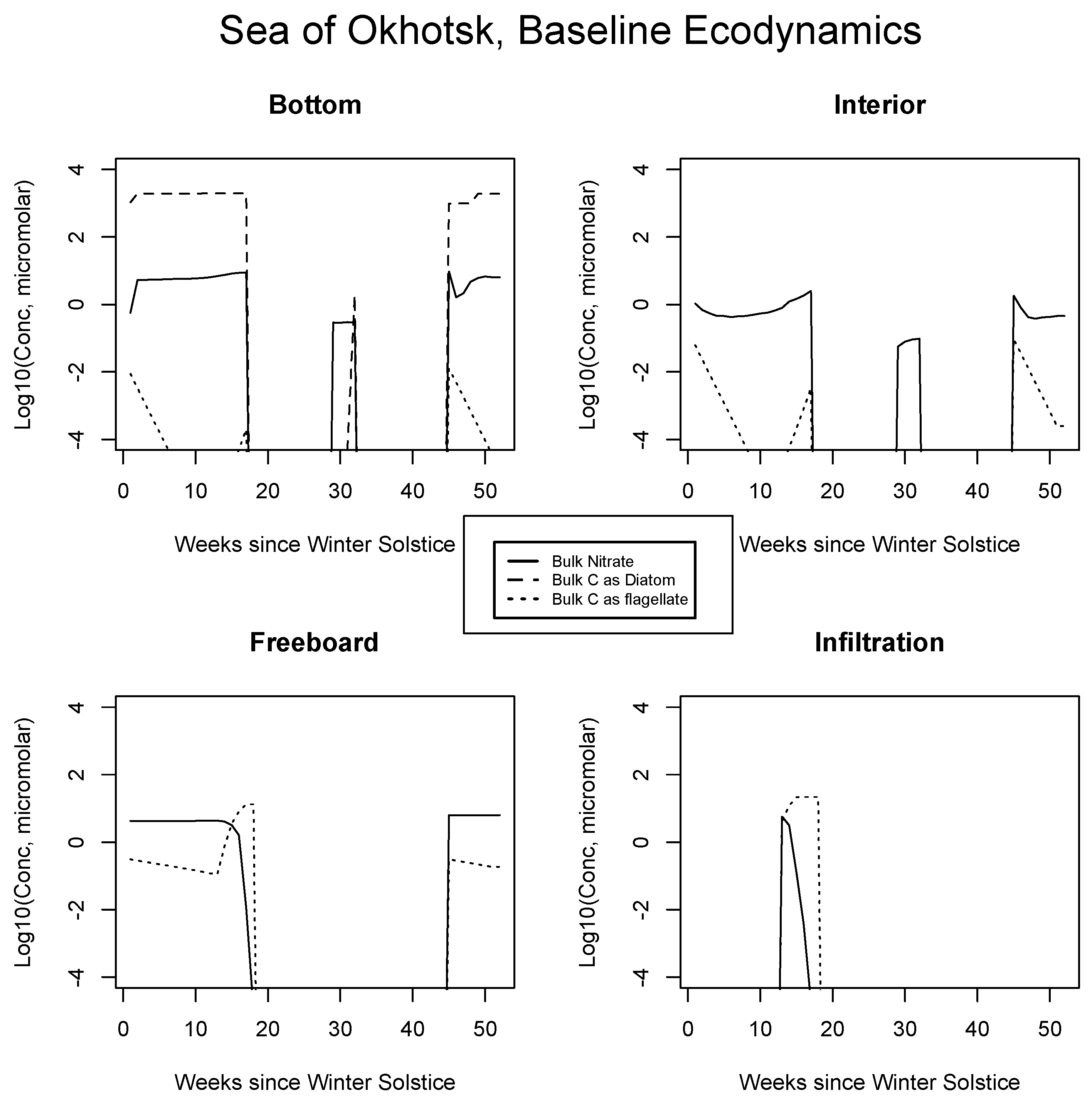
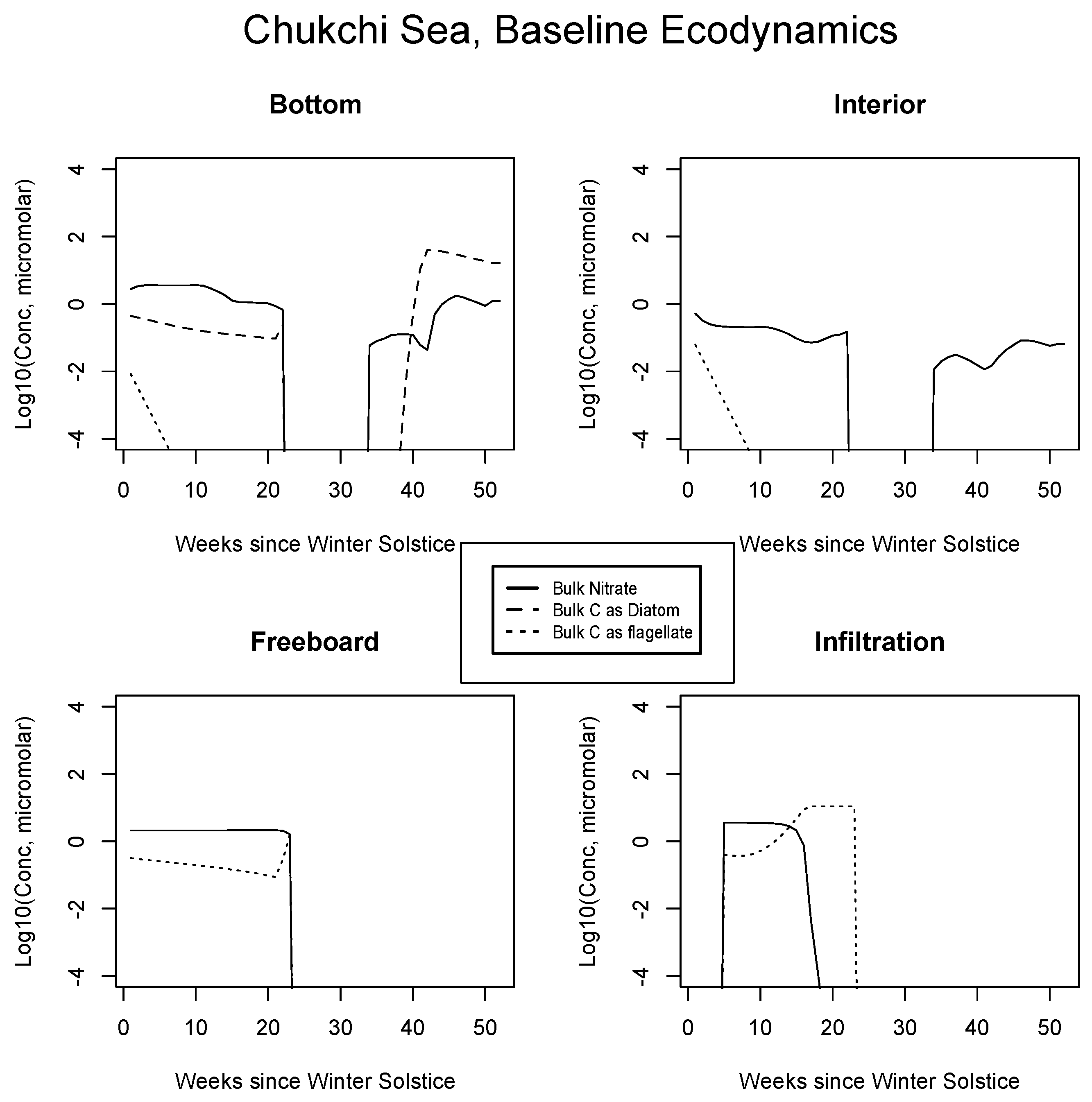
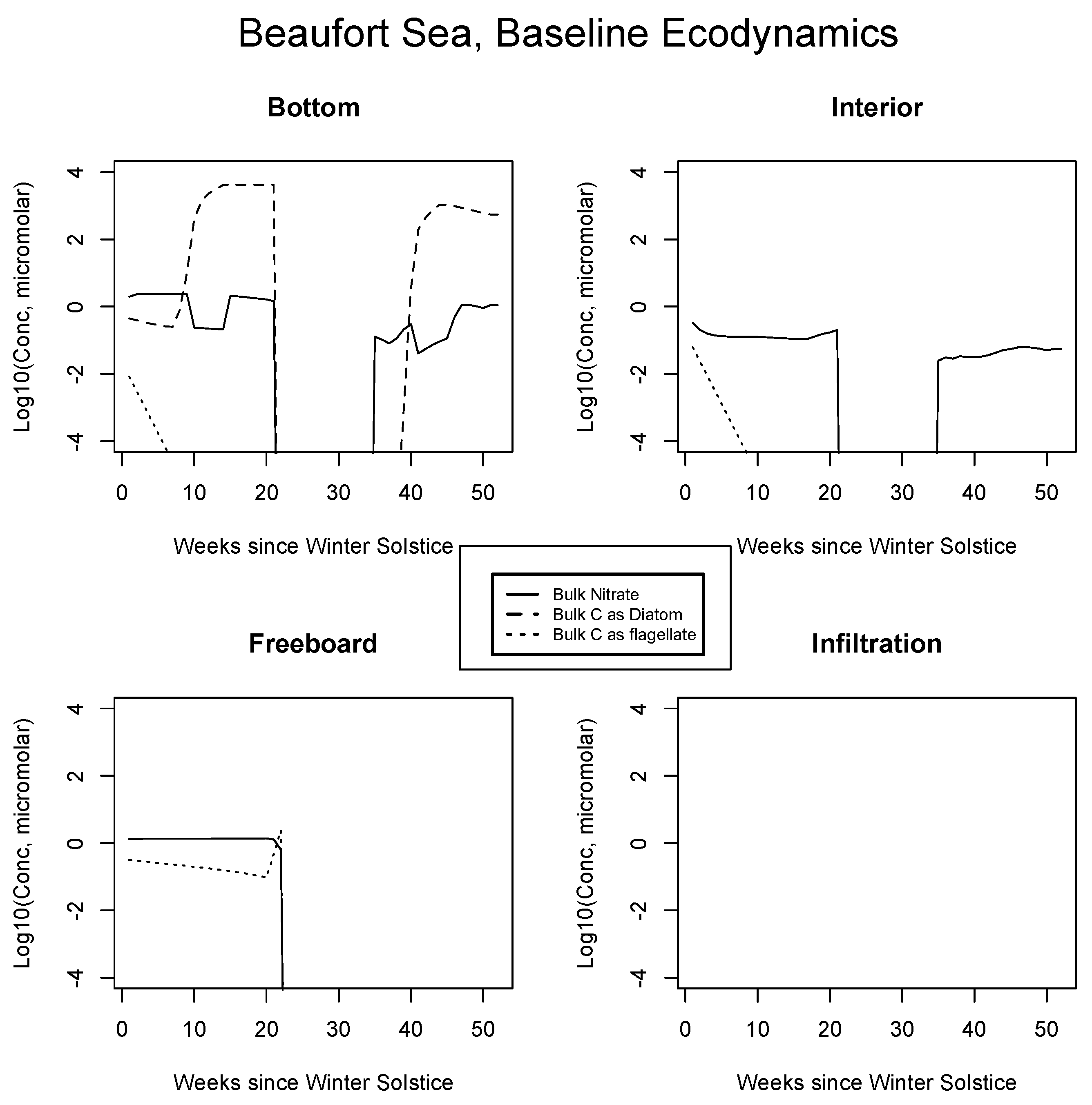
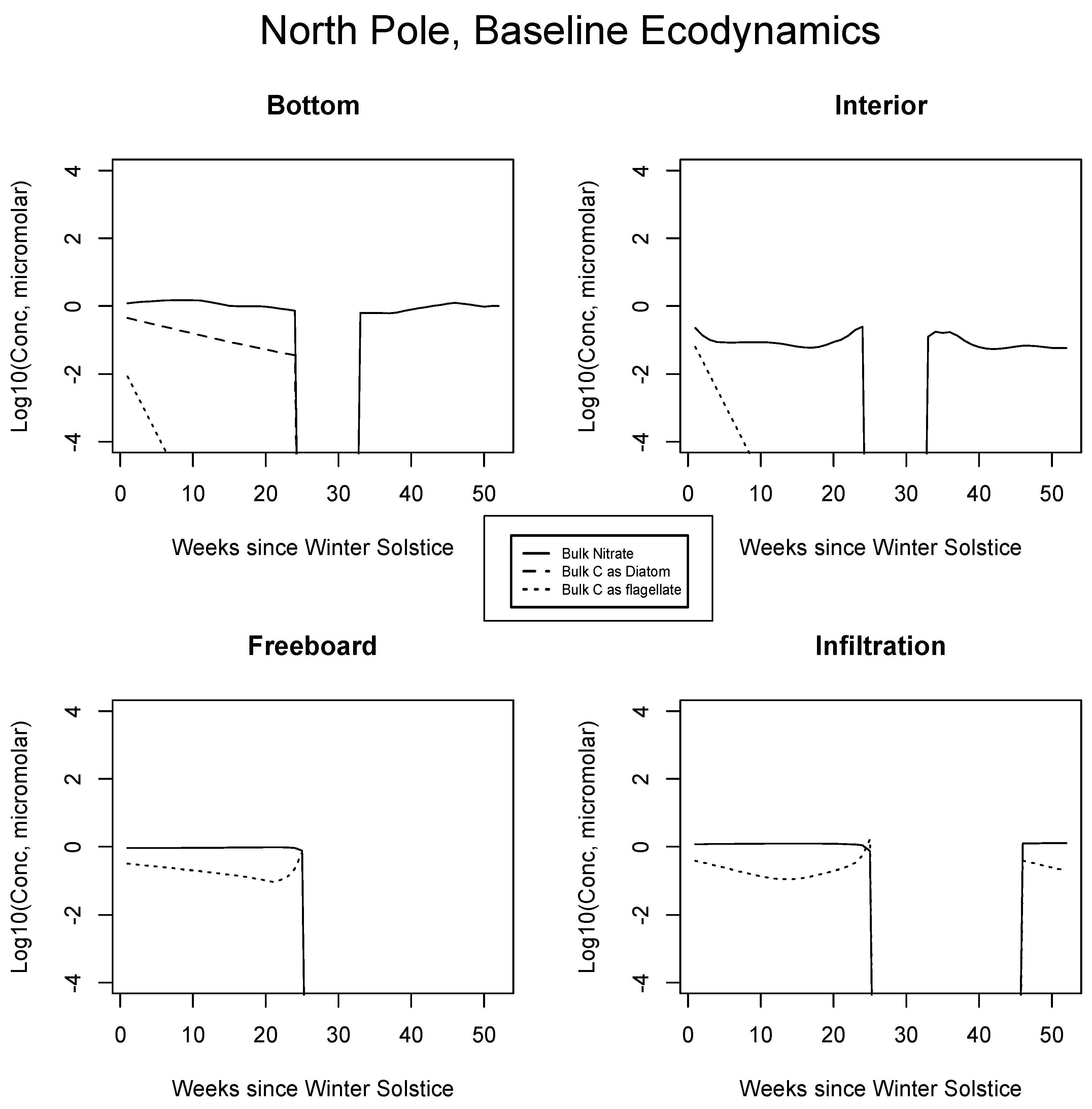
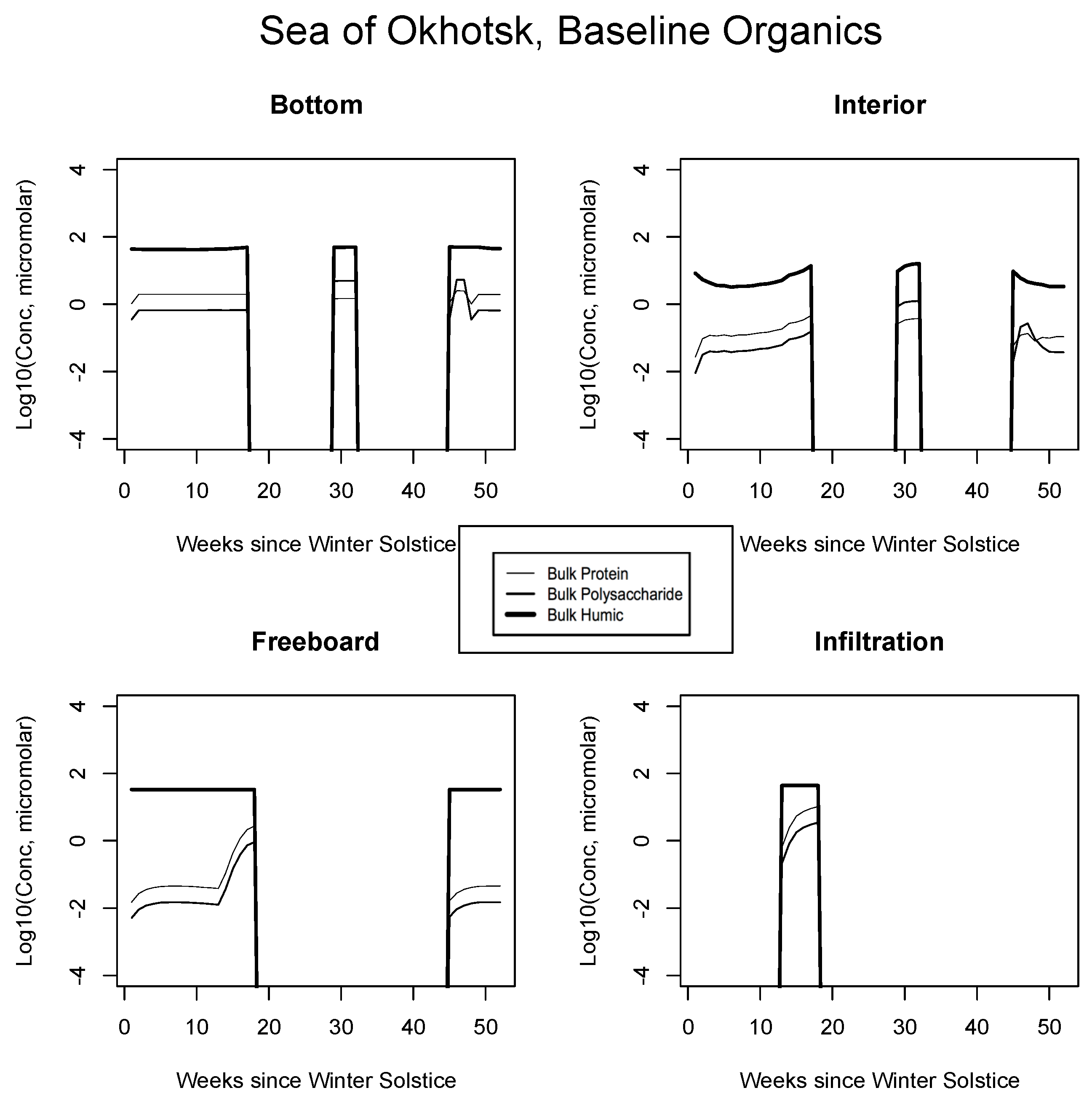
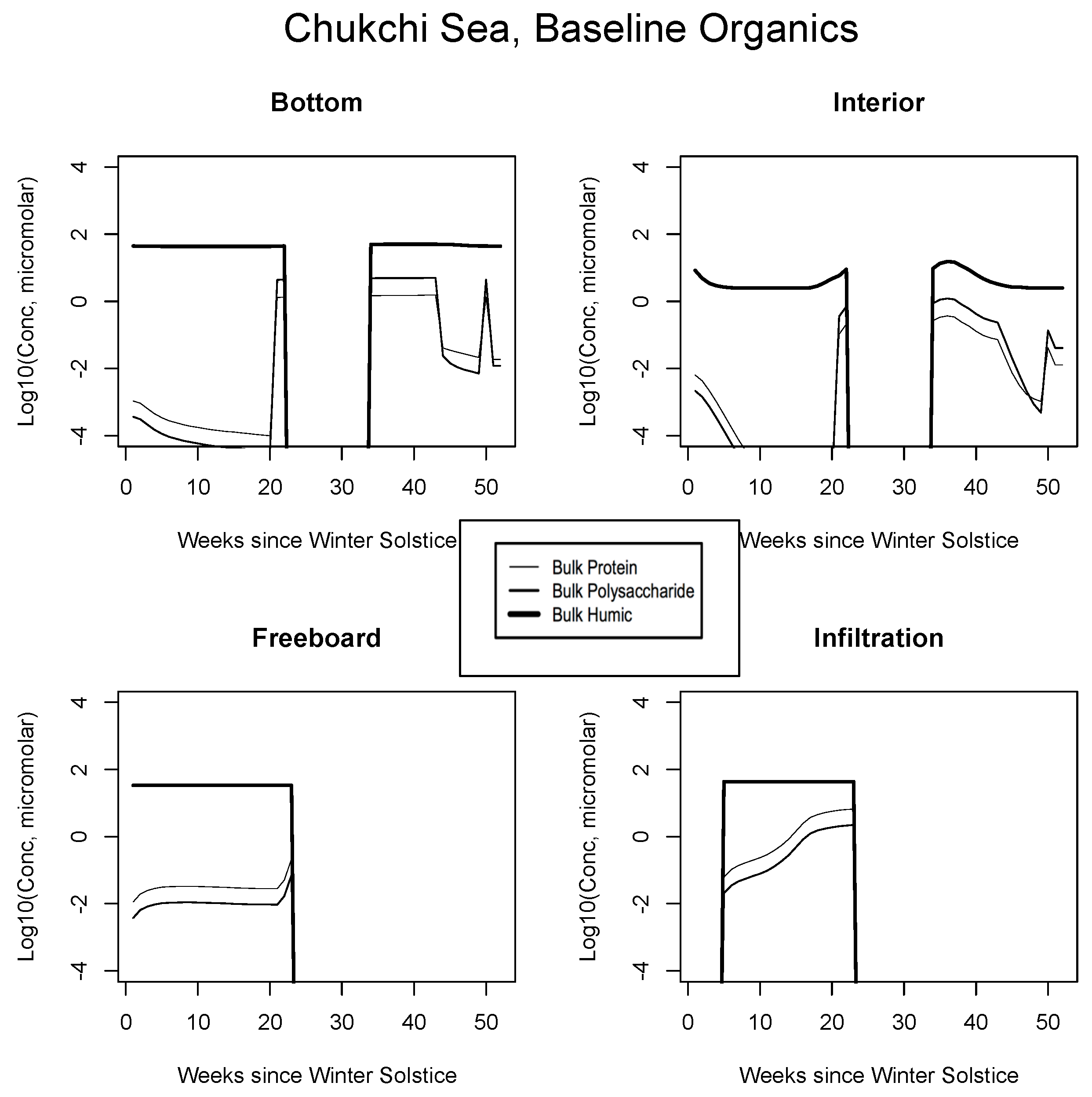
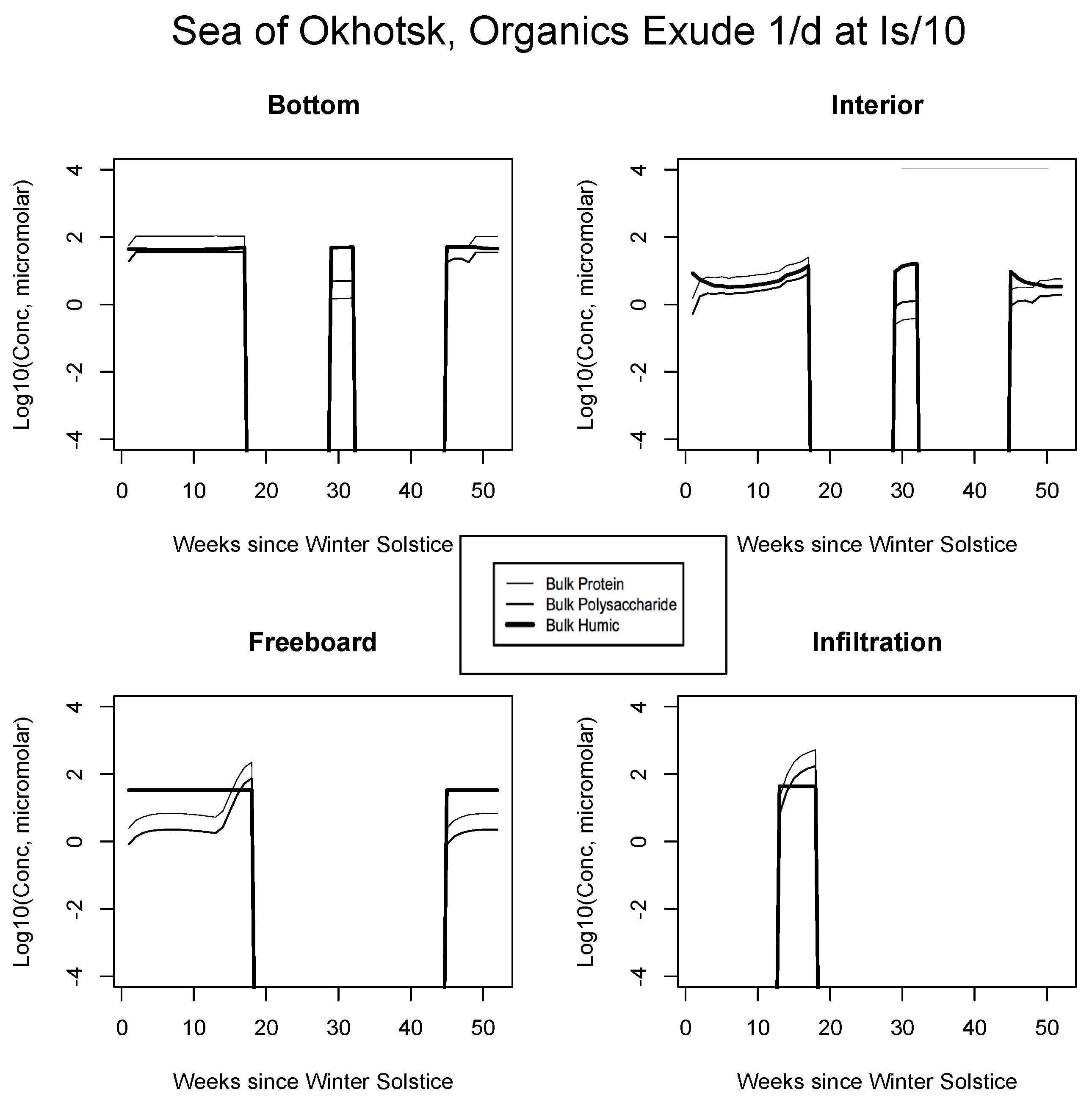
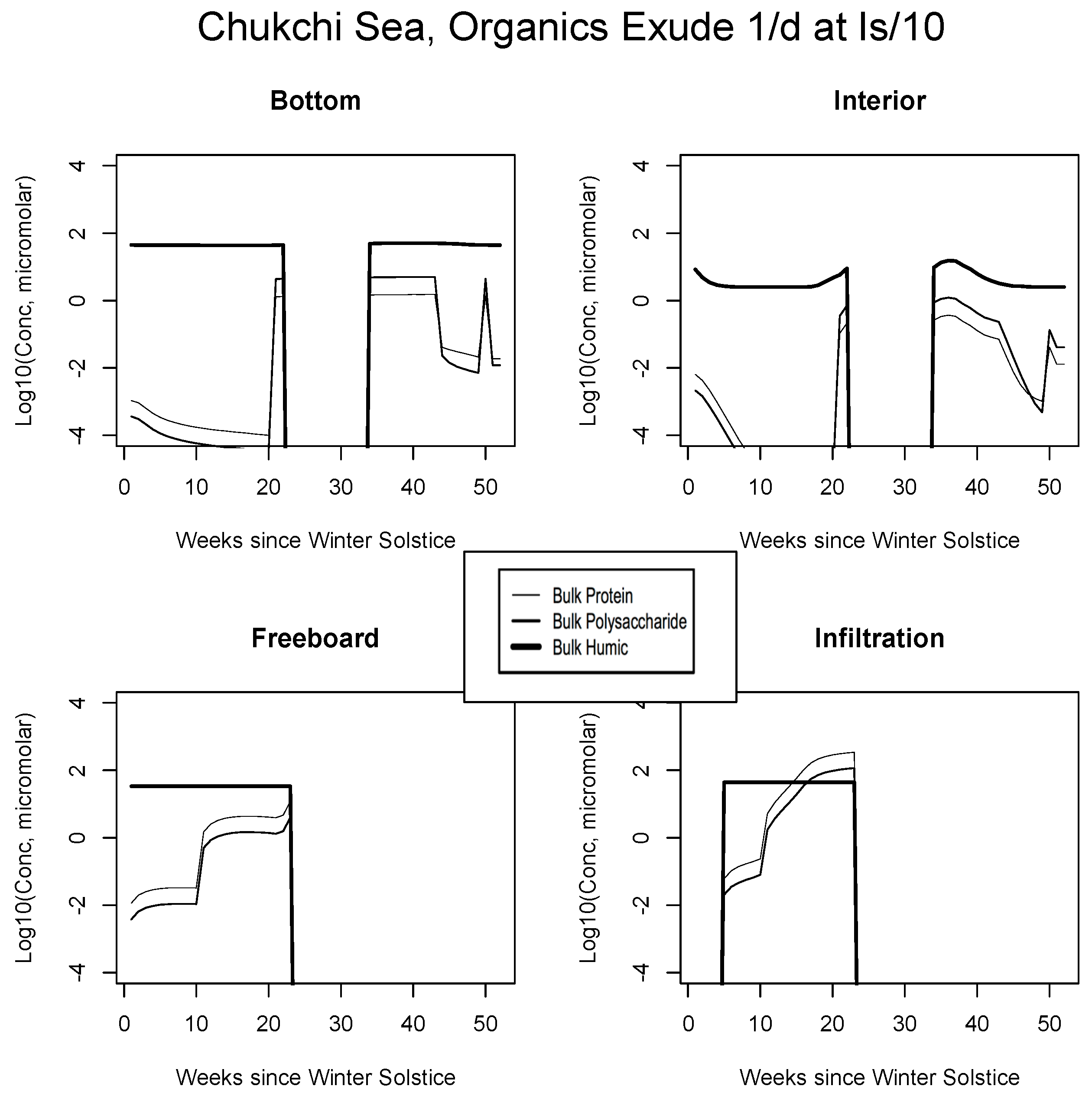
| JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | |
|---|---|---|---|---|---|---|---|---|---|
| Okhotsk | - | - | - | - | - | - | - | - | - |
| Okhotsk | - | - | - | - | - | - | - | - | - |
| Okhotsk | - | 300, 100 | 1000, 500 | - | - | - | - | - | - |
| Bering | - | - | - | - | - | - | - | - | - |
| GIN | - | - | 0, 0 | - | - | - | - | - | - |
| GIN | - | - | 0.3, 10 | - | - | - | - | - | NR, 100 |
| GIN | - | - | 1, 300 | - | - | 10 | - | - | - |
| Barents | - | - | - | - | - | - | - | - | - |
| Kara | - | - | - | - | - | - | - | - | - |
| Siberian | - | - | - | - | - | - | - | - | - |
| Chukchi | - | - | - | - | - | - | - | - | - |
| Chukchi | - | - | - | - | - | - | - | - | - |
| Chukchi | - | - | 100 | 500 | 30 | - | 30 | - | - |
| Beau | - | - | - | - | - | - | - | - | - |
| Beau | - | - | - | - | - | - | - | - | - |
| Beau | - | - | 100 | 500 | 300 | - | - | - | - |
| Arch | - | - | - | - | - | - | - | - | - |
| Arch | - | - | - | - | - | - | - | - | - |
| Arch | - | - | 3 | 1000, 300 | 2000, 3000 | 300 | - | - | - |
| Central | - | - | - | - | - | - | - | - | 0 |
| Central | - | - | - | - | - | - | - | - | 0.3 |
| Central | - | - | - | - | - | - | 30 | 100 | 3 |
| Sources | - | 84 | 71,84,85,103,104 | 71,84 | 25,71,72,84,103–105 | 25,106 | 107 | 107 | 15,41 |
| Zone | Model | Data | ||
|---|---|---|---|---|
| Maximum | Month | Maximum | Month | |
| Okhotsk | 600 | April | 1000 | March |
| Bering | 1100 | May | - | - |
| GIN | NB | - | 10 | June |
| Barents | 500 | June | - | - |
| Kara | 800 | June | - | - |
| Siberian | 60 | June | - | - |
| Chukchi | NB | - | 500 | April |
| Beau | 1200 | May | 500 | April |
| Arch | 900 | June | 2000 | May |
| Central | NB | - | 100 | August |
| Month | Zone | Level | DOC | Protein | Sacch | Lipid | Humic | Source |
|---|---|---|---|---|---|---|---|---|
| March | Chukchi | Top | - | - | 50 | - | - | 20 |
| Chukchi | Interior | - | - | 100 | - | - | ||
| Chukchi | Bottom | - | - | 50 | - | - | ||
| April | Arch | Bottom | 500 | - | 100 | - | - | 4 |
| May | Arch | Bottom | 1000 | - | 500 | - | - | |
| Chukchi | Top | - | - | 250 | - | - | 20 | |
| Chukchi | Interior | - | - | 250 | - | - | ||
| Chukchi | Bottom | - | - | 250 | - | - | ||
| September | GIN | Interior | 100 | 5 | 15 | - | - | 15 |
| Spring & Summer | Antarctic | Top | 100–300 | - | 20 | - | 10 | 7,29,30,60,93,108 |
| Antarctic | Interior | 50–300 | 50 | 50–100 | - | 10 | ||
| Antarctic | Bottom | - | - | - | - | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elliott, S.; Jeffery, N.; Hunke, E.; Deal, C.; Jin, M.; Wang, S.; Elliott Smith, E.; Oestreicher, S. Strategies for the Simulation of Sea Ice Organic Chemistry: Arctic Tests and Development. Geosciences 2017, 7, 52. https://doi.org/10.3390/geosciences7030052
Elliott S, Jeffery N, Hunke E, Deal C, Jin M, Wang S, Elliott Smith E, Oestreicher S. Strategies for the Simulation of Sea Ice Organic Chemistry: Arctic Tests and Development. Geosciences. 2017; 7(3):52. https://doi.org/10.3390/geosciences7030052
Chicago/Turabian StyleElliott, Scott, Nicole Jeffery, Elizabeth Hunke, Clara Deal, Meibing Jin, Shanlin Wang, Emma Elliott Smith, and Samantha Oestreicher. 2017. "Strategies for the Simulation of Sea Ice Organic Chemistry: Arctic Tests and Development" Geosciences 7, no. 3: 52. https://doi.org/10.3390/geosciences7030052
APA StyleElliott, S., Jeffery, N., Hunke, E., Deal, C., Jin, M., Wang, S., Elliott Smith, E., & Oestreicher, S. (2017). Strategies for the Simulation of Sea Ice Organic Chemistry: Arctic Tests and Development. Geosciences, 7(3), 52. https://doi.org/10.3390/geosciences7030052





