Abstract
The paper investigates the superficial layers of an archaeological landscape based on the integration of various remote sensing techniques. It is well known in the literature that shallow depths may be rich in archeological remains, which generate different signal responses depending on the applied technique. In this study three main technologies are examined, namely ground-penetrating radar (GPR), ground spectroscopy, and multispectral satellite imagery. The study aims to propose a methodology to enhance optical remote sensing satellite images, intended for archaeological research, based on the integration of ground based and satellite datasets. For this task, a regression model between the ground spectroradiometer and GPR is established which is then projected to a high resolution sub-meter optical image. The overall methodology consists of nine steps. Beyond the acquirement of the in-situ measurements and their calibration (Steps 1–3), various regression models are examined for more than 70 different vegetation indices (Steps 4–5). The specific data analysis indicated that the red-edge position (REP) hyperspectral index was the most appropriate for developing a local fusion model between ground spectroscopy data and GPR datasets (Step 6), providing comparable results with the in situ GPR measurements (Step 7). Other vegetation indices, such as the normalized difference vegetation index (NDVI), have also been examined, providing significant correlation between the two datasets (R = 0.50). The model is then projected to a high-resolution image over the area of interest (Step 8). The proposed methodology was evaluated with a series of field data collected from the Vésztő-Mágor Tell in the eastern part of Hungary. The results were compared with in situ magnetic gradiometry measurements, indicating common interpretation results. The results were also compatible with the preliminary archaeological investigations of the area (Step 9). The overall outcomes document that fusion models between various types of remote sensing datasets frequently used to support archaeological research can further expand the current capabilities and applications for the detection of buried archaeological remains.
1. Introduction
The scientific field of remote sensing has exhibited great potential over the last years for archaeological investigations, even in challenging environments [1,2,3,4,5,6,7]. Optical and radar satellite datasets have been used to reconstruct the archaeo-environment [8,9], to map recent land use and land cover changes in areas with archaeological interest [10,11,12], to detect traces linked with archaeological remains [13,14] or even to investigate spatial patterns between archaeological sites [15].
The integration of various remote sensing data has attracted the interest of scholars. For instance, in [16,17], the potential use of multispectral satellite images and archive aerial imageries with ground geophysical prospection was demonstrated over the same archaeological area. In addition, Morehart [18] has exploited various forms of landscape information like historic records and maps together with archive aerial images, and medium- and high-resolution satellite multispectral datasets, in order to study and identify buried features. Others have applied a multi-disciplinary study in the area of the Vésztő-Mágor tell, Hungary, using archive aerial images, high resolution multispectral datasets, ground spectroscopy and geophysics to reconstruct pre-historic landscapes [16].
Despite the wide use of various such non-invasive remote sensing techniques, these are frequently employed separately. Indeed, in most cases the different processed and geocoded remote sensing data were inserted in a Geographical Information System (GIS), followed by simple superimposition of the diverse ortho-rectified datasets for visual and/or semi-automatic multilayer analysis (e.g., [8,9,19,20]). Some studies have also presented interesting results on data integration and fusion by employing quantitative means for multiple data sources [21,22,23,24,25]. Some other similar cases studies related to the exploitation of multi-sensor data for archaeological research can be found in [24,25].
The synthesis and interpretation of the overall results from the different remote sensing sensors help researchers to identify “hot spots” which can be considered as potential archaeological targets. Table 1 summarizes some of the most basic advantages and limitations of the three remote sensing methods used here: (a) satellite datasets; (b) ground-penetrating radar (GPR) and (c) ground spectroscopy. The table provides basic attributes of these methods, such as spatial resolution and spectral range; spatial extent; potential extraction of 3D underground information; soil penetration, and the capability to use archive datasets. It is therefore understood that none of these technologies can be considered as “ideal” for archaeological research. For instance, high-resolution multispectral images can see beyond the visible part of the spectrum and therefore detect vegetation anomalies but at the same time their spatial resolution (e.g., 0.5 m in the panchromatic band) can be problematic for identification of small-scale localized buried features. In contrast, ground spectroscopy can be used to collect “accurate” spectral signatures (ground truth) for small targets with limited spatial extent. The GPR method is the only one of the three methods that penetrates the upper layers of ground surface and produces a 3D reconstruction of the underground targets with increased spatial resolution.

Table 1.
General characteristics of satellite remote sensing; ground-penetrating radar (GPR) and ground spectroscopy for archaeological research.
2. Aims
Buried archaeological remains can have a different response to the backscattering signal captured by the various remote sensing sensors, which are used either on top of the ground surface or located in a distance (Figure 1). For example, both satellite images and ground spectral signatures have the capability to record the vegetation status over archaeological landscapes and therefore sense any vegetation-stressed conditions. This vegetation stress formed due to the presence of buried archaeological remains (known in the archaeological research as “crop marks phenomenon”), is detectable in the near infrared part of the electromagnetic spectrum (i.e., passive sensors). This indirect approach allows researchers to “examine” the upper layers of the archaeological context (up to 0.50 m below the surface) without any real penetration as occurs with active sensors like GPR.
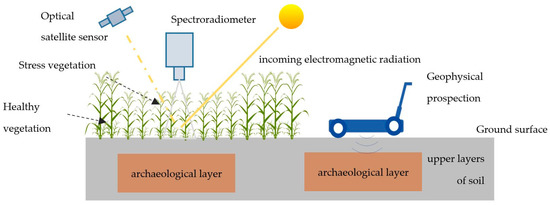
Figure 1.
Detection of buried remains either using an indirect method (left, passive sensors) or a direct method (right, active sensors). The first category can include both satellite and ground spectroradiometer measurements (i.e., reflectance values in several bands) over cultivated areas where vegetation stress is used as a proxy for the presence of buried archaeological remains in the upper layers of soil. In contrast, direct methods such as GPR can penetrate soil and record the backscattering signal.
Since each remote sensing technique uses different technology, their results can provide useful but still partial information regarding the concealed archaeological remains. Thus, the integration of various technologies is considered as a key step towards the holistic understanding of the landscape. However, the fusion and integration of data gathered from different sensors is quite challenging. Although some fusion techniques already exist, like pan-sharpening between multi-spectral and panchromatic bands of the same or different satellite sensors [26,27], or as more recently shown, fusion between archive greyscale and recent multispectral satellite images [28], fusion methodologies of more diverse datasets need to be developed and tested for archaeological research. Studies have shown that it is feasible to scale-up ground spectroradiometric data (i.e., ground spectral signatures) to existing [29] or even forthcoming satellite sensors [30].
This study aims to go a step forward by investigating the integration of ground spectroradiometric and GPR data, based on a fusion regression model and then projected to a high resolution optical image. The result is an enhanced optical satellite image capable of improving the initial raw satellite information.
3. Methodology
The enhancement of the final satellite image was based exploring three different datasets: (a) a high-resolution GeoEye image with spatial resolution of 50 cm; (b) ground hyperspectral signatures collected from the GER-1500 spectroradiometer (Spectra Vista Corporation, New York, NY, USA ) with a spectral range between 350–1050 nm (Visible-Near Infrared spectrum) and (c) GPR measurements with a 250 MHz antenna. Both GER-1500 and GPR measurements were collected moving along parallel transects 0.5 m apart with 5 cm sampling along the lines. The ground spectroradiometer and GPR data have been used to develop the local fusion regression model.
All the datasets have undergone the initial pre-processing steps: geometric and radiometric corrections have been applied to the GeoEye image, while during the collection of the ground spectral signatures, sun irradiance was measured using a calibrated spectralon panel. The latter allows us to standardize the results and minimize the sun illumination noise. More details regarding the different datasets and their result can be found in [16,31]. The methodology applied consists of nine (9) steps, described in Figure 2.
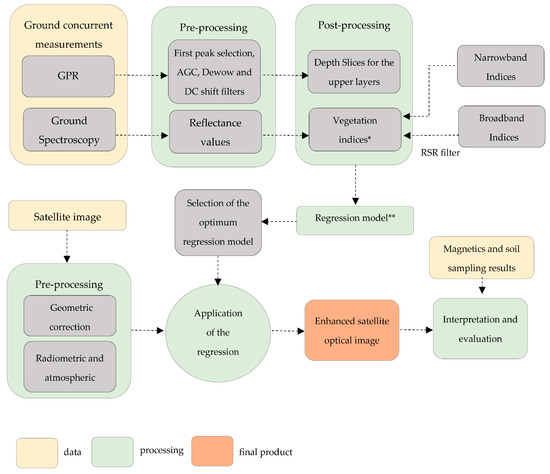
Figure 2.
Overall proposed methodology for the enhancement of the optical remote sensing image based on the application of the fusion regression model between the ground data gathered from GPR and ground spectroscopy (* see Supplementary Table S1; ** see Table 2). RSR: relative spectral response; AGC: Automatic Gain Control; DC: Direct Current.
Step 1 is with regard to the collection of ground remote sensing data over an archaeological area of interest. GPR and spectroradiometric measurements have been collected concurrently to minimize any background noise from climatic changes such as rainfall, humidity etc. These datasets were then processed separately using standard techniques which are described in more detail in [16] (Step 2). Several filters have been applied for the GPR measurements, while hyperspectral reflectance values with a 1 nm interval have been calculated based on the incoming and backscattering radiance values. The following step (Step 3) employs the calculation of the broadband reflectance values of the selected satellite sensor (i.e., GeoEye-1) using its relative spectral response (RSR) filter (see more in [16]). The RSR filter is used as the band-average relative spectral radiance response of the specific sensor. As is known, each satellite sensor has its own RSR filter which describes the capability of the sensor to capture the electromagnetic radiation. The calculation of vegetation indices, including both the broadband (i.e., based on multispectral bands—Step 3) and narrowband (i.e., based on hyperspectral bands—Step 2) reflectance values is performed in Step 4. Overall, 71 vegetation indices have been estimated upon the equations shown in the Supplementary Table S1 (see also more details in [32]). The next step (Step 5) considers the regression analysis between these 71 vegetation indices and the GPR measurements for the upper layers of soil (i.e., 0.00–0.60 m). In detail, linear; exponential; Fourier; Gaussian; polynomial (second–third order); power; rational and sum of sin regression models have been evaluated. In the various regression models the GPR measurements were considered as the independent X variable, while the vegetation indices (from the spectroradiometer) were considered as the dependent Y variable. Based on the regression analysis (Pearson correlation coefficient—R) the optimum fusion model was selected (Step 6). Before the application of the selected model to the satellite image (Step 8), an evaluation of the proposed model was performed over the common area of interest using the ground data (see Step 7). Finally, the overall results are evaluated (Step 9). It should be mentioned that the proposed enhancement technique to the GeoEye-1 image or in any other satellite image is easily applicable to any GIS environment using raster calculators.
4. Case Study: The Vésztő-Mágor Tell
The Vésztő-Mágor Tell is located in the southeastern Great Hungarian Plain, at a latitude of 46°56′24.36″ and longitude of 21°12′32.67″ (Figure 3). The tell covers about 4.25 hectares and rises to a height of about 9 m above mean sea level. A monastery on top of the tell was the main focus of the archaeological excavations that were initiated in 1968. Excavations revealed cultural layers dated from the Late Middle Neolithic period continuing until the Late Neolithic period (ca. 5000–4600 B.C). After the Late Neolithic (Tisza Culture) the site was abandoned to be reoccupied in the Early Copper Age (Tiszapolgár Culture). Habitation of the settlement continued until the Early/Middle Bronze Age (Gyulavarsánd Culture) with a small interruption during the end of the Middle Copper Age [33,34,35,36]. In the 11th century AD a church and then a monastery of the Csolt-clan were established on the Vésztő-Mágor Tell. The monastery continued to operate until the end of the 14th century, while the two towers of the church were standing until 1798. During the early 19th century, the monastery, which was constructed at the southern part of the tell was completely destroyed by the operations carried out during the construction works of a wine cellar [33,35,37]. Since the 1980s the site has been one of the Hungarian National Parks.
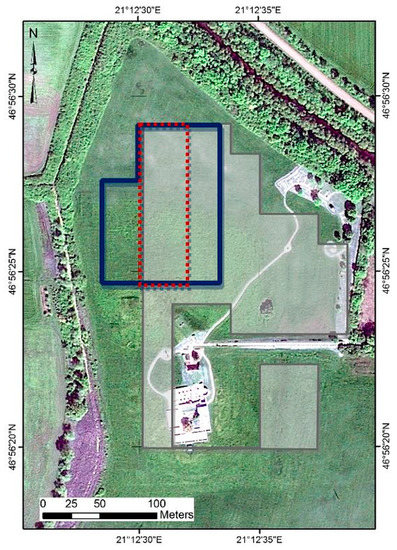
Figure 3.
Area covered from the different techniques: Grey and blue polygons indicate the areas covered from the geophysical surveys (magnetic and GPRsurvey, respectively), the red polygon indicates the area covered from the ground spectroradiometric measurements while the whole area is covered by the GeoEye image (no polygon used) (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84).
The area was intensively investigated in the previous years as part of the Körös Regional Archaeological Project [38] with various non-invasive techniques aiming to reconstruct the organization of Neolithic tell-based settlements of Vésztő-Mágor and Szeghalom-Kovácshalom. These techniques included intensive, gridded and surface collections as well as magnetometry, ground-penetrating radar, electrical resistance tomography, hyperspectral spectroradiometry, and soil chemistry. Based on the stylistic attributes of the recovered ceramics, it appears that the tell at Vésztő-Mágor was inhabited during the Neolithic period, possibly for several centuries [38].
The area covered by ground spectroscopy is indicated in Figure 3 with red dashed polygon, while geophysical surveys from GPR and magnetic methods are shown with blue and grey polygons, respectively. Measurements taken from ground spectroradiometer and GPR were used to set up the model (see Steps 1 and 5).
5. Results
5.1. Results from GPR and Spectroradiometer
Details regarding the overall results of the in-situ investigation around the Vésztő-Mágor tell can be found in [16]. Sometimes similar interpretations were noticeable, for instance the NDVI—as calculated from the ground spectroradiometer—with the first GPR depth slice of 0.00–0.20 m below ground surface (Figure 4). Indeed, a linear anomaly at around 80 m in the Y-axis (indicated with red arrow in Figure 4) was highlighted by both techniques. This feature is supposed to be part of a ditch which surrounded the tell (see more in [38]). In the GPR depth slice of Figure 4 (right) positive waveform values indicate that the polarity of the signal is same as the incident wave, or negative if the polarity of the reflected wave is opposite to the incident wave.
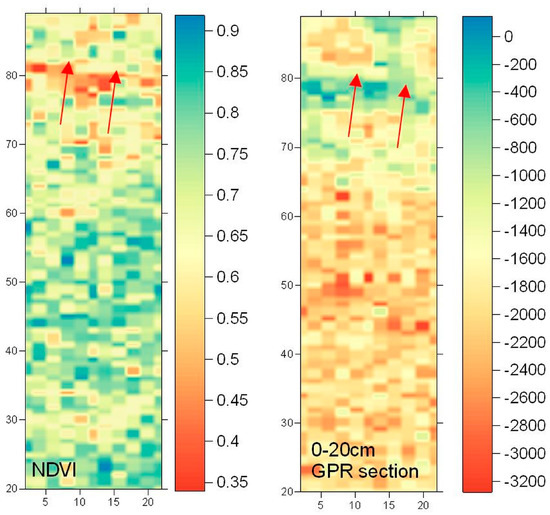
Figure 4.
The normalized difference vegetation index (NDVI) as calculated from the ground spectroradiometer over the red area of Figure 3 (left) and the first depth slice (i.e., 0.00–0.20 m below ground surface) from the GPR measurements. A linear anomaly, indicated with red arrows, at around 80 m of the Y-axis was detected by both methodologies.
GPR sensor could penetrate up to a depth of 2 m below ground surface, providing 10 depth slices, each with a thickness of 20 cm. The GPR slices with increasing depth were created after the application of the first peak selection; AGC (Automatic Gain Control), Dewow and DC (Direct Current ) shift filters were used to amplify the average signal amplitude and remove the initial DC bias. A velocity of 0.1 m/ns for the transmission of the electromagnetic waves (250 MHz antennas) was assumed based on the hyperbola fitting. GPR interpretation can be very complicated since each slice should be treated separately, but at the same time the overall interpretation is linked with the archaeological context of the site. As shown in Figure 5, scatterplots between the first depth slice of the GPR (0–20 cm below the ground surface) and the last depth slices beyond the 1 m depth, are completely uncorrelated. Pearson correlation coefficient (R) starting from top of the surface until a depth of 2 m is shown in Table 2. The R value was selected to be shown (instead of R square) since the aim was to identify any existing correlation between the two datasets. The upper layers of soil, which are considered as the “optimum depth” for indirect methods such as satellite images and ground spectroscopy, are indicated in the first row (i.e., 0.00–0.60 m) of Figure 5.
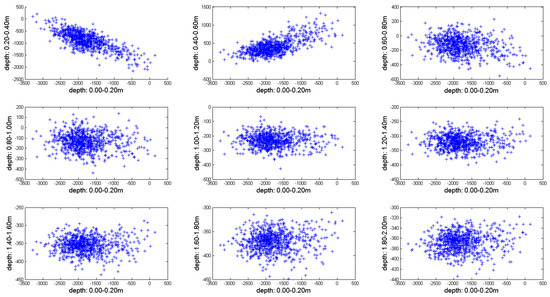
Figure 5.
Scatterplots of the first slice of the GPR results (i.e., depth 0.00–0.20 m below ground surface) against the rest of the depth slices of thickness 0.20 m until 2.00 m below ground surface. The Pearson correlation coefficient starting from the top of the surface to a 2 m depth was estimated as −0.74 for the slice 0.20–0.40 m; 0.67 for the slice 0.40–0.60 m; −0.22 for the slice 0.60–0.80 m; −0.07 for the slice 0.80–1.00 m; −0.04 for the slice 1.00–1.20 m; −0.01 for the slice 1.20–1.40 m; 0.03 for the slice 1.40–1.60 m; 0.06 for the slice 1.60–1.80 m and 0.10 for the slice 1.80–2.00 m. The upper layers of soil (i.e. 0.00–0.80 m) are shown in the first row.

Table 2.
The Pearson correlation coefficient (R) starting from top of the surface down to a 2 m depth for GPR results of the first slice compared to the rest of the slices.
Similarly, Figure 6 presents the scatterplot of the NDVI index against the GPR measurements for various depth slices. It is noticeable that the variance of the data in the slices representing depths larger than 0.80 m below ground surface is increasing. The R value from this analysis is shown in Table 3. The variance observed in Figure 6 is linked to the fact that both NDVI and GPR results are influenced by different factors: on one hand NDVI indicates vegetation status on top of the surface, while on the other hand GPR results depend on the electromagnetic properties of the underground targets and the surrounding soil. Figure 6 also demonstrates the difficulty in achieving a high correlation regression model between different remote sensing datasets even though the spectroradiometer and GPR measurements have been acquired concurrently over the same area and in the same conditions.
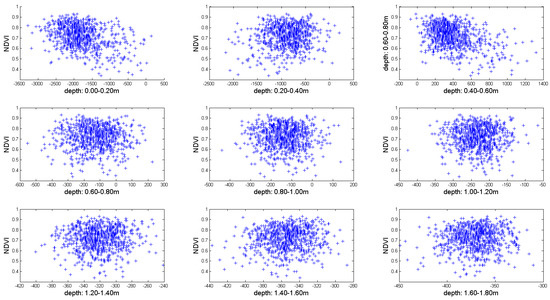
Figure 6.
Scatterplots of the NDVI index against the 10 depth slices with a width 0.20 to 2 m below ground surface. The Pearson correlation coefficient of the NDVI compared to the GPR measurements starting from top of the surface to a depth of 1.80 meters was estimated as −0.35 for the slice 0.00–0.20 m; 0.12 for the slice 20–0.40 m; −0.39 for the slice 0.40–0.60 m; −0.01 for the slice 0.60–0.80 m; −0.03 for the slice 0.80–1.00 m; 0.01 for the slice 1.00–1.20 m; 0.05 for the slice 1.20–1.40 m; 0.08 for the slice 1.40–1.60 m and 0.05 for the slice 1.60–1.80 m. The upper layers of soil (i.e. 0.00–0.80 m) are shown in the first row.

Table 3.
The Pearson correlation coefficient (R) starting from top of the surface until a 2 m depth between GPR results and the NDVI.
5.2. Setting up the Local Regression Model for the Enchacement of the Optical Data
In order to find an “optimum” fusion model between the spectroradiometric and the GPR measurements, the first three upper layers corresponding to a depth up to 0.60 m have been used. The GPR measurements and the various vegetation indices mentioned in the Supplementary Table S1 (including also the Vis—NIR bands) were correlated with the following mathematical models shown in Table 4:

Table 4.
General mathematical equations used for the regression model between the spectroradiometric measurements and the different GPR amplitude value slices.
The Pearson correlation coefficient (R) was estimated for each combination (i.e., 10 slices of GPR × 71 vegetation indices and four spectral bands). The final analysis indicated that the linear model (Model 1 of Table 4), despite its simplicity, performed superior results compared to the rest of the mathematical models mentioned in Table 4. Some of them showed very low performance (e.g., power models, numbers 10–11 of Table 4) and therefore could not assist towards the aims of this study.
Table 5 displays the Pearson correlation coefficient (R) results of the linear regression model (Model 1 of Table 5) for each vegetation index (see Table S1) and depth slice (up to 0.80 m). Below this depth, the coefficient was found to be extremely low (R → 0.00). Within the first three depths of GPR slices (i.e., depth range 0.00–0.60 m, “optimum depth” for the passive remote sensing techniques) a higher Pearson correlation coefficient (R) (up to almost R = 0.5) is recorded, which indicates that a regression model between the optical images and geophysical measurements can be established. Among the various vegetation indices examined, it seems that the red-edge position (REP) index (Equation (37), of Table S1) is the most suitable for use, at least for this linear correlation and for the specific depth between the two datasets. However, the REP (hyperspectral) index cannot be applied to multispectral and high spatial resolution sensors such as the GeoEye. On the contrary, the broadband NDVI index, which has also provided some promising results for a couple of surface depth slices, is more applicable to these sensors.

Table 5.
The results of the Pearson correlation coefficient (R) with range of −1 to +1 for each vegetation index and for each depth slice (up to 0.80 m) for the linear regression model. Higher correlation (either negative or positive) is highlighted in the table.
5.3. Comparison of the Fusion Model from the Spectroradiometric Measurements with the GPR Results
Based on the previous findings a linear enhancement was applied to the spectroradiometric data using the REP and NDVI results. The first three columns of Figure 7 demonstrate the original GPR depth slices for the upper layers of soil (range from 0.0 to 0.60 m depth) which have been collected over the area indicated with red polygon at Figure 3, while the next six columns of Figure 7 show the enhanced images derived from the linear regression models after the REP and NDVI indices. All the results of Figure 7 share the same range as the original GPR measurements for direct visual comparison. The interpolation between the point samples of the GPR measurements and enhanced spectroradiometric results was performed using the kriging method.
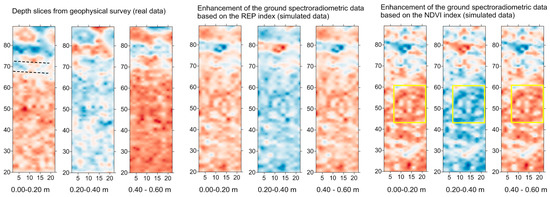
Figure 7.
First three columns from the left: GPR real data for the upper layer of soil (depth from 0.0–0.6 m); next three columns: enhanced results generated from the red-edge position (REP) regression model; the last three columns: enhanced results generated from the NDVI regression model. The two parallel linear features are indicated in the first column while some circular false positive marks are indicated within the yellow sqaure in the NDVI regression results (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84).
Enhanced images derived from the REP index tend to give generally very comparative interpretation results with the actual GPR section for the upper layers of soil. Enhanced images below this “optimum” depth (i.e., >0.60 m below ground surface) cannot be considered reliable as shown earlier from the correlation coefficient and therefore these results are not demonstrated here. The linear anomaly indicated in the first upper layers of the GPR section at around 80 m in the Y-axis (see dashed parallel lines in the first image of Figure 7) is also visible in the enhanced vegetation image generated from the REP index. According to the GPR data, this anomaly seems to consist of two parallel features, about 2 m apart, running in a west to east direction [16]. This feature has been hypothesized to belong to the north boundary of the old monastery’s yard which acted possibly as Neolithic fortifications ditches [38].
Similar interpretation results between the original GPR data and the enhanced NDVI sections are also observed for the first three depth slices (i.e., 0.0–0.60 m depth). Again, the results are very poor below this “optimum” depth. Some circular “false positive” marks were also observed at around 50 m in the Y-axis of the enhanced NDVI images for all slices (see Figure 7, yellow squares). Overall, the results and especially those originated by the employment of the REP index, are found to be very promising in enabling the enhancement of the optical remote sensing data.
5.4. Application to the Vésztő-Mágor Tell Case Study
The final steps (Steps 8 and 9 of the overall methodology) refer to the application of the regression model to a satellite imagery. Due to current limitations (i.e., spatial resolution) of existing hyperspectral satellite sensors—such as the Earth Observing (EO)-1 Hyperion sensor with 30 meters of spatial resolution—the projection of any fusion model generated from hyperspectral vegetation index—like the REP index—is still restricted. In contrast, fusion models generated from broadband vegetation indices—such as the NDVI index—can be applied to high resolution multispectral images. A GeoEye image was selected since the spatial resolution of the sensor (0.50 m) is similar to the ground transects applied for both GPR and spectroradiometric measurements. The Red Green Blue (RGB) composite of the GeoEye image is shown in Figure 8a, while the overall results from the GPR and magnetic prospection are shown in Figure 8b,c, respectively. Figure 8d is an enhanced NVDI image after the linear regression model was applied to the GeoEye image (shown in Figure 8a). Some linear features have been already identified from the GPR prospection in the northern part of the site, while other anomalies have been also detected around the old monastery’s yard (see more about the geophysical results in references [16,38]). Magnetic survey, GPR and soil coring suggest that the Vésztő-Mágor tell may have been surrounded by a system of three large ditches and palisades, with a possible entrance in the northwest. Preliminary coring into the linear anomalies also suggests that some of the ditches may exceed 4 m in depth. Structural similarities with other Neolithic fortifications led archaeologists to suspect that part of the ditch and palisade system at the Vésztő-Mágor Tell was established during this period. The number of geophysical anomalies located outside the ditch and palisade system drops dramatically, suggesting that the Late Neolithic occupations were restricted to the tell itself (i.e., no evidence for a surrounding settlement around the tell), and a substantial horizontal settlement was not established in the surrounding area [38].
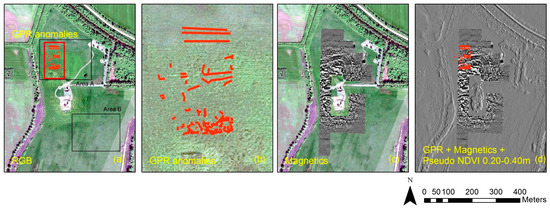
Figure 8.
(a) GeoEye image shown in the RGB composite; (b) GPR anomalies results; (c) magnetic prospection results and (d) enhanced NDVI image for the upper layer between 0.20–0.40 m below the surface, overlaid with GPR and magnetic results (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84). Two areas (Area A and Area B) have been selected for further interpretation (see Figure 12).
A comparison between the enhanced NDVI images and the magnetic prospection results is provided in Figure 9. The magnetic data after despiking and equalization of dynamic range lay in the range of ±15 nT/m. Figure 9a,b shows the overall results from the magnetic prospection and the interpretation of the magnetic anomalies, respectively (see more in [16]). The NDVI index derived from the GeoEye image is presented in Figure 9c. The next figure (Figure 9d) presents the enhanced NDVI image for the upper layer between 0.00 and 0.20 m below ground surface, derived from the linear regression model. The latest image can provide additional information compared to the initial NDVI image. Linear features on the north of the Tell (part of the large ditches and palisades acting as fortification of the Tell?) are clearly identified in the enhanced image (Figure 9d) as well as in the magnetic results (Figure 9b). The eastern part of the same feature and other circular features on the southern part are also noticeable. It should be mentioned that this region was explored in past by excavations. All these features, indicated with arrows in Figure 9d, are aligned with the magnetometer results and the rest of the non-invasive techniques applied in the area around the Tell. Of course, magnetic results provide more details and visible results compared to the enhanced NDVI image, since the correlation results and the regression model could explain only a portion of the in-situ geophysical measurements. It should be mentioned that similar outcomes (features) have been also spotted in the following slices (i.e., 0.20–0.60 m) thus permitting all this information to be used for extracting the 3D profile of the hidden features.

Figure 9.
(a) Magnetic prospection results around the Vésztő-Mágor Tell (see more in [14,36]); (b) interpretation results of the magnetic prospection (see more in [16,38]); (c) raw NDVI image and (d) enhanced NDVI image for the upper layers at 0.00–0.20 m below the surface. Linear and circular features in correspondence to the 8b interpretation are indicated with yellow arrows (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84).
It is important to stress the advantages of the proposed methodology in relation to the standard interpretation of the satellite images. As seen in the RGB GeoEye and the NDVI images (Figure 8a and Figure 9c respectively), the interpretation results of these images are limited, while only a small part can be detected through interpretation process (e.g., part of the lower circular feature south to the tell in Figure 9c). In contrast, the enhanced NDVI image overcomes these interpretation limitations, providing additional information for the area around the Vésztő-Mágor Tell.
In order to further improve the interpretation of the enhanced NDVI images, pseudo color composites and spatial filters have been also applied. Figure 10, shows the pseudo RGB color composite of the enhanced NDVI image for three different slices (i.e., 0.00–0.60 m below surface, with a 20 cm depth interval). The pseudo RGB color composite could enhance further the results derived from the individual NDVI enhanced image. As revealed, several linear and circular features found near the Tell are detectible and in line with the magnetometer interpretation results (see Figure 9b). The southern and eastern fortification ditches (?), with an either linear or circular ground plan (shown with yellow arrows in Figure 9), are outlined due to their different contrast from the surrounding area. Other anomalies with lower contrast values on the northern part of the Tell can also be noticed, especially a feature which is linked to a path or wall going to the north and then running to the west, nowadays invisible. Based on the geophysical prospection results these are signs of the surrounding ditches of the Tell which become visible from the reflective signals of the GPR and in a relative good correlation to the magnetic results. Figure 11, presents the same pseudo RGB color composite as in Figure 10, superimposed to a Sobel spatial filter image. The latest filter has been applied for the most top upper layer of soil (i.e., 0.00–0.20 m). A Sobel filter can improve the enhancement of various edges, detected in the images and therefore can be used to advance the interpretation practice. The gain of this approach, in addition to enhancing the above-mentioned anomalies, is that it allows for capture of the linear anomaly on the north of the Tell which was not detected before (i.e., in Figure 10). According to the GPR data this anomaly seems to consist of two parallel features, about 2 m apart, running in the direction west to east.

Figure 10.
Pseudo RGB composite of the enhanced NDVI images for three different slices of the “optimum” depth (i.e., 0.00–0.60 m below the surface). Linear and circular features in correspondence to the 8b interpretation are indicated with yellow arrows (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84).

Figure 11.
Pseudo RGB composite of the enhanced NDVI images for three different slices of the “optimum” depth (i.e., 0.00–0.60 m below surface) superimposed to a Sobel spatial filter applied to the most top upper layer of soil. Linear and circular features, in correspondence to the 8b interpretation, are indicated with yellow arrows (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84).
The Sobel spatial filter was also found to be very useful in enhancing other linear features around the Vésztő-Mágor tell. Figure 12 demonstrates this application with specific focus on two areas (see Area A and Area B in Figure 8). The Sobel filter could minimize the background noise, and enhance some of the most prominent edges of the image. Slices below the “optimum” depth (i.e., >0.60 m depth) bear much noise (see Figure 12, slice 0.60–0.80 m) and therefore are difficult to be interpreted. In contrast, the upper layers of soil (i.e., 0.00–0.60 m) have revealed some linear and circular features. While a good contrast can be observed in the most top layer of soil (i.e., 0.00–0.20 m) of Figure 12, this is decreasing as we move lower in depth (i.e., similar findings with the model 1 of Table 4). However, for the next two slices (i.e., 0.20–0.60 m) some linear features are still visible, as indicated with the arrows of Figure 12. It should be mentioned that these features go beyond the area of investigation of the geophysical prospection, providing therefore some additional “hot spot” areas for future investigations.

Figure 12.
Enhanced images using the NDVI index for the slices between 0.00 and 0.80 m below the ground surface after the application of the Sobel filter. Top: Focus on the northern area (Area A) for each depth. Bottom: Focus on the southern area (Area B) for each depth. Area A and Area B are indicated in Figure 8 (Latitude: 46°56′24.36″; Longitude: 21°12′32.67″, WGS84).
6. Discussion
The proposed methodology aims to enhance optical satellite data intended for archaeological research based on the integration of different remote sensing datasets. The proposed regression approach provided acceptable but not completely satisfactory results. Evidently, there are many considerations regarding the regression model and some of the most important ones are discussed here. Essentially, when the regression model is established between the ground data and then projected to the satellite image (or part of this image) it is normally considered that the areas have similar context (i.e., same soil properties; same archaeological findings etc.). However, this is only an assumption, which is not always valid. The proposed enhanced methodology can provide more reliable results in cases were the archaeological background knowledge permits us to assume a relatively “homogenous” area. In addition, as the results of Figure 7 indicated, someone should proceed with caution when interoperating the data as the enhancement processing might provide false positive alarms or by-products of the processing (e.g., the linear anomaly observed in Figure 7 at around 50 m from NDVI model). Moreover, it is also expected that reflectance values (either from satellite image or calculated from the spectroradiometer) have good correlation with the geophysical prospection measurements. This is only valid if either crop or soil marks can be detected from the reflectance values for the “optimum” depth. Therefore, a correlation threshold between the optical and active data (i.e., geophysical measurements) can be set by the researchers to avoid any potential errors.
Additionally, the correlations between GPR and the vegetation indices from the ground data seem to vary with each depth but nonetheless each regression model in this “optimum” depth is a linear function of the input optical data. Therefore, as a linear enhancement, the generated enhanced optical image can only improve the initial optical image and its information. Of course, this is a usual limitation for any other enhancement technique including also the vegetation indices. Moreover, GPR variations that are not already in the optical image, and therefore cannot be explained by the regression model, cannot be mapped in the enhanced optical image.
Concerning the collection of ground data, both spectroradiometer and GPR sensors have been collected simultaneously to eliminate the influence (i.e., noise) from other external factors (mainly climatic changes i.e., rainfall). Though this limits the applicability of the proposed technique, future research is expected to be carried by the authors in proposing an “image-based” regression model. It is expected that noise which will be recorded within these regression models will be removed by setting gains and offset values.
Most important is the fact that such enhanced methodology should be a primary step prior to a larger archaeolandscape analysis, and not the final “model”. As for every fusion, this technique will only work well in the case where both techniques produce satisfactory results. The purpose of enhanced techniques is primarily to identify “hot spot” areas where ground truth data (i.e., geophysical prospection) can take place. However, regression models—such as those discussed here—allow scientists to exploit the current capabilities of optical remote sensing to detect buried relics. Given the fact that such approach is quite new, further developments can additionally improve the final outcomes and provide more reliable results.
7. Conclusions
This paper discusses an approach applicable to any existing high-resolution satellite sensor in order to enhance image interpretation for the detection of hidden archaeological remains. The overall methodology consists of nine steps, with the most significant ones being those determining the optimum “regression” model based on the ground data (Steps 5 and 6).
The linear regression model developed in this study for the “optimum depth”, was found to be the most encouraging (with Pearson coefficient up to almost 50%), providing promising results especially when elaborating the various hyperspectral indices (see Figure 7, REP index). Even though such high resolution hyperspectral datasets are not currently available, the use of airborne/ unmanned aerial vehicles (UAVs) equipped with small hyperspectral sensors could be a reliable alternative solution. The proposed approach can be also applied in areas that have been partially examined through geophysical prospection in the past. In this case, these (archive) results can be further exploited for developing regression models and for calibration purposes in order to examine a wider area of interest. As in this case study presented here, archaeological excavations that will be carried out in the area can be used as a “calibration factor” to improve and enhance further the results.
Despite its simplicity, the linear regression model was found to be the most appropriate for the integration between the two datasets, which can be used for the enhancement of the satellite image. The application of the regression models in several satellite images acquired during different periods and therefore in different phenological stages of the crops can improve the interpretation for the detection of buried archaeological remains.
The final outcomes have demonstrated that further enhancement of optical remote sensing data is feasible, contributing in the prospection of archaeological targets. Nevertheless, additional experiments are expected to be carried out under different environmental conditions (e.g., climate and soil characteristics) and employing different satellite datasets. This will allow us to maximize its possible use as a supporting tool to archaeological investigation using also more advanced mathematical models such as machine learning and neural networks.
Supplementary Materials
The following are available online at www.mdpi.com/2076-3263/7/2/40/s1, Table S1: Vegetation indices applied in the study (see more details in [32]).
Acknowledgments
The present communication is under the “ATHENA” project H2020-TWINN2015 of European Commission. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 691936. The fieldwork campaign was supported by USA-NSF (U.S.-Hungarian-Greek Collaborative International Research Experience for Students on Origins and Development of Prehistoric European Villages) and the Wenner-Gren Foundation (International Collaborative Research Grant, “Early Village Social Dynamics: Prehistoric Settlement Nucleation on the Great Hungarian Plain”). William A. Parkinson, Richard W. Yerkes, Attila Gyucha and Paul R. Duffy provided their expertise and support in the fieldwork activities.
Author Contributions
Athos Agapiou conceived and performed the regression experiments; Vasiliki Lysandrou contributed to the interpretation of the regression model and its projection to the satellite image. Apostolos Sarris and Nikos Papadopoulos described the study area and performed the geophysical prospection. All authors have contributed to the interpretation of the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lasaponara, R.; Masini, N. Satellite remote sensing in archaeology: Past, present and future perspectives. J. Archaeol. Sci. 2011, 38, 1995–2002. [Google Scholar] [CrossRef]
- Giardino, J.M. A history of NASA remote sensing contributions to archaeology. J. Archaeol. Sci. 2011, 38, 2003–2009. [Google Scholar] [CrossRef]
- Agapiou, Α.; Lysandrou, V. Remote sensing archaeology: Tracking and mapping evolution in European scientific literature from 1999 to 2015. J. Archaeol. Sci. Rep. 2015, 4, 192–200. [Google Scholar] [CrossRef]
- Keay, J.S.; Parcak, H.S.; Strutt, D.K. High resolution space and ground-based remote sensing and implications for landscape archaeology: The case from Portus, Italy. J. Archaeol. Sci. 2014, 52, 277–292. [Google Scholar] [CrossRef]
- Reinhold, S.; Belinskiy, A.; Korobov, D. Caucasia top-down: Remote sensing data for survey in a high altitude mountain landscape. Quat. Int. 2016, 402, 46–60. [Google Scholar] [CrossRef]
- Barone, M.P.; Desibio, L. A remote sensing approach to understanding the archaeological potential: the case study of some Roman evidence in Umbria (Italy). Int. J. Archaeol. 2015, 3, 37–44. [Google Scholar] [CrossRef]
- Barone, M.P.; Desibio, L. Landscape archaeology of southern Umbria (Italy) using the GPR technique. In Proceedings of the 2015 8th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Florence, Italy, 7–10 July 2015. [Google Scholar]
- Alexakis, D.; Sarris, A.; Astaras, T.; Albanakis, Κ. Detection of neolithic settlements in thessaly (Greece) through multispectral and hyperspectral satellite imagery. Sensors 2009, 9, 1167–1187. [Google Scholar] [CrossRef] [PubMed]
- Alexakis, A.; Sarris, A.; Astaras, T.; Albanakis, K. Integrated GIS, remote sensing and geomorphologic approaches for the reconstruction of the landscape habitation of Thessaly during the Neolithic period. J. Archaeol. Sci. 2011, 38, 89–100. [Google Scholar] [CrossRef]
- Banerjee, R.; Srivastava, K.P. Reconstruction of contested landscape: Detecting land cover transformation hosting cultural heritage sites from Central India using remote sensing. Land Use Policy 2013, 34, 193–203. [Google Scholar] [CrossRef]
- Agapiou, A.; Alexakis, D.D.; Lysandrou, V.; Sarris, A.; Cuca, B.; Themistocleous, K.; Hadjimitsis, D.G. Impact of Urban Sprawl to archaeological research: the case study of Paphos area in Cyprus. J. Cult. Herit. 2015, 16, 671–680. [Google Scholar] [CrossRef]
- Cerra, D.; Plank, S.; Lysandrou, V.; Tian, J. Cultural Heritage Sites in Danger—Towards Automatic Damage Detection from Space. Remote Sens. 2016, 8, 781. [Google Scholar] [CrossRef]
- Chen, F.; Lasaponara, R.; Masini, N. An Overview of Satellite Synthetic Aperture Radar Remote Sensing in Archaeology: From Site Detection to Monitoring. J. Cult. Herit. 2017, 23, 5–11. [Google Scholar] [CrossRef]
- Stek, D.T. Drones over Mediterranean landscapes. The potential of small UAV's (drones) for site detection and heritage management in archaeological survey projects: A case study from Le Pianelle in the Tappino Valley, Molise (Italy). J. Cult. Herit. 2016, 22, 1066–1071. [Google Scholar] [CrossRef]
- Siart, C.; Eitel, B.; Panagiotopoulos, D. Investigation of past archaeological landscapes using remote sensing and GIS: a multi-method case study from Mount Ida, Crete. J. Archaeol. Sci. 2008, 35, 2918–2926. [Google Scholar] [CrossRef]
- Sarris, A.; Papadopoulos, N.; Agapiou, A.; Salvi, M.C.; Hadjimitsis, D.G.; Parkinson, A.; Yerkes, R.W.; Gyucha, A.; Duffy, R.P. Integration of geophysical surveys, ground hyperspectral measurements, aerial and satellite imagery for archaeological prospection of prehistoric sites: The case study of Vésztő-Mágor Tell, Hungary. J. Archaeol. Sci. 2013, 40, 1454–1470. [Google Scholar] [CrossRef]
- Malfitana, D.; Leucci, G.; Fragalà, G.; Masini, N.; Scardozzi, G.; Cacciaguerra, G.; Santagati, C.; Shehi, E. The potential of integrated GPR survey and aerial photographic analysis of historic urban areas: A case study and digital reconstruction of a Late Roman villa in Durrës (Albania). J. Archaeol. Sci. Rep. 2015, 4, 276–284. [Google Scholar] [CrossRef]
- Morehart, C.T. Mapping ancient chinampa landscapes in the Basin of Mexico: A remote sensing and GIS approach. J. Archaeol. Sci. 2012, 39, 2541–2551. [Google Scholar] [CrossRef]
- Traviglia, A.; Cottica, D. Remote sensing applications and archaeological research in the Northern Lagoon of Venice: the case of the lost settlement of Constanciacus. J. Archaeol. Sci. 2011, 38, 2040–2050. [Google Scholar] [CrossRef]
- Gallo, D.; Ciminale, M.; Becker, H.; Masini, N. Remote sensing techniques for reconstructing a vast Neolithic settlement in Southern Italy. J. Archaeol. Sci. 2009, 36, 43–50. [Google Scholar] [CrossRef]
- Keay, S.; Earl, G.; Hay, S.; Kay, S.; Ogden, J.; Strutt, K.D. The role of integrated survey methods in the assessment of archaeological landscapes: the case of Portus. Archaeol. Prospect. 2009, 15, 154–166. [Google Scholar] [CrossRef]
- Ciminale, M.; Gallo, D.; Lasaponara, R.; Masini, N. A multiscale approach for reconstructing archaeological landscapes: Applications in northern Apulia (Italy). Archaeol. Prospect. 2009, 16, 143–153. [Google Scholar] [CrossRef]
- Piro, S.; Mauriello, P.; Cammarano, F. Quantitative integration of geophysical methods for archaeological prospection. Archaeol. Prospect. 2000, 7, 203–213. [Google Scholar] [CrossRef]
- Kvamme, K.L. Integrating Multidimensional Geophysical Data. Archaeol. Prospect. 2006, 13, 57–72. [Google Scholar] [CrossRef]
- Kvamme, K.; Ernenwein, E.; Hargrave, M.; Sever, T.; Harmon, D.; Limp, F. New Approaches to the Use and Integration of Multi-Sensor Remote Sensing for Historic Resource. Identification and Evaluation, Report of SERDP Project, SI-1263, University of Arkansas, Center for Advanced Spatial Technologies. 10 November 2006. Available online: http://s3.amazonaws.com/academia.edu.documents/10387950/si-1263-part1.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&Expires=1496724950&Signature=BKPfKdlCCLxJ9Q%2BoU30JtrM3MP8%3D&response-content-disposition=inline%3B%20filename%3DNew_Approaches_to_the_Use_and_Integratio.pdf (accessed on 6 June 2017).
- Aiazzi, B.; Baronti, S.; Lotti, F.; Selva, M. A comparison between global and context-adaptive pansharpening of multispectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 302–306. [Google Scholar] [CrossRef]
- Garzelli, A. Pansharpening of Multispectral Images Based on Nonlocal Parameter Optimization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2096–2107. [Google Scholar] [CrossRef]
- Agapiou, A.; Alexakis, D.D.; Sarris, A.; Hadjimitsis, D.G. Colour to grayscale pixels: Re-seeing grayscale archived aerial photographs and declassified satellite CORONA images based on image fusion techniques. Archaeol. Prospect. 2016, 23, 231–241. [Google Scholar] [CrossRef]
- Schaepman, E.M.; Ustin, L.S.; Plaza, J.A.; Painter, H.T.; Verrelst, J.; Liang, S. Earth system science related imaging spectroscopy—An assessment. Remote Sens. Environ. 2009, 113, S123–S137. [Google Scholar] [CrossRef]
- Agapiou, A.; Alexakis, D.D.; Sarris, A.; Hadjimitsis, D.G. Evaluating the potentials of Sentinel-2 for archaeological perspective. Remote Sens. 2014, 6, 2176–2194. [Google Scholar] [CrossRef]
- Agapiou, A.; Sarris, A.; Papadopoulos, N.; Alexakis, D.D.; Hadjimitsis, D.G. 3D pseudo GPR sections based on NDVI values: Fusion of optical and active remote sensing techniques at the Vészto-Mágor tell, Hungary. In Archaeological Research in the Digital Age, Proceedings of the 1st Conference on Computer Applications and Quantitative Methods in Archaeology Greek Chapter (CAA-GR), Rethymno Crete, Greece, 6–8 March 2014; Papadopoulos, C., Paliou, E., Chrysanthi, A., Kotoula, E., Sarris, A., Eds.; Institute for Mediterranean Studies-Foundation of Research and Technology (IMS-Forth): Rethymno, Greece, 2015. [Google Scholar]
- Agapiou, A.; Hadjimitsis, D.G.; Alexakis, D.D. Evaluation of broadband and narrowband vegetation indices for the identification of archaeological crop marks. Remote Sens. 2012, 4, 3892–3919. [Google Scholar] [CrossRef]
- Hegedűs, K. Vésztő-Mágori-domb. In Magyarország Régészeti Topográfiája VI. Békés Megye Régészeti Topográfiája: A Szeghalmi Járás 1982 IV/1; Ecsedy, I., Kovács, L., Maráz, B., Torma, I., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1982; pp. 184–185. (In Hungarian) [Google Scholar]
- Hegedűs, K.; Makkay, J. Vésztő-Mágor: A Settlement of the Tisza Culture. In The Late Neolithic of the Tisza Region: A Survey of Recent Excavations and their Findings; Tálas, L., Raczky, P, Eds.; Szolnok County Museums: Budapest-Szolnok, Hungary, 1987; pp. 85–104. [Google Scholar]
- Makkay, J. Vésztő–Mágor. Ásatás a szülőföldön. Békés Megyei Múzeumok Igazgatósága, Békéscsaba. 2004. Available online: http://mek.oszk.hu/07600/07616/07616.pdf (accessed on 6 June 2017).
- Parkinson, W.A. Tribal boundaries: Stylistic variability and social boundary maintenance during the transition to the Copper Age on the Great Hungarian Plain. J. Anthropol. Archaeol. 2006, 25, 33–58. [Google Scholar] [CrossRef]
- Juhász, I. A Csolt nemzetség monostora. In A középkori Dél-Alföld és Szer; Kollár, T., Ed.; pp. 281–304. Available online: http://opac.regesta-imperii.de/lang_en/anzeige.php?sammelwerk=A+k%C3%B6z%C3%A9pkori+D%C3%A9l-Alf%C3%B6ld+%C3%A9s+Szer (accessed on 6 June 2017).
- Gyucha, A.; Yerkes, W.R.; Parkinson, A.W.; Sarris, A.; Papadopoulos, N.; Duffy, R.P.; Salisbury, B.R. Settlement Nucleation in the Neolithic: A Preliminary Report of the Körös Regional Archaeological Project’s Investigations at Szeghalom-Kovácshalom and Vésztő-Mágor. In Neolithic and Copper Age between the Carpathians and the Aegean Sea: Chronologies and Technologies from the 6th to the 4th Millennium BCE. International Workshop Budapest 2012; Hansen, S., Raczky, P., Anders, A., Reingruber, A., Eds.; Habelt-Verlag: Bonn, Germany, 2015; pp. 129–142. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).