Gibbs Free Energy of Formation for Selected Platinum Group Minerals (PGM)

Abstract

Thermodynamic data for platinum group (Os, Ir, Ru, Rh, Pd and Pt) minerals are very limited. The present study is focused on the calculation of the Gibbs free energy of formation (Δ_fG°) for selected PGM occurring in layered intrusions and ophiolite complexes worldwide, applying available experimental data on their constituent elements at their standard state (ΔG = G_(species) − ΔG_(elements)), using the computer program HSC Chemistry software 6.0. The evaluation of the accuracy of the calculation method was made by the calculation of (ΔG_f) of rhodium sulfide phases. The calculated values were found to be in good agreement with those measured in the binary system (Rh + S) as a function of temperature by previous authors (Jacob and Gupta (2014). The calculated Gibbs free energy (Δ_fG°) followed the order RuS₂ < (Ir,Os)S₂ < (Pt, Pd)S < (Pd, Pt)Te₂, increasing from compatible to incompatible noble metals and from sulfides to tellurides.

1. Introduction

The platinumgroup elements Os, Ir, Ru, Rh, Pd and Pt (PGE) are among the most valuable elements in nature with strategic importance, due to their growing use in advanced technologies and automobile catalyst converters. Platinum groupelements (PGE) can be classified into two subgroups: the Os-, Ir-, Ru-rich or IPGE (more refractory) and PPGE (low-melting and more soluble) (Ir group), interpreted to reflect compatible behavior (partition or distribution coefficient between solid and magma, D ≥ 1) during large-degree mantle melting and (Pt, Pd)-rich or PPGE assemblages, reflecting the incompatible behavior (D ≤ 1) of the PPGE, showing enrichment as a function of the differentiation degree [1]. The behavior of PGE during partial melting and crystal fractionation and which minerals are collectors of PGEs have been investigated and reviewed extensively [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].

Despite the great interest in the PGE, the thermo-chemical basis of their geochemical properties remains unclear. Thermodynamic data for PGE-minerals (PGM) are very limited, due probably to experimental difficulties and very limited data on the activity-composition models and relevant phase diagrams [21,22,23,24,25,26,27,28]. Assuming that the required thermodynamic data (enthalpy, entropy, Gibbs free energy) of the reactants and physical/chemical conditions (P, T) are available, then the mineral Gibbs free energy can be calculated [26,27,28]. This paper focuses on: (1) the calculation of the Gibbs free energy of formation for the selected PGM in PGE-bearing complexes worldwide, at standard state conditions (Δ_fG°), using the current state of knowledge from experimental data on the PGE; and (2) the application of the calculated Gibbs free energy (ΔG) values to predict the stability of PGM.

2. Methodology

Minerals have a Gibbs free energy of formation (∆_fG°) value, which describes the amount of energy that is released or consumed when a phase is created from its constituent elements in their standard state. It is well known that the Δ_fG° of a mineral varies with changes in pressure (P), temperature (T) and mineral composition (X) and that the more stable position is one of lower energy. The HSC Chemistry software 6.0, includes databases and various modules providing different types of chemical/thermodynamic calculation.

The Gibbs free energy is defined [26] by the following equation:

G = H − T × S

(1)

The enthalpy and entropy values are available in different databases (HSC 6.0 Thermo-chemical Data Source on PGE [29,30,31,32,33,34,35,36,37]). The standard Gibbs free energy (ΔG°) values of PGM were calculated (Table 1, [21,22,23,24,35]) as the difference between free energy (G) of the products and reactants (Equation (2) using data from the NBS tables of chemical thermodynamic properties [37]).

ΔG = G(species) − ΣG(elements)

(2)

Table 1. The calculated standard Gibbs free energy (Δ_fG°) values of formation for platinumgroup minerals are compared to available literature data.

Mineral			Literature Data				Ref.
Formula	Name	ΔfG°	ΔfG°	ΔfH°	S°	Cp
		kJ/mol	kJ/mol	kJ/mol	J/mol·K	J/mol·K
RuS2	Laurite	−204.1	−188.1	−199.2	55.2	66.46	[22,23]
OsS2	Erlichmanite	−135.1	−134.1	−146.9	54.8	--	[21]
IrS2	Unnamed iridium disulfide	−123.9	−131.8	−143.1	72.8	--	[21]
IrTe2	Shuangfengite	−68.0	--	−71.13	123.43	--	[35]
PtTe2	Moncheite	−52.9	−52.33	−58.19	120.95	75.09	[24,35]
PdTe2	Merenskyite	−60.6	−47.36	−50.40	126.67	76.30	[24,35]
Ir2S3	Kashinite	−196.4	−220.5	−241.4	97.1	--	[21]
PtS	Cooperite	−76.1	−76.22	−81.79	54.87	48.17	[24]
PdS	Vysotskite	−66.7	−72.25	−70.87	57.63	48.66	[24]
OsAs2	Omeiite	−75.8	--	−76.57	101.32	--	[35]
PtAs2	Sperrylite	−193.4	--	−217.57	31.928	--	[35]
Rh2S3	Bowieite	−252.4	--	−262.47	125.52	--	[35]
RuO2	Ru-oxide	−252.7	--	−305.01	58.158	--	[35]

Table 1. The calculated standard Gibbs free energy (Δ_fG°) values of formation for platinumgroup minerals are compared to available literature data.

Mineral			Literature Data				Ref.
Formula	Name	ΔfG°	ΔfG°	ΔfH°	S°	Cp
		kJ/mol	kJ/mol	kJ/mol	J/mol·K	J/mol·K
RuS2	Laurite	−204.1	−188.1	−199.2	55.2	66.46	[22,23]
OsS2	Erlichmanite	−135.1	−134.1	−146.9	54.8	--	[21]
IrS2	Unnamed iridium disulfide	−123.9	−131.8	−143.1	72.8	--	[21]
IrTe2	Shuangfengite	−68.0	--	−71.13	123.43	--	[35]
PtTe2	Moncheite	−52.9	−52.33	−58.19	120.95	75.09	[24,35]
PdTe2	Merenskyite	−60.6	−47.36	−50.40	126.67	76.30	[24,35]
Ir2S3	Kashinite	−196.4	−220.5	−241.4	97.1	--	[21]
PtS	Cooperite	−76.1	−76.22	−81.79	54.87	48.17	[24]
PdS	Vysotskite	−66.7	−72.25	−70.87	57.63	48.66	[24]
OsAs2	Omeiite	−75.8	--	−76.57	101.32	--	[35]
PtAs2	Sperrylite	−193.4	--	−217.57	31.928	--	[35]
Rh2S3	Bowieite	−252.4	--	−262.47	125.52	--	[35]
RuO2	Ru-oxide	−252.7	--	−305.01	58.158	--	[35]

It is notable that the ° (“not”) on Δ_fG° indicates that the ΔG value is based on the reaction at standard conditions (1 M solution concentration, 1 atm gas pressure). Temperature is not part of the standard conditions, but commonly, a temperature of 298 K is used. If the concentration is different from 1 M or 1 atm gas pressure, the change of the Gibbs free energy is written as ΔG.

Using the Reaction Equations mode, chemical compounds and reactions were analyzed, in order to calculate the change of the Gibbs free energy (Δ_fG°) at standard conditions. Calibrating a chemical reaction, Δ_rG° is calculated by Equation (3), when the chemical reaction follows Equation (5):

ΔG = G(Products) − G(Reactants)

(3)

ΣG(Products) − ΣG(Reactants) = (c × G_C + d × G_D + …) − (a × G_A + b × G_B + …)

(4)

aA + bB + … = cC + dD + …

(5)

Although the question of the original existence of bonds between metallic PGEs and sulfur, oxygen or other ligands remains unclear, the calculated Gibbs free energy values were calculated assuming the existence of metallic PGEs and sulfur [21,22,38] via the Equation (2).

Although thermodynamic calculations, which are derived by various computational methods based on the available reference data, and experimental methods yield considerable uncertainties [22,24], the calculated thermodynamic values for PGM appear to be in a good agreement with those given in the literature. In addition, to evaluate the accuracy of the method of the calculation of the Gibbs free energy of formation, the (Δ_fG) for the rhodium sulfide phases Rh₃S₄ and Rh₂S₃were calculated using the HSC program (Table 2 and Table 3). The Reaction Equations mode was used to estimate the free energy of Reactions (6) and (7) through Equation (3), combining data from the HSC main database.

3Rh(s) + 2S₂(g) = Rh₃S₄

(6)

4Rh₃S₄(s) + S₂(g) = 6Rh₂S₃

(7)

These values were compared to those obtained using a solid-state electrochemical technique [25]. The calculated values of Δ_fG for these rhodium sulfides (Table 2 and Table 3; Figure 1) were found to be in good agreement with those of temperature in the range from 925 to 1275 K.

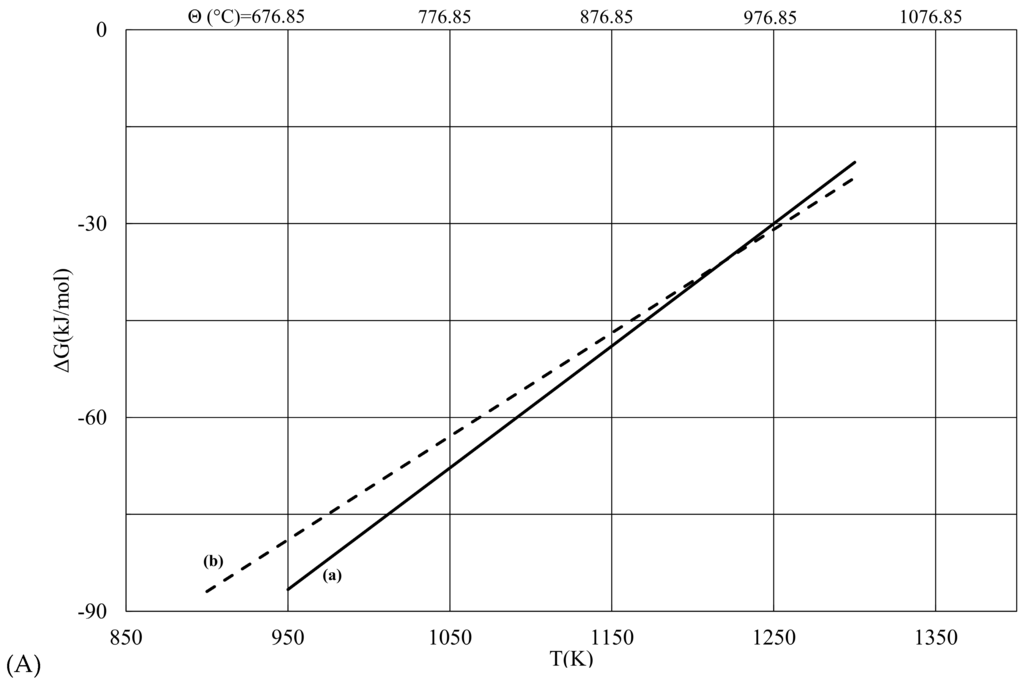
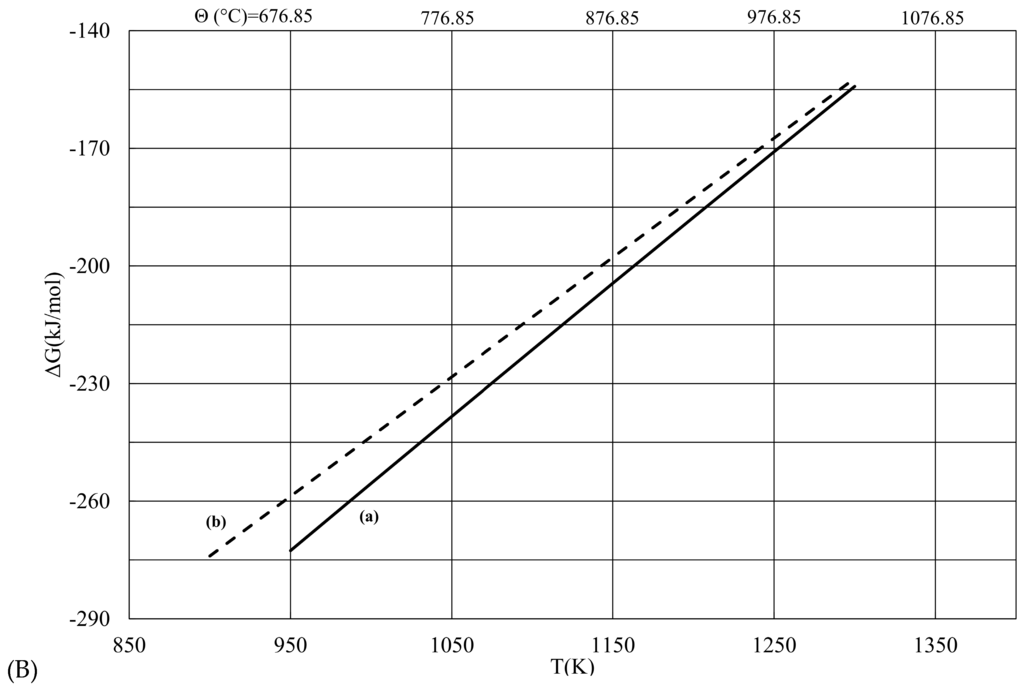
Figure 1. Comparison of the calculated Gibbs free energy (ΔG) against temperature, for two reactions. (A) 3Rh(s) + 2S₂(g) = Rh₃S₄(s) in this study with values obtained by previous authors [25]. Data for Line (a) from Table 2; data for Line (b): ΔGf(J·mol⁻¹) = −548026 + 304.5 × T (K) from [25]. (B) 4Rh₃S₄(s) + S₂(g) = 6Rh₂S₃(s) in this study with values obtained by previous authors [25]. Data for Line (a) from Table 3; data for Line (b): ΔGf(J·mol⁻¹)= −230957 + 160.03 × T (K) from [25].

Figure 1. Comparison of the calculated Gibbs free energy (ΔG) against temperature, for two reactions. (A) 3Rh(s) + 2S₂(g) = Rh₃S₄(s) in this study with values obtained by previous authors [25]. Data for Line (a) from Table 2; data for Line (b): ΔGf(J·mol⁻¹) = −548026 + 304.5 × T (K) from [25]. (B) 4Rh₃S₄(s) + S₂(g) = 6Rh₂S₃(s) in this study with values obtained by previous authors [25]. Data for Line (a) from Table 3; data for Line (b): ΔGf(J·mol⁻¹)= −230957 + 160.03 × T (K) from [25].

Table 2. Comparison between ΔG_f values of (a) this study and (b) [25] for the reaction: 3Rh(s) + 2S₂(g) = Rh₃S₄(s).

T (K)	ΔG (a) (kJ/mol)	ΔG (b) (kJ/mol)	|ΔG (b) − ΔG (a)|
900	−289.89	−273.98	15.92
950	−272.63	−258.75	13.88
1000	−255.46	−243.53	11.93
1050	−238.37	−228.3	10.07
1100	−221.37	−213.08	8.29
1150	−204.46	−197.85	6.60
1200	−187.62	−182.63	5.00
1250	−170.88	−167.4	3.48
1300	−154.22	−152.18	2.04

Table 2. Comparison between ΔG_f values of (a) this study and (b) [25] for the reaction: 3Rh(s) + 2S₂(g) = Rh₃S₄(s).

T (K)	ΔG (a) (kJ/mol)	ΔG (b) (kJ/mol)	|ΔG (b) − ΔG (a)|
900	−289.89	−273.98	15.92
950	−272.63	−258.75	13.88
1000	−255.46	−243.53	11.93
1050	−238.37	−228.3	10.07
1100	−221.37	−213.08	8.29
1150	−204.46	−197.85	6.60
1200	−187.62	−182.63	5.00
1250	−170.88	−167.4	3.48
1300	−154.22	−152.18	2.04

Table 3. Comparison between ΔG_f values of (a) this study and (b) [25] for the reaction: 4Rh₃S₄(s) + S₂(g) = 6Rh₂S₃(s).

T (K)	ΔG (a) (kJ/mol)	ΔG (b) (kJ/mol)	|ΔG (b) − ΔG (a)|
900	−96.016	−86.93	9.086
950	−86.619	−78.929	7.691
1000	−77.219	−70.927	6.292
1050	−67.812	−62.926	4.887
1100	−58.392	−54.924	3.468
1150	−48.956	−46.923	2.034
1200	−39.499	−38.921	0.578
1250	−30.018	−30.920	0.901
1300	−20.509	−22.918	2.409

Table 3. Comparison between ΔG_f values of (a) this study and (b) [25] for the reaction: 4Rh₃S₄(s) + S₂(g) = 6Rh₂S₃(s).

T (K)	ΔG (a) (kJ/mol)	ΔG (b) (kJ/mol)	|ΔG (b) − ΔG (a)|
900	−96.016	−86.93	9.086
950	−86.619	−78.929	7.691
1000	−77.219	−70.927	6.292
1050	−67.812	−62.926	4.887
1100	−58.392	−54.924	3.468
1150	−48.956	−46.923	2.034
1200	−39.499	−38.921	0.578
1250	−30.018	−30.920	0.901
1300	−20.509	−22.918	2.409

Near 1250 K, there is excellent agreement between the measured and calculated values. At lower temperatures, the calculated values fall below the measured values, and this discrepancy increases with decreasing temperature. The reason for this discrepancy is not obvious, but it is probably due to many experimental difficulties and uncertainties and/or a database collected from different methods.

3. Calculated Change of the Gibbs Free Energy (Δ_fG°)

The calculated changes of the free energy of formation (Δ_fG°) for selected PGM in layered intrusions and ophiolite complexes are negative (Table 1), supporting their stability compared to the separate elements (spontaneous reaction). They showed the following order: RuS₂ < (Ir, Os)S₂ < (Pt, Pd)S < (Pd, Pt)Te₂; that is, increasing from compatible to incompatible noble metals and from sulfides to tellurides. In addition, due to the common presence of (Os–Ir–Ru)-oxides in nature, the Δ_fG° for RuO₂ was calculated (Table 1). Using the equations of the HSC program, the calculated Δ_fG° values in standard conditions (Table 1) were extrapolated to a wide range of temperature, up to 1300 °C (Table 4), and the variation of the free energy versus temperature is plotted (Figure 2, Figure 3 and Figure 4). Since ∆H and ∆S are essentially constant with temperature unless a phase change occurs, the free energy versus temperature plot can be drawn as a series of straight lines, where ∆S is the slope and ∆H is the y-intercept [39,40]. Furthermore, since the ΔS values are always negative for these reactions, the ΔH-TΔS becomes larger with temperature, and the lines slope upwards (formation reactions are exothermic).

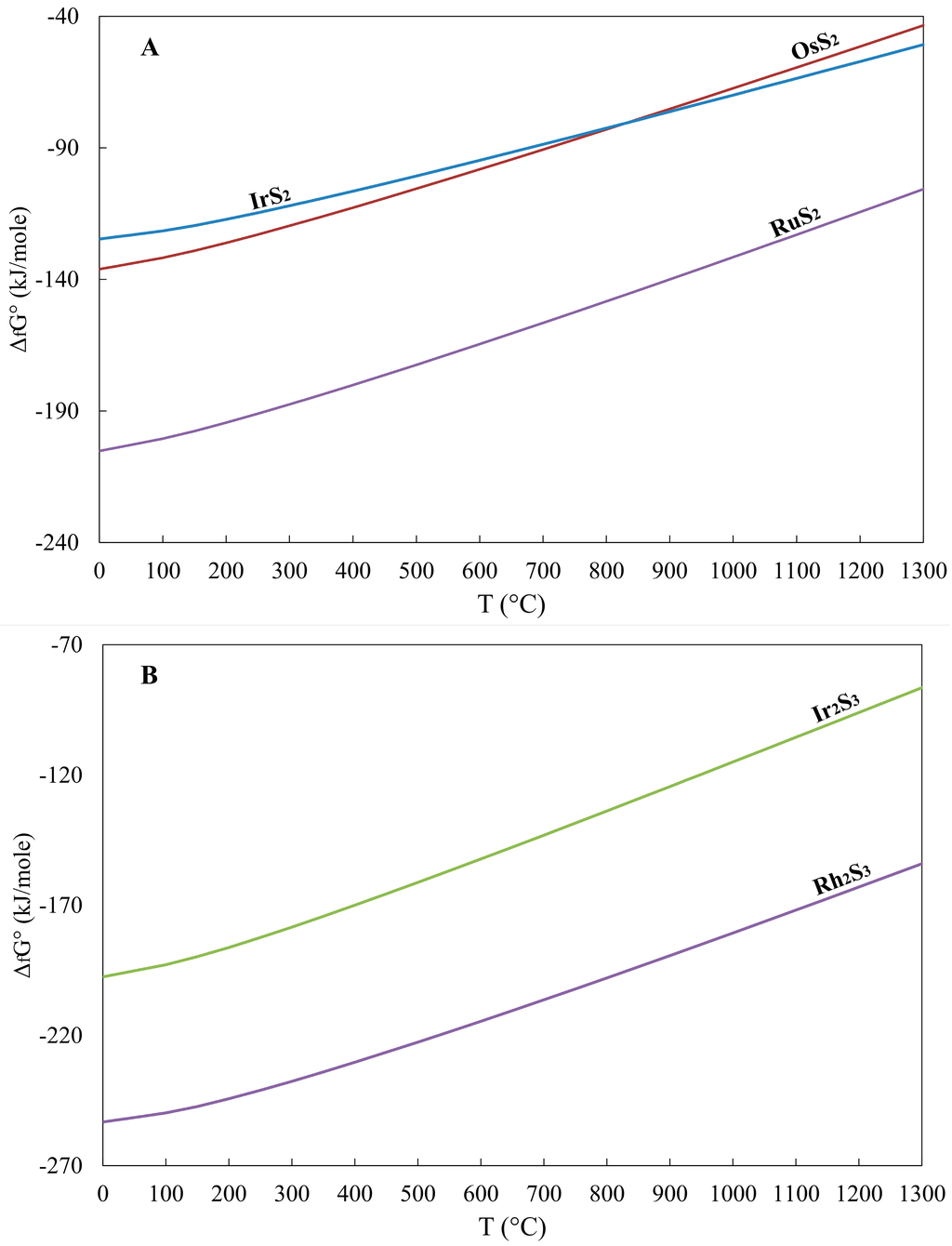
Figure 2. Plot of the Free energy (Δ_fG°) against temperature for (A) RuS₂ (laurite), OsS₂ (erlichmanite) and IrS₂ (unnamed iridium disulfide) and (B) Rh₂S₃ (bowieite) and Ir₂S₃ (kashinite). Data from Table 4.

Figure 2. Plot of the Free energy (Δ_fG°) against temperature for (A) RuS₂ (laurite), OsS₂ (erlichmanite) and IrS₂ (unnamed iridium disulfide) and (B) Rh₂S₃ (bowieite) and Ir₂S₃ (kashinite). Data from Table 4.

With respect to the recorded difference between the diagrams showing smooth curves (Figure 2A, Band 3B) and diagram for tellurides (PtTe₂, PdTe₂ and IrTe₂ (Figure 3A), showing an abrupt change of direction at 450 °C (Figure 3B)), it may be related to the phase changes, as is exemplified by a phase change at 449.51 °C, for compositions between PtTe₂ and Te (melting point of Te metal) in the related phase diagram [41,42].

Table 4. Extrapolation of the calculated free energy values at standard stage (Δ_fG°) (Table 1) to a wide range of temperatures.

T (°C)	RuS2	OsS2	IrS2	IrTe2	PtTe2	PdTe2	Ir2S3	Rh2S3	PtS	PdS	OsAs2	PtAs2	RuO2
25	−204.1	−135.1	−123.9	−68.0	−52.9	−60.6	−196.4	−252.4	−76.1	−66.7	−75.76	−193.4	−252.7
50	−202.9	−134.0	−123.2	−67.7	−52.4	−60.3	−195.2	−251.5	−75.7	−66.4	−75.6	−191.3	−248.3
100	−200.5	−131.8	−121.6	−66.5	−51.4	−59.9	−192.8	−249.8	−74.7	−65.6	−74.9	−186.7	−239.5
150	−197.7	−129.1	−119.6	−64.9	−50.5	−59.4	−189.8	−247.3	−73.5	−64.7	−73.7	−181.5	−230.9
200	−194.5	−126.2	−117.2	−62.8	−49.4	−58.9	−186.2	−244.3	−72.1	−63.6	−72.0	−175.9	−222.3
250	−191.1	−123.0	−114.7	−60.3	−48.4	−58.4	−182.4	−241.1	−70.6	−62.4	−70.0	−169.9	−213.9
300	−187.5	−119.7	−112.0	−57.4	−47.4	−57.9	−178.4	−237.6	−69.0	−61.1	−67.5	−163.5	−205.5
350	−183.9	−116.2	−109.3	−54.2	−46.3	−57.5	−174.2	−234.0	−67.5	−59.8	−64.7	−156.7	−197.2
400	−180.1	−112.7	−106.5	−50.6	−45.2	−57.0	−170.0	−230.3	−65.8	−58.4	−61.6	−149.6	−189.1
449.5	--	--	--	−46.7	−44.1	−56.6	--	--	--	--	--	--	--
450	−176.3	−109.2	−103.6	−46.7	−44.0	−56.5	−165.6	−226.5	−64.1	−57.0	−58.2	−142.2	−180.9
500	−172.5	−105.6	−100.7	−40.0	−40.4	−53.6	−161.2	−222.6	−62.4	−55.5	−54.3	−134.6	−172.9
550	−168.6	−101.9	−97.8	−33.1	−36.7	−50.7	−156.7	−218.6	−60.7	−54.1	−50.6	−126.7	−165.0
600	−164.6	−98.2	−94.8	−25.8	−32.8	−47.6	−152.2	−214.6	−59.0	−52.7	−46.4	−118.4	−157.1
626.8	--	--	--	--	--	−46.0	--	--	--	−51.9	--	--	--
650	−160.6	−94.4	−91.7	−18.2	−29.0	−44.6	−147.7	−210.5	−57.0	−51.2	−42.0	−110.0	−149.3
700	−156.6	−90.7	−88.7	−10.4	−25.0	−41.5	−143.1	−206.3	−55.4	−49.7	−37.3	−101.3	−141.5
750	−152.5	−86.9	−85.6	−2.3	−21.0	−38.4	−138.4	−202.1	−53.6	−48.2	−32.4	−92.4	−133.8
800	−148.4	−83.0	−82.5	6.0	−17.0	−35.3	−133.8	−197.9	−51.9	−46.8	−27.3	−83.3	−126.2
850	−144.2	−79.1	−79.4	14.5	−12.9	−32.2	−129.1	−193.6	−50.0	−45.2	−20.6	−72.5	−118.6
876.8	--	--	--	19.2	−10.7	−30.6	--	--	--	--	--	--	--
900	−140.0	−75.3	−76.3	23.3	−8.7	−29.1	−124.4	−189.3	−48.3	−43.8	−12.8	−60.8	−111.1
926.8	--	--	−74.6	28.1	--	--	−121.9	−187.0	--	--	--	--	--
950	−135.8	−71.3	−73.1	32.2	−4.5	−26.0	−119.7	−185.0	−46.5	−42.3	−4.9	−48.8	−103.6
1000	−131.6	−67.4	−70.0	41.4	−0.3	−22.9	−115.0	−180.7	−44.7	−40.8	−3.1	−36.7	−96.2
1026.8	−129.3	--	--	--	2.0	--	--	--	−43.7	--	−	−30.1	−92.3
1050	−127.3	−63.5	−66.8	50.7	3.9	−19.8	−110.2	−176.3	−42.9	−39.3	11.4	−24.4	−88.9
1100	−123.1	−59.5	−63.6	60.2	8.3	−16.7	−105.5	−171.9	−41.1	−37.8	19.8	−11.9	−81.5
1150	−118.8	−55.5	−60.4	69.9	12.6	−13.6	−100.7	−167.4	−39.3	−36.3	28.4	0.7	−74.3
1200	−114.4	−51.5	−57.2	79.7	17.0	−10.5	−96.0	−163.0	−37.5	−34.8	37.1	13.5	−67.0
1250	−110.1	−47.5	−54.0	89.8	21.4	−7.4	−91.2	−158.5	−35.7	−33.3	46.0	26.5	−59.9
1300	−105.7	−43.5	−50.8	99.9	25.8	−4.3	−86.4	−154.0	−34.0	−31.8	55.0	39.6	−52.7

Table 4. Extrapolation of the calculated free energy values at standard stage (Δ_fG°) (Table 1) to a wide range of temperatures.

T (°C)	RuS2	OsS2	IrS2	IrTe2	PtTe2	PdTe2	Ir2S3	Rh2S3	PtS	PdS	OsAs2	PtAs2	RuO2
25	−204.1	−135.1	−123.9	−68.0	−52.9	−60.6	−196.4	−252.4	−76.1	−66.7	−75.76	−193.4	−252.7
50	−202.9	−134.0	−123.2	−67.7	−52.4	−60.3	−195.2	−251.5	−75.7	−66.4	−75.6	−191.3	−248.3
100	−200.5	−131.8	−121.6	−66.5	−51.4	−59.9	−192.8	−249.8	−74.7	−65.6	−74.9	−186.7	−239.5
150	−197.7	−129.1	−119.6	−64.9	−50.5	−59.4	−189.8	−247.3	−73.5	−64.7	−73.7	−181.5	−230.9
200	−194.5	−126.2	−117.2	−62.8	−49.4	−58.9	−186.2	−244.3	−72.1	−63.6	−72.0	−175.9	−222.3
250	−191.1	−123.0	−114.7	−60.3	−48.4	−58.4	−182.4	−241.1	−70.6	−62.4	−70.0	−169.9	−213.9
300	−187.5	−119.7	−112.0	−57.4	−47.4	−57.9	−178.4	−237.6	−69.0	−61.1	−67.5	−163.5	−205.5
350	−183.9	−116.2	−109.3	−54.2	−46.3	−57.5	−174.2	−234.0	−67.5	−59.8	−64.7	−156.7	−197.2
400	−180.1	−112.7	−106.5	−50.6	−45.2	−57.0	−170.0	−230.3	−65.8	−58.4	−61.6	−149.6	−189.1
449.5	--	--	--	−46.7	−44.1	−56.6	--	--	--	--	--	--	--
450	−176.3	−109.2	−103.6	−46.7	−44.0	−56.5	−165.6	−226.5	−64.1	−57.0	−58.2	−142.2	−180.9
500	−172.5	−105.6	−100.7	−40.0	−40.4	−53.6	−161.2	−222.6	−62.4	−55.5	−54.3	−134.6	−172.9
550	−168.6	−101.9	−97.8	−33.1	−36.7	−50.7	−156.7	−218.6	−60.7	−54.1	−50.6	−126.7	−165.0
600	−164.6	−98.2	−94.8	−25.8	−32.8	−47.6	−152.2	−214.6	−59.0	−52.7	−46.4	−118.4	−157.1
626.8	--	--	--	--	--	−46.0	--	--	--	−51.9	--	--	--
650	−160.6	−94.4	−91.7	−18.2	−29.0	−44.6	−147.7	−210.5	−57.0	−51.2	−42.0	−110.0	−149.3
700	−156.6	−90.7	−88.7	−10.4	−25.0	−41.5	−143.1	−206.3	−55.4	−49.7	−37.3	−101.3	−141.5
750	−152.5	−86.9	−85.6	−2.3	−21.0	−38.4	−138.4	−202.1	−53.6	−48.2	−32.4	−92.4	−133.8
800	−148.4	−83.0	−82.5	6.0	−17.0	−35.3	−133.8	−197.9	−51.9	−46.8	−27.3	−83.3	−126.2
850	−144.2	−79.1	−79.4	14.5	−12.9	−32.2	−129.1	−193.6	−50.0	−45.2	−20.6	−72.5	−118.6
876.8	--	--	--	19.2	−10.7	−30.6	--	--	--	--	--	--	--
900	−140.0	−75.3	−76.3	23.3	−8.7	−29.1	−124.4	−189.3	−48.3	−43.8	−12.8	−60.8	−111.1
926.8	--	--	−74.6	28.1	--	--	−121.9	−187.0	--	--	--	--	--
950	−135.8	−71.3	−73.1	32.2	−4.5	−26.0	−119.7	−185.0	−46.5	−42.3	−4.9	−48.8	−103.6
1000	−131.6	−67.4	−70.0	41.4	−0.3	−22.9	−115.0	−180.7	−44.7	−40.8	−3.1	−36.7	−96.2
1026.8	−129.3	--	--	--	2.0	--	--	--	−43.7	--	−	−30.1	−92.3
1050	−127.3	−63.5	−66.8	50.7	3.9	−19.8	−110.2	−176.3	−42.9	−39.3	11.4	−24.4	−88.9
1100	−123.1	−59.5	−63.6	60.2	8.3	−16.7	−105.5	−171.9	−41.1	−37.8	19.8	−11.9	−81.5
1150	−118.8	−55.5	−60.4	69.9	12.6	−13.6	−100.7	−167.4	−39.3	−36.3	28.4	0.7	−74.3
1200	−114.4	−51.5	−57.2	79.7	17.0	−10.5	−96.0	−163.0	−37.5	−34.8	37.1	13.5	−67.0
1250	−110.1	−47.5	−54.0	89.8	21.4	−7.4	−91.2	−158.5	−35.7	−33.3	46.0	26.5	−59.9
1300	−105.7	−43.5	−50.8	99.9	25.8	−4.3	−86.4	−154.0	−34.0	−31.8	55.0	39.6	−52.7

A particular case of the free energy change accompanying a chemical reaction is the standardfree energy of formation, which is the free energy change accompanying the formation of one mole of a compound from the constituent elements, all being in their standard states. The change in the standard free energy with temperature is due to the changes ΔH° and ΔS° (this is related to the standard enthalpy and entropy ΔG° (ΔG° =ΔH°−T·ΔS°) and, of course, to the change in the temperature itself. It has been assumed that the free energies of formation of the elements in their standard states are, by convention, taken to be zero; the enthalpy scale is fixed by defining H = 0, describing the most stable phase of the pure elements, and the enthalpy of compounds contains the enthalpy of formation H_f from elements, which is usually measured calorimetrically [25,26,27,28]. Thus, the enthalpy of the compound is calculated by adding the enthalpy of formation to the experimental enthalpy difference H(T)–H [27].

$$H(T)=H_f(298.15)+{\int }_{298.15}^T{C}_{p}dT+\mathsf{\sum }{H}_{tr}$$

(8)

where H_f(298.15) is the enthalpy of formation at 298.15 K and H_tr is the enthalpy of transformation of the substance.

Absolute entropy values can be calculated from the experimental heat capacity values through the equation:

$$S=S(298.15)+{\int }_{298.15}^T(C_p/dT)+\mathsf{\sum }{H}_{tr}/T_{tr}$$

(9)

where S(298.15) is the standard entropy of the substance, which can be calculated by integrating C_p/T function from 0 to 298.15 K, T is temperature and H_tr is the enthalpy of phase transformation at a temperature T_tr.

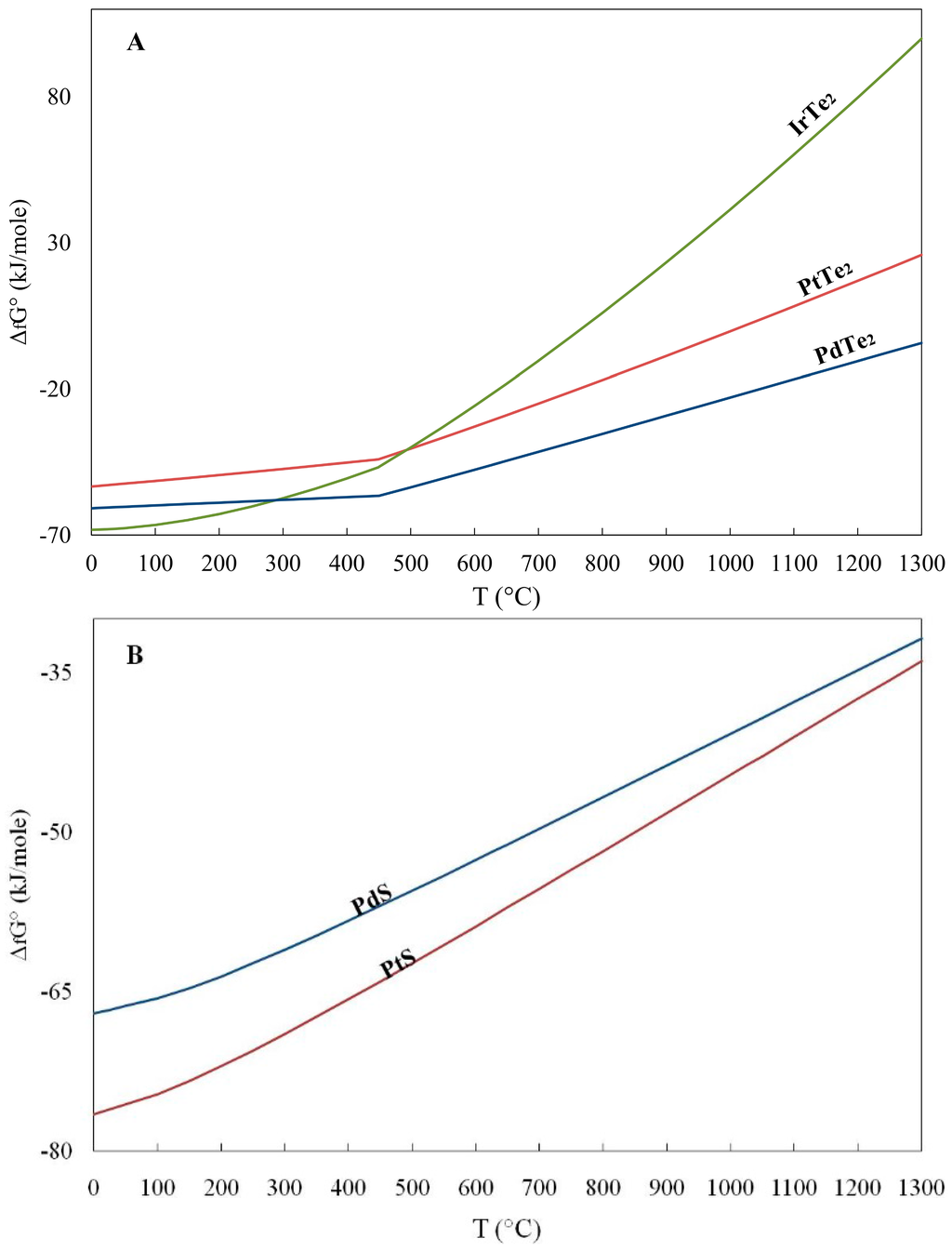
Figure 3. Plot of the Free energy (Δ_fG°) against temperature for (A) PtTe₂ (moncheite), PdTe₂ (merenskyite), IrTe₂ (shuangfengite) and (B) PtS (cooperite) and PdS (braggite). Data from Table 4.

Figure 3. Plot of the Free energy (Δ_fG°) against temperature for (A) PtTe₂ (moncheite), PdTe₂ (merenskyite), IrTe₂ (shuangfengite) and (B) PtS (cooperite) and PdS (braggite). Data from Table 4.

Entropies of crystalline substances approach zero at 0 K (−273.15 °C). This fundamental experimental observation is compatible with the third law of thermodynamics [27]. If entropy is understood as a measure of disorder, the disorder reaches its minimum at absolute zero and in perfect crystal structures. The heat capacity values of crystalline substances in equilibrium approaches the zero value at 0 K. Theoretical thermodynamic modeling cannot predict the temperature dependence of heat capacity at elevated temperatures. The term ΔC_p is usually small, but seldom zero. Plots of ΔG° versus T are, therefore, slightly curved. The term ΔC_p can usually be expressed as a function of temperature by an empirical equation, and the inclusion of this in the expression for ΔG° leads to the following fully-mathematical correlation, which is therefore adopted for fitting experimental heat capacities:

C_p = A + B × 10⁻³ × T + C × 10⁵ × T⁻² + D × 10⁻⁶ × T²

(10)

where A, B, C and D are coefficients estimated from experimental data [26].

Figure 4. Plot of the free energy (Δ_fG°) against temperature for (A) PtAs₂ (sperrylite), OsAs₂ (Omeiite) and (B) RuO_2, and RuS₂ (laurite). Data from Table 4.

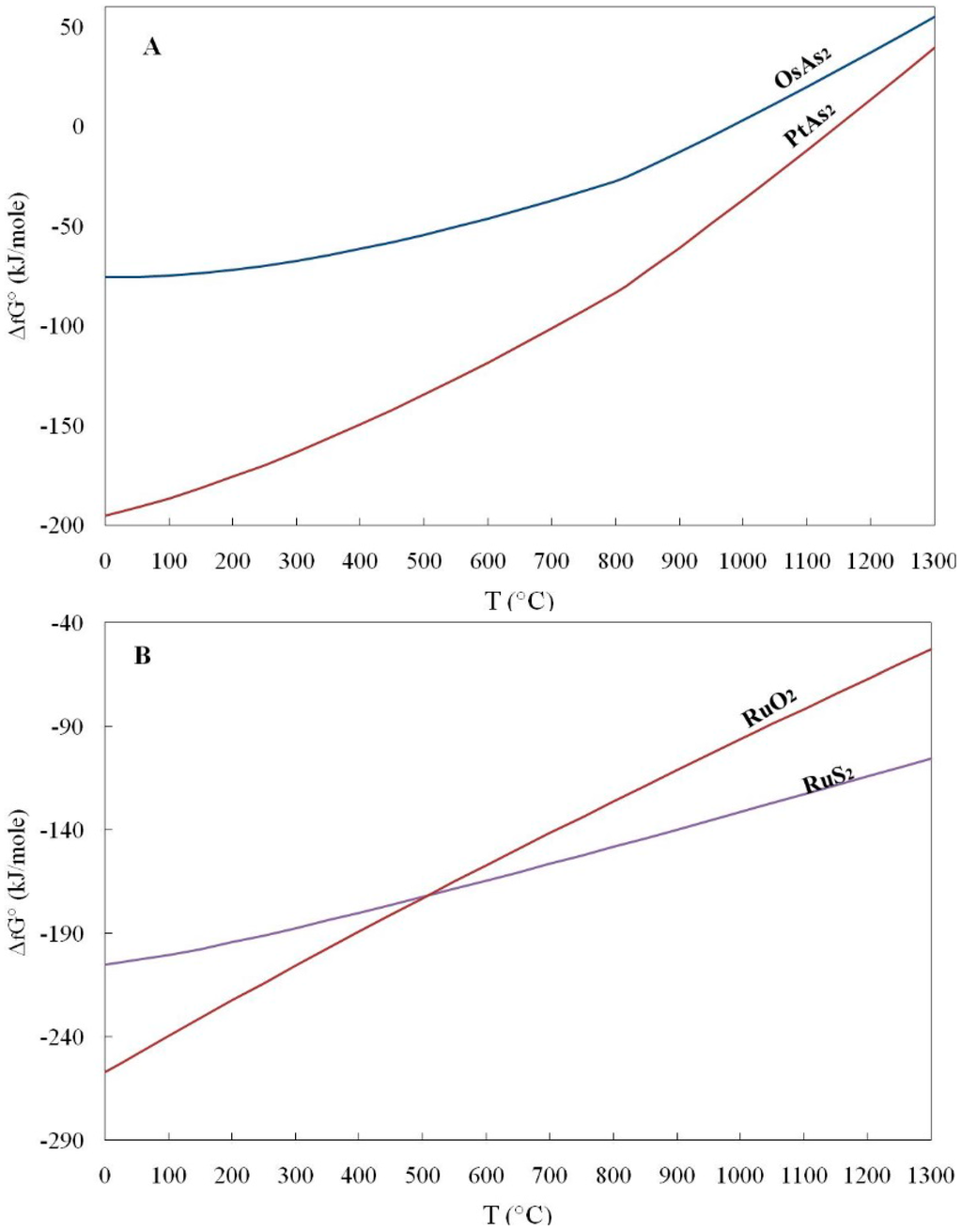
Figure 4. Plot of the free energy (Δ_fG°) against temperature for (A) PtAs₂ (sperrylite), OsAs₂ (Omeiite) and (B) RuO_2, and RuS₂ (laurite). Data from Table 4.

Since ∆H and ∆S are essentially constant with temperature unless a phase change occurs, the free energy versus temperature plot can be drawn as a series of straight lines, where ∆S is the slope and ∆H is the y-intercept [26,27,28]. The lines slope for selected PGM (Figure 5) upwards because ΔS for these reactions is always negative, therefore ΔH-TΔS becomes larger with temperature because the formation reactions are exothermic (Δ H< 0).

4. Application of (Δ_fG) Values to the Origin of PGM

The mineral stability, depending mainly on the availability of PGE/reactants and/or differences in pressure and temperature relative to standard conditions, may have an effect on the equilibrium constants [26,27,28]. Although the stability relationships between various phases can be studied using the experimental method, thermodynamics may give us an approach to the calculation of the Gibbs free energy and phase diagrams [28]. However, the requirements for the PGM stability and re-deposition remain still unclear, since the activity-composition models and relevant phase diagrams for PGM are very limited, and the PGM forming processes in natural systems are complicated [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,28].

The calculated Gibbs free energy values may contribute to better understanding of the knowledge provided by geochemical data, mineral chemistry and structure relationships (microscopic scale) as they are obtained from the investigation of PGE/PGM in nature [43,44,45,46,47,48,49,50]. The more negative Gibbs free energy values for the RuO₂ compared to those for the RuS₂, in the range of temperature lower than 500 °C (Table 4, Figure 5), seems to be in good agreement with the common transformation of laurite to oxides/hydroxides in small chromite occurrences [13,48], in placer deposits [49], in the oxidized zone of the Great Dyke of Zimbabwe layered intrusion [50], in laterite deposits [51,52,53] and elsewhere. The equilibrium constant for the transfer of an ion from one phase to another is directly related to Gibbs free energy and the partition coefficient, which are defined by the behavior of the elements. The apparent epigenetic desulfurization at relatively low (350–500 °C) temperature and partial oxidation of primary laurite crystals has been facilitated by strong brittle deformation and crystal deformation and dislocations, making it possible to remove the sulfur [3,13,48].

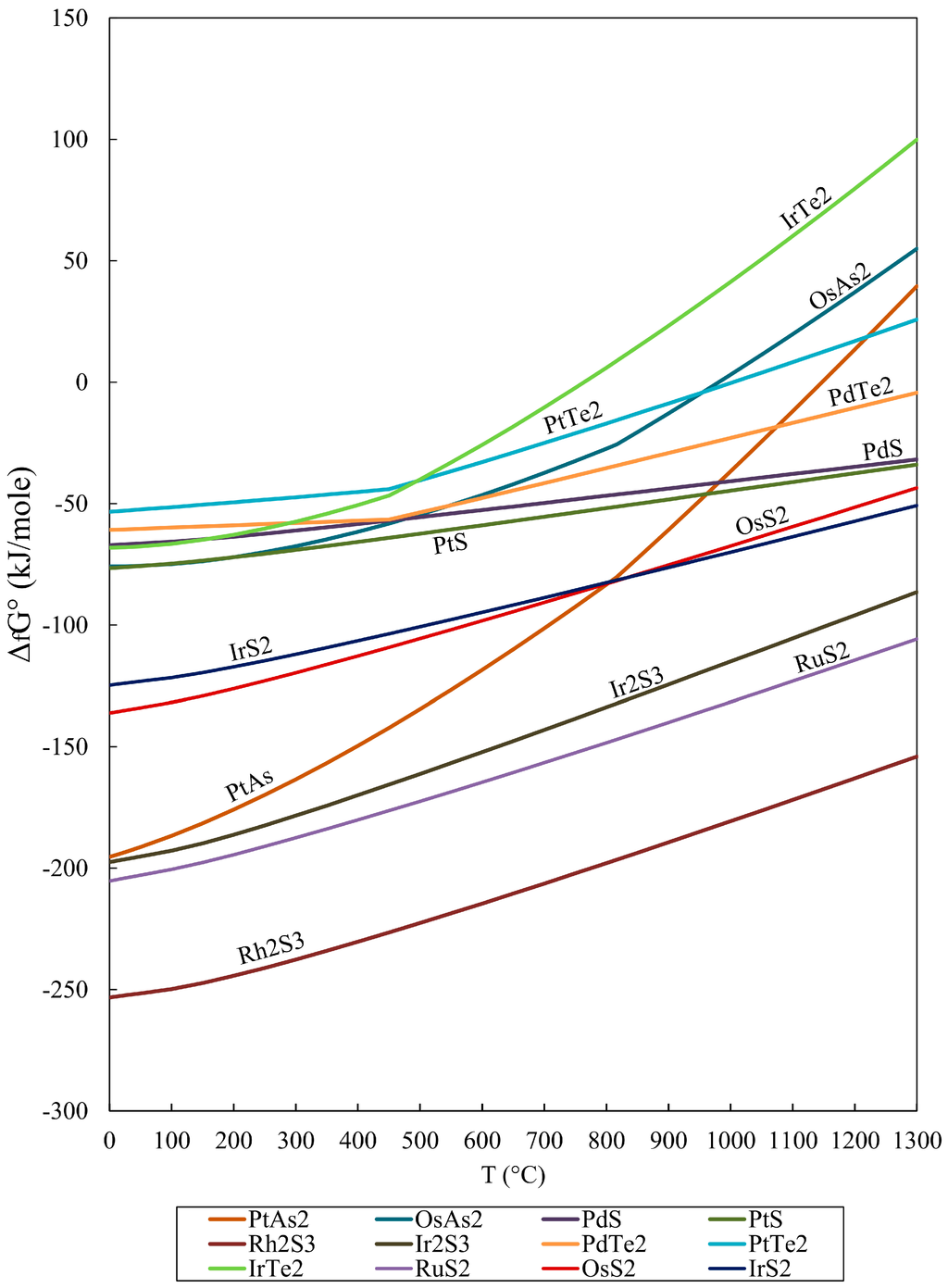
Figure 5. A comparative diagram plotting the free energy (Δ_fG°) against temperature. Data from Table 4.

Figure 5. A comparative diagram plotting the free energy (Δ_fG°) against temperature. Data from Table 4.

Thus, a differential stress driving the deformation of ores, in particular those associated with ophiolite complexes, and changes in temperature, pressure, surface energies, solubility and the diffusion process, have a potential effect on PGM reactions [54]. Although the relative stability of RuO₂ and RuS₂ phases as functions of fO₂ and fS₂ (a redox reaction) is not constrained, the change of a mineral assemblage into a different assemblage means that the new association at the given pressure, temperature and mineral association has a lower free energy than the initial one [55].

On the basis of the calculated Gibbs free energy of formation for the RuS₂ (−204.1 kJ/mol), which is lower compared to that for the OsS₂ (−135.1 kJ/mol) (Table 1, Figure 2A), the reaction Os + RuS₂ ↔Ru + OsS₂ is not favorable thermodynamically (positive Δ_fG°), although the substitution reaction of Ru by Os has been recorded in nature: laurite in chromitites associated with ophiolite complexes is commonly characterized by the general formula (Ru > Os > Ir)S₂, but in the Othrys complex and other ophiolites of the Balkan Peninsula, it is Os-rich (Os > Ru > Ir)S₂, reaching the composition of erlichmanite [4]. Such a composition has been interpreted as Os–Ru substitution during crystal fractionation, while the metal-sulfide equilibrium curves for PGE indicate that at given T, the formation of RuS₂ requires fS₂ lower than that for OsS₂ [56].

Furthermore, the role of fS₂, fTe₂ and temperature has been emphasized for the composition and crystallization of sulfides and tellurides, scavenging Pt and Pd originally contained in the sulfide melt [41,42]. In addition, the earlier deposition of (Pt, Pd)S compared to (Pd, Pt)Te₂, since (Pt, Pd)S is dominant in the UG2chromitite unit (Bushveld), which is located at a lower stratigraphic level compared to the Merensky Reef, where (Pd, Pt)Te₂ are dominant PGM [18,43], seems to be consistent with the more negative free energy values in the former than in the latter (Table 1).

The occurrence of (Pd, Pt)-tellurides, such as moncheite (PtTe₂), merenskyite (PdTe₂), melonite [(Ni, Pd)Te₂], kotulskite [(Pd, Ni)Te] and bismuth-tellurides [(Pt, Pd)(Te, Bi)₂] in certain porphyry-Cu–Au ± Pd ± Pt systems [44,45,46,47], may be related to fS₂, fTe₂ and temperature, as well [41,42]. Assuming that the elevated values of the Pd/Pt ratios, the extremely low Cr contents (<1 ppm) in high Cu–Pd–Pt-grade ores, negative correlation between Cr content and the Pd/Pt, δ¹⁸O values in porphyry deposits of the Balkan Peninsula suggest genesis from more evolved mineralized fluids in porphyry Cu–Au–Pd–Pt deposits [44,45,46,47], the dominance of (Pd-Pt)-tellurides versus (Pt, Pd)S may be related to fS₂, fTe₂ and temperature variation. In addition, the common occurrence of the (Pd, Pt ± Bi)Te₂, merenskyite (the main PGM in porphyry Cu–Au–Pd–Pt deposits), at the peripheral parts of chalcopyrite [44,45,46,47], may be related to the lower free energy of formation (Δ_fG) values for chalcopyrite (−369.6 kJ/mol [57]) compared to that for merenskyite (−70 kJ/mol), suggesting the subsequent deposition of the latter, under appropriate fTe₂ and temperature conditions. Thus, the combination of geochemical characteristics of a porphyry deposit indicating an evolved mineralized system, texture relationships of minerals and free energy data for those minerals data may provide evidence for the existence of (Pd, Pt)-mineralization.

The strong effect of As on PGE partitioning has been documented by the formation of stable high-temperature phases between As and Pt or Rh, including sperrylite (PtAs2), hollingworthite (Rh, Pt, Pd)AsS, and platarsite (Pt, Rh, Ru)AsS [5,13,14,15]. The presented (ΔG_f) values for sperrylite (PtAs₂) (Table 1; Figure 5) seem to be consistent with its common occurrence in chromitites as an interstitial phase between chromite grains [5,13,14,15].

Therefore, although the application of calculated Gibbs free energy values for selected PGM (Table 1) is not clear on the PGE behavior during the evolution of the mineralized systems, the free energy of PGM formation values can be compared to geological and mineralogy data and structure relationships observed in rocks associated with PGM to predict their occurrence and stability.

5. Conclusions

Although there are uncertainties in heat capacity and enthalpy data for PGM and the applications of thermodynamic experiments are limited, the application of thermodynamics to the study of nature systems can be compared to phase relations observed in rocks associated with PGM to predict their occurrence and stability. The preliminary results presented for the Gibbs free energy of the PGM allow us to present the following conclusions:

• The calculated free energy of formation (ΔG_f) for selected PGM were negative values, indicating that these minerals are more stable than the separate elements at standard conditions (the process is spontaneous).
• The calculated Gibbs free energy of formation in the order RuS₂ < OsS₂ < (Pt, Pd)S < (Pd, Pt)Te₂ is increasing from sulfides to tellurides, and they are consistent with their compatibility.
• The evaluation of the accuracy of the method of calculation of the Gibbs free energy of formation using the HSC program was made by comparison with those obtained using a solid-state electrochemical technique by previous authors and was found to be in a good agreement.
• The lower values of the calculated Gibbs free energy of formation (ΔG°_f) for the oxide RuO₂ compared to that for RuS₂ at temperatures lower than 500 °C are consistent with the observed transformation of laurite to oxides/hydroxides at relatively low temperatures.
• Although much more experimental work is required, the compilation of preliminary Gibbs free energy values with geological, mineralogical data and phase relations in natural systems suggests that a thermodynamic approach on PGM may contribute to the better understanding of the PGM thermodynamic behavior and PGE mineralization.