Hydrothermal Modeling of Groundwater–Surface Water Interactions Under an Evolving Climate
Abstract
1. Introduction
2. Materials and Methods
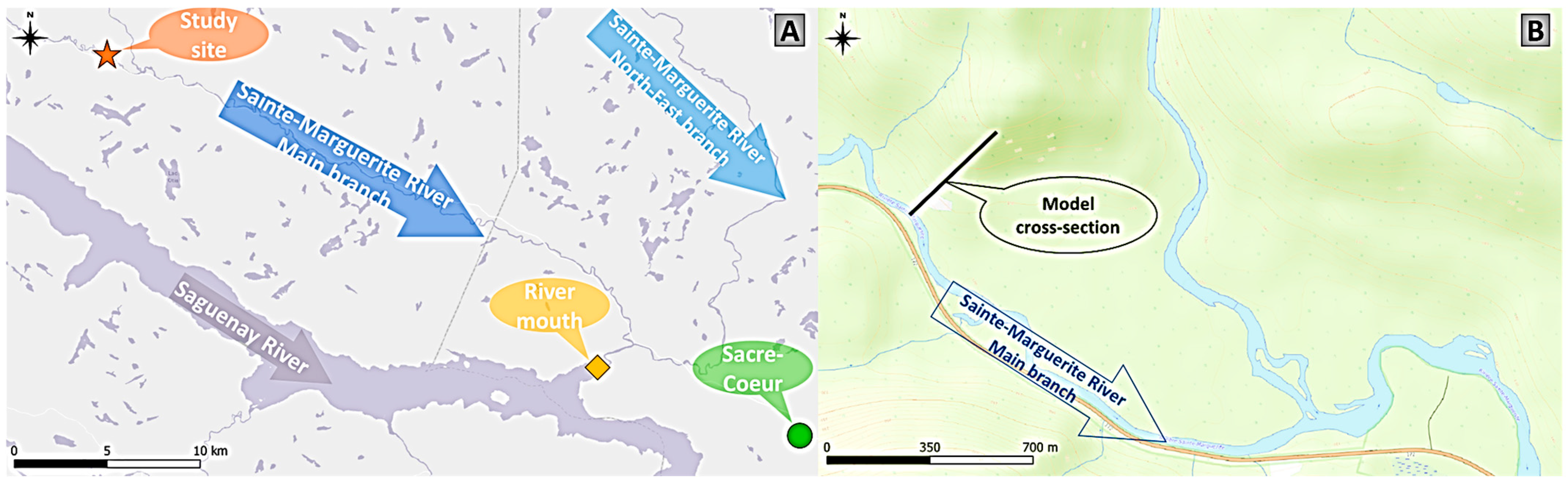
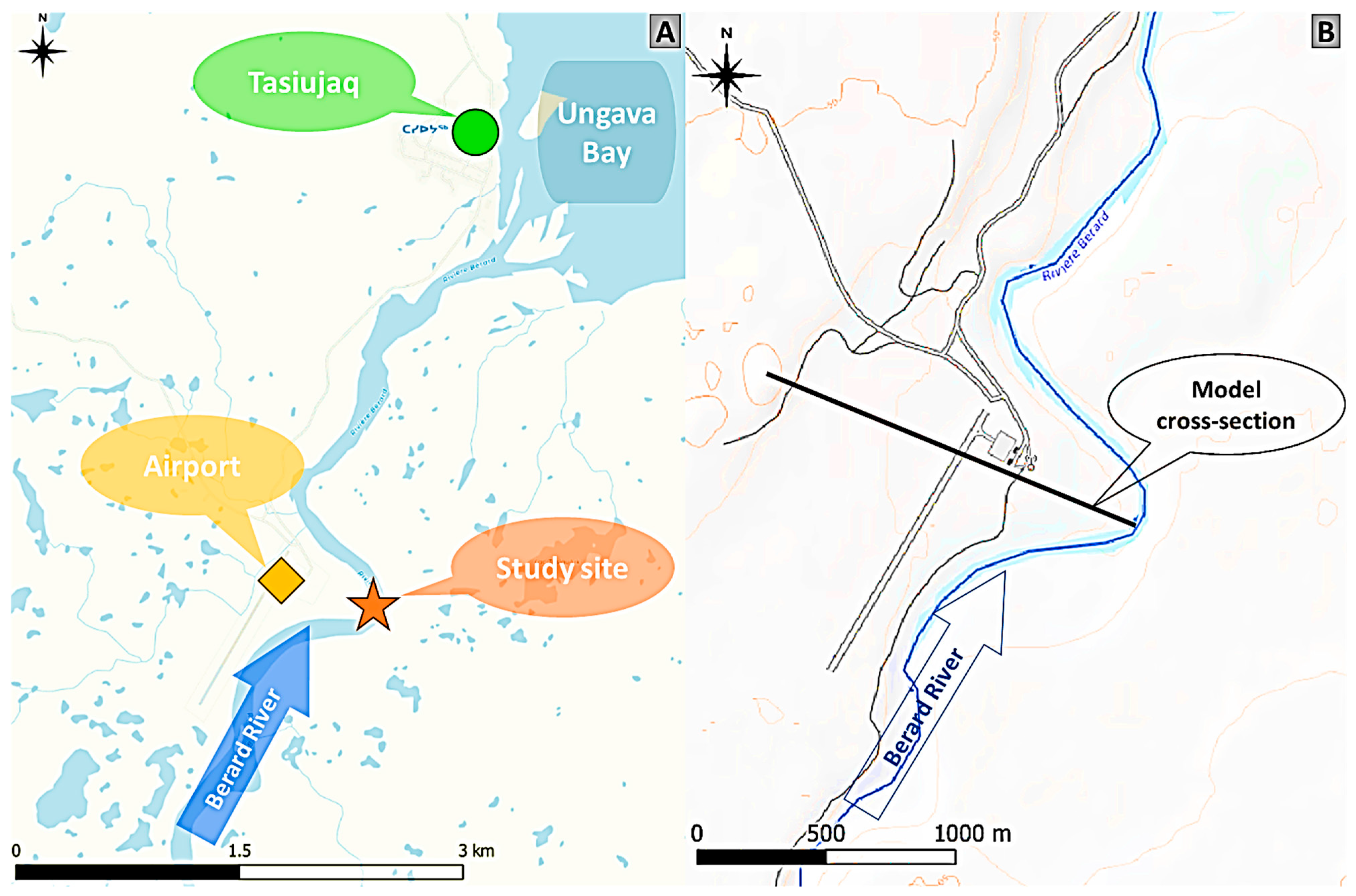
2.1. Study Area
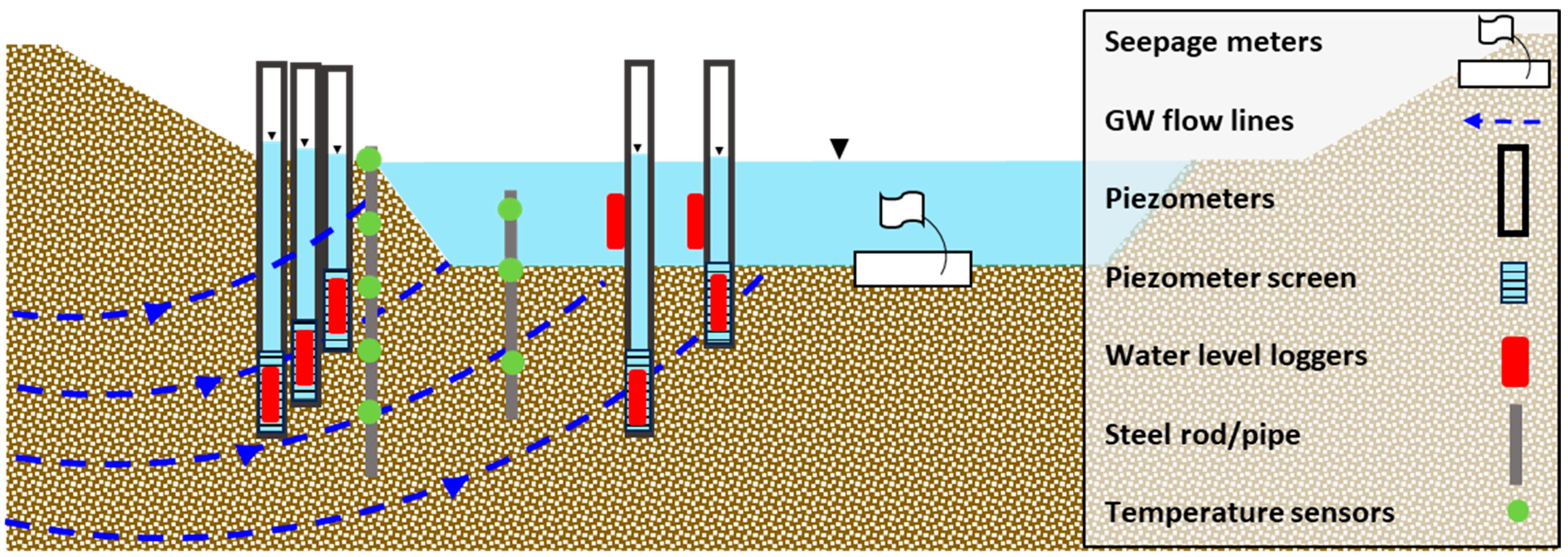
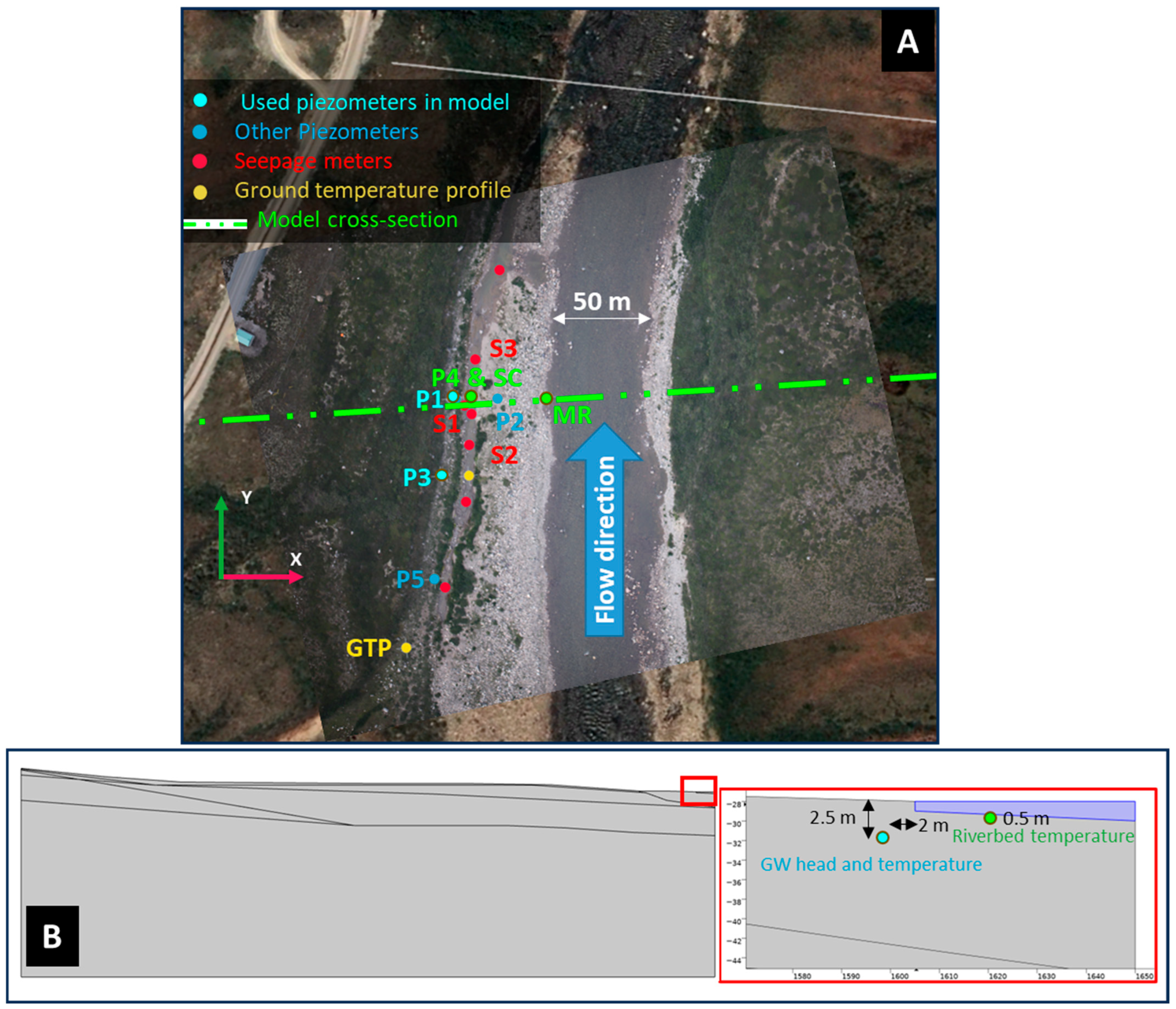
2.2. Data Collection
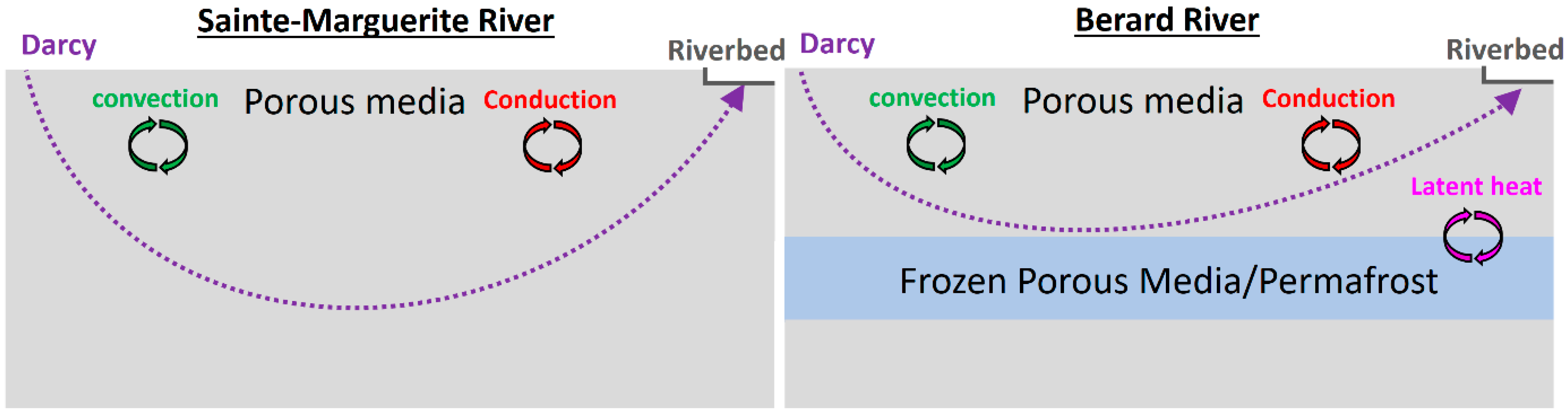
2.3. Hydrothermal Modeling Framework
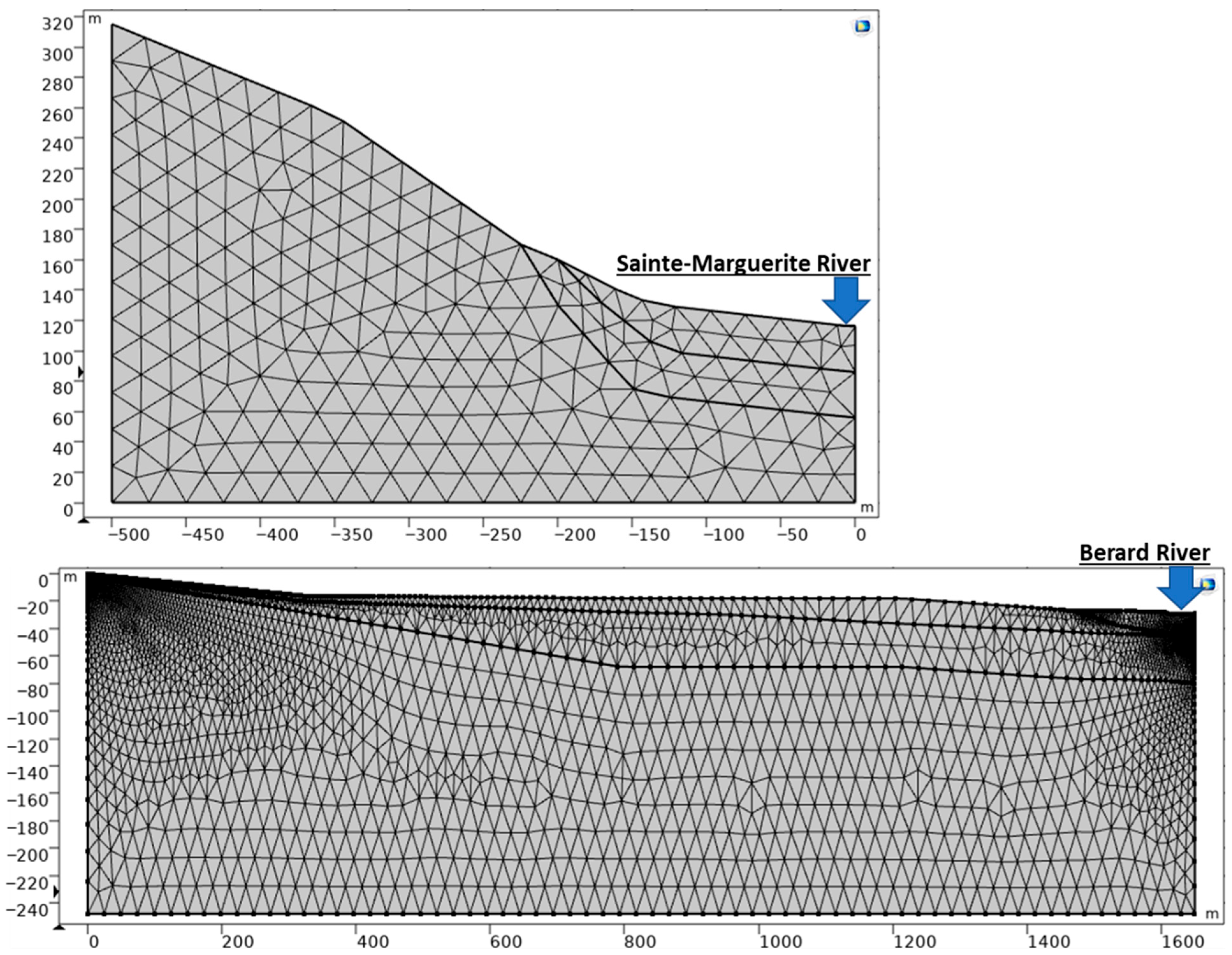
2.4. Geometry of Subsurface Geology
2.5. Inputs and Parameter Estimation
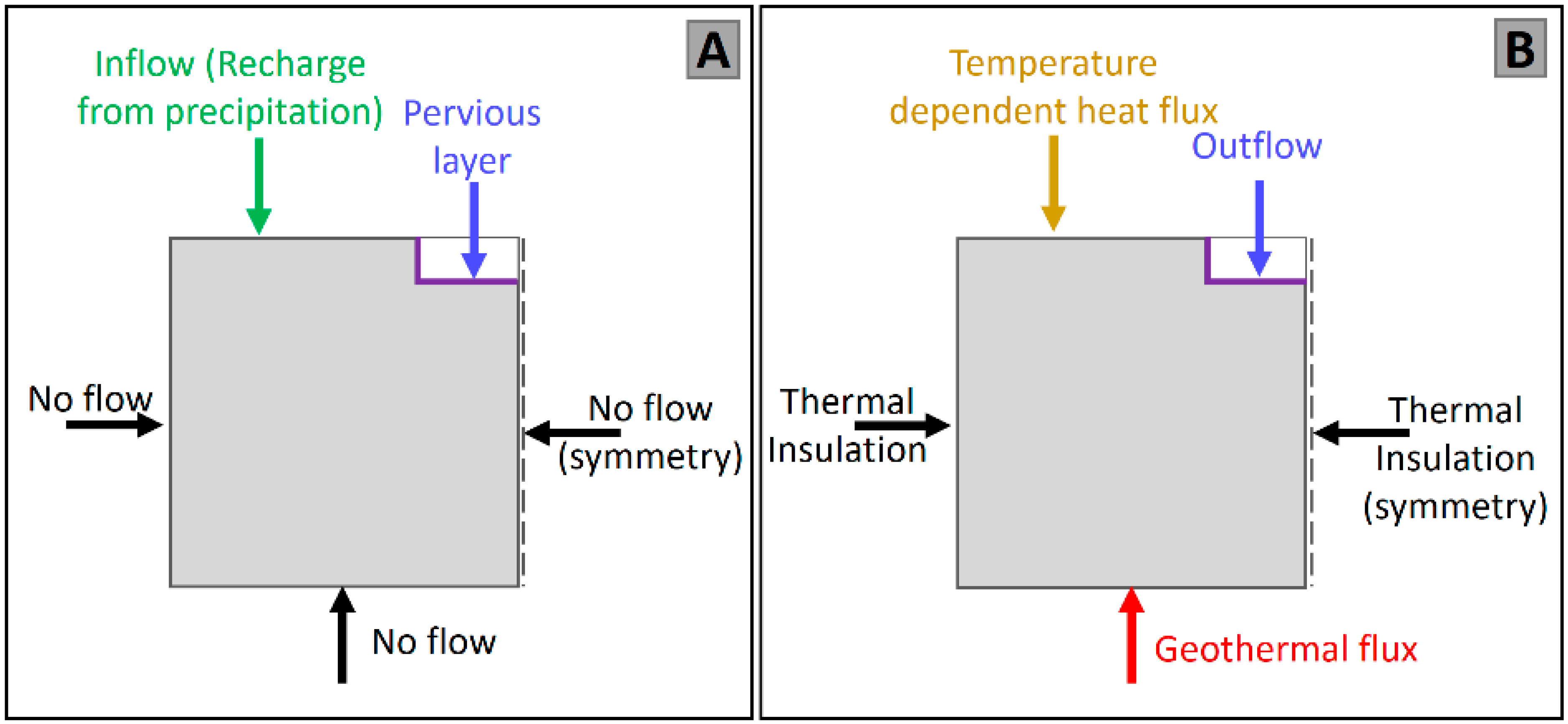
2.6. Boundary Conditions
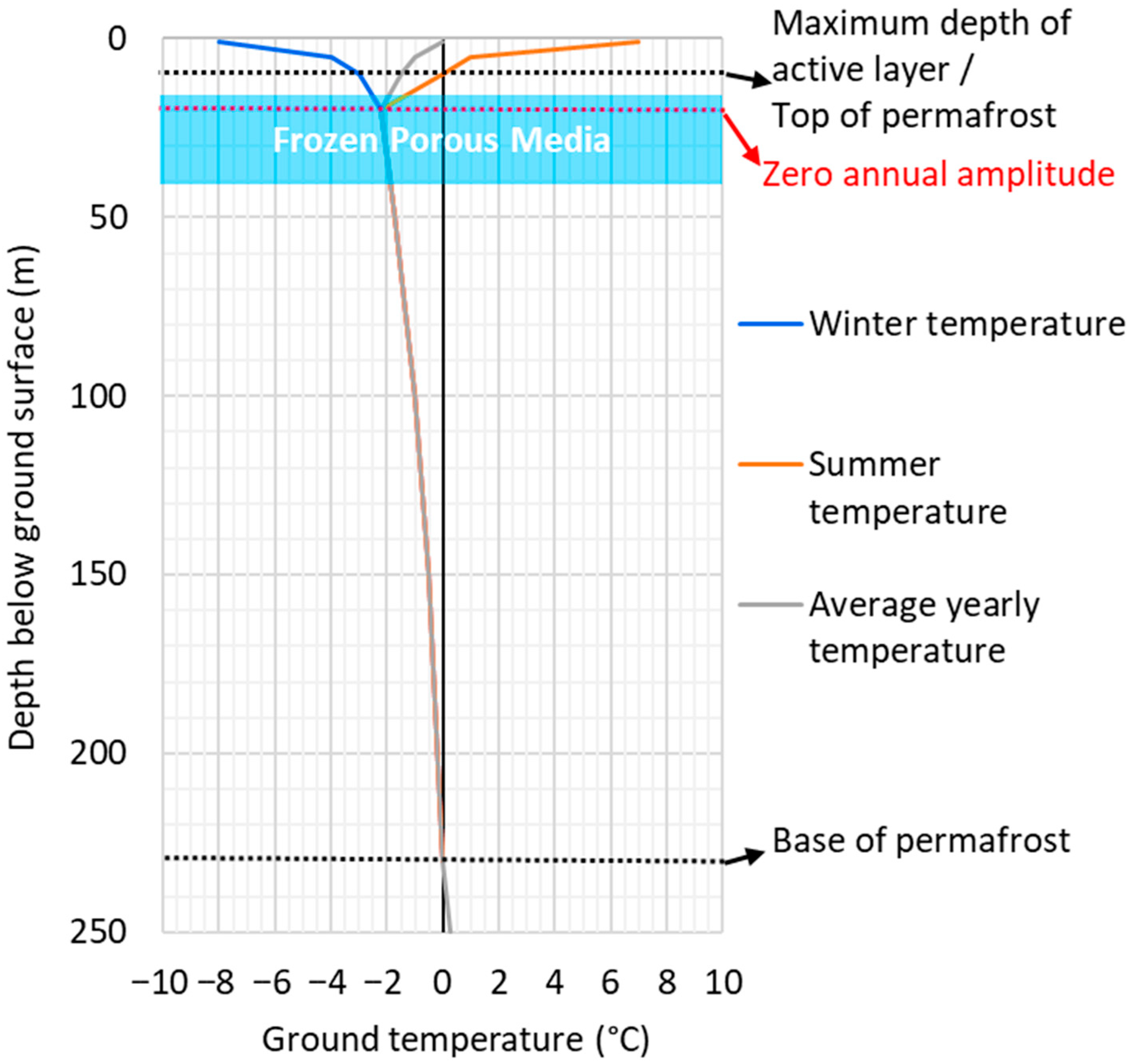
2.7. Initial Conditions
2.8. Mesh
2.9. Time Step
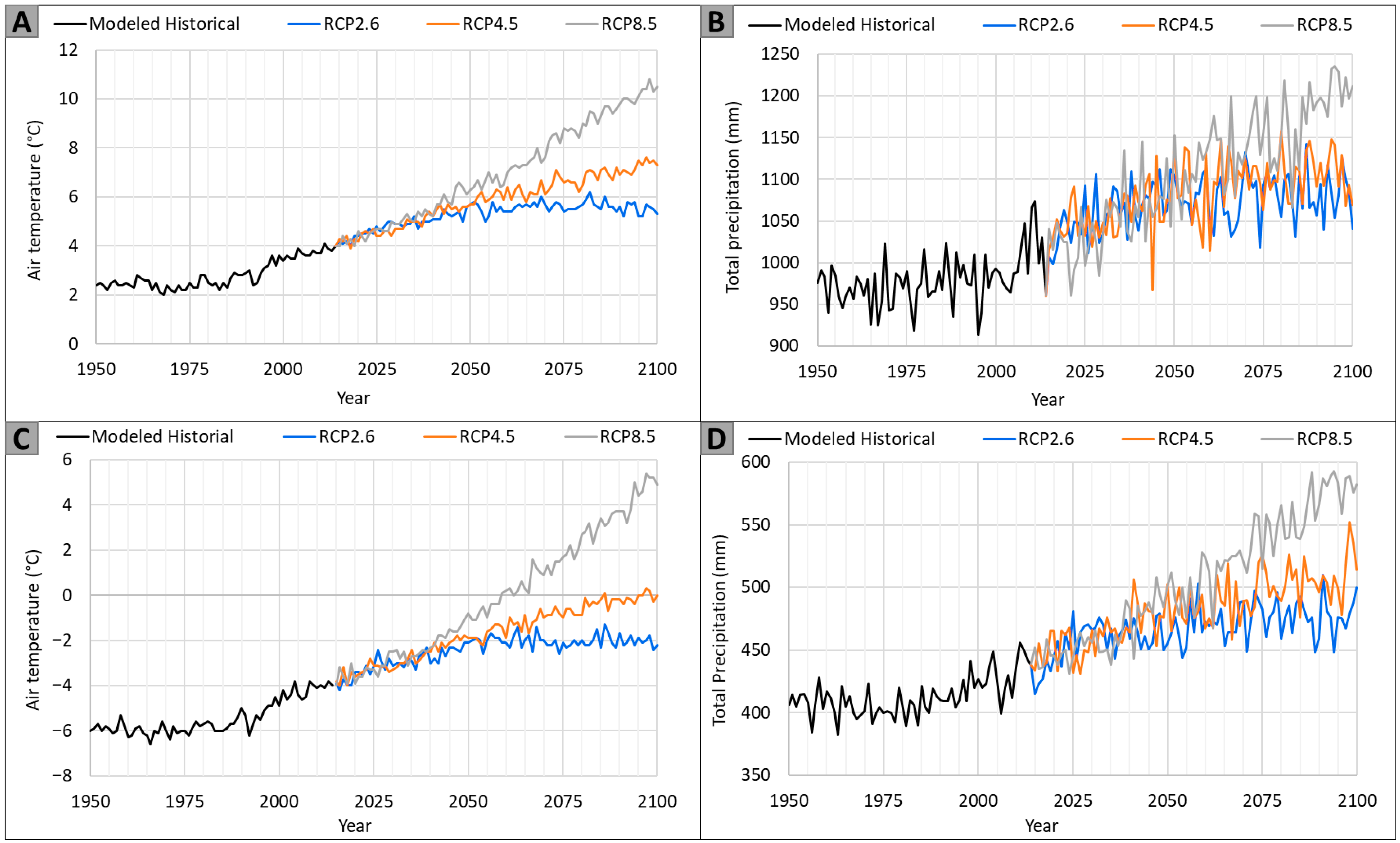
2.10. Simulated Scenarios
3. Results
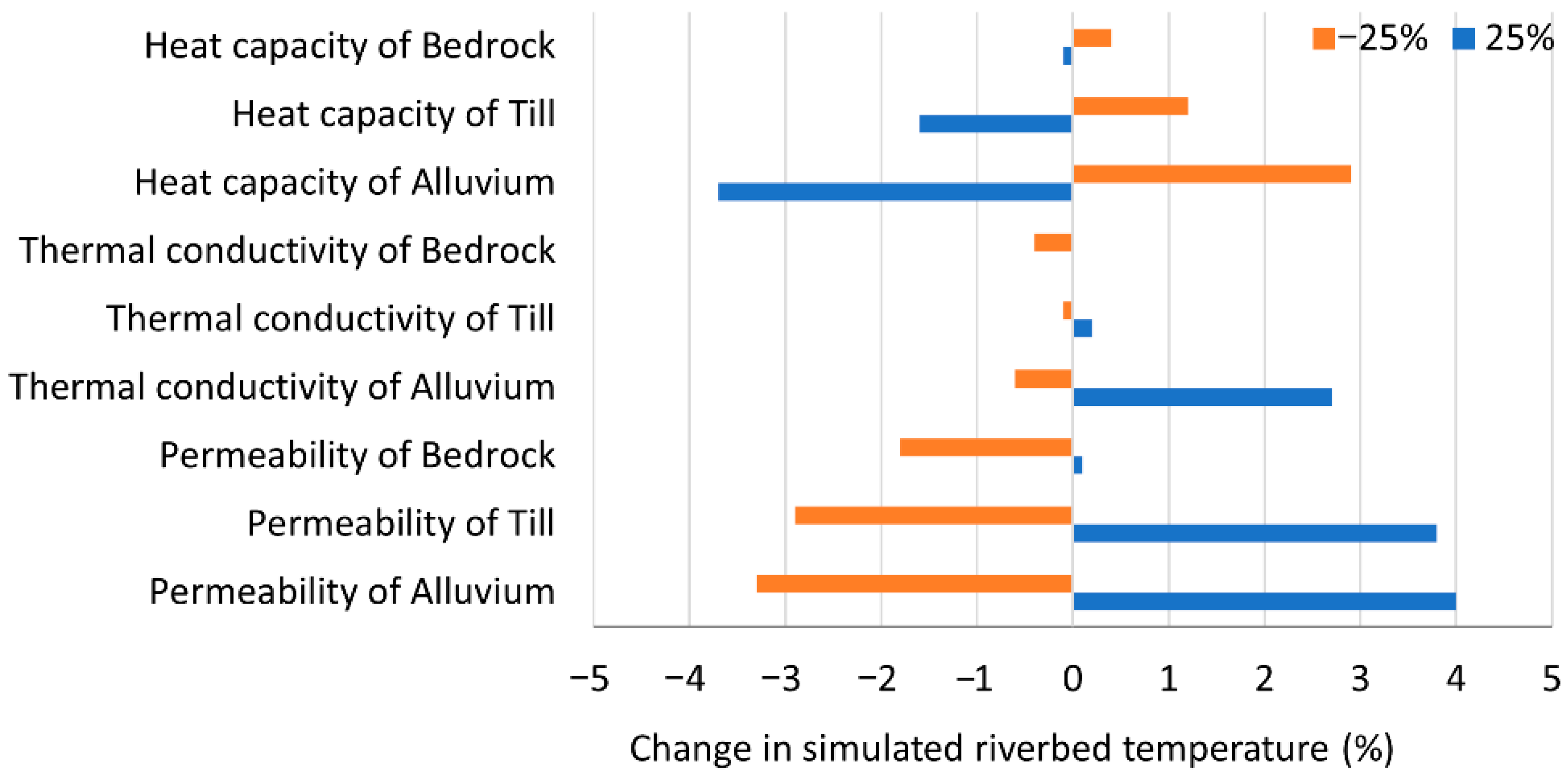
3.1. Sensitivity Analysis and Calibration
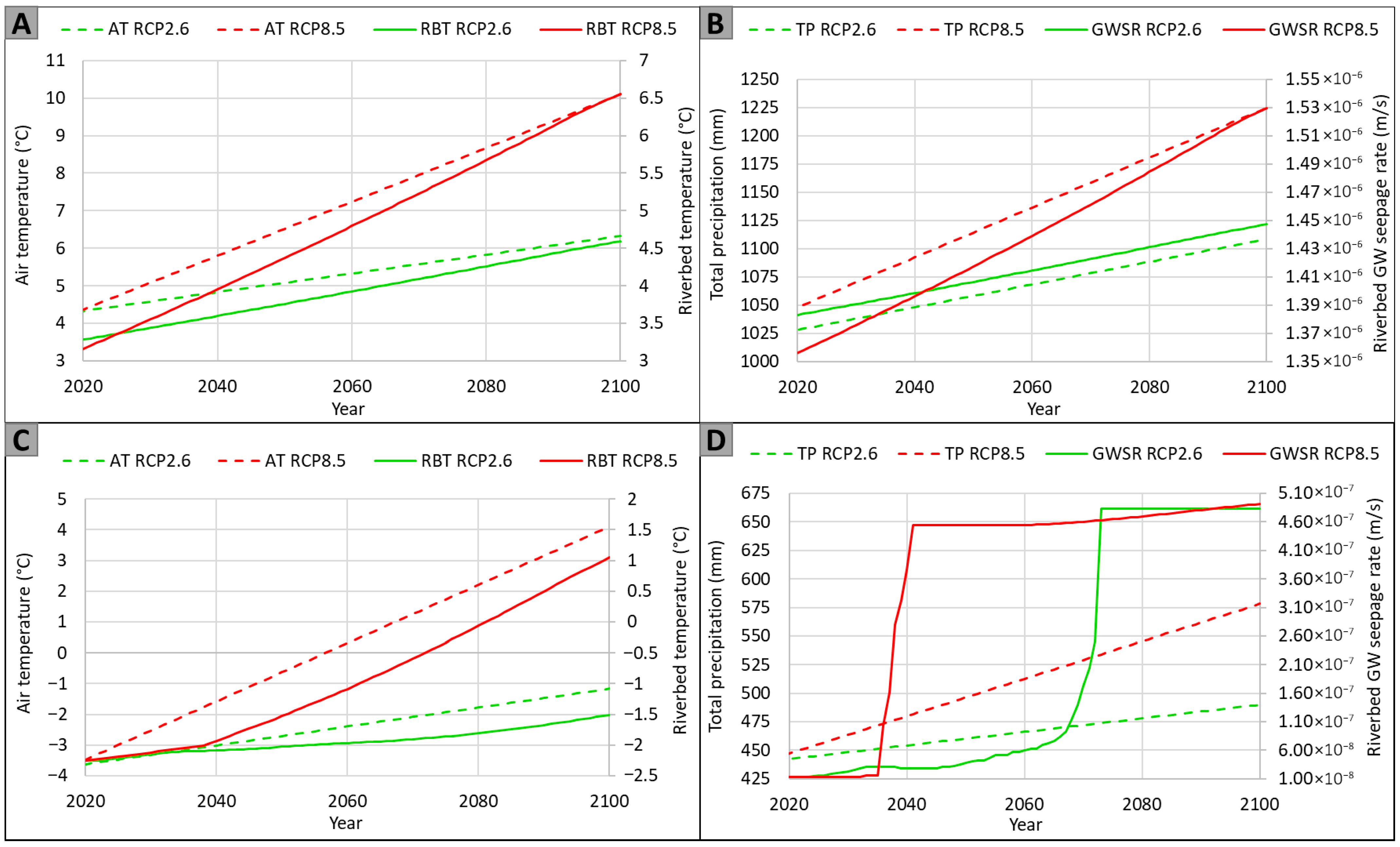
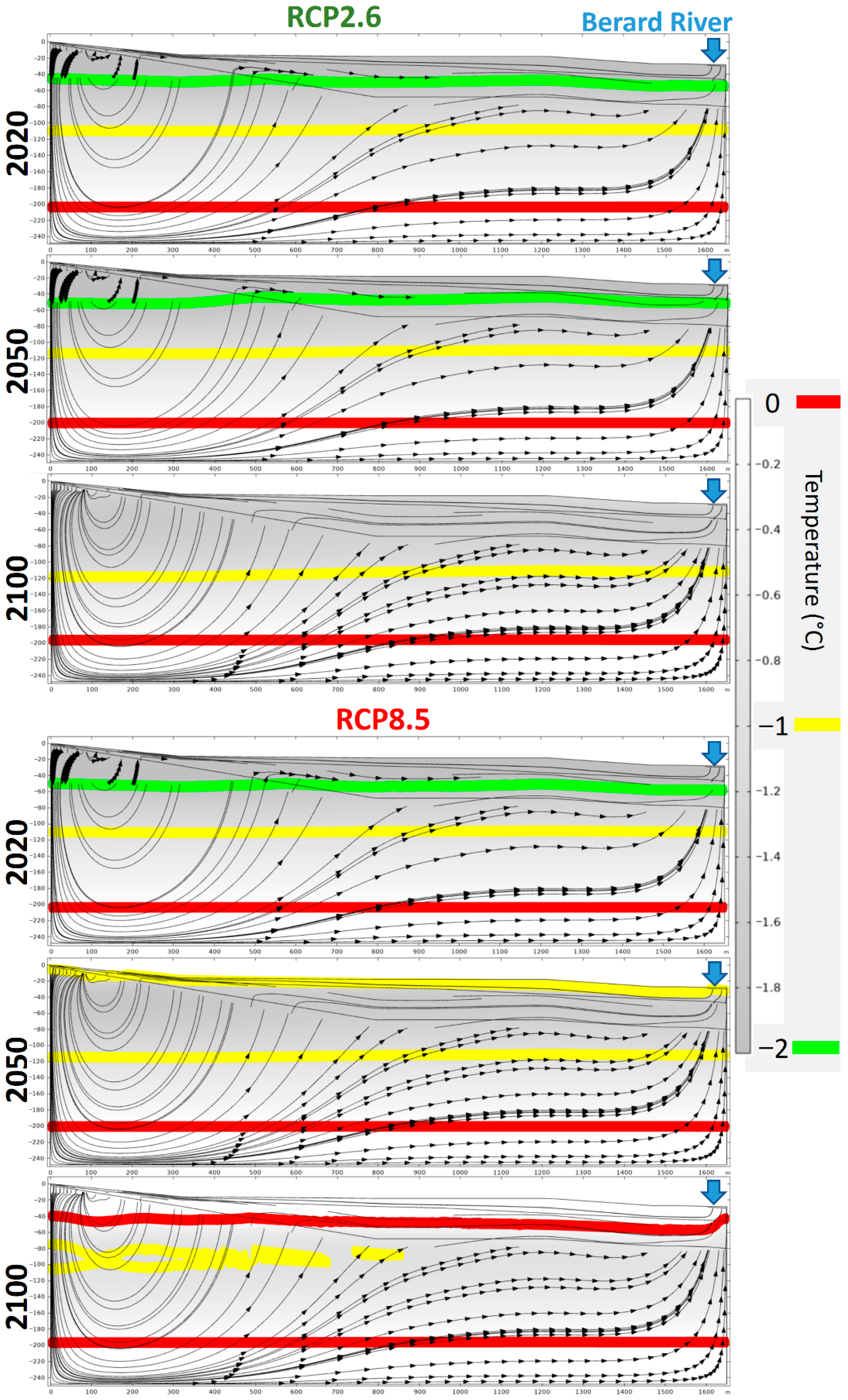
3.2. Long-Term Climate Change Scenarios
4. Discussion
4.1. Limitations and Prospects for Improvement
4.2. Impacts of Climate Change
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Additional Equations
Appendix A.2. Additional Data
| Case Study | Parameter | Measured | Simulated | Difference (%) |
|---|---|---|---|---|
| Sainte-Marguerite River | Ground temperature (°C) | 5.2 | 4.9 | −4 |
| GW head (MASL) | 113.6 | 116.7 | 3 | |
| Riverbed temperature (°C) | 4.9 | 4.3 | −13 | |
| Riverbed seepage rate (m3/s) | 5.9 × 10−7 | 5.0 × 10−7 | −14 | |
| Berard River | Ground temperature (°C) | 1.1 | 1.0 | −11 |
| GW head (MASL) | 15.4 | 13.2 | −14 | |
| Riverbed temperature (°C) | −3.5 | −4.4 | 19 | |
| Riverbed seepage rate (m3/s) | 6.4 × 10−8 | 5.5 × 10−8 | −13 |
| Logger | P1 | P2 | P3 | P4 | R1 | R2 |
|---|---|---|---|---|---|---|
| Average yearly hydraulic head (MASL) | 113.54 | 113.66 | 113.57 | 113.38 | 113.21 | 113.22 |
| Average yearly water temperature (°C) | 3.95 | 4.22 | 3.64 | 10.31 | 7.58 | 10.46 |
| Logger | P1 | P2 | P3 | P4 | P5 | Side Channel (SC) | Main River (MR) |
|---|---|---|---|---|---|---|---|
| Average yearly hydraulic head (MASL) | 15.14 | 15.19 | 15.32 | 15.22 | 14.87 | 14.97 | 15.17 |
| Average yearly water temperature (°C) | 1.63 | 7.34 | 0.80 | 8.37 | 3.69 | 7.52 | 4.75 |
| Seepage Meter | Riverbed Seepage Rate (m3/s) |
|---|---|
| S1 | 3.62 × 10−7 |
| S2 | 3.59 × 10−7 |
| S3 | 5.65 × 10−7 |
| S4 | 3.97 × 10−7 |
| S5 | 3.64 × 10−7 |
| S6 | 8.52 × 10−7 |
| S7 | 1.12 × 10−6 |
| S8 | 7.55 × 10−7 |
| Seepage Meter | Riverbed Seepage Rate (m3/s) |
|---|---|
| S1 | 3.99 × 10−7 |
| S2 | 4.77× 10−8 |
| S3 | 1.06 × 10−7 |
| Others | Inconclusive results |
| Depth Below Ground Surface (cm) | Average Yearly Ground Temperature (°C) |
|---|---|
| 0 | 6.55 |
| 24 | 6.40 |
| 63 | 5.81 |
| 87 | 5.46 |
| 131 | 5.03 |
| Depth Below Ground Surface (cm) | Average Yearly Ground Temperature (°C) |
|---|---|
| 9 | 0.79 |
| 25 | 0.84 |
| 45 | 0.80 |
| 72 | 0.80 |
| 100 | 0.78 |
| 129 | 0.76 |
| 157 | 0.72 |
Appendix A.3. Additional Figures



References
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Hayashi, M.; Rosenberry, D.O. Effects of ground water exchange on the hydrology and ecology of surface water. Ground Water 2002, 40, 309–316. [Google Scholar] [CrossRef] [PubMed]
- Spanoudaki, K.; Stamou, A.I.; Nanou-Giannarou, A. Development and verification of a 3-D integrated surface water-groundwater model. J. Hydrol. 2009, 375, 410–427. [Google Scholar] [CrossRef]
- Hancock, P.J. Human impacts on the stream-groundwater exchange zone. Environ. Manag. 2002, 29, 763–781. [Google Scholar] [CrossRef] [PubMed]
- Saha, G.C.; Li, J.; Thring, R.W.; Hirshfield, F.; Paul, S.S. Temporal dynamics of groundwater-surface water interaction under the effects of climate change: A case study in the Kiskatinaw River Watershed, Canada. J. Hydrol. 2017, 551, 440–452. [Google Scholar] [CrossRef]
- Havril, T.; Tóth, Á.; Molson, J.W.; Galsa, A.; Mádl-Szőnyi, J. Impacts of predicted climate change on groundwater flow systems: Can wetlands disappear due to recharge reduction? J. Hydrol. 2018, 563, 1169–1180. [Google Scholar] [CrossRef]
- Rossetto, R.; Barbagli, A.; De Filippis, G.; Marchina, C.; Vienken, T.; Mazzanti, G. Importance of the induced recharge term in riverbank filtration: Hydrodynamics, hydrochemical, and numerical modelling investigations. Hydrology 2020, 7, 96. [Google Scholar] [CrossRef]
- Lamontagne, S.; Leaney, F.W.; Herczeg, A.L. Groundwater-surface water interactions in a large semi-arid floodplain: Implications for salinity management. Hydrol. Process. 2005, 19, 3063–3080. [Google Scholar] [CrossRef]
- Hassan, S.M.T.; Lubczynski, M.W.; Niswonger, R.G.; Su, Z. Surface-groundwater interactions in hard rocks in Sardon Catchment of western Spain: An integrated modeling approach. J. Hydrol. 2014, 517, 390–410. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, Y.; Wu, B.; Wu, X.; Liu, J.; Zheng, C. Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Model. Softw. 2015, 63, 170–184. [Google Scholar] [CrossRef]
- Floriancic, M.G.; Abhervé, R.; Bouchez, C.; Jimenez-Martinez, J.; Roques, C. Evidence of Groundwater Seepage and Mixing at the Vicinity of a Knickpoint in a Mountain Stream. Geophys. Res. Lett. 2024, 51, e2024GL111325. [Google Scholar] [CrossRef]
- Poesch, M.S.; Chavarie, L.; Chu, C.; Pandit, S.N.; Tonn, W. Climate Change Impacts on Freshwater Fishes: A Canadian Perspective. Fisheries 2016, 41, 385–391. [Google Scholar] [CrossRef]
- Jensen, A.J.; Johnsen, B.O.; Saksgard, L. Temperature requirements in Atlantic salmon (Salmo salar), brown trout (Salmon trutta), and Arctic char (Salvelinus alpinus) from hatching to initial feeding compared with geographic distribution. Can. J. Fish. Aquat. Sci. 1989, 46, 786–789. [Google Scholar] [CrossRef]
- Finstad, A.G.; Jonsson, B. Effect of incubation temperature on growth performance in Atlantic salmon. Mar. Ecol. Prog. Ser. 2012, 454, 75–82. [Google Scholar] [CrossRef]
- Nyanti, L.; Soo, C.L.; Ahmad-Tarmizi, N.N.; Abu-Rashid, N.N.K.; Ling, T.Y.; Sim, S.F.; Grinang, J.; Ganyai, T.; Lee, K.S.P. Effects of water temperature, dissolved oxygen and total suspended solids on juvenile barbonymus schwanenfeldii (Bleeker, 1854) and Oreochromis niloticus (Linnaeus, 1758). AACL Bioflux 2018, 11, 394–406. [Google Scholar]
- Lorenz, J.M.; Filer, J.H. Spawning Habitat and Redd Characteristics of Sockeye Salmon in the Glacial Taku River, British Columbia and Alaska. Trans. Am. Fish. Soc. 1989, 118, 495–502. [Google Scholar] [CrossRef]
- Geist, D.R.; Dauble, D.D. Redd site selection and spawning habitat use by fall chinook salmon: The importance of geomorphic features in large rivers. Environ. Manag. 1998, 22, 655–669. [Google Scholar] [CrossRef] [PubMed]
- Power, G.; Brown, R.S.; Imhof, J.G. Groundwater and fish—Insights from northern North America. Hydrol. Process. 1999, 13, 401–422. [Google Scholar] [CrossRef]
- Fakhari, M.; Raymond, J.; Martel, R.; Dugdale, S.J.; Bergeron, N. Identification of Thermal Refuges and Water Temperature Patterns in Salmonid-Bearing Subarctic Rivers of Northern Quebec. Geographies 2022, 2, 528–548. [Google Scholar] [CrossRef]
- Fakhari, M.; Raymond, J.; Martel, R.; Drolet, J.-P.; Dugdale, S.; Bergeron, N. Analysis of Large-Scale Groundwater-Driven Cooling Zones in Rivers Using Thermal Infrared Imagery and Radon Measurements. Water 2023, 15, 873. [Google Scholar] [CrossRef]
- Saltveit, S.J.; Brabrand, Å. Incubation, hatching and survival of eggs of Atlantic salmon (Salmo salar) in spawning redds influenced by groundwater. Limnologica 2013, 43, 325–331. [Google Scholar] [CrossRef]
- Caissie, D. The thermal regime of rivers: A review. Freshw. Biol. 2006, 51, 1389–1406. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Voss, C.I.; Wellman, T.P. Influence of permafrost distribution on groundwater flow in the context of climate-driven permafrost thaw: Example from Yukon Flats Basin, Alaska, United States. Water Resour. Res. 2012, 48, 1–17. [Google Scholar] [CrossRef]
- Evans, S.G.; Ge, S. Contrasting hydrogeologic responses to warming in permafrost and seasonally frozen ground hillslopes. Geophys. Res. Lett. 2017, 44, 1803–1813. [Google Scholar] [CrossRef]
- Allard, M.; Chiasson, A.; St-amour, A.B.; Aubé-michaud, S.; Mathon-dufour, V.; Hérault, E.L.; Bilodeau, S.; Deslauriers, C. Caractérisation Géotechnique et Cartographie Améliorée Du Pergélisol Dans Les Communautés Nordiques Du Nunavik; Final Report; Centre D’études Nordiques, Université Laval: Québec, QC, Canada, 2020; 76p. [Google Scholar] [CrossRef]
- Perreault, J.; Fortier, R.; Molson, J.W. Numerical Modelling of Permafrost Dynamics under Climate Change and Evolving Ground Surface Conditions: Application to an Instrumented Permafrost Mound at Umiujaq, Nunavik (Québec), Canada. Ecoscience 2021, 28, 377–397. [Google Scholar] [CrossRef]
- Neilson, B.T.; Cardenas, M.B.; O’Connor, M.T.; Rasmussen, M.T.; King, T.V.; Kling, G.W. Groundwater Flow and Exchange Across the Land Surface Explain Carbon Export Patterns in Continuous Permafrost Watersheds. Geophys. Res. Lett. 2018, 45, 7596–7605. [Google Scholar] [CrossRef]
- Ingebritsen, S.E.; Sanford, W.E.; Neuzil, C.E. Groundwater in Geologic Processes; Cambridge University Press: Cambridge, UK, 1998; ISBN 052149608X. [Google Scholar]
- Raymond, J.; Therrien, R. Optimizing the design of a geothermal district heating and cooling system located at a flooded mine in Canada. Hydrogeol. J. 2014, 22, 217–231. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; Hayashi, M.; Quinton, W.L.; McKenzie, J.M.; Voss, C.I. Influence of vertical and lateral heat transfer on permafrost thaw, peatland landscape transition, and groundwater flow. Water Resour. Res. 2016, 52, 1286–1305. [Google Scholar] [CrossRef]
- Cho, J.; Mostaghimi, S.; Kang, M.S. Development and application of a modeling approach for surface water and groundwater interaction. Agric. Water Manag. 2010, 97, 123–130. [Google Scholar] [CrossRef]
- Tian, W.; Li, X.; Cheng, G.D.; Wang, X.S.; Hu, B.X. Coupling a groundwater model with a land surface model to improve water and energy cycle simulation. Hydrol. Earth Syst. Sci. 2012, 16, 4707–4723. [Google Scholar] [CrossRef]
- Hunt, R.J.; Westenbroek, S.M.; Walker, J.F.; Selbig, W.R.; Regan, R.S.; Leaf, A.T.; Saad, D.A. Simulation of Climate Change Effects on Streamflow, Groundwater, and Stream Temperature Using GSFLOW and SNTEMP in the Black Earth Creek Watershed, Wisconsin; USGS: Reston, VA, USA, 2016.
- Smith, S.L.; Burgess, M.M. A Digital Database of Permafrost Thickness in Canada; Natural Resources Canada: Ottawa, ON, Canada, 2002. [Google Scholar]
- Lévesque, R.; Allard, M.; Seguin, M.K.; Pilon, J.-A. Données préliminaires sur la régime thermique du pergélisol dans quelques localités du Nunavik, Québec. In Proceedings of the Fifth Canadian Permafrost Conference, Nordicana no 54, Quebec City, QC, Canada, 5–8 June 1990; pp. 207–213. [Google Scholar]
- Gray, J.T.; Pilon, J.A.; Poitevin, J. Le pergélisol et la couche active dans la toundra forestière au sud de la baie aux Feuilles, Nouveau-Québec. Geogr. Phys. Quat. 1979, 33, 253–264. [Google Scholar] [CrossRef][Green Version]
- ClimateData.ca Data Source: Environment and Climate Change Canada and (ClimateData.ca). Available online: https://climatedata.ca/maps/?var=hottest_day&th=tx_max&dataset=216&dataOpacity=100&labelOpacity=100&lat=57.55615&lng=-70.20264&zoom=6 (accessed on 1 June 2020).[Green Version]
- Mookerji, N.; Weng, Z.; Mazumder, A. Food partitioning between coexisting Atlantic salmon and brook trout in the Sainte-Marguerite River ecosystem, Quebec. J. Fish. Biol. 2004, 64, 680–694. [Google Scholar] [CrossRef]
- Mainguy, J.; Beaupré, L. Établissement D’un État de Référence Pour la Population D’omble Chevalier de la Rivière BÉRARD à Tasiujaq; Ministère des Forêts, de la Faune et des Parcs, Direction de L’expertise Sur la Faune Aquatique et Direction de la Gestion de la Faune du Nord-du-Québec: Québec, QC, Canada, 2019.
- SIGÉOM Surface Deposits Map. Available online: https://sigeom.mines.gouv.qc.ca/signet/classes/I1108_afchCarteIntr (accessed on 1 June 2020).
- Fakhari, M.; Raymond, J.; Martel, R.; Klepikova, M.; Bour, O. Complementarity of multiple in-situ techniques for spatiotemporal assessment of groundwater/surface-water exchanges. Hydrogeol. J. 2025, 33, 219–235. [Google Scholar] [CrossRef]
- COMSOL. COMSOL Multiphysics® Simulation Software. Available online: https://www.comsol.com/comsol-multiphysics (accessed on 1 June 2023).
- Chesnaux, R.; Lambert, M.; Walter, J.; Fillastre, U.; Hay, M.; Rouleau, A.; Daigneault, R.; Moisan, A.; Germaneau, D. Building a geodatabase for mapping hydrogeological features and 3D modeling of groundwater systems: Application to the Saguenay-Lac-St.-Jean region, Canada. Comput. Geosci. 2011, 37, 1870–1882. [Google Scholar] [CrossRef]
- Chesnaux, R. Using ArcHydro Groundwater for 3D modeling of quaternary deposits in the Saguenay-Lac-St.-Jean region. In Proceedings of the ESRI Canada User Conferences, San Diego, CA, USA, 11–15 July 2011. [Google Scholar]
- Comeau, F.A.; Raymond, J.; Malo, M.; Dezayes, C.; Carreau, M. Geothermal potential of Northern Québec: A regional assessment. Trans. Geotherm. Resour. Counc. 2017, 41, 1076–1094. [Google Scholar]
- Freeze, A.; Cherry, J. Groundwater; Prentice-Hall Inc.: Saddle River, NJ, USA, 1979; ISBN 0133653129. [Google Scholar]
- Dagher, E.E.; Su, G.; Nguyen, T.S. Verification of the Numerical Simulation of Permafrost Using COMSOL Multiphysics® Software. In Proceedings of the COMSOL Conference 2014, Boston, MA, USA, 8–10 October 2014; pp. 1–9. [Google Scholar]
- Hu, R.; Liu, Q.; Xing, Y. Case study of heat transfer during artificial ground freezing with groundwater flow. Water 2018, 10, 1322. [Google Scholar] [CrossRef]
- Osborne, P.E.; Alvares-Sanches, T. Quantifying how landscape composition and configuration affect urban land surface temperatures using machine learning and neutral landscapes. Comput. Environ. Urban Syst. 2019, 76, 80–90. [Google Scholar] [CrossRef]
- Yusuf, Y.A.; Pradhan, B.; Idrees, M.O. Spatio-temporal Assessment of Urban Heat Island Effects in Kuala Lumpur Metropolitan City Using Landsat Images. J. Indian Soc. Remote Sens. 2014, 42, 829–837. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. CMIP5 permafrost degradation projection: A comparison among different regions. J. Geophys. Res. Atmos. 2016, 121, 4449–4517. [Google Scholar] [CrossRef]
- Anisimov, O.; Reneva, S. Permafrost and changing climate: The Russian perspective. Ambio J. Hum. Environ. 2006, 35, 169–175. [Google Scholar] [CrossRef]
- Adiya, S.; Erdenebat, E. 21st century permafrost distribution under the scenario of RCP2.6 and RCP8.5 in Mongolia. Proc. Mong. Acad. Sci. 2021, 61, 9–14. [Google Scholar] [CrossRef]
- Koven, C.D.; Riley, W.J.; Stern, A. Analysis of permafrost thermal dynamics and response to climate change in the CMIP5 earth system models. J. Clim. 2013, 26, 1877–1900. [Google Scholar] [CrossRef]
- Buteau, S.; Fortier, R.; Delisle, G.; Allard, M. Numerical simulation of the impacts of climate warming on a permafrost mound. Permafr. Periglac. Process. 2004, 15, 41–57. [Google Scholar] [CrossRef]
- Frampton, A.; Painter, S.; Lyon, S.W.; Destouni, G. Non-isothermal, three-phase simulations of near-surface flows in a model permafrost system under seasonal variability and climate change. J. Hydrol. 2011, 403, 352–359. [Google Scholar] [CrossRef]
- Frechette, D.M.; Dugdale, S.J.; Dodson, J.J.; Bergeron, N.E. Understanding summertime thermal refuge use by adult Atlantic salmon using remote sensing, river temperature monitoring, and acoustic telemetry1. Can. J. Fish. Aquat. Sci. 2018, 75, 1999–2010. [Google Scholar] [CrossRef]
- Linnansaari, T.; O’Sullivan, A.M.; Breau, C.; Corey, E.M.; Collet, E.N.; Curry, R.A.; Cunjak, R.A. The Role of Cold-Water Thermal Refuges for Stream Salmonids in a Changing Climate—Experiences from Atlantic Canada. Fishes 2023, 8, 471. [Google Scholar] [CrossRef]
- Snyder, M.N.; Schumaker, N.H.; Dunham, J.B.; Ebersole, J.L.; Keefer, M.L.; Halama, J.; Comeleo, R.L.; Leinenbach, P.; Brookes, A.; Cope, B.; et al. Tough places and safe spaces: Can refuges save salmon from a warming climate? Ecosphere 2022, 13, e4265. [Google Scholar] [CrossRef] [PubMed]
- Oyinlola, M.A.; Khorsandi, M.; Penman, R.; Earhart, M.L.; Arsenault, R.; Brauner, C.J.; St-Hilaire, A. Hydrothermal impacts of water release on early life stages of white Sturgeon in the Nechako river (B.C. Canada). J. Therm. Biol. 2023, 53, 125–134. [Google Scholar] [CrossRef]

| Geological Unit | Unfrozen Hydraulic Conductivity (m·s−1) | Frozen Hydraulic Conductivity (m·s−1) | Porosity (−) |
|---|---|---|---|
| Alluvial | 1 × 10−4 | 1 × 10−7 | 0.25 |
| Till | 1 × 10−7 | 1 × 10−10 | 0.35 |
| Bedrock | 1 × 10−10 | 1 × 10−13 | 0.05 |
| Material/Geological Unit | Thermal Conductivity (W·m−1·K−1) | Heat Capacity (J·kg−1·K−1) | Density (kg·m−3) |
|---|---|---|---|
| Alluvial (Solid) | 0.5 | 300 | 1500 |
| Till (Solid) | 1 | 500 | 1300 |
| Bedrock (Solid) | 2 | 1000 | 2500 |
| Water | 0.6 | 4200 | 1000 |
| Ice | 2.14 | 2100 | 920 |
| Scenario | RCP2.6 | RCP8.5 | ||
|---|---|---|---|---|
| River | AT (°C/yr) | TP (mm/yr) | AT (°C/yr) | TP (mm/yr) |
| Sainte-Marguerite | 0.02 | 1.00 | 0.07 | 2.20 |
| Berard | 0.03 | 0.60 | 0.09 | 1.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fakhari, M.; Raymond, J.; Martel, R. Hydrothermal Modeling of Groundwater–Surface Water Interactions Under an Evolving Climate. Geosciences 2025, 15, 370. https://doi.org/10.3390/geosciences15090370
Fakhari M, Raymond J, Martel R. Hydrothermal Modeling of Groundwater–Surface Water Interactions Under an Evolving Climate. Geosciences. 2025; 15(9):370. https://doi.org/10.3390/geosciences15090370
Chicago/Turabian StyleFakhari, Milad, Jasmin Raymond, and Richard Martel. 2025. "Hydrothermal Modeling of Groundwater–Surface Water Interactions Under an Evolving Climate" Geosciences 15, no. 9: 370. https://doi.org/10.3390/geosciences15090370
APA StyleFakhari, M., Raymond, J., & Martel, R. (2025). Hydrothermal Modeling of Groundwater–Surface Water Interactions Under an Evolving Climate. Geosciences, 15(9), 370. https://doi.org/10.3390/geosciences15090370






