A Novel Probabilistic Approach for Debris Flow Accumulation Volume Prediction Using Bayesian Neural Networks with Synthetic and Real-World Data
Abstract
1. Introduction
2. Materials and Methods
2.1. General Introduction to Bayesian Neural Network Architecture
2.1.1. “Bayes by Backprop”: Weight Uncertainty in Neural Networks
2.1.2. Implementation of “Bayes by Backprop” in TensorFlow
2.2. Datasets
2.2.1. Real Datasets
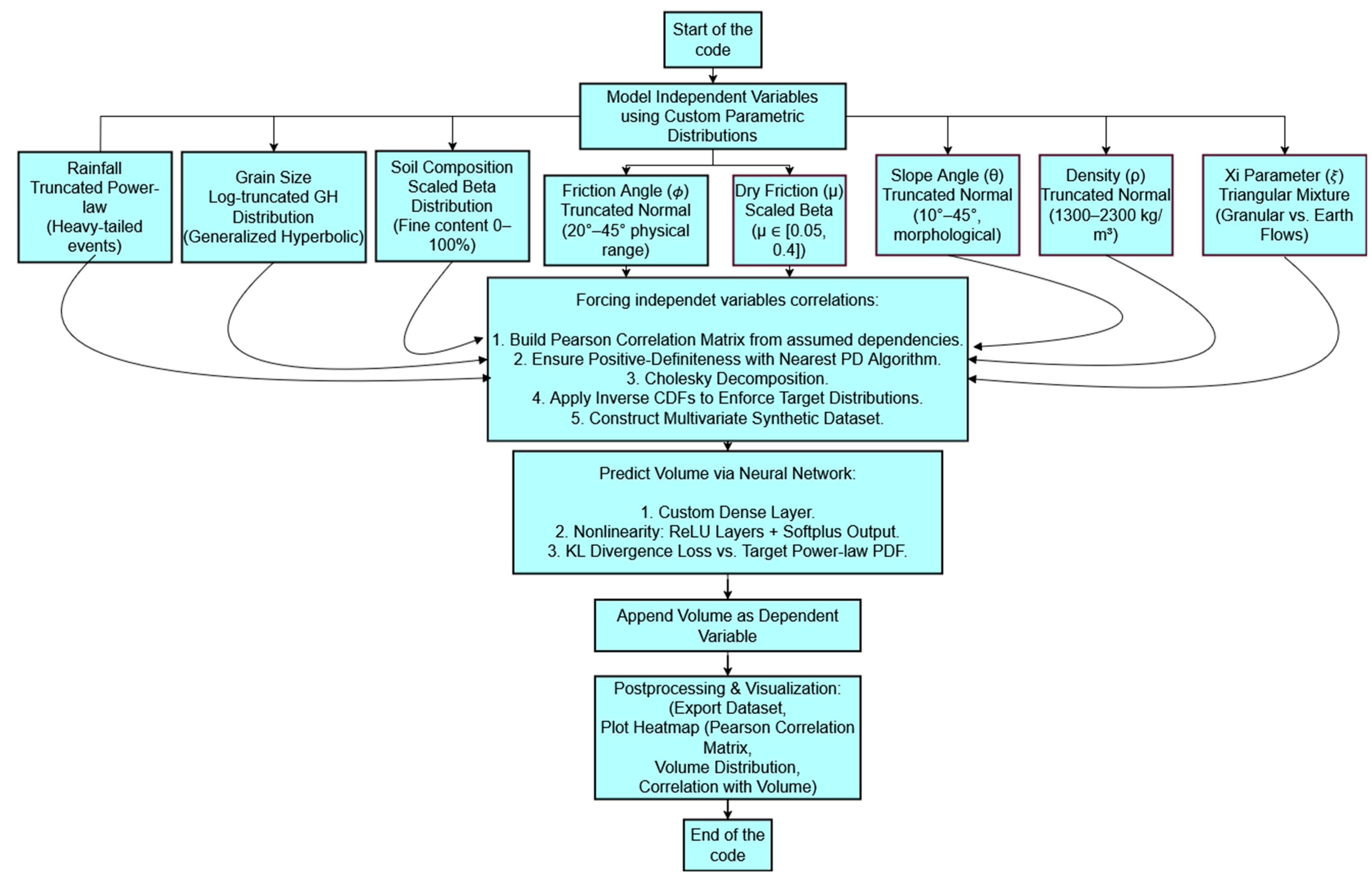
2.2.2. General Description of Synthetic Dataset Generation
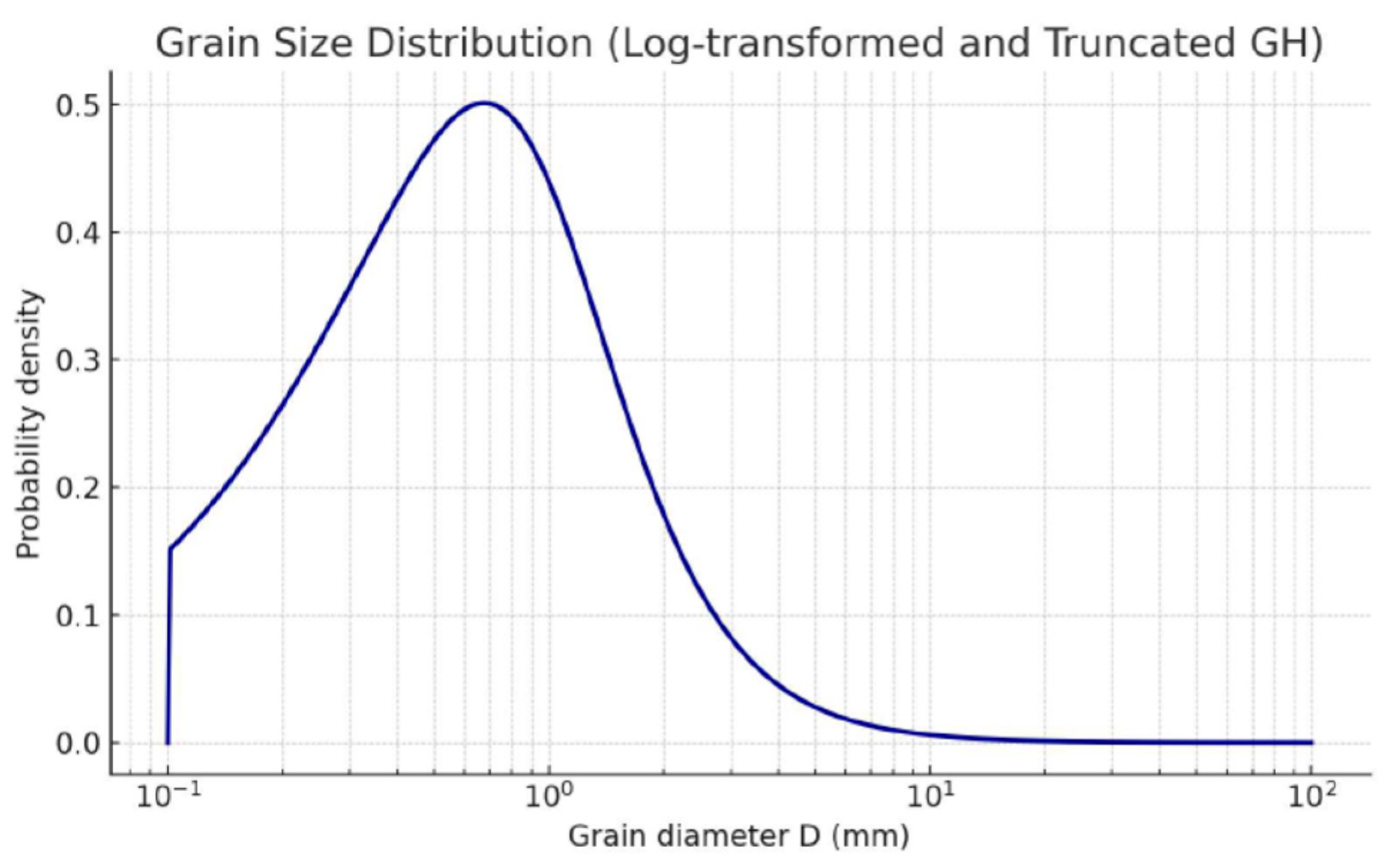
Modeling of Independent Variables and Distributions
Imposition of Inter-Variable Correlation Structure
Dependent Variable Volume Generation
2.3. Application of Bayesian Neural Networks
2.3.1. Data Preparation and Preprocessing
2.3.2. Selected Bayesian Neural Network Architecture
2.3.3. Training, Evaluation, and Uncertainty Analysis
2.3.4. Application to Synthetic Data
2.3.5. Application to Real-World Debris Flow Data
3. Results
3.1. Generation of Synthetic Dataset
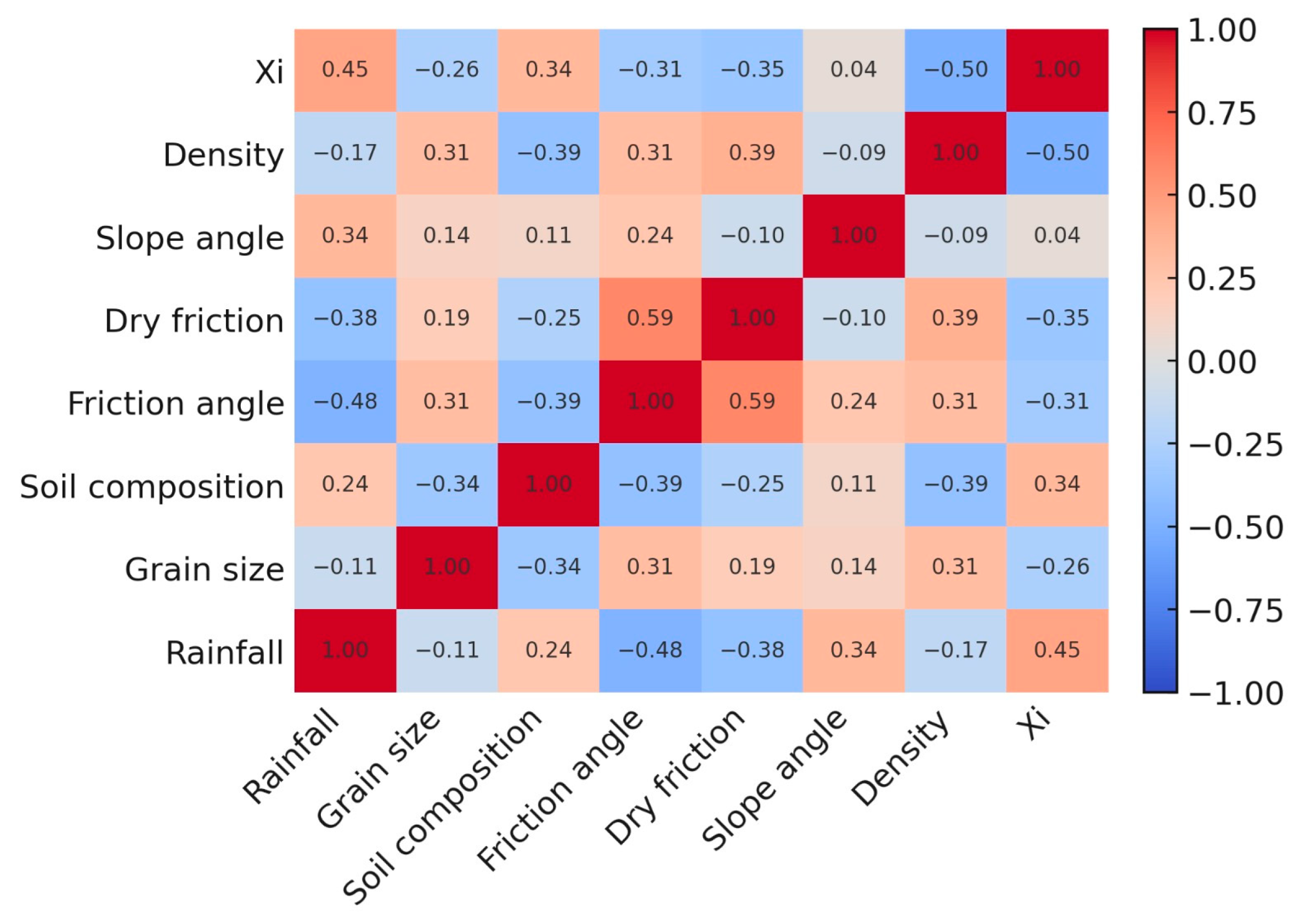
3.1.1. Independent Variable Correlation Matrix
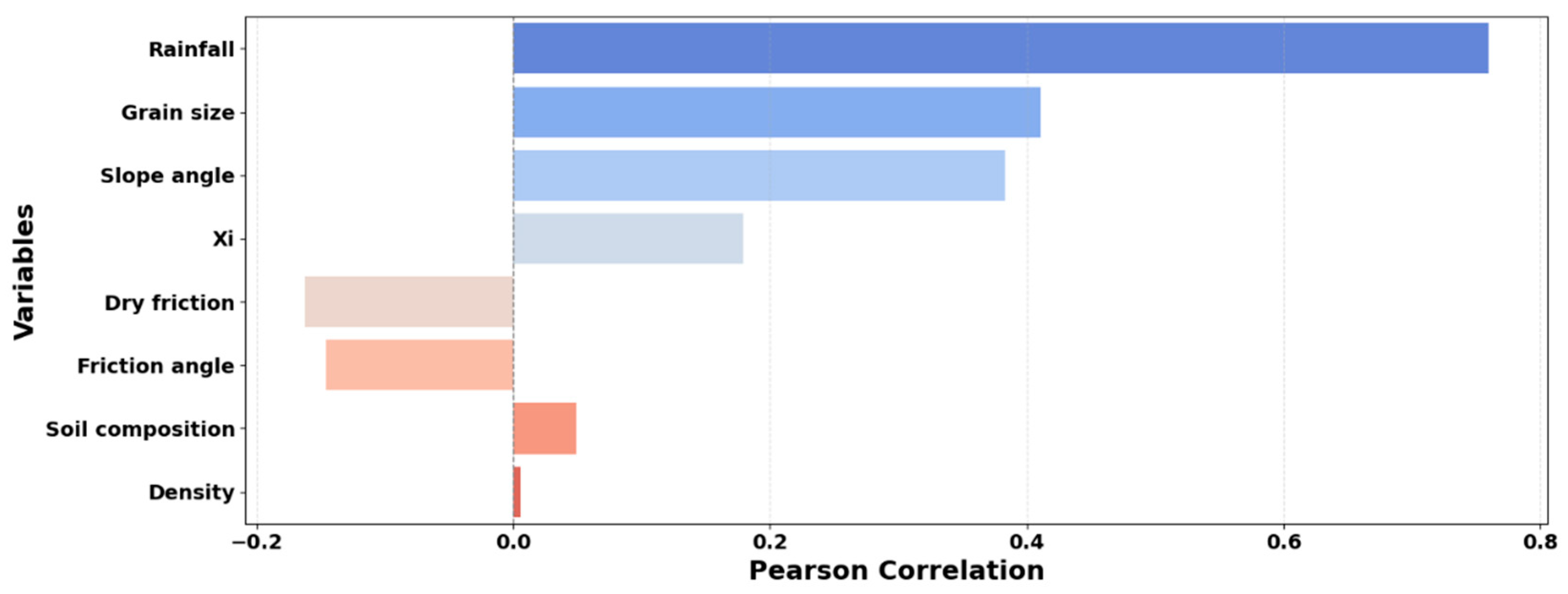
3.1.2. Correlation of Independent Variables with the Dependent Variable
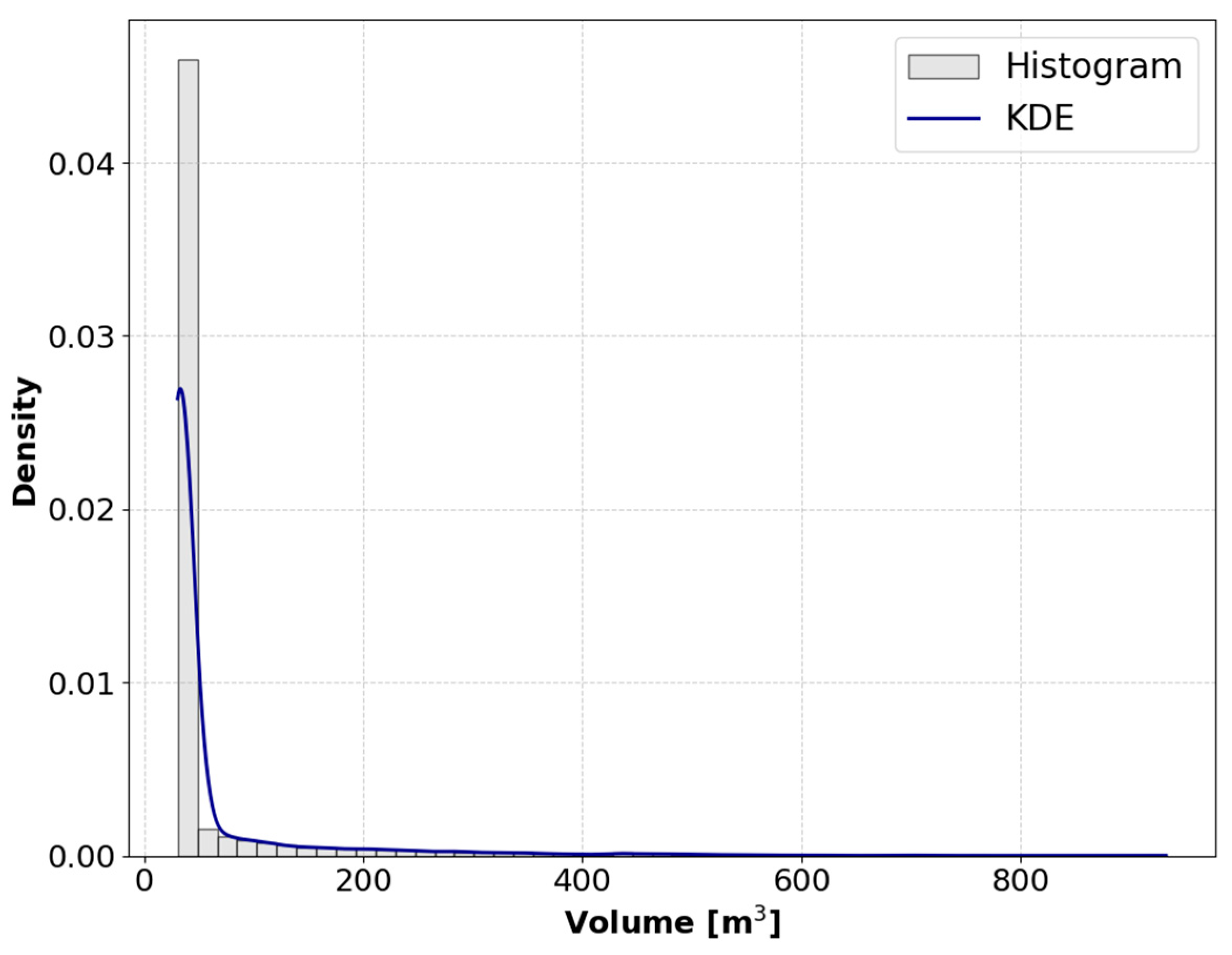
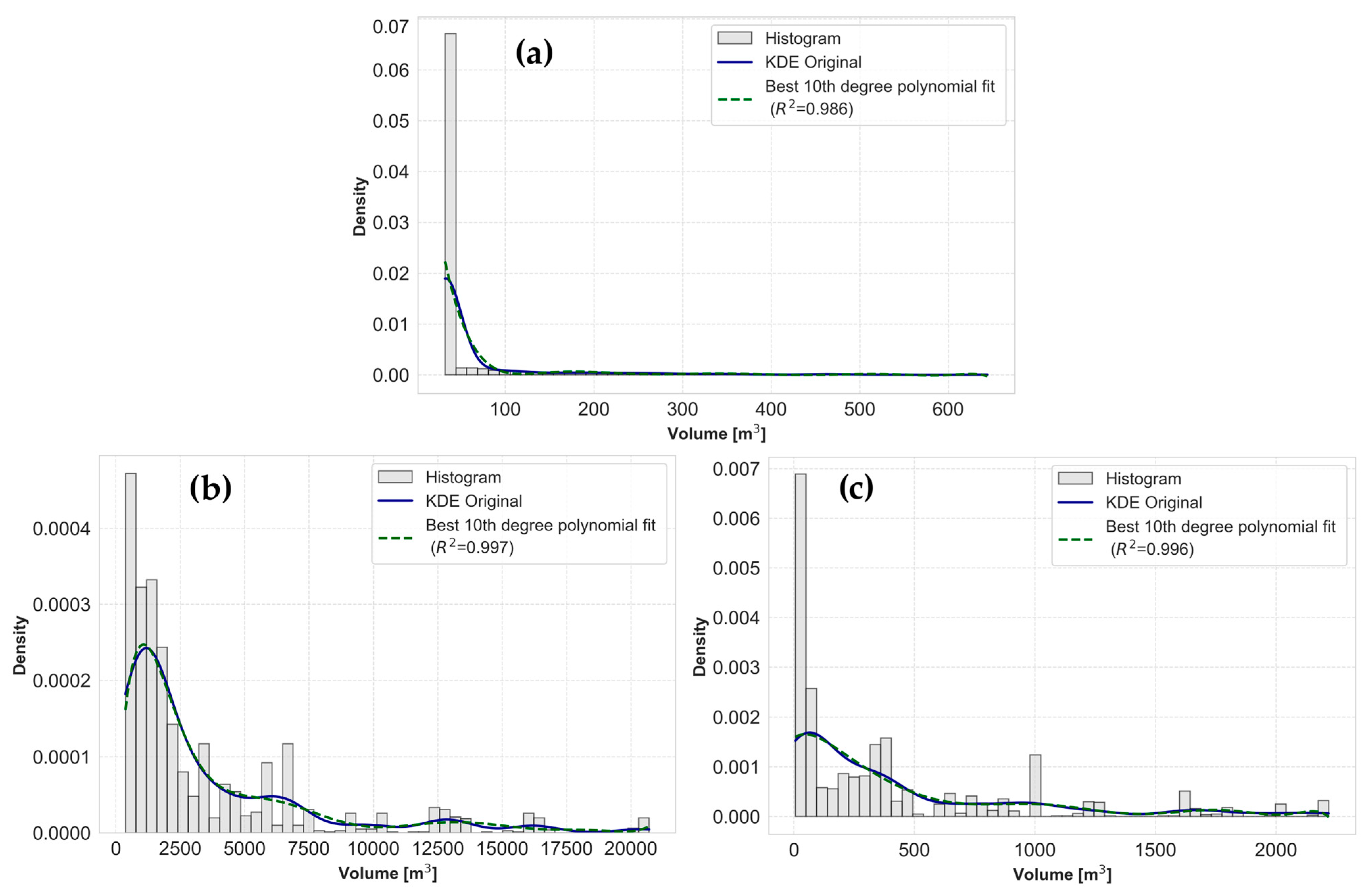
3.1.3. Predicted Volume Distribution
3.2. BNN Performance
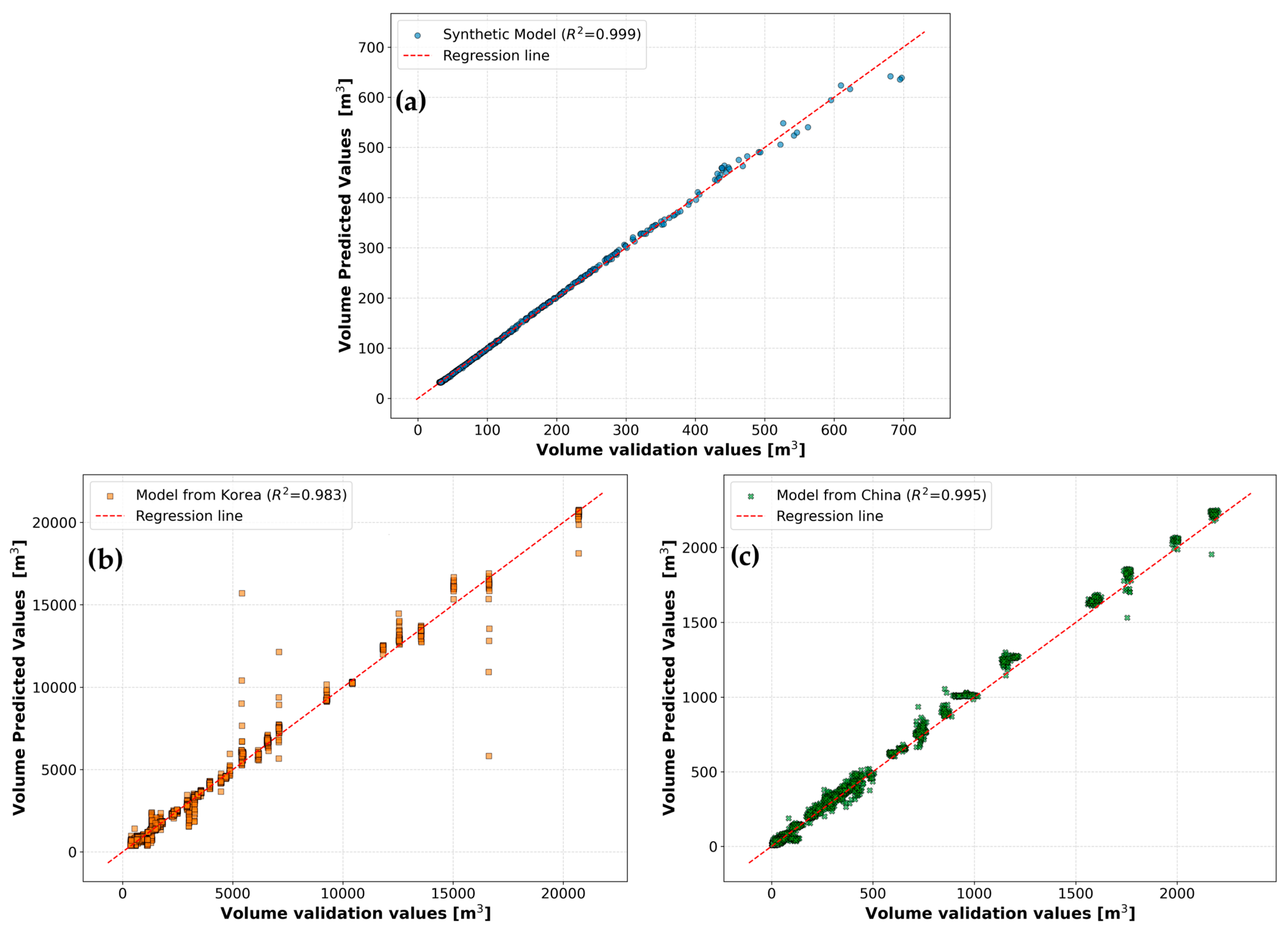
3.2.1. Model Performance Evaluation
3.2.2. Prediction Uncertainty Analysis
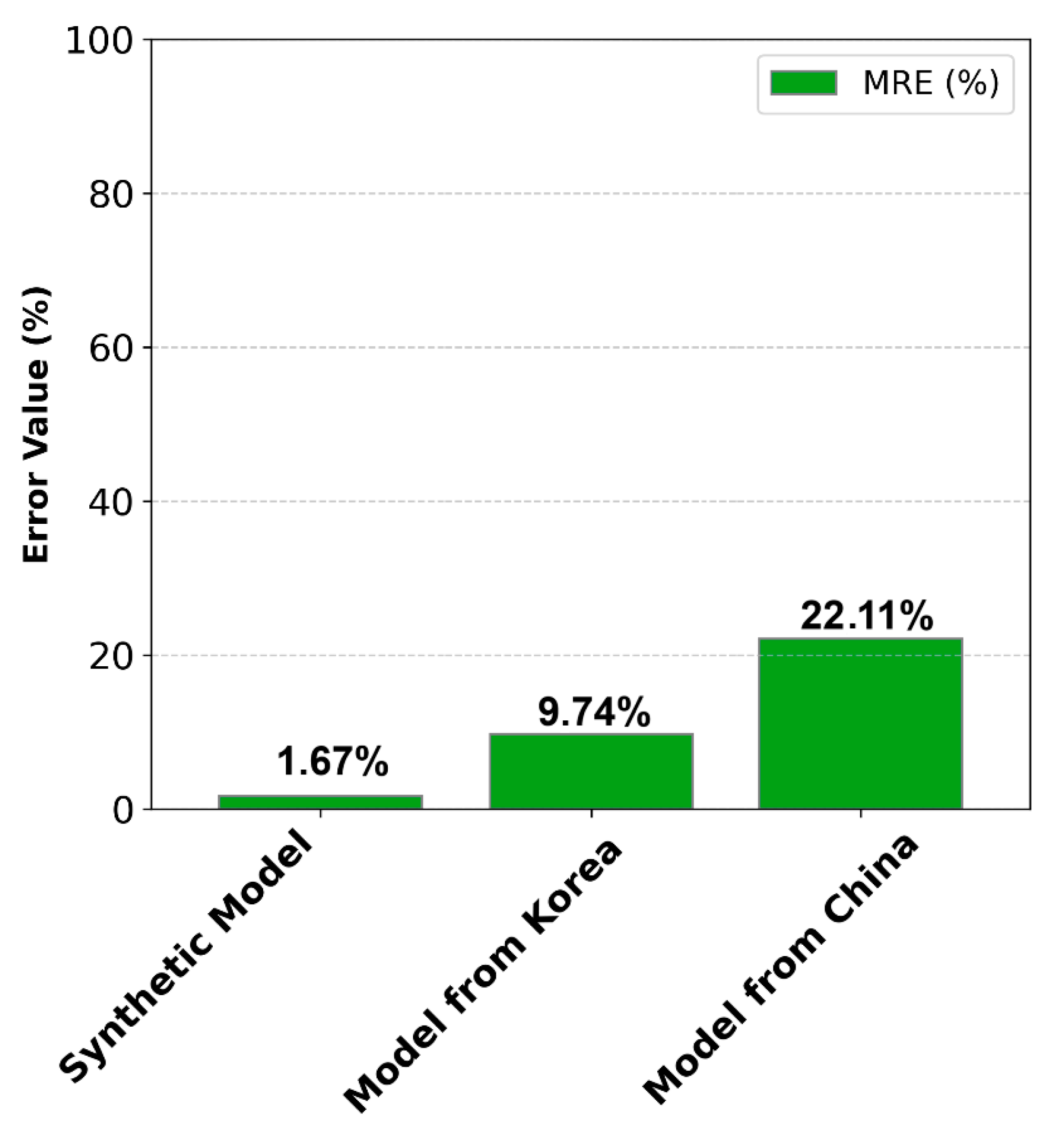
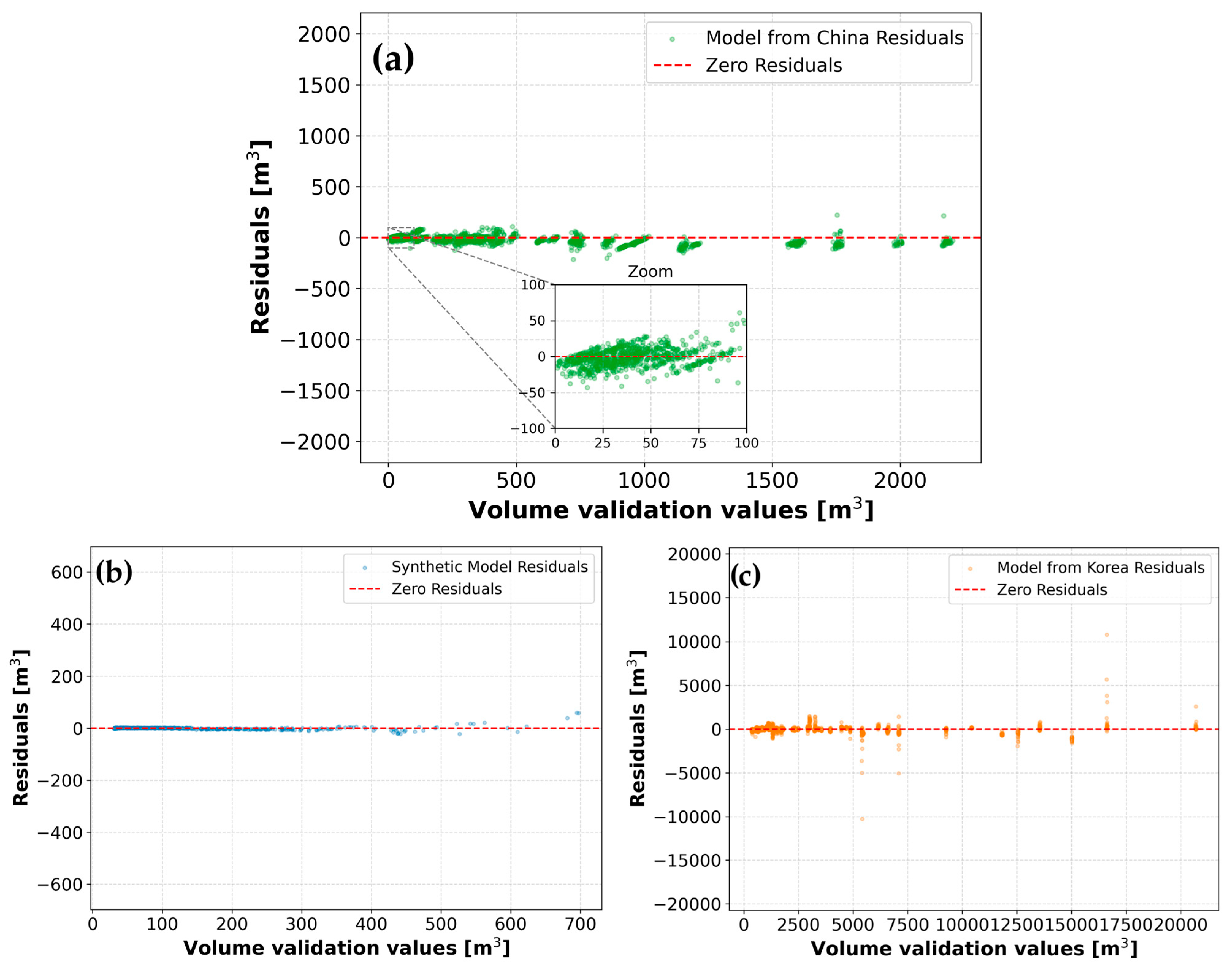
3.2.3. Error Metric Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Correction Statement
References
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, J.; Denzler, J.; Oh, N.K.; Tomioka, R. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Falah, F.; Rahmati, O.; Rostami, M.; Ahmadisharaf, E.; Daliakopoulos, I.N.; Pourghasemi, H.R. Artificial Neural Networks for Flood Susceptibility Mapping in Data-Scarce Urban Areas. In Data-Driven Approaches for Water Resources Management; Elsevier: Amsterdam, The Netherlands, 2019; pp. 317–332. [Google Scholar]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide Susceptibility Assessment and Factor Effect Analysis: Back Propagation Artificial Neural Networks and Their Comparison with Frequency Ratio and Bivariate Logistic Regression Modeling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: A systematic review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslide in a changing climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Debris flow Types and Processes. In Debris Flows: Investigation and Mitigation; Special Report No. 247; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board: Washington, DC, USA; National Research Council: Ottawa, ON, Canada, 1996; pp. 36–75. [Google Scholar]
- Petley, D. Global patterns of loss of life from debris flows. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Chung, T.J. Computational Fluid Dynamics, 4th ed.; Cambridge University Press: Cambridge, UK, 2006; p. 1012. [Google Scholar]
- Pasculli, A.; Zito, C.; Sciarra, N.; Mangifesta, M. Back analysis of a real debris flow, the Morino-Rendinara test case (Italy), using RAMMS software. Land 2024, 13, 2078. [Google Scholar] [CrossRef]
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method for Solid and Structural Mechanics, 6th ed.; Elsevier: London, UK, 2006; p. 631. [Google Scholar]
- Minatti, L.; Pasculli, A. Dam break Smoothed Particle Hydrodynamic modeling based on Riemann solvers. In Advances in Fluid Mechanics VIII; Algarve (Spain); WIT Transactions on Engineering Sciences; WIT Press: Southampton, UK, 2010; Volume 69, pp. 145–156. [Google Scholar] [CrossRef]
- Pastor, M.; Haddad, B.; Sorbino, G.; Cuomo, S.; Drempetic, V. A depth integrated coupled SPH model for flow-like debris flows and related phenomena. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 143–172. [Google Scholar] [CrossRef]
- Pasculli, A.; Minatti, L.; Audisio, C.; Sciarra, N. Insights on the application of some current SPH approaches for the study of muddy debris flow: Numerical and experimental comparison. In Advances in Fluid Mechanics X, Proceedings of the 10th International Conference on Advances in Fluid Mechanics, AFM 2014, A Coruna, Spain, 1–3 July 2014; WIT Press: Southampton, UK, 2014; Volume 82, pp. 3–14. [Google Scholar] [CrossRef]
- Idelsohn, S.R.; Oñate, E.; Del Pin, F. A lagrangian meshless finite element method applied to fluid-structure interaction problems. Comput. Struct. 2003, 81, 655–671. [Google Scholar] [CrossRef]
- Del Pin, F.; Aubry, R. The particle finite element method. An overview. Int. J. Comput. Methods 2004, 1, 267–307. [Google Scholar] [CrossRef]
- Idelsohn, S.R.; Oñate, E.; Del Pin, F. The particle finite element method: A powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int. J. Numer. Methods Eng. 2004, 61, 964–989. [Google Scholar] [CrossRef]
- Calista, M.; Pasculli, A.; Sciarra, N. Reconstruction of the geotechnical model considering random parameters distributions. In Engineering Geology for Society and Territory; Springer: Cham, Switzerland, 2015; Volume 2, pp. 1347–1351. [Google Scholar]
- Bossi, G.; Borgatti, L.; Gottardi, G.; Marcato, G. The Boolean Stochastic Generation method—BoSG: A tool for the analysis of the error associated with the simplification of the stratigraphy in geo-technical models. Eng. Geol. 2016, 203, 99–106. [Google Scholar] [CrossRef]
- Pasculli, A. Viscosity Variability Impact on 2D Laminar and Turbulent Poiseuille Velocity Profiles; Characteristic-Based Split (CBS) Stabilization. In Proceedings of the 2018 5th International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Corfù, Greece, 25–27 August 2018; ISBN 978-1-5386-7500-7. [Google Scholar] [CrossRef]
- Pasculli, A.; Sciarra, N. (2026). A probabilistic approach to determine the local erosion of a watery debris flow. In Proceedings of the XI IAEG International Congress, Paper S08-08, Liege, Belgium, 3–8 September 2006; ISBN 978-296006440-7. [Google Scholar]
- Bayes, T. An essay towards solving a problem in the doctrine of chances. Philos. Trans. R. Soc. Lond. 1763, 53, 370–418. [Google Scholar] [CrossRef]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. Adv. Neural Inf. Process. Syst. 2017, 30, 6405–6416. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: London, UK, 1994. [Google Scholar]
- Huang, J.; Hales, T.C.; Huang, R.; Ju, N.; Li, Q.; Huang, Y. A hybrid machine-learning model to estimate potential debris-flow volumes. Geomorphology 2020, 367, 107333. [Google Scholar] [CrossRef]
- Lee, D.-H.; Cheon, E.; Lim, H.-H.; Choi, S.-K.; Kim, Y.-T.; Lee, S.-R. An artificial neural network model to predict debris-flow volumes caused by extreme rainfall in the central region of South Korea. Eng. Geol. 2021, 281, 105979. [Google Scholar] [CrossRef]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight Uncertainty in Neural Networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1398–1406. [Google Scholar]
- Neal, R.M.; Hinton, G.E. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models; Springer: Berlin/Heidelberg, Germany, 1998; pp. 355–368. [Google Scholar]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Generalized belief propagation. In Advances in Neural Information Processing Systems (NIPS); MIT Press: Cambridge, MA, USA, 2000; Volume 13, pp. 689–695. [Google Scholar]
- Friston, K.; Mattout, J.; Trujillo-Barreto, N.; Ashburner, J.; Penny, W. Variational free energy and the Laplace approximation. Neuroimage 2007, 34, 220–234. [Google Scholar] [CrossRef]
- Saul, L.K.; Jaakkola, T.; Jordan, M.I. Mean field theory for sigmoid belief networks. J. Artif. Intell. Res. 1996, 4, 61–76. [Google Scholar] [CrossRef]
- Jaakkola, T.S.; Jordan, M.I. Bayesian parameter estimation via variational methods. Stat. Comput. 2000, 10, 25–37. [Google Scholar] [CrossRef]
- Dürr, O.; Sick, B.; Murina, E. Probabilistic Deep Learning: With Python, Keras and TensorFlow Probability, 1st ed.; Manning Publications: New York, NY, USA, 2020; 296p, ISBN 978-1617296079. [Google Scholar]
- TensorFlow Probability Team. TensorFlow Probability Documentation; TensorFlow: Mountain View, CA, USA, 2024. [Google Scholar]
- Peters, O.; Deluca, A.; Corral, A.; Neelin, J.D.; Holloway, C.E. Universality of rain event size distributions. J. Stat. Mech. Theory Exp. 2010, 2010, P11030. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O. Exponentially decreasing distributions for the logarithm of particle size. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 353, 401–419. [Google Scholar] [CrossRef]
- Del Soldato, M.; Rosi, A.; Delli Passeri, L.; Cacciamani, C.; Catani, F.; Casagli, N. Ten years of pluviometric analyses in Italy for civil protection purposes. Sci. Rep. 2021, 11, 20302. [Google Scholar] [CrossRef]
- Haskett, J.D.; Pachepsky, Y.A.; Acock, B. Use of the beta distribution for parameterizing variability of soil properties at the regional level for crop yield estimation. Agric. Syst. 1995, 48, 73–86. [Google Scholar] [CrossRef]
- Vico, G.; Porporato, A. Probabilistic description of topographic slope and aspect. J. Geophys. Res. Earth Surf. 2009, 114, F01011. [Google Scholar] [CrossRef]
- Higham, N.J. Computing the nearest correlation matrix—A problem from finance. IMA J. Numer. Anal. 2002, 22, 329–343. [Google Scholar] [CrossRef]
- Cholesky, A. Sur la résolution numérique des systèmes d’équations linéaires. Bull. Sabix 2005, 39, 81–95. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Foundations of the Theory of Probability; Morrison, N., Translator; Chelsea Publishing Company: New York, NY, USA, 1950. [Google Scholar]
- Griswold, J.P.; Iverson, R.M. Mobility Statistics and Automated Hazard Mapping for Debris Flows and Rock Avalanches; Scientific Investigations Report 2007–5276; U.S. Geological Survey: Reston, VA, USA, 2008. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Routledge: Oxfordshire, UK, 2003. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Mendez, F.J.; Mendez, M.A.; Sciarra, N.; Pasculli, A. Multi-objective analysis of the Sand Hypoplasticity model calibration. Acta Geotech. 2024, 19, 4241–4254. [Google Scholar] [CrossRef]
- Franceschini, R.; Rosi, A.; Del Soldato, M.; Catani, F.; Casagli, N. Integrating multiple information sources for landslide hazard assessment: The case of Italy. Sci. Rep. 2022, 12, 20724. [Google Scholar] [CrossRef] [PubMed]



| Model Name | ||||
|---|---|---|---|---|
| Synthetic Model | 32.7 | 32.4 | 0.26 | (31.87, 32.92) |
| Model from Sichuan region (China) | 45.57 | 44.63 | 3.62 | (37.39, 51.87) |
| Model from Korea | 5445.99 | 5953.52 | 233.94 | (5485.64, 6421.41) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasculli, A.; Secchi, M.; Mangifesta, M.; Cencetti, C.; Sciarra, N. A Novel Probabilistic Approach for Debris Flow Accumulation Volume Prediction Using Bayesian Neural Networks with Synthetic and Real-World Data. Geosciences 2025, 15, 362. https://doi.org/10.3390/geosciences15090362
Pasculli A, Secchi M, Mangifesta M, Cencetti C, Sciarra N. A Novel Probabilistic Approach for Debris Flow Accumulation Volume Prediction Using Bayesian Neural Networks with Synthetic and Real-World Data. Geosciences. 2025; 15(9):362. https://doi.org/10.3390/geosciences15090362
Chicago/Turabian StylePasculli, Antonio, Mauricio Secchi, Massimo Mangifesta, Corrado Cencetti, and Nicola Sciarra. 2025. "A Novel Probabilistic Approach for Debris Flow Accumulation Volume Prediction Using Bayesian Neural Networks with Synthetic and Real-World Data" Geosciences 15, no. 9: 362. https://doi.org/10.3390/geosciences15090362
APA StylePasculli, A., Secchi, M., Mangifesta, M., Cencetti, C., & Sciarra, N. (2025). A Novel Probabilistic Approach for Debris Flow Accumulation Volume Prediction Using Bayesian Neural Networks with Synthetic and Real-World Data. Geosciences, 15(9), 362. https://doi.org/10.3390/geosciences15090362






