Impact of Aerosols on Cloud Microphysical Processes: A Theoretical Review
Abstract
1. Introduction
2. General Theoretical Aspects of Aerosol-Cloud Interaction
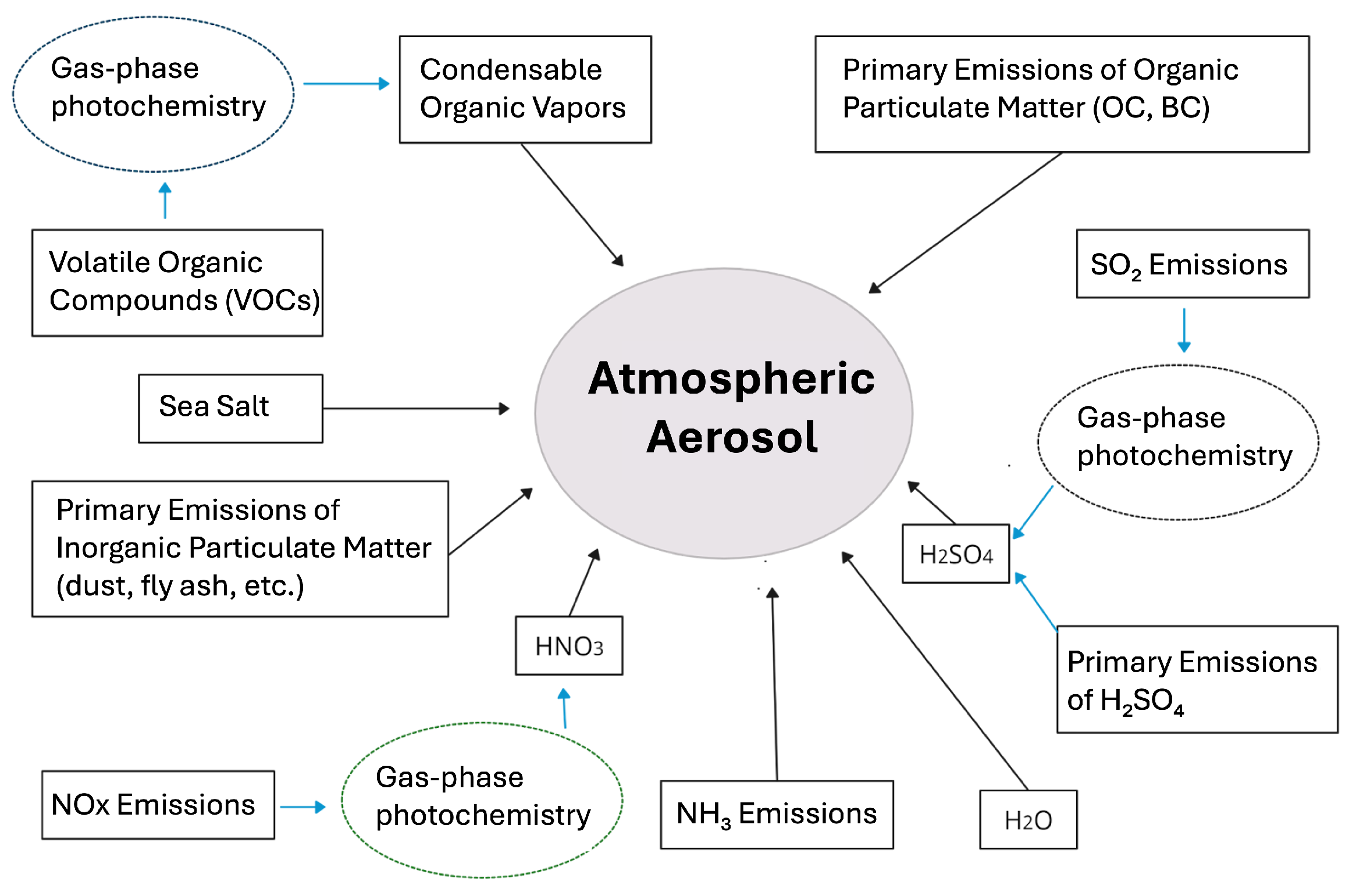
2.1. Aerosols
2.1.1. Primary Aerosols
2.1.2. Secondary Aerosols
- Sulfate aerosol
- Nitrate aerosol
- Organic aerosol
2.1.3. Gas-to-Particle Conversion (Partitioning)
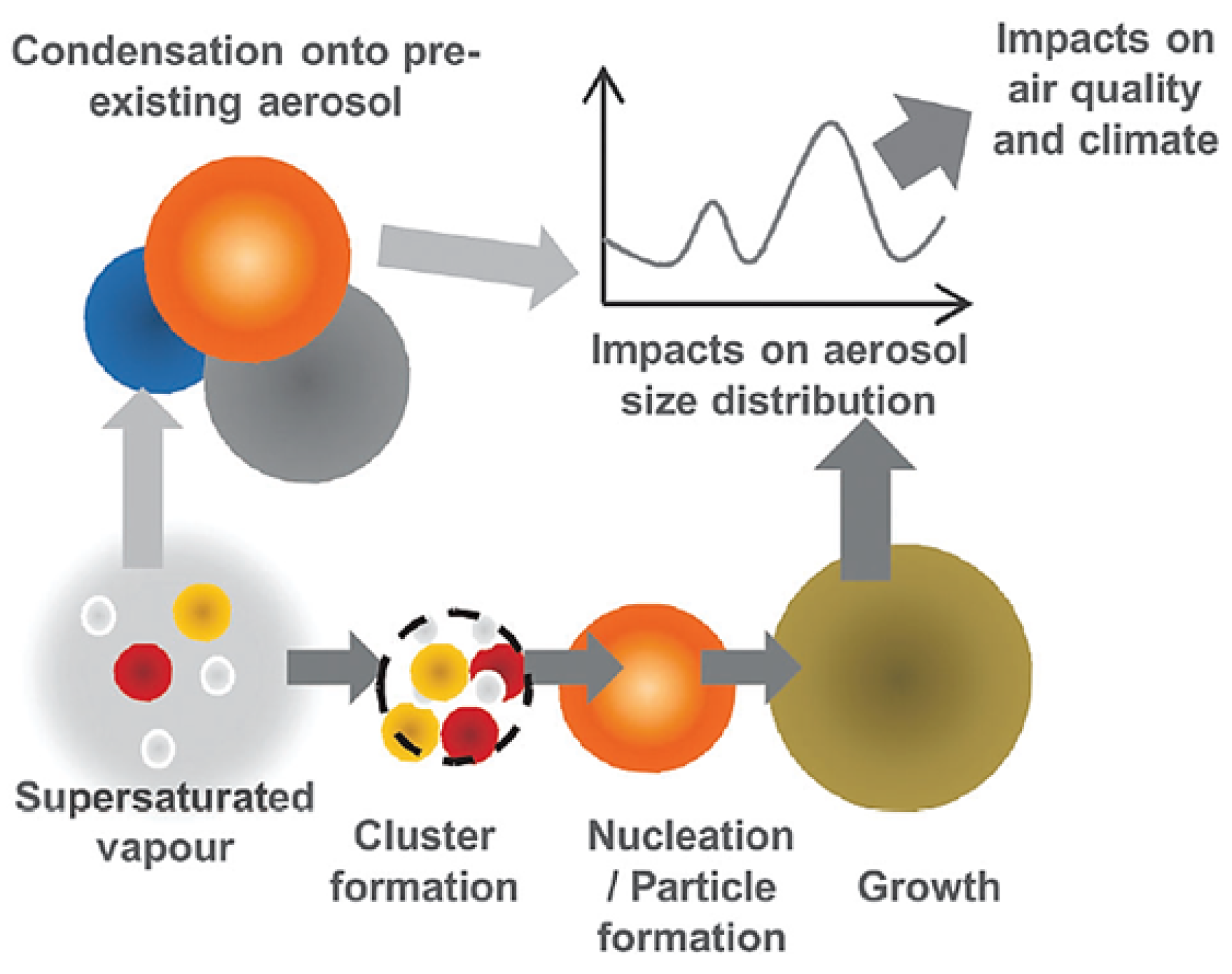
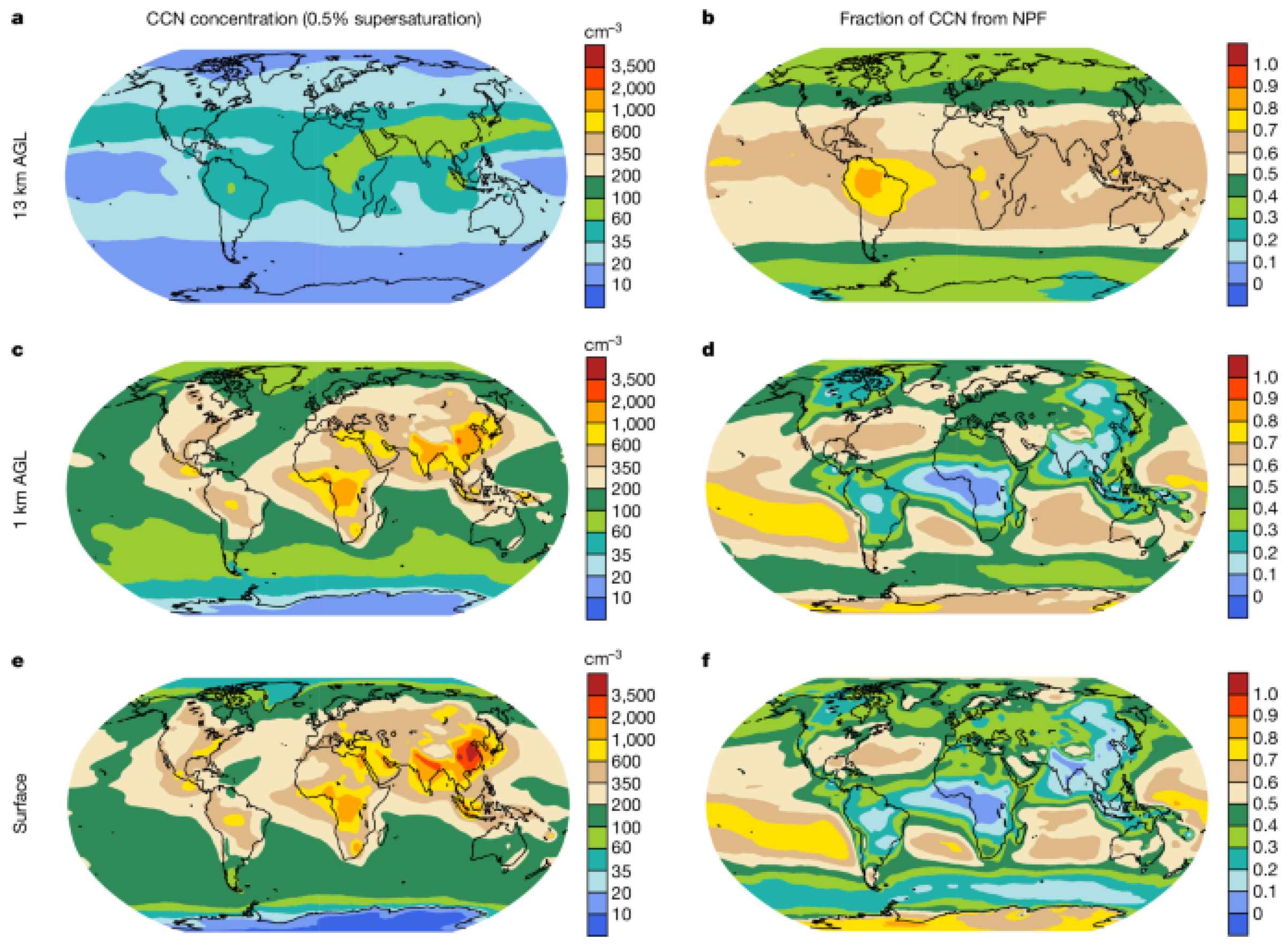
2.1.4. New Particle Formation (NPF)
3. Indirect Aerosol Effects: Twomey and Albrecht
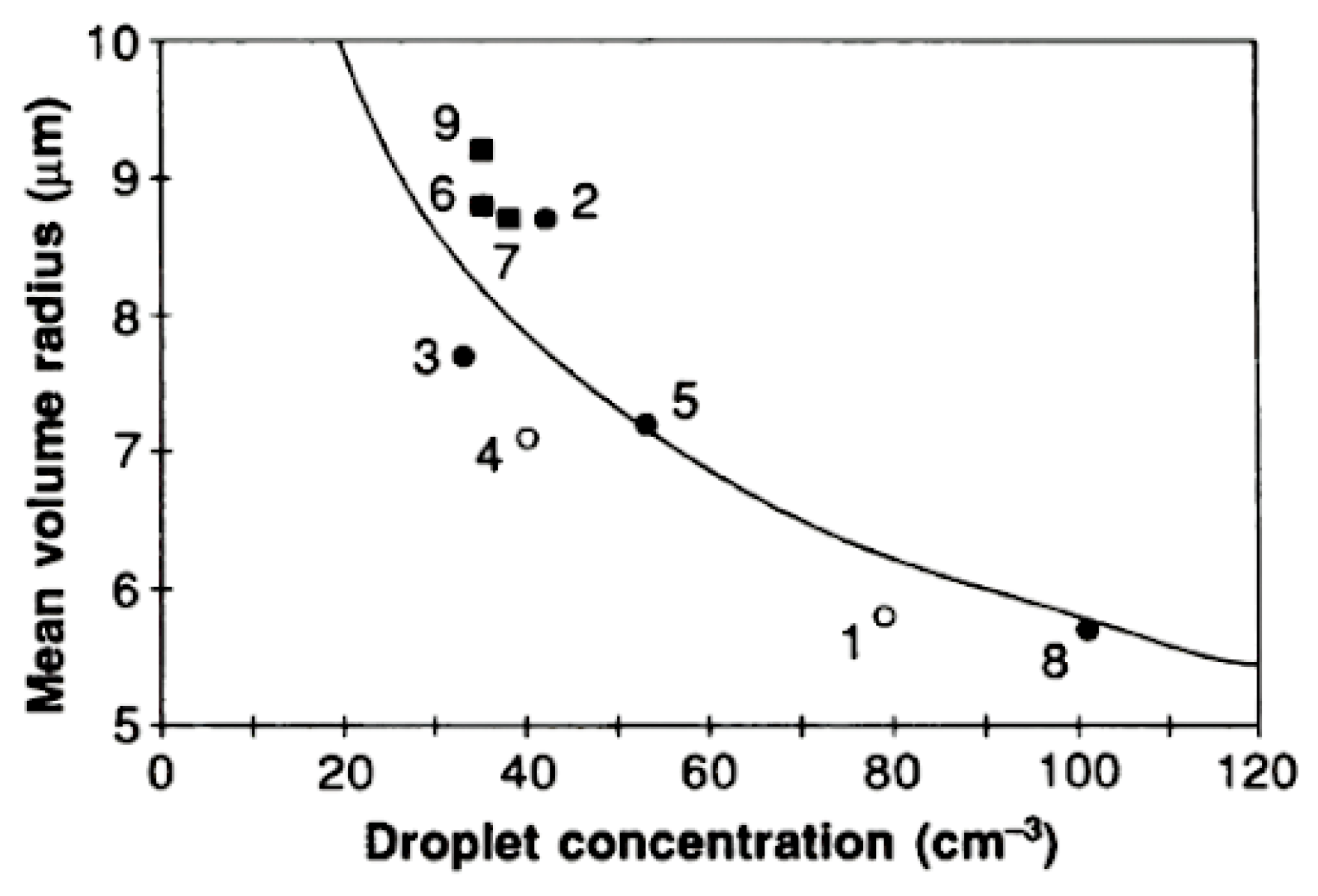
3.1. First Indirect Effect, Twomey (1977) [23]
3.2. Second Indirect Effect, Albrecht (1989) [10]
4. Droplet Nucleation
4.1. Homogeneous Nucleation and Heterogeneous Nucleation
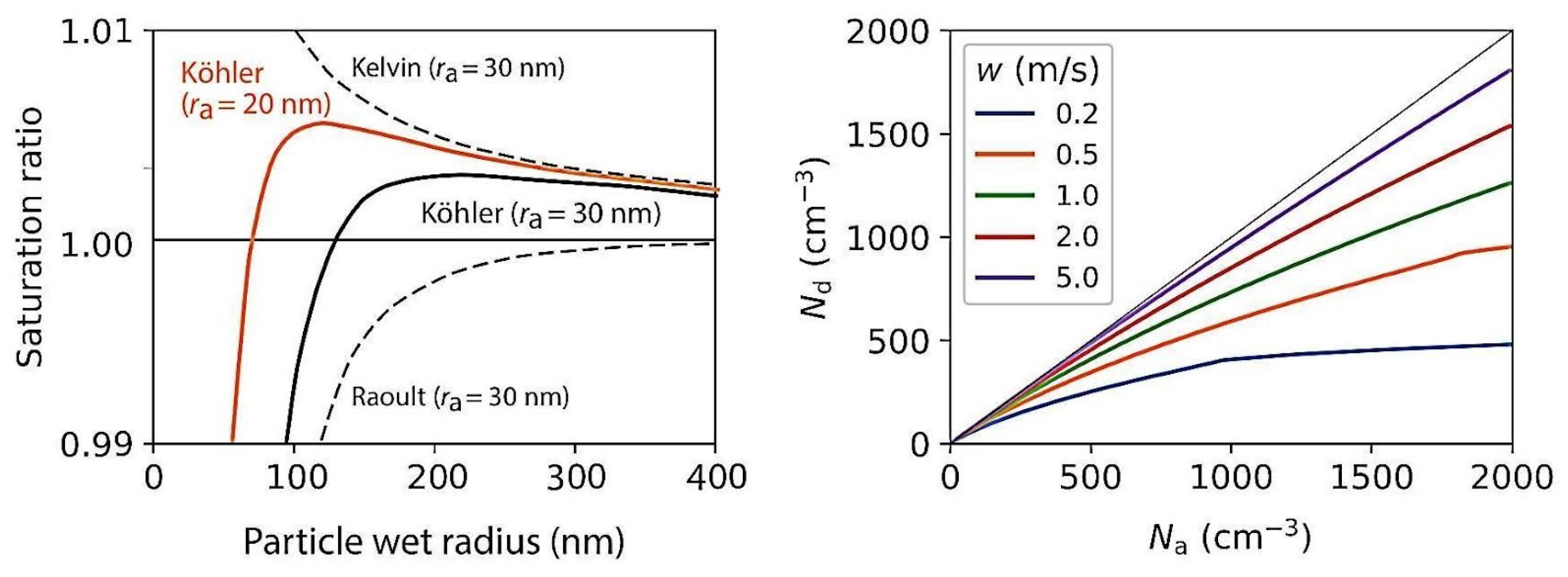
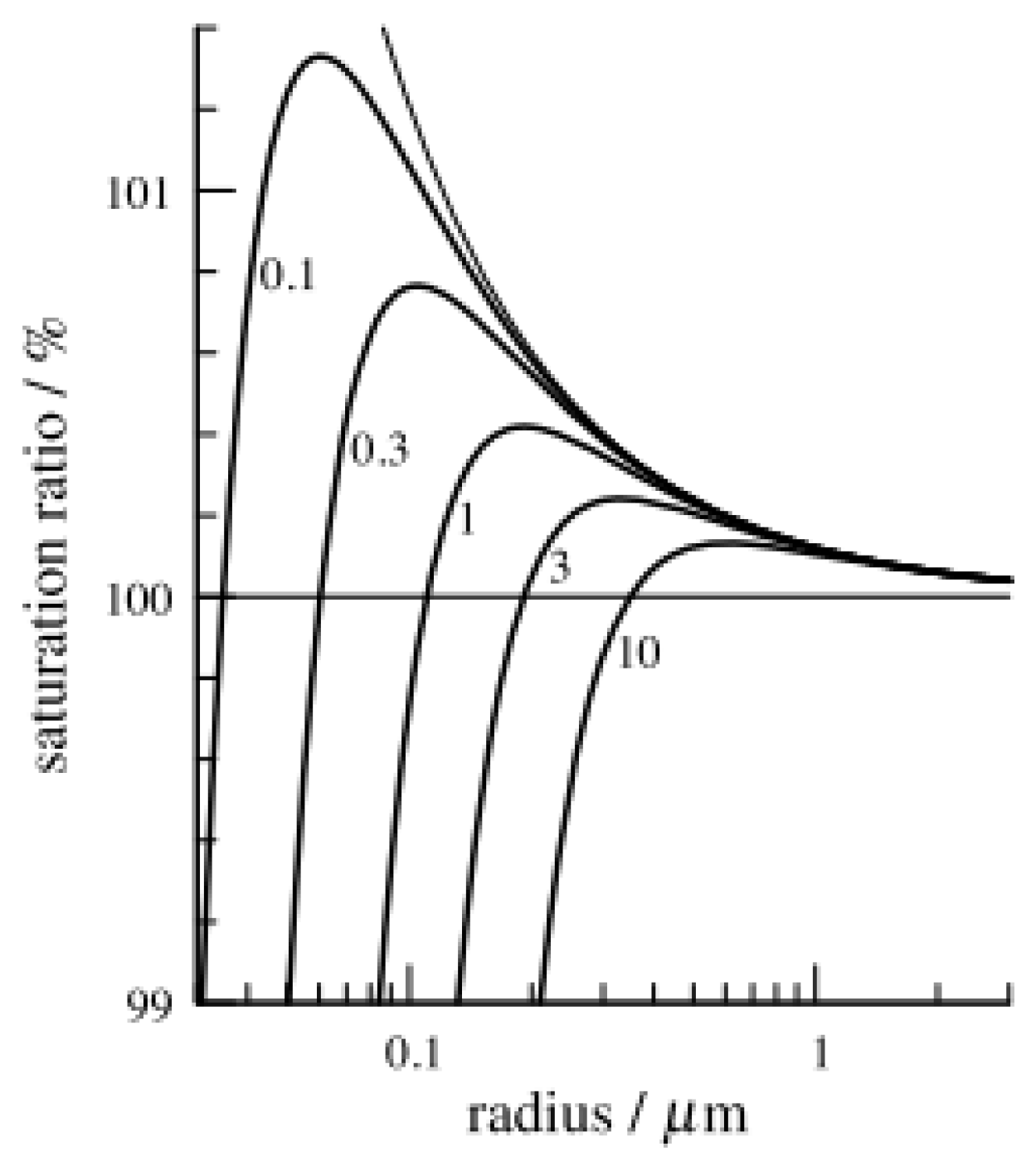
4.2. Köhler Theory or Köhler Curve
4.2.1. Kelvin Effect
4.2.2. Raoult Effect
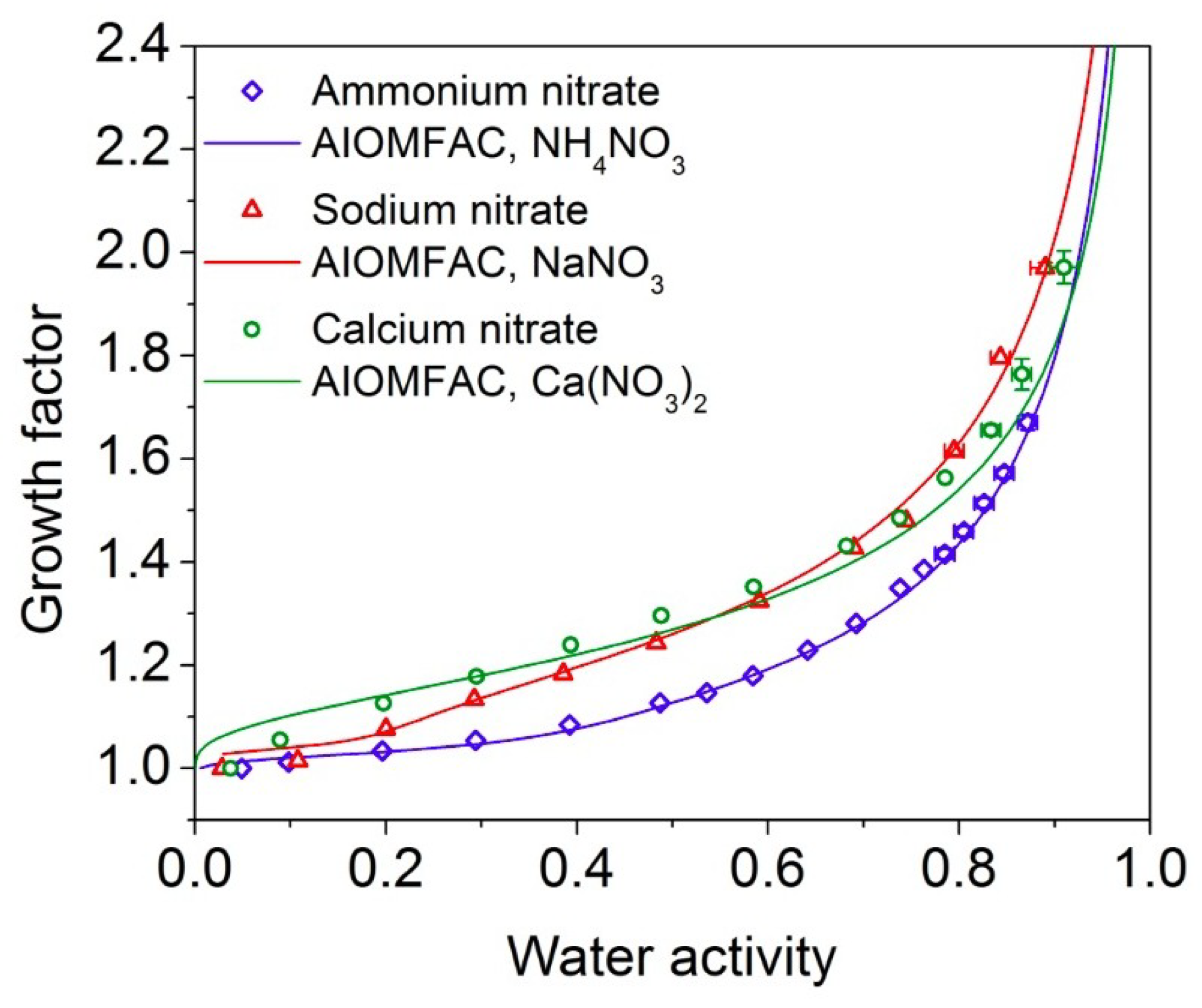
4.2.3. Hygroscopicity Factor
4.2.4. Water Activity Coefficient and Solution Ideality
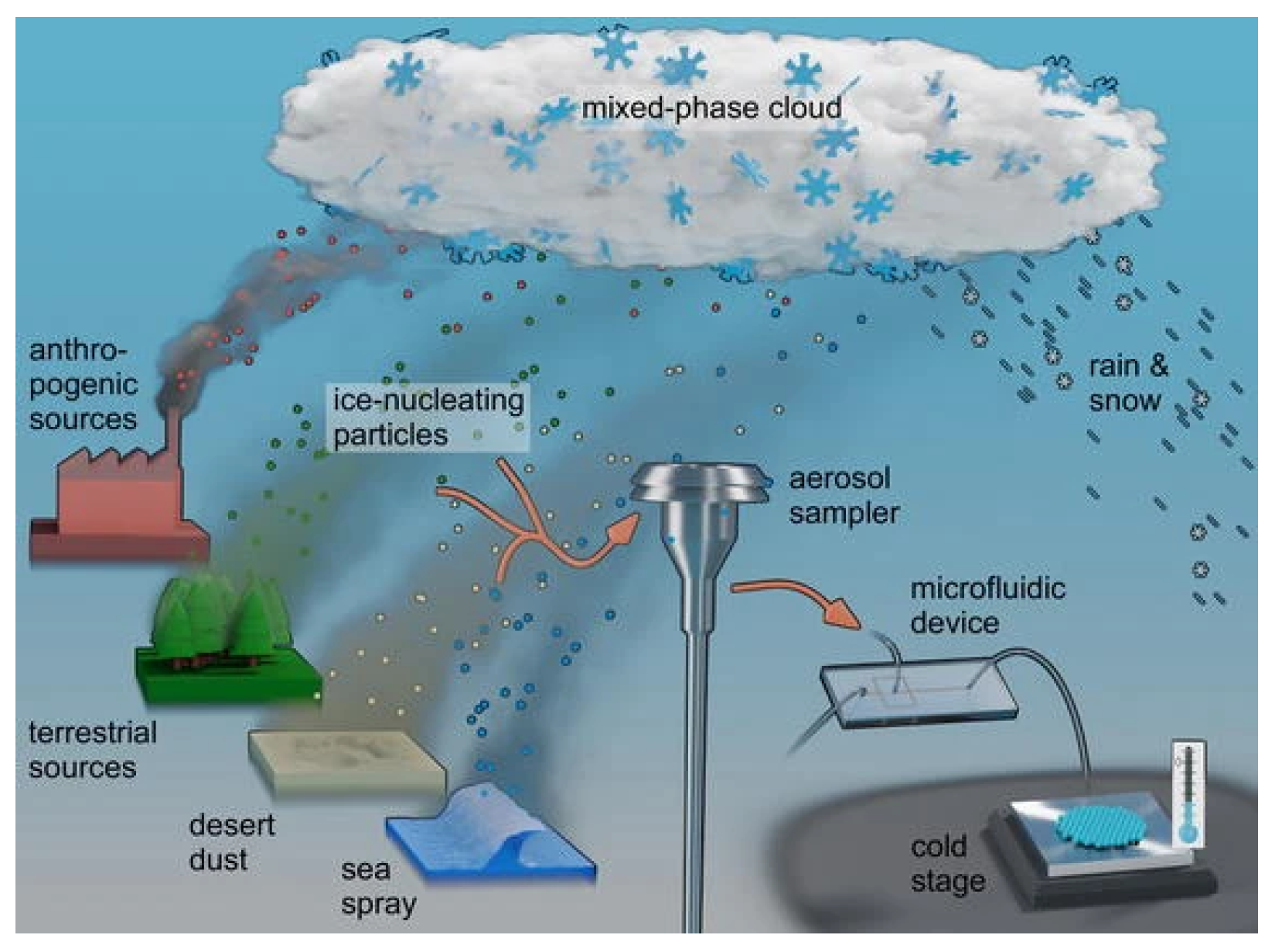
5. Ice Nucleation
5.1. Modes of Ice Nucleation
- Immersion freezing: In this process, an insoluble particle (IN), such as mineral dust, is immersed in a supercooled water body. This is dominant in the atmosphere [118].
- Condensation freezing: Similar to immersion freezing, but it occurs when a particle acts as a CCN, e.g., salt, and immediately induces the freezing of the water condensate [119].
- Deposition nucleation: Deposition ice nucleation occurs when ice forms on an INP from the supersaturated vapor phase, requiring low values of supersaturation and ice temperature [117].
- Inside-out freezing: When a residual solid core (organic aerosol) is coated with a water shell and immersion freezing can proceed [121].
5.2. Aerosol Types Involved in Ice Nucleation
5.3. Uncertainties in Ice Nucleation Understanding
- Improve the accuracy of INP measurements in both field and laboratory settings;
- Understand heterogeneous and homogeneous nucleation mechanisms across different environments;
- Incorporate more realistic parameterizations of ice formation and evolution into climate models;
- Investigate the effects of different aerosol types (e.g., BC, SSA) and their surface properties;
- Include stacking-disordered ice in microphysical approaches to nucleation and ice growth.
6. Cloud Microphysical Processes
6.1. Droplet Growth by Condensation
- Growth of aerosol particles to their equilibrium size;
- Nucleation or activation of droplets;
- Growth by diffusion of droplets.
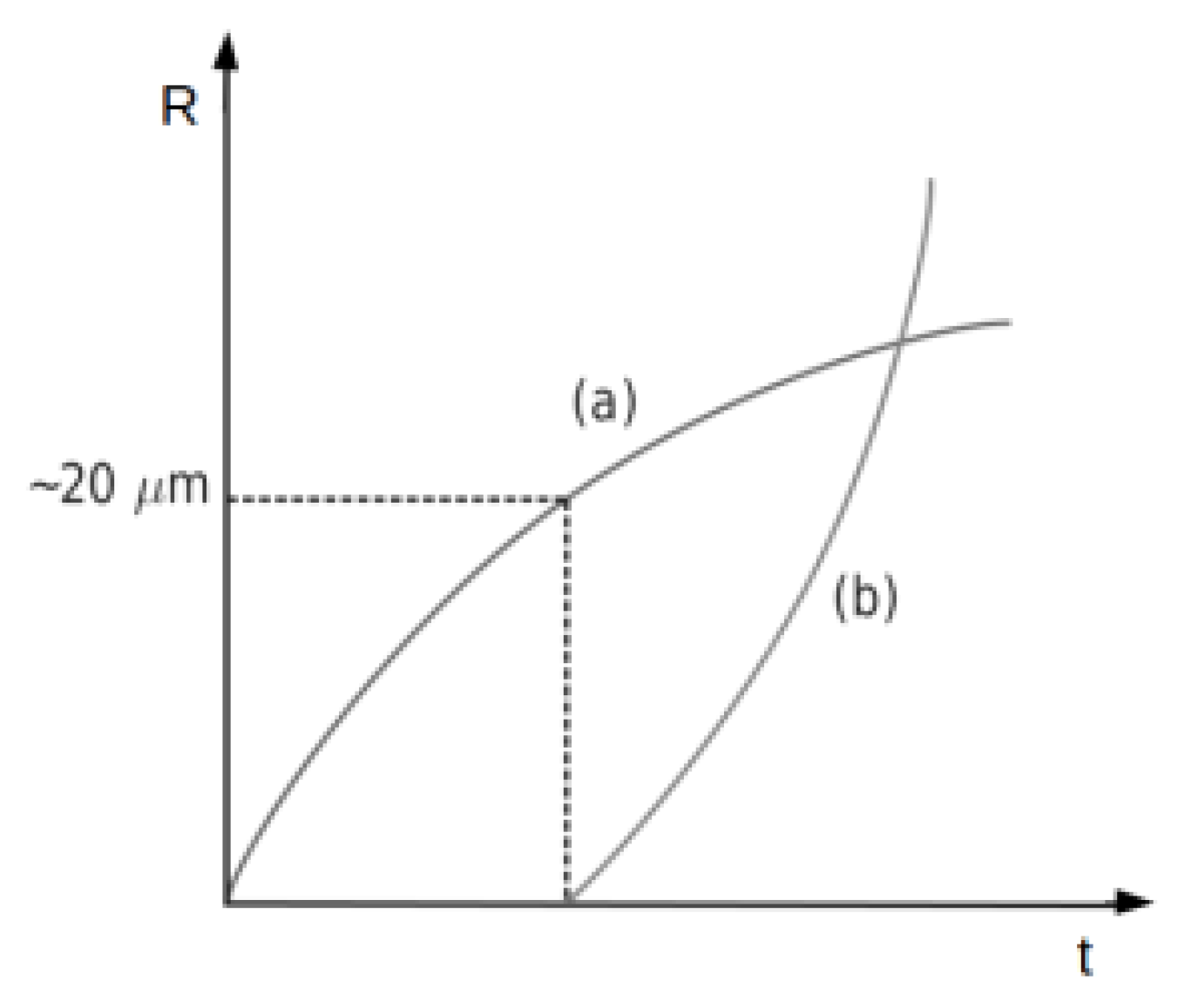
6.2. Droplet Growth by Collision-Coalescence
6.3. Growth of Ice by Vapor Diffusion, Bergeron, Riming, and Aggregation
6.3.1. Vapor Diffusion
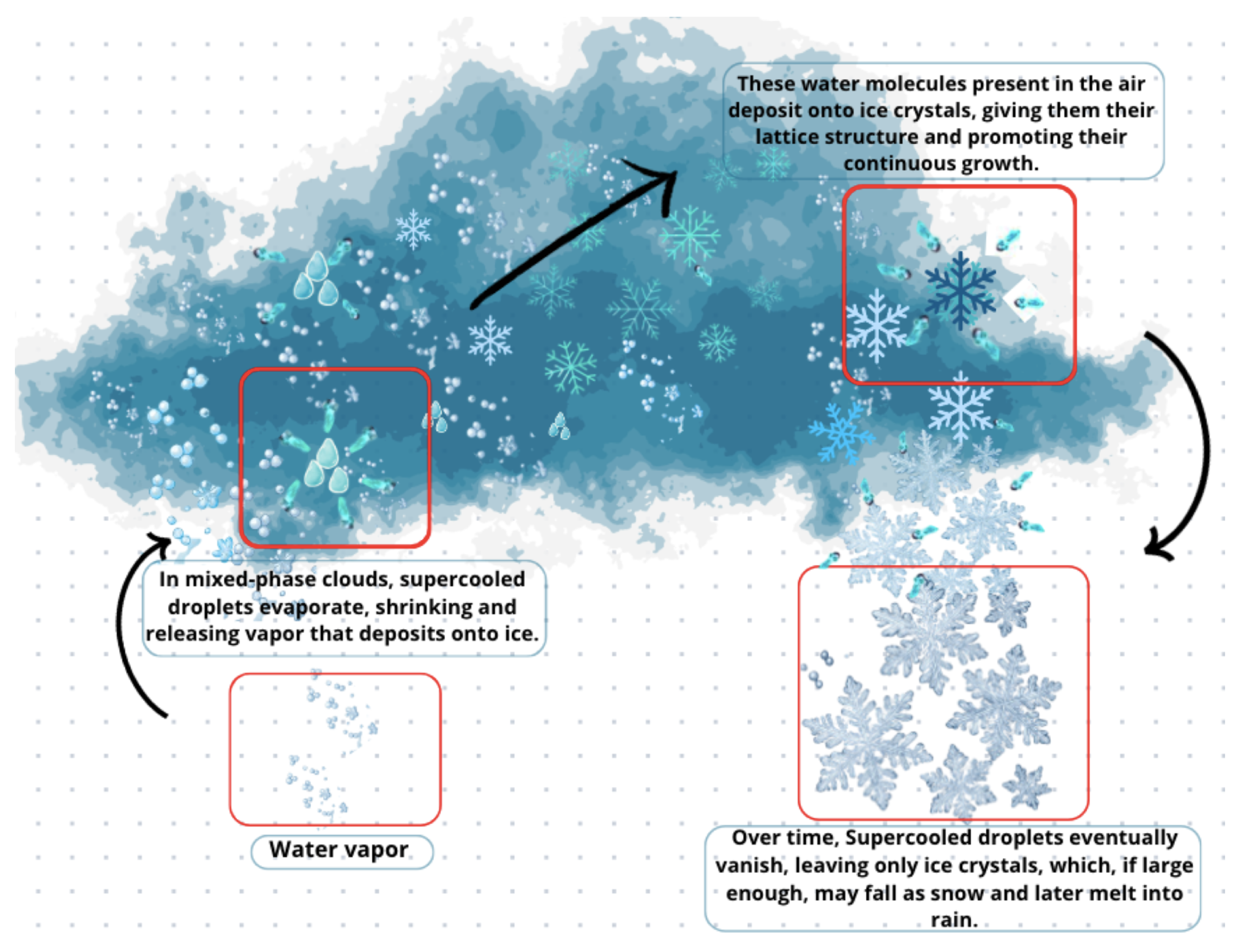
6.3.2. Wegener–Bergeron–Findeisen (WBF)
- For and , both droplets and ice particles grow simultaneously when the upward velocity exceeds .
- For , the WBF process can occur in both upward and downward currents when .
- For , and , the simultaneous evaporation of ice particles and liquid droplets can occur in downward currents when .
6.3.3. Riming
- —rimed particles (graupel);
- —moderately rimed particles;
- —aggregates with insignificant riming.
6.3.4. Aggregation
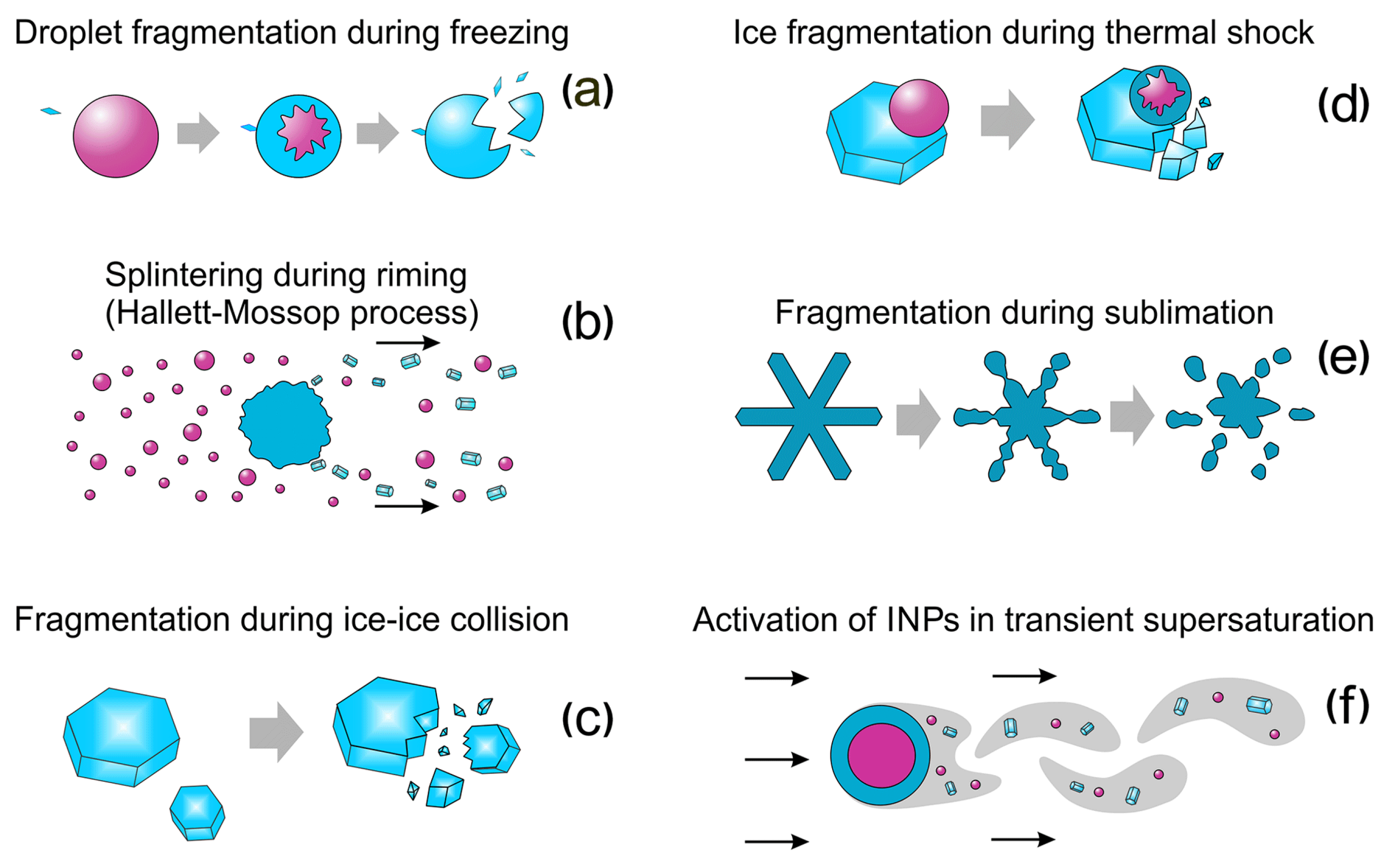
6.4. Secondary Ice Production (SIP)
- Shattering during droplet freezing: During the freezing of a supercooled droplet, an ice shell forms around the liquid core. As freezing progresses inward, the volumetric expansion of ice traps the remaining liquid water under increasing internal pressure. Once a critical threshold is exceeded, the shell may rupture, releasing ice fragments that act as secondary ice crystals [185,186].
- Rime-splintering (Hallett–Mossop) process: This occurs when supercooled droplets collide with and freeze upon falling ice particles, such as graupel or ice crystals. During this process, small droplets, typically with diameters greater than , freeze upon impact with the ice surface. Under certain conditions, typically between and , this freezing can generate small ice fragments (splinters) that detach and act as secondary ice crystals, significantly increasing the ice concentration in the cloud [187].
- Fragmentation due to ice–ice collision: Process by which ice particles mechanically break upon collision, producing small fragments that act as secondary ice [188].
- Ice particle fragmentation due to thermal shock: Process by which ice particles break due to internal stresses generated by rapid localized heating caused by the freezing of a supercooled droplet attached to the surface of the ice crystal. When the droplet freezes, it releases latent heat that raises the local temperature of the crystal to the melting point, causing differential expansion of the ice and generating thermal stresses that can lead to cracking and fragmentation of the crystal [189].
- Fragmentation of sublimating ice: Process in which ice particles, especially those with edges or dendritic shapes, mechanically break apart while sublimating in cloud regions with relative humidity below saturation (subsaturated). During sublimation, the transition from solid ice to vapor creates stresses within the crystal structure, which can lead to the detachment of fragments [190].
- Activation of ice-nucleating particles in transient supersaturation around freezing drops: Process in which freezing droplets temporarily create a region around them with high water vapor supersaturation, activating ice nuclei (INPs) that would normally not be activated, leading to the formation of new ice crystals [189,191].
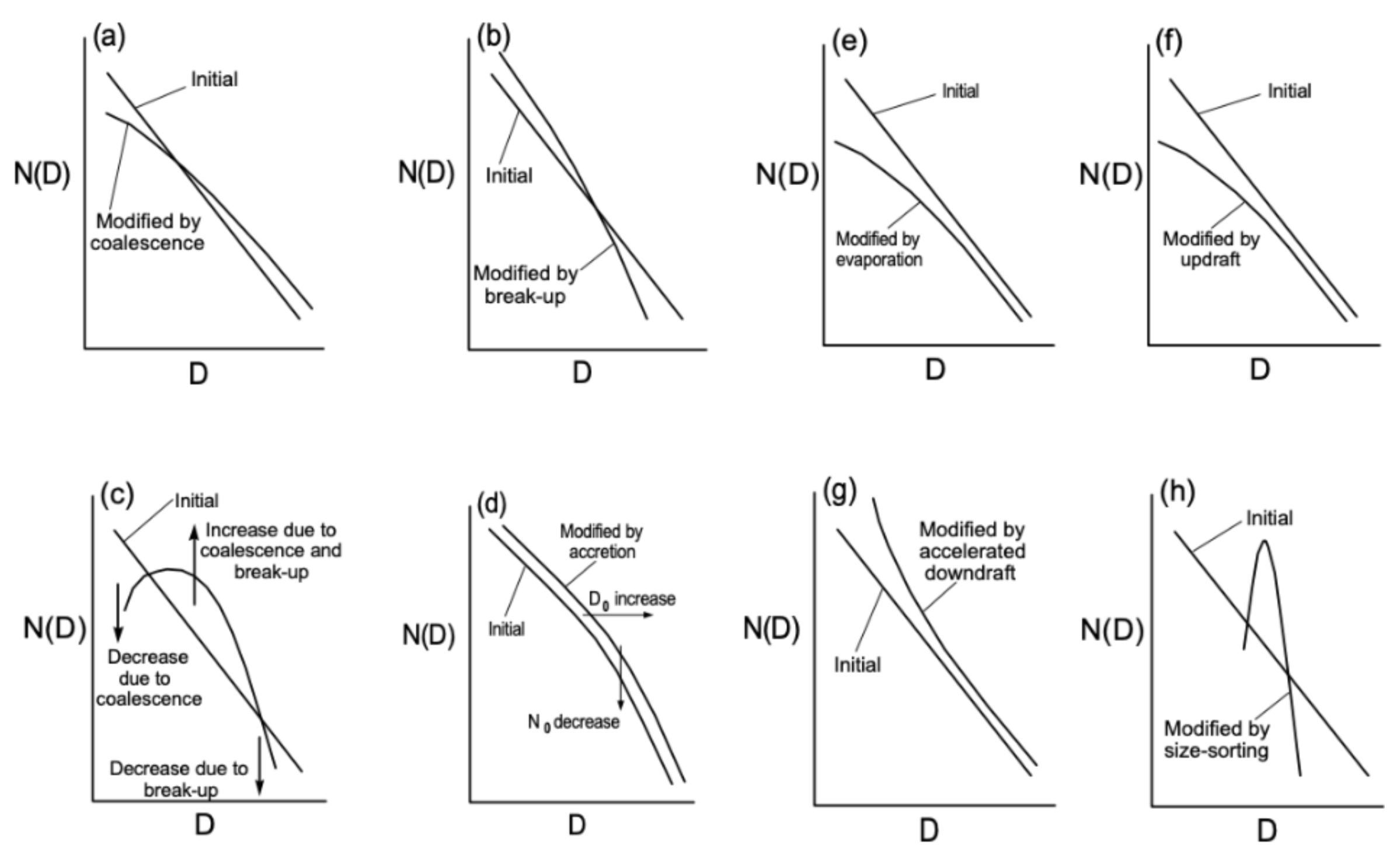
6.5. Drop Size Distribution (DSD)
- Coalescence: Decreases the number of small drops, thus reducing the total number of drops in the distribution [201].
- Break-up: As the number of larger drops decreases, the number of smaller drops increases [202].
- Combined coalescence and break-up: The increase and decrease in drop size, through coalescence and break-up, respectively, impact the reduction of very small and very large droplets, increasing the number of medium-sized droplets [202].
- Accretion: Works to increase size, and the drops grow at the same rate [203].
- Evaporation: Leads to a greater loss of small droplets compared to larger ones. Consequently, the total number of drops should decrease [204].
- Updrafts: Eliminate smaller drops at lower levels of the cloud. The effect is the same as evaporation [205].
- Downdraft: A downdraft would increase the downward flow of particles of all diameters, especially the smaller ones. A change in the shape is likely, but the details of these changes are uncertain [206].
- Size sorting: Tends to make the distribution narrower, significantly increasing the average drop size and decreasing the total drop concentration [207].
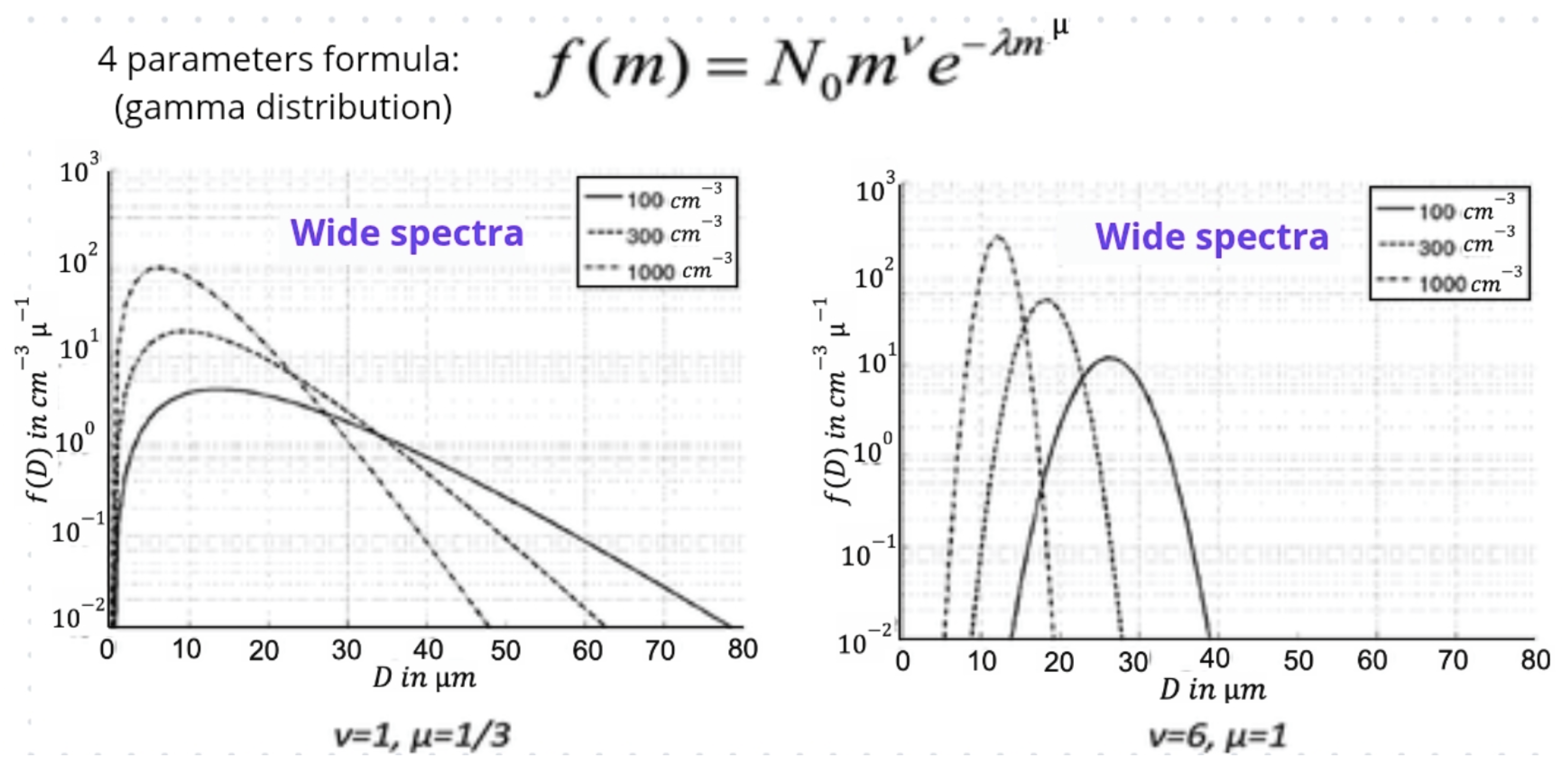
Gamma Function
6.6. Terminal Velocity of Hydrometeors
7. Clouds and Precipitation
7.1. Warm-Phase Clouds
7.2. Cold/Mixed-Phase Clouds
7.3. Warm and Cold Precipitation
8. Aerosol–Cloud Interactions (ACI) in Current and Future Climate Models
9. Observational Limitations
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khatri, P.; Hayasaka, T.; Holben, B.N.; Singh, R.P.; Letu, H.; Tripathi, S.N. Increased aerosols can reverse Twomey effect in water clouds through radiative pathway. Sci. Rep. 2022, 12, 20666. [Google Scholar] [CrossRef] [PubMed]
- Carslaw, K.S.; Lee, L.A.; Reddington, C.L.; Pringle, K.J.; Pierce, J.R.; Gordon, H.; Mann, G.W.; Spracklen, D.V. The global impact of aerosols on cloud condensation nuclei and the role of new particle formation. Nature 2022, 610, 557–562. [Google Scholar]
- McCoy, D.T.; Burrows, S.M.; Wood, R.; Grosvenor, D.P.; Elliott, S.M.; Ma, P.L.; Rasch, P.J.; Hartmann, D.L. Natural aerosols explain seasonal and spatial patterns of Southern Ocean cloud albedo. Sci. Adv. 2015, 1, e1500157. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Reissell, A.; Andreae, M.O. Flood or drought: How do aerosols affect precipitation? Science 2008, 321, 1309–1313. [Google Scholar] [CrossRef]
- Williams, E.; Rosenfeld, D.; Madden, N.; Gerlach, J.; Gears, N.; Atkinson, L.; Dunnemann, N.; Frostrom, G.; Antonio, M.; Biazon, B.; et al. Contrasting convective regimes over the Amazon: Implications for cloud electrification. J. Geophys. Res. Atmos. 2002, 107, LBA 50-1–LBA 50-19. [Google Scholar] [CrossRef]
- Fan, J.; Leung, L.R.; Rosenfeld, D.; Chen, Q.; Li, Z.; Zhang, J.; Yan, H. Microphysical effects determine macrophysical response for aerosol impacts on deep convective clouds. Proc. Natl. Acad. Sci. USA 2013, 110, E4581–E4590. [Google Scholar] [CrossRef]
- Tao, W.K.; Chen, J.P.; Li, Z.; Wang, C.; Zhang, C. Impact of aerosols on convective clouds and precipitation. Rev. Geophys. 2012, 50, RG2001. [Google Scholar] [CrossRef]
- Nakajima, T.; Higurashi, A.; Kawamoto, K.; Penner, J.E. A possible correlation between satellite-derived cloud and aerosol microphysical parameters. Geophys. Res. Lett. 2001, 28, 1171–1174. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y.; Rosenfeld, D.; Liu, X. Review of aerosol–cloud interactions: Mechanisms, significance, and challenges. J. Atmos. Sci. 2016, 73, 4221–4252. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, cloud microphysics, and fractional cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, U.; Diehl, K. Sensitivity studies of the importance of dust ice nuclei for the indirect aerosol effect on stratiform mixed-phase clouds. J. Atmos. Sci. 2006, 63, 968–982. [Google Scholar] [CrossRef]
- Stohl, A.; Forster, C.; Huntrieser, H.; Mannstein, H.; McMillan, W.; Petzold, A.; Schlager, H.; Weinzierl, B. Aircraft measurements over Europe of an air pollution plume from Southeast Asia–aerosol and chemical characterization. Atmos. Chem. Phys. 2007, 7, 913–937. [Google Scholar] [CrossRef]
- Khain, A.; Pokrovsky, A.; Sednev, I. Some effects of cloud–aerosol interaction on cloud microphysics structure and precipitation formation: Numerical experiments with a spectral microphysics cloud ensemble model. Atmos. Res. 1999, 52, 195–220. [Google Scholar] [CrossRef]
- Liu, S.; Chen, M.; Zhuang, Q. Aerosol effects on global land surface energy fluxes during 2003–2010. Geophys. Res. Lett. 2014, 41, 7875–7881. [Google Scholar] [CrossRef]
- Yeom, J.M.; Fahandezh Sadi, H.; Anderson, J.C.; Yang, F.; Cantrell, W.; Shaw, R.A. Cloud microphysical response to entrainment of dry air containing aerosols. Npj Clim. Atmos. Sci. 2025, 8, 8. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Lu, P. Improvement of cloud microphysics in the aerosol-climate model BCC_AGCM2. 0.1 _CUACE/Aero, evaluation against observations, and updated aerosol indirect effect. J. Geophys. Res. Atmos. 2014, 119, 8400–8417. [Google Scholar] [CrossRef]
- La, I.; Yum, S.S. Relationship between vertical variation of cloud microphysical properties and thickness of the entrainment interfacial layer in Physics of Stratocumulus Top stratocumulus clouds. Q. J. R. Meteorol. Soc. 2024, 150, 5037–5056. [Google Scholar] [CrossRef]
- Lee, S.; Donner, L.; Penner, J. Thunderstorm and stratocumulus: How does their contrasting morphology affect their interactions with aerosols? Atmos. Chem. Phys. 2010, 10, 6819–6837. [Google Scholar] [CrossRef]
- Storer, R.L.; Van Den Heever, S.C.; Stephens, G.L. Modeling aerosol impacts on convective storms in different environments. J. Atmos. Sci. 2010, 67, 3904–3915. [Google Scholar] [CrossRef]
- Carslaw, K.; Boucher, O.; Spracklen, D.; Mann, G.; Rae, J.; Woodward, S.; Kulmala, M. A review of natural aerosol interactions and feedbacks within the Earth system. Atmos. Chem. Phys. 2010, 10, 1701–1737. [Google Scholar] [CrossRef]
- Artaxo, P.; Rizzo, L.V.; Paixão, M.; De Lucca, S.; Oliveira, P.H.; Lara, L.L.; Wiedemann, K.T.; Andreae, M.O.; Holben, B.; Schafer, J.; et al. Aerosol particles in Amazonia: Their composition, role in the radiation balance, cloud formation, and nutrient cycles. Amazon. Glob. Chang. 2009, 186, 233–250. [Google Scholar] [CrossRef]
- Koren, I.; Feingold, G.; Jiang, H.; Altaratz, O. Aerosol effects on the inter-cloud region of a small cumulus cloud field. Geophys. Res. Lett. 2009, 36, L14805. [Google Scholar] [CrossRef]
- Twomey, S. The influence of pollution on the shortwave albedo of clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Carslaw, K.S.; Pringle, K. Global aerosol properties. In Aerosols and Climate; Elsevier: Amsterdam, The Netherlands, 2022; pp. 101–133. [Google Scholar] [CrossRef]
- Kalkavouras, P.; Bougiatioti, A.; Grivas, G.; Stavroulas, I.; Pilinis, C.; Pandis, S.N.; Nenes, A.; Mihalopoulos, N. Regional new particle formation as modulators of cloud condensation nuclei and cloud droplet number in the eastern Mediterranean. Atmos. Chem. Phys. 2019, 19, 6185–6203. [Google Scholar] [CrossRef]
- Mahowald, N.; Carslaw, K.S. Aerosol in the Earth System. In Aerosols and Climate; Carslaw, K.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Chapter 3; pp. 53–99. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef]
- Creamean, J.M.; Suski, K.J.; Rosenfeld, D.; Cazorla, A.; DeMott, P.J.; Sullivan, R.C.; White, A.B.; Ralph, F.M.; Minnis, P.; Comstock, J.M.; et al. Dust and biological aerosols from the Sahara and Asia influence precipitation in the western US. Science 2013, 339, 1572–1578. [Google Scholar] [CrossRef]
- Schrod, J.; Thomson, E.S.; Weber, D.; Kossmann, J.; Pöhlker, C.; Saturno, J.; Weller, R.; Ullrich, R.; Schneider, J.; Tatzelt, C.; et al. Long-term deposition and condensation ice-nucleating particle measurements from four stations across the globe. Atmos. Chem. Phys. 2020, 20, 15983–16006. [Google Scholar] [CrossRef]
- Schulz, M.; McConnell, J.R. Historical changes in aerosol. In Aerosols and Climate; Elsevier: Amsterdam, The Netherlands, 2022; pp. 249–297. [Google Scholar]
- Murray, B.J.; Liu, X. Ice-nucleating particles and their effects on clouds and radiation. In Aerosols and Climate; Elsevier: Amsterdam, The Netherlands, 2022; pp. 619–649. [Google Scholar] [CrossRef]
- Mahowald, N.; Albani, S.; Kok, J.F.; Engelstaeder, S.; Scanza, R.; Ward, D.S.; Flanner, M.G. The size distribution of desert dust aerosols and its impact on the Earth system. Aeolian Res. 2014, 15, 53–71. [Google Scholar] [CrossRef]
- Alves, C. Aerossóis atmosféricos: Perspectiva histórica, fontes, processos químicos de formação e composição orgânica. Química Nova 2005, 28, 859–870. [Google Scholar] [CrossRef]
- Holanda, B.A. Absorção da Radiação por Aerossóis na Amazônia. Master’s Thesis, Instituto de Física, Departamento de Física Aplicada, Universidade de São Paulo, São Paulo, Brazil, 2015. [Google Scholar]
- Zender, C.S.; Bian, H.; Newman, D. Mineral Dust Entrainment and Deposition (DEAD) model: Description and 1990s dust climatology. J. Geophys. Res. Atmos. 2003, 108, 4416. [Google Scholar] [CrossRef]
- Sullivan, R.C. Heterogeneous Chemistry of Atmospheric Mineral Dust Particles and Their Resulting Cloud-Nucleation Properties. Ph.D. Thesis, University of California, San Diego, San Diego, CA, USA, 2008. [Google Scholar]
- Andreae, M.; Rosenfeld, D. Aerosol–cloud–precipitation interactions. Part 1. The nature and sources of cloud-active aerosols. Earth-Sci. Rev. 2008, 89, 13–41. [Google Scholar] [CrossRef]
- Andreae, M.O.; Rosenfeld, D.; Artaxo, P.; Costa, A.A.; Frank, G.P.; Longo, K.M.; Silva-Dias, M.A.F. Smoking rain clouds over the Amazon. Science 2004, 303, 1337–1342. [Google Scholar] [CrossRef]
- Cavalli, F.; Facchini, M.C.; Decesari, S.; Mircea, M.; Emblico, L.; Fuzzi, S.; Ceburnis, D.; Yoon, Y.J.; Putaud, P. Advances in characterization of size-resolved organic matter in marine aerosol over the North Atlantic. J. Geophys. Res. Atmos. 2004, 109, D24. [Google Scholar] [CrossRef]
- Hill, T.C.J.; Wilson, T.W.; Hill, S.; Rangno, A.L.; Leck, C.; Bigg, E.K.; Svensson, A.; Rogers, D.C.; Orellana, M.V.; Murray, B.J. Measurement of Ice Nucleation-Active Bacteria on Plants and in Precipitation by Quantitative PCR. Appl. Environ. Microbiol. 2014, 80, 1256–1267. [Google Scholar] [CrossRef]
- Maki, L.R.; Galyan, E.L.; Chang-Chien, M.M.; Caldwell, D.R. Ice Nucleation Induced by Pseudomonas syringae. Appl. Microbiol. 1974, 28, 456–459. [Google Scholar] [CrossRef]
- Hansson, H.C.; Bhend, J. Causes of Regional Change—Aerosols. In Second Assessment of Climate Change for the Baltic Sea Basin; Springer International Publishing: Cham, Switzerland, 2015; pp. 441–452. [Google Scholar]
- Dentener, F.; Kinne, S.; Bond, T.; Boucher, O.; Cofala, J.; Generoso, S.; Ginoux, P.; Gong, S.; Hoelzemann, J.J.; Ito, A.; et al. Emissions of primary aerosol and precursor gases in the years 2000 and 1750 prescribed data-sets for AeroCom. Atmos. Chem. Phys. 2006, 6, 4321–4344. [Google Scholar] [CrossRef]
- Orel, A.E.; Seinfeld, J.H. Nitrate formation in atmospheric aerosols. Environ. Sci. Technol. 1977, 11, 1000–1007. [Google Scholar] [CrossRef]
- Ayres, B.R.; Allen, H.M.; Draper, D.C.; Brown, S.S.; Wild, R.J.; Jimenez, J.L.; Fry, J.L. Organic nitrate aerosol formation via NO3 + biogenic volatile organic compounds in the southeastern United States. Atmos. Chem. Phys. 2015, 15, 13377–13392. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pankow, J.F. Organic atmospheric particulate material. Annu. Rev. Phys. Chem. 2003, 54, 121–140. [Google Scholar] [CrossRef] [PubMed]
- Metzger, A.; Verheggen, B.; Dommen, J.; Duplissy, J.; Prevot, A.S.; Weingartner, E.; Baltensperger, U. Evidence for the role of organics in aerosol particle formation under atmospheric conditions. Proc. Natl. Acad. Sci. USA 2010, 107, 6646–6651. [Google Scholar] [CrossRef] [PubMed]
- Fuzzi, S.; Andreae, M.O.; Huebert, B.J.; Kulmala, M.; Bond, T.C.; Boy, M.; Doherty, S.J.; Guenther, A.; Kanakidou, M.; Kawamura, K.; et al. Critical assessment of the current state of scientific knowledge, terminology, and research needs concerning the role of organic aerosols in the atmosphere, climate, and global change. Atmos. Chem. Phys. 2006, 6, 2017–2038. [Google Scholar] [CrossRef]
- Shrivastava, M.; Cappa, C.D.; Fan, J.; Goldstein, A.H.; Guenther, A.B.; Jimenez, J.L.; Kuang, C.; Laskin, A.; Martin, S.T.; Ng, N.L.; et al. Recent advances in understanding secondary organic aerosol: Implications for global climate forcing. Rev. Geophys. 2017, 55, 509–559. [Google Scholar] [CrossRef]
- Kanakidou, M.; Seinfeld, J.H.; Pandis, S.N.; Barnes, I.; Dentener, F.J.; Facchini, M.C.; Dingenen, R.V.; Ervens, B.; Nenes, A.; Nielsen, C.J.; et al. Organic aerosol and global climate modelling: A review. Atmos. Chem. Phys. 2005, 5, 1053–1123. [Google Scholar] [CrossRef]
- Vehkamäki, H.; Riipinen, I. Thermodynamics and kinetics of atmospheric aerosol particle formation and growth. Chem. Soc. Rev. 2012, 41, 5160–5173. [Google Scholar] [CrossRef]
- Zhao, B.; Donahue, N.M.; Zhang, K.; Mao, L.; Shrivastava, M.; Ma, P.L.; Shen, J.; Wang, S.; Sun, J.; Gordon, H.; et al. Global variability in atmospheric new particle formation mechanisms. Nature 2024, 631, 98–105. [Google Scholar] [CrossRef]
- Artaxo, P.; Hansson, H.C.; Andreae, M.O.; Bäck, J.; Alves, E.G.; Barbosa, H.M.J.; Bender, F.; Bourtsoukidis, E.; Carbone, S.; Chi, J. Tropical and Boreal Forest–Atmosphere Interactions: A review. Tellus B Chem. Phys. Meteorol. 2022, 74, 24. [Google Scholar] [CrossRef]
- Matsui, H.; Koike, M.; Takegawa, N.; Kondo, Y. Spatial and temporal variations of new particle formation in East Asia using an NPF-explicit WRF-chem model: North-south contrast in new particle formation frequency. J. Geophys. Res. Atmos. 2013, 118, 11649–11663. [Google Scholar] [CrossRef]
- Yu, F.; Luo, G.; Nair, A.A.; Schwab, J.J.; Sherman, J.P.; Zhang, Y. Wintertime new particle formation and its contribution to cloud condensation nuclei in the Northeastern United States. Atmos. Chem. Phys. 2020, 20, 2591–2601. [Google Scholar] [CrossRef]
- Zhao, B.; Shrivastava, M.; Donahue, N.M.; Gordon, H.; Schervish, M.; Shilling, J.E.; Zaveri, R.A.; Wang, J.; Andreae, M.O.; Zhao, C. High concentration of ultrafine particles in the Amazon free troposphere produced by organic new particle formation. Proc. Natl. Acad. Sci. USA 2020, 117, 25344–25351. [Google Scholar] [CrossRef]
- Dada, L.; Stolzenburg, D.; Simon, M.; Fischer, L.; Heinritzi, M.; Wang, M.; Xiao, M.; Vogel, A.L.; Ahonen, L.; Amorim, A.; et al. Role of sesquiterpenes in biogenic new particle formation. Sci. Adv. 2023, 9, eadi5297. [Google Scholar] [CrossRef] [PubMed]
- Scott, C.E.; Spracklen, D.V.; Pierce, J.R.; Riipinen, I.; D’Andrea, S.D.; Rap, A.; Carslaw, K.S.; Forster, P.M.; Artaxo, P.; Kulmala, M.; et al. Impact of gas-to-particle partitioning approaches on the simulated radiative effects of biogenic secondary organic aerosol. Atmos. Chem. Phys. 2015, 15, 12989–13001. [Google Scholar] [CrossRef]
- Schulz, C.; Schneider, J.; Holanda, B.A.; Appel, O.; Costa, A.; Sá, S.S.d.; Dreiling, V.; Fütterer, D.; Jurkat-Witschas, T.; Klimach, T. Aircraft-based observations of isoprene-epoxydiol-derived secondary organic aerosol (IEPOX-SOA) in the tropical upper troposphere over the Amazon region. Atmos. Chem. Phys. 2018, 18, 14979–15001. [Google Scholar] [CrossRef]
- Bardakov, R.; Thornton, J.A.; Riipinen, I.; Krejci, R.; Ekman, A.M.L. Transport and chemistry of isoprene and its oxidation products in deep convective clouds. Tellus B Chem. Phys. Meteorol. 2021, 73, 1–21. [Google Scholar] [CrossRef]
- Zhang, C.; Hai, S.; Gao, Y.; Wang, Y.; Zhang, S.; Sheng, L.; Zhao, B.; Wang, S.; Jiang, J.; Huang, X.; et al. Substantially positive contributions of new particle formation to cloud condensation nuclei under low supersaturation in China based on numerical model improvements. Atmos. Chem. Phys. 2023, 23, 10713–10730. [Google Scholar] [CrossRef]
- Pöhlker, C.; Wiedemann, K.T.; Sinha, B.; Shiraiwa, M.; Gunthe, S.S.; Smith, M.; Su, H.; Artaxo, P.; Chen, Q.; Cheng, Y.; et al. Biogenic potassium salt particles as seeds for secondary organic aerosol in the Amazon. Science 2012, 337, 1075–1078. [Google Scholar] [CrossRef]
- Palmer, P.I.; Marvin, M.R.; Siddans, R.; Kerridge, B.J.; Moore, D.P. Nocturnal survival of isoprene linked to formation of upper tropospheric organic aerosol. Science 2022, 375, 562–566. [Google Scholar] [CrossRef]
- Franco, M.A. Transporte Vertical, Processos de Crescimento e Caracterização de Aerossóis na Amazônia. Ph.D. Thesis, Universidade de São Paulo, Sao Paulo, Brazil, 2021. Available online: https://web.archive.org/web/20211102183215id_/https://teses.usp.br/teses/disponiveis/43/43134/tde-07102021-174257/publico/MarcoAureliodeMenezesFranco_DO_Thesis_Final.pdf (accessed on 22 July 2025).
- Liu, Y.; Su, H.; Wang, S.; Wei, C.; Tao, W.; Pöhlker, M.L.; Pöhlker, C.; Holanda, B.A.; Krüger, O.O.; Hoffmann, T. Strong particle production and condensational growth in the upper troposphere sustained by biogenic VOCs from the canopy of the Amazon Basin. Atmos. Chem. Phys. 2023, 23, 251–272. [Google Scholar] [CrossRef]
- Shrivastava, M.; Fan, J.; Zhang, Y.; Rasool, Q.Z.; Zhao, B.; Shen, J.; Pierce, J.R.; Jathar, S.H.; Akherati, A.; Zhang, J.; et al. Intense formation of secondary ultrafine particles from Amazonian vegetation fires and their invigoration of deep clouds and precipitation. One Earth 2024, 7, 1029–1043. [Google Scholar] [CrossRef]
- Andreae, M.O.; Afchine, A.; Albrecht, R.; Holanda, B.A.; Artaxo, P.; Barbosa, H.M.J.; Borrmann, S.; Cecchini, M.A.; Costa, A.; Dollner, M. Aerosol characteristics and particle production in the upper troposphere over the Amazon Basin. Atmos. Chem. Phys. 2018, 18, 921–961. [Google Scholar] [CrossRef]
- Trabert, W. Die Extinktion des Lichtes in einem trüben Medium (Sehweite in Wolken). Meteor. Z 1901, 18, 518–520. [Google Scholar]
- Aufm Kampe, H.; Weickmann, H. Trabert’s formula and the determination of the water content in clouds. J. Atmos. Sci. 1952, 9, 167–171. [Google Scholar] [CrossRef]
- Kim, B.G.; Schwartz, S.E.; Miller, M.A.; Min, Q. Effective radius of cloud droplets by ground-based remote sensing: Relationship to aerosol. J. Geophys. Res. Atmos. 2003, 108, 4740. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Zhou, W.; Ma, X.; Li, S.; Wang, X. Cloud ability to produce precipitation over arid and semiarid regions of Central and East Asia. Int. J. Climatol. 2020, 40, 1824–1837. [Google Scholar] [CrossRef]
- Khain, A.; Ovtchinnikov, M.; Pinsky, M.; Pokrovsky, A.; Krugliak, H. Notes on the state-of-the-art numerical modeling of cloud microphysics. Atmos. Res. 2000, 55, 159–224. [Google Scholar] [CrossRef]
- Ambaum, M.H. Thermal Physics of the Atmosphere; Elsevier: Amsterdam, The Netherlands, 2021; Volume 1. [Google Scholar]
- Benoit, J.B.; McCluney, K.E.; DeGennaro, M.J.; Dow, J.A. Dehydration dynamics in terrestrial arthropods: From water sensing to trophic interactions. Annu. Rev. Entomol. 2023, 68, 129–149. [Google Scholar] [CrossRef]
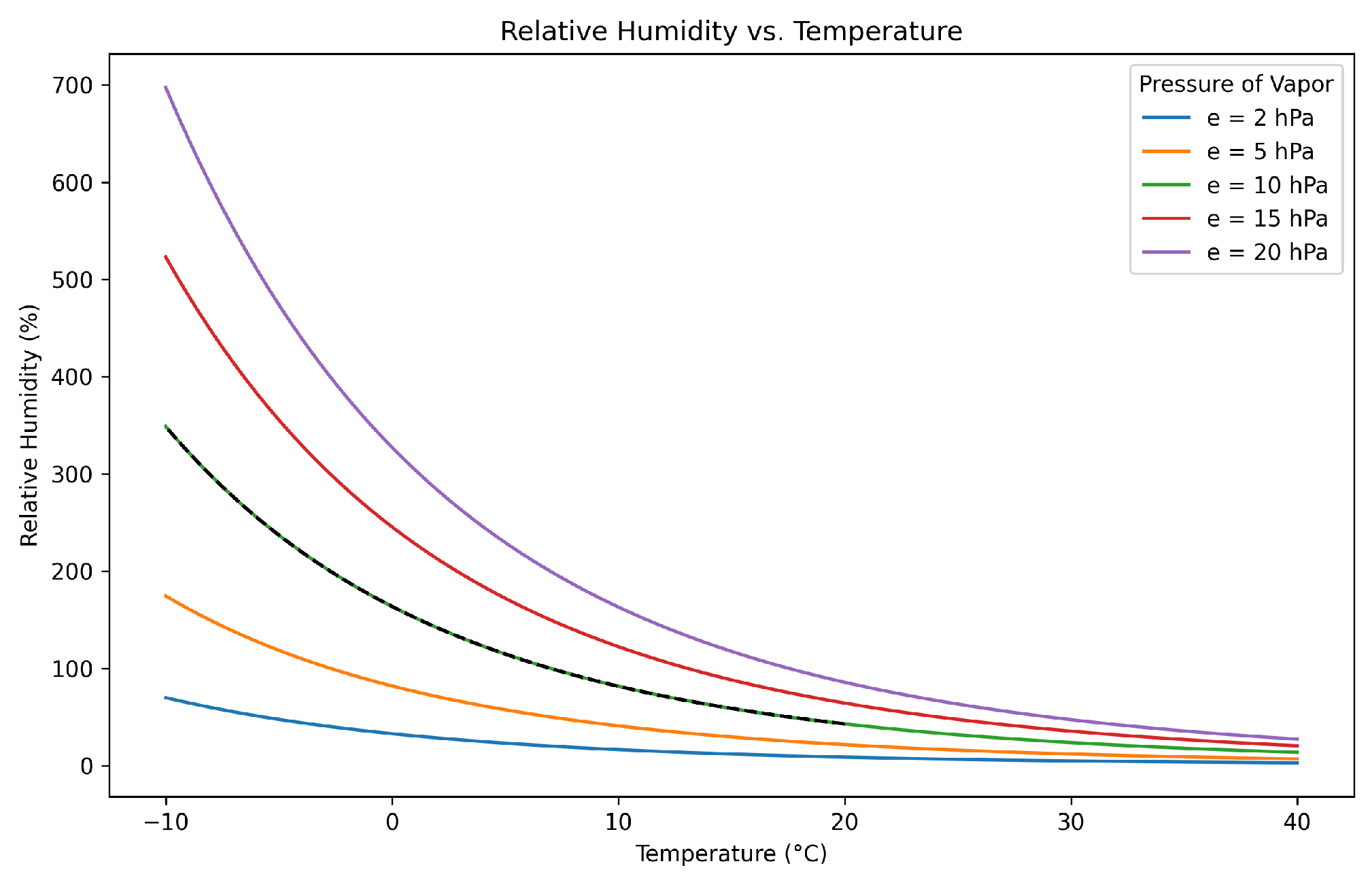
- Saha, K. Water Vapour in the Atmosphere: Thermodynamics of Moist Air. In The Earth’s Atmosphere; Springer: Berlin/Heidelberg, Germany, 2008; pp. 43–58. [Google Scholar]
- Braga, R.C. Influências das Concentrações de Aerossóis na Microfísica de Nuvens Convectivas Formadas Sobre a Amazônia. Ph.D. Thesis, Graduate Program in Meteorology, National Institute for Space Research (INPE), São José dos Campos, SP, Brazil, 2017. Available online: http://urlib.net/8JMKD3MGP3W34P/3PELPDE (accessed on 22 July 2025).
- Quaas, J.; Gryspeerdt, E. Aerosol-cloud interactions in liquid clouds. In Aerosols and Climate; Elsevier: Amsterdam, The Netherlands, 2022; pp. 489–544. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Meteorological Instruments and Methods of Observation; WMO-No. 8; World Meteorological Organization: Geneva, Switzerland, 2008; Appendix 4B (CIMO Guide).
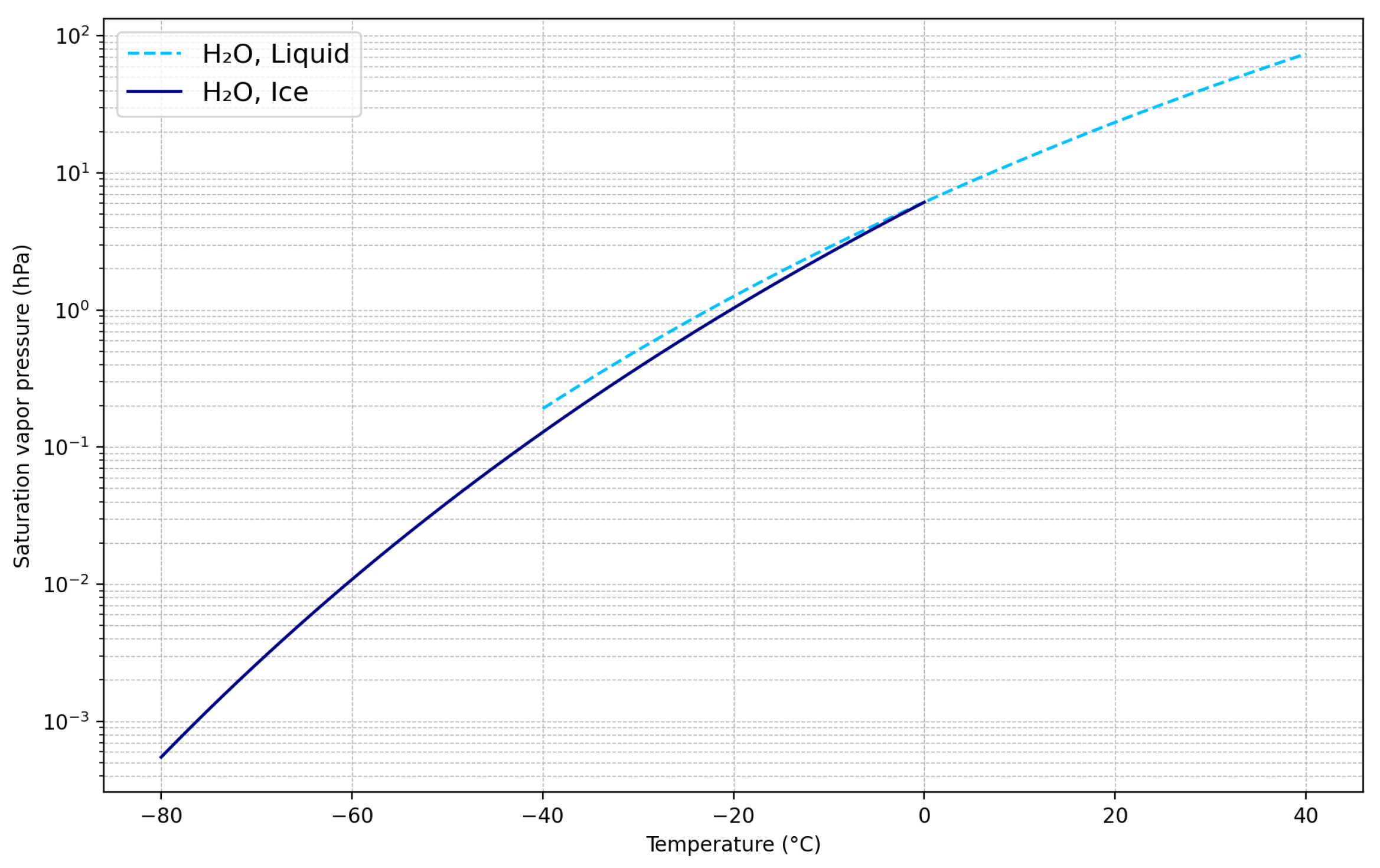
- Goff, J.A. Saturation Pressure of Water on the New Kelvin Temperature Scale. In Transactions of the American Society of Heating and Ventilating Engineers: Proceedings of the Semi-Annual Meeting of the American Society of Heating and Ventilating Engineers, Murray Bay, QC, Canada, 24–26 June 1957; American Society of Heating and Ventilating Engineers (ASHVE): New York, NY, USA, 1957; pp. 347–354. [Google Scholar]
- Davies, J.F.; Wilson, K.R. Heterogeneous reactions in aerosol. In Physical Chemistry of Gas-Liquid Interfaces; Elsevier: Amsterdam, The Netherlands, 2018; pp. 403–433. [Google Scholar] [CrossRef]
- Spichtinger, P.; Leschner, M. Horizontal scales of ice-supersaturated regions. Tellus B Chem. Phys. Meteorol. 2016, 68, 1. [Google Scholar] [CrossRef]
- Wex, H.; Stratmann, F.; Topping, D.; McFiggans, G. The Kelvin versus the Raoult term in the Köhler equation. J. Atmos. Sci. 2008, 65, 4004–4016. [Google Scholar] [CrossRef]
- Wex, H.; Stratmann, F.; Hennig, T.; Hartmann, S.; Niedermeier, D.; Nilsson, E.; Ocskay, R.; Rose, D.; Salma, I.; Ziese, M. Connecting hygroscopic growth at high humidities to cloud activation for different particletypes. Environ. Res. Lett. 2008, 3, 035004. [Google Scholar] [CrossRef]
- Grabowski, W.W.; Wang, L.P. Growth of Cloud Droplets in a Turbulent Environment. Annu. Rev. Fluid Mech. 2009, 41, 231–254. [Google Scholar] [CrossRef]
- Lewis, E.R. The effect of surface tension (Kelvin effect) on the equilibrium radius of a hygroscopic aqueous aerosol particle. J. Aerosol Sci. 2006, 37, 1605–1617. [Google Scholar] [CrossRef]
- Heidenreich, S.; Büttner, H. Investigations about the influence of the Kelvin effect on droplet growth rates. J. Aerosol Sci. 1995, 26, 335–339. [Google Scholar] [CrossRef]
- Kim, S.; Kim, D.; Kim, J.; An, S.; Jhe, W. Direct evidence for curvature-dependent surface tension in capillary condensation: Kelvin equation at molecular scale. Phys. Rev. X 2018, 8, 041046. [Google Scholar] [CrossRef]
- Durigon, A.; Rodriguez, C.A.M.; Biscaro, T.S.; Massambani, O. Impacto da distribuição de tamanho de hidrometeoros no cálculo das temperaturas de brilho na região de microondas. In Anais. A Meteorologia a Serviço da Sociedade; Sociedade Brasileira de Meteorologia: Florianópolis, Brazil, 2006; Available online: https://repositorio.usp.br/item/001590153 (accessed on 22 July 2025).
- Pruppacher, H.R.; Klett, J.D.; Wang, P.K. Microphysics of clouds and precipitation. Aerosol Sci. Technol. 1998, 28, 381–382. [Google Scholar] [CrossRef]
- Yau, M.K.; Rogers, R.R. A Short Course in Cloud Physics, 3rd ed.; Butterworth-Heinemann (Elsevier Science): Oxford, UK, 1996; pp. 60–96. [Google Scholar]
- Krueger, S.K. Equilibrium droplet size distributions in a turbulent cloud chamber with uniform supersaturation. Atmos. Chem. Phys. 2020, 20, 7895–7909. [Google Scholar] [CrossRef]
- Jing, B.; Wang, Z.; Qi, L.; Zhang, Y.; Sun, Y.; Wang, X.; He, H. Hygroscopic behavior of atmospheric aerosols containing nitrate salts and water-soluble organic acids. Atmos. Chem. Phys. 2018, 18, 5115–5127. [Google Scholar] [CrossRef]
- Kuang, Y.; He, Y.; Xu, W.; Zhao, P.; Cheng, Y.; Zhao, G.; Tao, J.; Ma, N.; Su, H.; Zhang, Y.; et al. Distinct diurnal variation in organic aerosol hygroscopicity and its relationship with oxygenated organic aerosol. Atmos. Chem. Phys. 2020, 20, 865–880. [Google Scholar] [CrossRef]
- Kang, H.; Jung, C.H.; Lee, B.Y.; Krejci, R.; Heslin-Rees, D.; Aas, W.; Yoon, J.J. Aerosol hygroscopicity influenced by seasonal chemical composition variations in the Arctic region. J. Aerosol Sci. 2025, 186, 106551. [Google Scholar] [CrossRef]
- Petters, M.D.; Kreidenweis, S.M. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity. Atmos. Chem. Phys. 2007, 7, 1961–1971. [Google Scholar] [CrossRef]
- Petters, M.D.; Kreidenweis, S.M. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity—Part 3: Including surfactant partitioning. Atmos. Chem. Phys. 2013, 13, 1081–1091. [Google Scholar] [CrossRef]
- Pöhlker, M.L.; Shiraiwa, M.; Yli-Juuti, T.; Cheng, Y.; Petters, M.D.; Rastak, N.; Gunthe, S.S.; Carbone, S.; Zaveri, R.A.; Andreae, M.O.; et al. Global organic and inorganic aerosol hygroscopicity and its effect on radiative forcing. Nat. Commun. 2023, 14, 6139. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Dou, J.; Klein, L.; Krieger, U.K.; Bain, A.; Wallace, B.J.; Preston, T.C.; Zuend, A. Extension of the AIOMFAC model by iodine and carbonate species: Applications for aerosol acidity and cloud droplet activation. Atmos. Chem. Phys. 2022, 22, 973–1013. [Google Scholar] [CrossRef]
- Raatikainen, T.; Laaksonen, A. Application of several activity coefficient models to water-organic-electrolyte aerosols of atmospheric interest. Atmos. Chem. Phys. 2005, 5, 2475–2495. [Google Scholar] [CrossRef]
- Hemming, B.L.; Seinfeld, J.H. On the Hygroscopic Behavior of Atmospheric Organic Aerosols. Ind. Eng. Chem. Res. 2001, 40, 4162–4171. [Google Scholar] [CrossRef]
- Zuend, A.; Marcolli, C.; Peter, T.; Krieger, U.K. New and extended parameterization of the thermodynamic model AIOMFAC: Calculation of activity coefficients for organic–inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups. Atmos. Chem. Phys. 2011, 11, 9155–9206. [Google Scholar] [CrossRef]
- Clegg, S.L.; Qiu, C.; Zhang, R. The deliquescence behaviour, solubilities, and densities of aqueous solutions of five methyl- and ethyl-aminium sulphate salts. Atmos. Environ. 2013, 73, 145–158. [Google Scholar] [CrossRef]
- Kärcher, B.; DeMott, P.J.; Jensen, E.J.; Harrington, J.Y. Studies on the Competition Between Homogeneous and Heterogeneous Ice Nucleation in Cirrus Formation. J. Geophys. Res. Atmos. 2022, 127, e2021JD035805. [Google Scholar] [CrossRef]
- Ren, C.; Mackenzie, A.R. Cirrus parametrization and the role of ice nuclei. Q. J. R. Meteorol. Soc. 2005, 131, 1585–1605. [Google Scholar] [CrossRef]
- Morrison, H.; van Lier-Walqui, M.; Fridlind, A.M.; Grabowski, W.W.; Harrington, J.Y.; Hoose, C.; Korolev, A.; Kumjian, M.R.; Milbrandt, J.A.; Pawlowska, H.; et al. Confronting the challenge of modeling cloud and precipitation microphysics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001689. [Google Scholar] [CrossRef]
- Burrows, S.M.; McCluskey, C.S.; Cornwell, G.; Steinke, I.; Zhang, K.; Zhao, B.; Zawadowicz, M.; Raman, A.; Kulkarni, G.; China, S.; et al. Ice-nucleating particles that impact clouds and climate: Observational and modeling research needs. Rev. Geophys. 2022, 60, e2021RG000745. [Google Scholar] [CrossRef]
- Krämer, M.; Rolf, C.; Spelten, N.; Afchine, A.; Fahey, D.; Jensen, E.; Khaykin, S.; Kuhn, T.; Lawson, P.; Lykov, A.; et al. A microphysics guide to cirrus–Part 2: Climatologies of clouds and humidity from observations. Atmos. Chem. Phys. 2020, 20, 12569–12608. [Google Scholar] [CrossRef]
- DeMott, P.J.; Kreidenweis, S.M.; Rogers, D.C. The susceptibility of ice formation in upper tropospheric clouds to insoluble aerosol components. J. Geophys. Res. 1997, 102, 19575–19584. [Google Scholar] [CrossRef]
- Martinsson, B. Aerosol, Water and Clouds. Extract from a Textbook on Airborne Particles by the Consortium of Aerosol Science and Technology (CAST), Lund University, 1992. Available online: https://www.nuclear.lu.se/fileadmin/nuclear/Undervisning/Atmosfaerskurs/Aerosol_water_and_clouds.pdf (accessed on 22 July 2025).
- Korolev, A.; McFarquhar, G.; Field, P.R.; Franklin, C.; Lawson, P.; Wang, Z.; Williams, E.; Abel, S.J.; Axisa, D.; Borrmann, S.; et al. Mixed-Phase Clouds: Progress and Challenges. In Formation and Evolution of Ice in Clouds and Precipitation: Measurement and Modeling Challenges; Meteorological Monographs, 58; American Meteorological Society: Boston, MA, USA, 2017; pp. 5.1–5.50. [Google Scholar] [CrossRef]
- Kanji, Z.A.; Ladino, L.A.; Wex, H.; Boose, Y.; Burkert-Kohn, M.; Cziczo, D.J.; Krämer, M. Overview of Ice Nucleating Particles. Meteorol. Monogr. 2017, 58, 1.1–1.33. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Springer: Dordrecht, The Netherlands, 2010; p. 954. [Google Scholar]
- Schröd, J.; Bingemer, H.G. A view on recent ice-nucleating particle intercomparison studies: Why the uncertainty of the activation temperature matters. Atmos. Meas. Tech. 2025, 18, 2591–2605. [Google Scholar] [CrossRef]
- Knopf, D.A.; Alpert, P.A.; Wang, B. The role of organic aerosol in atmospheric ice nucleation: A review. ACS Earth Space Chem. 2018, 2, 168–202. [Google Scholar] [CrossRef]
- Karlsruher Institut für Technologie (KIT). Modes of Ice Nucleation—IMK-AAF, n.d. Available online: https://www.imk-aaf.kit.edu/417.php (accessed on 10 March 2025).
- Zhang, Z.; Liu, X.Y. Control of ice nucleation: Freezing and antifreeze strategies. Chem. Soc. Rev. 2018, 47, 7116–7139. [Google Scholar] [CrossRef]
- Kasparoglu, S.; Perkins, R.; Ziemann, P.J.; DeMott, P.J.; Kreidenweis, S.M.; Finewax, Z.; Deming, B.L.; DeVault, M.P.; Petters, M.D. Experimental Determination of the Relationship Between Organic Aerosol Viscosity and Ice Nucleation Under Upper Tropospheric Conditions. J. Geophys. Res. Atmos. 2022, 127, e2021JD036296. [Google Scholar] [CrossRef]
- Mehndiratta, L.; Lyp, A.E.; Slade, J.H.; Grassian, V.H. Immersion ice nucleation of atmospherically relevant lipid particles. Environ. Sci. Atmos. 2024, 4, 1239–1254. [Google Scholar] [CrossRef]
- Rinaldi, M.; Nicosia, A.; Paglione, M.; Mansour, K.; Decesari, S.; Mazzola, M.; Belosi, F. Seasonal Trends of Ice Nucleating Particles at Ny-Ålesund: A Study of Condensation-Freezing by the Dynamic Filter Processing Chamber. Aerosol Res. Discuss. 2025, 1–29. [Google Scholar] [CrossRef]
- Ladino Moreno, L.A.; Stetzer, O.; Lohmann, U. Contact freezing: A review of experimental studies. Atmos. Chem. Phys. 2013, 13, 9745–9769. [Google Scholar] [CrossRef]
- Durant, A.J.; Shaw, R.A. Evaporation freezing by contact nucleation inside-out. Geophys. Res. Lett. 2005, 32, L20814. [Google Scholar] [CrossRef]
- Zhao, L.; Xue, J.; Wang, S.; Tian, P.; Huang, M.; Bi, K.; Wang, B. Single particle characteristics and ice nucleation potential of particles collected during Asian dust storms in 2021. Sci. Total Environ. 2024, 948, 174829. [Google Scholar] [CrossRef] [PubMed]
- Korhonen, K.; Kristensen, T.B.; Falk, J.; Lindgren, R.; Andersen, C.; Carvalho, R.L.; Malmborg, V.; Eriksson, A.; Boman, C.; Pagels, J.; et al. Ice-nucleating ability of particulate emissions from solid-biomass-fired cookstoves: An experimental study. Atmos. Chem. Phys. 2020, 20, 4951–4968. [Google Scholar] [CrossRef]
- Hoose, C.; Möhler, O. Heterogeneous ice nucleation on atmospheric aerosols: A review of results from laboratory experiments. Atmos. Chem. Phys. 2012, 12, 9817–9854. [Google Scholar] [CrossRef]
- Yang, F.; Liu, X. The Role of Anthropogenic Aerosols in Heterogeneous Ice Nucleation: A Review. Atmosphere 2022, 13, 286. [Google Scholar]
- Cziczo, D.J.; Froyd, K.D.; Hoose, C.; Jensen, E.J.; Diao, M.; Zondlo, M.A.; Hudson, P.K.; Stone, E.M.; Danforth, W. Clarifying the dominant sources and mechanisms of cirrus cloud formation. Science 2013, 340, 1320–1324. [Google Scholar] [CrossRef]
- Hill, T.C.J.; DeMott, P.J.; Tobo, Y.; Fröhlich-Nowoisky, J.; Moffett, B.F.; Franc, G.D.; Kreidenweis, S.M. Sources of organic ice nucleating particles in soils. Atmos. Chem. Phys. 2016, 16, 7195–7211. [Google Scholar] [CrossRef]
- Franks, F. Nucleation of ice and its management in ecosystems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 557–574. [Google Scholar] [CrossRef]
- Li, T.; Yu, Y.; Wang, X.; Liu, X.; Mao, Q.; Yuan, Y. A review of aerosol–cloud interactions: Mechanisms, climate effects, and observational methods. Atmos. Res. 2025, 325, 108267. [Google Scholar] [CrossRef]
- Patnaude, R.J.; Moore, K.A.; Perkins, R.J.; Hill, T.C.J.; DeMott, P.J.; Kreidenweis, S.M. Low-temperature ice nucleation of sea spray and secondary marine aerosols under cirrus cloud conditions. Atmos. Chem. Phys. 2024, 24, 911–926. [Google Scholar] [CrossRef]
- Schill, G.P.; Jathar, S.H.; Kodros, J.K.; Levin, E.J.T.; Galang, A.M.; Friedman, B.; Link, M.F.; Farmer, D.K.; Pierce, J.R.; Kreidenweis, S.M.; et al. Ice-nucleating particle emissions from photochemically aged diesel and biodiesel exhaust. Geophys. Res. Lett. 2016, 43, 5524–5531. [Google Scholar] [CrossRef]
- Mahrt, F.; Wang, B.; Wang, C.; Shen, H.; Martin, S.T.; Knopf, D.A. Aging induced changes in ice nucleation activity of combustion aerosol as determined by near edge X-ray absorption fine structure (NEXAFS) spectroscopy. Environ. Sci. Process. Impacts 2020, 22, 895–907. [Google Scholar] [CrossRef]
- Rapp, C.N.; Niu, S.; Armstrong, N.C.; Shen, X.; Berkemeier, T.; Surratt, J.D.; Zhang, Y.; Cziczo, D.J. Ice-nucleating properties of glassy organic and organosulfate aerosol. Atmos. Chem. Phys. 2025, 25, 5519–5536. [Google Scholar] [CrossRef]
- Sato, K.; Inoue, J. Seasonal Change in Satellite-Retrieved Lower-Tropospheric Ice-Cloud Fraction over the Southern Ocean. Geophys. Res. Lett. 2021, 48, e2021GL095295. [Google Scholar] [CrossRef]
- Tarn, M.D.; Sikora, S.N.; Porter, G.C.; O’Sullivan, D.; Adams, M.; Whale, T.F.; Harrison, A.D.; Vergara-Temprado, J.; Wilson, T.W.; Shim, J.u.; et al. The study of atmospheric ice-nucleating particles via microfluidically generated droplets. Microfluid. Nanofluid. 2018, 22, 52. [Google Scholar] [CrossRef] [PubMed]
- Herbert, R.J.; Sanchez-Marroquin, A.; Grosvenor, D.P.; Pringle, K.J.; Arnold, S.R.; Murray, B.J.; Carslaw, K.S. Gaps in our understanding of ice-nucleating particle sources exposed by global simulation of the UK climate model. EGUsphere 2024, 1–47. [Google Scholar] [CrossRef]
- Herbert, R.J.; Sanchez-Marroquin, A.; Grosvenor, D.P.; Pringle, K.J.; Arnold, S.R.; Murray, B.J.; Carslaw, K.S. Gaps in our understanding of ice-nucleating particle sources exposed by global simulation of the UK Earth System Model. Atmos. Chem. Phys. 2025, 25, 291–325. [Google Scholar] [CrossRef]
- Miller, A.J.; Fuchs, C.; Ramelli, F.; Zhang, H.; Omanovic, N.; Spirig, R.; Marcolli, C.; Kanji, Z.A.; Lohmann, U.; Henneberger, J. Quantified ice-nucleating ability of AgI-containing seeding particles in natural clouds. Atmos. Chem. Phys. 2025, 25, 5387–5407. [Google Scholar] [CrossRef]
- Gardner, D.B.; Wang, H. Critical review of modeling, measurement, and prediction of ice nucleation on surfaces. Int. J. Refrig. 2024, 163, 32–44. [Google Scholar] [CrossRef]
- Gettelman, A.; Liu, X.; Barahona, D.; Lohmann, U.; Chen, C. Climate impacts of ice nucleation. J. Geophys. Res. Atmos. 2012, 117, D20. [Google Scholar] [CrossRef]
- Song, X.; Zhang, G.J.; Li, J.L. Evaluation of microphysics parameterization for convective clouds in the NCAR Community Atmosphere Model CAM5. J. Clim. 2012, 25, 8568–8590. [Google Scholar] [CrossRef]
- McFarquhar, G.M. Rainfall microphysics. In Rainfall: Modeling, Measurement and Applications; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1–26. ISBN 978-0-12-822544-8. [Google Scholar]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 92. [Google Scholar]
- Barnet, P. Rain Drop Growth by Collision and Coalescence. Ph.D. Thesis, University of Reading, 2011. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=68cd79b4440ea3d547008d31bbb3e85f05f07d4a (accessed on 22 July 2025).
- Xue, Y.; Wang, L.P.; Grabowski, W.W. Growth of cloud droplets by turbulent collision–coalescence. J. Atmos. Sci. 2008, 65, 331–356. [Google Scholar] [CrossRef]
- Jonas, P.R. Turbulence and cloud microphysics. Atmos. Res. 1996, 40, 283–306. [Google Scholar] [CrossRef]
- Fowler, L.D.; Randall, D.A. Liquid and ice cloud microphysics in the CSU general circulation model. Part III: Sensitivity to modeling assumptions. J. Clim. 1996, 9, 561–586. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Ulbrich, C.W. Cloud Microphysical Properties, Processes, and Rainfall Estimation Opportunities. Meteorol. Monogr. 2003, 30, 237–258. [Google Scholar] [CrossRef]
- Stevens, B.; Seifert, A. Understanding macrophysical outcomes of microphysical choices in simulations of shallow cumulus convection. J. Meteorol. Soc. Jpn. Ser. II 2008, 143–162. [Google Scholar] [CrossRef]
- Zmijewski, P.; Dziekan, P.; Pawlowska, H. Modeling collision–coalescence in particle microphysics: Numerical convergence of mean and variance of precipitation in cloud simulations using the University of Warsaw Lagrangian Cloud Model (UWLCM) 2.1. Geosci. Model Dev. 2024, 17, 759–780. [Google Scholar] [CrossRef]
- Shima, S.; Kusano, K.; Kawano, A.; Sugiyama, T.; Kawahara, S. The super-droplet method for the numerical simulation of clouds and precipitation: A particle-based and probabilistic microphysics model coupled with a non-hydrostatic model. Q. J. R. Meteorol. Soc. 2009, 135, 1307–1320. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact Method for Numerically Simulating the Stochastic Coalescence Process in a Cloud. J. Atmos. Sci. 1975, 32, 1977–1989. [Google Scholar] [CrossRef]
- Bailey, M.; Hallett, J. Growth Rates and Habits of Ice Crystals between −20° and −70 °C. J. Atmos. Sci. 2004, 61, 514–544. [Google Scholar] [CrossRef]
- Gonda, T. The influence of vapor and heat diffusion on the morphology of ice crystals grown from the vapor phase. J. Cryst. Growth 1980, 49, 173–181. [Google Scholar] [CrossRef]
- Fourteau, K.; Domine, F.; Hagenmuller, P. Macroscopic water vapor diffusion is not enhanced in snow. Cryosphere 2021, 15, 389–406. [Google Scholar] [CrossRef]
- Chiruta, M.; Wang, P.K. The Capacitance of Rosette Ice Crystals. J. Atmos. Sci. 2003, 60, 836–846. [Google Scholar] [CrossRef]
- Zhang, C.; Harrington, J.Y. Including Surface Kinetic Effects in Simple Models of Ice Vapor Diffusion. J. Atmos. Sci. 2014, 71, 372–390. [Google Scholar] [CrossRef]
- Korolev, A. Limitations of the Wegener-Bergeron-Findeisen mechanism in the evolution of mixed-phase clouds. J. Atmos. Sci. 2007, 64, 3372–3375. [Google Scholar] [CrossRef]
- Storelvmo, T.; Tan, I. The Wegener-Bergeron-Findeisen process - Its discovery and vital importance for weather and climate. Meteorol. Z. 2015, 24, 455–461. [Google Scholar] [CrossRef]
- Khain, A.; Pinsky, M.; Korolev, A. Combined Effect of the Wegener–Bergeron–Findeisen Mechanism and Large Eddies on Microphysics of Mixed-Phase Stratiform Clouds. J. Atmos. Sci. 2022, 79, 383–407. [Google Scholar] [CrossRef]
- Yang, J.; Lu, J.; Deng, Y.; Wang, Y.; Lu, C.; Yin, Y.; Yang, K. Parameterizing the heterogeneous liquid-ice mixing in modeling ice growth through the Wegener-Bergeron-Findeisen process in CAM6. Geophys. Res. Lett. 2025, 52, e2024GL114036. [Google Scholar] [CrossRef]
- von Blohn, N.; Diehl, K.; Mitra, S.K.; Borrmann, S. Riming of graupel: Wind tunnel investigations of collection kernels and growth regimes. J. Atmos. Sci. 2009, 66, 2359–2366. [Google Scholar] [CrossRef]
- Garrett, T.J.; Yuter, S.E. Observed influence of riming, temperature, and turbulence on the fallspeed of solid precipitation. Geophys. Res. Lett. 2014, 41, 6515–6522. [Google Scholar] [CrossRef]
- Maherndl, N.; Maahn, M.; Tridon, F.; Leinonen, J.; Ori, D.; Kneifel, S. A riming-dependent parameterization of scattering by snowflakes using the self-similar Rayleigh–Gans approximation. Q. J. R. Meteorol. Soc. 2023, 149, 3562–3581. [Google Scholar] [CrossRef]
- Hogan, R.J.; Honeyager, R.; Tyynelä, J.; Kneifel, S. Calculating the millimetre-wave scattering phase function of snowflakes using the self-similar Rayleigh–Gans Approximation. Q. J. R. Meteorol. Soc. 2016, 143, 834–844. [Google Scholar] [CrossRef]
- Seifert, A.; Leinonen, J.; Siewert, C.; Kneifel, S. The Geometry of Rimed Aggregate Snowflakes: A Modeling Study. J. Adv. Model. Earth Syst. 2019, 11, 712–731. [Google Scholar] [CrossRef]
- Fitch, K.E.; Garrett, T.J. Measurement and analysis of the microphysical properties of Arctic precipitation showing frequent occurrence of riming. J. Geophys. Res. Atmos. 2022, 127, e2022JD037609. [Google Scholar] [CrossRef]
- Morrison, H.; Milbrandt, J.A. Parameterization of cloud microphysics based on the prediction of bulk ice particle properties. Part I: Scheme description and idealized tests. J. Atmos. Sci. 2015, 72, 287–311. [Google Scholar] [CrossRef]
- Lin, Y.; Donner, L.J.; Colle, B.A. Parameterization of riming intensity and its impact on ice fall speed using ARM data. Mon. Weather Rev. 2011, 139, 1180–1193. [Google Scholar] [CrossRef]
- Sulia, K.J.; Lebo, Z.J.; Przybylo, V.M.; Schmitt, C.G. A New Method for Ice–Ice Aggregation in the Adaptive Habit Model. J. Atmos. Sci. 2021, 78, 133–154. [Google Scholar] [CrossRef]
- Connolly, P.J.; Emersic, C.; Field, P.R. A laboratory investigation into the aggregation efficiency of small ice crystals. Atmos. Chem. Phys. 2012, 12, 2055–2076. [Google Scholar] [CrossRef]
- Korolev, A.; Heckman, I.; Wolde, M.; Ackerman, A.S.; Fridlind, A.M.; Ladino, L.A.; Williams, E. A new look at the environmental conditions favorable to secondary ice production. Atmos. Chem. Phys. 2020, 20, 1391–1429. [Google Scholar] [CrossRef]
- Waitz, F.; Afchine, A.; Wendisch, M.; Spichtinger, P.; Rolf, D.E.P.; Schwarzenboeck, A.; Schnaiter, M. PHIPS-HALO: The airborne Particle Habit Imaging and Polar Scattering probe–Part 3: Single-particle phase discrimination and particle size distribution based on the angular-scattering function. Atmos. Meas. Tech. 2021, 14, 3049–3070. [Google Scholar] [CrossRef]
- Baran, A.J. A review of the light scattering properties of cirrus. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1239–1260. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, P.; Kattawar, G.W.; Baum, B.A.; Hu, Y. Optical properties of plate aggregates for remote sensing applications in cirrus clouds. Appl. Opt. 2011, 50, 1065–1081. [Google Scholar] [CrossRef]
- Han, C.; Lower, C.; Dürlich, V. Secondary Ice Production in Simulated Deep Convective Clouds: A Sensitivity Study. J. Atmos. Sci. 2024, 81, 903–921. [Google Scholar] [CrossRef]
- Cholette, M.; Milbrandt, J.A.; Morrison, H.; Kirk, S.; Lalonde, L.-É. Secondary Ice Production Improves Simulations of Freezing Rain. Geophys. Res. Lett. 2024, 51, e2024GL108490. [Google Scholar] [CrossRef]
- Qu, Z.; Korolev, A.; Milbrandt, J.A.; Heckman, I.; Huang, Y.; McFarquhar, G.M.; Morrison, H.; Wolde, M.; Nguyen, C. The impacts of secondary ice production on microphysics and dynamics in tropical convection. Atmos. Chem. Phys. 2022, 22, 12287–12310. [Google Scholar] [CrossRef]
- Dedekind, Z.; Lauber, A.; Ferrachat, S.; Lohmann, U. Sensitivity of precipitation formation to secondary ice production in mixed-phase winter orographic clouds. Atmos. Chem. Phys. 2021, 21, 15115–15134. [Google Scholar] [CrossRef]
- Georgakaki, P.; Sotiropoulou, G.; Vignon, É.; Billault-Roux, A.C.; Berne, A.; Nenes, A. Secondary Ice Production Processes in Wintertime Alpine Mixed-Phase Clouds. Atmos. Chem. Phys. 2022, 22, 1965–1988. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, X. Primary and secondary ice production: Interactions and their relative importance. Atmos. Chem. Phys. 2022, 22, 2585–2600. [Google Scholar] [CrossRef]
- Sullivan, S.C.; Barthlott, C.; Crosier, J.; Zhukov, I.; Nenes, A.; Hoose, C. The effect of secondary ice production parameterization on the simulation of a cold frontal rainband. Atmos. Chem. Phys. 2018, 18, 16461–16480. [Google Scholar] [CrossRef]
- Karalis, M.; Sotiropoulou, G.; Abel, S.J.; Bossioli, E.; Georgakaki, P.; Methymaki, G.; Nenes, A.; Tombrou, M. Effects of secondary ice processes on a stratocumulus to cumulus transition during a cold-air outbreak. Atmos. Res. 2022, 277, 106302. [Google Scholar] [CrossRef]
- Korolev, A.; Leisner, T. Review of experimental studies of secondary ice production. Atmos. Chem. Phys. 2020, 20, 11767–11790. [Google Scholar] [CrossRef]
- Langham, E.J.; Mason, B.J. Heterogeneous and homogeneous nucleation of supercooled water. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1958, 247, 493–504. [Google Scholar]
- Mason, B.J.; Maybank, J. The fragmentation and electrification of freezing water drops. Q. J. R. Meteorol. Soc. 1960, 86, 176–185. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Mossop, S.C. Temperature dependence of secondary ice crystal production during soft hail growth by riming. Q. J. R. Meteorol. Soc. 1984, 110, 765–770. [Google Scholar] [CrossRef]
- Vardiman, L. The Generation of Secondary Ice Particles in Clouds by Crystal–Crystal Collision. J. Atmos. Sci. 1978, 35, 2168–2180. [Google Scholar] [CrossRef]
- Dye, J.E.; Hobbs, P.V. The Influence of Environmental Parameters on the Freezing and Fragmentation of Suspended Water Drops. J. Atmos. Sci. 1968, 25, 82–96. [Google Scholar] [CrossRef]
- Oraltay, R.G.; Hallett, J. Evaporation and melting of ice crystals: A laboratory study. Atmos. Res. 1989, 24, 169–189. [Google Scholar] [CrossRef]
- Muchnik, V.M.; Rudko, J.S. Peculiarities of freezing supercooled water drops. Trans. Ukr. Hydro Meteorol. Inst. (Trudi UkrNIGMI) 1961, 26, 64–73. [Google Scholar]
- Field, P.R.; Lawson, R.P.; Brown, P.R.A.; Lloyd, G.; Westbrook, C.; Moisseev, D.; Miltenberger, A.; Nenes, A.; Blyth, A.; Choularton, T.; et al. Secondary Ice Production: Current State of the Science and Recommendations for the Future. Meteorol. Monogr. 2017, 58, 7.1–7.20. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, X. Global Importance of Secondary Ice Production. Geophys. Res. Lett. 2021, 48, e2021GL092581. [Google Scholar] [CrossRef]
- Best, A.C. The size distribution of raindrops. Q. J. R. Meteorol. Soc. 1950, 76, 16–36. [Google Scholar] [CrossRef]
- Smith, P.L. Raindrop Size Distributions: Exponential or Gamma—Does the Difference Matter? J. Appl. Meteorol. 2003, 42, 1031–1034. [Google Scholar] [CrossRef]
- Igel, A.L.; van den Heever, S.C. The role of the gamma function shape parameter in determining differences between condensation rates in bin and bulk microphysics schemes. Atmos. Chem. Phys. 2017, 17, 4599–4609. [Google Scholar] [CrossRef]
- Khain, A.P.; Beheng, K.D.; Heymsfield, A.; Korolev, A.; Krichak, S.O.; Levin, Z.; Pinsky, M.; Phillips, V.; Prabhakaran, T.; Teller, A.; et al. Representation of microphysical processes in cloud-resolving models: Spectral (bin) microphysics versus bulk parameterization. Rev. Geophys. 2015, 53, 247–322. [Google Scholar] [CrossRef]
- Benmoshe, N.; Reisin, G.; Khain, A.; Koren, I. Turbulent effects on the microphysics and initiation of warm rain in deep convective clouds: 2-D simulations by a spectral mixed-phase microphysics cloud model. J. Geophys. Res. Atmos. 2012, 117, D06205. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Rasch, P.J.; Carslaw, K.S. Aerosol–Climate Modeling. In Aerosols and Climate; Carslaw, K.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Chapter 6; pp. 187–248. [Google Scholar]
- Chandrakar, K.K.; Morrison, H.; Grabowski, W.W.; Lawson, R.P. Are turbulence effects on droplet collision–coalescence a key to understanding observed rain formation in clouds? Proc. Natl. Acad. Sci. USA 2024, 121, e2319664121. [Google Scholar] [CrossRef]
- Singh, N.; Das, S.; Sahoo, U.K.; Kundu, S.S.; Chakraborty, S. On collisional drop breakup in orographic rain. Atmos. Res. 2024, 300, 107232. [Google Scholar] [CrossRef]
- Jin, H.G. Development of New Accretion Parameterizations and Their Applications to Cloud and Precipitation Modeling. Ph.D. Thesis, Seoul National University Graduate School, 2021. Available online: https://dcollection.snu.ac.kr/common/orgView/000000165497 (accessed on 20 July 2025).
- Lu, C.; Zhang, J.; Li, R.; Wang, S.; Fan, J.; Zhang, L. Reconciling contrasting relationships between relative dispersion and volume-mean radius of cloud droplet size distributions. J. Geophys. Res. Atmos. 2020, 125, e2019JD031868. [Google Scholar] [CrossRef]
- Gupta, S.; Rodrigues, E.S.; Silva, M.T.; Oliveira, C.A.; Souza, L.F. Lifecycle of Updrafts and Mass Flux in Isolated Deep Convection over the Amazon Forest: Insights from Cell Tracking. Atmos. Chem. Phys. 2024, 24, 4487–4510. [Google Scholar] [CrossRef]
- Rooney, G.G.; Shipway, B.J.; Parker, D.J. Rain in Convective Downdraughts. Quart. J. Roy. Meteorol. Soc. 2025, 151, e4923. [Google Scholar] [CrossRef]
- Terrell, M.L. Investigating the Effect of Size Sorting on the Vertical Variation of Rain Drop Size Distributions Using Parsivel Disdrometers and WSR-88D Radars During Vortex-SE. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2021. Available online: https://hammer.purdue.edu/articles/thesis/INVESTIGATING_THE_EFFECT_OF_SIZE_SORTING_ON_THE_VERTICAL_VARIATION_OF_RAIN_DROP_SIZE_DISTRIBUTIONS_USING_PARSIVEL_DISDROMETERS_AND_WSR-88D_RADARS_DURING_VORTEX-SE/15067314?utm_source=chatgpt.com&file=28973964 (accessed on 15 July 2025).
- Shan, Y.; Wilcox, E.M.; Gao, L.; Lin, L.; Mitchell, D.L.; Yin, Y.; Zhao, T.; Zhang, L.; Shi, H.; Gao, M. Evaluating Errors in Gamma-Function Representations of the Raindrop Size Distribution: A Method for Determining the Optimal Parameter Set for Use in Bulk Microphysics Schemes. J. Atmos. Sci. 2020, 77, 513–529. [Google Scholar] [CrossRef]
- Noppel, H.; Pokrovsky, A.; Lynn, B.; Khain, A.; Beheng, K. A spatial shift of precipitation from ocean to land induced by submicron soluble aerosol: Numerical modeling. J. Geophys. Res. Atmos. 2010, 115, D18212. [Google Scholar] [CrossRef]
- Cecchini, M.A.; Machado, L.A.T.; Wendisch, M.; Costa, A.; Krämer, M.; Andreae, M.O.; Afchine, A.; Albrecht, R.I.; Artaxo, P.; Borrmann, S.; et al. Illustration of microphysical processes in Amazonian deep convective clouds in the gamma phase space: Introduction and potential applications. Atmos. Chem. Phys. 2017, 17, 14727–14746. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Hsieh, T.; Freer, M.; Mascio, J.; Jewett, B.F. The Characterization of Ice Hydrometeor Gamma Size Distributions as Volumes in N0–rλ–μ Phase Space: Implications for Microphysical Process Modeling. J. Atmos. Sci. 2015, 72, 892–909. [Google Scholar] [CrossRef]
- Luo, L.; Xue, M.; Zhu, K.; Wang, Z. Diagnosing the shape parameters of the gamma particle size distributions in a two-moment microphysics scheme and improvements to explicit hail prediction. Atmos. Res. 2021, 258, 105651. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Morrison, H. Parameterization of cloud microphysics based on the prediction of bulk ice particle properties. Part III: Introduction of multiple free categories. J. Atmos. Sci. 2016, 73, 975–995. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water droplets in stagnant air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef]
- McDonald, J.E. The physics of cloud modification. Adv. Geophys. 1958, 5, 223–303. [Google Scholar] [CrossRef]
- Costa, A.A.; Campos Filho, M.C.; Santos, A.C.S. Características de cristais de gelo observados em um sistema de nuvens na Amazônia durante o experimento TRMM-LBA. Rev. Bras. Meteorol. 2012, 27, 139–151. [Google Scholar] [CrossRef][Green Version]
- Huang, J.; Minnis, P.; Yan, H.; Yi, Y.; Chen, B.; Zhang, L.; Ayers, J.K. Dust aerosol effect on semi-arid climate over Northwest China detected from A-Train satellite measurements. Atmos. Chem. Phys. 2010, 10, 6863–6872. [Google Scholar] [CrossRef]
- Lohmann, U.; Lüönd, F.; Mahrt, F. An Introduction to Clouds: From the Microscale to Climate; Cambridge University Press: Cambridge, UK, 2016; ISBN 9781139087513. [Google Scholar] [CrossRef]
- Koren, I.; Remer, L.A.; Altaratz, O.; Martins, J.V.; Davidi, A. Aerosol-induced changes of convective cloud anvils produce strong climate warming. Atmos. Chem. Phys. 2010, 10, 5001–5010. [Google Scholar] [CrossRef]
- Diehl, K.; Mitra, S.K.; Pruppacher, H.R. A laboratory study of the uptake of HNO3 and HCl vapor by snow crystals and ice spheres at temperatures between 0 and −40 ∘C. Atmos. Environ. 1995, 29, 975–981. [Google Scholar] [CrossRef]
- Gupta, A.K.; Deshmukh, A.; Waman, D.; Patade, S.; Jadav, A.; Phillips, V.T.J.; Bansemer, A.; Martins, J.A.; Gonçalves, F.L.T. The microphysics of warm-rain and ice-crystal precipitation processes in simulated continental convective storms. Earth Environ. Commun. Nat. 2023, 4, 226. [Google Scholar] [CrossRef]
- van den Heever, S.C.; Carrió, G.G.; Cotton, W.R.; Demott, P.J.; Prenni, A.J. Impacts of nucleating aerosol on Florida storms. Part I: Mesoscale simulations. J. Atmos. Sci. 2006, 63, 1752–1775. [Google Scholar] [CrossRef]
- Wang, J.; Wang, T.; Yasheng, D.; Wang, X.; Lei, Y.; Li, X.; Wang, Z.; Shi, B. Modulations of dust aerosols on precipitation: Evidence from a typical heavy sandstorm event. Atmos. Res. 2024, 304, 107411. [Google Scholar] [CrossRef]
- Henao, J.J.; Mejia, J.F.; McDonough, F. Impacts of anthropogenic aerosols on orographic precipitation in Arizona. Urban Clim. 2023, 49, 101561. [Google Scholar] [CrossRef]
- Chen, T.; Li, Z.; Kahn, R.A.; Zhao, C.; Rosenfeld, D.; Guo, J.; Han, W.; Chen, D. Potential impact of aerosols on convective clouds revealed by Himawari-8 observations over different terrain types in eastern China. Atmos. Chem. Phys. 2021, 21, 6199–6220. [Google Scholar] [CrossRef]
- López-Romero, J.M.; Montávez, J.P.; Jerez, S.; Lorente-Plazas, R.; Palacios-Peña, L.; Jiménez-Guerrero, P. Precipitation response to aerosol–radiation and aerosol–cloud interactions in regional climate simulations over Europe. Atmos. Chem. Phys. 2021, 21, 415–430. [Google Scholar] [CrossRef]
- Su, T.; Li, Z.; Roldan Henao, N.; Luan, Q.; Yu, F. Restrictive Effects of Aerosol–Cloud Interaction When Considering Cloud–Surface Coupling. Sci. Adv. 2024, 10, eadl5044. [Google Scholar] [CrossRef]
- Kumar, H.; Tiwari, S. Aerosol loading over the Northern Indian Ocean using space-borne measurements. In Atmospheric Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2023; pp. 191–210. [Google Scholar] [CrossRef]
- Rautela, K.S.; Singh, S.; Goyal, M.K. Aerosol atmospheric rivers: Patterns, impacts, and societal insights. In Environmental Science and Pollution Research; Springer Nature: Heidelberg, Germany, 2024; pp. 1–16. [Google Scholar] [CrossRef]
- Rautela, K.S.; Singh, S.; Goyal, M.K. Characterizing the spatio-temporal distribution, detection, and prediction of aerosol atmospheric rivers on a global scale. J. Environ. Manag. 2024, 351, 119675. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Kokhanovsky, A.; Goren, T.; Gryspeerdt, E.; Hasekamp, O.; Jia, S.; Lopatin, A.; Quaas, J.; Zengxin, P.; Sourdeval, O. Frontiers in Satellite-Based Estimates of Aerosol-Cloud-Mediated Forcing. Rev. Geophys. 2023, 61, e2022RG000799. [Google Scholar] [CrossRef]
- Zelinka, M.D.; Myers, T.A.; McCoy, D.T.; Po-Chedley, S.; Caldwell, P.M.; Ceppi, P.; Klein, S.A.; Taylor, K.E. Causes of Higher Climate Sensitivity in CMIP6 Models. Geophys. Res. Lett. 2020, 47, e2019GL085782. [Google Scholar] [CrossRef]
- Lutsko, N.J.; Luongo, M.T.; Wall, C.J.; Myers, T.A. Correlation Between Cloud Adjustments and Cloud Feedbacks Responsible for a Greater Spread in Climate Sensitivities in CMIP6. J. Geophys. Res. Atmos. 2022, 127, e2022JD037486. [Google Scholar] [CrossRef]
- Tiwari, S.; Kumar, H.; Singh, S.; Kumar, A. Current state of aerosol–cloud interactions and their impact over the northern Indian Ocean: A comprehensive review. Atmos. Res. 2023, 283, 106555. [Google Scholar] [CrossRef]
- Cairo, F.; Liberto, L.D.; Dionisi, D.; Snels, M. Understanding Aerosol-Cloud Interactions Using Lidar Techniques: A Review. Remote Sens. 2024, 16, 2788. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Gao, H. Impacts of laser beam divergence on lidar multiple scattering polarization returns from water clouds. J. Quant. Spectrosc. Radiat. Transf. 2021, 268, 107618. [Google Scholar] [CrossRef]
- Li, T.; Yu, Y.; Wang, X.; Liu, X.; Mao, Q.; Yuan, Y. Uma revisão das interações aerossol-nuvem: Mecanismos, efeitos climáticos e métodos de observação. Pesqui. Atmosférica 2025, 325, 108267. [Google Scholar]
- Lv, M.; Wang, T.; Huang, J.; Sun, Y.; Wang, Z.; Chen, L.; Zhang, J.; Zhao, C.; Shen, L.; Wu, Z. Hygroscopic growth of atmospheric aerosol particles based on lidar, radiosonde, and in situ measurements: Case studies from the Xinzhou field campaign. J. Quant. Spectrosc. Radiat. Transf. 2017, 188, 60–70. [Google Scholar] [CrossRef]
- Shen, X.; Liu, Q.; Sun, J.; Kong, W.; Ma, Q.; Qi, B.; Han, L.; Zhang, Y.; Liang, L.; Liu, L.; et al. Measurement report: The influence of particle number size distribution and hygroscopicity on the microphysical properties of cloud droplets at a mountain site. Atmos. Chem. Phys. 2025, 25, 5711–5725. [Google Scholar] [CrossRef]
- Jiang, F.; Zheng, Z.; Coe, H.; Healy, R.M.; Poulain, L.; Gros, V.; Zhang, H.; Li, W.; Liu, D.; West, M.; et al. Integrating Simulations and Observations: A Foundation Model for Estimating the Aerosol Mixing State Index. ACS ES&T Air 2025, 2, 877–890. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, K.M.R.d.; Herdies, D.L.; Kubota, P.Y.; Bresciani, C.; Figueroa, S.N. Impact of Aerosols on Cloud Microphysical Processes: A Theoretical Review. Geosciences 2025, 15, 312. https://doi.org/10.3390/geosciences15080312
Silva KMRd, Herdies DL, Kubota PY, Bresciani C, Figueroa SN. Impact of Aerosols on Cloud Microphysical Processes: A Theoretical Review. Geosciences. 2025; 15(8):312. https://doi.org/10.3390/geosciences15080312
Chicago/Turabian StyleSilva, Kécia Maria Roberto da, Dirceu Luís Herdies, Paulo Yoshio Kubota, Caroline Bresciani, and Silvio Nilo Figueroa. 2025. "Impact of Aerosols on Cloud Microphysical Processes: A Theoretical Review" Geosciences 15, no. 8: 312. https://doi.org/10.3390/geosciences15080312
APA StyleSilva, K. M. R. d., Herdies, D. L., Kubota, P. Y., Bresciani, C., & Figueroa, S. N. (2025). Impact of Aerosols on Cloud Microphysical Processes: A Theoretical Review. Geosciences, 15(8), 312. https://doi.org/10.3390/geosciences15080312







