Seasonal Sea Surface Temperatures from Mercenaria spp. During the Plio-Pleistocene: Oxygen Isotope Versus Clumped Isotope Paleothermometers
Abstract
1. Introduction
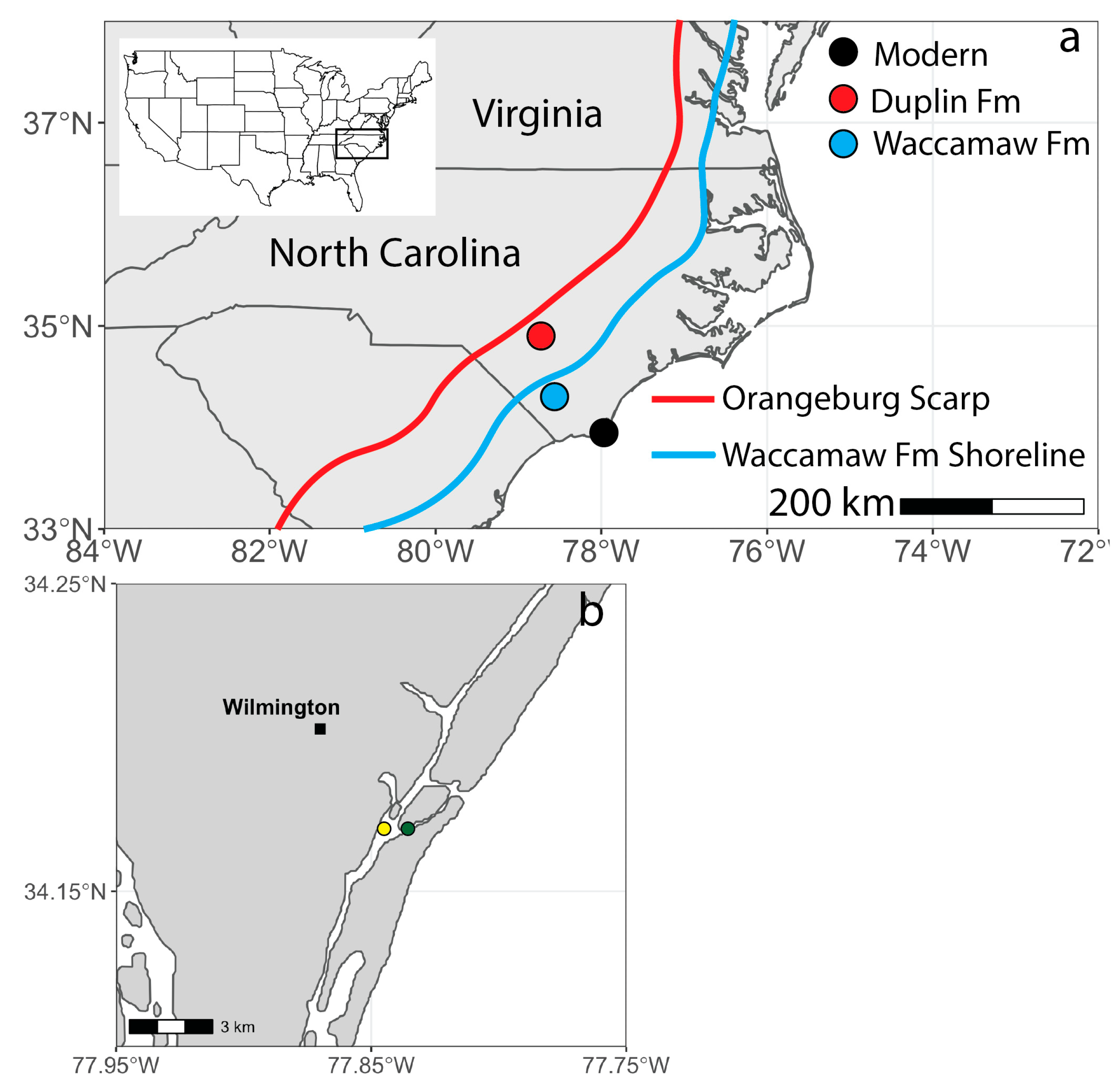
2. Geologic Context
2.1. Pliocene Formations (Duplin/Yorktown)
2.2. Pleistocene Formations (Waccamaw/Chowan River)
2.3. Mercenaria Ecology
3. Methods
3.1. Modern and Fossil Shell Collection
3.2. Taphonomic and Diagenetic Assessments and Shell Preparation
3.3. Micromilling and Isotopic Analysis
3.4. δ18O-Derived Temperature Calculations
3.5. Age Model
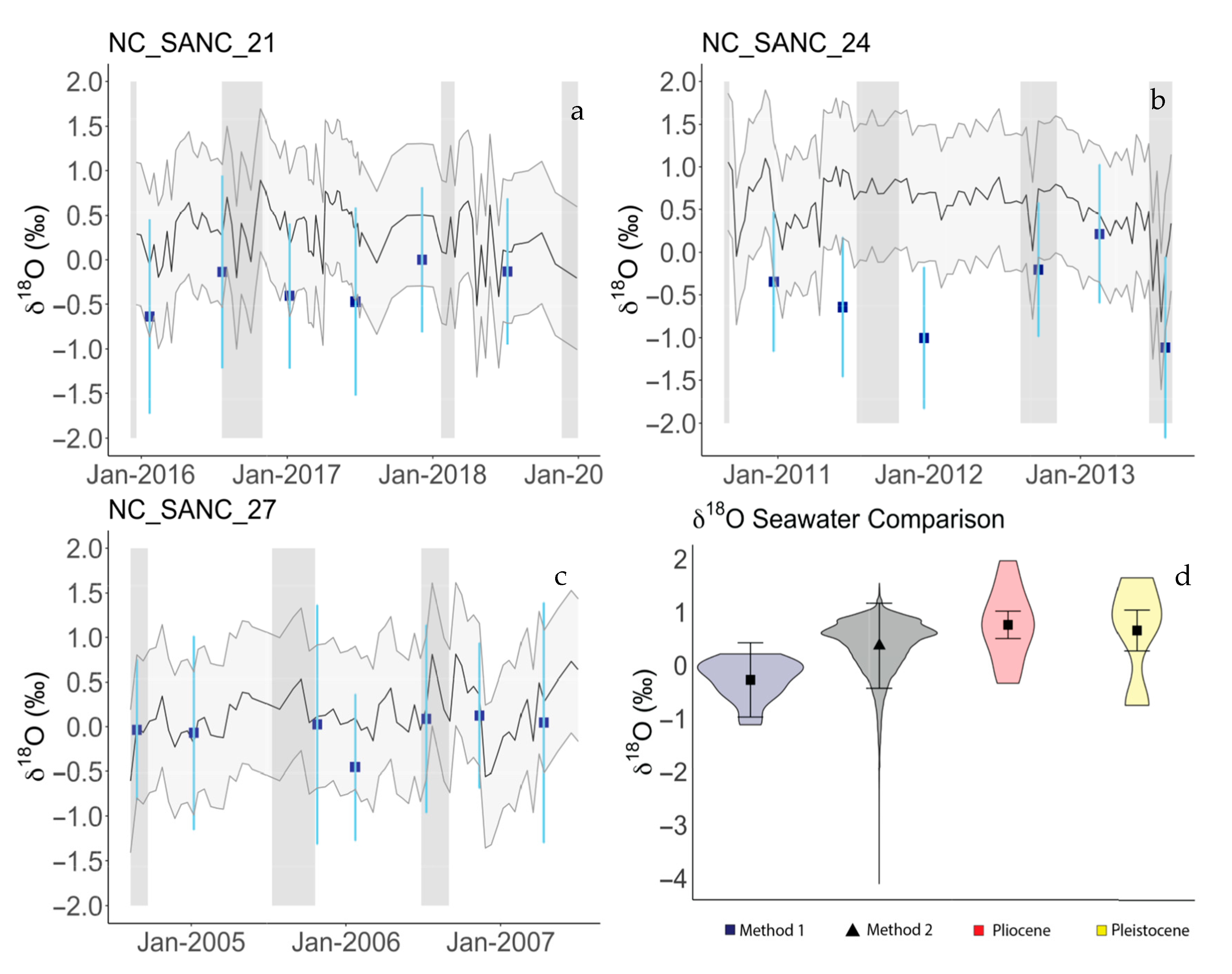
3.6. δ18Osw Calculations
3.7. Bootstrap Analysis
4. Results
4.1. Isotopic Compositions of Modern Shells
4.2. Isotopic Compositions of Fossil Shells
5. Discussion
5.1. Modern Clumped Isotope Validation
5.2. Validation of Clumped Isotope Temperatures vs. Modern Conditions
5.3. Comparison of Estimation Methods of Modern δ18Osw
5.4. Paleo SST Reconstructions: Δ47 Versus δ18Oshell
5.5. Comparing Seasonal SSTΔ47 Across Time Intervals
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dowsett, H.; Poore, R. Pliocene sea surface temperatures of the North Atlantic Ocean at 3.0 Ma. Quat. Sci. Rev. 1991, 10, 189–204. [Google Scholar] [CrossRef]
- Thompson, R.S.; Fleming, R.F. Middle Pliocene vegetation: Reconstructions, paleoclimatic inferences, and boundary conditions for climate modeling. Mar. Micropaleontol. 1996, 27, 27–49. [Google Scholar] [CrossRef]
- Dowsett, H.J.; Chandler, M.A.; Robinson, M.M. Surface temperatures of the Mid-Pliocene North Atlantic Ocean: Implications for future climate. Philos. Trans. Math. Phys. Eng. Sci. 2009, 367, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Dowsett, H.; Dolan, A.; Rowley, D.; Moucha, R.; Forte, A.M.; Mitrovica, J.X.; Pound, M.; Salzmann, U.; Robinson, M.; Chandler, M.; et al. The PRISM4 (mid-Piacenzian) paleoenvironmental reconstruction. Clim. Past 2016, 12, 1519–1538. [Google Scholar] [CrossRef]
- Arias, P.; Bellouin, N.; Coppola, E.; Jones, R.; Krinner, G.; Marotzke, J.; Naik, V.; Palmer, M.; Plattner, G.-K.; Rogelj, J. Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Summary; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Bretherton, F.; Bryan, K.; Woods, J. Time-Dependent Greenhouse-Gas-Induced Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1990; pp. 173–194. [Google Scholar]
- National Weather Service. Annual Average Temperature by Year. U.S. Department of Commerce. Available online: https://www.weather.gov/media/slc/ClimateBook/Annual%20Average%20Temperature%20By%20Year.pdf (accessed on 15 May 2025).
- Jansen, E.; Overpeck, J.; Briffa, K.R.; Duplessy, J.-C.; Joos, F.; Masson-Delmotte, V.; Olago, D.; Otto-Bliesner, B.; Peltier, W.R.; Rahmstorf, S.; et al. Palaeoclimate. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Johnson, A.L.A.; Valentine, A.; Leng, M.J.; Sloane, H.J.; Schöne, B.R.; Balson, P.S. Isotopic temperatures from the early and mid-pliocene of the US Middle Atlantic coastal plain, and their implications for the cause of regional marine climate change. Palaios 2017, 32, 250–269. [Google Scholar] [CrossRef]
- Burke, K.D.; Williams, J.W.; Chandler, M.A.; Haywood, A.M.; Lunt, D.J.; Otto-Bliesne, B.L. Pliocene and Eocene provide best analogs for near-future climates. Proc. Natl. Acad. Sci. USA 2018, 115, 13288–13293. [Google Scholar] [CrossRef]
- Adopted, I. Climate Change 2014 Synthesis Report; IPCC: Geneva, Switzerland, 2014; pp. 1059–1072. [Google Scholar]
- Martínez-Botí, M.A.; Foster, G.L.; Chalk, T.B.; Rohling, E.J.; Sexton, P.F.; Lunt, D.J.; Pancost, R.D.; Badger, M.P.S.; Schmidt, D.N. Plio-Pleistocene climate sensitivity evaluated using high-resolution CO2 records. Nature 2015, 518, 49–54. [Google Scholar] [CrossRef]
- Beierlein, L.; Salvigsen, O.; Schöne, B.R.; Mackensen, A.; Brey, T. The seasonal water temperature cycle in the Arctic Dicksonfjord (Svalbard) during the Holocene Climate Optimum derived from subfossil Arctica islandica shells. Holocene 2015, 25, 1197–1207. [Google Scholar] [CrossRef]
- Mouchi, V.; Godbillot, C.; Forest, V.; Ulianov, A.; Lartaud, F.; de Rafélis, M.; Emmanuel, L.; Verrecchia, E.P. Rare earth elements in oyster shells: Provenance discrimination and potential vital effects. Biogeosciences 2020, 17, 2205–2217. [Google Scholar] [CrossRef]
- Quitmyer, I.R.; Hale, H.S.; Jones, D.S. Paleoseasonality Determination Based on Incremental Shell Growth in the Hard Clam, Mercenaria mercenaria, and its Implications for the Analysis of Three Southeast Georgia Coastal Shell Middens. Southeast. Archaeol. 1985, 4, 27–40. [Google Scholar]
- Krantz, D.E. Mollusk-isotope records of Plio-Pleistocene marine paleoclimate, U.S. Middle Atlantic Coastal Plain. Palaios 1990, 5, 317–335. [Google Scholar] [CrossRef]
- Ward, L.W.; Bailey, R.; Carter, J.; Horton, J.; Zullo, V.A. Pliocene and early Pleistocene stratigraphy, depositional history, and molluscan paleobiogeography of the Coastal Plain. In The Geology Of The Carolinas; University of Tennessee Press: Knoxville, TN, USA, 1991; pp. 274–289. [Google Scholar]
- Jones, D.S.; Allmon, W.D. Records of upwelling, seasonality and growth in stable-isotope profiles of Pliocene mollusk shells from Florida. Lethaia 1995, 28, 61–74. [Google Scholar] [CrossRef]
- Jones, D.S.; Quitmyer, I.R. Marking Time with Bivalve Shells: Oxygen Isotopes and Season of Annual Increment Formation. Palaios 1996, 11, 340–346. [Google Scholar] [CrossRef]
- Winkelstern, I.; Surge, D.; Hudley, J.W. Multiproxy Sclerochronological Evidence for Plio-Pleistocene Regional Warmth: United State Mid-Atlantic Coastal Plain. Palaios 2013, 28, 649–660. [Google Scholar] [CrossRef]
- Goodwin, D.H.; Scho, B.R.; Dettman, D.L. Resolution and Fidelity of Oxygen Isotopes as Paleotemperature Proxies in Bivalve Mollusk Shells: Models and Observations. Palaios 2003, 18, 110–125. [Google Scholar] [CrossRef]
- Gillikin, D.P.; De Ridder, F.; Ulens, H.; Elskens, M.; Keppens, E.; Baeyens, W.; Dehairs, F. Assessing the reproducibility and reliability of estuarine bivalve shells (Saxidomus giganteus) for sea surface temperature reconstruction: Implications for paleoclimate studies. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2005, 228, 70–85. [Google Scholar] [CrossRef]
- Quitmyer, I.R.; Jones, D.S.; Arnold, W.S. The Sclerochronology of Hard Clams, Mercenaria spp., from the South-Eastern U.S.A.: A Method of Elucidating the Zooarchaeological Records of Seasonal Resource Procurement and Seasonality in Prehistoric Shell Middens. J. Archaeol. Sci. Rep. 1997, 24, 825–840. [Google Scholar] [CrossRef]
- Ansell, A.D. The Rate of Growth of the Hard Clam (Mercenaria mercenaria) throughout the Geographical Range. ICES J. Mar. Sci. 1968, 31, 364–409. [Google Scholar] [CrossRef]
- Wang, T.; Surge, D.; Walker, K.J. Isotopic evidence for climate change during the Vandal Minimum from Ariopsis felis otoliths and Mercenaria campechiensis shells, southwest Florida, USA. Holocene 2011, 21, 1081–1091. [Google Scholar] [CrossRef]
- Stenzel, H.B. Ancestors of the quahog. J. Sediment. Res. 1955, 25, 145. [Google Scholar] [CrossRef]
- Harte, M.E. Chapter 1 Systematics and taxonomy. In Developments in Aquaculture and Fisheries Science; Kraeuter, J.N., Castagna, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 3–51. [Google Scholar]
- Zachos, J.; Pagani, M.; Sloan, L.; Thomas, E.; Billups, K. Trends, Rhythms, and Aberrations in Global Climate 65 Ma to Present. Science 2001, 292, 686–693. [Google Scholar] [CrossRef]
- Lutringer, A.; Blamart, D.; Frank, N.; Labeyrie, L. Paleotemperatures from deep-sea corals: Scale effects. In Cold-Water Corals and Ecosystems; Freiwald, A., Roberts, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1081–1096. [Google Scholar]
- Ghosh, P.; Adkins, J.; Affek, H.; Balta, B.; Guo, W.; Schauble, E.A.; Schrag, D.; Eiler, J.M. 13C–18O bonds in carbonate minerals: A new kind of paleothermometer. Geochim. Cosmochim. Acta 2006, 70, 1439–1456. [Google Scholar] [CrossRef]
- Schauble, E.A.; Ghosh, P.; Eiler, J.M. Preferential formation of 13C–18O bonds in carbonate minerals, estimated using first-principles lattice dynamics. Geochim. Cosmochim. Acta 2006, 70, 2510–2529. [Google Scholar] [CrossRef]
- Huntington, K.W.; Budd, D.A.; Wernicke, B.P.; Eiler, J.M. Use of Clumped-Isotope Thermometry To Constrain the Crystallization Temperature of Diagenetic Calcite. J. Sediment. Res. 2011, 81, 656–669. [Google Scholar] [CrossRef]
- Briggs, J.C.; Bowen, B.W. A realignment of marine biogeographic provinces with particular reference to fish distributions. J. Biogeogr. 2012, 39, 12–30. [Google Scholar] [CrossRef]
- Rovere, A.; Hearty, P.J.; Austermann, J.; Mitrovica, J.X.; Gale, J.; Moucha, R.; Forte, A.M.; Raymo, M.E. Mid-Pliocene shorelines of the US Atlantic Coastal Plain—An improved elevation database with comparison to Earth model predictions. Earth-Sci. Rev. 2015, 145, 117–131. [Google Scholar] [CrossRef]
- Braniecki, G.F.; Surge, D.; Hyland, E.G.; Goodwin, D.H. Reconstructed seasonality during the Mid Piacenzian Warm Interval and early Pleistocene cooling as recorded by growth temperatures from Mercenaria shells. Quat. Sci. Rev. 2024, 328, 108524. [Google Scholar] [CrossRef]
- Ward, L.W.; Blackwelder, B.W. Stratigraphic Revision of Upper Miocene and Lower Pliocene Beds of the Chesapeake Group, Middle Atlantic Coastal Plain; Bulletin; U.S. Geological Survey: Reston, VA, USA, 1980. [Google Scholar]
- Blackwelder, B.W. Late Cenozoic Stages and Molluscan Zones of the U.S. Middle Atlantic Coastal Plain. J. Paleontol. 1981, 55 (Suppl. S12), 1–34. [Google Scholar] [CrossRef]
- Krantz, D.E. A chronology of Pliocene sea-level fluctuations: The U.S. Middle Atlantic Coastal Plain record. Quat. Sci. Rev. 1991, 10, 163–174. [Google Scholar] [CrossRef]
- Ward, L.W.; Gilinsky, N.L. Molluscan Assemblages of the Chowan River Formation; Virginia Museum of Natural History: Martinsville, VA, USA, 1993. [Google Scholar]
- Groot, J.J. Palynological evidence for late Miocene, Pliocene and early Pleistocene climate changes in the middle US Atlantic coastal plain. Quat. Sci. Rev. 1991, 10, 147–162. [Google Scholar] [CrossRef]
- Snyder, S.W.; Mauger, L.L.; Ames, D. Benthic Foraminifera and Paleecology of the Pliocene Yorktown and Chowan River Formations, Lee Creek Mine, North Carolina, USA. J. Foraminifer. Res. 2001, 31, 244–274. [Google Scholar] [CrossRef]
- Ward, L.W. Geology and Paleontology of the James River: Richmond to Hampton Roads; Virginia Museum of Natural History: Martinsville, VA, USA, 2008. [Google Scholar]
- Cronin, T.W. Evolution of marine climates of the US Atlantic coast during the past four million years. Philos. Trans. R. Soc. B Biol. Sci. 1988, 318, 661–678. [Google Scholar]
- Dowsett, H.J.; Cronin, T.M. High eustatic sea level during the middle Pliocene: Evidence from the southeastern US Atlantic Coastal Plain. Geology 1990, 18, 435–438. [Google Scholar] [CrossRef]
- Williams, M.; Haywood, A.M.; Harper, E.M.; Johnson, A.L.A.; Knowles, T.; Leng, M.J.; Lunt, D.J.; Okamura, B.; Taylor, P.D.; Zalasiewicz, J. Pliocene climate and seasonality in North Atlantic shelf seas. Philos. Trans. R. Soc. A 2009, 367, 85–108. [Google Scholar] [CrossRef] [PubMed]
- Dowsett, H.; Robinson, M.; Haywood, A.M.; Salzmann, U.; Hill, D.; Sohl, L.E.; Chandler, M.; Williams, M.; Foley, K.; Stoll, D.K. The PRISM3D paleoenvironmental reconstruction. Stratigraphy 2010, 7, 123–139. [Google Scholar] [CrossRef]
- Haywood, A.M.; Hill, D.J.; Dolan, A.M.; Otto-Bliesner, B.L.; Bragg, F.; Chan, W.L.; Chandler, M.A.; Contoux, C.; Dowsett, H.J.; Jost, A.; et al. Large-scale features of Pliocene climate: Results from the Pliocene Model Intercomparison Project. Clim. Past 2013, 9, 191–209. [Google Scholar] [CrossRef]
- Dowsett, H.J.; Wiggs, L.B. Planktonic foraminiferal assemblage of the Yorktown Formation, Virginia, USA. Micropaleontology 1992, 38, 75–86. [Google Scholar] [CrossRef]
- Dowsett, H.J.; Robinson, M.M.; Foley, K.M.; Herber, T.D. The Yorktown Formation: Improved stratigraphy, chronology, and paleoclimate interpretations from the US mid-Atlantic Coastal Plain. Geosciences 2021, 11, 486. [Google Scholar] [CrossRef]
- Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records. Paleoceanography 2005, 20, PA1003. [Google Scholar]
- Hazel, J.E. Distribution of some biostratigraphically diagnostic ostracodes in the Pliocene and lower Pleistocene of Virginia and northern North Carolina. Bull. U.S. Geol. J. Res. 1977, 5, 373–388. [Google Scholar]
- Gibbard, P.L.; Head, M.J.; Walker, M.J.C.; Subcommission on Quaternary Stratigraph. Formal ratification of the Quaternary System/Period and the Pleistocene Series/Epoch with a base at 2.58 Ma. J. Quat. Sci. 2010, 25, 96–102. [Google Scholar] [CrossRef]
- Merrill, A.S.; Ropes, J. Distribution of southern quahogs off the middle Atlantic coast. Commer. Fish. Rev. 1967, 29, 62–64. [Google Scholar]
- Arnold, W.; Bert, T.; Quitmyer, I.; Jones, D. Contemporaneous deposition of annual growth bands in Mercenaria mercenaria (Linnaeus), Mercenaria campechiensis (Gmelin), and their natural hybrid forms. J. Exp. Mar. Biol. Ecol. 1998, 223, 93–109. [Google Scholar] [CrossRef]
- MacKenzie, C.L., Jr.; Morrison, A.; Taylor, D.L.; Burrell, V.G., Jr.; Arnold, W.S.; Wakida-Kusunoki, A.T. Quahogs in eastern North America: Part I, biology, ecology, and historical uses. Mar. Fish. Rev. 2002, 64, 1–56. [Google Scholar]
- National Marine Fisheries Service. Fisheries of the United States, 2019; U.S. Department of Commerce, NOAA Current Fishery Statistics No. 2019; 2021. Available online: https://media.fisheries.noaa.gov/2021-05/FUS2019-FINAL-webready-2.3.pdf (accessed on 1 April 2021).
- Kraeuter, J.N.; Castagna, M. Biology of the Hard Clam; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Grizzle, R.E.; Bricelj, V.M.; Shumway, S.E. Chapter 8 Physiological ecology of Mercenaria mercenaria. In Developments in Aquaculture and Fisheries Science; Kraeuter, J.N., Castagna, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 305–382. [Google Scholar]
- Jones, D.S.; Arthur, M.A.; Allard, D.J. Sclerochronological records of temperature and growth from shells of Mercenaria mercenaria from Narragansett Bay, Rhode Island. Mar. Biol. 1989, 102, 225–234. [Google Scholar] [CrossRef]
- Briggs, J.C. Global Biogeography; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Sato, S.i. Spawning periodicity and shell microgrowth patterns of the venerid bivalve Phacosoma japonicum (Reeve, 1850). Veliger 1995, 38, 61–72. [Google Scholar]
- Kennedy, H.; Richardson, C.; Duarte, C.; Kennedy, D. Oxygen and carbon stable isotopic profiles of the fan mussel, Pinna nobilis, and reconstruction of sea surface temperatures in the Mediterranean. Mar. Biol. 2001, 139, 1115–1124. [Google Scholar] [CrossRef]
- Fritz, L.W. Shell Structure and Age Determination, in Developments in Aquaculture and Fisheries Science; Elsevier: Amsterdam, The Netherlands, 2001; pp. 53–76. [Google Scholar]
- Pannella, G.; MacClintock, C. Biological and Environmental Rhythms Reflected in Molluscan Shell Growth. Mem. (Paleontol. Soc.) 1968, 2, 64–80. [Google Scholar] [CrossRef]
- Rhoads, D.C.; Pannella, G. The use of molluscan shell growth patterns in ecology and paleoecology. Lethaia 1970, 3, 143–161. [Google Scholar] [CrossRef]
- Clark, G.R. Seasonal growth variations in the shells of recent and prehistoric specimens of Mercenaria mercenaria from St. Catherines Island, Georgia. Anthropol. Pap. Am. Mus. Nat. Hist. 1979, 51, 161–179. [Google Scholar]
- Fritz, L.W. Annulus Formation and Microstructure of Hard Clam (Mercenaria mercenaria) Shells. Master’s Thesis, School of Marine Science, College of William and Mary, Virginia Institute of Marine Science, Gloucester Point, VA, USA, 1982. [Google Scholar]
- Jones, D.S.; Quitmyer, I.R.; Arnold, W.S.; Marelli, D. Annual shell banding, age, and growth rate of hard clams (Mercenaria spp.) from Florida. J. Shellfish Res. 1990, 9. [Google Scholar]
- Arnold, W.S.; Marelli, D.C.; Bert, T.M.; Jones, D.S.; Quitmyer, I.R. Habitat-specific growth of hard clams Mercenaria mercenaria (L.) from the Indian River, Florida. J. Exp. Mar. Biol. Ecol. 1991, 147, 245–265. [Google Scholar] [CrossRef]
- Surge, D.; Wang, T.; Gutièrrez-Zugasti, I.; Kelley, P.H. Isotope Sclerochronology and Season of Annual Growt Line Formation in Limpet Shells (Patella Vulgata) from Warm- and Cold- Temperate Zones in the Eastern North Atlantic. Palaios 2013, 28, 386–393. [Google Scholar] [CrossRef]
- Henry, K.M.; Cerrato, R.M. The Annual Macroscopic Growth Pattern Of The Northern Quahog [=Hard Clam, Mercenaria mercenaria (L.)], In Narragansett Bay, Rhode Island. J. Shellfish Res. 2007, 26, 985–993, 9. [Google Scholar] [CrossRef]
- Elliot, M.; de Menocal, P.B.; Linsley, B.K.; Howe, S.S. Environmental controls on the stable isotopic composition of Mercenaria mercenaria: Potential application to paleoenvironmental studies. Geochem. Geophys. Geosyst. 2003, 4, 7. [Google Scholar] [CrossRef]
- Kubota, K.; Shirai, K.; Murakami-Sugihara, N.; Seike, K.; Hori, M.; Tanabe, K. Annual shell growth pattern of the Stimpson’s hard clam Mercenaria stimpsoni as revealed by sclerochronological and oxygen stable isotope measurements. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2017, 465, 307–315. [Google Scholar] [CrossRef]
- Palmer, K.L.; Moss, D.K.; Surge, D.; Turek, S. Life history patterns of modern and fossil Mercenaria spp. from warm vs. cold climates. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2021, 566, 110227. [Google Scholar] [CrossRef]
- Kidwell, S. Time-averaging in the marine fossil record: Overview of strategies and uncertainties. Oceanogr. Lit. Rev. 1998, 9, 1546–1547. [Google Scholar] [CrossRef]
- Bernasconi, S.M.; Daëron, M.; Bergmann, K.D.; Bonifacie, M.; Meckler, A.N.; Affek, H.P.; Anderson, N.; Bajnai, D.; Barkan, E.; Beverly, E.; et al. InterCarb: A Community Effort to Improve Interlaboratory Standardization of the Carbonate Clumped Isotope Thermometer Using Carbonate Standards. Geochem. Geophys. Geosyst. 2021, 22, e2020GC009588. [Google Scholar] [CrossRef]
- John, C.M.; Bowen, D. Community software for challenging isotope analysis: First applications of ‘Easotope’ to clumped isotopes. Rapid Commun. Mass Spectrom. 2016, 30, 2285–2300. [Google Scholar] [CrossRef]
- Daëron, M. Full Propagation of Analytical Uncertainties in Δ47 Measurements. Geochem. Geophys. Geosystems 2021, 22, e2020GC009592. [Google Scholar] [CrossRef]
- Anderson, N.T.; Kelson, J.R.; Kele, S.; Daëron, M.; Bonifacie, M.; Horita, J.; Mackey, T.J.; John, C.M.; Kluge, T.; Petschnig, P.; et al. A Unified Clumped Isotope Thermometer Calibration (0.5–1,100°C) Using Carbonate-Based Standardization. Geophys. Res. Lett. 2021, 48, e2020GL092069. [Google Scholar] [CrossRef]
- Brand, W.A.; Assonov, S.S.; Coplen, T.B. Correction for the 17O interference in δ(13C) measurements when analyzing CO2 with stable isotope mass spectrometry. Pure Appl. Chem. 2010, 82, 1719–1733. [Google Scholar] [CrossRef]
- Urey, H.C. Oxygen Isotopes in Nature and in the Laboratory. Science 1948, 108, 489–496. [Google Scholar] [CrossRef]
- Epstein, S.; Buchsbaum, R.; Lowenstam, H.A.; Urey, H.C. Revised Carbonate-Water Isotopic Temperature Scale. GSA Bull. 1953, 64, 1315–1326. [Google Scholar] [CrossRef]
- Grossman, E.L.; Ku, T.-L. Oxygen and carbon isotope fractionation in biogenic aragonite: Temperature effects. Chem. Geol. Isot. Geosci. Sect. 1986, 59, 59–74. [Google Scholar] [CrossRef]
- Dettman, D.L.; Reische, A.K.; Lohmann, K.C. Controls on the stable isotope composition of seasonal growth bands in aragonitic fresh-water bivalves (unionidae). Geochim. Cosmochim. Acta 1999, 63, 1049–1057. [Google Scholar] [CrossRef]
- Gonfiantini, R.; Stichler, W.; Rozanski, K. Standards and Intercomparison Materials Distributed by the International Atomic Energy Agency for Stable Isotope Measurements; IAEA: Vienna, Austria, 1995. [Google Scholar]
- Beck, J.W.; Edwards, R.L.; Ito, E.; Taylor, F.W.; Recy, J.; Rougerie, F.; Joannot, P.; Henin, C. Sea-surface temperature from coral skeletal strontium/calcium ratios. Science 1992, 257, 644–647. [Google Scholar] [CrossRef]
- Klein, R.T.; Lohmann, K.C.; Thayer, C.W. Bivalve skeletons record sea-surface temperature and δ18O via Mg/Ca and 18O/16O ratios. Geology 1996, 24, 415–418. [Google Scholar] [CrossRef]
- Surge, D.; Lohmann, K.C.; Dettman, D.L. Controls on isotopic chemistry of the American oyster, Crassostrea virginica: Implications for growth patterns. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2001, 172, 283–296. [Google Scholar] [CrossRef]
- Petersen, S.V.; Defliese, W.F.; Saenger, C.; Daëron, M.; Huntington, K.W.; John, C.M.; Kelson, J.R.; Bernasconi, S.M.; Colman, A.S.; Kluge, T.; et al. Effects of Improved 17O Correction on Interlaboratory Agreement in Clumped Isotope Calibrations, Estimates of Mineral-Specific Offsets, and Temperature Dependence of Acid Digestion Fractionation. Geochem. Geophys. Geosyst. 2019, 20, 3495–3519. [Google Scholar] [CrossRef]
- Jautzy, J.J.; Savard, M.M.; Dhillon, R.S.; Bernasconi, S.M.; Smirnoff, A. Clumped isotope temperature calibration for calcite: Bridging theory and experimentation. Geochem. Perspect. Lett. 2020, 14, 36–41. [Google Scholar] [CrossRef]
- Huyghe, D.; Daëron, M.; de Rafelis, M.; Blamart, D.; Sébilo, M.; Paulet, Y.-M.; Lartaud, F. Clumped isotopes in modern marine bivalves. Geochim. Cosmochim. Acta 2022, 316, 41–58. [Google Scholar] [CrossRef]
- Eagle, R.A.; Eiler, J.M.; Tripati, A.K.; Ries, J.B.; Freitas, P.S.; Hiebenthal, C.; Wanamaker, A.D., Jr.; Taviani, M.; Elliot, M.; Marenssi, S.; et al. The influence of temperature and seawater carbonate saturation state on 13C–18O bond ordering in bivalve mollusks. Biogeosciences 2013, 10, 4591–4606. [Google Scholar] [CrossRef]
- Cummins, R.C.; Finnegan, S.; Fike, D.A.; Eiler, J.M.; Fischer, W.W. Carbonate clumped isotope constraints on Silurian ocean temperature and seawater δ18O. Geochim. Cosmochim. Acta 2014, 140, 241–258. [Google Scholar] [CrossRef]
- Henkes, G.A.; Passey, B.H.; Grossman, E.L.; Shenton, B.J.; Yancey, T.E.; Pérez-Huerta, A. Temperature evolution and the oxygen isotope composition of Phanerozoic oceans from carbonate clumped isotope thermometry. Earth Planet. Sci. Lett. 2018, 490, 40–50. [Google Scholar] [CrossRef]
- Swart, P.K. The geochemistry of carbonate diagenesis: The past, present and future. Sedimentology 2015, 62, 1233–1304. [Google Scholar] [CrossRef]
- Henkes, G.A.; Passey, B.H.; Grossman, E.L.; Shenton, B.J.; Pérez-Huerta, A.; Yancey, T.E. Temperature limits for preservation of primary calcite clumped isotope paleotemperatures. Geochim. Cosmochim. Acta 2014, 139, 362–382. [Google Scholar] [CrossRef]
- Winkelstern, I.Z.; Lohmann, K.C. Shallow burial alteration of dolomite and limestone clumped isotope geochemistry. Geology 2016, 44, 467–470. [Google Scholar] [CrossRef]
- Staudigel, P.T.; Swart, P.K. Isotopic behavior during the aragonite-calcite transition: Implications for sample preparation and proxy interpretation. Chem. Geol. 2016, 442, 130–138. [Google Scholar] [CrossRef]
- Auderset, A.; Martínez-García, A.; Tiedemann, R.; Hasenfratz, A.P.; Eglinton, T.I.; Schiebel, R.; Sigman, D.M.; Haug, G.H. Gulf Stream intensification after the early Pliocene shoaling of the Central American Seaway. Earth Planet. Sci. Lett. 2019, 520, 268–278. [Google Scholar] [CrossRef]
- Lee, T.N.; Yoder, J.A.; Atkinson, L.P. Gulf Stream frontal eddy influence on productivity of the southeast U.S. continental shelf. J. Geophys. Res. Ocean. 1991, 96, 22191–22205. [Google Scholar] [CrossRef]
- Johnson, A.L.A.; Valentine, A.M.; Leng, M.J.; Schöne, B.R.; Sloane, H.J. Life History, Environment and Extinction of the Scallopcarolinapecten Eboreus(Conrad) in the Plio-Pleistocene of the U.S. Eastern Seaboard. Palaios 2019, 34, 49–70. [Google Scholar] [CrossRef]
- Johnson, A.L.A.; Schöne, B.R.; Petersen, S.V.; de Winter, N.J.; Dowsett, H.J.; Cudennec, J.-F.; Harper, E.M.; Winkelstern, I.Z. Molluscan isotope sclerochronology in marine palaeoclimatology: Taxa, technique and timespan issues. Quat. Sci. Rev. 2025, 350, 109068. [Google Scholar] [CrossRef]
- Hazel, J.E. Ostracode Biostratigraphy of the Yorktown Formation: (Upper Miocene and Lower Pliocene) of Virginia and North Carolina; US Government Printing Office: Washington, DC, USA, 1971; Volume 704.
- Hazel, J.E. Age and correlation of the Yorktown (Pliocene) and Croatan (Pliocene and Pleistocene) formations at the Lee Creek Mine. Smithson. Contrib. Paleobiol. 1983, 53, 81–199. [Google Scholar]




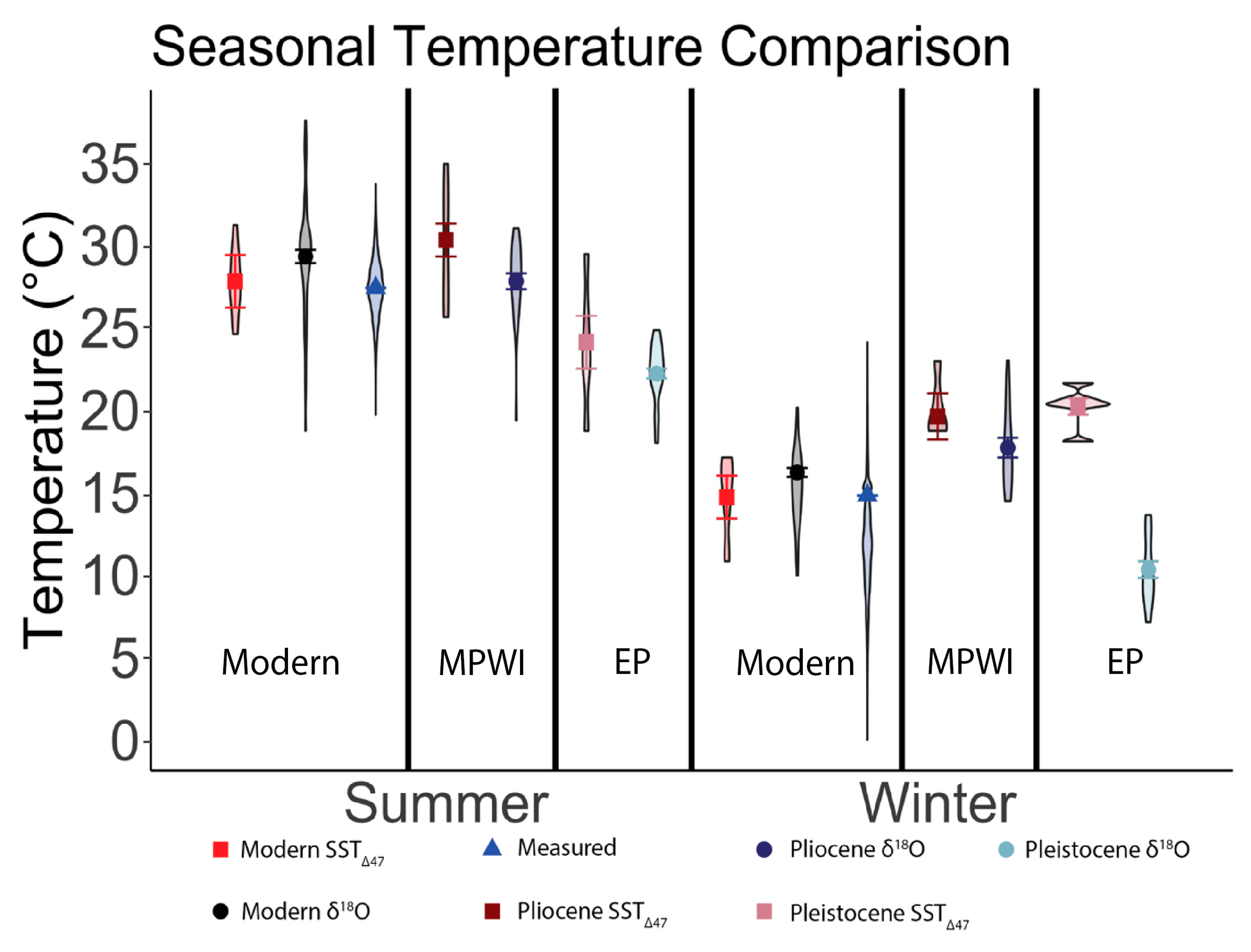
| Age/Formation/Location | Shell ID | Season | δ18O VPDB | Δ47 ICDES | Temperature (Δ47) |
|---|---|---|---|---|---|
| Modern | |||||
| North Carolina | NC_SANC_21 | Summer | −1.7 ± 0.4‰ | 0.586 ± 0.003‰ | 28 ± 1 °C |
| Winter | 0.9 ± 0.5‰ | 0.626 ± 0.011‰ | 15 ± 3 °C | ||
| North Carolina | NC_SANC_24 | Summer | −1.9 ± 0.1‰ | 0.588 ± 0.008‰ | 27 ± 3 °C |
| Winter | 0.9 ± 0.2‰ | 0.626 ± 0.009‰ | 15 ± 3 °C | ||
| North Carolina | NC_SANC_27 | Summer | −1.7 ± 0.3‰ | 0.581 ± 0.005‰ | 29 ± 2 °C |
| Winter | 1.0 ± 0.2‰ | 0.625 ± 0.005‰ | 15 ± 1 °C | ||
| Mid-Piacenzian | |||||
| Duplin Fm, NC | DUP-13 | Summer | −0.5 ± 0.2‰ | 0.582 ± 0.014‰ | 29 ± 5 °C |
| Winter | 0.7 ± 0.6‰ | 0.615 ± 0.005‰ | 18 ± 2 °C | ||
| Duplin Fm, NC | DUP-24 | Summer | −0.0 ± 0.3‰ | 0.577 ± 0.008‰ | 31 ± 3 °C |
| Winter | 0.3 ± 0.1‰ | 0.604 ± 0.005‰ | 22 ± 2 °C | ||
| Early Pleistocene | |||||
| Waccamaw Fm, NC | WAC-2 | Summer | −0.2 ± 0.1‰ | 0.587 ± 0.008‰ | 28 ± 3 °C |
| Winter | 1.3 ± 0.6‰ | 0.609 ± 0.006‰ | 20 ± 2 °C | ||
| Waccamaw Fm, NC | WAC-33 | Summer | −0.1 ± 0.6‰ | 0.600 ± 0.001‰ | 23 ± 1 °C |
| Winter | 1.3 ± 0.8‰ | 0.608 ± 0.001‰ | 20 ± 1 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braniecki, G.F.N.; Surge, D.; Hyland, E.G. Seasonal Sea Surface Temperatures from Mercenaria spp. During the Plio-Pleistocene: Oxygen Isotope Versus Clumped Isotope Paleothermometers. Geosciences 2025, 15, 295. https://doi.org/10.3390/geosciences15080295
Braniecki GFN, Surge D, Hyland EG. Seasonal Sea Surface Temperatures from Mercenaria spp. During the Plio-Pleistocene: Oxygen Isotope Versus Clumped Isotope Paleothermometers. Geosciences. 2025; 15(8):295. https://doi.org/10.3390/geosciences15080295
Chicago/Turabian StyleBraniecki, Garrett F. N., Donna Surge, and Ethan G. Hyland. 2025. "Seasonal Sea Surface Temperatures from Mercenaria spp. During the Plio-Pleistocene: Oxygen Isotope Versus Clumped Isotope Paleothermometers" Geosciences 15, no. 8: 295. https://doi.org/10.3390/geosciences15080295
APA StyleBraniecki, G. F. N., Surge, D., & Hyland, E. G. (2025). Seasonal Sea Surface Temperatures from Mercenaria spp. During the Plio-Pleistocene: Oxygen Isotope Versus Clumped Isotope Paleothermometers. Geosciences, 15(8), 295. https://doi.org/10.3390/geosciences15080295







