Carbon Isotopes in Magmatic Systems: Measurements, Interpretations, and the Carbon Isotopic Signature of the Earth’s Mantle
Abstract
1. Introduction
2. Carbon Isotope Measurements in Magmatic Systems
2.1. Carbon Isotope Measurements in Volcanic Gases
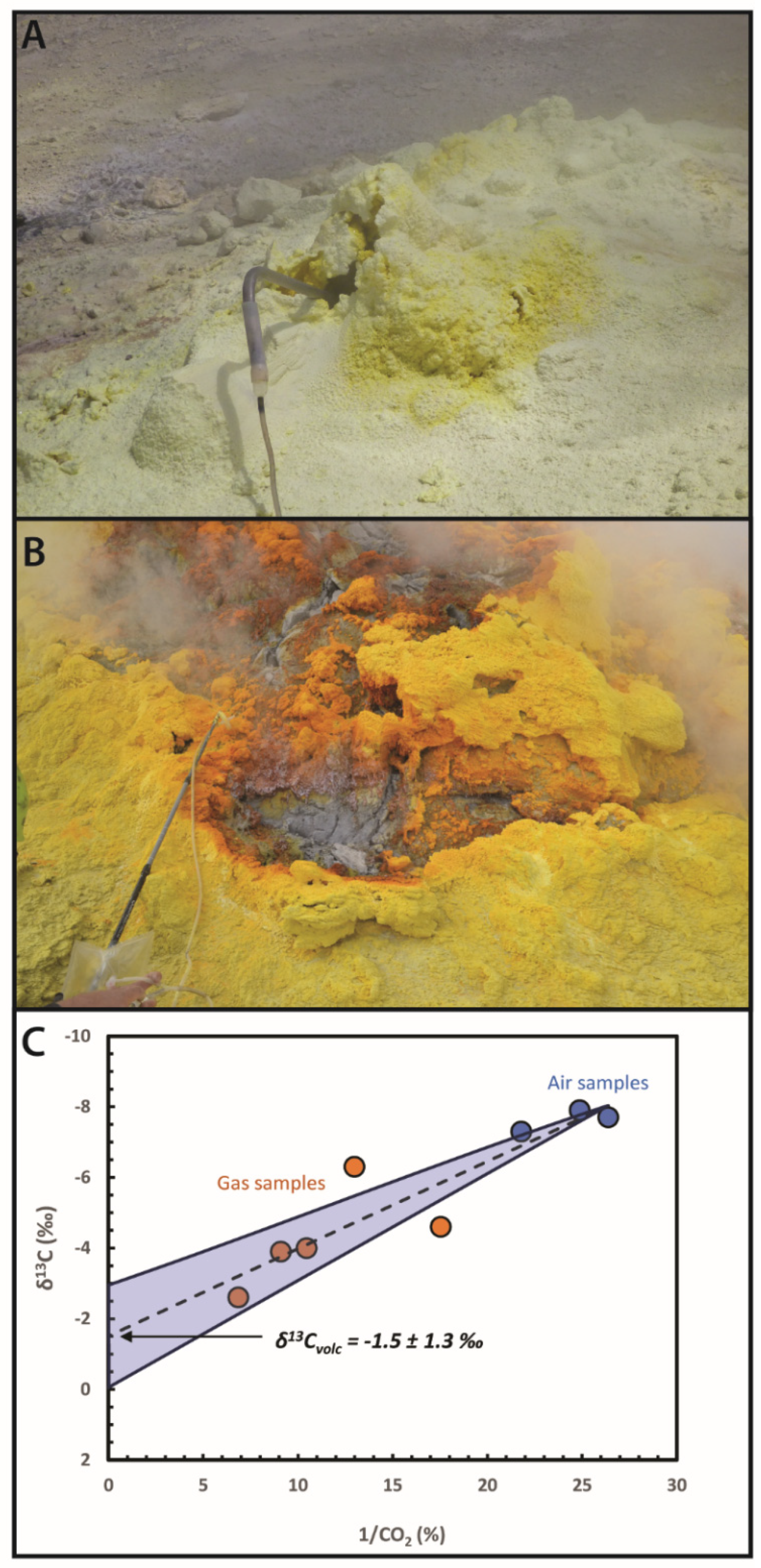
2.1.1. Traditional Technique (Direct Sampling + IRMS)
2.1.2. Novel Approach (Dilute Samples + IRIS)
2.2. Carbon Isotope Measurements in Vesicles
2.3. Carbon Isotope Measurements in Glasses and Melt Inclusions
2.3.1. Traditional Technique (Fusion-Extraction + IRMS)
2.3.2. Novel Approach (SIMS)
2.4. Carbon Isotope Measurements in Fluid Inclusions
2.4.1. Traditional Technique (Crushing-Extraction + IRMS)
2.4.2. Novel Approach (Raman Spectroscopy)
3. Carbon Isotope Behavior in Magmatic Systems
3.1. Carbon Isotopic Fractionation During Degassing
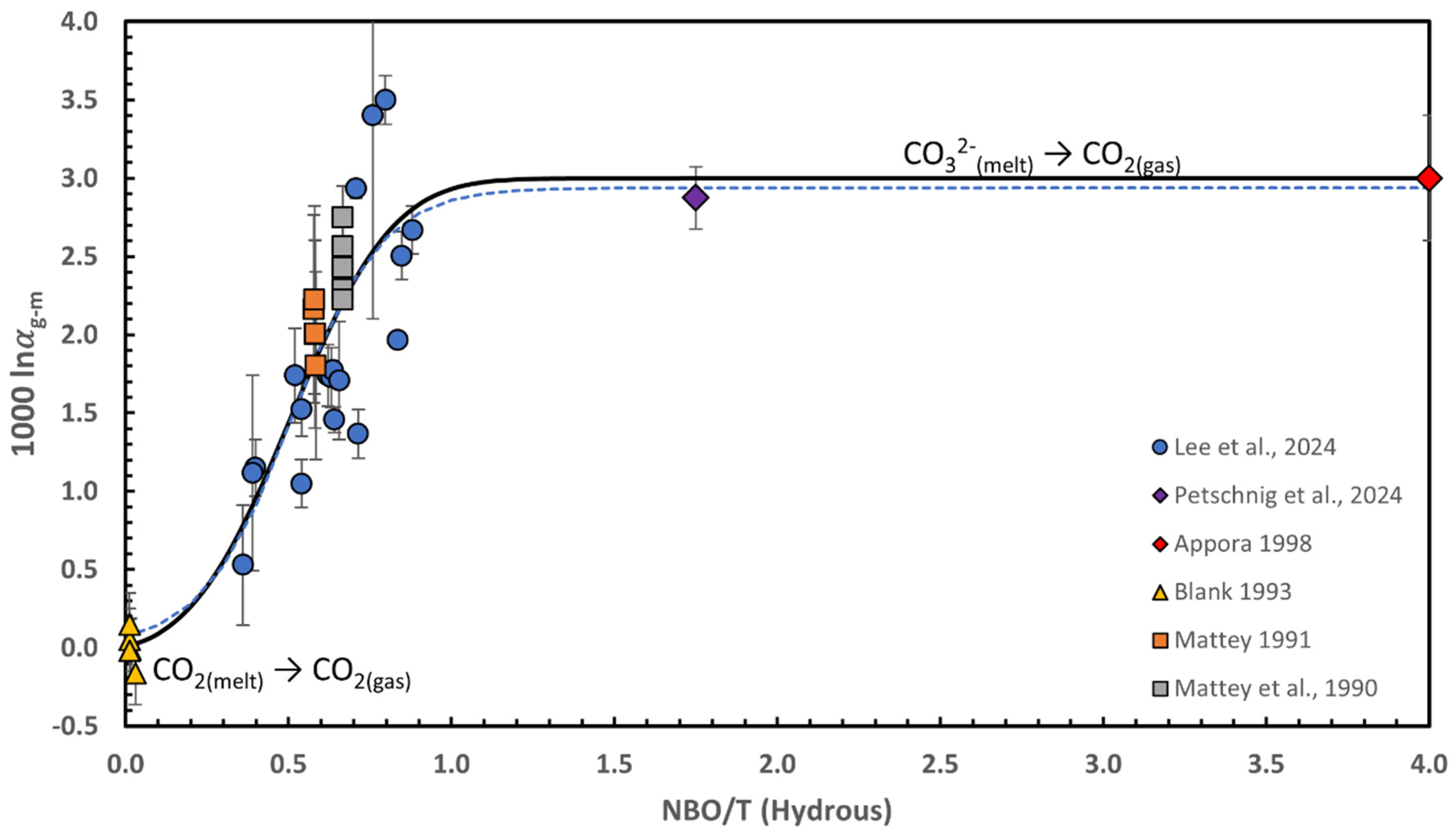
3.1.1. Isotopic Fractionation Between CO2 Gas and Dissolved Carbon in Silicate Melts; The Javoy-Mattey Conundrum and Its Resolution
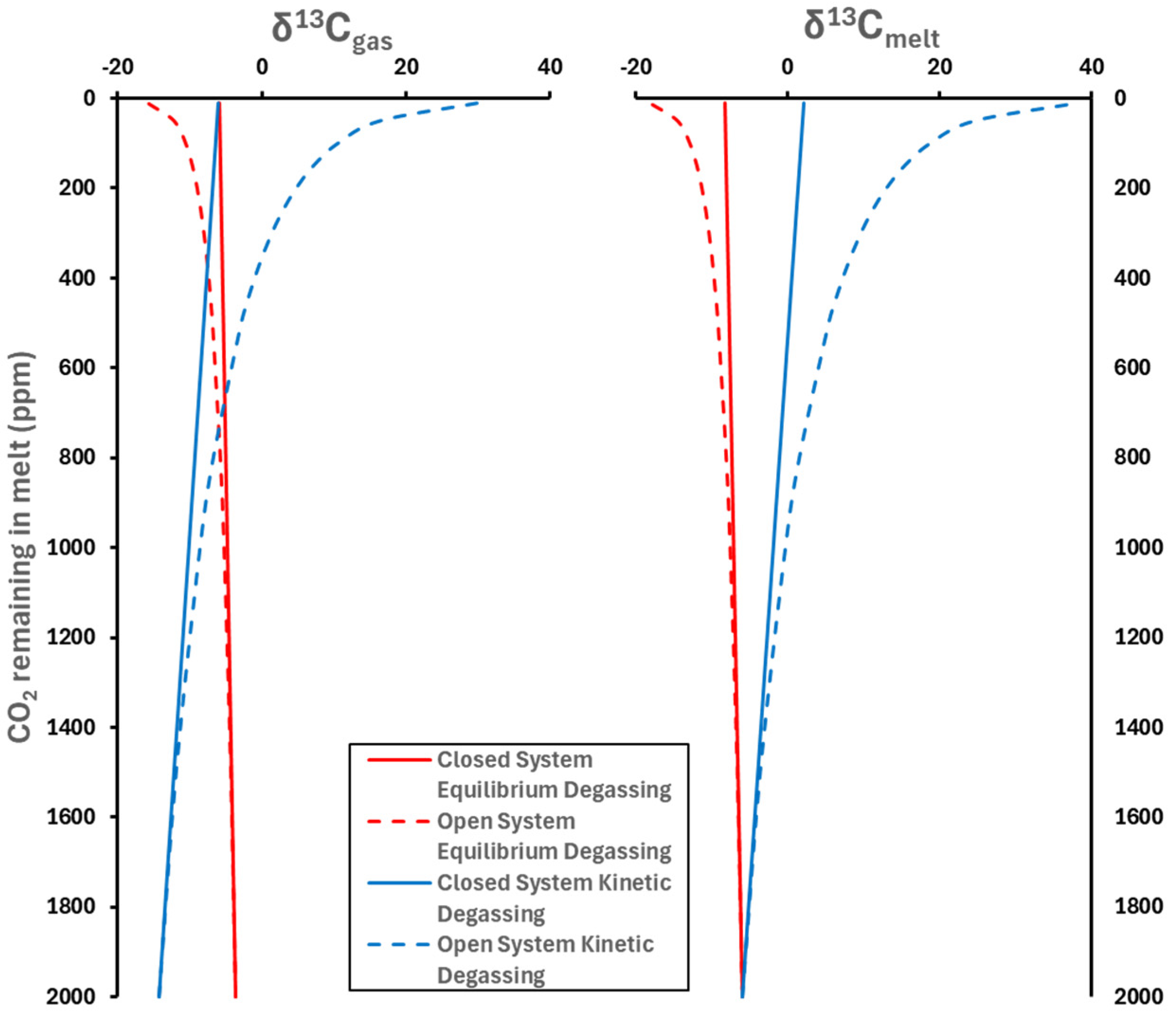
3.1.2. Degassing Styles and Carbon Isotope Evolution During Degassing
3.2. Isotopic Fractionation in Subduction and Mantle Processes
3.2.1. Isotopic Fractionation During Mantle Partial Melting
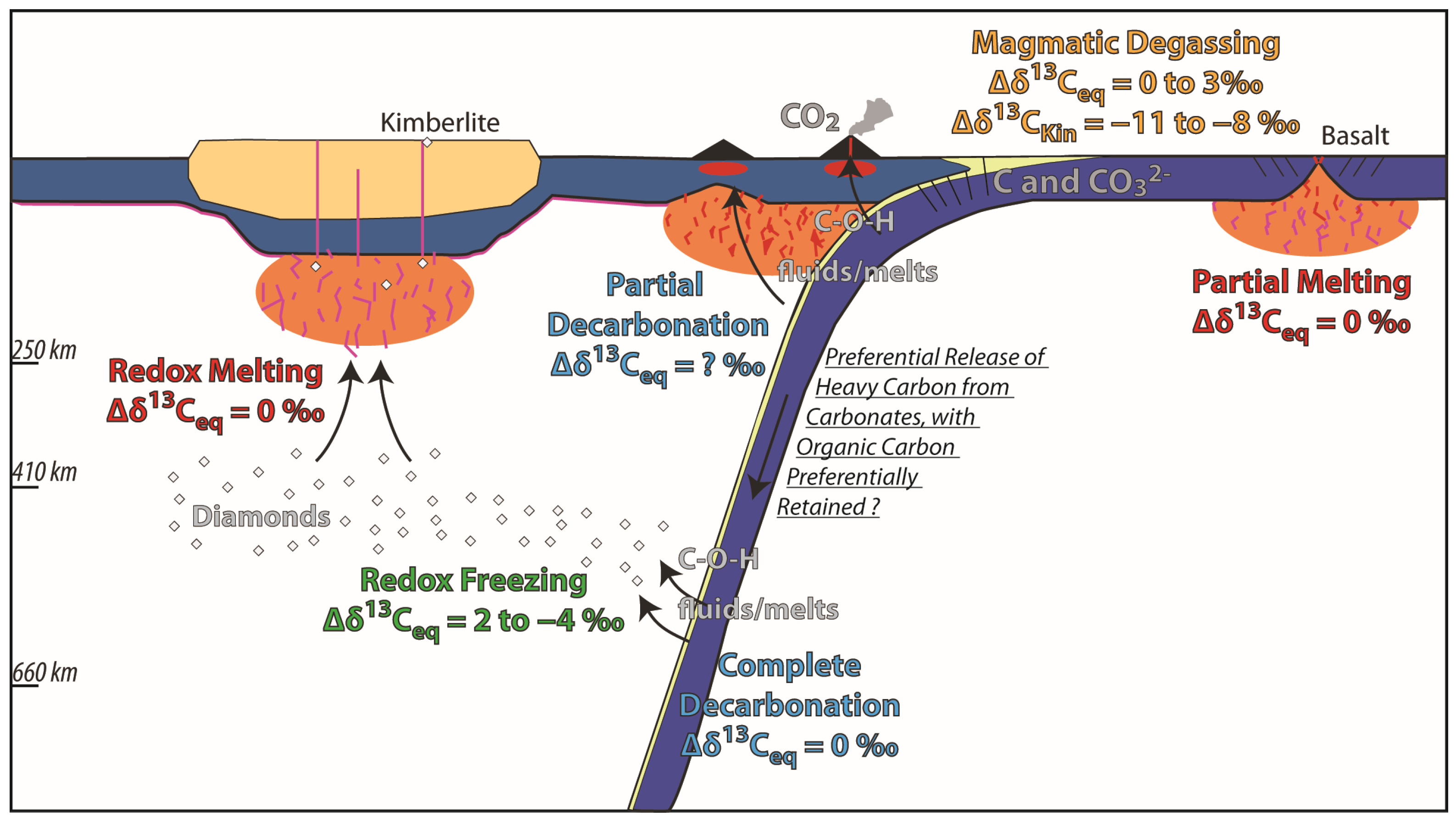
3.2.2. Isotopic Fractionation During Slab Release and Diamond Formation
4. Carbon Isotope Signature of Earth’s Upper Mantle
4.1. Review of Available Evidence
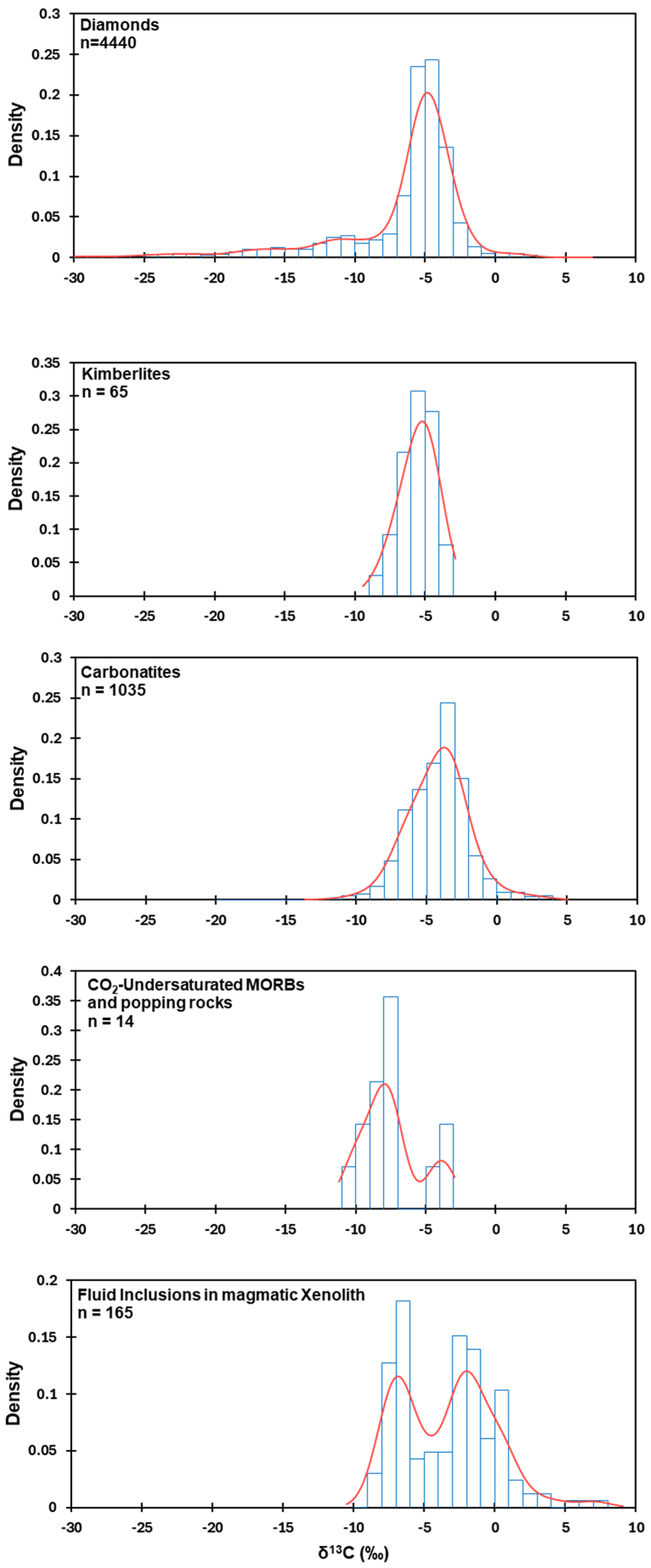
4.2. Carbon Isotope Signature of Earth’s Upper Mantle, Spatial, and Temporal Variability
5. Future Studies
Supplementary Materials
Funding
Conflicts of Interest
References
- Craig, H. The Geochemistry of the Stable Carbon Isotopes. Geochim. Cosmochim. Acta 1953, 3, 53–92. [Google Scholar] [CrossRef]
- Degens, E.T. Biogeochemistry of Stable Carbon Isotopes. In Organic Geochemistry: Methods and Results; Eglinton, G., Murphy, M.T.J., Eds.; Springer: Berlin, Heidelberg, 1969; pp. 304–329. ISBN 978-3-642-87734-6. [Google Scholar]
- Sano, Y.; Marty, B. Origin of Carbon in Fumarolic Gas from Island Arcs. Chem. Geol. 1995, 119, 265–274. [Google Scholar] [CrossRef]
- Mason, E.; Edmonds, M.; Turchyn, A.V. Remobilization of Crustal Carbon May Dominate Volcanic Arc Emissions. Science 2017, 357, 290–294. [Google Scholar] [CrossRef]
- Deines, P. The Carbon Isotope Geochemistry of Mantle Xenoliths. Earth-Sci. Rev. 2002, 58, 247–278. [Google Scholar] [CrossRef]
- Naughton, J.J.; Terada, K. Effect of Eruption of Hawaiian Volcanoes on the Composition and Carbon Isotope Content of Associated Volcanic and Fumarolic Gases. Science 1954, 120, 580–581. [Google Scholar] [CrossRef]
- Gerlach, T.M.; Taylor, B.E. Carbon Isotope Constraints on Degassing of Carbon Dioxide from Kilauea Volcano. Geochim. Cosmochim. Acta 1990, 54, 2051–2058. [Google Scholar] [CrossRef]
- Sakai, H.; Matsubaya, O. Stable Isotopic Studies of Japanese Geothermal Systems. Geothermics 1977, 5, 97–124. [Google Scholar] [CrossRef]
- Allard, P.; Le Guern, F.; Sabroux, J.C. Thermodynamic and Isotopic Studies in Eruptive Gases. Geothermics 1977, 5, 37–40. [Google Scholar] [CrossRef]
- Allard, P. 13C/12C and 34S/32S Ratios in Magmatic Gases from Ridge Volcanism in Afar. Nature 1979, 282, 56–58. [Google Scholar] [CrossRef]
- Allard, P. The Origin of Water, Carbon, Sulphur, Nitrogen and Rare Gases in Volcanic Exhalations; Evidence from Isotope Geochemistry. In Forecasting Volcanic Events; Tazieff, H., Sabroux, J.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1983; pp. 337–386. [Google Scholar]
- Shinohara, H.; Matsuo, S. Results of Analyses on Fumarolic Gases from F-1 and F-5 Fumaroles of Vulcano, Italy. Geothermics 1986, 15, 211–215. [Google Scholar] [CrossRef]
- Marty, B.; Giggenbach, W.F. Major and Rare Gases at White Island Volcano, New Zealand: Origin and Flux of Volatiles. Geophys. Res. Lett. 1990, 17, 247–250. [Google Scholar] [CrossRef]
- Allard, P.; Jean-Baptiste, P.; D’Alessandro, W.; Parello, F.; Parisi, B.; Flehoc, C. Mantle-Derived Helium and Carbon in Groundwaters and Gases of Mount Etna, Italy. Earth Planet. Sci. Lett. 1997, 148, 501–516. [Google Scholar] [CrossRef]
- Ellis, A.J. Chemical Equilibrium in Magmatic Gases. Am. J. Sci. 1957, 255, 416–431. [Google Scholar] [CrossRef]
- Elskens, I.; Tazieff, H.; Tonani, F. Investigations Nouvelles sur les Gaz Volcaniques. Bull. Volcanol. 1968, 32, 521–574. [Google Scholar] [CrossRef]
- Giggenbach, W.F. Chemical Composition of Volcanic Gases. In Monitoring and Mitigation of Volcano Hazards; Scarpa, R., Tilling, R.I., Eds.; Springer Nature: Dordrecht, The Netherlands, 1996; pp. 202–226. [Google Scholar]
- Symonds, R.B.; Gerlach, T.M.; Reed, M.H. Magmatic Gas Scrubbing: Implications for Volcano Monitoring. J. Volcanol. Geotherm. Res. 2001, 108, 303–341. [Google Scholar] [CrossRef]
- Sainte-Claire Deville, C.J. Mémoire sur les Emanations Volcaniques; Impr. L. Martinet: Paris, France, 1857. [Google Scholar]
- Sainte-Claire Deville, C.J.; Leblanc, F. Mémoire Sur la Composition Chimique Des Gaz Rejetés Par Les Events Volcaniques de L’Italie Méridionale; Mallet-Bachelier: Paris, France, 1858. [Google Scholar]
- Sano, Y.; Wakita, H. Geographical Distribution of 3He/4He Ratios in Japan: Implications for Arc Tectonics and Incipient Magmatism. J. Geophys. Res. Solid. Earth 1985, 90, 8729–8741. [Google Scholar] [CrossRef]
- Liotta, M.; Paonita, A.; Caracausi, A.; Martelli, M.; Rizzo, A.; Favara, R. Hydrothermal Processes Governing the Geochemistry of the Crater Fumaroles at Mount Etna Volcano (Italy). Chem. Geol. 2010, 278, 92–104. [Google Scholar] [CrossRef]
- Baxter, P.J.; Gresham, A. Deaths and Injuries in the Eruption of Galeras Volcano, Colombia, 14 January 1993. J. Volcanol. Geotherm. Res. 1997, 77, 325–338. [Google Scholar] [CrossRef]
- Keeling, C.D. The Concentration and Isotopic Abundances of Atmospheric Carbon Dioxide in Rural Areas. Geochim. Cosmochim. Acta 1958, 13, 322–334. [Google Scholar] [CrossRef]
- Rizzo, A.L.; Jost, H.-J.; Caracausi, A.; Paonita, A.; Liotta, M.; Martelli, M. Real-Time Measurements of the Concentration and Isotope Composition of Atmospheric and Volcanic CO2 at Mount Etna (Italy). Geophys. Res. Lett. 2014, 41, 2014GL059722. [Google Scholar] [CrossRef]
- Rizzo, A.L.; Liuzzo, M.; Ancellin, M.A.; Jost, H.J. Real-Time Measurements of δ13C, CO2 Concentration, and CO2/SO2 in Volcanic Plume Gases at Mount Etna, Italy, over 5 Consecutive Days. Chem. Geol. 2015, 411, 182–191. [Google Scholar] [CrossRef]
- Schipper, C.I.; Moussallam, Y.; Curtis, A.; Peters, N.; Barnie, T.; Bani, P.; Jost, H.J.; Hamilton, D.; Aiuppa, A.; Tamburello, G.; et al. Isotopically (δ13C and δ18O) Heavy Volcanic Plumes from Central Andean Volcanoes: A Field Study. Bull. Volcanol. 2017, 79, 65. [Google Scholar] [CrossRef]
- Malowany, K.S.; Stix, J.; de Moor, J.M.; Chu, K.; Lacrampe-Couloume, G.; Sherwood Lollar, B. Carbon Isotope Systematics of Turrialba Volcano, Costa Rica, Using a Portable Cavity Ring-down Spectrometer. Geochem. Geophys. Geosyst. 2017, 18, 2769–2784. [Google Scholar] [CrossRef]
- Shingubara, R.; Tsunogai, U.; Ito, M.; Nakagawa, F.; Yoshikawa, S.; Utsugi, M.; Yokoo, A. Development of a Drone-Borne Volcanic Plume Sampler. J. Volcanol. Geotherm. Res. 2021, 412, 107197. [Google Scholar] [CrossRef]
- D’Arcy, F.; Aiuppa, A.; Grassa, F.; Rizzo, A.L.; Stix, J. Large Isotopic Shift in Volcanic Plume CO2 Prior to a Basaltic Paroxysmal Explosion. Geophys. Res. Lett. 2024, 51, e2023GL107474. [Google Scholar] [CrossRef]
- Fischer, T.P.; Mandon, C.L.; Nowicki, S.; Ericksen, J.; Vilches, F.R.; Pfeffer, M.A.; Aiuppa, A.; Bitetto, M.; Vitale, A.; Fricke, G.M.; et al. CO2 Emissions during the 2023 Litli Hrútur Eruption in Reykjanes, Iceland: ẟ13C Tracks Magma Degassing. Bull. Volcanol. 2024, 86, 60. [Google Scholar] [CrossRef]
- Moussallam, Y.; Rose-Koga, E.F.; Fischer, T.P.; Georgeais, G.; Lee, H.J.; Birnbaum, J.; Pfeffer, M.A.; Barnie, T.; Regis, E. Kinetic Isotopic Degassing of CO2 During the 2021 Fagradalsfjall Eruption and the δ13C Signature of the Icelandic Mantle. Geochem. Geophys. Geosyst. 2024, 25, e2024GC011997. [Google Scholar] [CrossRef]
- Fischer, T.P.; Lopez, T.M. First Airborne Samples of a Volcanic Plume for δ13C of CO2 Determinations. Geophys. Res. Lett. 2016, 43, 2016GL068499. [Google Scholar] [CrossRef]
- D’Arcy, F.; de Moor, J.M.; Stix, J.; Alan, A.; Bogue, R.; Corrales, E.; Diaz, J.A.; Mick, E.; Salas-Navarro, J.; Lauzeral, R. New Insights into Carbon Isotope Systematics at Poás Volcano, Costa Rica. J. Volcanol. Geotherm. Res. 2022, 431, 107639. [Google Scholar] [CrossRef]
- Liu, E.J.; Aiuppa, A.; Alan, A.; Arellano, S.; Bitetto, M.; Bobrowski, N.; Carn, S.; Clarke, R.; Corrales, E.; de Moor, J.M.; et al. Aerial Strategies Advance Volcanic Gas Measurements at Inaccessible, Strongly Degassing Volcanoes. Sci. Adv. 2020, 6, eabb9103. [Google Scholar] [CrossRef] [PubMed]
- Pineau, F.; Javoy, M.; Bottinga, Y. 13C/12C Ratios of Rocks and Inclusions in Popping Rocks of the Mid-Atlantic Ridge and Their Bearing on the Problem of Isotopic Composition of Deep-Seated Carbon. Earth Planet. Sci. Lett. 1976, 29, 413–421. [Google Scholar] [CrossRef]
- Pineau, F.; Javoy, M. Strong Degassing at Ridge Crests: The Behaviour of Dissolved Carbon and Water in Basalt Glasses at 14°N, Mid-Atlantic Ridge. Earth Planet. Sci. Lett. 1994, 123, 179–198. [Google Scholar] [CrossRef]
- Nishio, Y.; Sasaki, S.; Gamo, T.; Hiyagon, H.; Sano, Y. Carbon and Helium Isotope Systematics of North Fiji Basin Basalt Glasses: Carbon Geochemical Cycle in the Subduction Zone. Earth Planet. Sci. Lett. 1998, 154, 127–138. [Google Scholar] [CrossRef]
- Alt, J.C.; Shanks, W.C.; Jackson, M.C. Cycling of Sulfur in Subduction Zones: The Geochemistry of Sulfur in the Mariana Island Arc and Back-Arc Trough. Earth Planet. Sci. Lett. 1993, 119, 477–494. [Google Scholar] [CrossRef]
- Macpherson, C.; Mattey, D. Carbon Isotope Variations of CO2 in Central Lau Basin Basalts and Ferrobasalts. Earth Planet. Sci. Lett. 1994, 121, 263–276. [Google Scholar] [CrossRef]
- Marty, B.; Sano, Y.; France-Lanord, C. Water-Saturated Oceanic Lavas from the Manus Basin: Volatile Behaviour during Assimilation–Fractional Crystallisation–Degassing (AFCD). J. Volcanol. Geotherm. Res. 2001, 108, 1–10. [Google Scholar] [CrossRef]
- Aubaud, C.; Pineau, F.; Hékinian, R.; Javoy, M. Degassing of CO2 and H2O in Submarine Lavas from the Society Hotspot. Earth Planet. Sci. Lett. 2005, 235, 511–527. [Google Scholar] [CrossRef]
- Aubaud, C.; Pineau, F.; Hékinian, R.; Javoy, M. Carbon and Hydrogen Isotope Constraints on Degassing of CO2 and H2O in Submarine Lavas from the Pitcairn Hotspot (South Pacific). Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Barry, P.H.; Hilton, D.R.; Füri, E.; Halldórsson, S.A.; Grönvold, K. Carbon Isotope and Abundance Systematics of Icelandic Geothermal Gases, Fluids and Subglacial Basalts with Implications for Mantle Plume-Related CO2 Fluxes. Geochim. Cosmochim. Acta 2014, 134, 74–99. [Google Scholar] [CrossRef]
- Graham, D.W.; Michael, P.J.; Truong, T.B. Carbon Isotope Composition of Basalts from Loihi Seamount: Primordial or Recycled Carbon in the Hawaiian Mantle Plume? Earth Planet. Sci. Lett. 2023, 617, 118248. [Google Scholar] [CrossRef]
- Moore, J.G.; Batchelder, J.N.; Cunningham, C.G. CO2-Filled Vesicles in Mid-Ocean Basalt. J. Volcanol. Geotherm. Res. 1977, 2, 309–327. [Google Scholar] [CrossRef]
- Pineau, F.; Javoy, M. Carbon Isotopes and Concentrations in Mid-Oceanic Ridge Basalts. Earth Planet. Sci. Lett. 1983, 62, 239–257. [Google Scholar] [CrossRef]
- Des Marais, D.J.; Moore, J.G. Carbon and Its Isotopes in Mid-Oceanic Basaltic Glasses. Earth Planet. Sci. Lett. 1984, 69, 43–57. [Google Scholar] [CrossRef]
- Marty, B.; Jambon, A. C3He in Volatile Fluxes from the Solid Earth: Implications for Carbon Geodynamics. Earth Planet. Sci. Lett. 1987, 83, 16–26. [Google Scholar] [CrossRef]
- Mattey, D.P.; Exley, R.A.; Pillinger, C.T. Isotopic Composition of CO2 and Dissolved Carbon Species in Basalt Glass. Geochim. Cosmochim. Acta 1989, 53, 2377–2386. [Google Scholar] [CrossRef]
- Jendrzejewski, N. Relations Entre Dynamique D’éruption et Géochimie Élémentaire et Isotopique Du Carbone et de L’eau Dans Les Basaltes de Rides. Ph.D. Thesis, Institut de physique du globe, Paris, France, 1994. [Google Scholar]
- Nishio, Y.; Ishii, T.; Gamo, T.; Sano, Y. Volatile Element Isotopic Systematics of the Rodrigues Triple Junction Indian Ocean MORB: Implications for Mantle Heterogeneity. Earth Planet. Sci. Lett. 1999, 170, 241–253. [Google Scholar] [CrossRef]
- Marty, B.; Zimmermann, L. Volatiles (He, C, N, Ar) in Mid-Ocean Ridge Basalts: Assesment of Shallow-Level Fractionation and Characterization of Source Composition. Geochim. Cosmochim. Acta 1999, 63, 3619–3633. [Google Scholar] [CrossRef]
- Cartigny, P.; Jendrzejewski, N.; Pineau, F.; Petit, E.; Javoy, M. Volatile (C, N, Ar) Variability in MORB and the Respective Roles of Mantle Source Heterogeneity and Degassing: The Case of the Southwest Indian Ridge. Earth Planet. Sci. Lett. 2001, 194, 241–257. [Google Scholar] [CrossRef]
- Pineau, F.; Shilobreeva, S.; Hekinian, R.; Bideau, D.; Javoy, M. Deep-Sea Explosive Activity on the Mid-Atlantic Ridge near 34°50′N: A Stable Isotope (C, H, O) Study. Chem. Geol. 2004, 211, 159–175. [Google Scholar] [CrossRef]
- Aubaud, C.; Pineau, F.; Jambon, A.; Javoy, M. Kinetic Disequilibrium of C, He, Ar and Carbon Isotopes during Degassing of Mid-Ocean Ridge Basalts. Earth Planet. Sci. Lett. 2004, 222, 391–406. [Google Scholar] [CrossRef]
- Cartigny, P.; Pineau, F.; Aubaud, C.; Javoy, M. Towards a Consistent Mantle Carbon Flux Estimate: Insights from Volatile Systematics (H2O/Ce, δD, CO2/Nb) in the North Atlantic Mantle (14° N and 34° N). Earth Planet. Sci. Lett. 2008, 265, 672–685. [Google Scholar] [CrossRef]
- Graham, D.W.; Michael, P.J.; Rubin, K.H. An Investigation of Mid-Ocean Ridge Degassing Using He, CO2, and δ13C Variations during the 2005–06 Eruption at 9°50′N on the East Pacific Rise. Earth Planet. Sci. Lett. 2018, 504, 84–93. [Google Scholar] [CrossRef]
- Mattey, D.P.; Carr, R.H.; Wright, I.P.; Pillinger, C.T. Carbon Isotopes in Submarine Basalts. Earth Planet. Sci. Lett. 1984, 70, 196–206. [Google Scholar] [CrossRef]
- Sakai, H.; Des Marais, D.J.; Ueda, A.; Moore, J.G. Concentrations and Isotope Ratios of Carbon, Nitrogen and Sulfur in Ocean-Floor Basalts. Geochim. Cosmochim. Acta 1984, 48, 2433–2441. [Google Scholar] [CrossRef] [PubMed]
- Exley, R.A.; Mattey, D.P.; Clague, D.A.; Pillinger, C.T. Carbon Isotope Systematics of a Mantle “Hotspot”: A Comparison of Loihi Seamount and MORB Glasses. Earth Planet. Sci. Lett. 1986, 78, 11. [Google Scholar] [CrossRef]
- Blank, J.G.; Delaney, J.R.; Marais, D.J.D. The Concentration and Isotopic Composition of Carbon in Basaltic Glasses from the Juan de Fuca Ridge, Pacific Ocean. Geochim. Cosmochim. Acta 1993, 57, 875–887. [Google Scholar] [CrossRef]
- Macpherson, C.G.; Hilton, D.R.; Newman, S.; Mattey, D.P. CO2, 13C/12C and H2O Variability in Natural Basaltic Glasses: A Study Comparing Stepped Heating and Ftir Spectroscopic Techniques. Geochim. Cosmochim. Acta 1999, 63, 1805–1813. [Google Scholar] [CrossRef]
- Macpherson, C.G.; Hilton, D.R.; Mertz, D.F.; Dunai, T.J. Sources, Degassing, and Contamination of CO2, H2O, He, Ne, and Ar in Basaltic Glasses from Kolbeinsey Ridge, North Atlantic. Geochim. Cosmochim. Acta 2005, 69, 5729–5746. [Google Scholar] [CrossRef]
- Shaw, A.M.; Hilton, D.R.; Macpherson, C.G.; Sinton, J.M. The CO2-He-Ar-H2O Systematics of the Manus Back-Arc Basin: Resolving Source Composition from Degassing and Contamination Effects. Geochim. Cosmochim. Acta 2004, 68, 1837–1855. [Google Scholar] [CrossRef]
- Aubaud, C. Carbon Stable Isotope Constraints on CO2 Degassing Models of Ridge, Hotspot and Arc Magmas. Chem. Geol. 2022, 605, 120962. [Google Scholar] [CrossRef]
- Exley, R.; Mattey, D.; Pillinger, C. Low Temperature Carbon Components in Basaltic Glasses—Reply to Comment by H. Craig. Earth Planet. Sci. Lett. 1987, 82, 387–390. [Google Scholar] [CrossRef]
- Hauri, E.H.; Shaw, A.M.; Wang, J.; Dixon, J.E.; King, P.L.; Mandeville, C. Matrix Effects in Hydrogen Isotope Analysis of Silicate Glasses by SIMS. Chem. Geol. 2006, 235, 352–365. [Google Scholar] [CrossRef]
- Eiler, J.M.; Graham, C.; Valley, J.W. SIMS Analysis of Oxygen Isotopes: Matrix Effects in Complex Minerals and Glasses. Chem. Geol. 1997, 138, 221–244. [Google Scholar] [CrossRef]
- Shimizu, K.; Ushikubo, T.; Murai, T.; Matsu’ura, F.; Ueno, Y. In Situ Analyses of Hydrogen and Sulfur Isotope Ratios in Basaltic Glass Using SIMS. Geochem. J. 2019, 53, 195–207. [Google Scholar] [CrossRef]
- Hauri, E.; Wang, J.; Dixon, J.E.; King, P.L.; Mandeville, C.; Newman, S. SIMS Analysis of Volatiles in Silicate Glasses: 1. Calibration, Matrix Effects and Comparisons with FTIR. Chem. Geol. 2002, 183, 99–114. [Google Scholar] [CrossRef]
- Lee, H.; Moussallam, Y.; Rose Koga, E.F.; Piani, L.; Villeneuve, J.; Bouden, N.; Gurenko, A.A.; Monteleone, B.; Gaetani, G.A. High–Precision Determination of Carbon Stable Isotope in Silicate Glasses by Secondary Ion Mass Spectrometry: Evaluation of International Reference Materials. Chem. Geol. 2024, 670, 122428. [Google Scholar] [CrossRef]
- Moussallam, Y.; Koga, K.T.; Rose–Koga, E.F.; Aubaud, C.; Lee, H.J.; Georgeais, G. The Carbon Isotopic Signature of the Upper Mantle Is Heterogeneous. Commun. Earth Environ. 2025, 6, 6. [Google Scholar] [CrossRef]
- Moussallam, Y.; Rose-Koga, E.F.; Aubaud, C.; Georgeais, G.; Cartigny, P.; Koga, K.T.; Devidal, J.-L.; Michael, P.J.; Shimizu, K.; Saal, A.E. Enigmatic Carbon Isotopic Variability in the Oceanic Upper Mantle. Proc. Natl. Acad. Sci. USA 2025, 122, e2502886122. [Google Scholar] [CrossRef]
- Hoefs, J. The Carbon Isotopic Composition of CO2 from Fluid Inclusions. Fortschr. Miner. 1975, 52, 475. [Google Scholar]
- Hoefs, J.; Touret, J. Fluid Inclusion and Carbon Isotope Study from Bamble Granulites (South Norway). Contr. Mineral. Petrol. 1975, 52, 165–174. [Google Scholar] [CrossRef]
- Jackson, D.H.; Mattey, D.P.; Harris, N.B.W. Carbon Isotope Compositions of Fluid Inclusions in Charnockites from Southern India. Nature 1988, 333, 167–170. [Google Scholar] [CrossRef]
- Hattori, K.; Sakai, H. D/H Ratios, Origins, and Evolution of the Ore-Forming Fluids for the Neogene Veins and Kuroko Deposits of Japan. Econ. Geol. 1979, 74, 535–555. [Google Scholar] [CrossRef]
- Kazahaya, K.; Matsuo, S. A New Ball-Milling Method for Extraction of Fluid Inclusions from Minerals. Geochem. J. 1985, 19, 45–54. [Google Scholar] [CrossRef]
- Nadeau, S.; Pineau, F.; Javoy, M.; Francis, D. Carbon Concentrations and Isotopic Ratios in Fluid-Inclusion-Bearing Upper-Mantle Xenoliths along the Northwestern Margin of North America. Chem. Geol. 1990, 81, 271–297. [Google Scholar] [CrossRef]
- Miller, M.F.; Pillinger, C.T. An Appraisal of Stepped Heating Release of Fluid Inclusion CO2 for Isotopic Analysis: A Preliminary to δ13C Characterisation of Carbonaceous Vesicles at the Nanomole Level. Geochim. Cosmochim. Acta 1997, 61, 193–205. [Google Scholar] [CrossRef]
- Luciani, N.; van der Lubbe, J.H.L.; Verdegaal-Warmerdam, S.J.A.; Postma, O.; Nikogosian, I.K.; Davies, G.R.; Koornneef, J.M. Carbon and Oxygen Isotope Analysis of CO2 Trapped in Silicate Minerals. Chem. Geol. 2022, 602, 120872. [Google Scholar] [CrossRef]
- Wilske, C.; Suckow, A.; Gerber, C.; Deslandes, A.; Crane, P.; Mallants, D. Mineral Crushing Methods for Noble Gas Analyses of Fluid Inclusions. Geofluids 2023, 2023, 8040253. [Google Scholar] [CrossRef]
- Roedder, E. Volume 12: Fluid Inclusions. Rev. Miner. 1984, 12, 644. [Google Scholar]
- Andersen, T.; Neumann, E.-R. Fluid Inclusions in Mantle Xenoliths. Lithos 2001, 55, 301–320. [Google Scholar] [CrossRef]
- Pineau, F.; Mathez, E.A. Carbon Isotopes in Xenoliths from the Hualalai Volcano, Hawaii, and the Generation of Isotopic Variability. Geochim. Cosmochim. Acta 1990, 54, 217–227. [Google Scholar] [CrossRef]
- Fermi, E. Über den Ramaneffekt des Kohlendioxyds. Z. Phys. 1931, 71, 250–259. [Google Scholar] [CrossRef]
- Cui, S.; Wang, W.; Cheng, C.; Yao, Y.; Qin, C.; Sun, Q. Raman Quantitative Measurement for Carbon Isotopic Composition of CO2: Theory and Method. Chem. Geol. 2021, 585, 120570. [Google Scholar] [CrossRef]
- Wang, W.; Lu, W. High-Precision Analysis of Carbon Isotopic Composition for Individual CO2 Inclusions via Raman Spectroscopy to Reveal the Multiple-Stages Evolution of CO2- Bearing Fluids and Melts. Geosci. Front. 2023, 14, 101528. [Google Scholar] [CrossRef]
- Remigi, S.; Frezzotti, M.-L.; Rizzo, A.L.; Esposito, R.; Bodnar, R.J.; Sandoval-Velasquez, A.; Aiuppa, A. Spatially Resolved CO2 Carbon Stable Isotope Analyses at the Microscale Using Raman Spectroscopy. Sci. Rep. 2023, 13, 18561. [Google Scholar] [CrossRef]
- Wang, H.; Lu, W.; Wang, W.; Liu, Q.; Yamamoto, J. High-Precision Analysis of Carbon Isotopic Composition for Individual CO2 Inclusions via Raman Spectroscopy: Addressing Issues Arising from the Laser-Heating Effects. Chem. Geol. 2024, 651, 122014. [Google Scholar] [CrossRef]
- Yokokura, L.; Hagiwara, Y.; Yamamoto, J. Pressure Dependence of Micro-Raman Mass Spectrometry for Carbon Isotopic Composition of Carbon Dioxide Fluid. J. Raman Spectrosc. 2020, 51, 997–1002. [Google Scholar] [CrossRef]
- Lu, W.; Wang, X.; Wan, Q.; Hu, W.; Chou, I.-M.; Wan, Y. In Situ Raman Spectroscopic Measurement of the 13C/12C Ratio in CO2: Experimental Calibrations on the Effects of Fluid Pressure, Temperature and Composition. Chem. Geol. 2023, 615, 121201. [Google Scholar] [CrossRef]
- Javoy, M.; Pineau, F.; Iiyama, I. Experimental Determination of the Isotopic Fractionation between Gaseous CO2 and Carbon Dissolved in Tholeiitic Magma. Contr. Mineral. Petrol. 1978, 67, 35–39. [Google Scholar] [CrossRef]
- Mattey, D.P.; Taylor, W.R.; Green, D.H.; Pillinger, C.T. Carbon Isotopic Fractionation between CO2 Vapour, Silicate and Carbonate Melts: An Experimental Study to 30 Kbar. Contr. Mineral. Petrol. 1990, 104, 492–505. [Google Scholar] [CrossRef]
- Mattey, D.P. Carbon Dioxide Solubility and Carbon Isotope Fractionation in Basaltic Melt. Geochim. Cosmochim. Acta 1991, 55, 3467–3473. [Google Scholar] [CrossRef]
- Appora Gnekindy, I. Etude Expérimentale Du Fractionnement Isotopique Du Carbone et de l’oxygène Dans Les Systèmes CO2-Carbonates Liquides: Application Aux Contextes Carbonatitiques. Ph.D. Thesis, Ministère chargé de l’Enseignement supérieur et de la Recherche, Paris, France, 1998. [Google Scholar]
- Lee, H.; Moussallam, Y.; Aubaud, C.; Iacono–Marziano, G.; Hammond, K.; Ebel, D. Carbon Isotope Fractionation between CO2 and Carbon in Silicate Melts at High Temperature. Geochim. Cosmochim. Acta 2024, 380, 208–219. [Google Scholar] [CrossRef]
- Blank, J.G. An Experimental Investigation of the Behavior of Carbon Dioxide in Rhyolitic Melt. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1993. [Google Scholar]
- Petschnig, P.; Schmidt, M.W.; Kueter, N.; Sartori, G.; Bernasconi, S.M. An Almost Universal CO2-CO32− Carbon Isotope Fractionation Function for High Temperatures. Earth Planet. Sci. Lett. 2024, 627, 118552. [Google Scholar] [CrossRef]
- Mysen, B.O.; Arculus, R.J.; Eggler, D.H. Solubility of Carbon Dioxide in Melts of Andesite, Tholeiite, and Olivine Nephelinite Composition to 30 Kbar Pressure. Contr. Mineral. Petrol. 1975, 53, 227–239. [Google Scholar] [CrossRef]
- Fine, G.; Stolper, E. Dissolved Carbon Dioxide in Basaltic Glasses: Concentrations and Speciation. Earth Planet. Sci. Lett. 1986, 76, 263–278. [Google Scholar] [CrossRef]
- Fine, G.; Stolper, E. The Speciation of Carbon Dioxide in Sodium Aluminosilicate Glasses. Contr. Mineral. Petrol. 1985, 91, 105–121. [Google Scholar] [CrossRef]
- Blank, J.G.; Brooker, R.A. Experimental Studies of Carbon Dioxide in Silicate Melts; Solubility, Speciation, and Stable Carbon Isotope Behavior. Rev. Mineral. Geochem. 1994, 30, 157–186. [Google Scholar]
- Fogel, R.A.; Rutherford, M.J. The Solubility of Carbon Dioxide in Rhyolitic Melts; a Quantitative FTIR Study. Am. Mineral. 1990, 75, 1311–1326. [Google Scholar]
- Giordano, D.; Romano, C.; Dingwell, D.B.; Poe, B.; Behrens, H. The Combined Effects of Water and Fluorine on the Viscosity of Silicic Magmas. Geochim. Cosmochim. Acta 2004, 68, 5159–5168. [Google Scholar] [CrossRef]
- Moussallam, Y.; Morizet, Y.; Massuyeau, M.; Laumonier, M.; Gaillard, F. CO2 Solubility in Kimberlite Melts. Chem. Geol. 2015, 418, 198–205. [Google Scholar] [CrossRef]
- Nowak, M.; Porbatzki, D.; Spickenbom, K.; Diedrich, O. Carbon Dioxide Speciation in Silicate Melts: A Restart. Earth Planet. Sci. Lett. 2003, 207, 131–139. [Google Scholar] [CrossRef]
- Guillot, B.; Sator, N. Carbon Dioxide in Silicate Melts: A Molecular Dynamics Simulation Study. Geochim. Cosmochim. Acta 2011, 75, 1829–1857. [Google Scholar] [CrossRef]
- Moussallam, Y.; Florian, P.; Corradini, D.; Morizet, Y.; Sator, N.; Vuilleumier, R.; Guillot, B.; Iacono-Marziano, G.; Schmidt, B.C.; Gaillard, F. The Molecular Structure of Melts along the Carbonatite–Kimberlite–Basalt Compositional Joint: CO2 and Polymerisation. Earth Planet. Sci. Lett. 2016, 434, 129–140. [Google Scholar] [CrossRef]
- Konschak, A.; Keppler, H. The Speciation of Carbon Dioxide in Silicate Melts. Contrib. Miner. Pet. 2014, 167, 1–13. [Google Scholar] [CrossRef]
- McGetchin, T.R.; Besancon, J.R. Carbonate Inclusions in Mantle-Derived Pyropes. Earth Planet. Sci. Lett. 1973, 18, 408–410. [Google Scholar] [CrossRef]
- Biellmann, C.; Gillet, P.; Guyot, F.; Peyronneau, J.; Reynard, B. Experimental Evidence for Carbonate Stability in the Earth’s Lower Mantle. Earth Planet. Sci. Lett. 1993, 118, 31–41. [Google Scholar] [CrossRef]
- Wang, A.; Pasteris, J.D.; Meyer, H.O.A.; Dele-Duboi, M.L. Magnesite-Bearing Inclusion Assemblage in Natural Diamond. Earth Planet. Sci. Lett. 1996, 141, 293–306. [Google Scholar] [CrossRef]
- Shcheka, S.S.; Wiedenbeck, M.; Frost, D.J.; Keppler, H. Carbon Solubility in Mantle Minerals. Earth Planet. Sci. Lett. 2006, 245, 730–742. [Google Scholar] [CrossRef]
- Wyllie, P.J.; Huang, W.-L. Carbonation and Melting Reactions in the System CaO–MgO–SiO2–CO2 at Mantle Pressures with Geophysical and Petrological Applications. Contr. Mineral. Petrol. 1976, 54, 79–107. [Google Scholar] [CrossRef]
- Eggler, D.H. The Effect of CO<2) upon Partial Melting of Peridotite in the System Na<2) O-CaO-Al<2) O<3) -MgO-SiO<2) -CO<2) to 35 Kb, with an Analysis of Melting in a Peridotite-H<2) O-CO<2) System. Am. J. Sci. 1978, 278, 305–343. [Google Scholar] [CrossRef]
- Wyllie, P.J. Origin of Carbonatites; Evidence from Phase Equilibrium Studies; Unwin Hyman: London, UK, 1989; pp. 500–545. ISBN 0-04-445068-0. [Google Scholar]
- Dalton, J.A.; Presnall, D.C. The Continuum of Primary Carbonatitic–Kimberlitic Melt Compositions in Equilibrium with Lherzolite: Data from the System CaO–MgO–Al2O3–SiO2–CO2 at 6 GPa. J. Petrol. 1998, 39, 1953–1964. [Google Scholar] [CrossRef]
- Gudfinnsson, G.H.; Presnall, D.C. Continuous Gradations among Primary Carbonatitic, Kimberlitic, Melilititic, Basaltic, Picritic, and Komatiitic Melts in Equilibrium with Garnet Lherzolite at 3–8 GPa. J. Petrol. 2005, 46, 1645–1659. [Google Scholar] [CrossRef]
- Dasgupta, R.; Hirschmann, M.M. Melting in the Earth’s Deep Upper Mantle Caused by Carbon Dioxide. Nature 2006, 440, 659–662. [Google Scholar] [CrossRef]
- Taylor, W.R.; Green, D.H. Measurement of Reduced Peridotite-C-O-H Solidus and Implications for Redox Melting of the Mantle. Nature 1988, 332, 349. [Google Scholar] [CrossRef]
- Foley, S.F. A Reappraisal of Redox Melting in the Earth’s Mantle as a Function of Tectonic Setting and Time. J. Petrol. 2010, 52, 1363–1391. [Google Scholar] [CrossRef]
- Rohrbach, A.; Schmidt, M.W. Redox Freezing and Melting in the Earth/’s Deep Mantle Resulting from Carbon-Iron Redox Coupling. Nature 2011, 472, 209–212. [Google Scholar] [CrossRef]
- Saal, A.; Hauri, E.; Langmuir, C.H.; Perfit, M. Vapour Undersaturation in Primitive Mid-Ocean-Ridge Basalt and the Volatile Content of Earth’s Upper Mantle. Nature 2002, 419, 451. [Google Scholar] [CrossRef]
- Michael, P.J.; Graham, D.W. The Behavior and Concentration of CO2 in the Suboceanic Mantle: Inferences from Undegassed Ocean Ridge and Ocean Island Basalts. Lithos 2015, 236–237, 338–351. [Google Scholar] [CrossRef]
- Le Voyer, M.; Kelley, K.A.; Cottrell, E.; Hauri, E.H. Heterogeneity in Mantle Carbon Content from CO2-Undersaturated Basalts. Nat. Commun. 2017, 8, 14062. [Google Scholar] [CrossRef]
- Moussallam, Y.; Georgeais, G.; Rose-Koga, E.F.; Koga, K.T.; Hartley, M.E.; Scaillet, B.; Oppenheimer, C.; Peters, N. CO2-Undersaturated Melt Inclusions From the South West Indian Ridge Record Surprisingly Uniform Redox Conditions. Geochem. Geophys. Geosyst. 2023, 24, e2023GC011235. [Google Scholar] [CrossRef]
- Kerrick, D.M.; Connolly, J.A.D. Metamorphic Devolatilization of Subducted Marine Sediments and the Transport of Volatiles into the Earth’s Mantle. Nature 2001, 411, 293–296. [Google Scholar] [CrossRef] [PubMed]
- Kerrick, D.M.; Connolly, J.A.D. Metamorphic Devolatilization of Subducted Oceanic Metabasalts: Implications for Seismicity, Arc Magmatism and Volatile Recycling. Earth Planet. Sci. Lett. 2001, 189, 19–29. [Google Scholar] [CrossRef]
- Kerrick, D.M.; Connolly, J.A.D. Subduction of Ophicarbonates and Recycling of CO2 and H2O. Geology 1998, 26, 375–378. [Google Scholar] [CrossRef]
- Gorman, P.J.; Kerrick, D.M.; Connolly, J.A.D. Modeling Open System Metamorphic Decarbonation of Subducting Slabs. Geochem. Geophys. Geosyst. 2006, 7. [Google Scholar] [CrossRef]
- Molina, J.F.; Poli, S. Carbonate Stability and Fluid Composition in Subducted Oceanic Crust: An Experimental Study on H2O–CO2-Bearing Basalts. Earth Planet. Sci. Lett. 2000, 176, 295–310. [Google Scholar] [CrossRef]
- Yaxley, G.M.; Green, D.H. Experimental Demonstration of Refractory Carbonate-Bearing Eclogite and Siliceous Melt in the Subduction Regime. Earth Planet. Sci. Lett. 1994, 128, 313–325. [Google Scholar] [CrossRef]
- Poli, S.; Franzolin, E.; Fumagalli, P.; Crottini, A. The Transport of Carbon and Hydrogen in Subducted Oceanic Crust: An Experimental Study to 5 GPa. Earth Planet. Sci. Lett. 2009, 278, 350–360. [Google Scholar] [CrossRef]
- Bebout, G.E.; Anderson, L.D.; Agard, P.; Bastoni, C.; Sills, G.; McCall, A.M. Retention of Metasedimentary Carbon during Subduction through Forearcs: Evidence from HP/UHP Rocks. AGU Fall Meet. Abstr. 2010, 2010, U21A-0004. [Google Scholar]
- Cook-Kollars, J.; Bebout, G.E.; Collins, N.C.; Angiboust, S.; Agard, P. Subduction Zone Metamorphic Pathway for Deep Carbon Cycling: I. Evidence from HP/UHP Metasedimentary Rocks, Italian Alps. Chem. Geol. 2014, 386, 31–48. [Google Scholar] [CrossRef]
- Farsang, S.; Louvel, M.; Zhao, C.; Mezouar, M.; Rosa, A.D.; Widmer, R.N.; Feng, X.; Liu, J.; Redfern, S.A.T. Deep Carbon Cycle Constrained by Carbonate Solubility. Nat. Commun. 2021, 12, 4311. [Google Scholar] [CrossRef]
- Tumiati, S.; Recchia, S.; Remusat, L.; Tiraboschi, C.; Sverjensky, D.A.; Manning, C.E.; Vitale Brovarone, A.; Boutier, A.; Spanu, D.; Poli, S. Subducted Organic Matter Buffered by Marine Carbonate Rules the Carbon Isotopic Signature of Arc Emissions. Nat. Commun. 2022, 13, 2909. [Google Scholar] [CrossRef]
- Arzilli, F.; Burton, M.; La Spina, G.; Macpherson, C.G.; van Keken, P.E.; McCann, J. Decarbonation of Subducting Carbonate-Bearing Sediments and Basalts of Altered Oceanic Crust: Insights into Recycling of CO2 through Volcanic Arcs. Earth Planet. Sci. Lett. 2023, 602, 117945. [Google Scholar] [CrossRef]
- Lan, C.; Tao, R.; Huang, F.; Jiang, R.; Zhang, L. High-Pressure Experimental and Thermodynamic Constraints on the Solubility of Carbonates in Subduction Zone Fluids. Earth Planet. Sci. Lett. 2023, 603, 117989. [Google Scholar] [CrossRef]
- Taran, Y.; Gavilanes, J.C.; Cortés, A. Chemical and Isotopic Composition of Fumarolic Gases and the SO2 Flux from Volcán de Colima, México, between the 1994 and 1998 Eruptions. J. Volcanol. Geotherm. Res. 2002, 117, 105–119. [Google Scholar] [CrossRef]
- Menyailov, I.A.; Nikitina, L.P.; Shapar, V.N.; Pilipenko, V.P. Temperature Increase and Chemical Change of Fumarolic Gases at Momotombo Volcano, Nicaragua, in 1982–1985: Are These Indicators of a Possible Eruption? J. Geophys. Res. Solid Earth 1986, 91, 12199–12214. [Google Scholar] [CrossRef]
- Boyd, S.R.; Mattey, D.P.; Pillinger, C.T.; Milledge, H.J.; Mendelssohn, M.; Seal, M. Multiple Growth Events during Diamond Genesis: An Integrated Study of Carbon and Nitrogen Isotopes and Nitrogen Aggregation State in Coated Stones. Earth Planet. Sci. Lett. 1987, 86, 341–353. [Google Scholar] [CrossRef]
- Boyd, S.R.; Pineau, F.; Javoy, M. Modelling the Growth of Natural Diamonds. Chem. Geol. 1994, 116, 29–42. [Google Scholar] [CrossRef]
- Smart, K.A.; Chacko, T.; Stachel, T.; Muehlenbachs, K.; Stern, R.A.; Heaman, L.M. Diamond Growth from Oxidized Carbon Sources beneath the Northern Slave Craton, Canada: A δ13C–N Study of Eclogite-Hosted Diamonds from the Jericho Kimberlite. Geochim. Cosmochim. Acta 2011, 75, 6027–6047. [Google Scholar] [CrossRef]
- Palot, M.; Pearson, D.G.; Stern, R.A.; Stachel, T.; Harris, J.W. Multiple Growth Events, Processes and Fluid Sources Involved in Diamond Genesis: A Micro-Analytical Study of Sulphide-Bearing Diamonds from Finsch Mine, RSA. Geochim. Cosmochim. Acta 2013, 106, 51–70. [Google Scholar] [CrossRef]
- Thomassot, E.; Cartigny, P.; Harris, J.; Viljoen, K.F. Methane-Related Diamond Crystallization in the Earth’s Mantle: Stable Isotope Evidences from a Single Diamond-Bearing Xenolith. Earth Planet. Sci. Lett. 2007, 257, 362–371. [Google Scholar] [CrossRef]
- Cartigny, P.; Palot, M.; Thomassot, E.; Harris, J.W. Diamond Formation: A Stable Isotope Perspective. Annu. Rev. Earth Planet. Sci. 2014, 42, 699–732. [Google Scholar] [CrossRef]
- Deines, P. The Carbon Isotopic Composition of Diamonds: Relationship to Diamond Shape, Color, Occurrence and Vapor Composition. Geochim. Cosmochim. Acta 1980, 44, 943–961. [Google Scholar] [CrossRef]
- Galimov, E. Isotope Fractionation Related to Kimberlite Magmatism and Diamond Formation. Geochim. Cosmochim. Acta 1991, 55, 1697–1708. [Google Scholar] [CrossRef]
- Cartigny, P.; Harris, J.W.; Javoy, M. Diamond Genesis, Mantle Fractionations and Mantle Nitrogen Content: A Study of δ13C–N Concentrations in Diamonds. Earth Planet. Sci. Lett. 2001, 185, 85–98. [Google Scholar] [CrossRef]
- Stachel, T.; Harris, J.W.; Muehlenbachs, K. Sources of Carbon in Inclusion Bearing Diamonds. Lithos 2009, 112, 625–637. [Google Scholar] [CrossRef]
- Horita, J.; Polyakov, V.B. Carbon-Bearing Iron Phases and the Carbon Isotope Composition of the Deep Earth. Proc. Natl. Acad. Sci. USA 2015, 112, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Knoche, R.; Sweeney, R.J.; Luth, R.W. Carbonation and Decarbonation of Eclogites: The Role of Garnet. Contrib. Miner. Pet. 1999, 135, 332–339. [Google Scholar] [CrossRef]
- Reutsky, V.; Borzdov, Y.; Palyanov, Y.; Sokol, A.; Izokh, O. Carbon Isotope Fractionation during Experimental Crystallisation of Diamond from Carbonate Fluid at Mantle Conditions. Contrib. Miner. Pet. 2015, 170, 41. [Google Scholar] [CrossRef]
- Kueter, N.; Schmidt, M.W.; Lilley, M.D.; Bernasconi, S.M. Experimental Determination of Equilibrium CH4–CO2–CO Carbon Isotope Fractionation Factors (300–1200 °C). Earth Planet. Sci. Lett. 2019, 506, 64–75. [Google Scholar] [CrossRef]
- Polyakov, V.B.; Horita, J. Equilibrium Carbon Isotope Fractionation Factors of Hydrocarbons: Semi-Empirical Force-Field Method. Chem. Geol. 2021, 559, 119948. [Google Scholar] [CrossRef]
- Shiryaev, A.A.; Polyakov, V.B.; Rols, S.; Rivera, A.; Shenderova, O. Inelastic Neutron Scattering: A Novel Approach towards Determination of Equilibrium Isotopic Fractionation Factors. Size Effects on Heat Capacity and Beta-Factor of Diamond. Phys. Chem. Chem. Phys. 2020, 22, 13261–13270. [Google Scholar] [CrossRef]
- Bottinga, Y. Carbon Isotope Fractionation between Graphite, Diamond and Carbon Dioxide. Earth Planet. Sci. Lett. 1968, 5, 301–307. [Google Scholar] [CrossRef]
- Polyakov, V.B.; Kharlashina, N.N.; Shiryaev, A.A. Thermodynamic Properties of 13C-Diamond. Diam. Relat. Mater. 1997, 6, 172–177. [Google Scholar] [CrossRef]
- Krylov, D.P. Comparative analysis of nitrogen and carbon isotopic fractionation during diamond formation based on β-factor determination. J. Min. Inst. 2025, 272, 40–50. [Google Scholar]
- Polyakov, V.B.; Kharlashina, N.N. The Use of Heat Capacity Data to Calculate Carbon Isotope Fractionation between Graphite, Diamond, and Carbon Dioxide: A New Approach. Geochim. Cosmochim. Acta 1995, 59, 2561–2572. [Google Scholar] [CrossRef]
- Stachel, T.; Chacko, T.; Luth, R.W. Carbon Isotope Fractionation during Diamond Growth in Depleted Peridotite: Counterintuitive Insights from Modelling Water-Maximum CHO Fluids as Multi-Component Systems. Earth Planet. Sci. Lett. 2017, 473, 44–51. [Google Scholar] [CrossRef]
- Stachel, T.; Cartigny, P.; Chacko, T.; Pearson, D.G. Carbon and Nitrogen in Mantle-Derived Diamonds. Rev. Mineral. Geochem. 2022, 88, 809–875. [Google Scholar] [CrossRef]
- Reutsky, V.N.; Borzdov, Y.M. Effect of Growth Rate on Diamond Composition. Diam. Relat. Mater. 2023, 135, 109865. [Google Scholar] [CrossRef]
- Wickman, F.E. The Cycle of Carbon and the Stable Carbon Isotopes. Geochim. Cosmochim. Acta 1956, 9, 136–153. [Google Scholar] [CrossRef]
- Javoy, M.; Pineau, F.; Allègre, C.J. Carbon Geodynamic Cycle. Nature 1982, 300, 171–173. [Google Scholar] [CrossRef]
- Sobolev, N.; Galimov, E.; Ivanovskaia, I.; Efimova, E. Isotopic Composition of Carbon from Diamonds Containing Crystalline Inclusions. Dokl. Akad. Nauk. SSSR 1979, 249, 1217–1220. [Google Scholar]
- Milledge, H.J.; Mendelssohn, M.J.; Seal, M.; Rouse, J.E.; Swart, P.K.; Pillinger, C.T. Carbon Isotopic Variation in Spectral Type II Diamonds. Nature 1983, 303, 791–792. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Mattey, D.P.; Lowry, D. Can Diamonds Be Dead Bacteria? Nature 1994, 367, 694. [Google Scholar] [CrossRef]
- De Stefano, A.; Kopylova, M.G.; Cartigny, P.; Afanasiev, V. Diamonds and Eclogites of the Jericho Kimberlite (Northern Canada). Contrib. Miner. Pet. 2009, 158, 295–315. [Google Scholar] [CrossRef]
- Vinogradov, A.; Kropotova, O.; Ustinov, V. Possible Source of Carbon in Diamonds as Indicated by the 12C/13C Ratios. Geochem. Int. 1965, 2, 495–503. [Google Scholar]
- Cartigny, P. Stable Isotopes and the Origin of Diamond. Elements 2005, 1, 79–84. [Google Scholar] [CrossRef]
- Moussallam, Y.; Morizet, Y.; Gaillard, F. H2O–CO2 Solubility in Low SiO2-Melts and the Unique Mode of Kimberlite Degassing and Emplacement. Earth Planet. Sci. Lett. 2016, 447, 151–160. [Google Scholar] [CrossRef]
- Giuliani, A.; Drysdale, R.N.; Woodhead, J.D.; Planavsky, N.J.; Phillips, D.; Hergt, J.; Griffin, W.L.; Oesch, S.; Dalton, H.; Davies, G.R. Perturbation of the Deep-Earth Carbon Cycle in Response to the Cambrian Explosion. Sci. Adv. 2022, 8, eabj1325. [Google Scholar] [CrossRef]
- Javoy, M.; Pineau, F. The Volatiles Record of a “Popping” Rock from the Mid-Atlantic Ridge at 14°N: Chemical and Isotopic Composition of Gas Trapped in the Vesicles. Earth Planet. Sci. Lett. 1991, 107, 598–611. [Google Scholar] [CrossRef]
- Bekaert, D.V.; Barry, P.H.; Curtice, J.; Blusztajn, J.; Hudak, M.; Seltzer, A.; Broadley, M.W.; Krantz, J.A.; Wanless, V.D.; Soule, S.A.; et al. A Carbon, Nitrogen, and Multi-Isotope Study of Basalt Glasses near 14°N on the Mid-Atlantic Ridge. Part A: Degassing Processes. Geochim. Cosmochim. Acta 2023, 369, 160–178. [Google Scholar] [CrossRef]
- Gennaro, M.E.; Grassa, F.; Martelli, M.; Renzulli, A.; Rizzo, A.L. Carbon Isotope Composition of CO2-Rich Inclusions in Cumulate-Forming Mantle Minerals from Stromboli Volcano (Italy). J. Volcanol. Geotherm. Res. 2017, 346, 95–103. [Google Scholar] [CrossRef]
- Lo Forte, F.M.; Boudoire, G.; Frezzotti, M.L.; Rotolo, S.G.; Sandoval-Velasquez, A.; Viveiros, F.; Zanon, V.; Aiuppa, A.; Rizzo, A.L. The Helium and Carbon Isotopic Signature of Ocean Island Basalts: Insights from Fogo Volcano (Cape Verde Archipelago). Earth Planet. Sci. Lett. 2024, 645, 118930. [Google Scholar] [CrossRef]
- Sandoval-Velasquez, A.; Casetta, F.; Ntaflos, T.; Aiuppa, A.; Coltorti, M.; Frezzotti, M.L.; Alonso, M.; Padrón, E.; Pankhurst, M.; Pérez, N.M.; et al. 2021 Tajogaite Eruption Records Infiltration of Crustal Fluids within the Upper Mantle beneath La Palma, Canary Islands. Front. Earth Sci. 2024, 12, 1303872. [Google Scholar] [CrossRef]
- Sandoval-Velasquez, A.; Rizzo, A.L.; Aiuppa, A.; Remigi, S.; Padrón, E.; Pérez, N.M.; Frezzotti, M.L. Recycled Crustal Carbon in the Depleted Mantle Source of El Hierro Volcano, Canary Islands. Lithos 2021, 400, 106414. [Google Scholar] [CrossRef]
- Boudoire, G.; Rizzo, A.L.; Di Muro, A.; Grassa, F.; Liuzzo, M. Extensive CO2 Degassing in the Upper Mantle beneath Oceanic Basaltic Volcanoes: First Insights from Piton de La Fournaise Volcano (La Réunion Island). Geochim. Cosmochim. Acta 2018, 235, 376–401. [Google Scholar] [CrossRef]
- Stachel, T.; Harris, J.; Aulbach, S.; Deines, P. Kankan Diamonds (Guinea) III: δ13C and Nitrogen Characteristics of Deep Diamonds. Contrib. Miner. Pet. 2002, 142, 465–475. [Google Scholar] [CrossRef]
- Tappert, R.; Stachel, T.; Harris, J.W.; Muehlenbachs, K.; Ludwig, T.; Brey, G.P. Diamonds from Jagersfontein (South Africa): Messengers from the Sublithospheric Mantle. Contrib. Miner. Pet. 2005, 150, 505–522. [Google Scholar] [CrossRef]
- Palot, M.; Cartigny, P.; Harris, J.W.; Kaminsky, F.V.; Stachel, T. Evidence for Deep Mantle Convection and Primordial Heterogeneity from Nitrogen and Carbon Stable Isotopes in Diamond. Earth Planet. Sci. Lett. 2012, 357–358, 179–193. [Google Scholar] [CrossRef]
- Howell, D.; Stachel, T.; Stern, R.A.; Pearson, D.G.; Nestola, F.; Hardman, M.F.; Harris, J.W.; Jaques, A.L.; Shirey, S.B.; Cartigny, P.; et al. Deep Carbon through Time: Earth’s Diamond Record and Its Implications for Carbon Cycling and Fluid Speciation in the Mantle. Geochim. Cosmochim. Acta 2020, 275, 99–122. [Google Scholar] [CrossRef]
- Smit, K.V.; Timmerman, S.; Aulbach, S.; Shirey, S.B.; Richardson, S.H.; Phillips, D.; Pearson, D.G. Geochronology of Diamonds. Rev. Mineral. Geochem. 2022, 88, 567–636. [Google Scholar] [CrossRef]
- Chapman, J.; Brown, G.; Sechos, B. The Typical Gemmological Characteristics of Argyle Diamonds. Aust. Gemmol. 1996, 19, 339–346. [Google Scholar]
- Timmerman, S.; Stachel, T.; Koornneef, J.M.; Smit, K.V.; Harlou, R.; Nowell, G.M.; Thomson, A.R.; Kohn, S.C.; Davies, J.H.F.L.; Davies, G.R.; et al. Sublithospheric Diamond Ages and the Supercontinent Cycle. Nature 2023, 623, 752–756. [Google Scholar] [CrossRef] [PubMed]
- Marty, B.; Avice, G.; Sano, Y.; Altwegg, K.; Balsiger, H.; Hässig, M.; Morbidelli, A.; Mousis, O.; Rubin, M. Origins of Volatile Elements (H, C, N, Noble Gases) on Earth and Mars in Light of Recent Results from the ROSETTA Cometary Mission. Earth Planet. Sci. Lett. 2016, 441, 91–102. [Google Scholar] [CrossRef]
- Mikhail, S.; Füri, E. On the Origin(s) and Evolution of Earth’s Carbon. Elements 2019, 15, 307–312. [Google Scholar] [CrossRef]



| Volcano | Location | Temperature (°C) | δ13C (‰ vs. PDB) | Reference |
|---|---|---|---|---|
| Mauna Loa | Hawaii | 700–800 | −13.1 | [6] |
| Kilauea | Hawaii | 905–935 | −7.82 | [7] |
| Usu | Japan | 750 | −4.4 | [8] |
| Satsuma-Iojima | Japan | 786 | −5.5 | [8] |
| Erta’ Ale | Afar | 1130 | −6.4 | [9] |
| Asal rift | Afar | 1070 | −6 | [10] |
| Merapi | Indonesia | 850 | −3.9 | [11] |
| Momotombo | Nicaragua | 880 | −2.6 | [11] |
| Etna | Italy | 1090 | −4.0 | [14] |
| Vesicle [CO2] (ppm) | Vesicle δ13C (‰) | Glass [CO2] (ppm) | Glass δ13C (‰) | |
|---|---|---|---|---|
| All data | ||||
| Average | 288 | −7 | 170 | −10 |
| 1-sigma | 682 | 4 | 93 | 5 |
| Min | 0 | −27 | 0 | −34 |
| Max | 5452 | −1 | 800 | −1 |
| N | 432 | 411 | 2474 | 341 |
| Arc | ||||
| Average | 102 | −7 | 103 | −12 |
| 1-sigma | 75 | 2 | 74 | 7 |
| Min | 4 | −13 | 0 | −34 |
| Max | 279 | −2 | 362 | −3 |
| N | 24 | 28 | 157 | 78 |
| Hotspot | ||||
| Average | 265 | −9 | 87 | −12 |
| 1-sigma | 707 | 6 | 101 | 6 |
| Min | 1 | −27 | 0 | −28 |
| Max | 5452 | −1 | 800 | −3 |
| N | 147 | 146 | 372 | 75 |
| Mid-Ocean Ridges | ||||
| Average | 319 | −5 | 191 | −9 |
| 1-sigma | 695 | 2 | 81 | 3 |
| Min | 0 | −11 | 0 | −24 |
| Max | 4539 | −1 | 674 | −1 |
| N | 261 | 237 | 1945 | 188 |
| Sample Type | Reference | Observations (n) | Minimum | Maximum | Mean | Std. Deviation |
|---|---|---|---|---|---|---|
| Diamonds (all) | [165] | 4308 | −41.4 | 2.5 | −6.9 | 5.5 |
| Diamonds (peridotitic) | [165] | 1906 | −34.5 | 2.3 | −4.9 | 1.9 |
| Kimberlites | [176] | 65 | −8.9 | −3.4 | −5.5 | 1.2 |
| Carbonatites | GEOROC | 1035 | −12.1 | 3.5 | −4.2 | 2.1 |
| CO2-Undersaturated MORBs, seamounts, and popping rocks | [73,74] | 14 | −10.5 | −3.6 | −7.5 | 2.2 |
| Fluid inclusions in magmatic xenoliths | [90,180,181,182,183] | 165 | −8.9 | 7.472 | −3.4 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moussallam, Y. Carbon Isotopes in Magmatic Systems: Measurements, Interpretations, and the Carbon Isotopic Signature of the Earth’s Mantle. Geosciences 2025, 15, 266. https://doi.org/10.3390/geosciences15070266
Moussallam Y. Carbon Isotopes in Magmatic Systems: Measurements, Interpretations, and the Carbon Isotopic Signature of the Earth’s Mantle. Geosciences. 2025; 15(7):266. https://doi.org/10.3390/geosciences15070266
Chicago/Turabian StyleMoussallam, Yves. 2025. "Carbon Isotopes in Magmatic Systems: Measurements, Interpretations, and the Carbon Isotopic Signature of the Earth’s Mantle" Geosciences 15, no. 7: 266. https://doi.org/10.3390/geosciences15070266
APA StyleMoussallam, Y. (2025). Carbon Isotopes in Magmatic Systems: Measurements, Interpretations, and the Carbon Isotopic Signature of the Earth’s Mantle. Geosciences, 15(7), 266. https://doi.org/10.3390/geosciences15070266






