A Novel Bimodal Hydro-Mechanical Coupling Model for Evaluating Rainfall-Induced Unsaturated Slope Stability
Abstract
1. Introduction
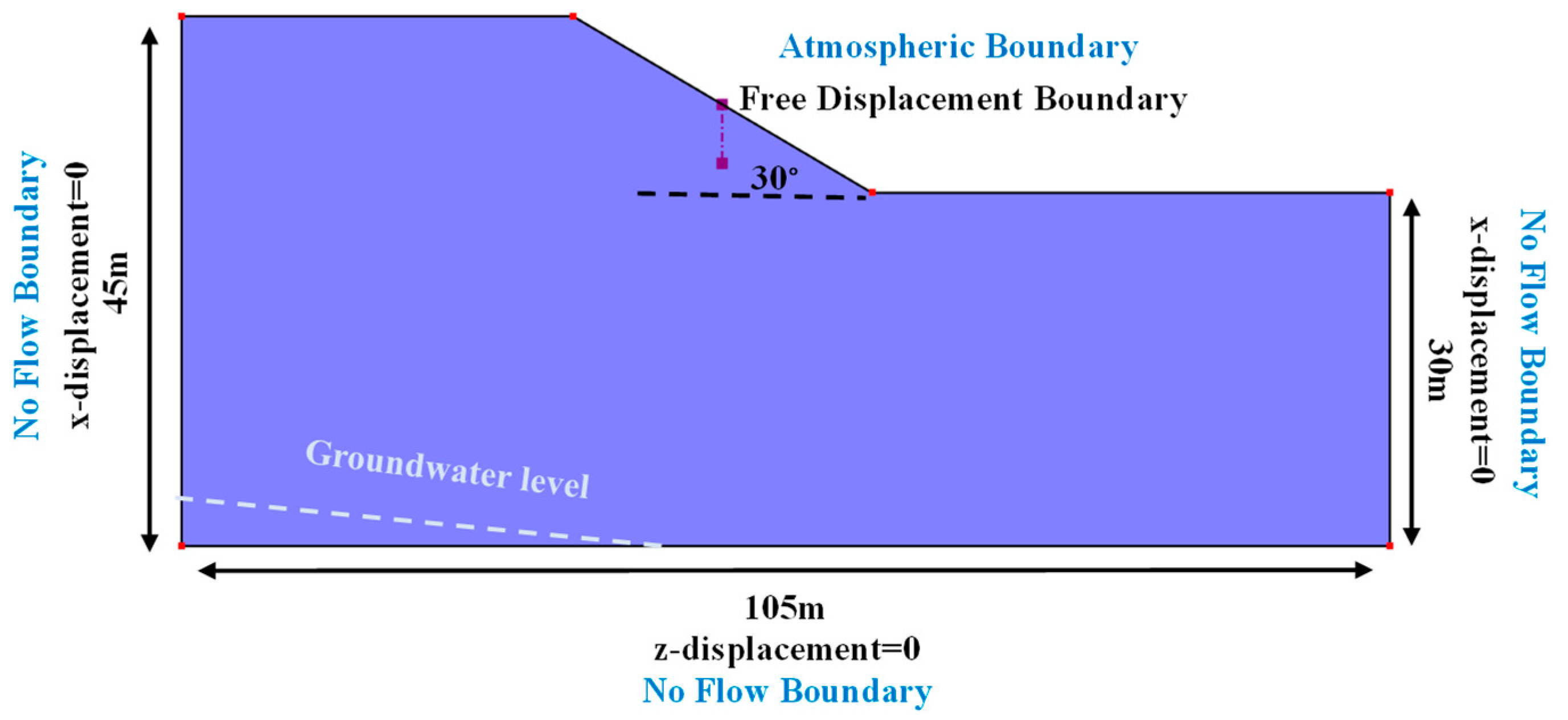
2. Materials and Methods
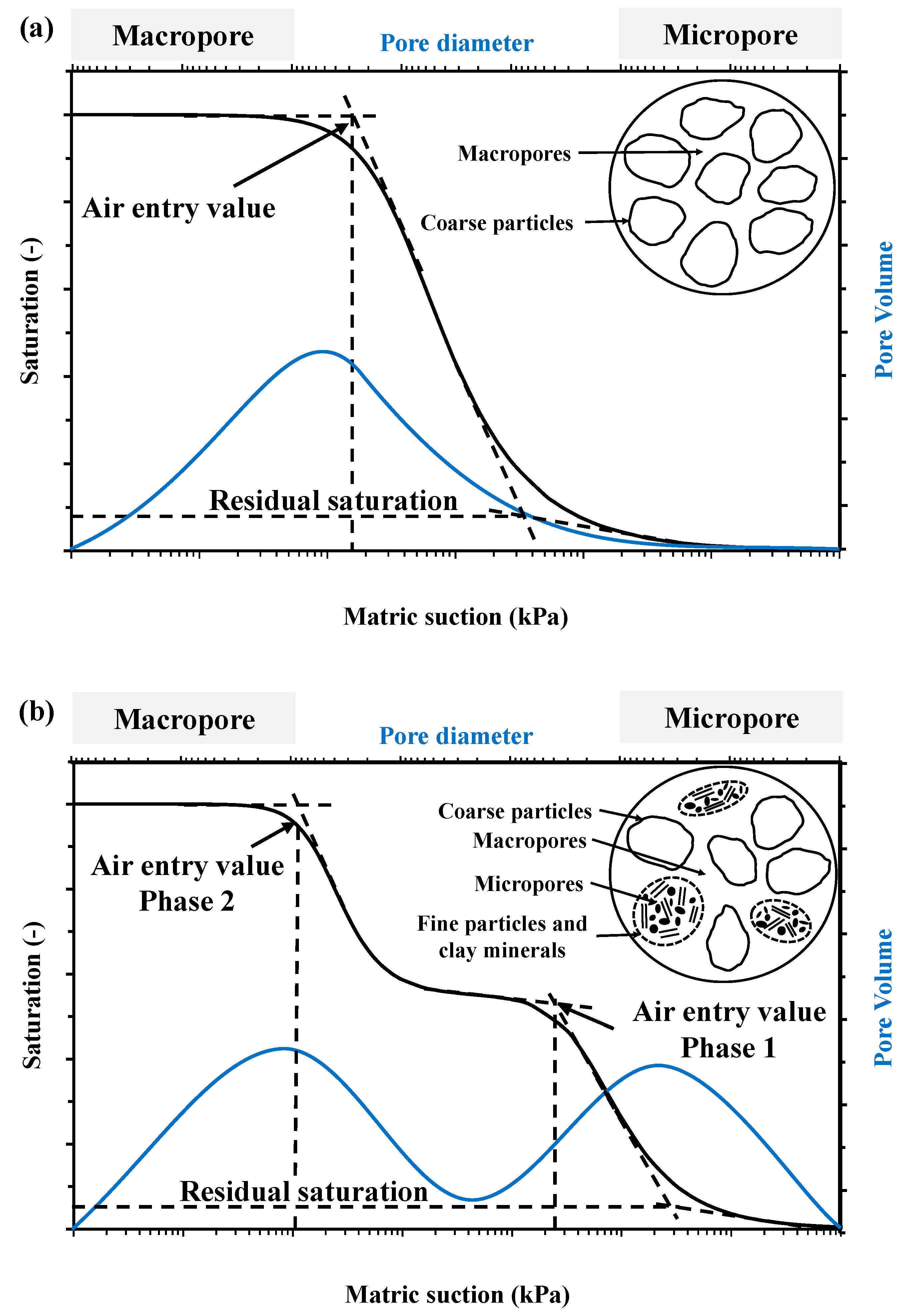
2.1. Typical Soil Water Characteristic Curve (SWCC)
2.2. Bimodal Soil Water Characteristic Curve (BSWCC)
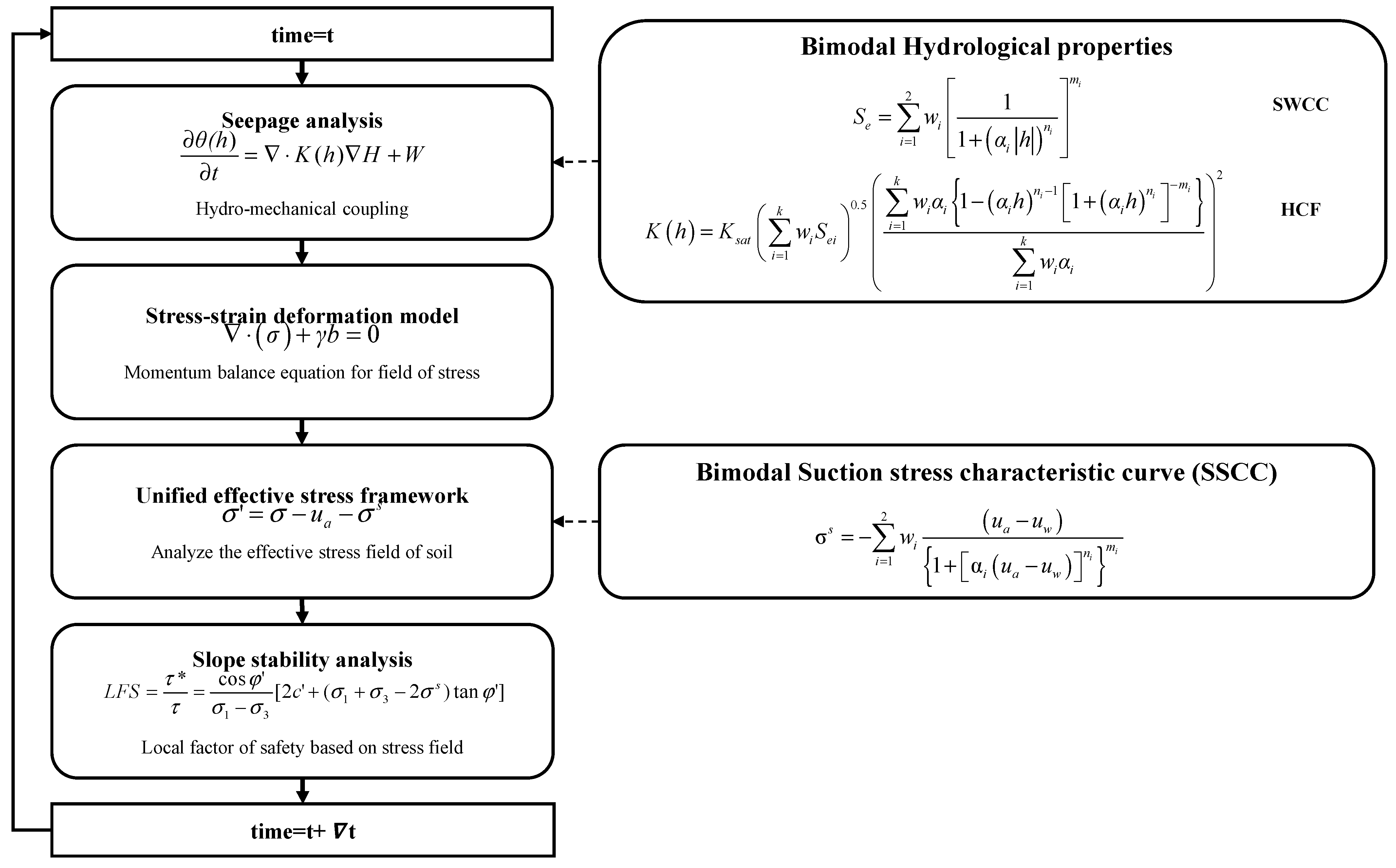
2.3. Coupled Hydro-Mechanical Framework
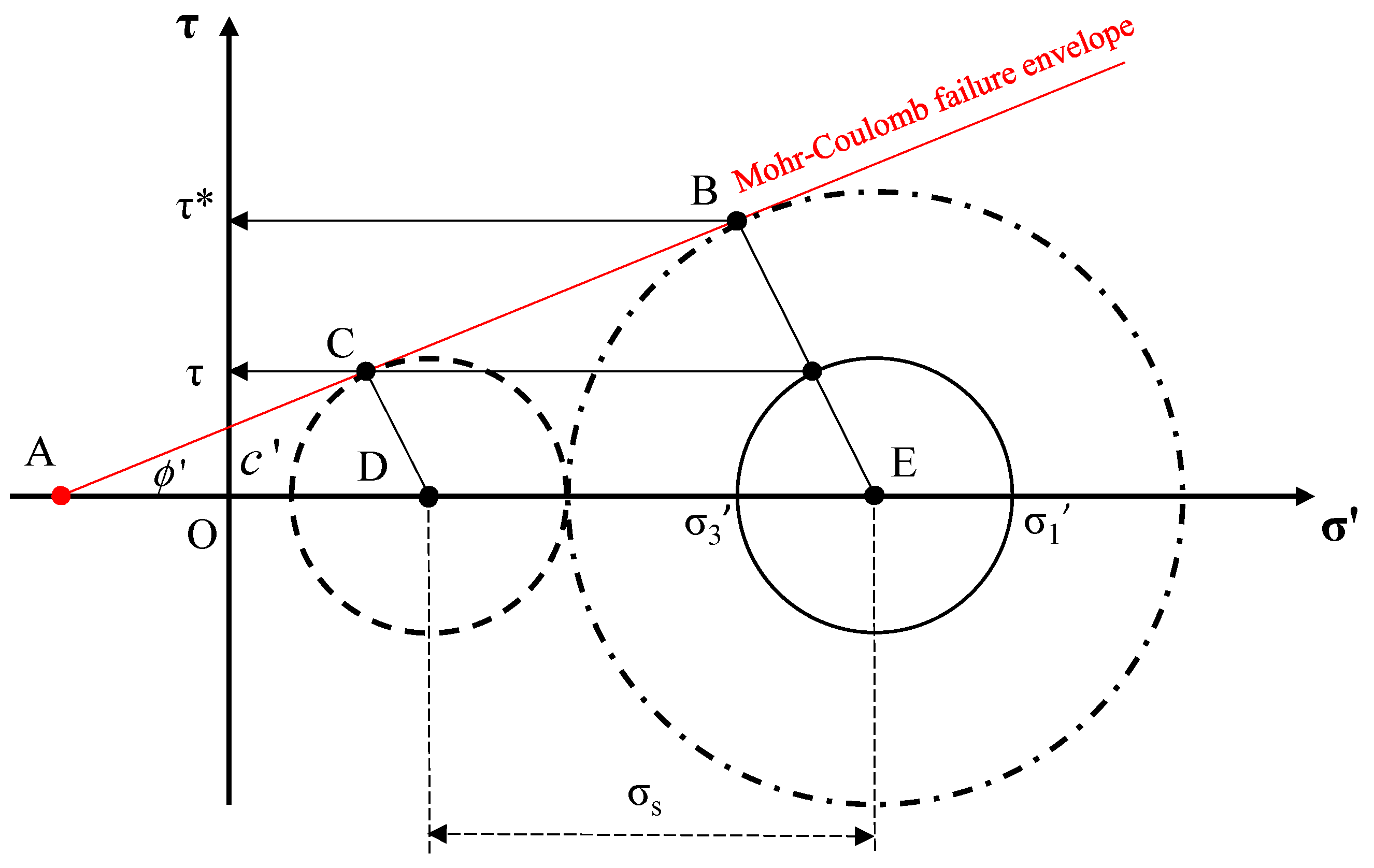
2.4. Concept of Effective Stress in Unsaturated Soils
2.5. Local Factor of Safety (LFS)
3. Results
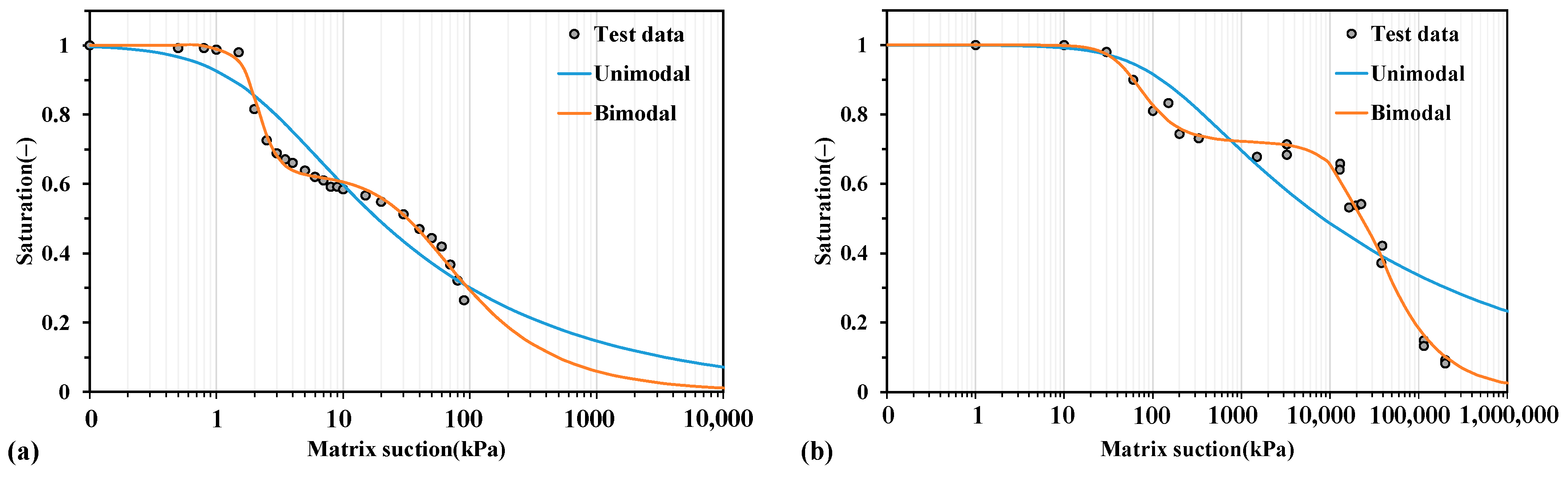
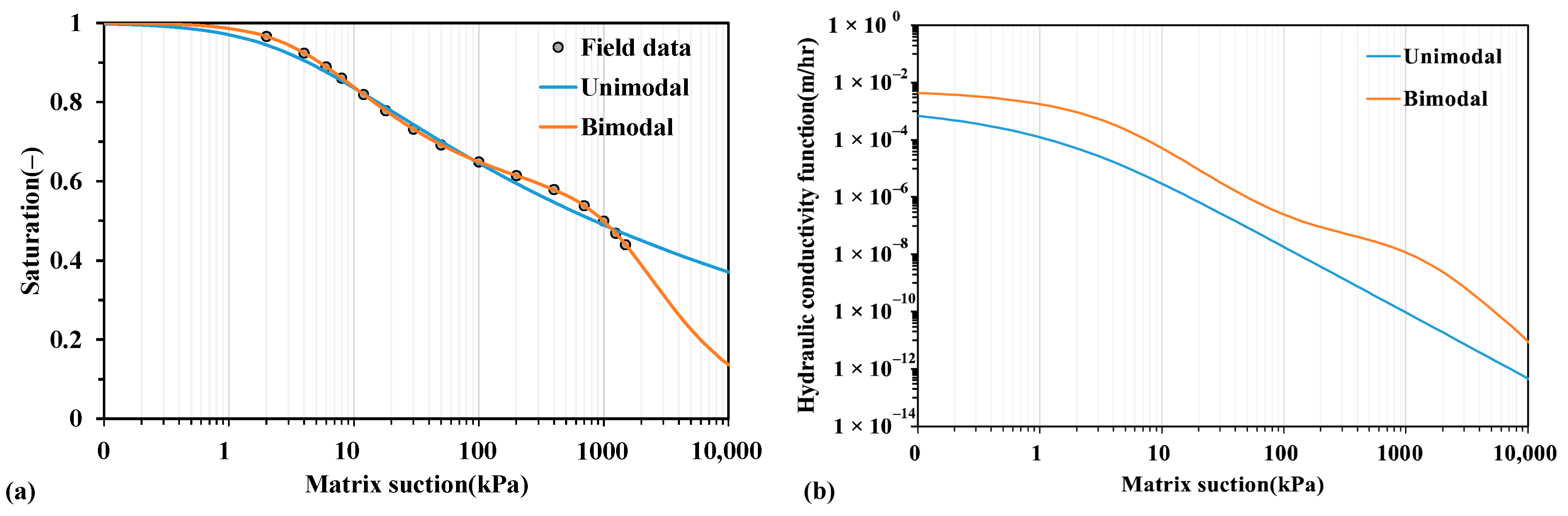
3.1. Comparative Analysis of Unimodal and Bimodal Soil Water Charateristic Curve Models
3.2. The Influence of Bimodal SWCC Models on SSCC
3.3. Fitting Results of Soil Hydraulic Parameters
4. Discussions
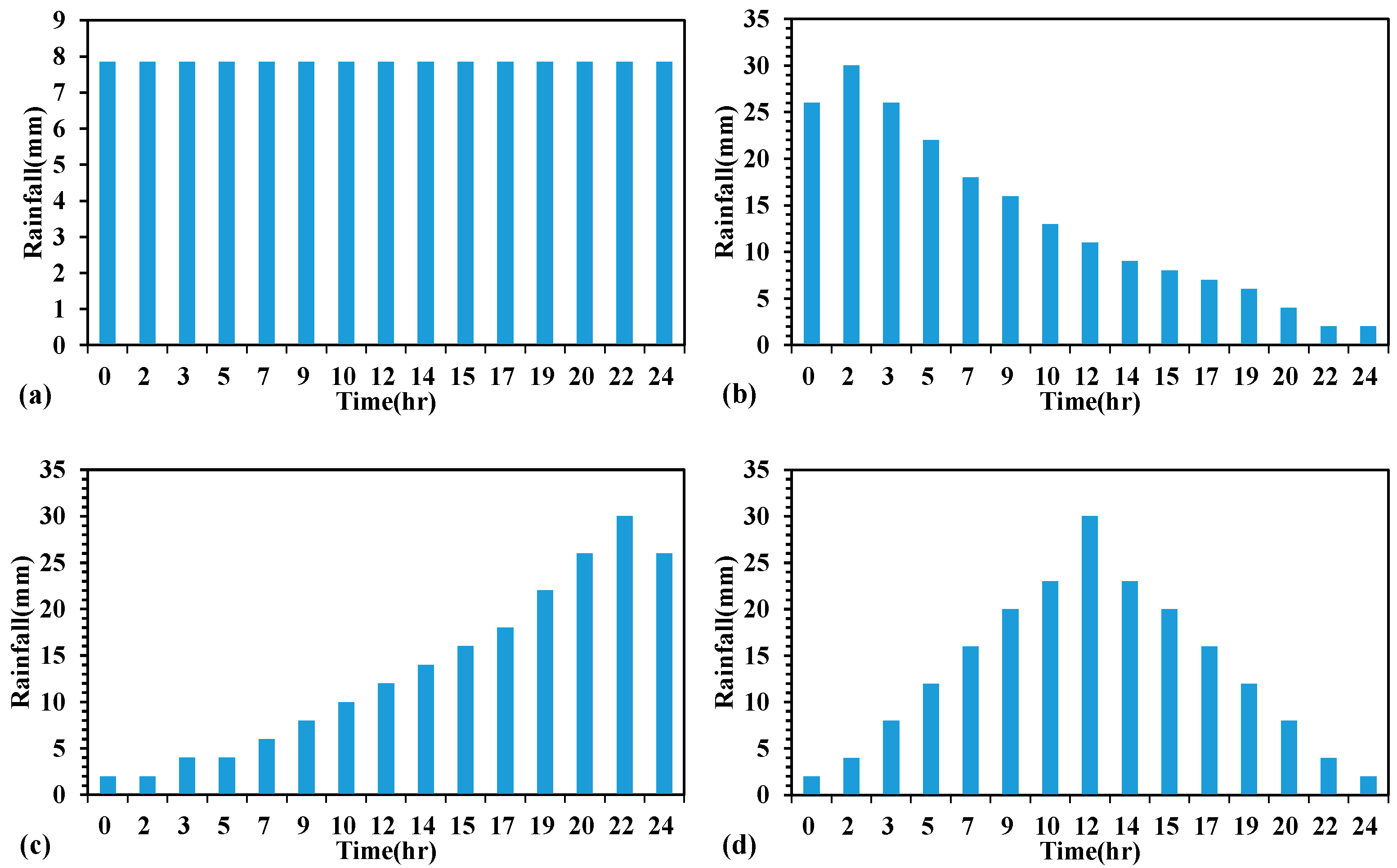
4.1. Effect of Different Rainfall Types on the Analysis of Unimodal and Bimodal Models
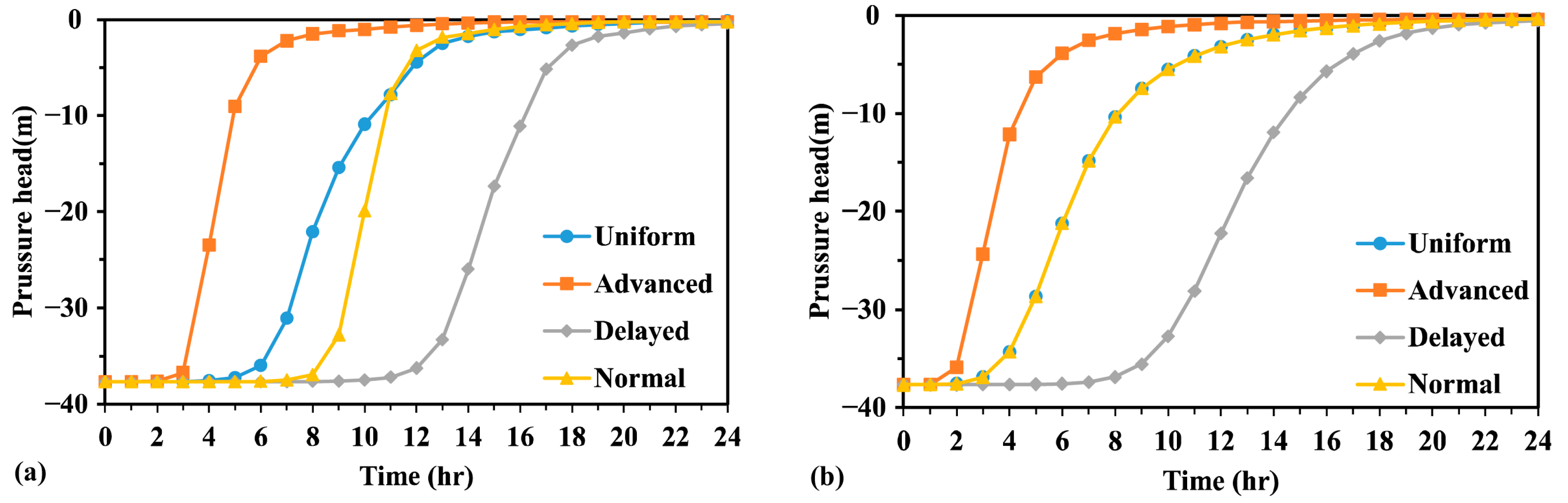
4.2. Evaluation of Seepage in Unimodal and Bimodal Models
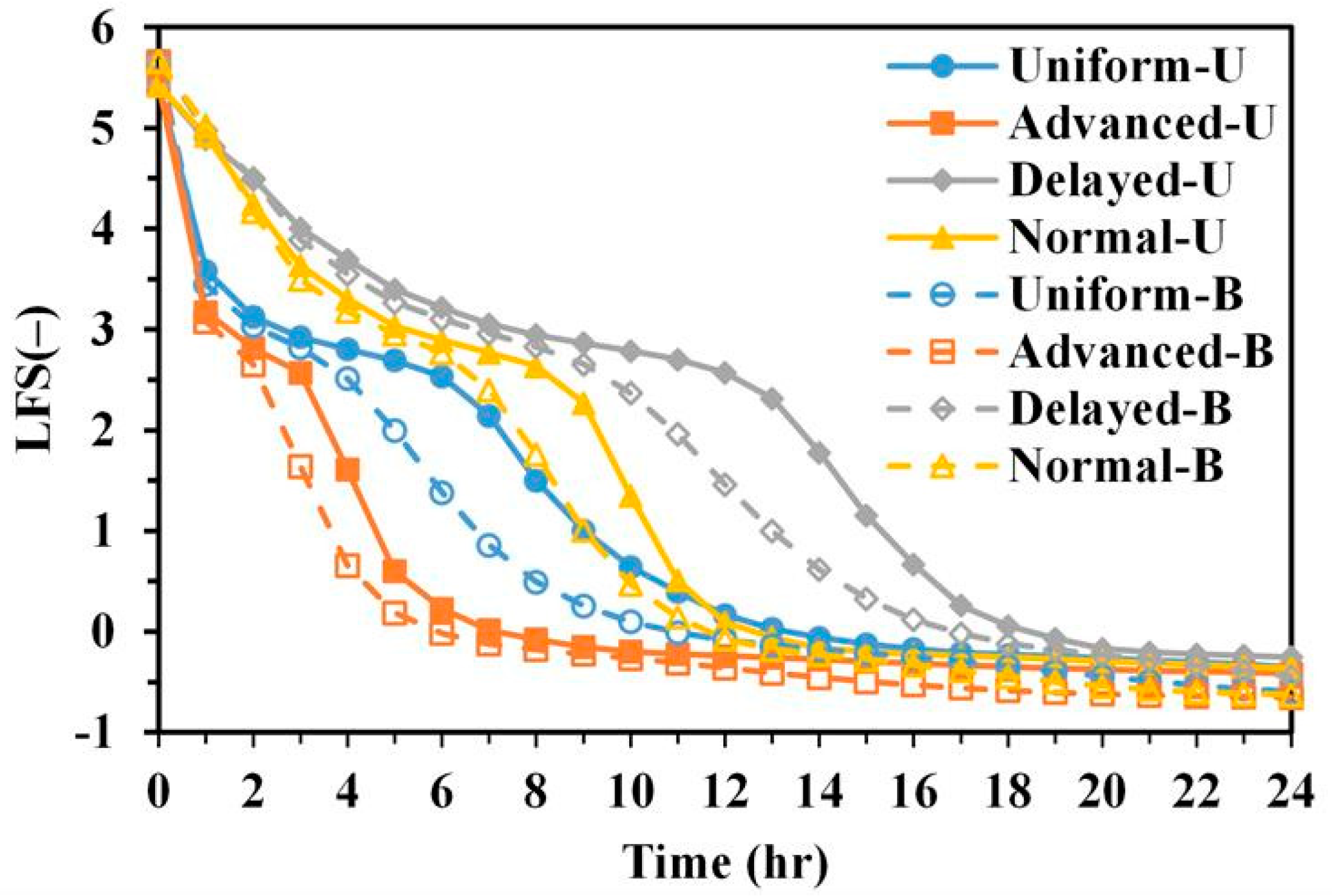
4.3. Slope Stability: Unimodal and Bimodal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SWCC | Soil Water Characteristic Curve |
| SSCC | Suction Stress Characteristic Curve |
| HCF | Hydraulic Conductivity Function |
| LFS | Local Factor of Safety |
| FEM | Finite Element Method |
References
- Chang, W.-J.; Chou, S.-H.; Huang, H.-P.; Chao, C.-Y. Development and verification of coupled hydro-mechanical analysis for rainfall-induced shallow landslides. Eng. Geol. 2021, 293, 106337. [Google Scholar]
- Jing, J.; Hou, J.; Sun, W.; Chen, G.; Ma, Y.; Ji, G. Study on influencing factors of unsaturated loess slope stability under dry-wet cycle conditions. J. Hydrol. 2022, 612, 128187. [Google Scholar]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of hysteresis on the stability of residual soil slope. Int. Soil Water Conserv. Res. 2019, 7, 226–238. [Google Scholar]
- Pham, K.; Kim, D.; Choi, H.-J.; Lee, I.-M.; Choi, H. A numerical framework for infinite slope stability analysis under transient unsaturated seepage conditions. Eng. Geol. 2018, 243, 36–49. [Google Scholar]
- Yang, S.-R.; Chen, X.-R. Assessing rainfall-induced wetting band depth for stability analysis of unsaturated soil slopes. Case Stud. Constr. Mater. 2023, 18, e02180. [Google Scholar]
- Yang, Y.-S.; Yeh, H.-F. Effects of hysteretic soil water characteristic curves on the hydromechanical behaviour. J. Earth Syst. Sci. 2023, 132, 136. [Google Scholar]
- Yang, Y.-S.; Yeh, H.-F.; Ke, C.-C.; Wei, L.-W. Assessing shallow slope stability using electrical conductivity data and soil hydraulic characteristics. Eng. Geol. 2024, 331, 107447. [Google Scholar]
- Yang, Y.-S.; Yeh, H.-F.; Ke, C.-C.; Wei, L.-W.; Chen, N.-C. The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory. Geosciences 2024, 14, 274. [Google Scholar] [CrossRef]
- Natalia, L.; Yang, J. Impact of hysteresis of unsaturated hydraulic properties on rainfall-induced slope failures. Eng. Geol. 2025, 354, 108175. [Google Scholar]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46, W05515. [Google Scholar]
- Lu, N.; Griffiths, D. Profiles of steady-state suction stress in unsaturated soils. J. Geotech. Geoenvironmental Eng. 2004, 130, 1063–1076. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar]
- Yeh, H.-F.; Huang, T.-T.; Yang, Y.-S.; Ke, C.-C. Influence of uncertainty of soil hydraulic parameters on stability of unsaturated slopes based on Bayesian updating. Geofluids 2021, 2021, 6629969. [Google Scholar]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A. Effect of bimodal soil-water characteristic curve on the estimation of permeability function. Eng. Geol. 2017, 230, 142–151. [Google Scholar]
- Zhou, A.-N.; Sheng, D.; Carter, J.P. Modelling the effect of initial density on soil-water characteristic curves. Géotechnique 2012, 62, 669–680. [Google Scholar]
- Li, X. Dual-Porosity Structure and Bimodal Hydraulic Property Functions for Unsaturated Coarse Granular Soils; Hong Kong University of Science and Technology (Hong Kong): Hong Kong, China, 2009. [Google Scholar]
- Li, X.; Li, J.H.; Zhang, L.M. Predicting bimodal soil–water characteristic curves and permeability functions using physically based parameters. Comput. Geotech. 2014, 57, 85–96. [Google Scholar]
- Satyanaga, A.; Rahardjo, H.; Leong, E.-C.; Wang, J.-Y. Water characteristic curve of soil with bimodal grain-size distribution. Comput. Geotech. 2013, 48, 51–61. [Google Scholar]
- Zhang, L.; Chen, Q. Predicting bimodal soil–water characteristic curves. J. Geotech. Geoenvironmental Eng. 2005, 131, 666–670. [Google Scholar]
- Brooks, R.H. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1965. [Google Scholar]
- Burdine, N.; Gournay, L.; Reichertz, P. Pore size distribution of petroleum reservoir rocks. J. Pet. Technol. 1950, 2, 195–204. [Google Scholar]
- Kosugi, K.i. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar]
- Liu, J.; Leung, A.K.; Dong, H.; Lai, N.T. A state-dependent bimodal soil water retention model considering evolutions of pore-scale soil–water interaction. Comput. Geotech. 2024, 175, 106704. [Google Scholar]
- Satyanaga, A.; Rahardjo, H. Unsaturated shear strength of soil with bimodal soil-water characteristic curve. Géotechnique 2019, 69, 828–832. [Google Scholar]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar]
- Qian, J.; Lin, Z.; Shi, Z. Experimental and modeling study of water-retention behavior of fine-grained soils with dual-porosity structures. Acta Geotech. 2022, 17, 3245–3258. [Google Scholar]
- Zhou, C.; Chen, R. Modelling the water retention behaviour of anisotropic soils. J. Hydrol. 2021, 599, 126361. [Google Scholar]
- Lin, Z.; Qian, J.; Shi, Z.; Zhai, Q. Bi-linear strength envelope of coarse-and fine-grained unsaturated soils with bimodal water-retention curve. Eng. Geol. 2022, 304, 106694. [Google Scholar]
- Giannini, L.M.; Varone, C.; Esposito, C.; Marmoni, G.M.; Scarascia Mugnozza, G.; Schilirò, L. Earthquake-induced reactivation of landslides under variable hydrostatic conditions: Evaluation at regional scale and implications for risk assessment. Landslides 2022, 19, 2005–2019. [Google Scholar]
- Yeh, H.-F.; Huang, T.-T.; Lee, J.-W. Effect of unimodal and bimodal soil hydraulic properties on slope stability analysis. Water 2021, 13, 1674. [Google Scholar] [CrossRef]
- De Luca, D.L.; Apollonio, C.; Petroselli, A. The benefit of continuous hydrological modelling for drought hazard assessment in small and coastal ungauged basins: A case study in Southern Italy. Climate 2022, 10, 34. [Google Scholar] [CrossRef]
- Li, D.-Q.; Wang, L.; Cao, Z.-J.; Qi, X.-H. Reliability analysis of unsaturated slope stability considering SWCC model selection and parameter uncertainties. Eng. Geol. 2019, 260, 105207. [Google Scholar]
- Pan, Y.; Wu, G.; Zhao, Z.; He, L. Analysis of rock slope stability under rainfall conditions considering the water-induced weakening of rock. Comput. Geotech. 2020, 128, 103806. [Google Scholar]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effect of antecedent rainfall patterns on rainfall-induced slope failure. J. Geotech. Geoenvironmental Eng. 2011, 137, 483–491. [Google Scholar]
- Wang, J.-H.; Xu, W.-J.; Liu, X.-X. A slope stability analysis method considering the rainfall hydrology process. Eng. Geol. 2024, 343, 107775. [Google Scholar]
- Wang, L.; Chen, Y.; Huang, X.; Zhang, L.; Li, X.; Wang, S. Displacement prediction method of rainfall-induced landslide considering multiple influencing factors. Nat. Hazards 2023, 115, 1051–1069. [Google Scholar]
- Yang, Y.-S.; Yeh, H.-F. Evaluate the Probability of Failure in Rainfall-Induced Landslides Using a Fuzzy Point Estimate Method. Geofluids 2019, 2019, 3587989. [Google Scholar]
- Gariano, S.; Rianna, G.; Petrucci, O.; Guzzetti, F. Assessing future changes in the occurrence of rainfall-induced landslides at a regional scale. Sci. Total. Environ. 2017, 596, 417–426. [Google Scholar]
- Song, Y.-S.; Chae, B.-G.; Lee, J. A method for evaluating the stability of an unsaturated slope in natural terrain during rainfall. Eng. Geol. 2016, 210, 84–92. [Google Scholar]
- Chen, P.; Mirus, B.; Lu, N.; Godt, J.W. Effect of hydraulic hysteresis on stability of infinite slopes under steady infiltration. J. Geotech. Geoenvironmental Eng. 2017, 143, 04017041. [Google Scholar]
- Nguyen, T.S.; Likitlersuang, S. Reliability analysis of unsaturated soil slope stability under infiltration considering hydraulic and shear strength parameters. Bull. Eng. Geol. Environ. 2019, 78, 5727–5743. [Google Scholar]
- Oh, S.; Lu, N. Slope stability analysis under unsaturated conditions: Case studies of rainfall-induced failure of cut slopes. Eng. Geol. 2015, 184, 96–103. [Google Scholar]
- Xu, F.; Hu, H.; Lin, H.; Xie, L. Bedding slope destabilization under rainfall: A case study of Zhuquedong slope in Hunan province, China. Appl. Sci. 2024, 14, 1394. [Google Scholar]
- Yang, Y.-S.; Yeh, H.-F.; Ke, C.-C.; Chen, N.-C.; Chang, K.-C. Assessment of probability of failure on rainfall-induced shallow landslides at slope scale using a physical-based model and fuzzy point estimate method. Front. Earth Sci. 2022, 10, 957506. [Google Scholar]
- Yeh, H.-F.; Tsai, Y.-J. Analyzing the effect of soil hydraulic conductivity anisotropy on slope stability using a coupled hydromechanical framework. Water 2018, 10, 905. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Tsai, Y.-J. Effect of variations in long-duration rainfall intensity on unsaturated slope stability. Water 2018, 10, 479. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; J. Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Duncan, J.M. State of the art: Limit equilibrium and finite-element analysis of slopes. J. Geotech. Eng. 1996, 122, 577–596. [Google Scholar]
- Duncan, J.M.; Wright, S.G.; Brandon, T.L. Soil Strength and Slope Stability; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Fellenius, W. Calculation of the stability of earth dams. In Proceedings of the Second Congress on Large Dams, Washington, DC, USA, 7–12 September 1936; pp. 445–463. [Google Scholar]
- Janbu, N. Slope Stability Computations; Wiley (John) and Sons, Incorporated: Hoboken, NJ, USA, 1973. [Google Scholar]
- Yu, H.; Salgado, R.; Sloan, S.; Kim, J. Limit analysis versus limit equilibrium for slope stability. J. Geotech. Geoenvironmental Eng. 1998, 124, 1–11. [Google Scholar]
- Lu, N.; Şener-Kaya, B.; Wayllace, A.; Godt, J.W. Analysis of rainfall-induced slope instability using a field of local factor of safety. Water Resour. Res. 2012, 48, W09524. [Google Scholar]
- Godt, J.W.; Şener-Kaya, B.; Lu, N.; Baum, R.L. Stability of infinite slopes under transient partially saturated seepage conditions. Water Resour. Res. 2012, 48, W05505. [Google Scholar]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar]
- Wijaya, M.; Leong, E. Equation for unimodal and bimodal soil–water characteristic curves. Soils Found. 2016, 56, 291–300. [Google Scholar]
- Simunek, J.; van Genuchten, M.T.; Sejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar]
- Reddy, J. An Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Terzaghi, K. Stress distribution in dry and in saturated sand above a yielding trap-door. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering (Harvard), Cambridge, UK, 22–26 June 1936. [Google Scholar]
- Bishop, A.W. The principal of effective stress. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- Chen, H.; Feng, S.-J. A simple water retention model of dual-porosity soils based on self-similarity of bimodal pore size distribution. Comput. Geotech. 2023, 162, 105684. [Google Scholar]
- Liu, J.; Leung, A.K.; Dong, H.; Jiang, Z. Pore-scale investigation of the hysteretic water retention behaviour of unsaturated soils by tracking preferential water transport. Comput. Geotech. 2025, 179, 107049. [Google Scholar]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenvironmental Eng. 2006, 132, 131–142. [Google Scholar]

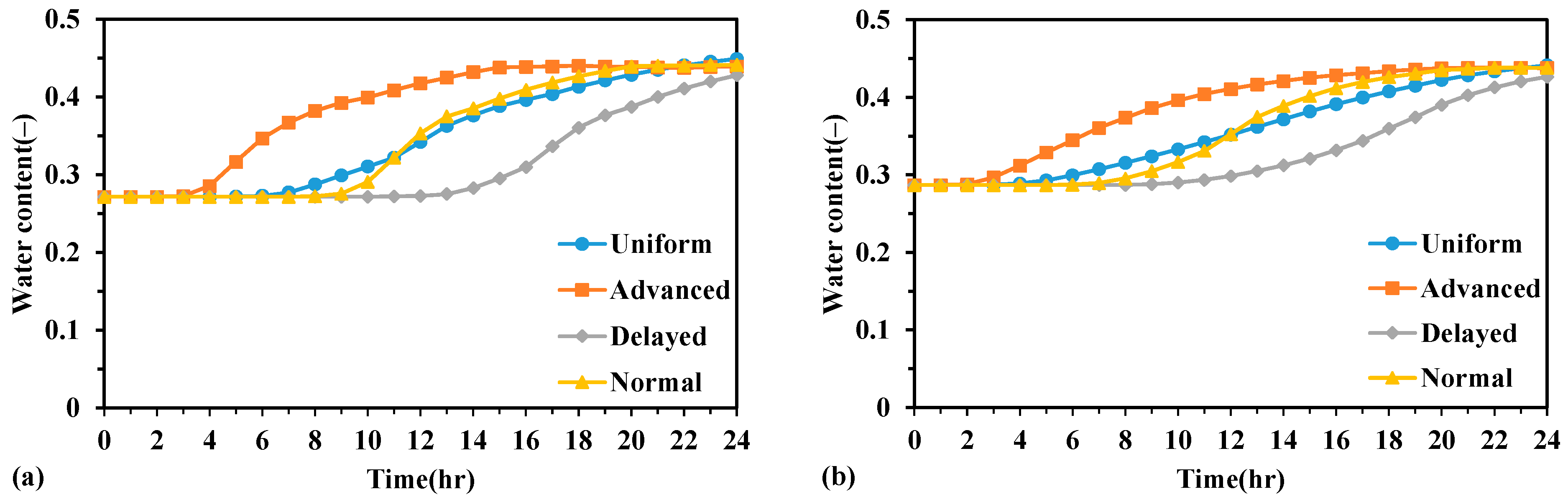
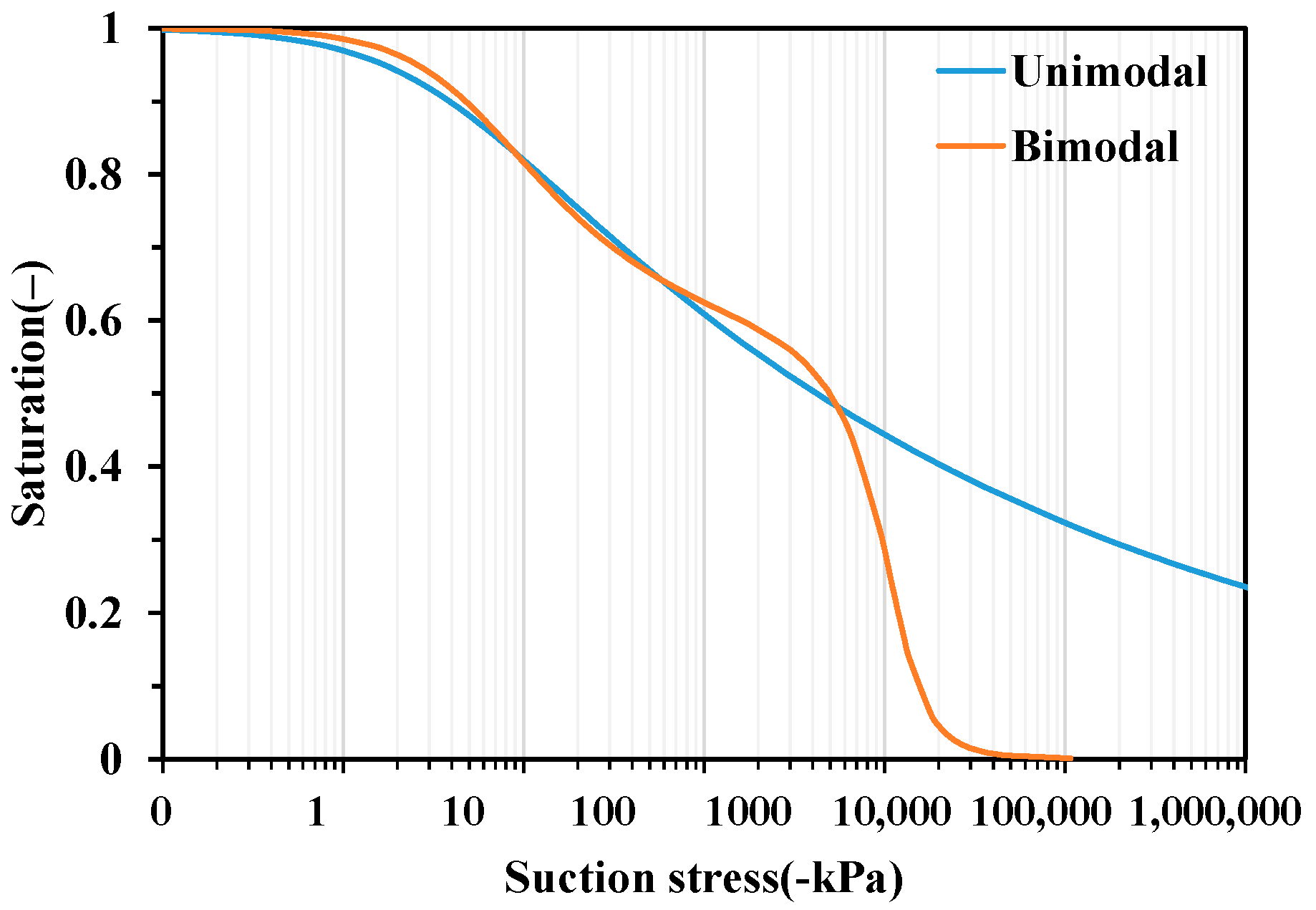
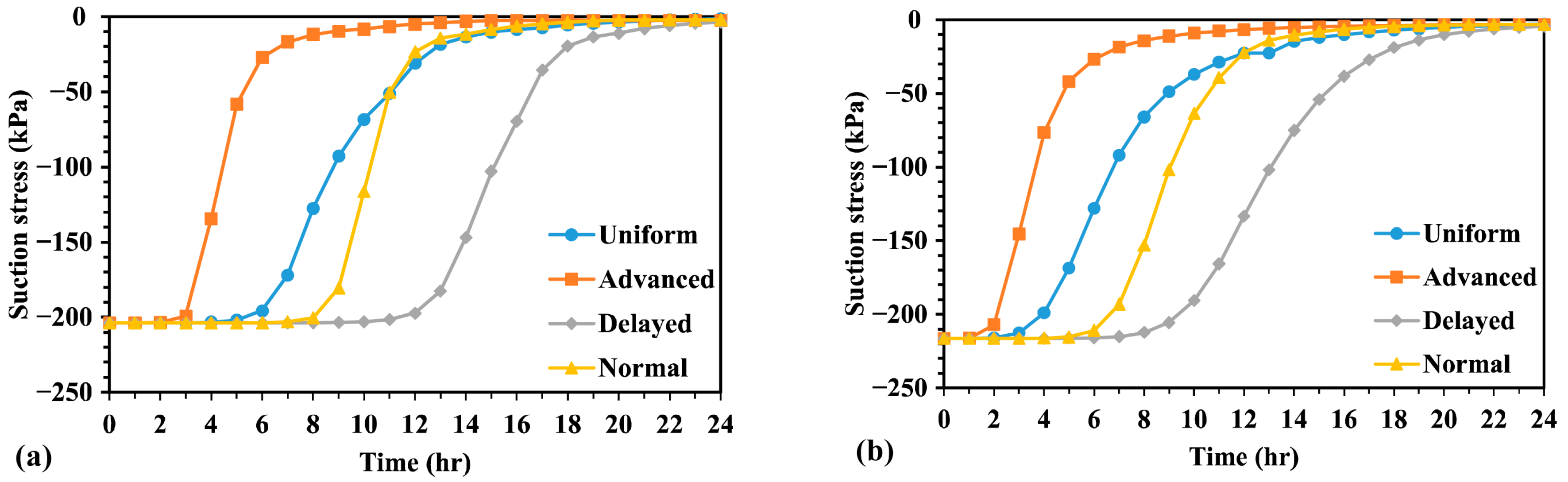
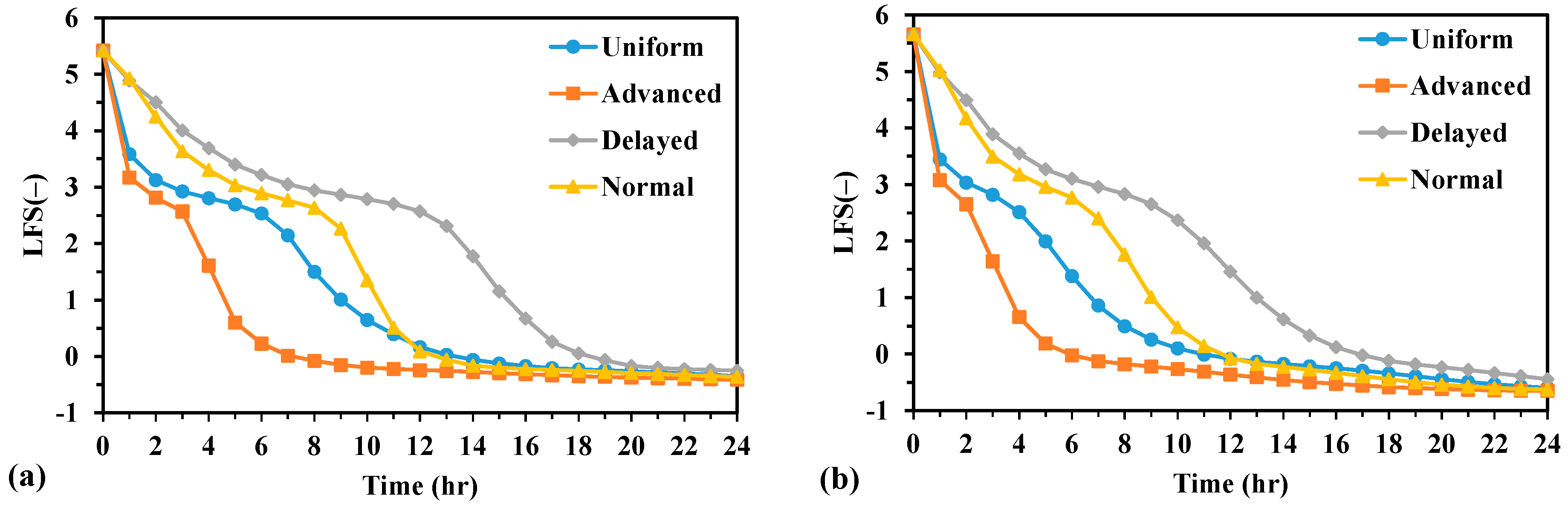
| Material | |||||
|---|---|---|---|---|---|
| Colluvium | 0.467 | 0.031 | 3.64 | 1.121 | 0.00626 |
| Material | ||||||||
|---|---|---|---|---|---|---|---|---|
| Colluvium | 0.467 | 0.031 | 2.08 | 1.461 | 0.46 | 0.0062 | 1.798 | 0.00626 |
| Material | |||||
|---|---|---|---|---|---|
| Colluvium | 2.62 | 27 | 5 | 0.33 | 40,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, T.-H.; Yang, Y.-S.; Yeh, H.-F. A Novel Bimodal Hydro-Mechanical Coupling Model for Evaluating Rainfall-Induced Unsaturated Slope Stability. Geosciences 2025, 15, 265. https://doi.org/10.3390/geosciences15070265
Huang T-H, Yang Y-S, Yeh H-F. A Novel Bimodal Hydro-Mechanical Coupling Model for Evaluating Rainfall-Induced Unsaturated Slope Stability. Geosciences. 2025; 15(7):265. https://doi.org/10.3390/geosciences15070265
Chicago/Turabian StyleHuang, Tzu-Hao, Ya-Sin Yang, and Hsin-Fu Yeh. 2025. "A Novel Bimodal Hydro-Mechanical Coupling Model for Evaluating Rainfall-Induced Unsaturated Slope Stability" Geosciences 15, no. 7: 265. https://doi.org/10.3390/geosciences15070265
APA StyleHuang, T.-H., Yang, Y.-S., & Yeh, H.-F. (2025). A Novel Bimodal Hydro-Mechanical Coupling Model for Evaluating Rainfall-Induced Unsaturated Slope Stability. Geosciences, 15(7), 265. https://doi.org/10.3390/geosciences15070265








