Integrating Soil Parameter Uncertainty into Slope Stability Analysis: A Case Study of an Open Pit Mine in Hungary
Abstract
1. Introduction
2. Geological Settings and Geotechnical Parameters
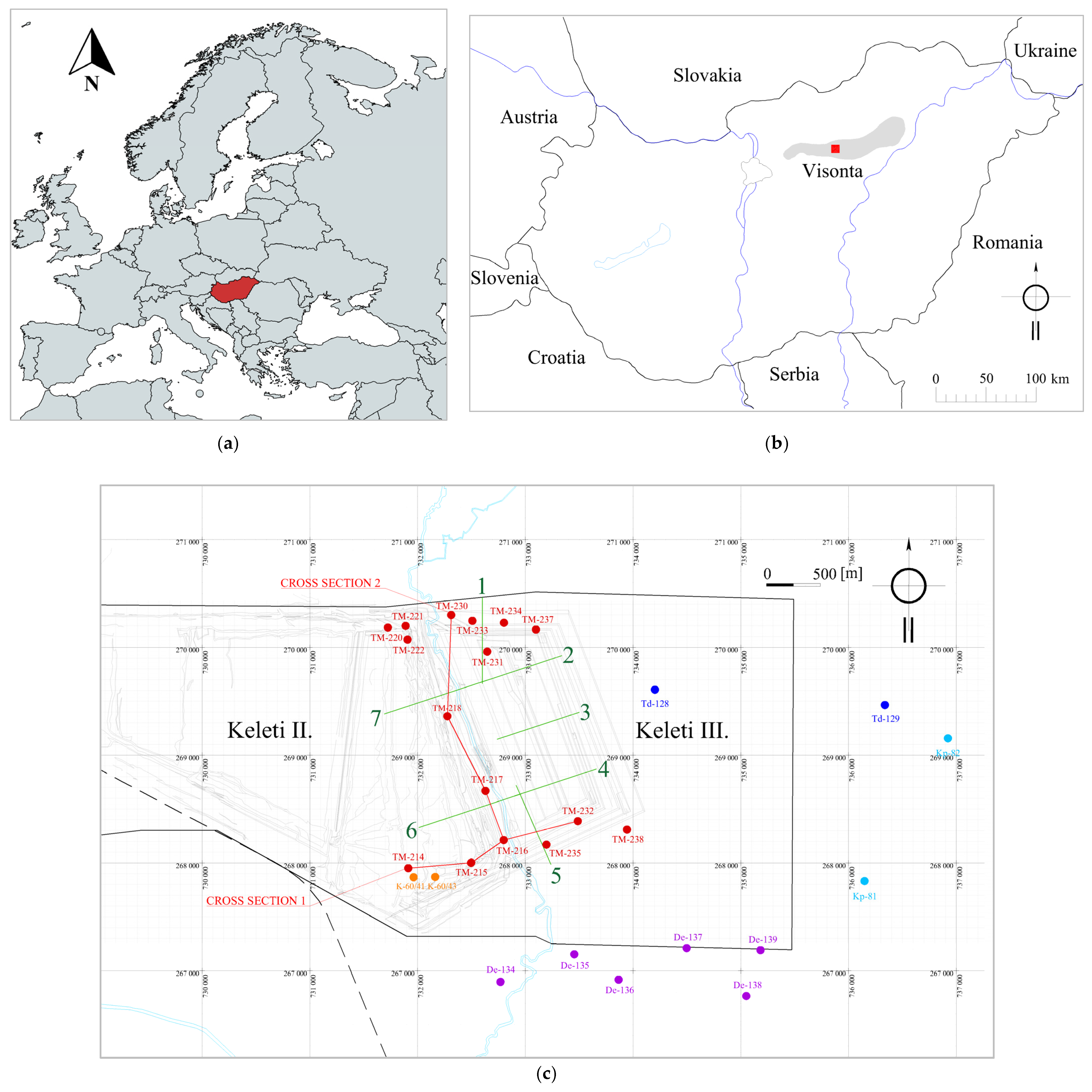
2.1. Geographical Location
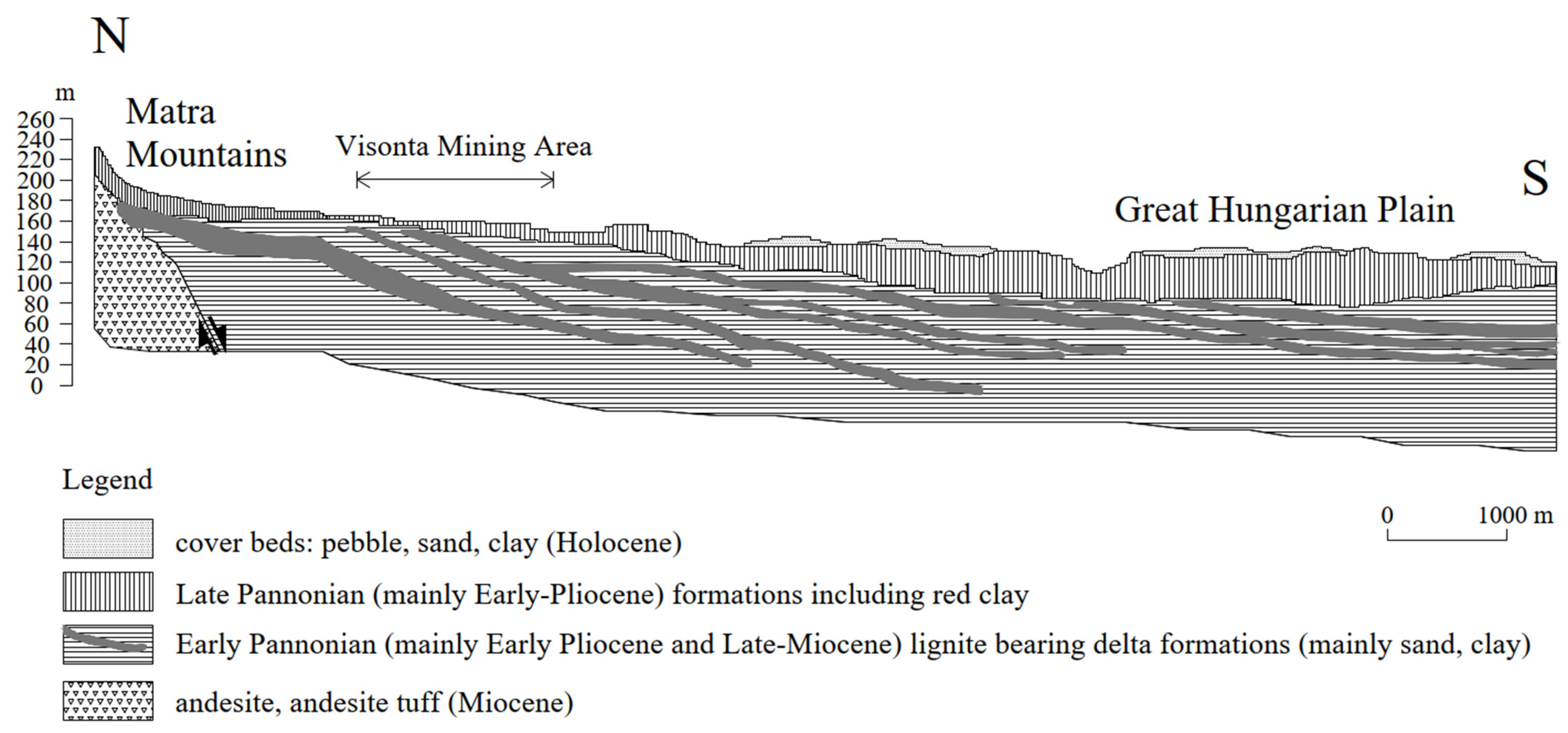
2.2. Interburden and Overburden Layer Characteristics
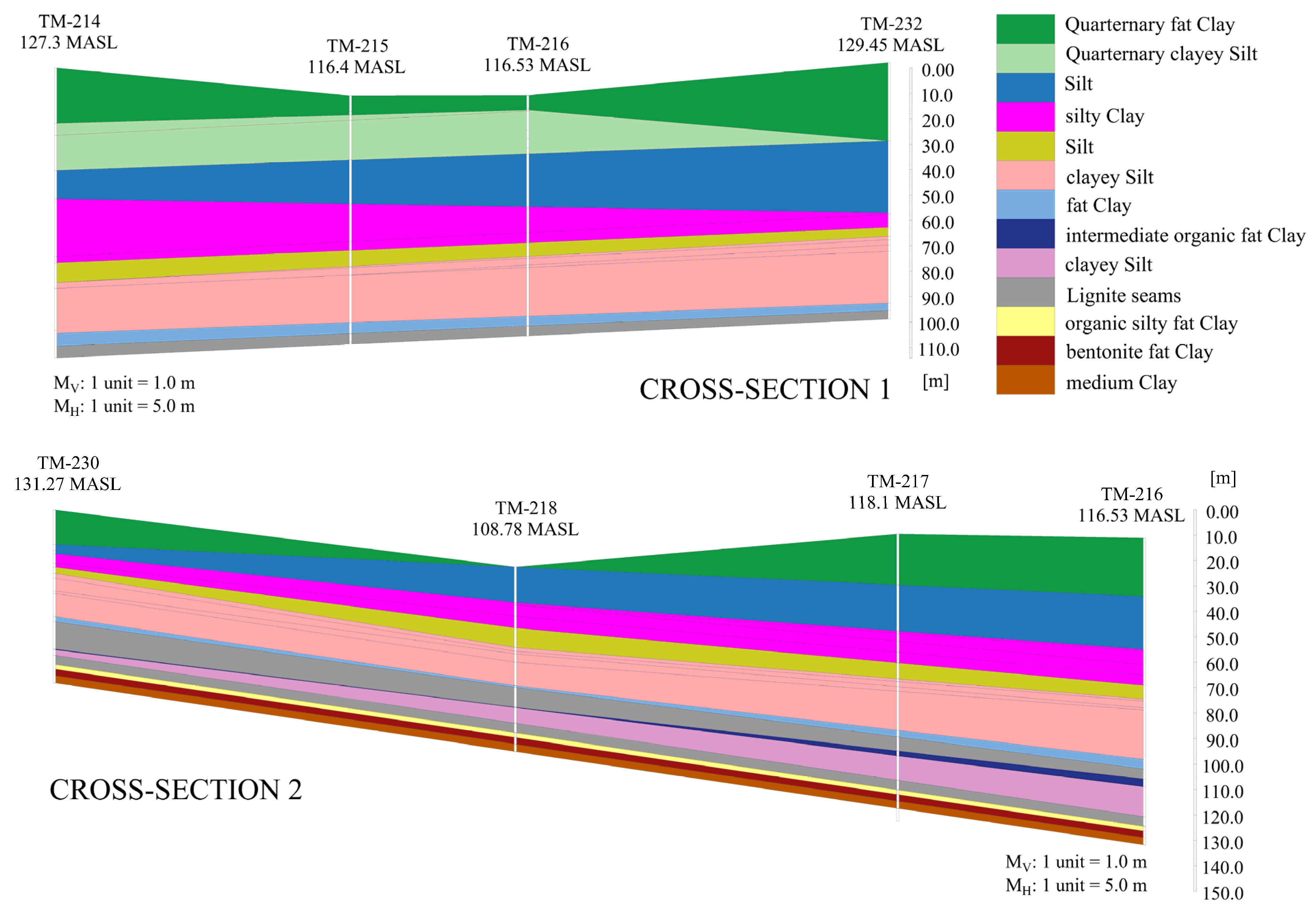
2.3. Geological Structure of Lignite Layers
2.4. Geotechnical Investigations
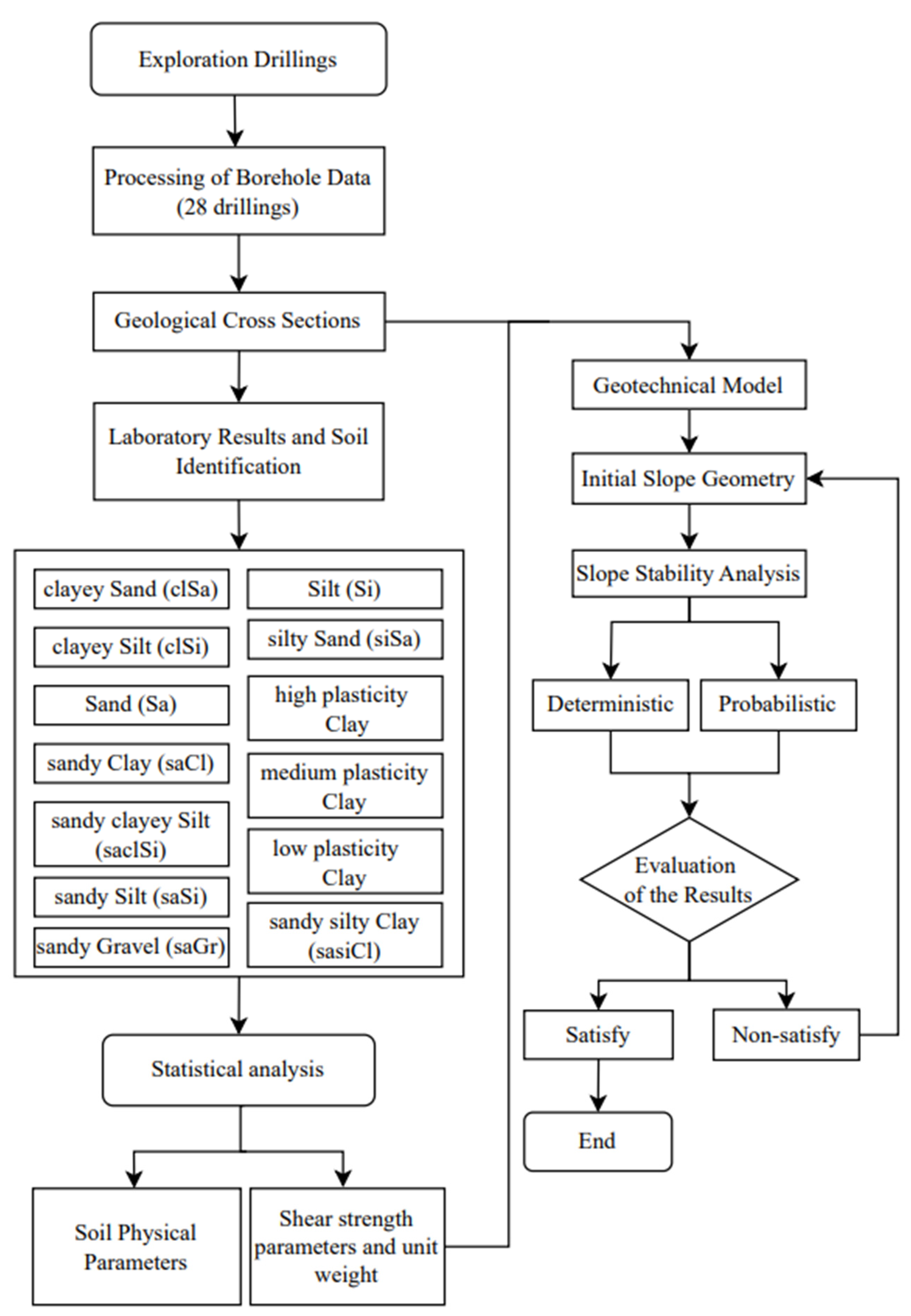
3. Methodology
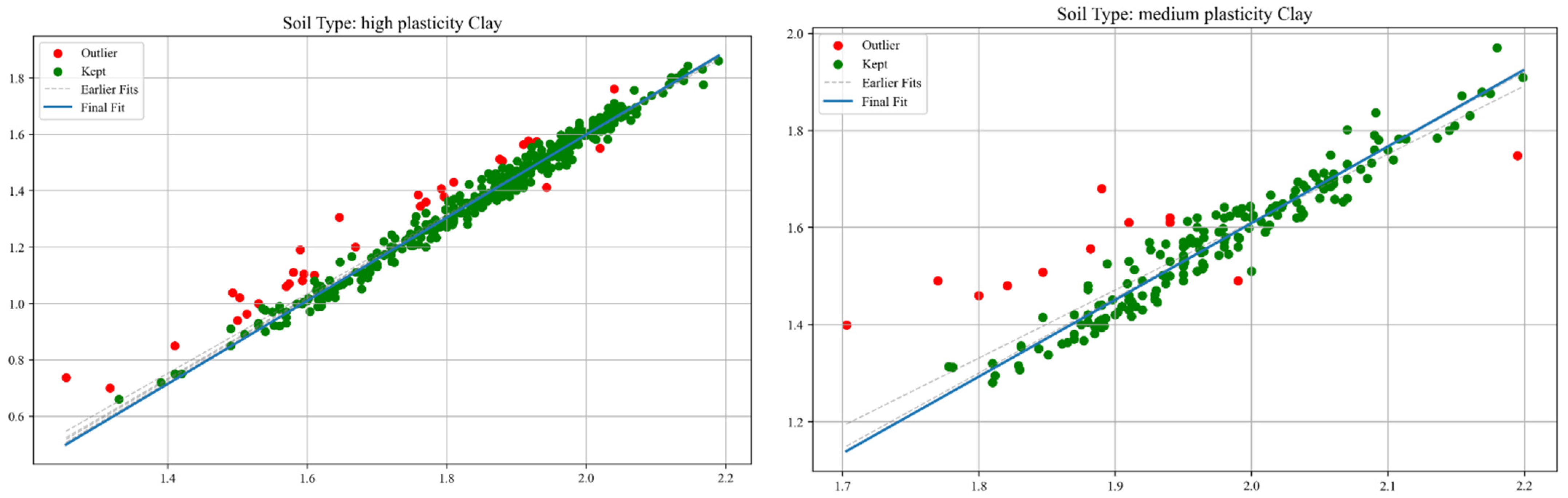
3.1. Methodology of Correlation Analysis
- def iterative_outlier_filtering(group):
- group = group.copy()
- all_outliers = []
- regression_lines = []
- num_iterations = 0
- while True:
- if len(group) < 2:
- break
- slope, intercept, _, _, _ = linregress(group[‘Value1’], group[‘Value2’])
- regression_lines.append((slope, intercept))
- num_iterations += 1
- group[‘Predicted_Value2’] = group[‘Value1’] * slope + intercept
- group[‘Residual’] = group[‘ Value2’] - group[‘Predicted_ Value2’]
- q1 = group[‘Residual’].quantile(0.25)
- q3 = group[‘Residual’].quantile(0.75)
- iqr = q3 - q1
- lower_bound = q1 - 1.5 * iqr
- upper_bound = q3 + 1.5 * iqr
- group[‘Outlier’] = ~group[‘Residual’].between(lower_bound, upper_bound)
- outliers = group[group[‘Outlier’]]
- if outliers.empty:
- break
- all_outliers.append(outliers)
- group = group[~group[‘Outlier’]]
- group[‘Outlier’] = False
- if all_outliers:
- all_outliers_df = pd.concat(all_outliers)
- all_outliers_df[‘Outlier’] = True
- final_group = pd.concat([group, all_outliers_df])
- else:
- final_group = group
- final_group = final_group.sort_index()
- final_slope, final_intercept = regression_lines[−1] if regression_lines else (0, 0)
- return final_group, final_slope, final_intercept, regression_lines, num_iterations
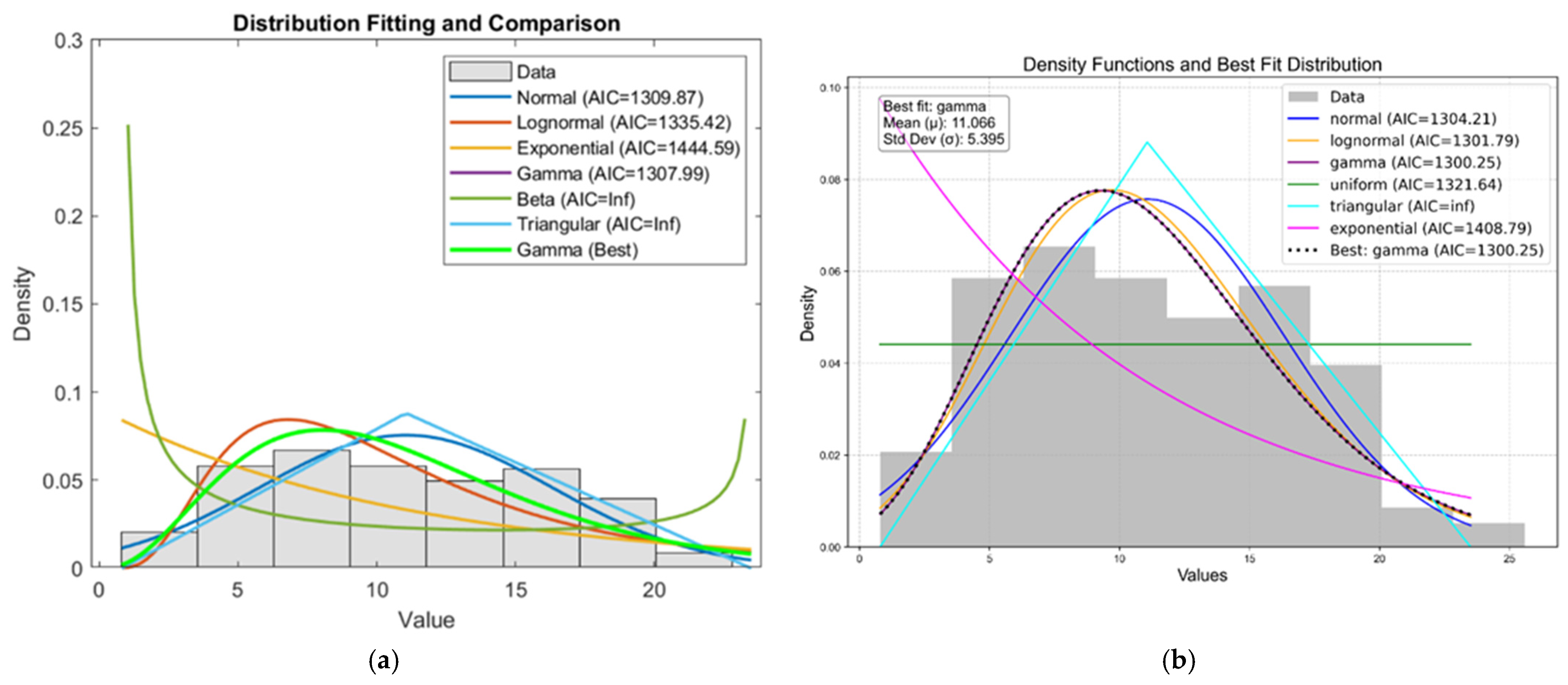
3.2. Methodology of the Statistical Analysis
- MATLAB code for selecting best-fit distribution:
- % Fit each distribution and compute AIC
- for i = 1:size(distributions, 1)
- distName = distributions{i, 1};
- distFunc = distributions{i, 2};
- try
- if strcmp(distName, ‘Beta’)
- normalized_data = (data - min(data))/(max(data) - min(data));
- pd = distFunc(normalized_data);
- else
- pd = distFunc(data);
- end
- logL = sum(log(pdf(pd, data)));
- k = length(pd.ParameterValues);
- AIC = 2 * k - 2 * logL;
- AIC_values(i) = AIC;
- if AIC < bestAIC
- bestAIC = AIC;
- bestDist = distName;
- bestParam = pd.ParameterValues;
- bestPD = pd;
- end
- catch ME
- fprintf(‘Error fitting %s distribution: %s\n’, distName, ME.message);
- end
- end
- Python code or selecting best-fit distribution:
- def fit_and_compare_distributions(data):
- results = []
- for name, dist in distributions.items():
- try:
- if name == “beta”:
- data_min, data_max = np.min(data), np.max(data)
- normalized_data = (data - data_min)/(data_max - data_min)
- params = dist.fit(normalized_data, floc=0, fscale=1)
- ll = np.sum(dist.logpdf(normalized_data, *params))
- mean, var = dist.stats(*params, moments=“mv”)
- mean = mean * (data_max - data_min) + data_min
- std = np.sqrt(var) * (data_max - data_min)
- elif name == “triangular”:
- a, c = np.min(data), np.max(data)
- b = np.mean(data)
- loc = a
- scale = c - a
- params = ((b - a)/scale, loc, scale)
- ll = np.sum(dist.logpdf(data, *params))
- mean, var = dist.stats(*params, moments=“mv”)
- std = np.sqrt(var)
- else:
- params = dist.fit(data)
- ll = np.sum(dist.logpdf(data, *params))
- mean, var = dist.stats(*params, moments=“mv”)
- std = np.sqrt(var)
- k = len(params)
- aic = 2 * k - 2 * ll
- results.append({
- “distribution”: name,
- “params”: params,
- “log_likelihood”: ll,
- “aic”: aic,
- “mean”: mean,
- “std”: std,
- })
- except Exception as e:
- warnings.warn(f”Error fitting {name} distribution: {e}”)
- if results:
- return results, min(results, key=lambda x: x[“aic”])
- else:
- warnings.warn(“No distributions successfully fitted to the data.”)
- return [], None
4. Results
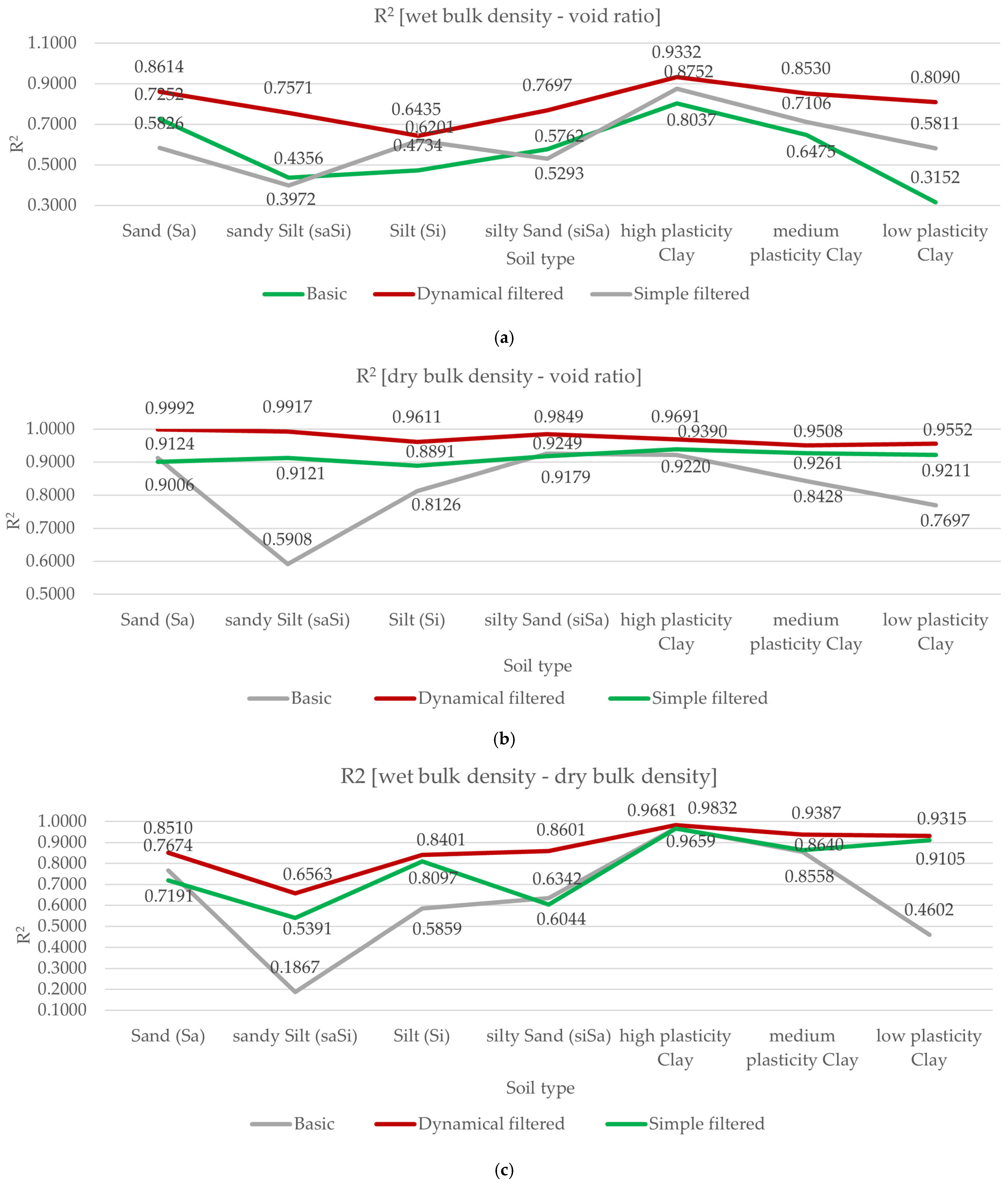
4.1. Correlation Analysis of Soil Physical Parameters
4.1.1. Wet Density—Void Ratio
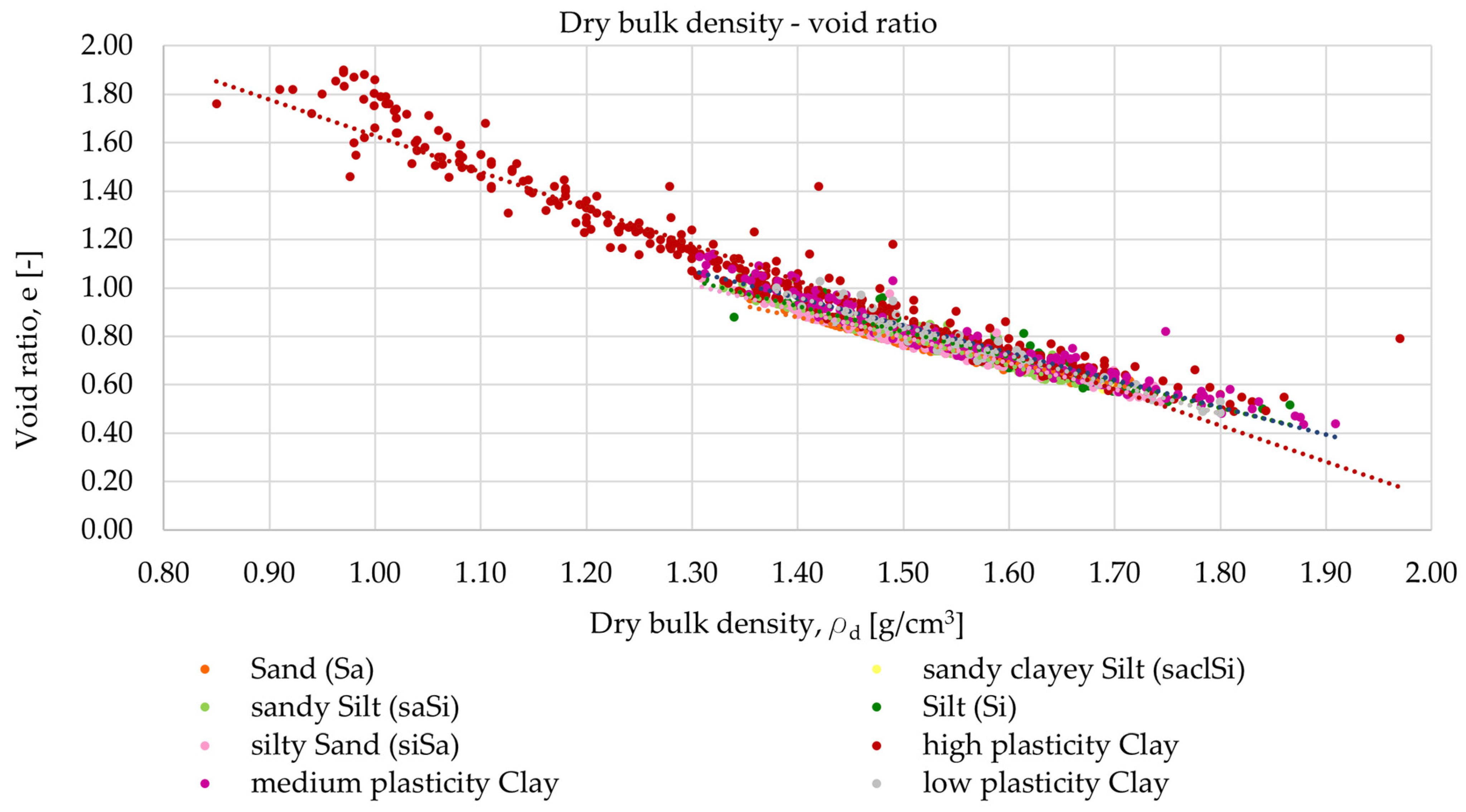
4.1.2. Dry Density—Void Ratio
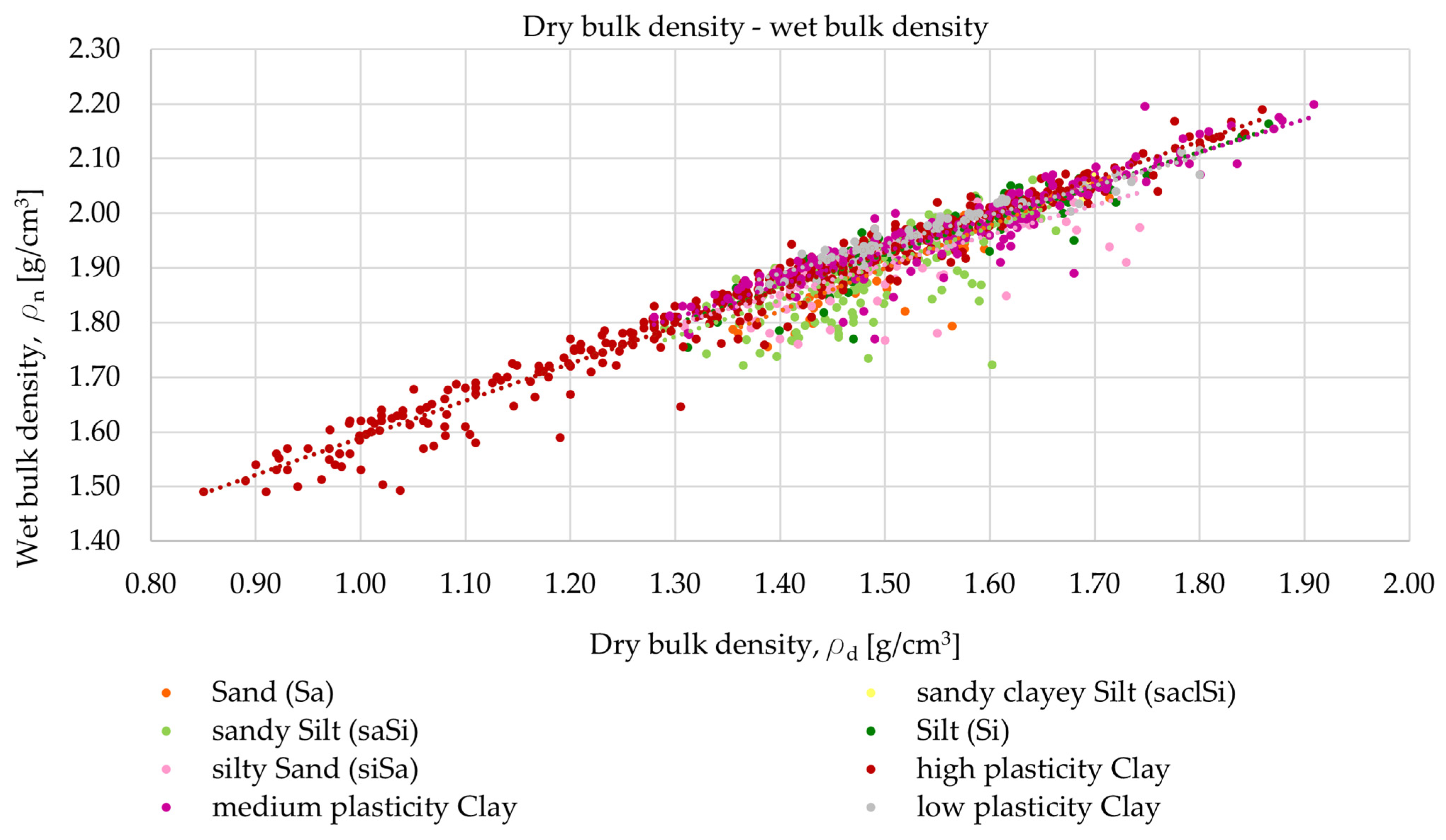
4.1.3. Wet Bulk Density—Dry Bulk Density
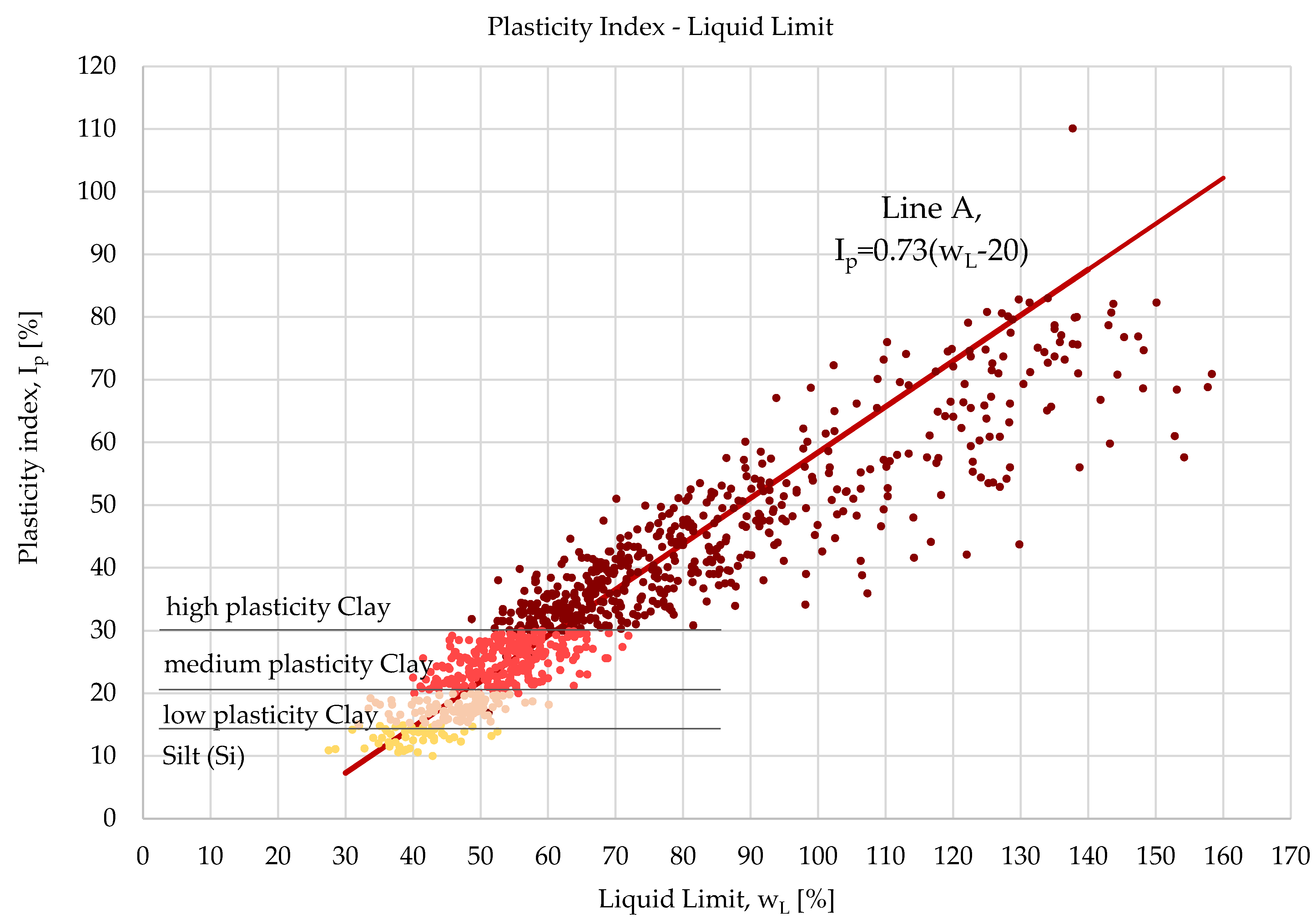
4.1.4. Plasticity Index—Liquid Limit
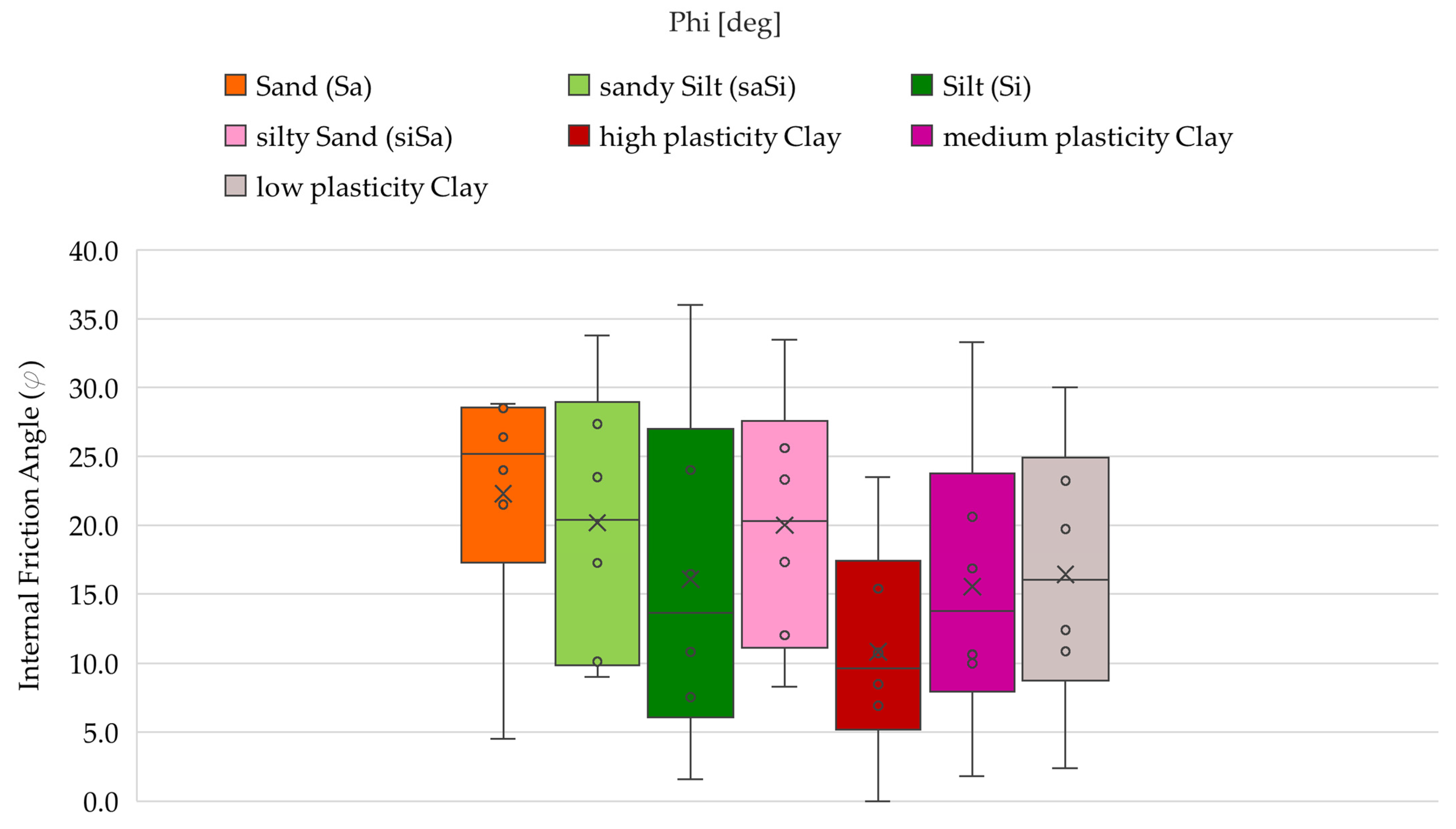
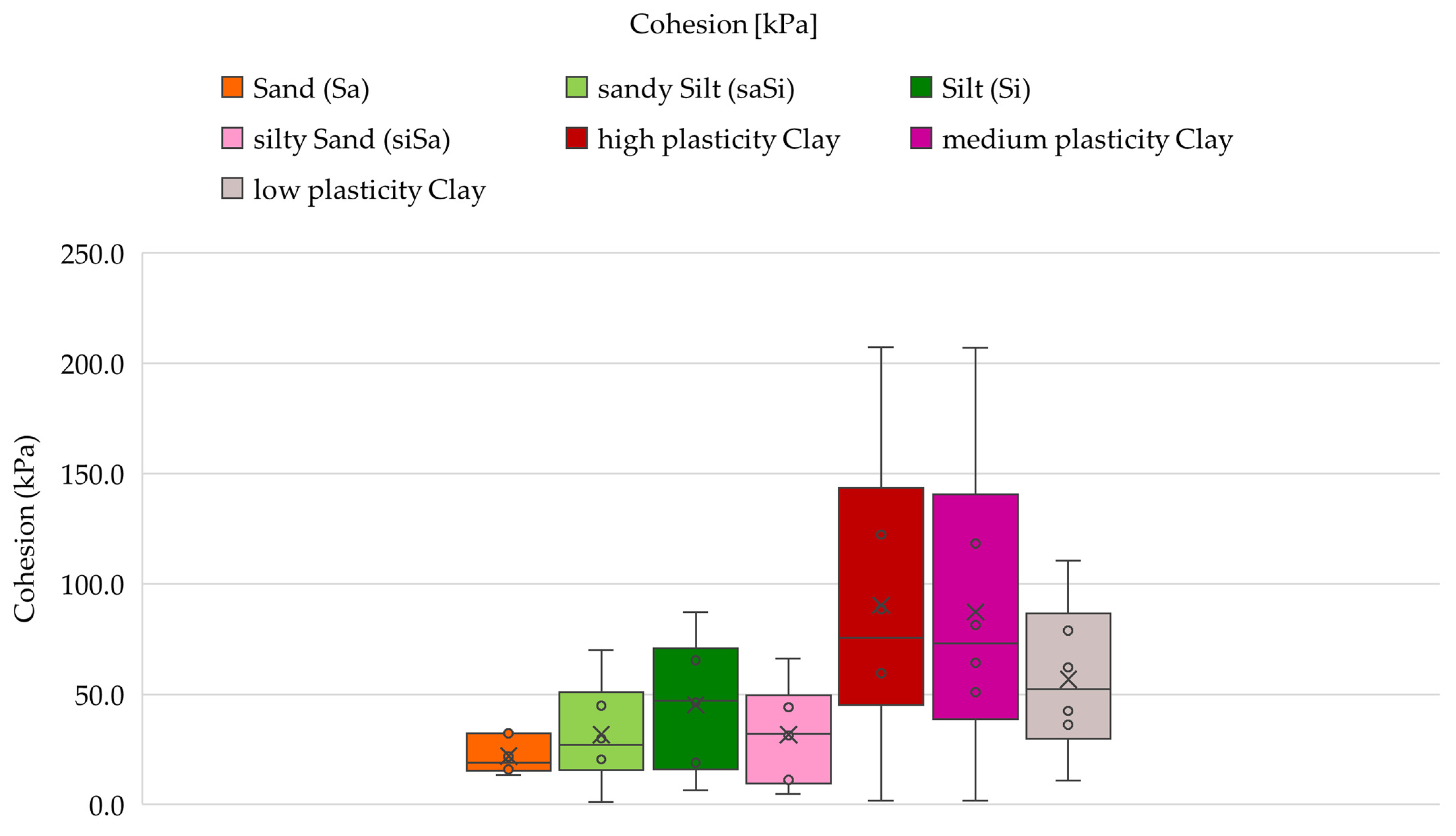
4.2. Statistical Analysis of Shear Strength Parameters
4.3. Application of the Statistical Analyses of the Investigated Soils for Probabilistic Slope Stability Calculations
4.3.1. Input Data
Characteristic Soil Properties
Probabilistic Soil Properties
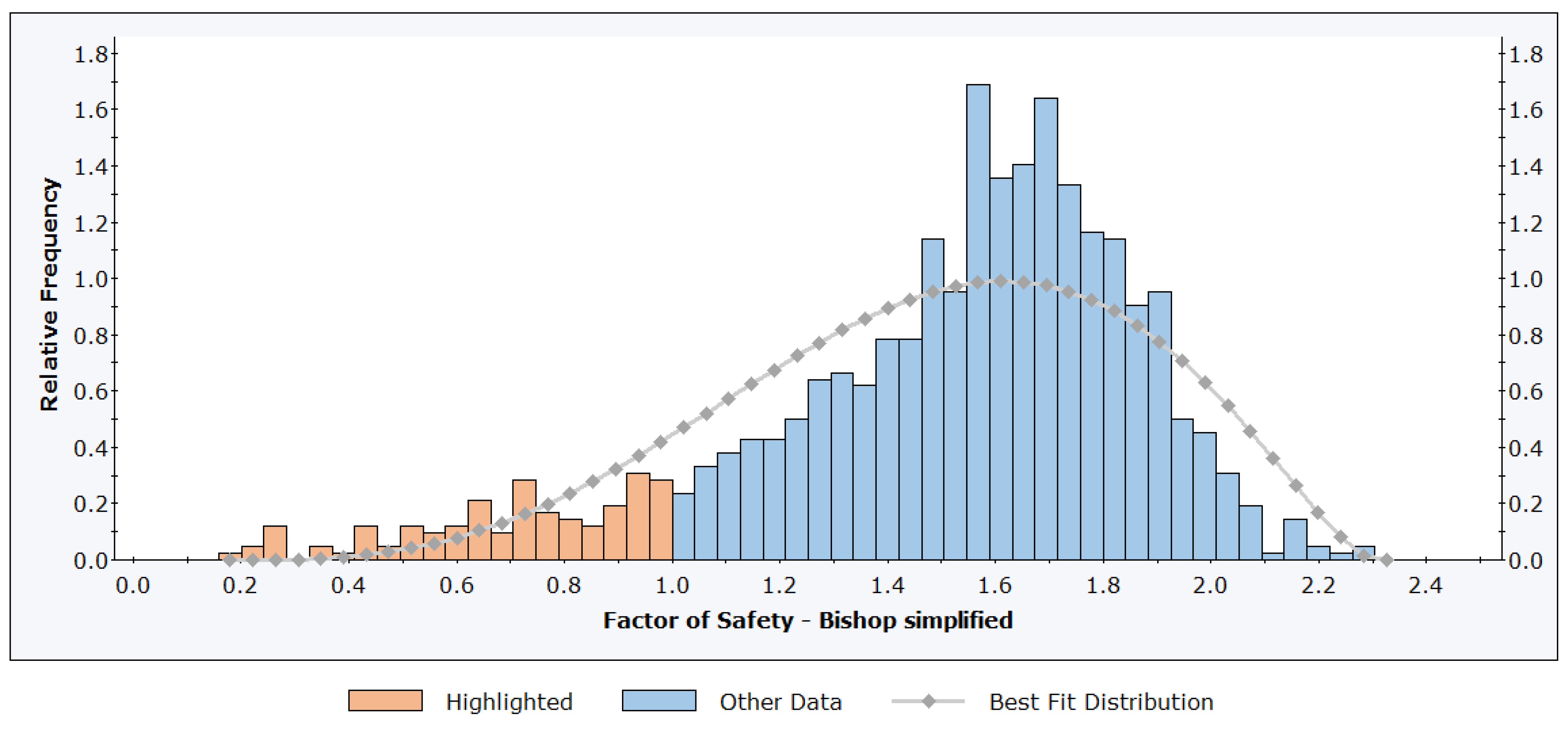
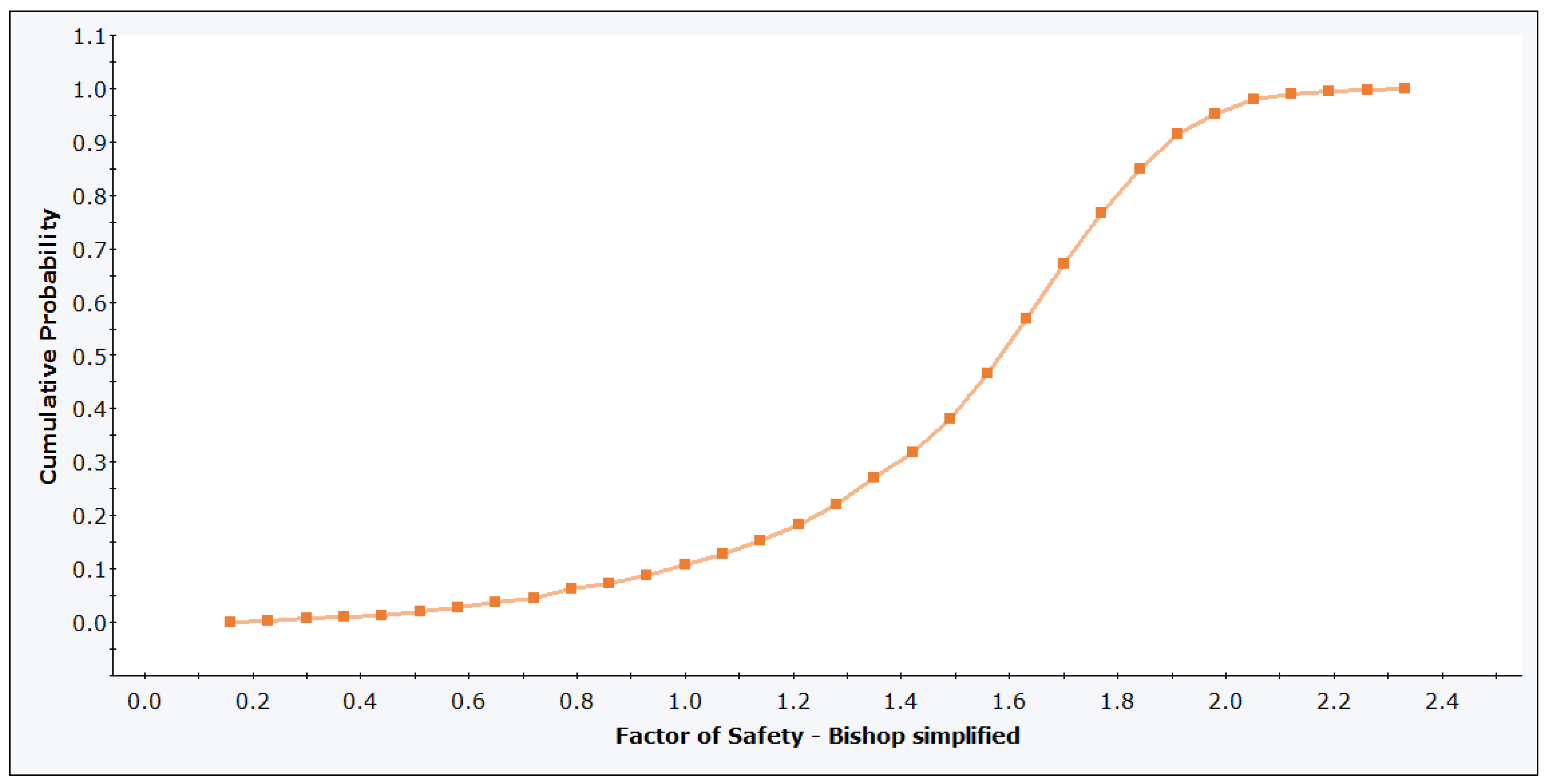
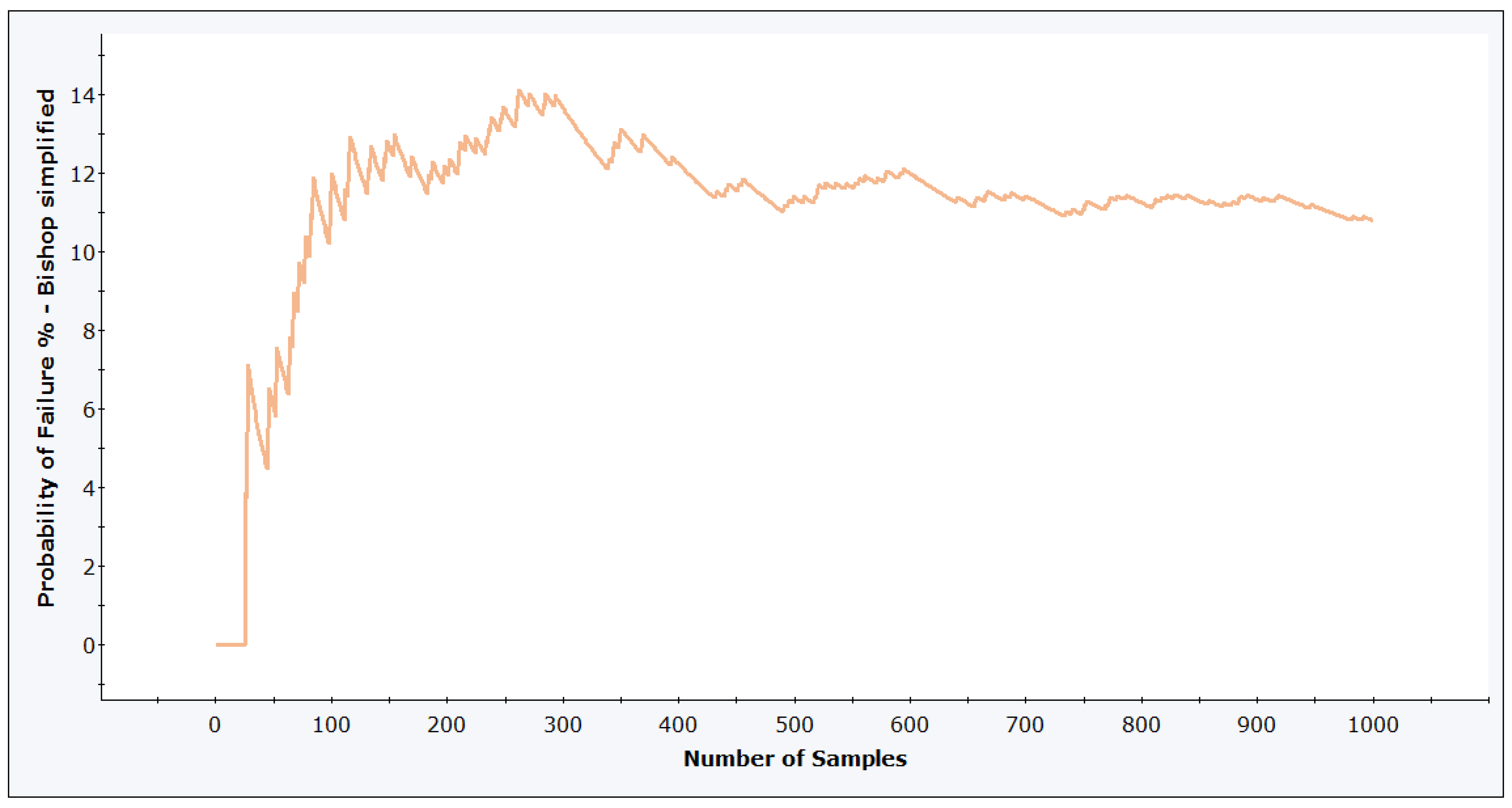
4.3.2. Results of the Slope Stability Analysis
Deterministic Calculation Results
Probabilistic Calculation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duncan, J.M.; Wright, S.G. Soil Strength and Slope Stability; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Harr, M.E. Reliability-Based Design in Civil Engineering; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Fenton, G.A.; Griffiths, D.V. Risk Assessment in Geotechnical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Selby, M.J. Hillslope Materials and Processes; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Bate, B.; McMahon, B.T. Numerical analysis of anisotropy in geotechnical engineering. J. Geotech. Res. 2017, 12, 45–60. [Google Scholar]
- Christian, J.T.; Baecher, G.B. Probabilistic analysis in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2003, 129, 307–317. [Google Scholar]
- Hammah, R.; Yacoub, T.; Curran, J. Probabilistic Slope Analysis with the Finite Element Method. In Proceedings of the 43rd US Symposium on Rock Mechanics & 4th US-Canada Rock Mechanics Symposium, Asheville, NC, USA, 28 June 28–1 July 2009. [Google Scholar]
- Chiwaye, H.T.; Stacey, T.R. A comparison of limit equilibrium and numerical modelling approaches to risk analysis for open pit mining. J. South. Afr. Inst. Min. Metall. 2010, 110, 571–580. [Google Scholar]
- Gibson, W. Probabilistic Methods for Slope Analysis and Design. Aust. Geomech. J. 2011, 46, 29. [Google Scholar]
- Chuaiwate, P.; Jaritngam, S.; Panedpojaman, P.; Konkong, N. Probabilistic Analysis of Slope against Uncertain Soil Parameters. Sustainability 2022, 14, 14530. [Google Scholar] [CrossRef]
- He, Y.; Li, Z.; Wang, W.; Yuan, R.; Zhao, X.; Nikitas, N. Slope stability analysis considering the strength anisotropy of c-φ soil. Sci. Rep. 2022, 12, 18372. [Google Scholar] [CrossRef]
- Teng, L.; He, Y.; Wang, Y.; Sun, C.; Yan, J. Numerical stability assessment of a mining slope using the synthetic rock mass modeling approach and strength reduction technique. Front. Earth Sci. 2024, 12, 1438277. [Google Scholar] [CrossRef]
- Vanneschi, C.; Eyre, M.; Burda, J.; Žižka, L.; Francioni, M.; Coggan, J.S. Investigation of landslide failure mechanisms adjacent to lignite mining operations in North Bohemia (Czech Republic) through a limit equilibrium/finite element modelling approach. Geomorphology 2018, 320, 142–153. [Google Scholar] [CrossRef]
- Masoudian, M.S.; Zevgolis, I.E.; Deliveris, A.V.; Marshall, A.M.; Heron, C.M.; Koukouzas, N.C. Stability and characterisation of spoil heaps in European surface lignite mines: A state-of-the-art review in light of new data. Environ. Earth Sci. 2019, 78, 505. [Google Scholar] [CrossRef]
- Pathan, S.M.; Pathan, A.G.; Siddiqui, F.I.; Memon, M.B.; Soomro, M.H.A.A. Open Pit Slope Stability Analysis in Soft Rock Formations. Arch. Min. Sci. 2022, 67, 437–454. [Google Scholar] [CrossRef]
- Horváth, Z.; Micheli, E.; Mindszenty, A.; Berényi Üveges, J. Soft-sediment deformation structures in Late Miocene–Pleistocene sediments on the pediment of the Mátra Hills (Visonta, Atkár, Verseg): Cryoturbation, load structures or seismites? Tectonophysics 2005, 410, 81–95. [Google Scholar] [CrossRef]
- Erdei, B.; Hably, L.; Selmeczi, I.; Kordos, L. Palaeogene and Neogene localities in the North-Hungarian Mountain Range. Guide to the post-congress fieldtrip of the 8th EPPC, 2010, Budapest, Hungary. Stud. Bot. Hung. 2011, 42, 153–183. [Google Scholar]
- Zeng, X.; Khajehzadeh, M.; Iraji, A.; Keawsawasvong, S. Probabilistic Slope Stability Evaluation Using Hybrid Metaheuristic Approach. Period. Polytech. Civ. Eng. 2022, 66, 1309–1322. [Google Scholar] [CrossRef]
- Priest, S.D.; Brown, E.T. Probabilistic stability analysis of variable rock slopes. Trans. Inst. Min. Metallurgy. Sect. A Min. Ind. 1983, 92, A1–A12. [Google Scholar]
- Pine, R.J.; Pascoe, D.M.; Howe, J.H. Assessment of the risk of failure in china clay deposits of south west England. In Proceedings of the 5th International Mine Water Congress, Nottingham, UK, 18–23 September 1994. [Google Scholar]
- Sullivan, T. Pit slope design and riskA view of the current state of the art. In Proceedings of the International Symposium on Stability of Rock Slopes in Open Pit Mining and Civil Engineering Situations, Cape Town, South Africa, 3–6 April 2006. [Google Scholar]
- Silva, F.; Lambe, T.W.; Marr, W.A. Probability and risk of slope failure. J. Geotech. Geoenviron. Eng. 2008, 134, 1691–1699. [Google Scholar] [CrossRef]
- Read, J.; Stacey, P. Guidelines for Open-Pit Slope Design; CSIRO: Collingwood, Australia, 2009. [Google Scholar]
- Wesseloo, J.; Read, J. Chapter 9—Acceptance criteria. In Guidelines for Open Pit Slope Design; Read, J., Stacey, P., Eds.; CIRSO Publishing: Clayton, Australia, 2009; pp. 221–236. [Google Scholar]
- Hormazabal, E.; Tapia, M.; Fuenzalida, R.; Zuniga, G. Slope optimization for the Hypogene Project at Carmen de Andacollo Pit, Chile. In Proceedings of the Slope Stability 2011, International Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering, Vancouver, BC, Canada, 18–21 September 2011. [Google Scholar]
- Adams, B. Slope Stability Acceptance Criteria for Opencast Mine Design. In Proceedings of the 12th Australia New Zealand Conference on Geomechanics, Wellington, New Zealand, 22–25 February 2015. [Google Scholar]
- Hawley, M.; Cunning, J. Guidelines for Mine Waste Dump and Stockpile Design; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Chakraborty, R.; Dey, A. Probabilistic Slope Stability Analysis: State-of-the-Art Review and Future Prospects. Innov. Infrastruct. Solut. 2022, 7, 177. [Google Scholar] [CrossRef]
- Che, W.; Chang, P.; Wang, W. Optimal Intensity Measures for Probabilistic Seismic Stability Assessment of Large Open-Pit Mine Slopes under Different Mining Depths. Shock Vib. 2023, 2023, 8851565. [Google Scholar] [CrossRef]
- Idris, M.A.; Kolade, A.S. Probabilistic Slope Stability Assessment for Sustainable Mining at Ankpa Coal Mine, Nigeria. Futa J. Eng. Eng. Technol. 2024, 18, 93–100. [Google Scholar]
- Ferreira Filho, F.A.; Bacellar, L.D.A.P.; Marques, E.A.G.; de Assis, A.P.; Gomes, R.C.; da Costa, T.A.V. Failure Susceptibility Analysis of Open Pit Slopes: A Case Study from the Quadrilátero Ferrífero Mine, Brazil. Geotech. Geol. Eng. 2025, 43, 59. [Google Scholar] [CrossRef]
- Department of Minerals and Energy of Western Australia. Guideline of Geotechnical Considerations in Open Pit Mines; Department of Minerals and Energy of Western Australia: Perth, Australia, 1999. [Google Scholar]
- Kirsten, H.A.D. Significance of the probability of failure in slope engineering. Civ. Eng. Siviele Ingenieurswese 1983, 1983, 17–29. [Google Scholar]
- Shien, N.G.K.O.K. Reliability Analysis on the Stability of Slope; UTM: Skudai, Malaysia, 2005. [Google Scholar]
- Peñalba, R.F.; Luo, Z.; Juang, C.H. Framework for probabilistic assessment of landslide: A case study of El Berrinche. Environ. Earth Sci. 2009, 59, 489–499. [Google Scholar] [CrossRef]
- Bi, R.; Ehret, D.; Xiang, W.; Rohn, J.; Schleier, M.; Jiang, J. Landslide reliability analysis based on transfer coefficient method: A case study from Three Gorges Reservoir. J. Earth Sci. 2012, 23, 187–198. [Google Scholar] [CrossRef]
- Moradi, A.; Osanloo, M. Determination and stability analysis of ultimate open-pit slope under geomechanical uncertainty. Int. J. Min. Sci. Technol. 2014, 24, 105–110. [Google Scholar] [CrossRef]
- Wang, L.; Hwang, J.-H.; Luo, Z.; Juang, C.H.; Xiao, J. Probabilistic back analysis of slope failure—A case study in Taiwan. Comput. Geotech. 2013, 51, 12–23. [Google Scholar] [CrossRef]
- Hamedifar, H.; Bea, R.; Pestana, J.; Roe, E. Role of Probabilistic Methods in Sustainable Geotechnical Slope Stability Analysis. Procedia Earth Planet. Sci. 2014, 9, 132–142. [Google Scholar] [CrossRef]
- Kulatilake, P.; Shu, B.; Sherizadeh, T.; Jh, D. Probabilistic block theory analysis for a rock slope at an open pit mine in USA. Comput. Geotech. 2014, 61, 254–265. [Google Scholar] [CrossRef]
- Chaulagai, R.; Osouli, A.; Clemente, J. Probabilistic Slope Stability Analyses—A Case Study. Geotech. Front. 2017, 2017, 444–452. [Google Scholar] [CrossRef]
- Mandal, J.; Narwal, S.; Gupte, D. Back Analysis of Failed Slopes—A Case Study. Int. J. Eng. Res. Technol. 2017, 6, 1070–1078. [Google Scholar] [CrossRef]
- Neman, N.; Zakaria, Z.; Sophian, I.; Adriansyah, Y. Probability of Failure and Slope Safety Factors Based on Geological Structure of Plane failure on Open Pit Batu Hijau Nusa Tenggara Barat. IOP Conf. Ser. Earth Environ. Sci. 2018, 145, 012077. [Google Scholar] [CrossRef]
- Obregon, C.; Mitri, H. Probabilistic approach for open pit bench slope stability analysis—A mine case study. Int. J. Min. Sci. Technol. 2019, 29, 629–640. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Hegde, A.M. A Case Study of Probabilistic Seismic Slope Stability Analysis of Rock Fill Tailing Dam. Int. J. Geotech. Earthq. Eng. 2019, 10, 43–60. [Google Scholar] [CrossRef]
- Sjöberg, J. Analysis of Large Scale Rock Slopes. Ph.D. Thesis, Luleå Tekniska Universitet, Luleå, Sweden, 1999. Available online: https://urn.kb.se/resolve?urn=urn:nbn:se:ltu:diva-18773 (accessed on 6 January 2025).
- Rafiei Renani, H.; Martin, D.; Varona, P.; Lorig, L. Stability Analysis of Slopes with Spatially Variable Strength Properties. Rock Mech. Rock Eng. 2019, 52, 1–18. [Google Scholar] [CrossRef]
- Mathe, L.; Ferentinou, M. Rock slope stability analysis adopting Eurocode 7, a limit state design approach for an open pit. IOP Conf. Ser. Earth Environ. Sci. 2021, 833, 012201. [Google Scholar] [CrossRef]
- Sachpazis, D.C. Probabilistic Slope Stability Evaluation. In Encyclopedia; 2019; Available online: https://encyclopedia.pub/entry/116 (accessed on 23 April 2025).
- Sdvyzhkova, O.; Moldabayev, S.; Bascetin, A.; Babets, D.; Kuldeyev, E.; Sultanbekova, Z.; Amankulov, M.; Issakov, B. Probabilistic assessment of slope stability at ore mining with steep layers in deep open pits. Min. Miner. Depos. 2022, 16, 11–18. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Pham, H.D.; Do Nguyen, V. Integrating Soil Property Variability In Sensitivity and Probabilistic Analysis of Unsaturated Slope: A Case Study. Int. J. Geomate 2023, 25, 132–139. [Google Scholar]
- Li, T.; Gong, W.; Zhu, C.; Tang, H. Stability evaluation of gentle slopes in spatially variable soils using discretized limit analysis method: A probabilistic study. Acta Geotech. 2024, 19, 6319–6335. [Google Scholar] [CrossRef]
- Nguyen, P.M.V.; Marciniak, M. Stochastic Rock Slope Stability Analysis: Open Pit Case Study with Adjacent Block Caving. Geotech. Geol. Eng. 2024, 42, 5827–5845. [Google Scholar] [CrossRef]
- Ajith, A.; Pillai, R.J. TRIGRS-FOSM: Probabilistic slope stability tool for rainfall-induced landslide susceptibility assessment. Nat. Hazards 2024, 121, 3401–3430. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. Engineering and Design: Introduction to Probability and Reliability Methods for Use in Geotechnical Engineering; Engineer Technical Letter 1110-2-547; Department of the Army: Washington, DC, USA, 1997. [Google Scholar]



| Borehole | 28 | |
|---|---|---|
| Drilling Depth (m) | 3305 | |
| Grain Size Distribution | 1205 | |
| Direct Shear Test | Internal Friction Angle f (deg) | 237 |
| Cohesion c (kPa) | 238 | |
| Residual Internal Friction frez (deg) | 264 | |
| Residual Cohesion crez (kPa) | 265 | |
| Triaxial Compression Test | Water Content W (%) | 196 |
| Saturated Bulk Density rs (g/cm3) | 155 | |
| Void Ratio e | 184 | |
| Degree of Saturation Sr | 188 | |
| Wet Bulk Density rn (g/cm3) | 205 | |
| Dry Bulk Density rd (g/cm3) | 197 | |
| Internal Friction Angle f (deg) | 166 | |
| Cohesion c (kPa) | 166 | |
| Natural Water Content–Wn (%) | 1265 | |
| Median Grain Size–Dm (mm) | 1206 | |
| Coefficient of Uniformity–Cu | 816 | |
| Grain Size Corresponding to 10% Finer–D10 (mm) | 1206 | |
| Grain Size Corresponding to 20% Finer–D20 (mm) | 1008 | |
| Grain Size Corresponding to 60% Finer (mm) | 1171 | |
| Liquid Limit–WL (%) | 653 | |
| Plastic Limit–Wp (%) | 654 | |
| Consistency Index–Ic | 360 | |
| Plasticity Index–Ip (%) | 1046 | |
| Water Content–W (%) | 1225 | |
| Void Ratio–e (-) | 1258 | |
| Porosity–n (-) | 121 | |
| Degree of Saturation–Sr (-) | 1221 | |
| Dry Unit Weight–rd (g/cm3) | 1286 | |
| Wet Unit Weight–rn (g/cm3) | 1291 | |
| Undrained Shear Strength (kPa) | 471 | |
| Number of Samples | 3307 | |
| Soil Type | Wet Bulk Density—Void Ratio | Dry Bulk Density—Void Ratio | Wet Bulk Density—Dry Bulk Density | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No. Samples (Basic) | No. Samples (Simple Filtered) | No. Samples (Dynamical Filtered) | No. Samples (Basic) | No. Samples (Simple Filtered) | No. Samples (Dynamical Filtered) | No. Samples (Basic) | No. Samples (Simple Filtered) | No. Samples (Dynamical Filtered) | |
| Sand (Sa) | 60 | 58 | 56 | 59 | 57 | 28 | 59 | 57 | 56 |
| sandy Silt (saSi) | 206 | 197 | 164 | 206 | 197 | 159 | 206 | 196 | 195 |
| Silt (Si) | 67 | 64 | 63 | 67 | 65 | 56 | 67 | 65 | 64 |
| silty Sand (siSa) | 113 | 107 | 99 | 113 | 108 | 91 | 113 | 105 | 100 |
| high plasticity Clay | 429 | 413 | 396 | 428 | 414 | 374 | 428 | 421 | 396 |
| medium plasticity Clay | 189 | 186 | 175 | 188 | 185 | 179 | 188 | 186 | 176 |
| low plasticity Clay | 68 | 64 | 65 | 68 | 64 | 59 | 68 | 62 | 61 |
| Name of the Layer | Equation of the Line | Correlation Coefficient |
|---|---|---|
| Sand (Sa) | y = −0.8137x + 2.3326 | R2 = 0.5826 |
| Silt (Si) | y = −1.2425x + 3.1965 | R2 = 0.6201 |
| sandy clayey Silt (saclSi) | y = 0.2077x + 0.1810 | R2 = 0.0994 |
| silty Sand (siSa) | y = −1.1796x + 3.0429 | R2 = 0.5293 |
| sandy Silt (saSi) | y = −0.8417x + 2.4086 | R2 = 0.3972 |
| high plasticity Clay | y = −2.1004x + 4.9338 | R2 = 0.8752 |
| medium plasticity Clay | y = −1.5081x + 3.7403 | R2 = 0.7106 |
| low plasticity Clay | y = −1.5859x + 3.9098 | R2 = 0.5811 |
| Name of the Layer | Equation of the Line | Correlation Coefficient |
|---|---|---|
| Sand (Sa) | y = −0.9326x + 2.1856 | R2 = 0.9006 |
| Silt (Si) | y = −0.1054x + 2.4012 | R2 = 0.8891 |
| sandy clayey Silt (saclSi) | y = 0.3155x + 0.068 | R2 = 0.0067 |
| silty Sand (siSa) | y = −1.0814x + 2.4185 | R2 = 0.9179 |
| sandy Silt (saSi) | y = −1.1642x + 2.5428 | R2 = 0.9121 |
| high plasticity Clay | y = −1.4969x + 3.1246 | R2 = 0.9390 |
| medium plasticity Clay | y = −1.1280x + 2.5379 | R2 = 0.9261 |
| low plasticity Clay | y = −1.2018x + 2.6427 | R2 = 0.92111 |
| Name of the Layer | Equation of the Line | Correlation Coefficient |
|---|---|---|
| Sand (Sa) | y = 0.7808x + 0.7282 | R2 = 0.7191 |
| Silt (Si) | y = 0.6276x + 0.9829 | R2 = 0.8097 |
| sandy clayey Silt (saclSi) | y = 2.7087x + 2.5308 | R2 = 0.3727 |
| silty Sand (siSa) | y = 0.5431x + 1.0908 | R2 = 0.6044 |
| sandy Silt (saSi) | y = 0.6626x + 0.9133 | R2 = 0.5391 |
| high plasticity Clay | y = 0.6780x + 0.9117 | R2 = 0.9659 |
| medium plasticity Clay | y = 0.6064x + 1.0197 | R2 = 0.8640 |
| low plasticity Clay | y = 0.5348x + 1.1413 | R2 = 0.9105 |
| Unit Weight (kN/m3) | Cohesion (kPa) | Phi (°) | |
|---|---|---|---|
| Quaternary fat clay (high plasticity clay) | 19.1 | 103 | 13 |
| Quaternary clayey Silt (clSi) | 20.0 | 56 | 22 |
| Quaternary Pannonian sandstone formation | 20.0 | 30 | 33 |
| Silt (silt) (Si) | 20.0 | 45 | 22 |
| Silty clay (clayey Silt) (clSi) | 20.0 | 67 | 16 |
| Lignite seam | 13.0 | 100 | 26 |
| Silt (silt) (Si) | 20.0 | 42 | 23 |
| Sandy clay (low plasticity clay) | 19.5 | 56 | 22 |
| Cover fat clay (high plasticity clay) | 19.5 | 103 | 13 |
| Intermediate organic fat clay (high plasticity clay) | 20.0 | 87 | 7 |
| Clayey silt (clSi) | 20.0 | 56 | 22 |
| Organic silty fat clay (high plasticity clay) | 20.3 | 87 | 7 |
| Medium clay (medium plasticity clay) | 20.0 | 56 | 23 |
| Bentonite fat clay (high plasticity clay) | 20.0 | 103 | 13 |
| Sandy silt (saSi) | 20.3 | 42 | 23 |
| Aquifer (sand) (Sa) | 20.3 | 20 | 20 |
| Waste material | 17.3 | 11 | 28 |
| Clayey Sand (clSa) | Sand (Sa) | Sandy Clayey Silt (saclSi) | Sandy Silt (saSi) | Silt (Si) | Silty Sand (siSa) | High Plasticity Clay | Medium Plasticity Clay | Low Plasticity Clay | |
|---|---|---|---|---|---|---|---|---|---|
| CumFreq [Mean Absolute Error (MAE)] | Lognormal | Lognormal | Normal | Normal | Normal | Lognormal | Lognormal | Lognormal | Lognormal |
| EasyFit [Kolmogorov–Smirnov] | Uniform | Triangular | Uniform | Gamma | Beta | Gamma | Beta | Beta | Beta |
| EasyFit [Anderson Darling] | Gamma | Gamma | Uniform | Normal | Beta | Lognormal | Beta | Gamma | Lognormal |
| EasyFit [Chi Squared] | N/A | Beta | N/A | Lognormal | Lognormal | Normal | Beta | Gamma | Beta |
| MATLAB [Akaike information criterion (AIC)] | Gamma | Lognormal | Gamma | Normal | Normal | Lognormal | Normal | Lognormal | Lognormal |
| Python [Akaike information criterion (AIC)] | Lognormal | Normal | Lognormal | Normal | Normal | Normal | Normal | Normal | Lognormal |
| Distribution | Mean | Std.dev. | Abs.max. | Rel.max. | Abs.min. | Rel.min. | |
|---|---|---|---|---|---|---|---|
| Quaternary fat clay (high plasticity clay) | Normal | 18.57 | 1.48 | 21.90 | 3.33 | 14.90 | 3.67 |
| Quaternary clayey silt (clSi) | 20.00 | ||||||
| Quaternary Pannonian sandstone formation | 20.00 | ||||||
| Silt (silt) (Si) | Normal | 19.56 | 0.83 | 21.64 | 2.08 | 17.54 | 2.02 |
| Silty clay (clayey silt) (clSi) | 20.00 | ||||||
| Lignite seam | 13.00 | ||||||
| Silt (silt) (Si) | Normal | 19.56 | 0.83 | 21.64 | 2.08 | 17.54 | 2.02 |
| Sandy clay (low plasticity clay) | Lognormal | 19.78 | 0.62 | 21.40 | 1.62 | 18.60 | 1.18 |
| Cover fat clay (high plasticity clay) | Normal | 18.57 | 1.48 | 21.90 | 3.33 | 14.90 | 3.67 |
| Intermediate organic fat clay (high plasticity clay) | Normal | 18.57 | 1.48 | 21.90 | 3.33 | 14.90 | 3.67 |
| Clayey silt (clSi) | 20.00 | ||||||
| Organic silty fat clay (high plasticity clay) | Normal | 18.57 | 1.48 | 21.90 | 3.33 | 14.90 | 3.67 |
| Medium clay (medium plasticity clay) | Lognormal | 19.70 | 0.88 | 21.99 | 2.29 | 17.36 | 2.34 |
| Bentonite fat clay (high plasticity clay) | Normal | 18.57 | 1.48 | 21.90 | 3.33 | 14.90 | 3.67 |
| Sandy silt (saSi) | Normal | 19.04 | 0.70 | 20.70 | 1.66 | 17.34 | 1.70 |
| Aquifer (sand) (Sa) | Lognormal | 18.99 | 0.68 | 20.33 | 1.34 | 17.56 | 1.43 |
| Waste material | 17.30 |
| High Plasticity Clay | Medium Plasticity Clay | Low Plasticity Clay | Sandy Silt (saSi) | Silt (Si) | Silty Sand (siSa) | Sand (Sa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| phi [deg] | c [kPa] | phi [deg] | c [kPa] | phi [deg] | c [kPa] | phi [deg] | c [kPa] | phi [deg] | c [kPa] | phi [deg] | c [kPa] | phi [deg] | c [kPa] | |
| CumFreq [Mean Absolute Error (MAE)] | Normal | Normal | Normal | Gamma | Normal | Normal | Normal | Normal | Lognormal | Normal | Normal | Normal | Normal | Lognormal |
| EasyFit [Kolmogorov–Smirnov] | Beta | Gamma | Normal | Gamma | Beta | Uniform | Triangular | Normal | Lognormal | Uniform | Normal | Uniform | Beta | N/A |
| EasyFit [Anderson Darling] | Beta | Gamma | Gamma | Gamma | Triangular | Normal | Triangular | Normal | Lognormal | Uniform | Normal | Normal | Normal | N/A |
| EasyFit [Chi Squared] | Triangular | Triangular | Beta | Gamma | Beta | Triangular | Triangular | Normal | Exponential | Lognormal | Lognormal | Beta | N/A | N/A |
| MATLAB [Akaike information criterion (AIC)] | Gamma | Normal | Normal | Gamma | Normal | Normal | Normal | Normal | Gamma | Gamma | Normal | Gamma | Normal | Lognormal |
| Python [Akaike information criterion (AIC)] | Gamma | Gamma | Uniform | Gamma | Uniform | Uniform | Uniform | Uniform | Lognormal | Gamma | Uniform | Uniform | Lognormal | Lognormal |
| Distribution | Mean | Std.dev. | Abs.max. | Rel.max. | Abs.min. | Rel.min. | |
|---|---|---|---|---|---|---|---|
| Quaternary fat clay (high plasticity clay) | Normal | 91.4 | 43.1 | 207.4 | 116 | 1.7 | 89.7 |
| Quaternary clayey silt (clSi) | 56.0 | ||||||
| Quaternary Pannonian sandstone formation | 30.0 | ||||||
| Silt (silt) (Si) | Gamma | 46.1 | 31 | 87.1 | 41 | 6.6 | 39.5 |
| Silty clay (clayey silt) (clSi) | 67.0 | ||||||
| Lignite seam | 100.0 | ||||||
| Silt (silt) (Si) | Gamma | 46.1 | 31 | 87.1 | 41 | 6.6 | 39.5 |
| Sandy clay (low plasticity clay) | Normal | 58.3 | 28.7 | 110.6 | 52.3 | 10.9 | 47.4 |
| Cover fat clay (high plasticity clay) | Normal | 91.4 | 43.1 | 207.4 | 116 | 1.7 | 89.7 |
| Intermediate organic fat clay (high plasticity clay) | Normal | 91.4 | 43.1 | 207.4 | 116 | 1.7 | 89.7 |
| Clayey silt (clSi) | 56.0 | ||||||
| Organic silty fat clay (high plasticity clay) | Normal | 91.4 | 43.1 | 207.4 | 116 | 1.7 | 89.7 |
| Medium clay (medium plasticity clay) | Gamma | 86.3 | 49.9 | 207 | 120.7 | 1.7 | 84.6 |
| Bentonite fat clay (high plasticity clay) | Normal | 91.4 | 43.1 | 207.4 | 116 | 1.7 | 89.7 |
| Sandy silt (saSi) | Normal | 30.9 | 17.2 | 70 | 39.1 | 1.3 | 29.6 |
| Aquifer (sand) (Sa) | Lognormal | 21.3 | 8.4 | 32.3 | 11 | 13.5 | 7.8 |
| Waste material | 11.0 |
| Distribution | Mean | Std.dev. | Abs.max. | Rel.max. | Abs.min. | Rel.min. | |
|---|---|---|---|---|---|---|---|
| Quaternary fat clay (high plasticity clay) | Gamma | 11.00 | 5.80 | 23.50 | 12.50 | 0.00 | 11.00 |
| Quaternary clayey silt (clSi) | 22.00 | ||||||
| Quaternary Pannonian sandstone formation | 33.00 | ||||||
| Silt (silt) (Si) | Lognormal | 15.20 | 10.40 | 36.00 | 20.80 | 1.60 | 13.60 |
| Silty clay (clayey silt) (clSi) | 16.00 | ||||||
| Lignite seam | 26.00 | ||||||
| Silt (silt) (Si) | Lognormal | 15.20 | 10.40 | 36.00 | 20.80 | 1.60 | 13.60 |
| Sandy clay (low plasticity clay) | Normal | 17 | 8.4 | 30 | 12.96 | 2.4 | 14.64 |
| Cover fat clay (high plasticity clay) | Gamma | 11.00 | 5.80 | 23.50 | 12.50 | 0.00 | 11.00 |
| Intermediate organic fat Clay (high plasticity Clay) | Gamma | 11.00 | 5.80 | 23.50 | 12.50 | 0.00 | 11.00 |
| Clayey silt (clSi) | 22.00 | ||||||
| Organic silty fat clay (high plasticity clay) | Gamma | 11.00 | 5.80 | 23.50 | 12.50 | 0.00 | 11.00 |
| Medium clay (medium plasticity clay) | Normal | 15.4 | 7.2 | 33.30 | 17.86 | 1.8 | 13.64 |
| Bentonite fat clay (high plasticity clay) | Gamma | 11.00 | 5.80 | 23.50 | 12.50 | 0.00 | 11.00 |
| Sandy silt (saSi) | Normal | 22 | 7 | 33.8 | 11.78 | 9.02 | 13 |
| Aquifer (sand) (Sa) | Normal | 25.80 | 3.10 | 28.80 | 3.00 | 21.50 | 4.30 |
| Waste material | 28.00 |
| Section 1 | Section 2 | Section 3 | Section 4 | Section 5 | Section 6 | Section 7 | |
|---|---|---|---|---|---|---|---|
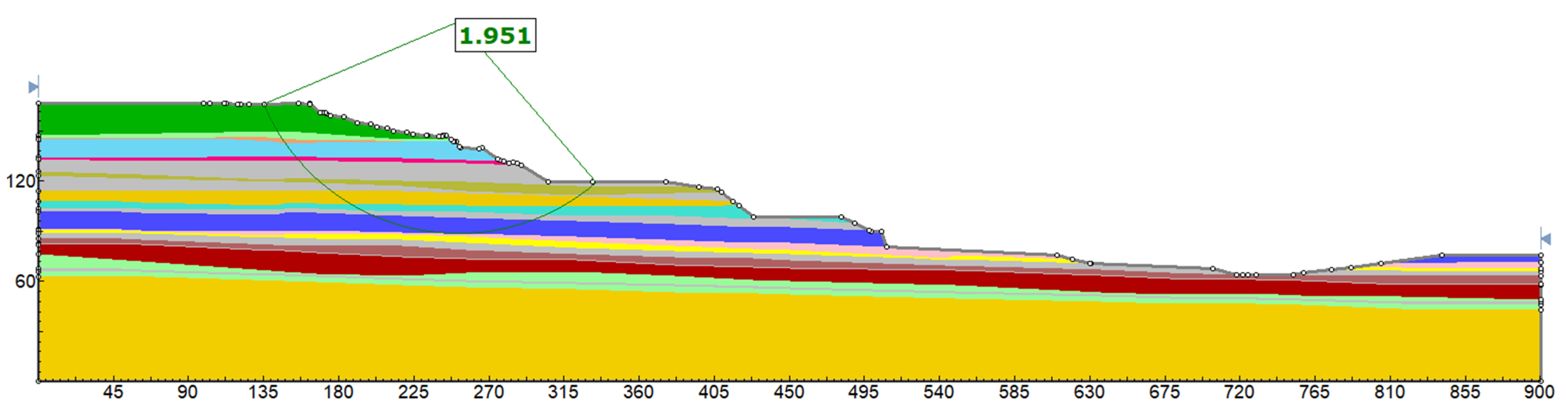
| FS (basic) [-] | 1.951 | 1.379 | 1.305 | 1.226 | 1.653 | 1.583 | 1.334 |
| FS (optimized) [-] | 1.951 | 1.379 | 2.108 | 1.646 | 1.653 | 1.583 | 1.826 |
| Section 1 | Section 2 | Section 3 | Section 4 | Section 5 | Section 6 | Section 7 | ||
|---|---|---|---|---|---|---|---|---|
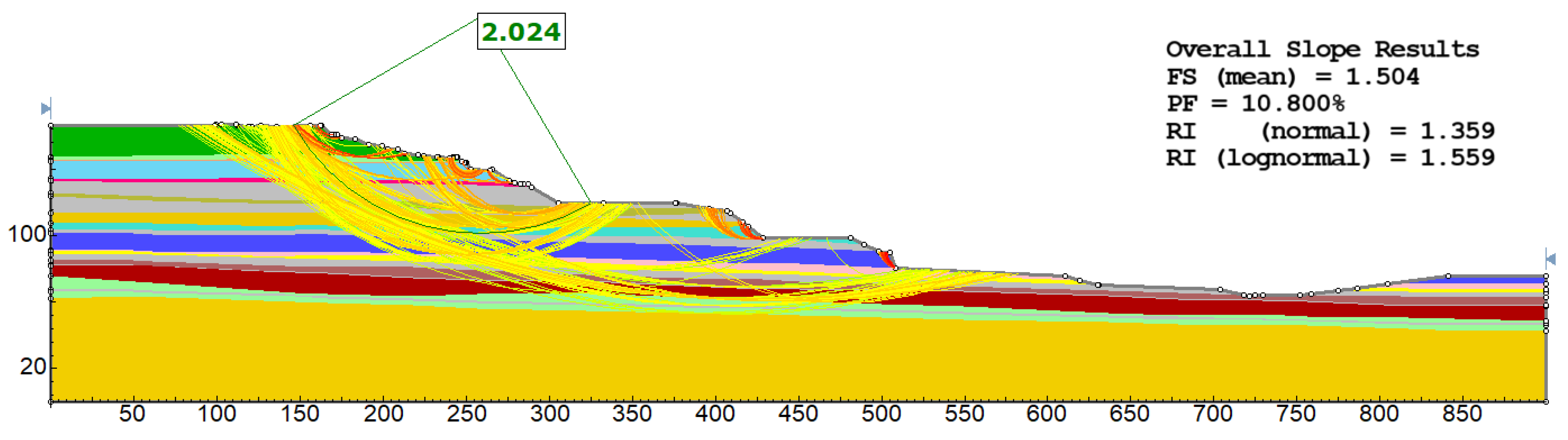
| Basic Geometry | FS [-] | 2.024 | 1.219 | 1.172 | 1.052 | 1.731 | 1.582 | 1.334 |
| FS (mean) | 1.504 | 1.041 | 0.949 | 0.866 | 1.195 | 1.522 | 1.334 | |
| PF [%] | 10.8% | 42.8% | 53.5% | 67.5% | 25.7% | 0.80% | 0.0% | |
| RI (normal) | 1.359 | 0.136 | −0.164 | −0.428 | 0.635 | 4.067 | 7687.336 | |
| RI (lognormal) | 1.559 | 0.002 | −0.325 | −0.586 | 0.578 | 4.947 | 8849.537 | |
| Optimized Geometry | FS [-] | 2.024 | 1.219 | 2.081 | 1.646 | 1.731 | 1.582 | 1.826 |
| FS (mean) | 1.054 | 1.041 | 1.538 | 1.209 | 1.195 | 1.522 | 1.826 | |
| PF [%] | 10.8% | 42.8% | 10% | 29% | 25.7% | 0.80% | 0.0% | |
| RI (normal) | 1.359 | 0.136 | 1.429 | 0.609 | 0.635 | 4.067 | 258.712 | |
| RI (lognormal) | 1.559 | 0.002 | 1.663 | 0.542 | 0.578 | 4.947 | 344.357 |
| Literature Source | Min.FS [-] | Max.PF [%] | Conditions of Applicability |
|---|---|---|---|
| Read and Stacey (2009) [24] | 1.3–1.5 | <5 | Overall slopes with high failure consequences |
| Priest and Brown (1983) [20] | >2 | <0.3; P (FoS < 1.5) < 5 | Medium-sized (50–100 m) and high slopes (<150 m) carrying major haulage roads or underlying permanent mine installations with “very serious” failure consequences |
| DME (1999) [33] | >2 | <0.3 | Permanent pit walls near public infrastructure with “high” failure consequences |
| Hormazabal et al. (2011) [26] | >1.5 | <3 | Slopes affecting infrastructure or public roads |
| Wesseloo and Read (2009) [25] | 1.2–1.3 | <10 | Inter-ramp (high consequence of failure) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oláh, P.; Görög, P. Integrating Soil Parameter Uncertainty into Slope Stability Analysis: A Case Study of an Open Pit Mine in Hungary. Geosciences 2025, 15, 222. https://doi.org/10.3390/geosciences15060222
Oláh P, Görög P. Integrating Soil Parameter Uncertainty into Slope Stability Analysis: A Case Study of an Open Pit Mine in Hungary. Geosciences. 2025; 15(6):222. https://doi.org/10.3390/geosciences15060222
Chicago/Turabian StyleOláh, Petra, and Péter Görög. 2025. "Integrating Soil Parameter Uncertainty into Slope Stability Analysis: A Case Study of an Open Pit Mine in Hungary" Geosciences 15, no. 6: 222. https://doi.org/10.3390/geosciences15060222
APA StyleOláh, P., & Görög, P. (2025). Integrating Soil Parameter Uncertainty into Slope Stability Analysis: A Case Study of an Open Pit Mine in Hungary. Geosciences, 15(6), 222. https://doi.org/10.3390/geosciences15060222






